Liquid–Liquid Flows with Non-Newtonian Dispersed Phase in a T-Junction Microchannel
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
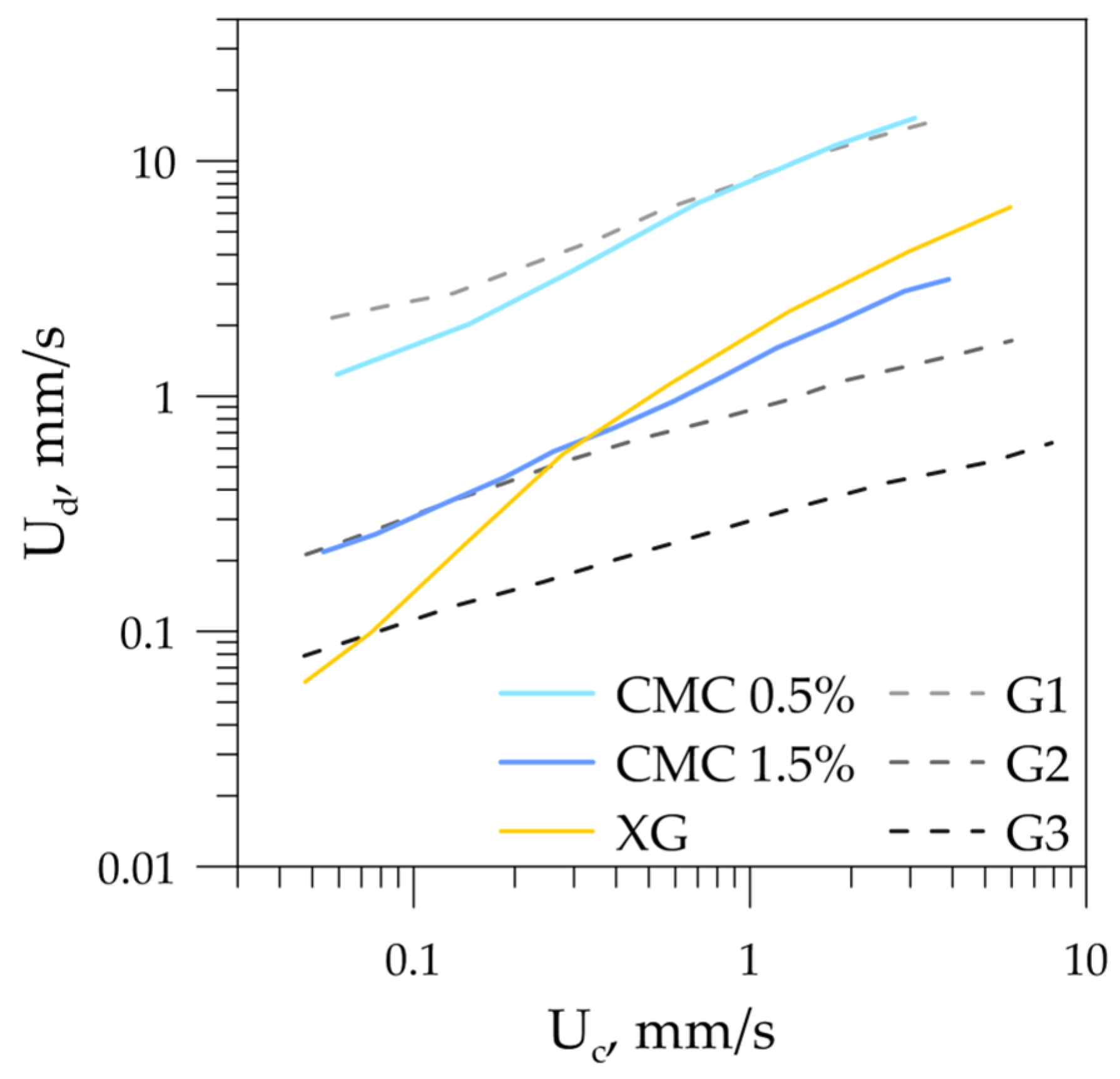
3.1. Flow Patterns
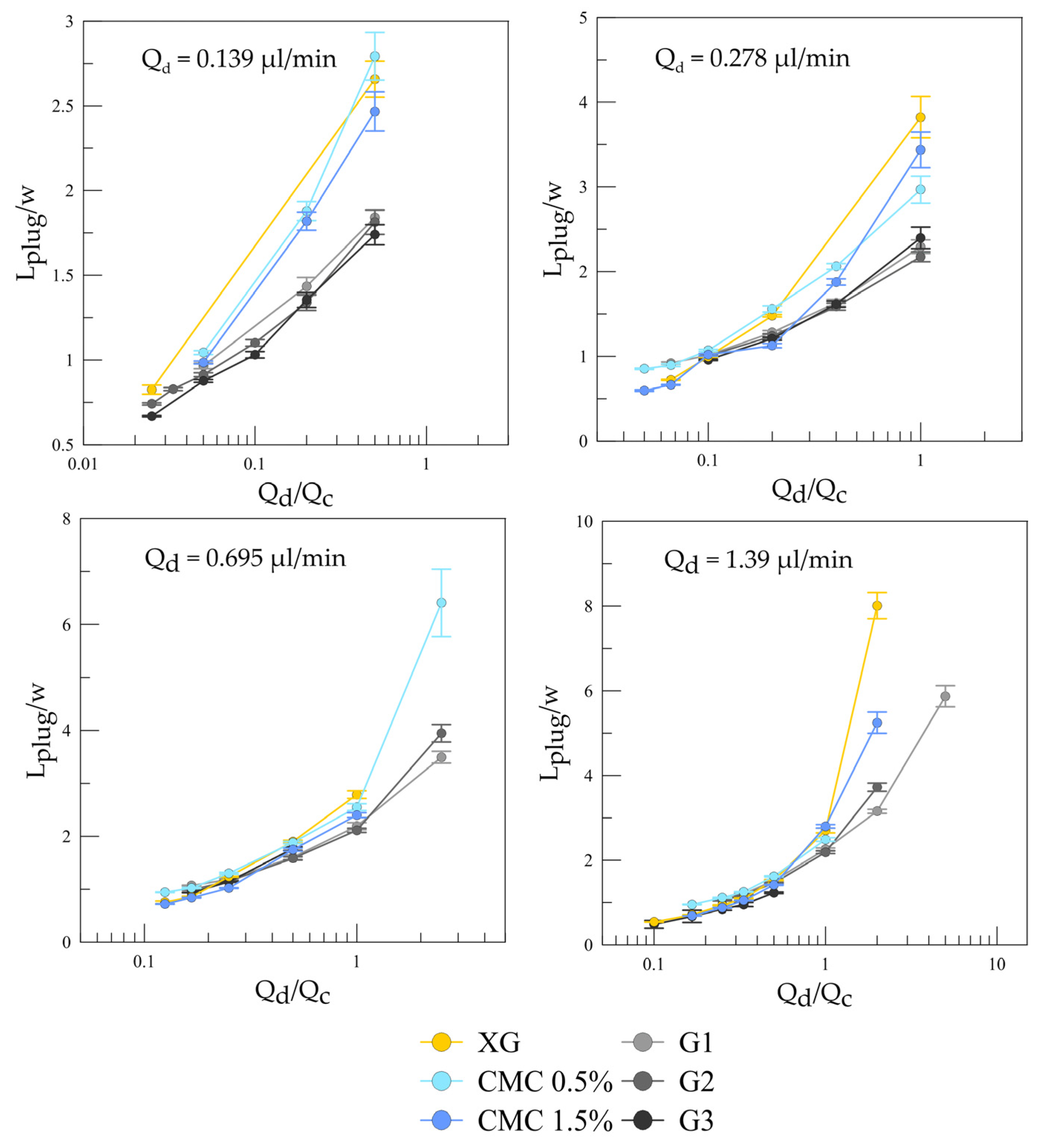
3.2. Slug Flow
4. Conclusions
- The boundaries between segmented and continuous-flow patterns drawn on the flow-pattern maps in terms of superficial velocities of the phases were shifted relative to each other for the cases of shear-thinning and Newtonian dispersed phases with different viscosities. While the boundaries for Newtonian liquids were parallel to each other, the boundaries for the case of the non-Newtonian dispersed phase were not.
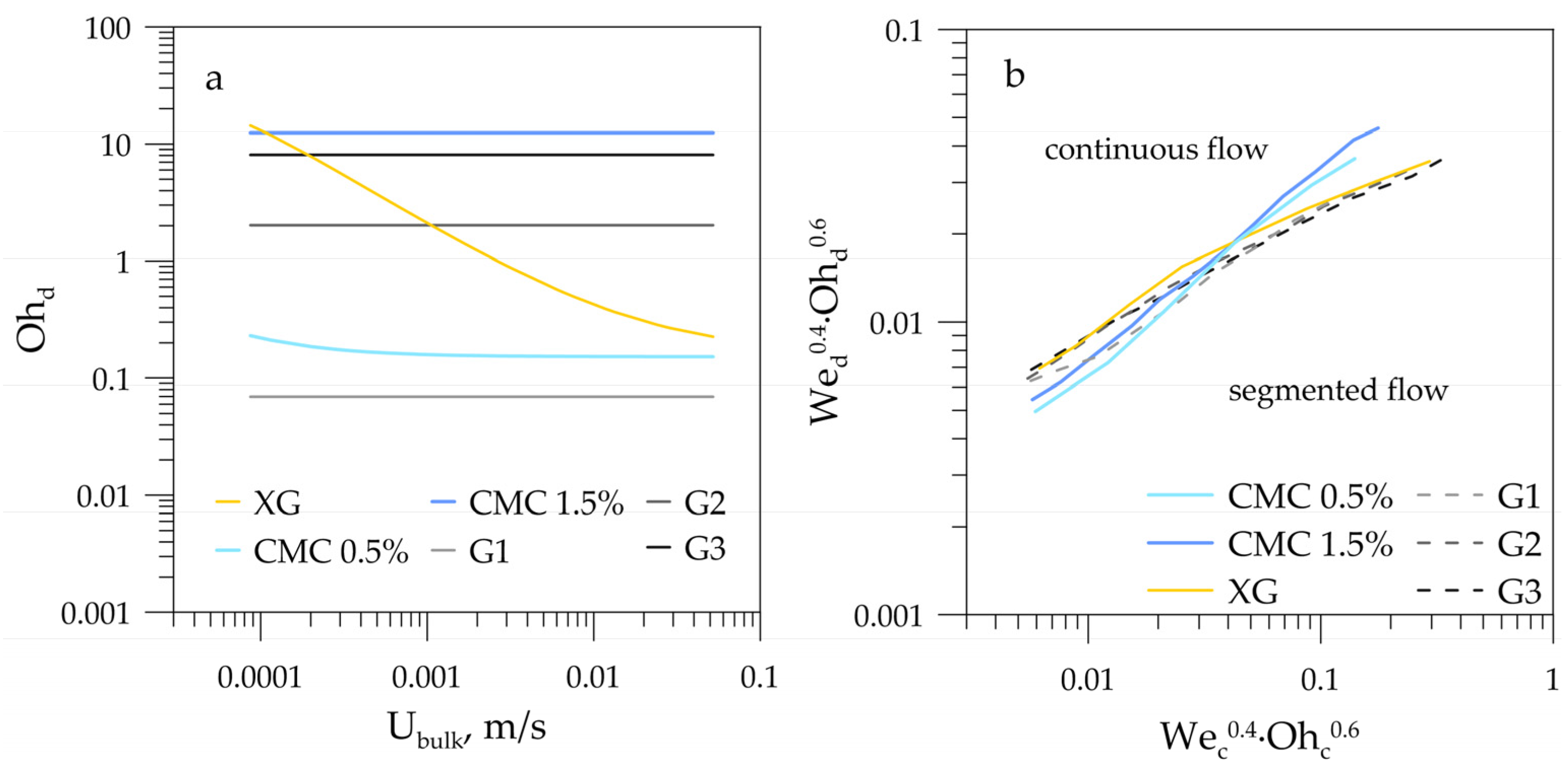
- The most appropriate model of average shear-rate estimation based on bulk velocity was chosen and applied to evaluate an effective dynamic viscosity of a shear-thinning fluid.
- The nondimensional complex We0.4·Oh0.6 could be successfully utilized for universal flow-pattern-map construction for both Newtonian and non-Newtonian dispersed phases, for which the Ohnesorge number was calculated using an effective viscosity based on the average shear rate in a microchannel.
- Comparison with the experimental data from literature showed that the proposed nondimensional complex We0.4·Oh0.6 unified flow-pattern boundaries when the continuous phase exhibited non-Newtonian properties.
- The shear-thinning dispersed phase influenced the slug-formation mechanism and slug length. At low flow rates of the dispersed and continuous phases, a jetting regime of slug formation was established, leading to a dramatic increase in slug length.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Formula | Description |
| Dh, m | hydraulic diameter | |
| w, m | microchannel width | |
| U, m/s | superficial velocity | |
| Ubulk, m/s | bulk velocity | |
| Q, m3/s | flow rate | |
| µ, Pa·s | dynamic viscosity | |
| σ, N/m | interfacial tension | |
| ρ, kg/m3 | density | |
| θ, ° | contact angle | |
| Ca | capillary number | |
| Oh | Ohnesorge number | |
| Re | Reynolds number | |
| We | Weber number | |
| d | dispersed phase | |
| c | continuous phase |
References
- Angeli, P.; Ortega, E.G.; Tsaoulidis, D.; Earle, M. Intensified Liquid-Liquid Extraction Technologies in Small Channels: A Review. Johns. Matthey Technol. Rev. 2019, 63, 299–310. [Google Scholar] [CrossRef]
- Wang, K.; Li, L.; Xie, P.; Luo, G. Liquid-liquid microflow reaction engineering. React. Chem. Eng. 2017, 2, 611–627. [Google Scholar] [CrossRef]
- Abdollahi, A.; Sharma, R.N.; Vatani, A. Fluid flow and heat transfer of liquid-liquid two phase flow in microchannels: A review. Int. Commun. Heat Mass Transf. 2017, 84, 66–74. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Hensel, A.; Brandner, J.J.; Zhang, K.; Du, X.; Yang, Y. A review on emulsification via microfluidic processes. Front. Chem. Sci. Eng. 2020, 14, 350–364. [Google Scholar] [CrossRef]
- Samiei, E.; Tabrizian, M.; Hoorfar, M. A review of digital microfluidics as portable platforms for lab-on a-chip applications. Lab Chip 2016, 16, 2376–2396. [Google Scholar] [CrossRef]
- Mosavati, B.; Oleinikov, A.V.; Du, E. Development of an Organ-on-a-Chip-Device for Study of Placental Pathologies. Int. J. Mol. Sci. 2020, 21, 8755. [Google Scholar] [CrossRef]
- Liu, J.; Mosavati, B.; Oleinikov, A.V.; Du, E. Biosensors for Detection of Human Placental Pathologies: A Review of Emerging Technologies and Current Trends. Transl. Res. 2019, 213, 23–49. [Google Scholar] [CrossRef]
- Jagdale, P.P.; Li, D.; Shao, X.; Bostwick, J.B.; Xuan, X. Fluid Rheological Effects on the Flow of Polymer Solutions in a Contraction–Expansion Microchannel. Micromachines 2020, 11, 278. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow and Applied Rheology: Engineering Applications; Butterworth-Heinemann: Oxford, UK, 2011; ISBN 0080951600. [Google Scholar]
- Triplett, K.A.; Ghiaasiaan, S.M.; Abdel-Khalik, S.I.; Sadowski, D.L. Gas-liquid two-phase flow in microchannels part I: Two-phase flow patterns. Int. J. Multiph. Flow 1999, 25, 377–394. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, G.; Yuan, Q. Liquid-Liquid Two-Phase Flow Patterns in a Rectangular Microchannel. AIChE J. 2006, 52, 4052–4060. [Google Scholar] [CrossRef]
- Waelchli, S.; Rudolf von Rohr, P. Two-phase flow characteristics in gas–liquid microreactors. Int. J. Multiph. Flow 2006, 32, 791–806. [Google Scholar] [CrossRef]
- Cao, Z.; Wu, Z.; Sundén, B. Dimensionless analysis on liquid-liquid flow patterns and scaling law on slug hydrodynamics in cross-junction microchannels. Chem. Eng. J. 2018, 344, 604–615. [Google Scholar] [CrossRef]
- Kashid, M.; Kiwi-Minsker, L. Quantitative prediction of flow patterns in liquid-liquid flow in micro-capillaries. Chem. Eng. Process. Process Intensif. 2011, 50, 972–978. [Google Scholar] [CrossRef]
- Yao, C.; Zhao, Y.; Chen, G. Multiphase processes with ionic liquids in microreactors: Hydrodynamics, mass transfer and applications. Chem. Eng. Sci. 2018, 189, 340–359. [Google Scholar] [CrossRef]
- Yagodnitsyna, A.A.; Kovalev, A.V.; Bilsky, A.V. Flow patterns of immiscible liquid-liquid flow in a rectangular microchannel with T-junction. Chem. Eng. J. 2016, 303, 547–554. [Google Scholar] [CrossRef]
- Kovalev, A.V.; Yagodnitsyna, A.A.; Bilsky, A.V. Viscosity Ratio Influence on Liquid-Liquid Flow in a T-shaped Microchannel. Chem. Eng. Technol. 2021, 44, 365–370. [Google Scholar] [CrossRef]
- Yang, Z.C.; Bi, Q.C.; Liu, B.; Huang, K.X. Nitrogen/non-Newtonian fluid two-phase upward flow in non-circular microchannels. Int. J. Multiph. Flow 2010, 36, 60–70. [Google Scholar] [CrossRef]
- Zhang, T.; Cao, B.; Fan, Y.; Gonthier, Y.; Luo, L.; Wang, S. Gas-liquid flow in circular microchannel. Part I: Influence of liquid physical properties and channel diameter on flow patterns. Chem. Eng. Sci. 2011, 66, 5791–5803. [Google Scholar] [CrossRef]
- Fu, T.; Wei, L.; Zhu, C.; Ma, Y. Flow patterns of liquid-liquid two-phase flow in non-Newtonian fluids in rectangular microchannels. Chem. Eng. Process. Process Intensif. 2015, 91, 114–120. [Google Scholar] [CrossRef]
- Husny, J.; Cooper-White, J.J. The effect of elasticity on drop creation in T-shaped microchannels. J. Nonnewton. Fluid Mech. 2006, 137, 121–136. [Google Scholar] [CrossRef]
- Arratia, P.E.; Gollub, J.P.; Durian, D.J. Polymeric filament thinning and breakup in microchannels. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2008, 77, 1–6. [Google Scholar] [CrossRef]
- Arratia, P.E.; Cramer, L.A.; Gollub, J.P.; Durian, D.J. The effects of polymer molecular weight on filament thinning and drop breakup in microchannels. New J. Phys. 2009, 11. [Google Scholar] [CrossRef]
- Lee, W.; Walker, L.M.; Anna, S.L. Competition between viscoelasticity and surfactant dynamics in flow focusing microfluidics. Macromol. Mater. Eng. 2011, 296, 203–213. [Google Scholar] [CrossRef]
- Sang, L.; Hong, Y.; Wang, F. Investigation of viscosity effect on droplet formation in T-shaped microchannels by numerical and analytical methods. Microfluid. Nanofluidics 2009, 6, 621–635. [Google Scholar] [CrossRef]
- Roumpea, E.; Chinaud, M.; Angeli, P. Experimental investigations of non-Newtonian/Newtonian liquid-liquid flows in microchannels. AIChE J. 2017, 63, 3599–3609. [Google Scholar] [CrossRef]
- Garstecki, P.; Fuerstman, M.J.; Stone, A.; Whitesides, G.M. Formation of droplets and bubbles in a microfluidic T-junction—Scaling and mechanism of break-up. Lab Chip 2006, 6, 437–446. [Google Scholar] [CrossRef] [PubMed]
- Bird, R.B.; Carreau, P.J. A nonlinear viscoelastic model for polymer solutions and melts-I. Chem. Eng. Sci. 1968, 23, 427–434. [Google Scholar] [CrossRef]
- Kovalev, A.V.; Yagodnitsyna, A.A.; Bilsky, A.V. Flow hydrodynamics of immiscible liquids with low viscosity ratio in a rectangular microchannel with T-junction. Chem. Eng. J. 2018, 352, 120–132. [Google Scholar] [CrossRef]
- Eberhard, U.; Seybold, H.J.; Floriancic, M.; Bertsch, P.; Jiménez-Martínez, J.; Andrade, J.S.; Holzner, M. Determination of the effective viscosity of non-Newtonian fluids flowing through porous media. Front. Phys. 2019, 7, 71. [Google Scholar] [CrossRef]
- Lindner, A.; Bonn, D.; Meunier, J. Viscous fingering in a shear-thinning fluid. Phys. Fluids 2000, 12, 256–261. [Google Scholar] [CrossRef]
- Chiarello, E.; Gupta, A.; Mistura, G.; Sbragaglia, M.; Pierno, M. Droplet breakup driven by shear thinning solutions in a microfluidic T-junction. Phys. Rev. Fluids 2017, 2, 123602. [Google Scholar] [CrossRef]
- Basu, A.S. Droplet morphometry and velocimetry (DMV): A video processing software for time-resolved, label-free tracking of droplet parameters. Lab Chip 2013, 13, 1892–1901. [Google Scholar] [CrossRef] [PubMed]






| Physical Property | Castor Oil | CMC 0.5% | CMC 1.5% | XG 0.5% | G1 | G2 | G3 |
|---|---|---|---|---|---|---|---|
| ρ, g/cm3 | 0.962 | 0.99 | 0.99 | 0.99 | 1.128 | 1.213 | 1.226 |
| σ, mN/m | - | 14.6 | 13.7 | 10.7 | 15 | 12.8 | 11.97 |
| θ, ° | - | 159.3 | 151.9 | 165.3 | 168.4 | 167 | 168.5 |
| µ, mPa·s | 760 | 9.4–14.3 | 107.1–108 | 29–1232 | 4.7 | 130 | 506 |
| Parameter | CMC 0.5% | CMC 1.5% | XG 0.5% |
|---|---|---|---|
| , mPa∙s | 200 | 372.9 | 1313 |
| , mPa∙s | 9.44 | 107.1 | 8.7 |
| k, s | 10.68 | 8.9 | 0.457 |
| −0.014 | −0.67 | 0.129 |
| Authors | Comments on the Estimation of Effective Viscosity | |
|---|---|---|
| Zhang et al. [19] and Yang et al. [18] | ||
| Roumpea et al. [26] | ||
| Chiarello et al. [32] | Here δ is a smallest size of a rectangular channel cross-section. The authors introduced effective capillary number Ca’ = n Ca(µeff) | |
| Fu et al. [20] | Viscosity was calculated using the Bird–Carreau model (Equation (1)) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yagodnitsyna, A.; Kovalev, A.; Bilsky, A. Liquid–Liquid Flows with Non-Newtonian Dispersed Phase in a T-Junction Microchannel. Micromachines 2021, 12, 335. https://doi.org/10.3390/mi12030335
Yagodnitsyna A, Kovalev A, Bilsky A. Liquid–Liquid Flows with Non-Newtonian Dispersed Phase in a T-Junction Microchannel. Micromachines. 2021; 12(3):335. https://doi.org/10.3390/mi12030335
Chicago/Turabian StyleYagodnitsyna, Anna, Alexander Kovalev, and Artur Bilsky. 2021. "Liquid–Liquid Flows with Non-Newtonian Dispersed Phase in a T-Junction Microchannel" Micromachines 12, no. 3: 335. https://doi.org/10.3390/mi12030335
APA StyleYagodnitsyna, A., Kovalev, A., & Bilsky, A. (2021). Liquid–Liquid Flows with Non-Newtonian Dispersed Phase in a T-Junction Microchannel. Micromachines, 12(3), 335. https://doi.org/10.3390/mi12030335







