The Correctness of the Simplified Bernoulli Trial (SBT) Collision Scheme of Calculations of Two-Dimensional Flows
Abstract
1. Introduction
2. DSMC Collision Scheme with Explanations Based on the Cumulative Distribution Function
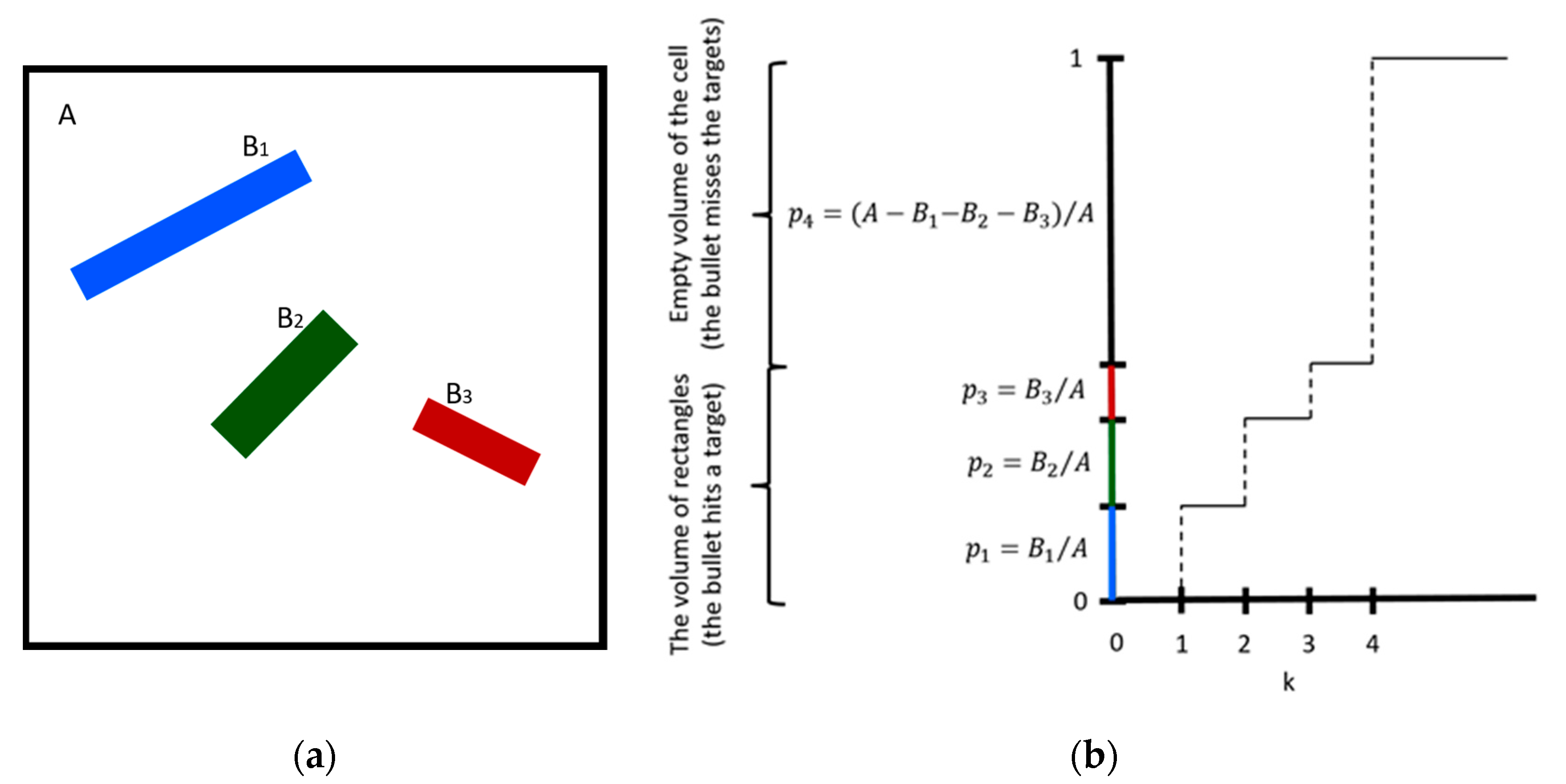
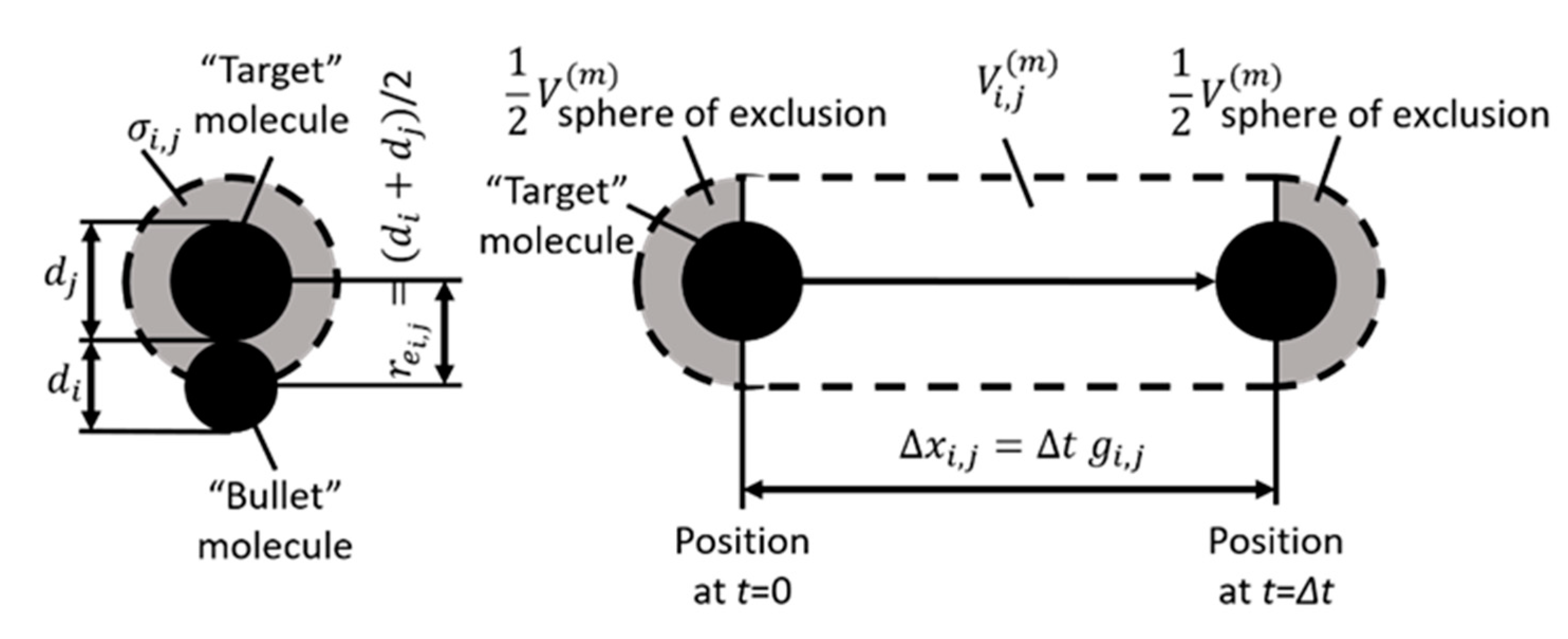
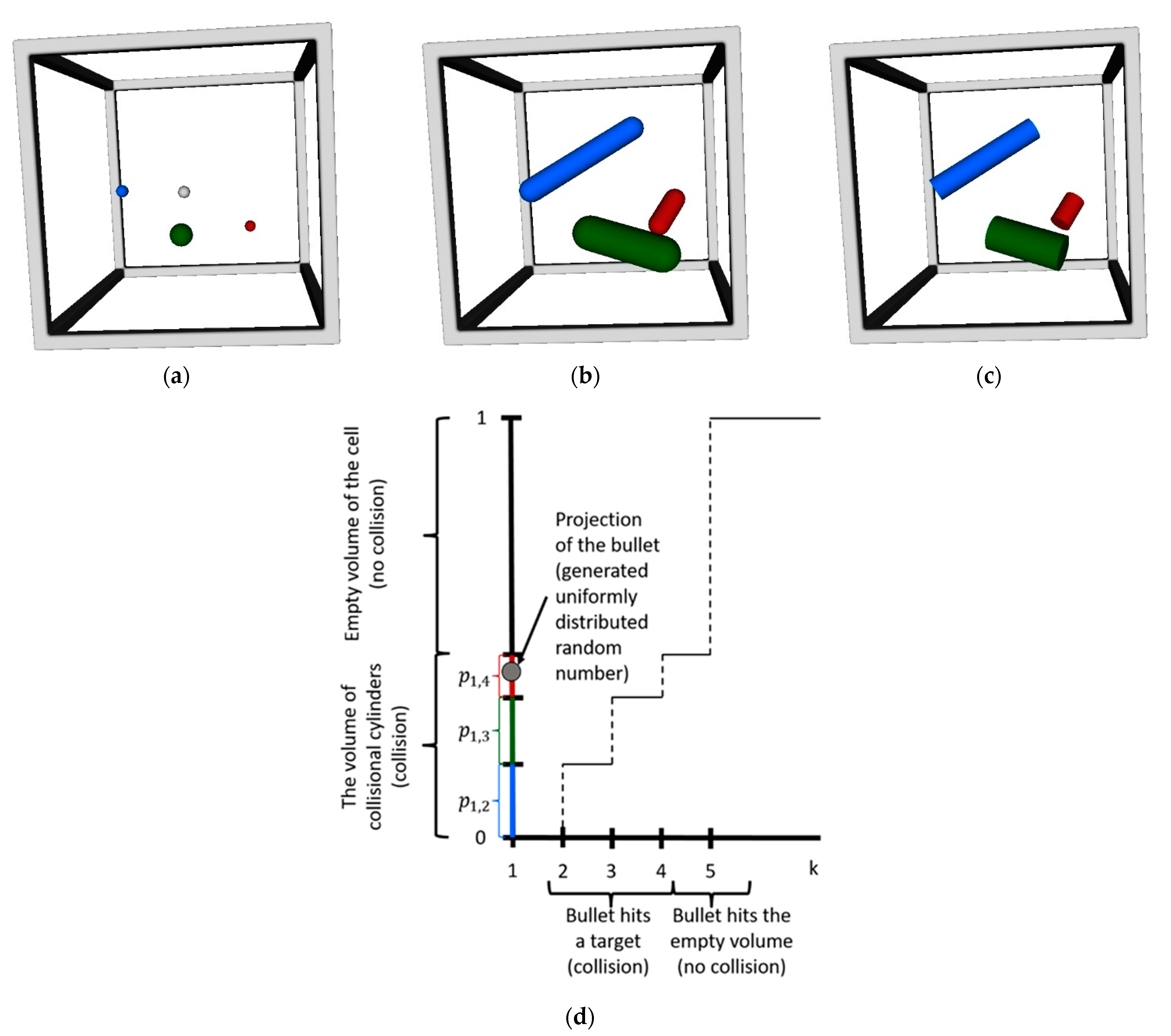
2.1. Preliminary Considerations
2.2. DSMC Collision Scheme with Explanations Based on the Cumulative Distribution Function
- 1.
- If the bullet is projected into an empty volume, there will be no collision, and
- 2.
- If the bullet hits any one of the targets, then
- 2.1.
- The hit target and bullet are collision pairs, and
- 2.2.
- We can determine when the collision occurs (considering the ratio of the travelled path to the collision to the path of the time step).
- The first particle i is the particle with index i in the particle list created for cell l, and
- The second particle is chosen with probability from particles on the list after particle i.
- The first particle i is the particle with index i in the particle list created for cell l, and
- Calculate j using CDF (6), taking into account the particles with indexes .
3. Results
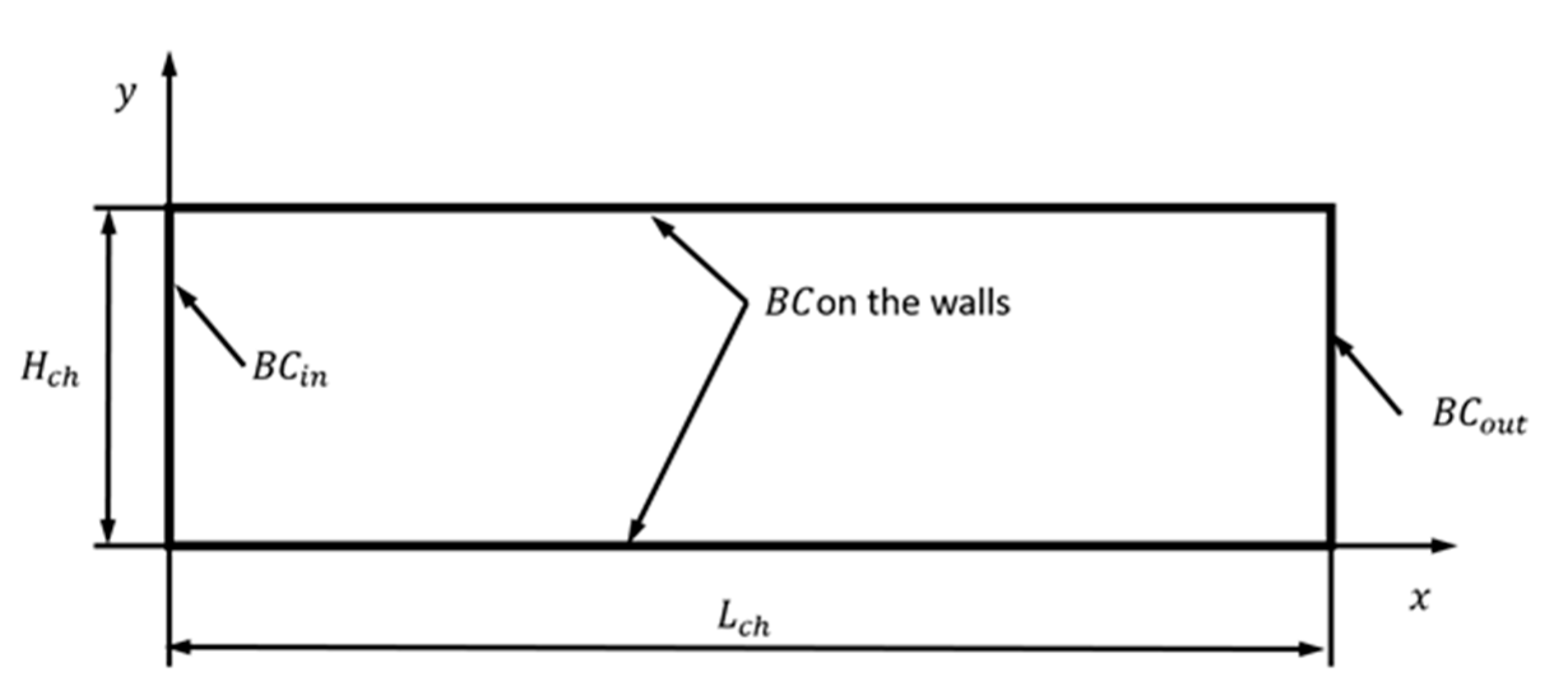
3.1. Pressure-Driven Gas Flow in a Microchannel
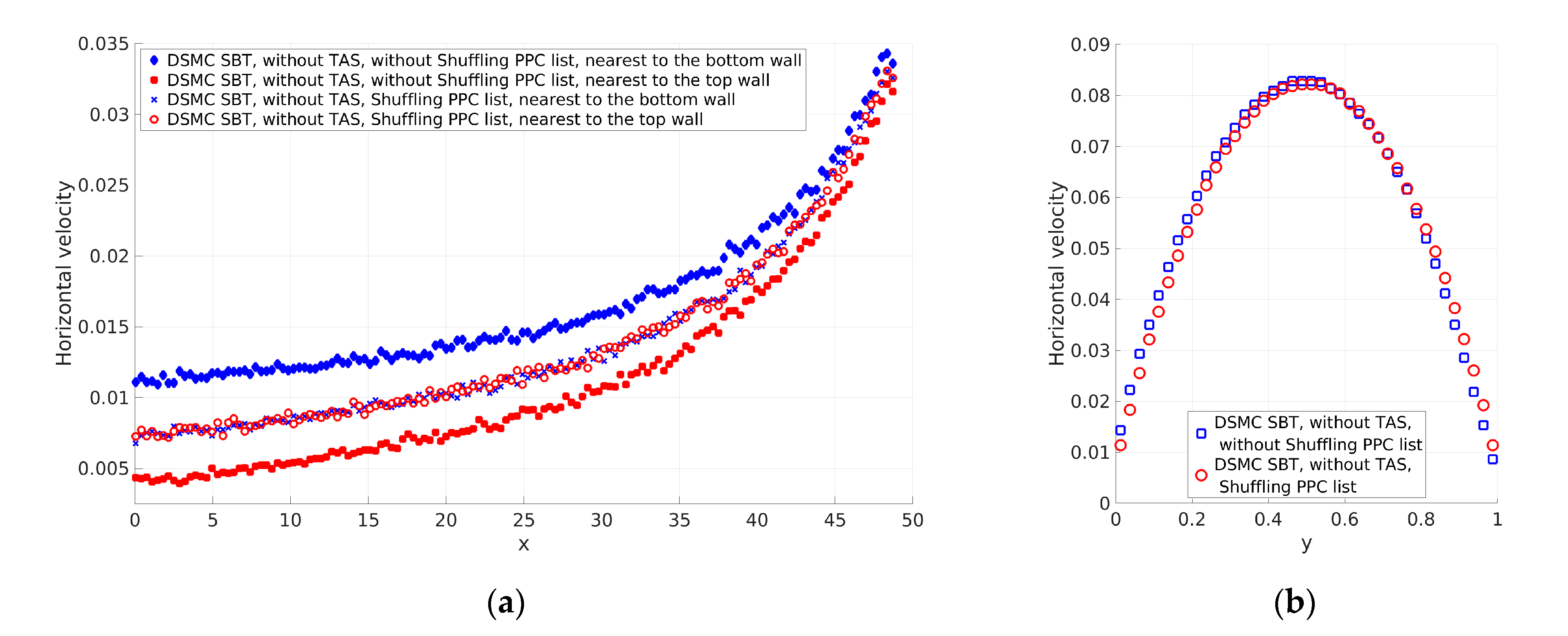
3.1.1. Influence of the Shuffling of the PPC List in the Collision Scheme on the Solution
- 1st group of particles were in cell (I − 1, J − 1);
- 2nd group of particles were in cell (I, J − 1);
- 3rd group of particles were in cell (I + 1, J − 1);
- 4th group of particles were in cell (I − 1, J);
- 5th group of particles were in cell (I, J);
- 6th group of particles were in cell (I + 1, J);
- 7th group of particles were in cell (I − 1, J + 1);
- 8th group of particles were in cell (I, J + 1);
- 9th group of particles were in cell (I + 1, J + 1).
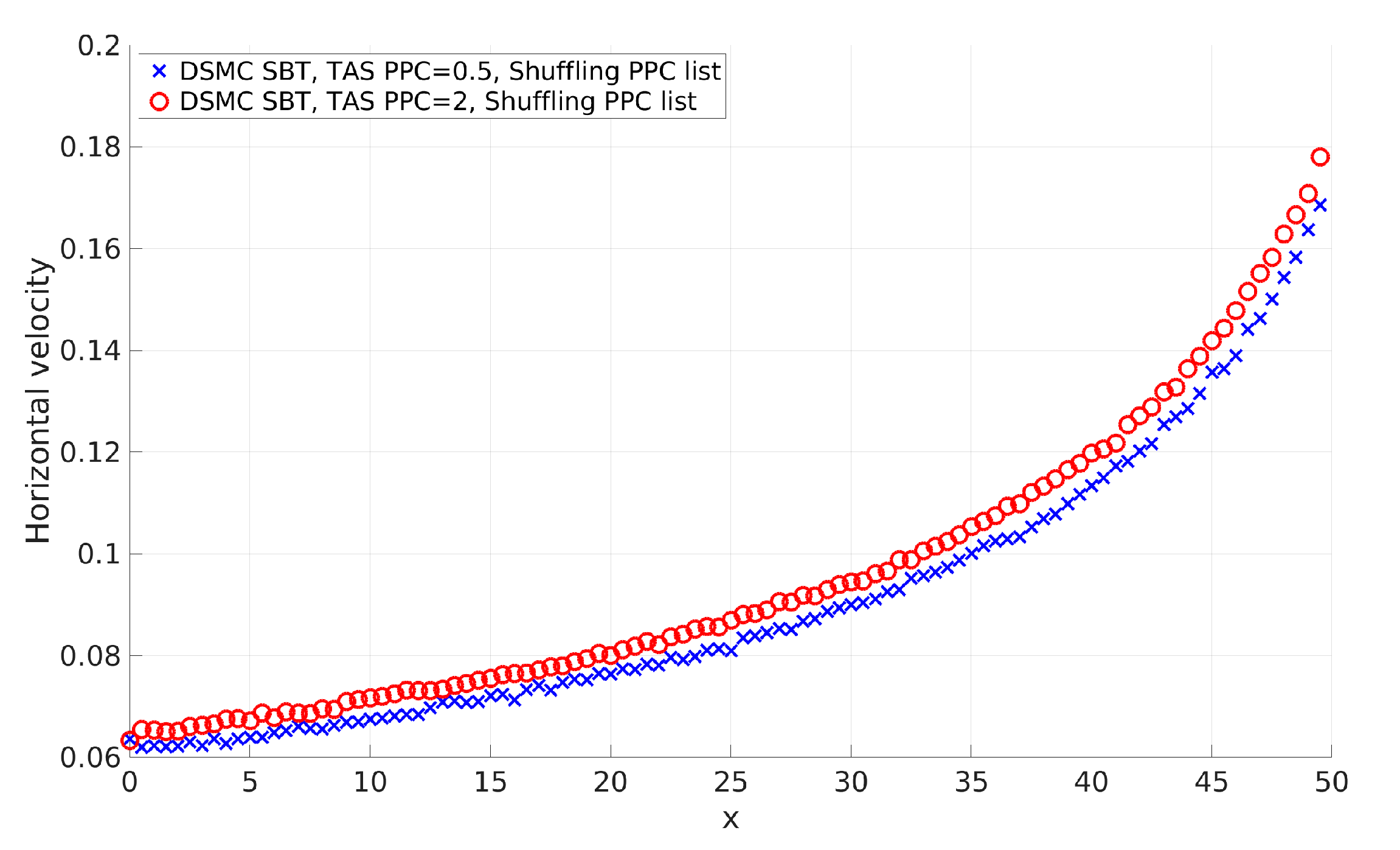
3.1.2. The Minimal Number of PPC in 2D Fluid Flows
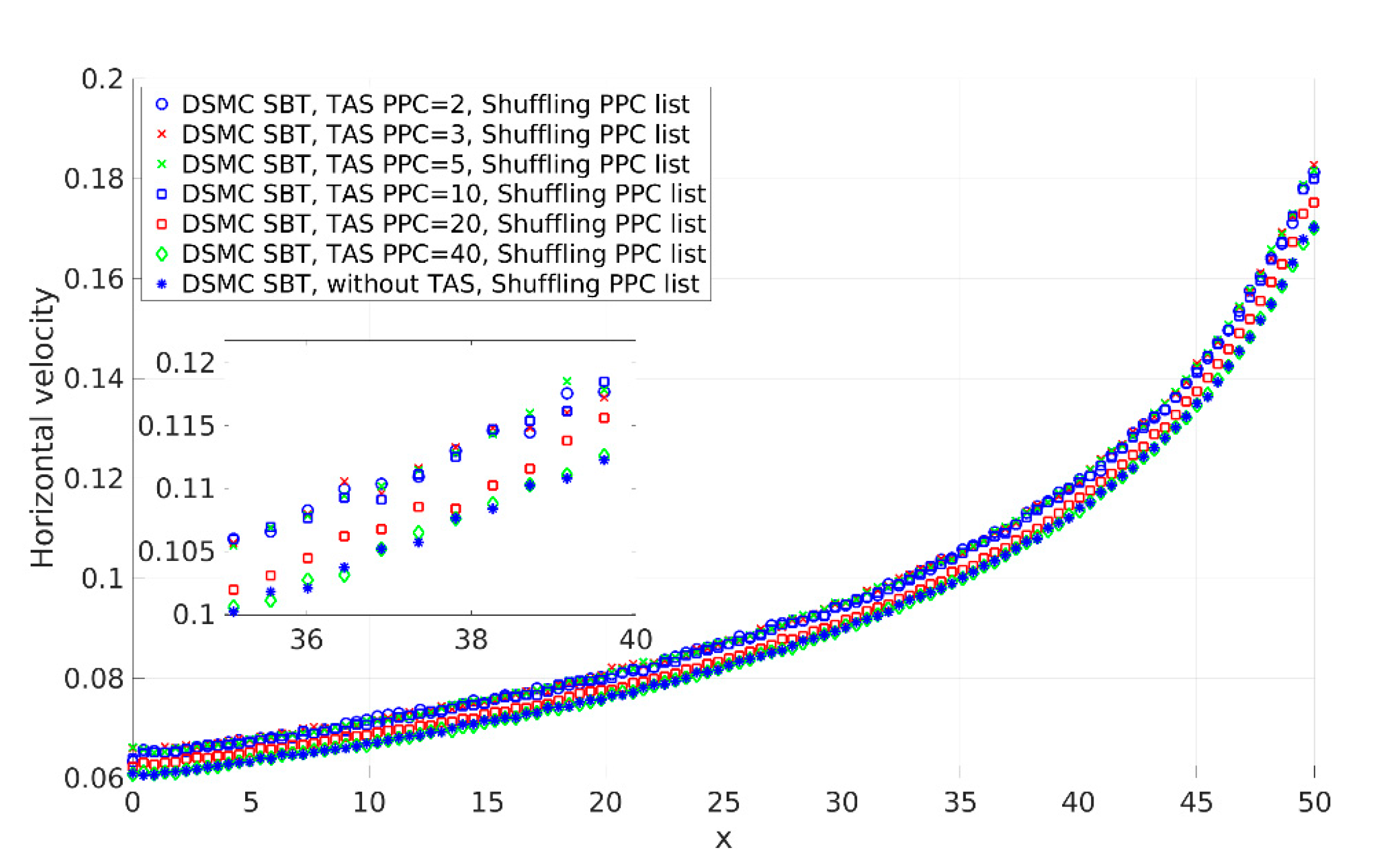
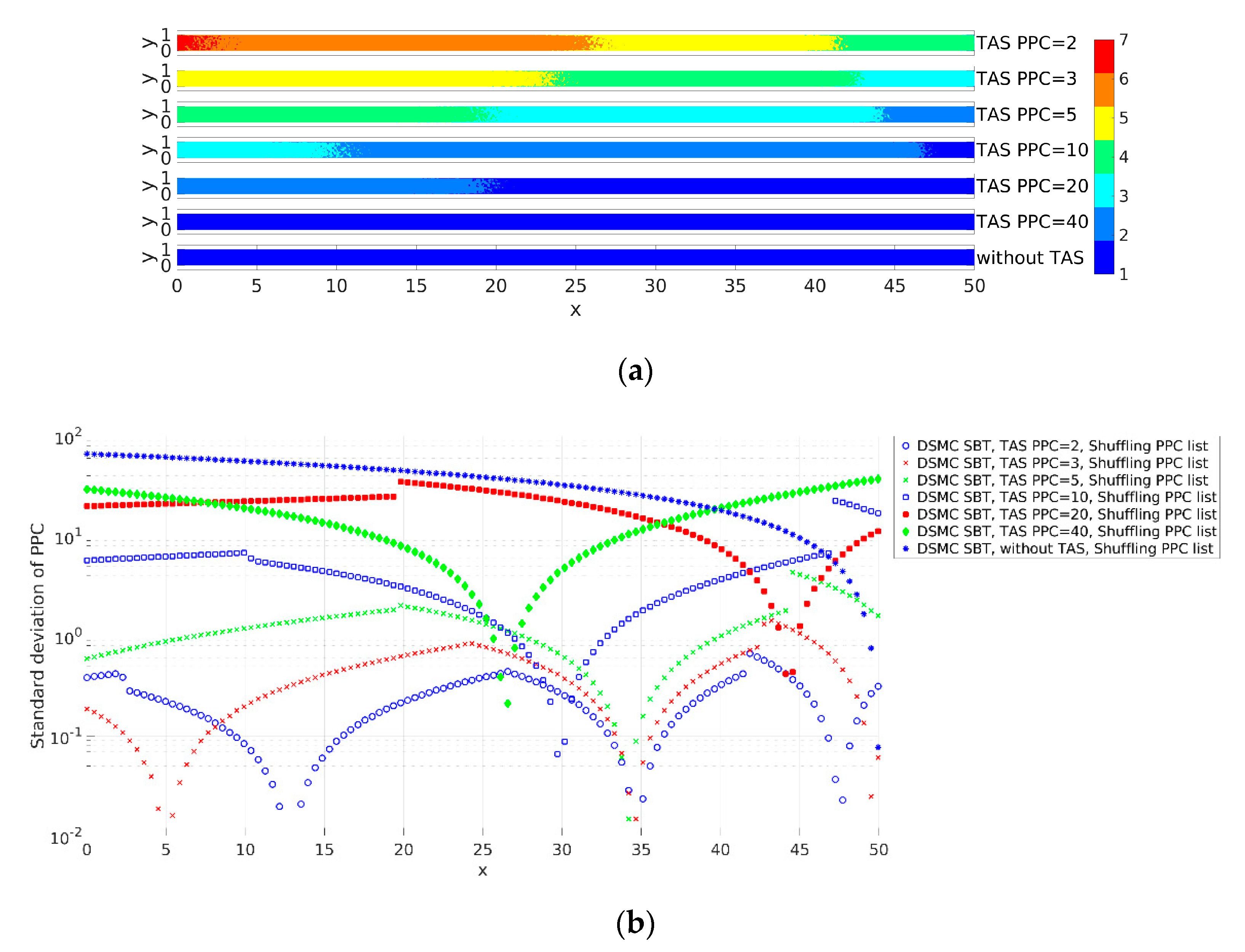
3.1.3. Influence of the Number of PPC on a Solution
3.1.4. The Computational Times of SBT and SBT-CDF Collision Schemes
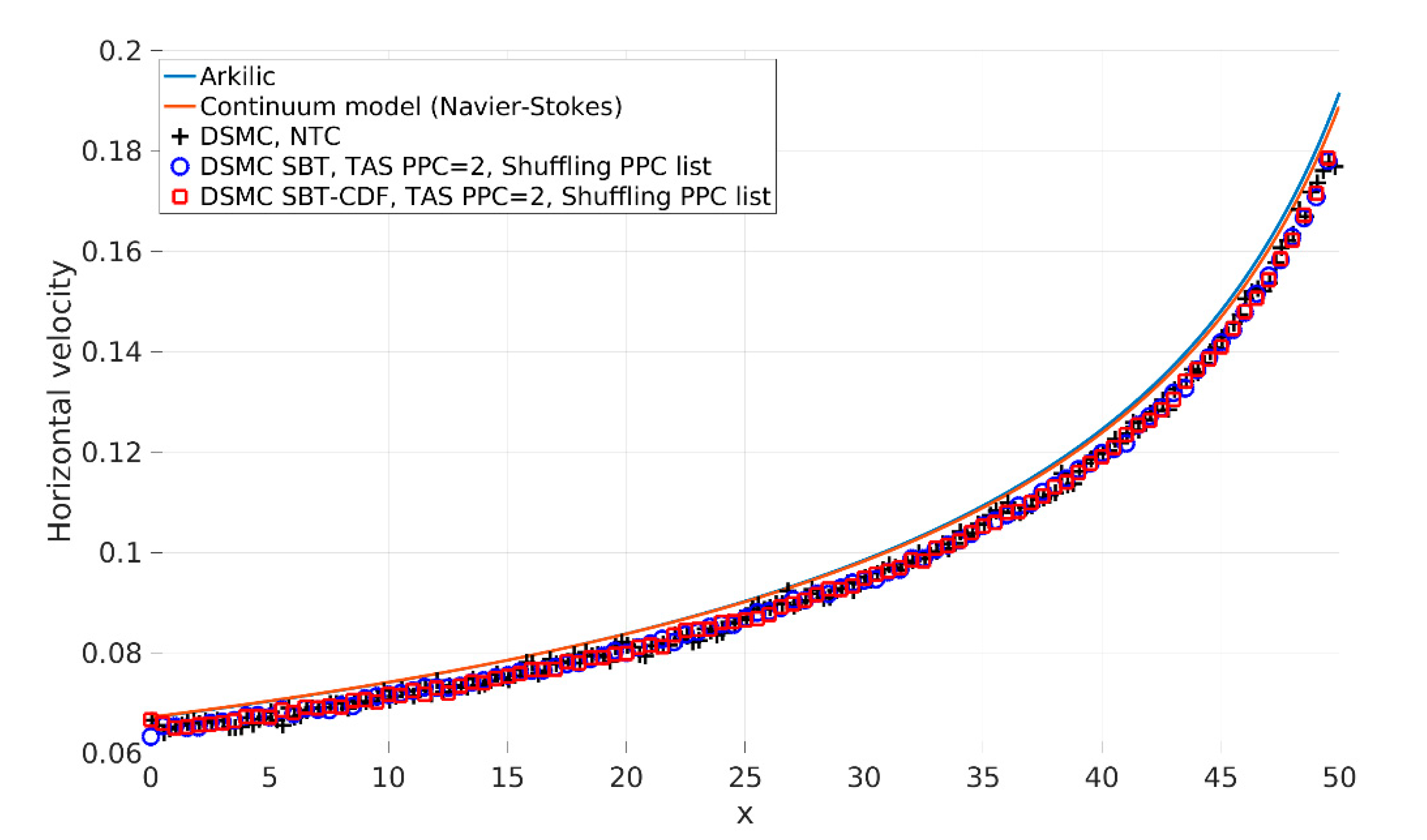
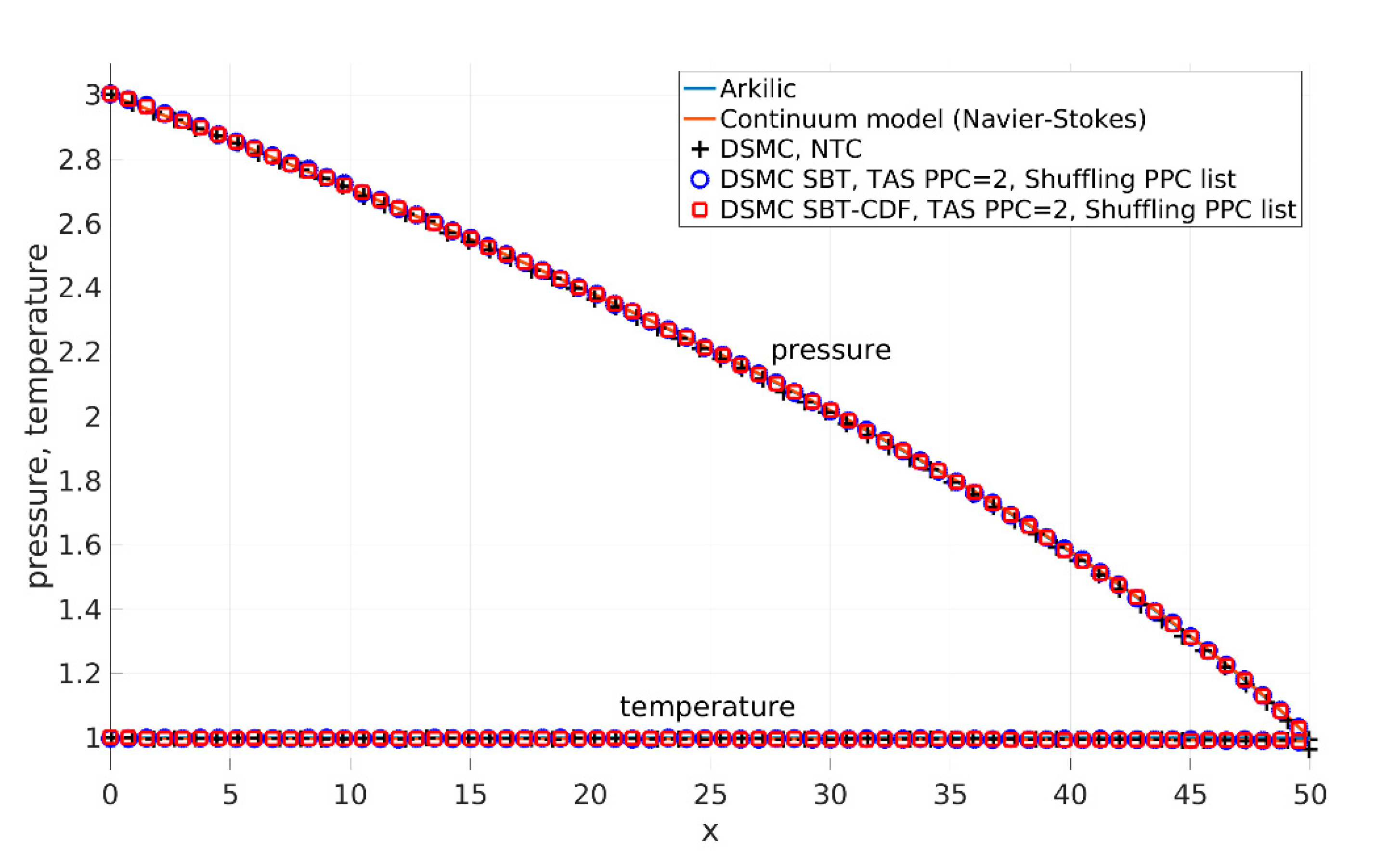
3.1.5. Validation of SBT and SBT-CDF Collision Schemes
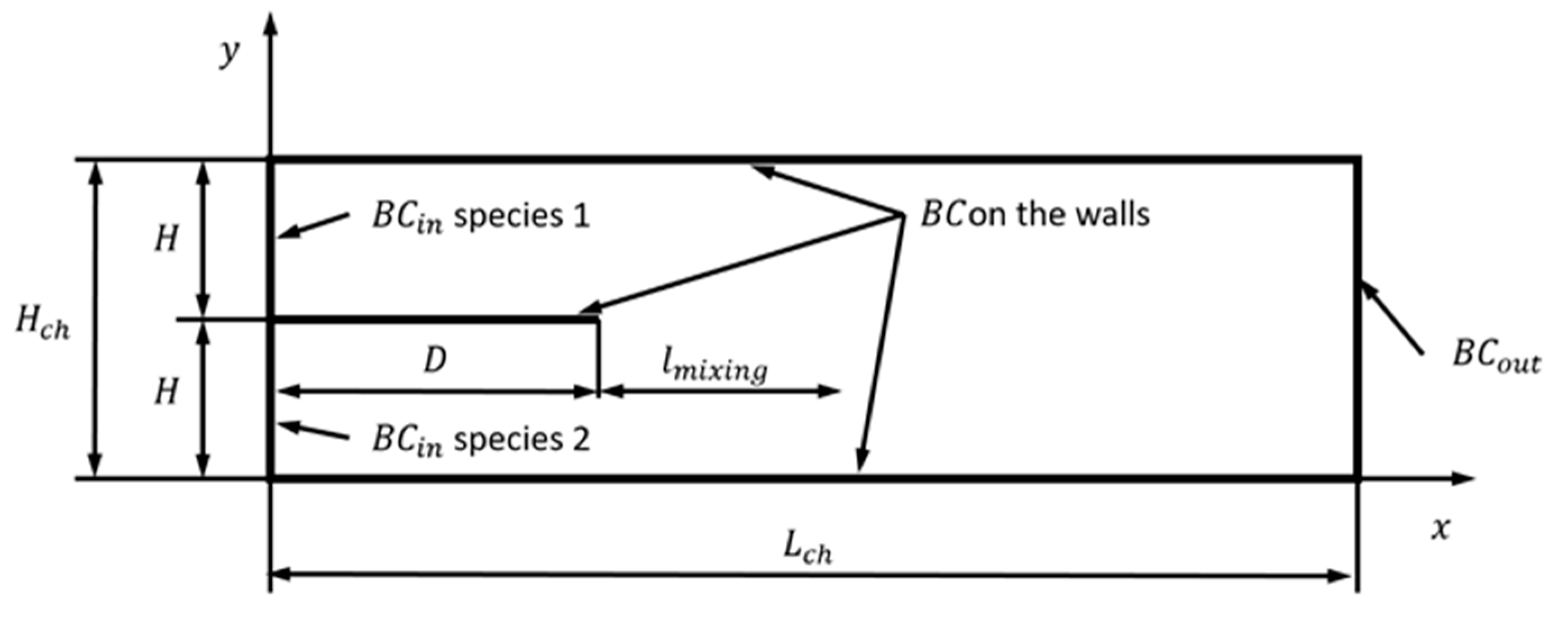
3.2. Gas Mixing
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Bird, G. Molecular, Gas Dynamics and the Direct Simulation of Gas Flows; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Yang, L.M.; Chen, Z.; Shu, C.; Wu, J.; Zhang, L.Q. Improved fully implicit discrete-velocity method for efficient simulation of flows in all flow regimes. Phys. Rev. E 2018, 98, 063313. [Google Scholar] [CrossRef]
- Yang, L.M.; Shu, C.; Chen, Z.; Dong, H. An improved discrete velocity method (DVM) for efficient simulation of flows in all flow regimes. Phys. Fluids 2018, 30, 062005. [Google Scholar] [CrossRef]
- Paidoussis, M.P. Fluid-Structure Interactions, 2nd ed.; Academic Press: Cambridge, MA, USA, 2014; ISBN 9780123973122. [Google Scholar]
- Shterev, K.; Manoach, E.; Stefanov, S. Hybrid numerical approach to study the interaction of the rarefied gas flow in a microchannel with a cantilever. Int. J. Non-Linear Mech. 2019, 117, 103239. [Google Scholar] [CrossRef]
- Stefanov, S. Particle Monte Carlo Algorithms with Small Number of Particles in Grid Cells. In Numerical Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2010; pp. 110–117. [Google Scholar]
- Stefanov, S.K. On DSMC calculations of rarefied gas flows with small number of particles in cells. SIAM J. Sci. Comput. 2011, 33, 677–702. [Google Scholar] [CrossRef]
- Roohi, E.; Stefanov, S. Collision partner selection schemes in DSMC: From micro/nano flows to hypersonic flows. Phys. Rep. 2016, 656, 1–38. [Google Scholar] [CrossRef]
- Stefanov, S. On the basic concepts of the direct simulation Monte Carlo method. Phys. Fluids 2019, 31, 067104. [Google Scholar] [CrossRef]
- Gallis, M.A.; Torczynski, J.R.; Rader, D.J.; Bird, G.A. Convergence behavior of a new DSMC algorithm. J. Comput. Phys. 2009, 228, 4532–4548. [Google Scholar] [CrossRef]
- Bird, G.A.; Gallis, M.A.; Torczynski, J.R.; Rader, D.J. Accuracy and efficiency of the sophisticated direct simulation Monte Carlo algorithm for simulating noncontinuum gas flows. Phys. Fluids 2009, 21, 017103. [Google Scholar] [CrossRef]
- Gallis, M.A.; Torczynski, J.R. Effect of collision-partner selection schemes on the accuracy and efficiency of the direct simulation Monte Carlo method. Int. J. Numer. Methods Fluids 2010, 67, 1057–1072. [Google Scholar] [CrossRef]
- Bird, G.A. The DSMC Method, 1st ed.; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2013. [Google Scholar]
- Ivanov, M.S.; Rogasinsky, S.V. Analysis of numerical techniques of the direct simulation Monte Carlo method in the rarefied gas dynamics. Russ. J. Numer. Anal. Math. Model. 1988, 3, 453–466. [Google Scholar] [CrossRef]
- Belotserkovskii, O.; Yanitskii, V. The statistical particles-in-cells method for solving rarefied gas dynamics problems. USSR Comput. Math. Math. Phys. 1975, 15, 101–114. [Google Scholar] [CrossRef]
- Yanitskiy, V. Operator approach to direct simulation Monte Carlo theory in rarefied gas dynamics. In Proceedings of the 17th Symposium on Rarefied Gas Dynamics, Aachen, Germany, 8–14 July 1990; pp. 770–777. [Google Scholar]
- Kac, M. Probability and Related Topics in Physical Sciences; Interscience Publishers: New York, NY, USA, 1959. [Google Scholar]
- Taheri, E.; Roohi, E.; Stefanov, S. On the convergence of the simplified Bernoulli trial collision scheme in rarefied Fourier flow. Phys. Fluids 2017, 29, 062003. [Google Scholar] [CrossRef]
- Roohi, E.; Stefanov, S.; Shoja-Sani, A.; Ejraei, H. A generalized form of the Bernoulli Trial collision scheme in DSMC: Derivation and evaluation. J. Comput. Phys. 2018, 354, 476–492. [Google Scholar] [CrossRef]
- Shonkwiler, R.W.; Mendivil, F. Explorations in Monte Carlo Methods; Springer Science and Business Media, LLC: New York, NY, USA, 2009. [Google Scholar]
- Sears, F.W.; Salinger, G.L. Thermodynamics, Kinetic Theory, and Statistical Thermodynamics, 3rd ed.; Addison-Wesley: Boston, MA, USA, 1975. [Google Scholar]
- Courant, R.; Friedrichs, K.; Lewy, H. Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 1928, 100, 32–74. [Google Scholar] [CrossRef]
- Bird, G.A. Visual DSMC Program for Two-Dimensional and Axially Symmetric Flows. The DS2V Program User’s Guide; Version 2.1; G.A.B. Consulting Pty Ltd.: Sydney, Australia, 2003. [Google Scholar]
- Shterev, K.S.; Stefanov, S.K. On DSMC calculations of high speed gas flows on adaptive meshes. In Proceedings of the 1st MIGRATE Summer Workshop, Strasbourg, France, 30 June–1 July 2016. [Google Scholar]
- Arkilic, E.B.; Schmidt, M.A.; Breuer, K.S. Gaseous slip flow in long microchannels. J. Microelectromechanical Syst. 1997, 6, 167–178. [Google Scholar] [CrossRef]
- Stefanov, S.; Roussinov, V.; Cercignani, C. Rayleigh-Bénard flow of a rarefied gas and its attractors. I. Convection regime. Phys. Fluids 2002, 14, 2255–2269. [Google Scholar] [CrossRef]
- Shterev, K.; Stefanov, S. Pressure based finite volume method for calculation of compressible viscous gas flows. J. Comput. Phys. 2010, 229, 461–480. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Meskos, S.; Stefanov, S.; Valougeorgis, D. Gas mixing and final mixture composition control in simple geometry micro-mixers via DSMC analysis. Micromachines 2019, 10, 178. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shterev, K. The Correctness of the Simplified Bernoulli Trial (SBT) Collision Scheme of Calculations of Two-Dimensional Flows. Micromachines 2021, 12, 127. https://doi.org/10.3390/mi12020127
Shterev K. The Correctness of the Simplified Bernoulli Trial (SBT) Collision Scheme of Calculations of Two-Dimensional Flows. Micromachines. 2021; 12(2):127. https://doi.org/10.3390/mi12020127
Chicago/Turabian StyleShterev, Kiril. 2021. "The Correctness of the Simplified Bernoulli Trial (SBT) Collision Scheme of Calculations of Two-Dimensional Flows" Micromachines 12, no. 2: 127. https://doi.org/10.3390/mi12020127
APA StyleShterev, K. (2021). The Correctness of the Simplified Bernoulli Trial (SBT) Collision Scheme of Calculations of Two-Dimensional Flows. Micromachines, 12(2), 127. https://doi.org/10.3390/mi12020127





