Design and Optimization of a Novel SAW Gyroscope Structure Based on Amplitude Modulation with 1-D Phononic Crystals
Abstract
:1. Introduction
2. Design and Theory
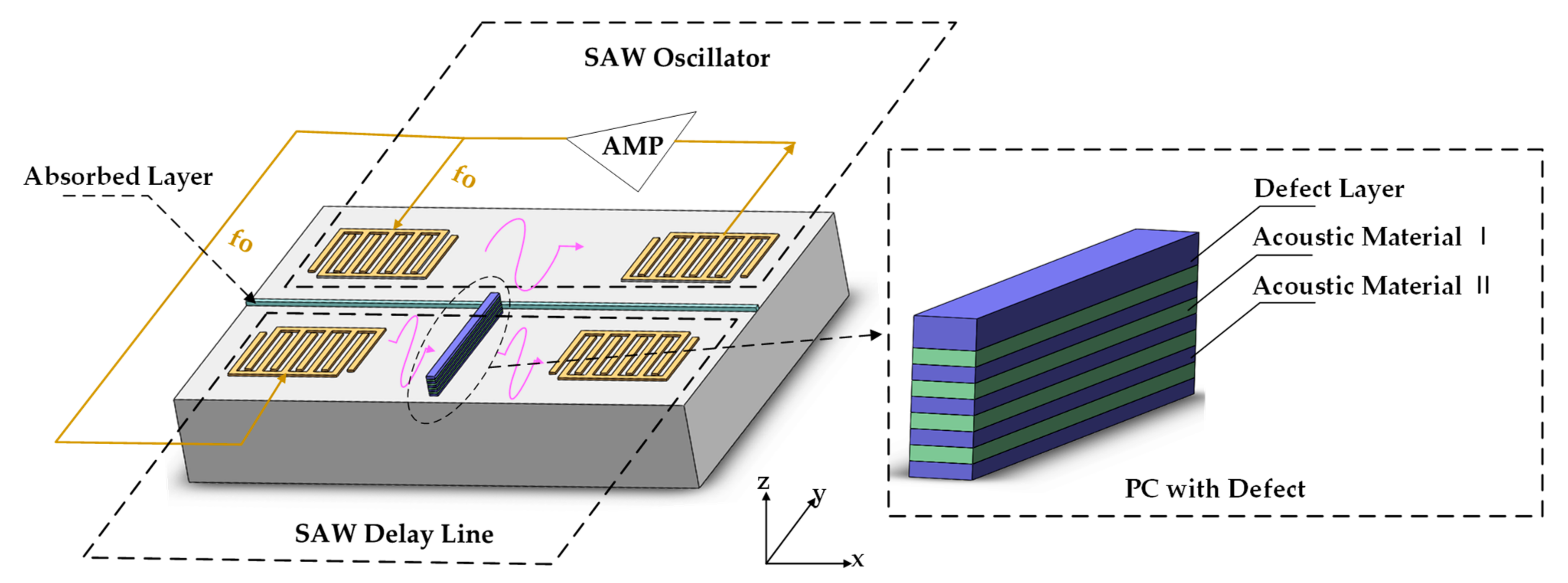
2.1. Design of Basic Structure and Working Principle
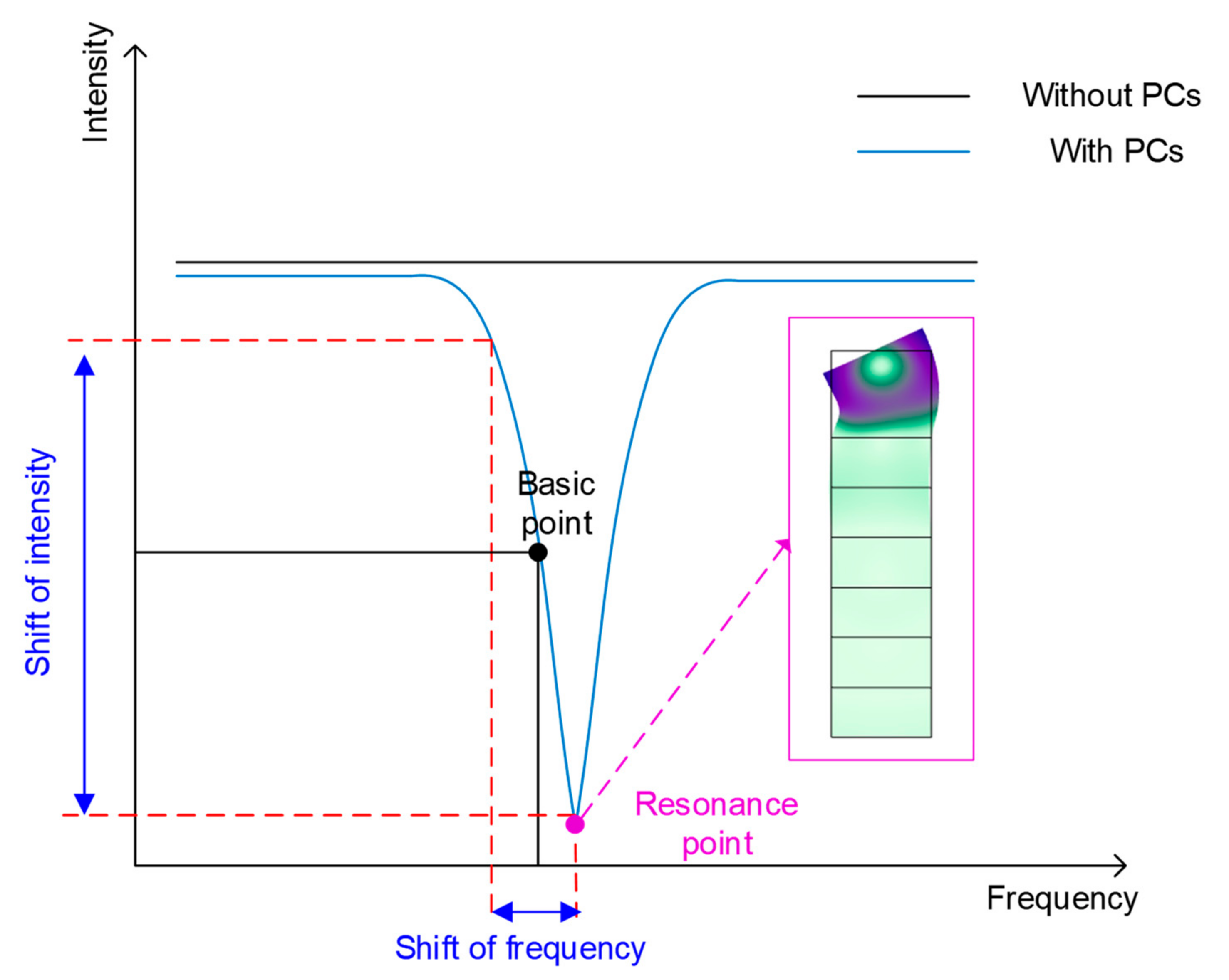
2.2. Theoretical Analysis
3. Optimization and Analysis
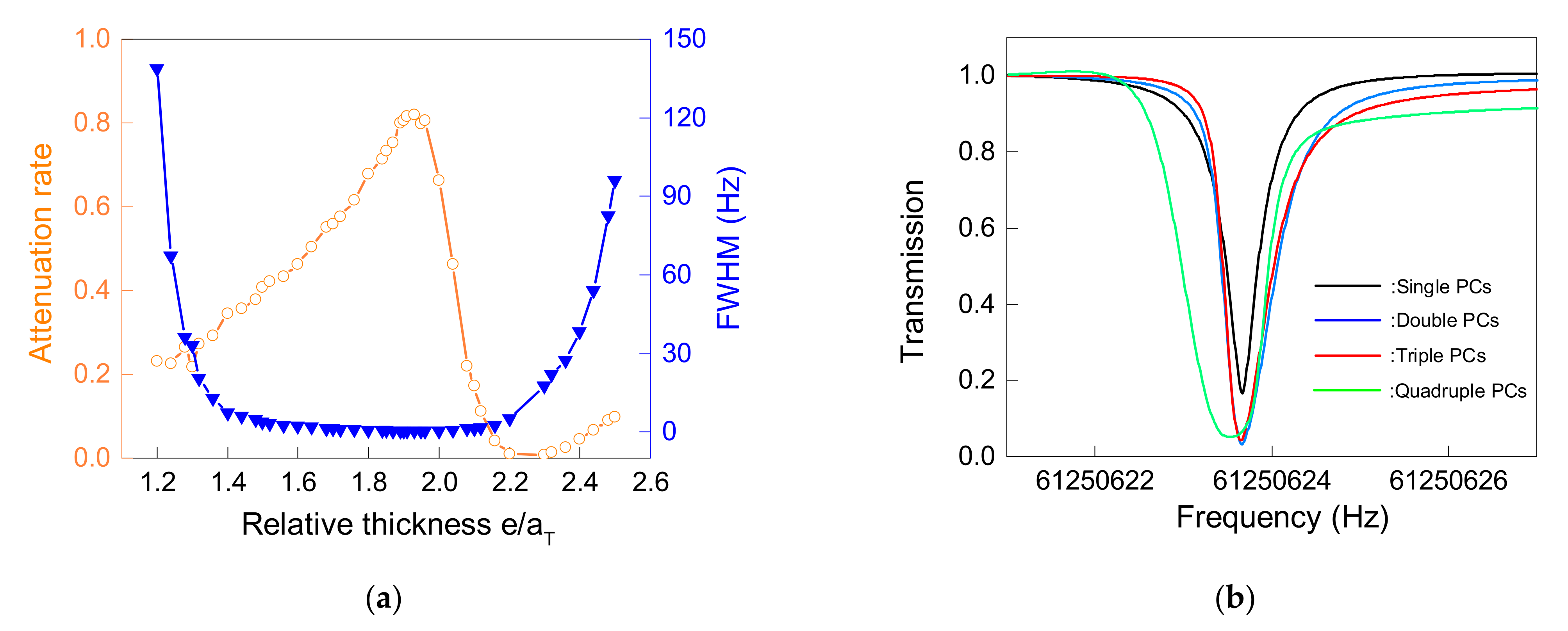
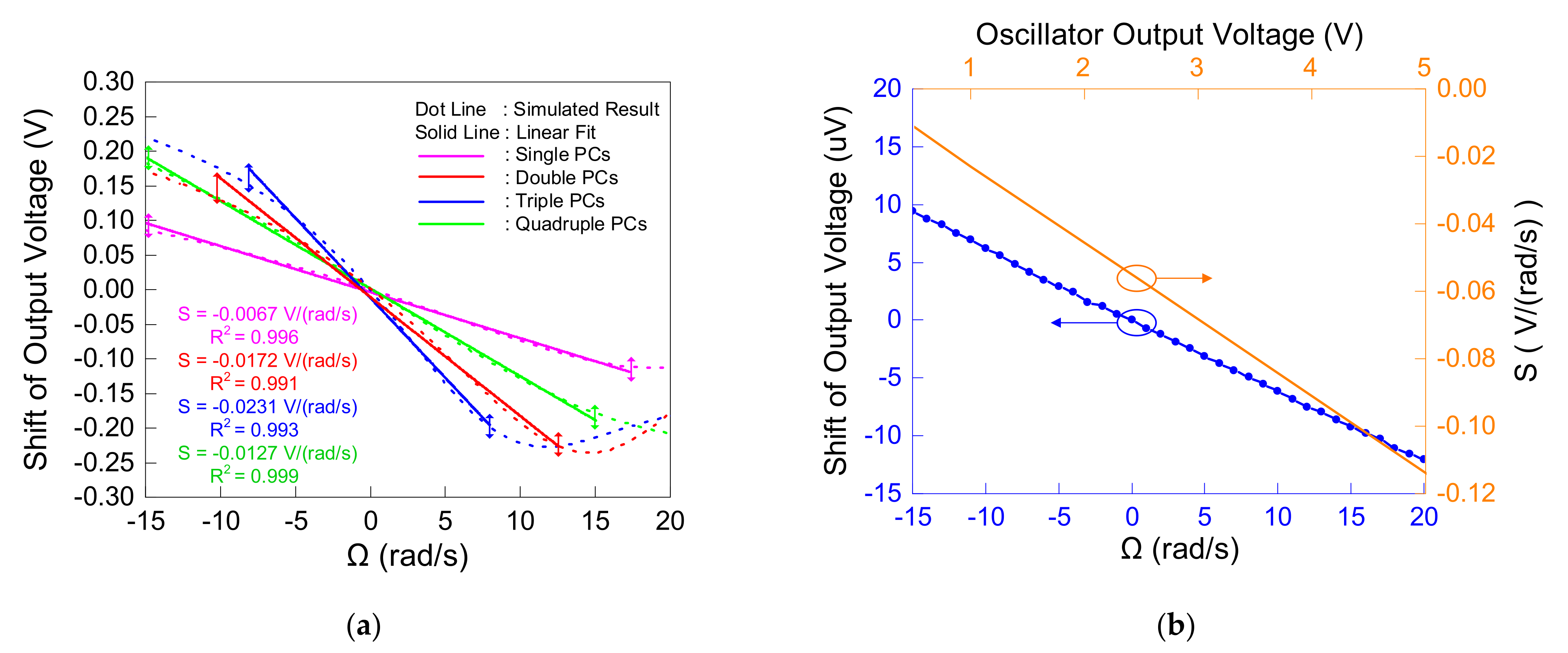
3.1. Optimization and Analysis of PCs
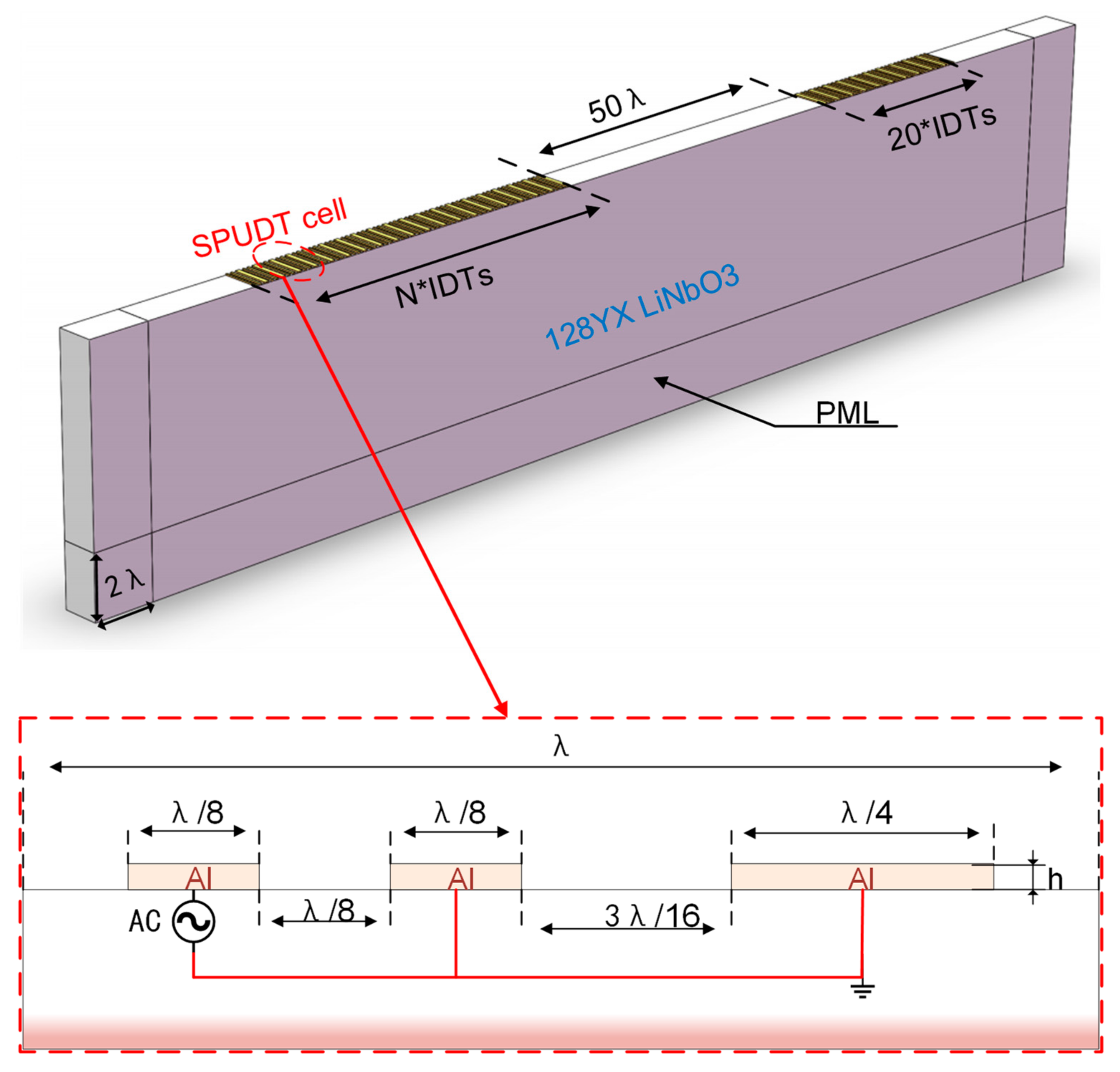
3.2. Optimization and Analysis of IDTs
3.3. Comprehensive Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sarapuloff, S.A.; Skrypkovsky, G.A.; Rhim, J. Inertial effects in surface and bulk elastic waves and possibility of their use in high-G solid-state micro gyroscopes. In Proceedings of the 12th Saint Petersburg International Conference on Integrated Navigation Systems, ICINS, Saint Petersburg, Russia, 23–25 May 2005; pp. 355–361. [Google Scholar]
- Oh, H.; Lee, K.J.; Lee, K.; Yang, S.S. Gyroscopes based on surface acoustic waves. Micro Nano Syst. Lett. 2015, 3, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Kurosawa, M.; Fukuda, Y.; Takasaki, M.; Higuchi, T. A surface-acoustic-wave gyro sensor. Sens. Actuators A Phys. 1998, 66, 33–39. [Google Scholar] [CrossRef]
- Woods, R.C.; Kalami, H.; Johnson, B. Evaluation of a novel surface acoustic wave gyroscope. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2002, 49, 136–141. [Google Scholar] [CrossRef]
- Varadan, V.K.; Suh, W.D.; Xavier, P.B.; Jose, K.A.; Varadan, V.V. Design and development of a MEMS-IDT gyroscope. Smart Mater. Struct. 2000, 9, 898. [Google Scholar] [CrossRef]
- Lee, M.; Lee, K. Enhancing the sensitivity of three-axis detectable surface acoustic wave gyroscope by using a floating thin piezoelectric membrane. Jpn. J. Appl. Phys. 2017, 56, 06GN14. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.W.; Rhim, J.W.; Park, S.W.; Yang, S.S. A micro rate gyroscope based on the SAW gyroscopic effect. J. Micromechanics Microengineering 2007, 17, 2272. [Google Scholar] [CrossRef]
- Wang, W.; Oh, H.; Lee, K.; Yoon, S.; Yang, S. Enhanced sensitivity of novel surface acoustic wave microelectromechanical system-interdigital transducer gyroscope. Jpn. J. Appl. Phys. 2009, 48, 06FK09. [Google Scholar] [CrossRef] [Green Version]
- Oh, H.; Wang, W.; Yang, S.; Lee, K. Development of SAW based gyroscope with high shock and thermal stability. Sens. Actuators A Phys. 2011, 165, 8–15. [Google Scholar] [CrossRef]
- Oh, H.; Fu, C.; Yang, S.S.; Wang, W.; Lee, K. A novel shock and heat tolerant gyrosensor utilizing a one-port surface acoustic wave reflective delay line. J. Micromech. Microeng. 2012, 22, 045007. [Google Scholar] [CrossRef]
- Oh, H.; Lee, K.; Yang, S.S.; Wang, W. Enhanced sensitivity of a surface acoustic wave gyroscope using a progressive wave. J. Micromech. Microeng. 2011, 21, 075015. [Google Scholar] [CrossRef]
- Oh, H.; Yang, S.; Lee, K. Development of surface acoustic wave-based microgyroscope utilizing progressive wave. Jpn. J. Appl. Phys. 2010, 49, 06GN16. [Google Scholar] [CrossRef]
- Oh, H.; Lee, K.J.; Yang, S.S.; Lee, K. Development of novel dual-axis sensing gyroscope using surface acoustic wave. Microelectron. Eng. 2012, 97, 259–264. [Google Scholar] [CrossRef]
- Khateib, F.; Mehaney, A.; Amin, R.M.; Aly, A.H. Ultra-sensitive acoustic biosensor based on a 1D phononic crystal. Phys. Scr. 2020, 95, 075704. [Google Scholar] [CrossRef]
- He, J.; Li, H.; Tian, Y.; Zhang, Q.; Lu, Z.; Lan, J. Numerical Analysis of Viscous Dissipation in Microchannel Sensor Based on Phononic Crystal. Micromachines 2021, 12, 994. [Google Scholar] [CrossRef] [PubMed]
- Hatanaka, D.; Yamaguchi, H. Real-space characterization of cavity-coupled waveguide systems in hypersonic phononic crystals. Phys. Rev. Appl. 2020, 13, 024005. [Google Scholar] [CrossRef] [Green Version]
- Dong, H.W.; Wang, Y.S.; Zhang, C. Inverse design of high-Q wave filters in two-dimensional phononic crystals by topology optimization. Ultrasonics 2017, 76, 109–124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Faiz, M.S.; Addouche, M.; Zain, A.R.M.; Siow, K.S.; Chaalane, A.; Khelif, A. Experimental demonstration of a multichannel elastic wave filter in a phononic crystal slab. Appl. Sci. 2020, 10, 4594. [Google Scholar] [CrossRef]
- Mohammadi, S.; Eftekhar, A.A.; Hunt, W.D.; Adibi, A. High-Q micromechanical resonators in a two-dimensional phononic crystal slab. Appl. Phys. Lett. 2009, 94, 051906. [Google Scholar] [CrossRef]
- Mohammadi, S.; Adibi, A. Waveguide-Based Phononic Crystal Micro/Nanomechanical High-$ Q $ Resonators. J. Microelectromechanical Syst. 2012, 21, 379–384. [Google Scholar] [CrossRef]
- Oudich, M.; Djafari-Rouhani, B.; Bonello, B.; Pennec, Y.; Sarry, F. Phononic crystal made of multilayered ridges on a substrate for Rayleigh waves manipulation. Crystals 2017, 7, 372. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.; Matheny, M.H.; MacCabe, G.S.; Luo, J.; Pfeifer, H.; Mirhosseini, M.; Painter, O. Two-dimensional optomechanical crystal cavity with high quantum cooperativity. Nat. Commun. 2020, 11, 1–10. [Google Scholar] [CrossRef]
- Wang, W.; Shao, X.; Liu, X.; Liu, J.; He, S. Enhanced sensitivity of surface acoustic wave-based rate sensors incorporating metallic dot arrays. Sensors 2014, 14, 3908–3920. [Google Scholar] [CrossRef] [Green Version]
- Kushibiki, J.; Takanaga, I.; Arakawa, M.; Sannomiya, T. Accurate measurements of the acoustical physical constants of LiNbO/sub 3/and LiTao/sub 3/single crystals. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 1315–1323. [Google Scholar] [CrossRef] [PubMed]
- Joshi, S.G.; White, R.M. Excitation and detection of surface elastic waves in piezoelectric crystals. J. Acoust. Soc. Am. 1969, 46, 17–27. [Google Scholar] [CrossRef]
- Kimura, N.; Takeuchi, M. A design of surface acoustic wave wideband single-phase-unidirectional transducers using coupling-of-modes theory. Jpn. J. Appl. Phys. 1999, 38, 3265. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Q.; Fu, S.; Wang, X.; Qiu, X.; Wu, H. Hybrid full-wave analysis of surface acoustic wave devices for accuracy and fast performance prediction. Micromachines 2021, 12, 5. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Phononic material | Al and W |
| Thickness of single-layer phononic material (aT) | 13 μm |
| Width of PCs (b) | 20 μm |
| Material of defect layer | Al |
| Relative thickness of defect layer (e/aT) | 1.91 |
| Number of PC walls | 1~4 |
| Parameter | Value |
|---|---|
| Substrate material | 128° XY LiNbO3 |
| Electrode material | Al |
| Period of SPUDTs () | 64.3 μm |
| Number of excitation electrodes | 50 |
| Number of receiving electrodes | 20 |
| Length of delay line | 50 |
| Operating frequency | 61.25 MHz |
| Insertion loss | −4 dB |
| Performance and Characteristic | The Proposed Gyro | Amplitude-Modulated | Frequency-Modulated | ||
|---|---|---|---|---|---|
| [4] | [6] | [7] | [11] | ||
| Sensitivity | 23.1 mV/(rad/s) under 1 V | 3.6 uV/(deg/s) | 27.5 uV/(deg/s) under 3.7 V | 0.431 Hz/(deg/s) | 62.57 Hz/(deg/s) |
| Linearity range | ±8 rad/s | 0 to 10 deg/s | 0 to 400 deg/s | 0 to 2000 deg/s | 0 to 1000 deg/s |
| Operating frequency | 61.25 MHz | 75 MHz | 160 MHz | 98.6 MHz | 80 MHz |
| Metallic array | No | Yes | Yes | No | Yes |
| Signal processing circuit | Simple | Simple | Simple | Complex | Complex |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, F.; Zhao, L.; Zhang, Y. Design and Optimization of a Novel SAW Gyroscope Structure Based on Amplitude Modulation with 1-D Phononic Crystals. Micromachines 2021, 12, 1485. https://doi.org/10.3390/mi12121485
Ge F, Zhao L, Zhang Y. Design and Optimization of a Novel SAW Gyroscope Structure Based on Amplitude Modulation with 1-D Phononic Crystals. Micromachines. 2021; 12(12):1485. https://doi.org/10.3390/mi12121485
Chicago/Turabian StyleGe, Fei, Liye Zhao, and Yang Zhang. 2021. "Design and Optimization of a Novel SAW Gyroscope Structure Based on Amplitude Modulation with 1-D Phononic Crystals" Micromachines 12, no. 12: 1485. https://doi.org/10.3390/mi12121485
APA StyleGe, F., Zhao, L., & Zhang, Y. (2021). Design and Optimization of a Novel SAW Gyroscope Structure Based on Amplitude Modulation with 1-D Phononic Crystals. Micromachines, 12(12), 1485. https://doi.org/10.3390/mi12121485





