Mechano-Triboelectric Analysis of Surface Charge Generation on Replica-Molded Elastomeric Nanodomes
Abstract
:1. Introduction
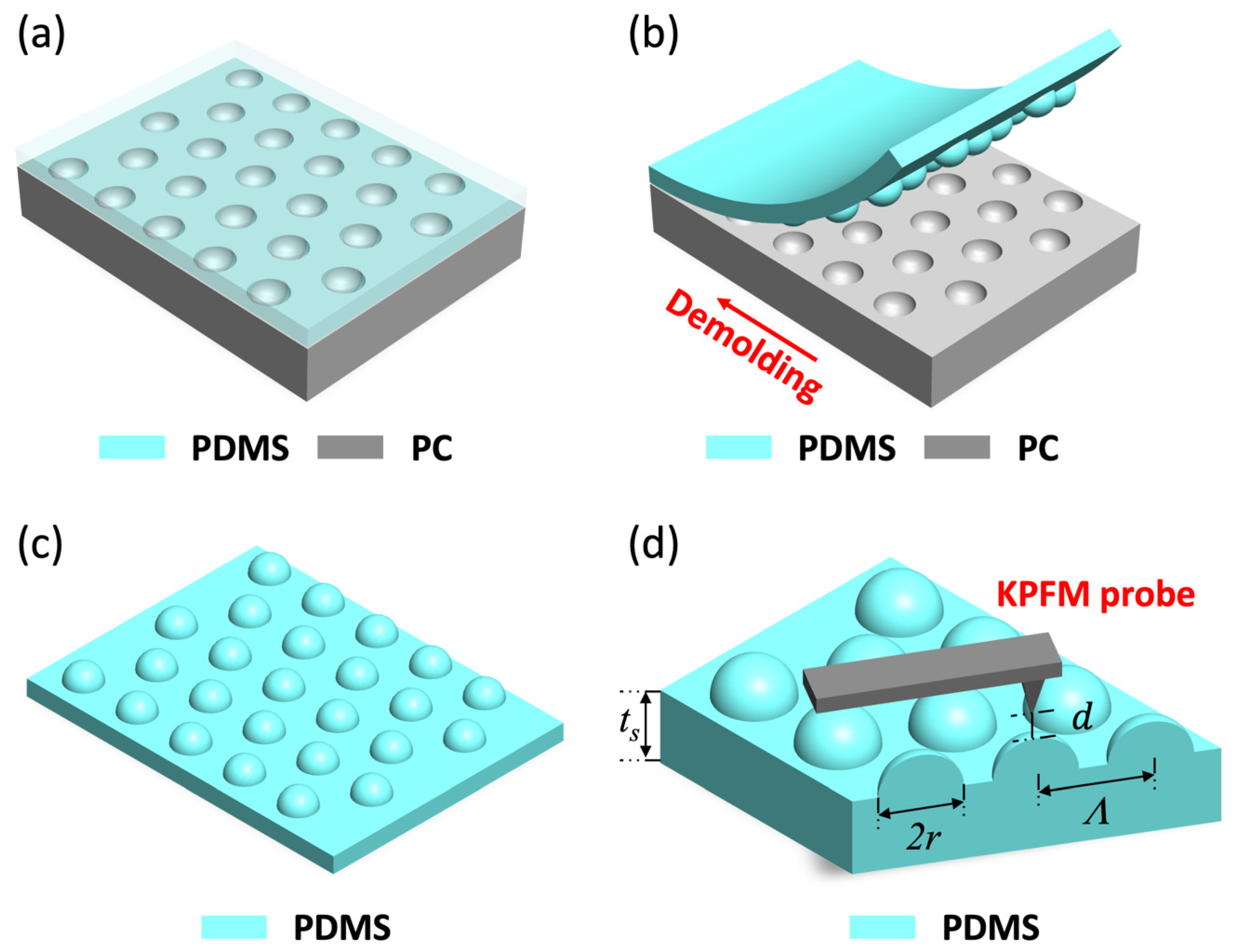
2. Materials and Methods
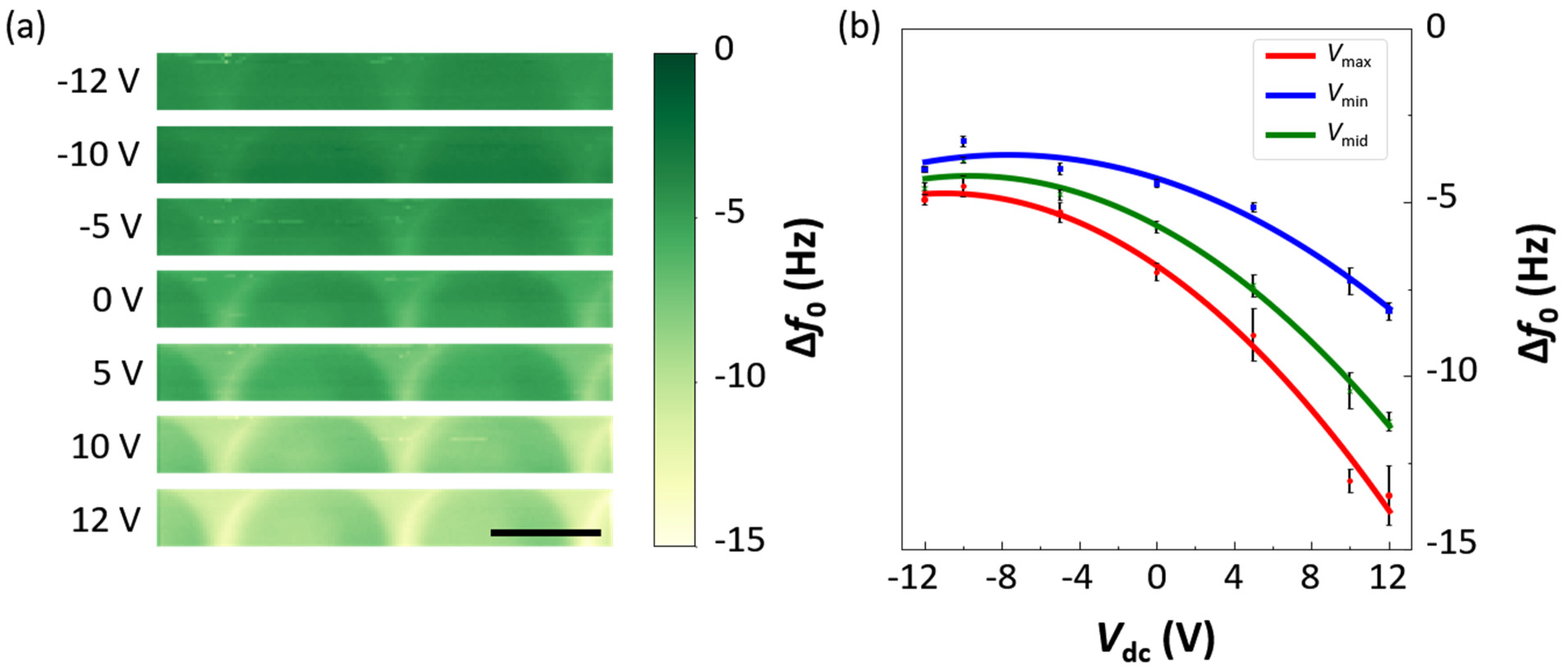
2.1. Tribocharging and Analysis
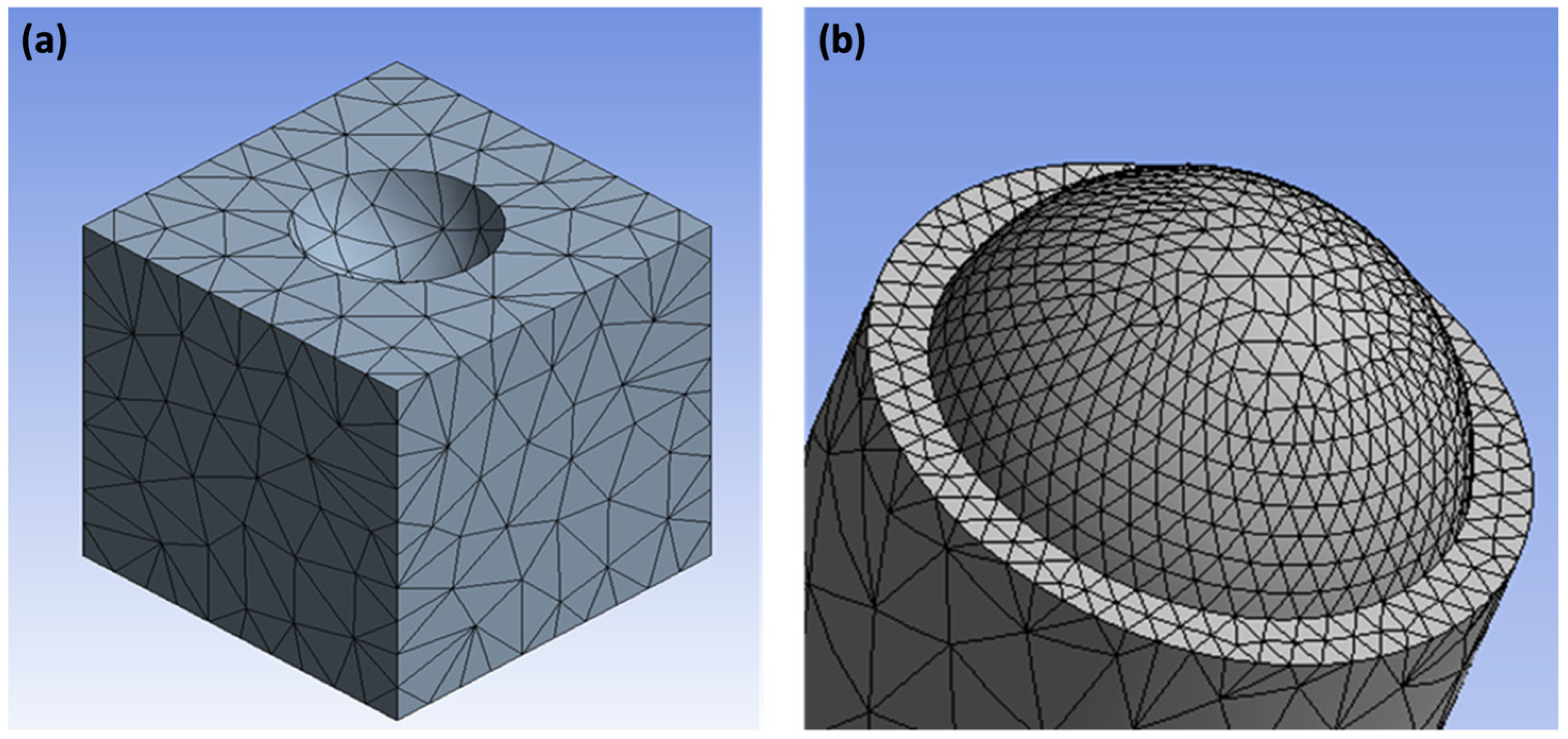
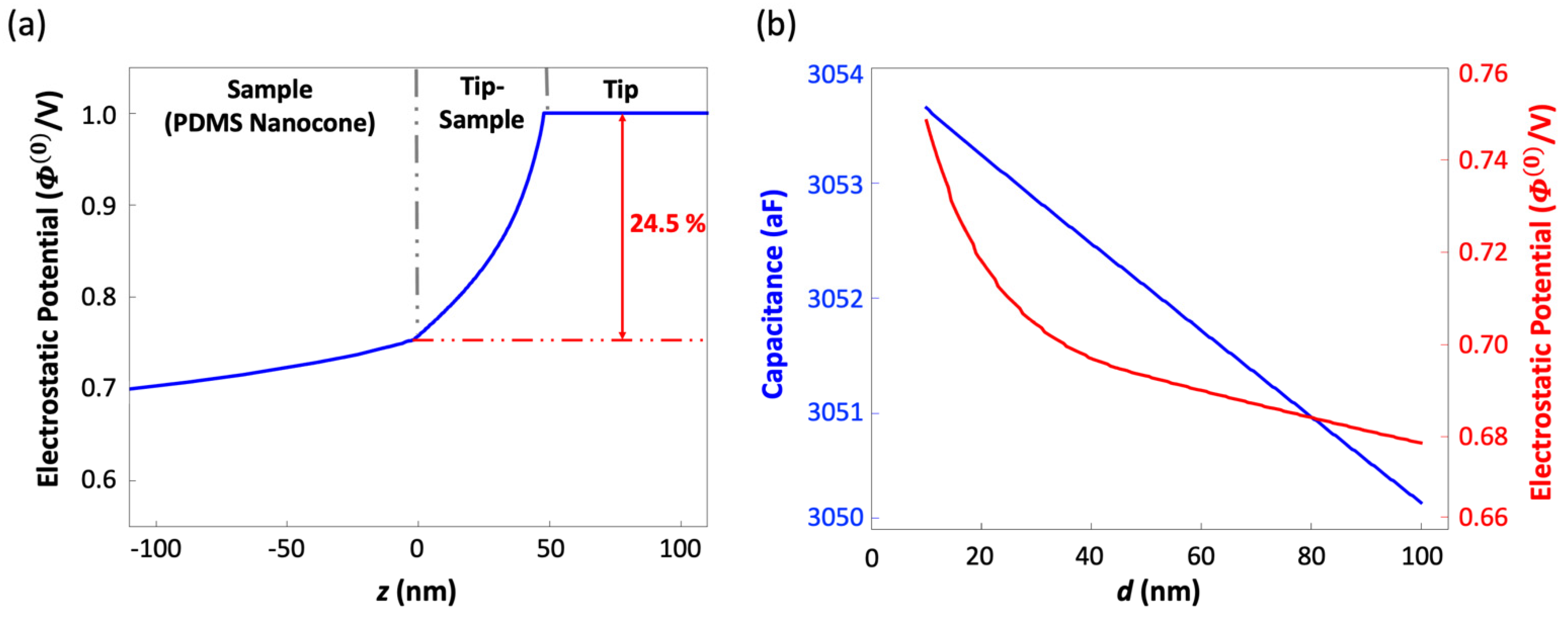
2.2. Mechano-Triboelectric Charging Model
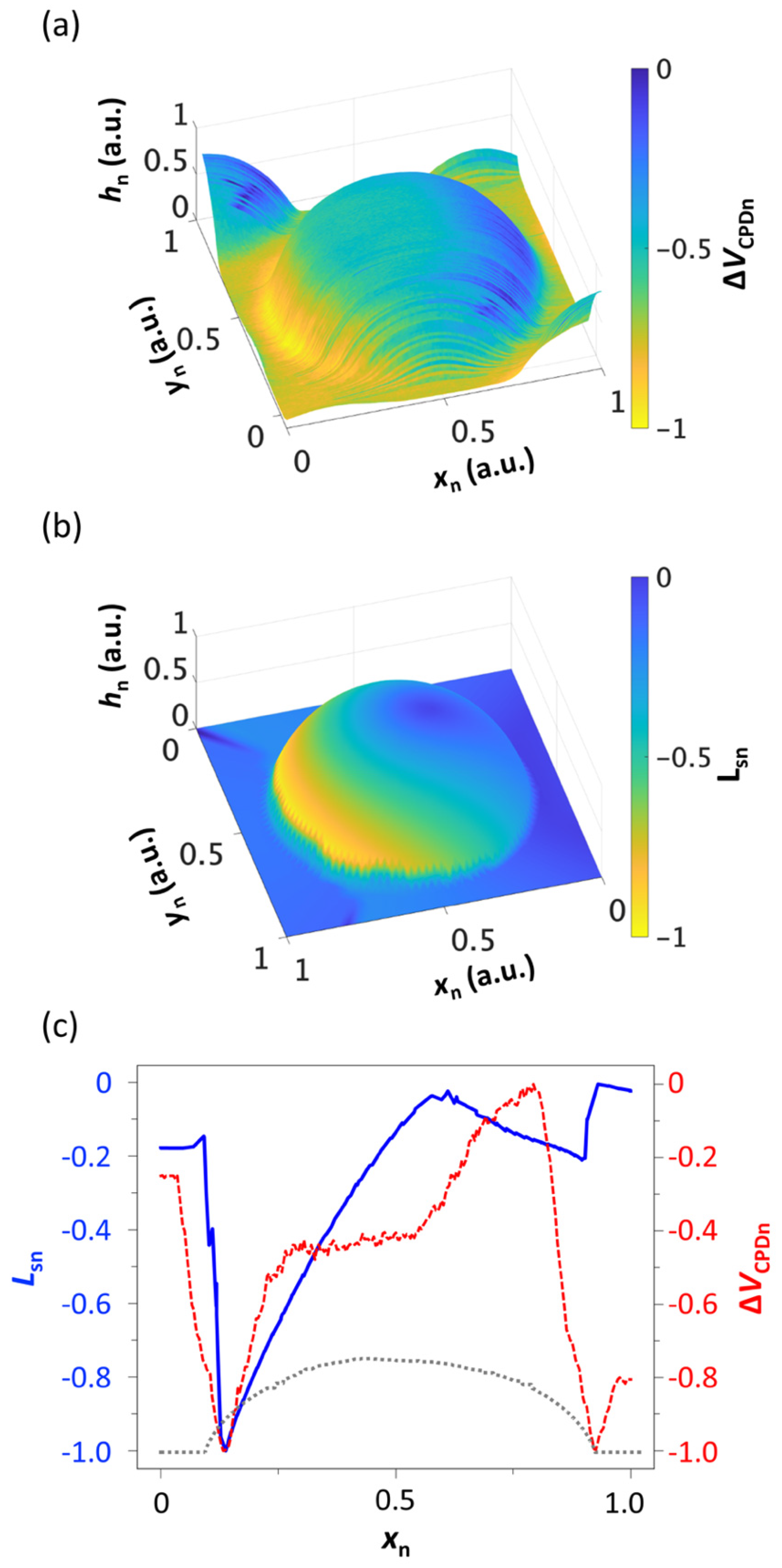
2.3. Surface Charge Density Estimation
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jacobs, H.O.; Campbell, S.A.; Steward, M.G. Approaching nanoxerography: The use of electrostatic forces to position nanoparticles with 100 nm scale resolution. Adv. Mater. 2002, 14, 1553–1557. [Google Scholar] [CrossRef]
- Palleau, E.; Ressier, L. Combinatorial Particle Patterning by Nanoxerography. Adv. Funct. Mater. 2018, 28, 4–7. [Google Scholar] [CrossRef]
- Kuang, S.Y.; Zhu, G.; Wang, Z.L. Triboelectrification-Enabled Self-Powered Data Storage. Adv. Sci. 2018, 5, 1700658. [Google Scholar] [CrossRef]
- Vallem, V.; Sargolzaeiaval, Y.; Ozturk, M.; Lai, Y.C.; Dickey, M.D. Energy Harvesting and Storage with Soft and Stretchable Materials. Adv. Mater. 2021, 33, 2004832. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Tcho, I.W.; Jin, I.K.; Park, S.J.; Jeon, S.B.; Kim, W.G.; Cho, H.S.; Lee, H.S.; Jeoung, S.C.; Choi, Y.K. Direct-laser-patterned friction layer for the output enhancement of a triboelectric nanogenerator. Nano Energy 2017, 35, 379–386. [Google Scholar] [CrossRef]
- Lee, B.Y.; Kim, D.H.; Park, J.; Park, K.I.; Lee, K.J.; Jeong, C.K. Modulation of surface physics and chemistry in triboelectric energy harvesting technologies. Sci. Technol. Adv. Mater. 2019, 20, 758–773. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Xie, Y.; Niu, S.; Lin, L.; Liu, C.; Zhou, Y.S.; Wang, Z.L. Maximum surface charge density for triboelectric nanogenerators achieved by ionized-air injection: Methodology and theoretical understanding. Adv. Mater. 2014, 26, 6720–6728. [Google Scholar] [CrossRef]
- Li, S.; Fan, Y.; Chen, H.; Nie, J.; Liang, Y.; Tao, X.; Zhang, J.; Chen, X.; Fu, E.; Wang, Z.L. Manipulating the triboelectric surface charge density of polymers by low-energy helium ion irradiation/implantation. Energy Environ. Sci. 2020, 13, 896–907. [Google Scholar] [CrossRef]
- Ko, Y.H.; Nagaraju, G.; Lee, S.H.; Yu, J.S. PDMS-based triboelectric and transparent nanogenerators with ZnO nanorod arrays. ACS Appl. Mater. Interfaces 2014, 6, 6631–6637. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Peer, A.; Cho, I.; Biswas, R.; Kim, J. Replica molding-based nanopatterning of tribocharge on elastomer with application to electrohydrodynamic nanolithography. Nat. Commun. 2018, 9, 974. [Google Scholar] [CrossRef] [PubMed]
- Ji, M.G.; Li, Q.; Biswas, R.; Kim, J. Stability and temporal decay of nanopatterned tribocharge on nanotextured elastomer surfaces. Nano Energy 2021, 79, 105441. [Google Scholar] [CrossRef]
- Li, Q.; Cho, I.; Biswas, R.; Kim, J. Nanoscale Modulation of Friction and Triboelectrification via Surface Nanotexturing. Nano Lett. 2019, 19, 850–856. [Google Scholar] [CrossRef]
- Cho, I.; Li, Q.; Biswas, R.; Kim, J. A framework for glass-box physics rule learner and its application to nano-scale phenomena. Commun. Phys. 2020, 3, 1–9. [Google Scholar] [CrossRef]
- Wolfe, D.B.; Love, J.C.; Whitesides, G.M. Nanostructures Replicated by Polymer Molding. In Encyclopedia of Nanoscience and Nanotechnology; Marcel Dekker, Inc.: New York, NY, USA, 2004; pp. 2657–2666. [Google Scholar]
- El Khoury, D.; Arinero, R.; Laurentie, J.C.; Castellon, J. Nanoscale surface charge detection in epoxy resin materials using electrostatic force spectroscopy. AIP Adv. 2016, 6, 035318. [Google Scholar] [CrossRef]
- Zou, H.; Zhang, Y.; Guo, L.; Wang, P.; He, X.; Dai, G.; Zheng, H.; Chen, C.; Wang, A.C.; Xu, C.; et al. Quantifying the triboelectric series. Nat. Commun. 2019, 10, 1427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, F.R.; Lin, L.; Zhu, G.; Wu, W.; Zhang, R.; Wang, Z.L. Transparent triboelectric nanogenerators and self-powered pressure sensors based on micropatterned plastic films. Nano Lett. 2012, 12, 3109–3114. [Google Scholar] [CrossRef] [Green Version]
- Mannsfeld, S.C.B.; Tee, B.C.K.; Stoltenberg, R.M.; Chen, C.V.H.H.; Barman, S.; Muir, B.V.O.; Sokolov, A.N.; Reese, C.; Bao, Z. Highly sensitive flexible pressure sensors with microstructured rubber dielectric layers. Nat. Mater. 2010, 9, 859–864. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Qian, S.; Yu, J.; Zhang, Q.; Yuan, Z.; Sang, S.; Zhou, X.; Sun, L. Flexible and wearable PDMS-based triboelectric nanogenerator for self-powered tactile sensing. Nanomaterials 2019, 9, 1304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, X.; Song, Y.; Su, Z.; Chen, H.; Cheng, X.; Zhang, J.; Han, M.; Zhang, H. Flexible fiber-based hybrid nanogenerator for biomechanical energy harvesting and physiological monitoring. Nano Energy 2017, 38, 43–50. [Google Scholar] [CrossRef]
- Seung, W.; Gupta, M.K.; Lee, K.Y.; Shin, K.S.; Lee, J.H.; Kim, T.Y.; Kim, S.; Lin, J.; Kim, J.H.; Kim, S.W. Nanopatterned textile-based wearable triboelectric nanogenerator. ACS Nano 2015, 9, 3501–3509. [Google Scholar] [CrossRef] [PubMed]
- Kantorovich, L.N.; Livshits, A.I.; Stoneham, M. Electrostatic energy calculation for the interpretation of scanning probe microscopy experiments. J. Phys. Condens. Matter 2000, 12, 795–814. [Google Scholar] [CrossRef]
- Neff, J.L.; Rahe, P. Insights into Kelvin probe force microscopy data of insulator-supported molecules. Phys. Rev. B-Condens. Matter Mater. Phys. 2015, 91, 1–11. [Google Scholar] [CrossRef]
- Sadeghi, A.; Baratoff, A.; Ghasemi, S.A.; Goedecker, S.; Glatzel, T.; Kawai, S.; Meyer, E. Multiscale approach for simulations of Kelvin probe force microscopy with atomic resolution. Phys. Rev. B 2012, 86, 75407. [Google Scholar] [CrossRef] [Green Version]
- Orihuela, M.F.; Somoza, A.M.; Colchero, J.; Ortuño, M.; Palacios-Lidón, E. Localized charge imaging with scanning Kelvin probe microscopy. Nanotechnology 2017, 28, 025703. [Google Scholar] [CrossRef]
- Sadeghi, A. Precise Modeling of Electrostatic Interactions with Dielectric Samples in Kelvin Probe Force Microscopy; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; Volume 65, ISBN 9783319756875. [Google Scholar]
- Goswami, A.; Alam, K.M.; Kumar, P.; Kar, P.; Thundat, T.; Shankar, K. Mapping the surface potential, charge density and adhesion of cellulose nanocrystals using advanced scanning probe microscopy. Carbohydr. Polym. 2020, 246, 116393. [Google Scholar] [CrossRef] [PubMed]
- Riedel, C.; Arinero, R.; Tordjeman, P.; Ramonda, M.; Lévêque, G.; Schwartz, G.A.; De Oteyza, D.G.; Alegria, A.; Colmenero, J. Determination of the nanoscale dielectric constant by means of a double pass method using electrostatic force microscopy. J. Appl. Phys. 2009, 106. [Google Scholar] [CrossRef] [Green Version]
- Portes, L.; Girard, P.; Arinero, R.; Ramonda, M. Force gradient detection under vacuum on the basis of a double pass method. Rev. Sci. Instrum. 2006, 77. [Google Scholar] [CrossRef]


| Leading Edge (LE) | Trailing Edge (TE) | Interstitial (IS) Region | |
|---|---|---|---|
| EFM | 0.0337 1 | 0.0268 | 0.0304 |
| KPFM/CAPSOL | 0.1045 | 0.0136 | 0.0545 |
| Ratio | 3.101 | 0.507 | 1.793 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, M.G.; Bazroun, M.; Cho, I.H.; Slafer, W.D.; Biswas, R.; Kim, J. Mechano-Triboelectric Analysis of Surface Charge Generation on Replica-Molded Elastomeric Nanodomes. Micromachines 2021, 12, 1460. https://doi.org/10.3390/mi12121460
Ji MG, Bazroun M, Cho IH, Slafer WD, Biswas R, Kim J. Mechano-Triboelectric Analysis of Surface Charge Generation on Replica-Molded Elastomeric Nanodomes. Micromachines. 2021; 12(12):1460. https://doi.org/10.3390/mi12121460
Chicago/Turabian StyleJi, Myung Gi, Mohammed Bazroun, In Ho Cho, W. Dennis Slafer, Rana Biswas, and Jaeyoun Kim. 2021. "Mechano-Triboelectric Analysis of Surface Charge Generation on Replica-Molded Elastomeric Nanodomes" Micromachines 12, no. 12: 1460. https://doi.org/10.3390/mi12121460
APA StyleJi, M. G., Bazroun, M., Cho, I. H., Slafer, W. D., Biswas, R., & Kim, J. (2021). Mechano-Triboelectric Analysis of Surface Charge Generation on Replica-Molded Elastomeric Nanodomes. Micromachines, 12(12), 1460. https://doi.org/10.3390/mi12121460







