An Investigation on a Novel 3-RCU Flexible Micromanipulator
Abstract
1. Introduction
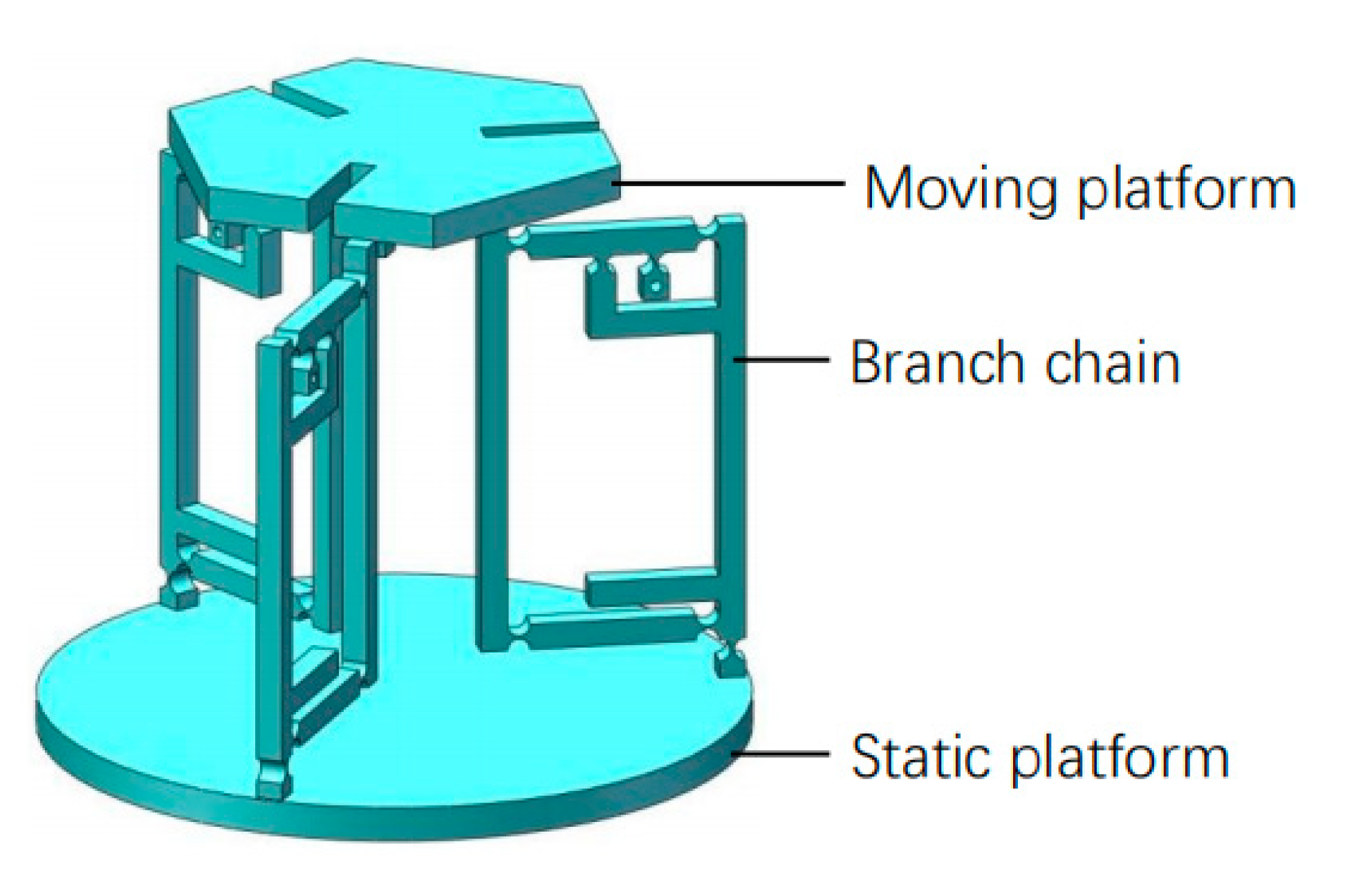
2. The Overall Design of Flexible Micro-Operation Platform
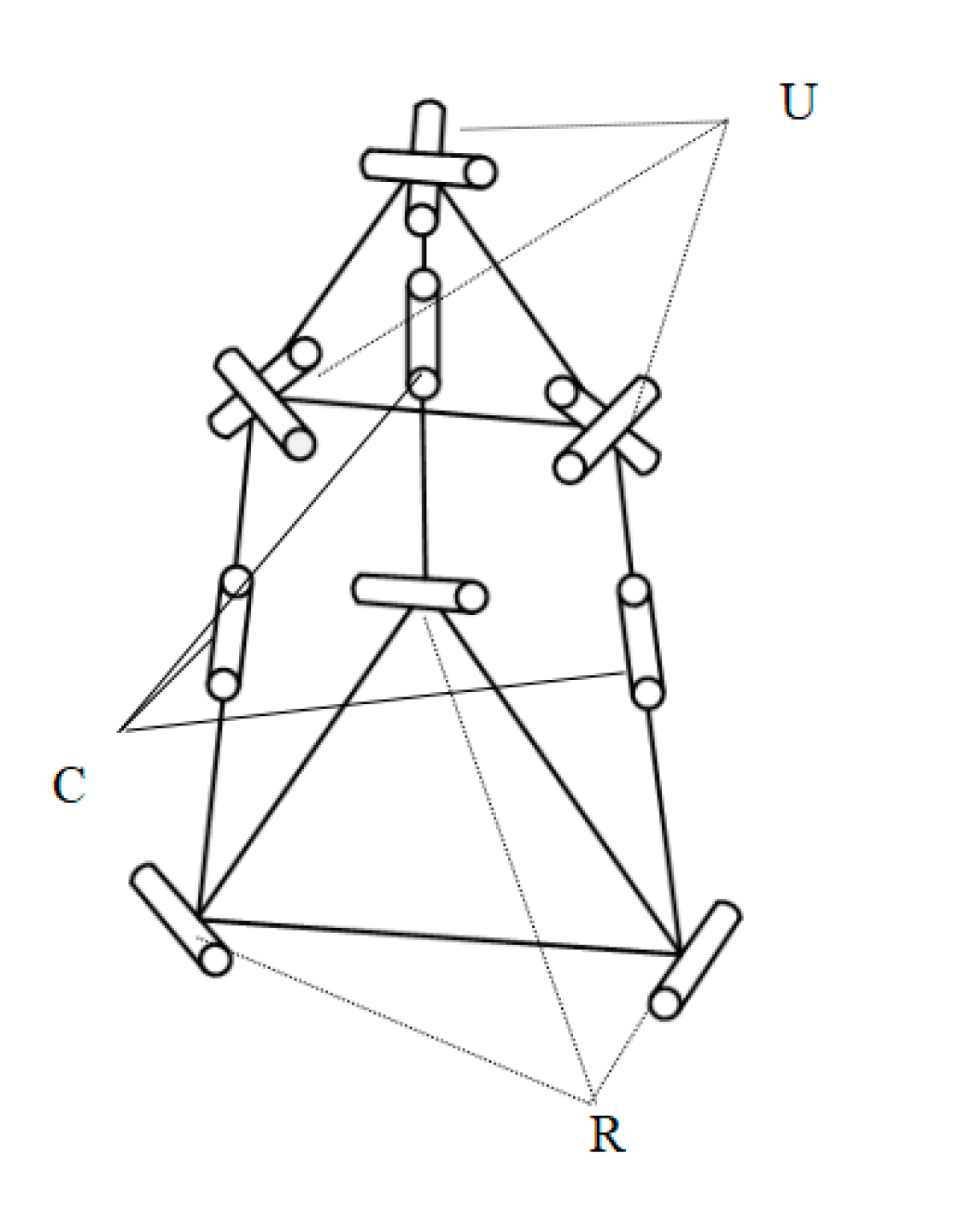
2.1. Structural Design of the Platform
2.2. Calculation of Platform Degrees of Freedom
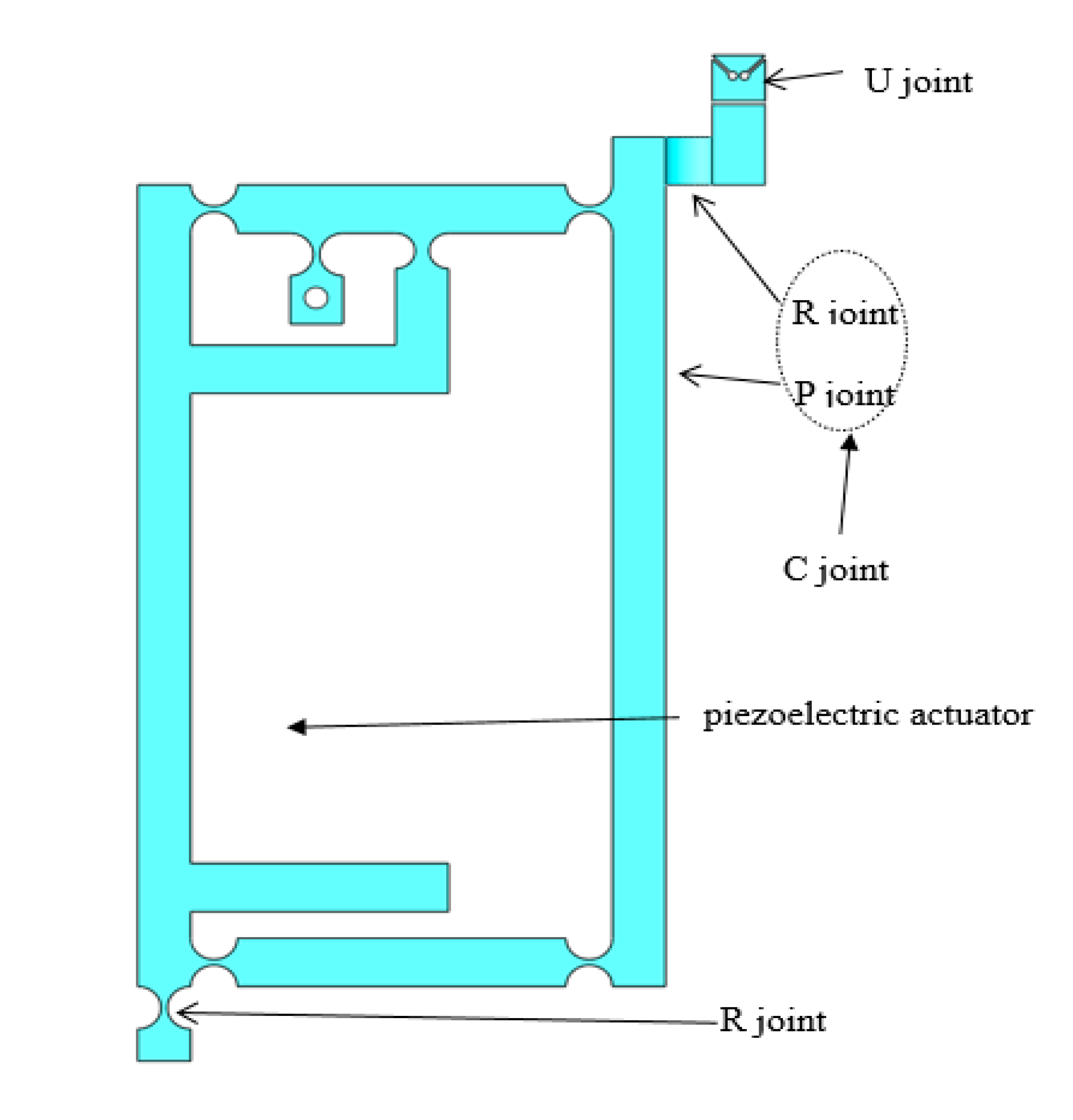
3. The Design of Branch Chain
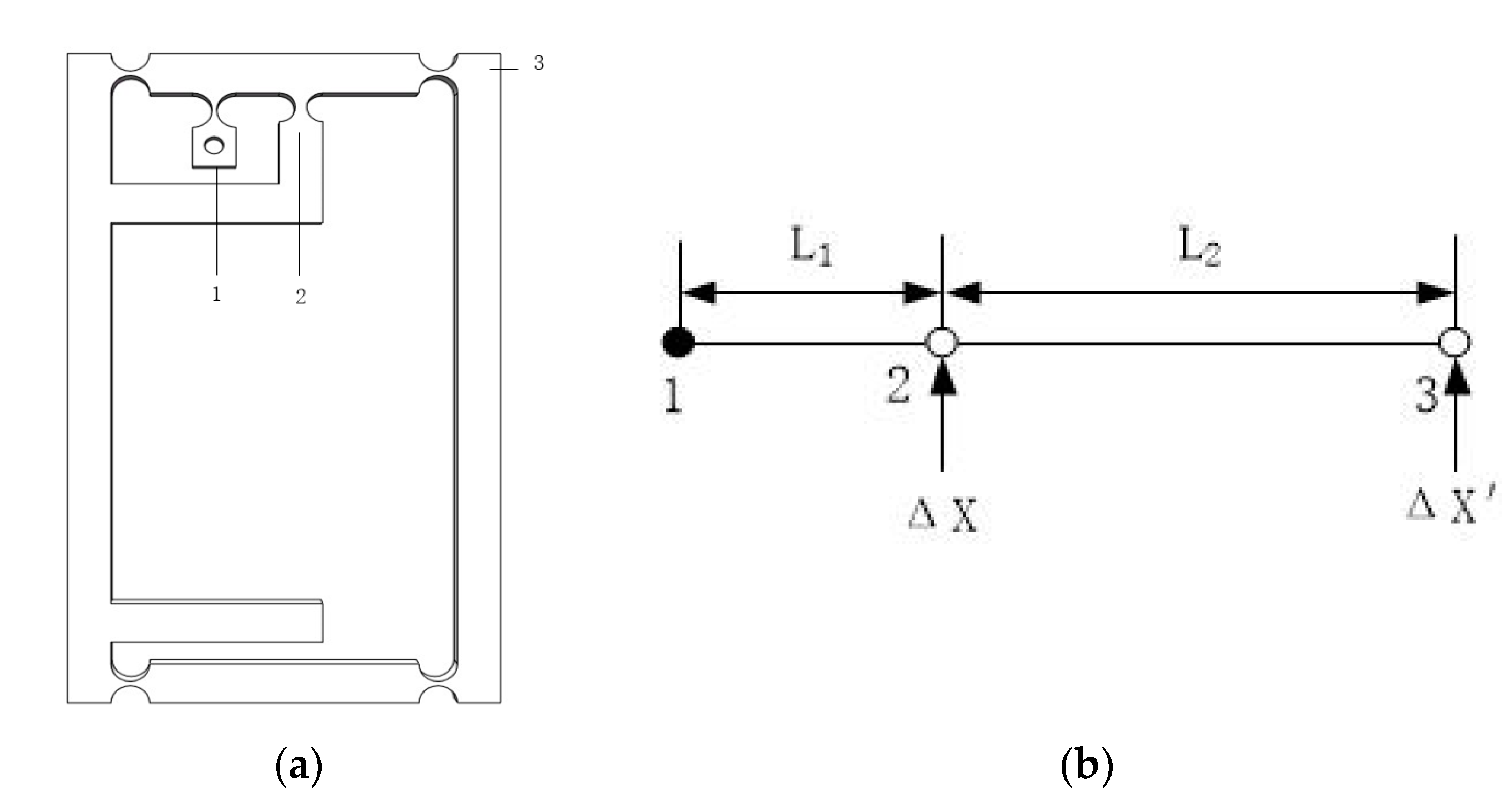
3.1. Branch Chain Structure Design
3.2. Design of Amplification Mechanism
4. Finite Element Analysis
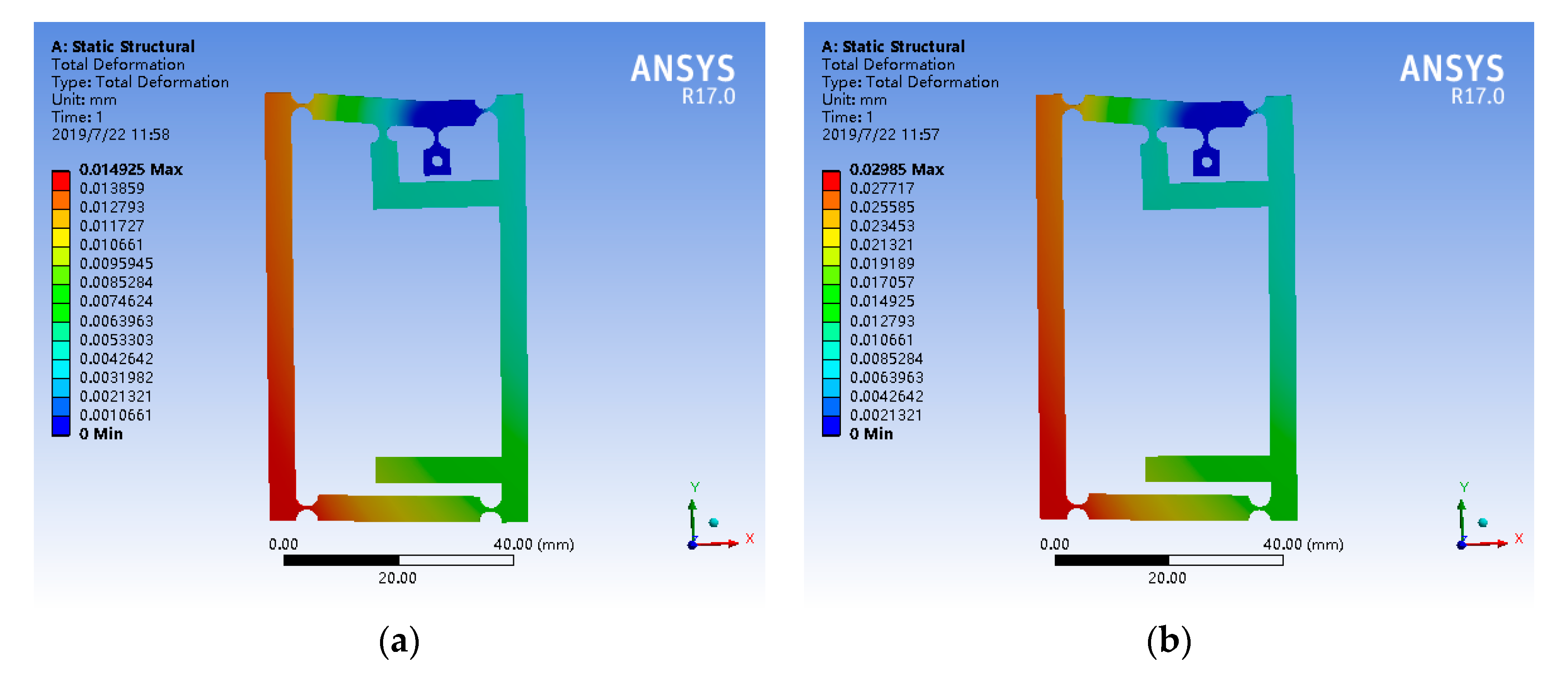
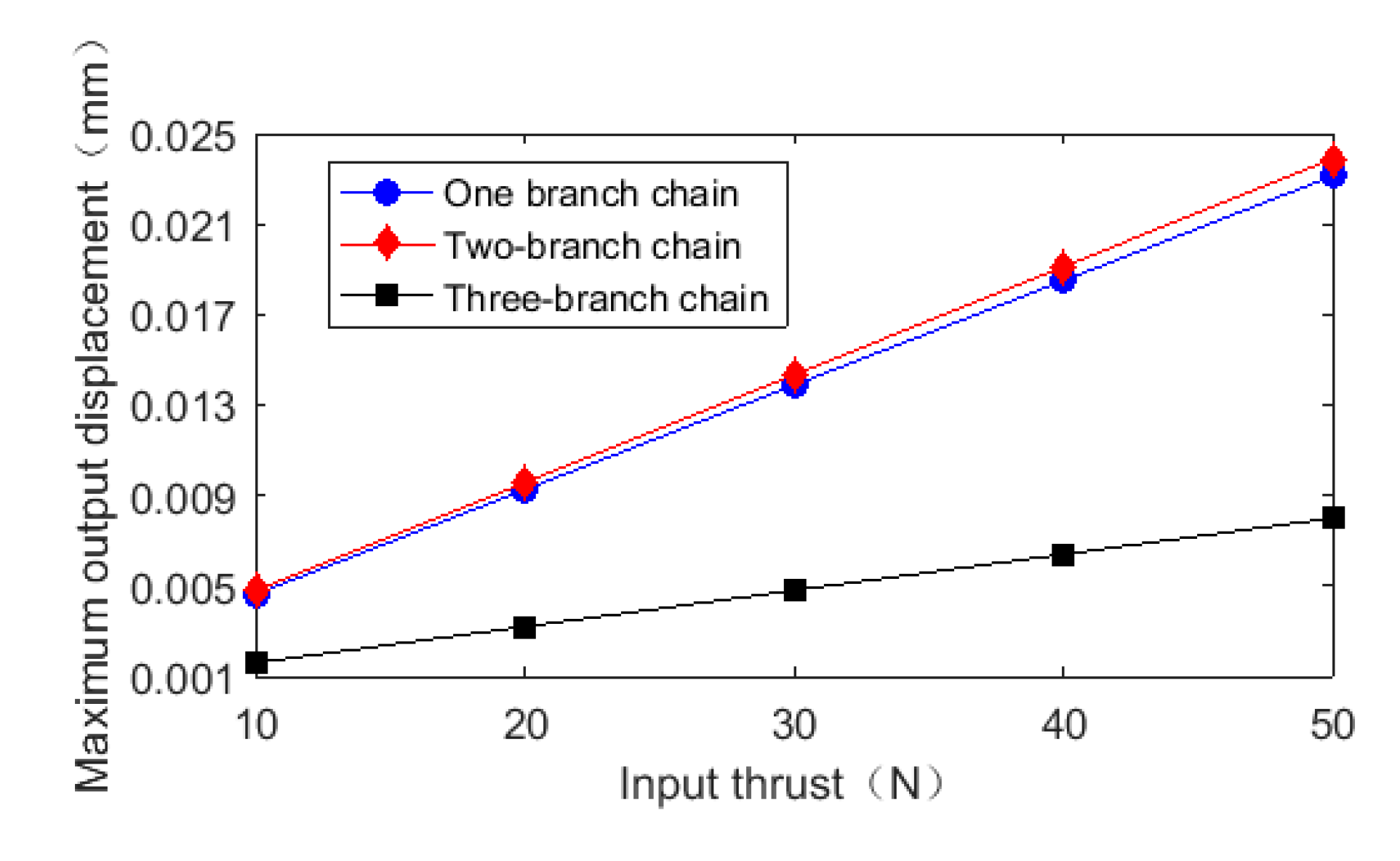
4.1. Simulation Analysis of Amplification Mechanism
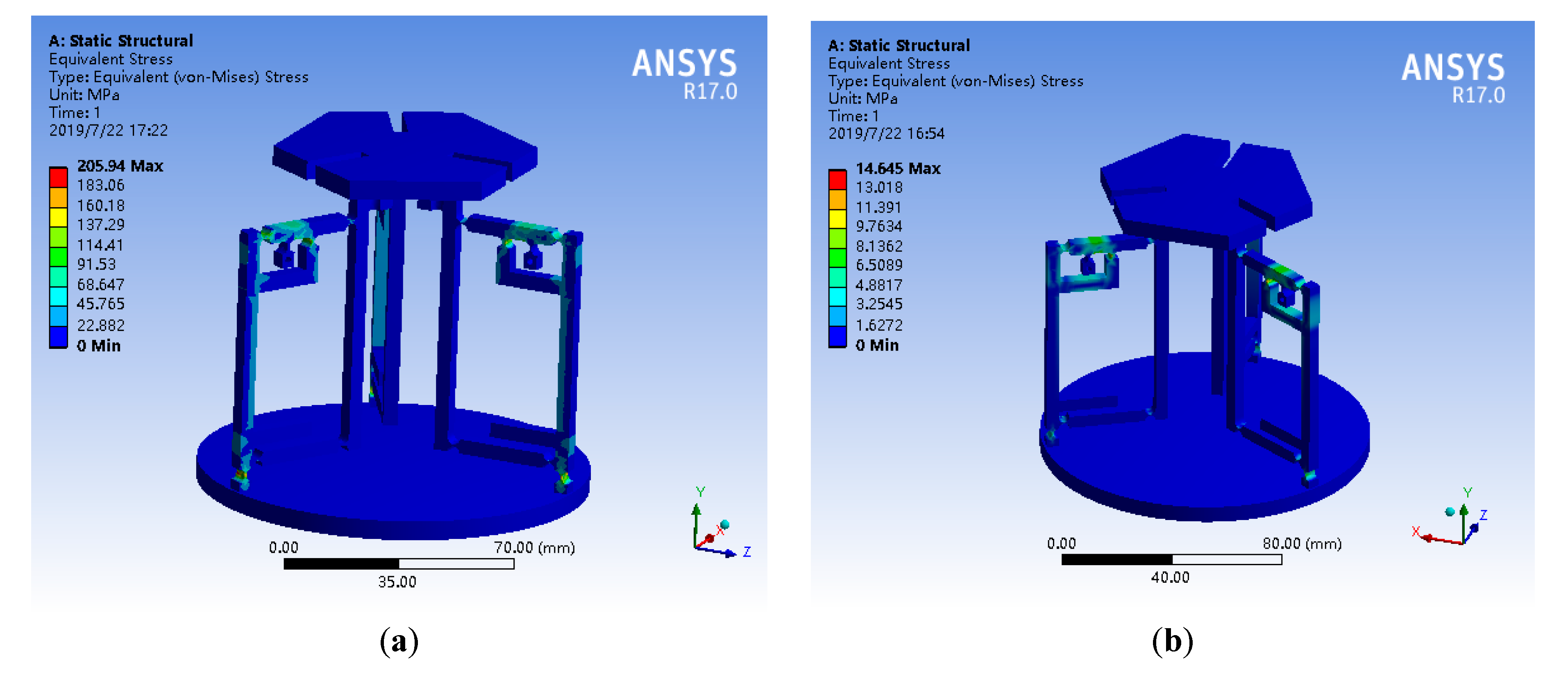
4.2. Verification of Material Properties Selected for the Platform
4.3. Modal Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, Y.M.; Tang, H.; Xu, Q.S. Development trend of micro-manipulation robot technology for biomedical applications. Chin. J. Mech. Eng. 2011, 47, 1–13. [Google Scholar] [CrossRef]
- Yun, Y.; Xu, Q.S.; Li, Y.M. Progress in parallel micro manipulation robot technology and its application. Chin. J. Mech. Eng. 2008, 44, 12–23. [Google Scholar] [CrossRef]
- Lin, H.B.; Yang, G.Z. Research on a precision positioning stage based on piezoelectric actuators and its validation. Piezoelectr. Acoustoopt. 2015, 37, 1030–1033. [Google Scholar]
- Feng, C.; Liang, Q.K. Design and Analysis of a Type of Three-Degree-of-Freedom Flexible Parallel Precision Positioning Platform; Dissertation; North University of China: Taiyuan, China, 2018. [Google Scholar]
- Howell, L.L. Compliant Mechanisms; Wiley Inter-Science: New York, NY, USA, 2001. [Google Scholar]
- Singh, A.V.; Hasandadansari, M.; Wang, S.; Laux, P.; Luch, A.; Kumar, A.; Patil, R.; Nussberger, S. The adoption of three-dimensional additive manufacturing from biomedical material design to 3d organ printing. Appl. Sci. 2019, 9, 811–823. [Google Scholar] [CrossRef]
- Zheng, W.Z.; Xin, H.B.; Zhao, F. Design of piezoelectric driven micro displacement amplification mechanism. Mech. Sci. Technol. 2003, 22, 966–967. [Google Scholar]
- Chen, Z.M.; Zhang, Y.; Huang, K. A symmetrical two-revolute-one-shift parallel mechanism without accompanying motion. J. Mech. Eng. 2016, 52, 15–23. [Google Scholar]
- Ding, B.X.; Xiao, X.; Li, Y.M. Design of large stroke parallel 3-DOF flexible micro-operating platform. J. Tianjin Univ. Technol. 2015, 31, 28–32. [Google Scholar]
- Xu, H.Y.; Li, Y.M.; Li, X.C. Design and analysis of spatial 3-DOF fully flexible micro motion platform. J. Tian Jin Univ. Technol. 2018, 34, 31–36. [Google Scholar]
- Tang, G.; Zou, P.J.; Xu, G.Y. Flexible hinge amplifying mechanism based on triangle and lever principle. Mech. Des. Res. 2018, 6, 46–49. [Google Scholar]
- Ma, L.; Xie, W.; Liu, B. Design of flexible hinge micro positioning platform. Opt. Precis. Eng. 2014, 22, 338–345. [Google Scholar]
- Meng, D.S.; Li, Y.M. Design and analysis of a new micro-displacement amplifier mechanism. J. Tianjin Univ. Technol. 2015, 31, 5–9. [Google Scholar]
- Li, Y.M.; Xiao, X.; Tang, H. Design and analysis of a new 3-DOF large stroke micro-positioning platform. J. Mech. Eng. 2013, 49, 48–54. [Google Scholar] [CrossRef]
- Tanikawa, T.; Arai, T. Two-finger micro hand. In Proceedings of the IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; pp. 1974–1679. [Google Scholar]
- Dong, W.; Sun, L.N.; Du, Z.J. Design of a precision compliant parallel position driven by dual Piezoelectric Actuator. J. Sens. Actuator 2017, 135, 250–256. [Google Scholar] [CrossRef]
- Yu, J.J.; Lu, D.F.; Xie, Y. Constraint design principle of large-displacement flexure systems. In Proceedings of the International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale, Taipei, Taiwan, 27–31 October 2014; pp. 255–260. [Google Scholar]
- Zhao, J.; Li, Y.M.; Xu, H.Y. Design and Analysis of a novel space flexible micro manipulator platform. In Proceedings of the IEEE The World Congress on Intelligent Control and Automation, Changsha, China, 4–8 July 2018; pp. 199–204. [Google Scholar]
- Xu, H.Y.; Li, Y.M.; Li, X.C. Kinematics analysis of space 3-DOF flexible parallel micro-motion platform. Manuf. Autom. 2018, 40, 23–26. [Google Scholar]
- Chen, X.G.; Li, Y.M. Design and analysis of a new high precision decoupled XY compact parallel micromanipulator. Micromachines 2017, 8, 82–94. [Google Scholar] [CrossRef]
- Chebbi, A.-H.; Affi, Z.; Romdhane, L. Prediction of the pose errors produced by joints clearance for a 3-UPU parallel robot. Mech. Mach. Theory 2009, 44, 1768–1783. [Google Scholar] [CrossRef]
- Huang, Z.; Zhao, Y.S.; Zhao, T.S. Advanced Spatial Mechanism; Higher Education Press: Beijing, China, 2014. [Google Scholar]
- Yu, J.J.; Bi, S.S. Flexible Design-Analysis and Synthesis of Flexible Mechanisms; Beijing Higher Education Press: Beijing, China, 2018. [Google Scholar]
- Hu, J.F.; Xu, G.Y. Comparison of performance of three-degree micro-positioning platform with four different flexible hinges. Mach. Des. Manuf. 2014, 2, 127–129. [Google Scholar]
- Wang, C.T.; Wang, Y.Q.; Yang, X.F.; Liu, Y.F. The stiffness characteristics of three four-bar flexure hinge mechanisms are analyzed based on ANSYS. Mech. Transm. 2017, 41, 59–63. [Google Scholar]
- Tian, Y.; Shirinzadeh, B.; Dawei, Z.; Alici, G. Development and dynamic modelling of a flexure-based scott-russell mechanism for nona manipulation. Mech. Syst. Signal Process. 2009, 23, 957–978. [Google Scholar] [CrossRef]
- Tian, Y.; Shirinzadeh, B.; Zhang, D.W.; Alici, G. Design and forward kinematics of the compliant micro-manipulator with lever mechanism. Precis. Eng. 2009, 33, 466–475. [Google Scholar] [CrossRef]
- Tang, Y.S.; Li, Y.M. Design and Analysis of Double Flexible Platform; Tianjin University of Technology: Tianjin, China, 2017. [Google Scholar]
- Yu, J.J.; Bi, S.S.; Zong, G.G. Research on design technology of fully flexible micro displacement amplifying mechanism. J. Aeronaut. 2004, 25, 74–78. [Google Scholar]
- Wang, N.; Gao, P.; Cui, G.H. Static stiffness and finite element analysis of two parallel mechanisms. J. Hebei Univ. Eng. Nat. Sci. 2013, 30, 87–90. [Google Scholar]
- Zhou, H.Y.; Liang, Q.K.; Liu, G.Q. Design and Analysis of Space 3-DOF Flexible Micro-Motor Control Platform; Hunan University: Changsha, China, 2015. [Google Scholar]
- Ge, J.Z.; Wang, Z.H. Analysis of the working space of the piezoceramic-driven micro-moving parallel robot. Piezoelectr. Acoustoopt. 2008, 30, 627–630. [Google Scholar]
- Zeng, P.; Lei, L.P.; Fang, G. Finite element analysis manual based on ANSYS platform. In Structure Modeling and Analysis; Mechanical Industry Press: Beijing, China, 2011; pp. 1–25. [Google Scholar]
- Li, Y.M.; Li, X.C.; Xu, H.Y.; Ding, B.X. An investigation of the dynamic performance of a new three degree of freedom micro-operating platform. Mach. Des. Manuf. 2019, 12, 255–258. [Google Scholar]
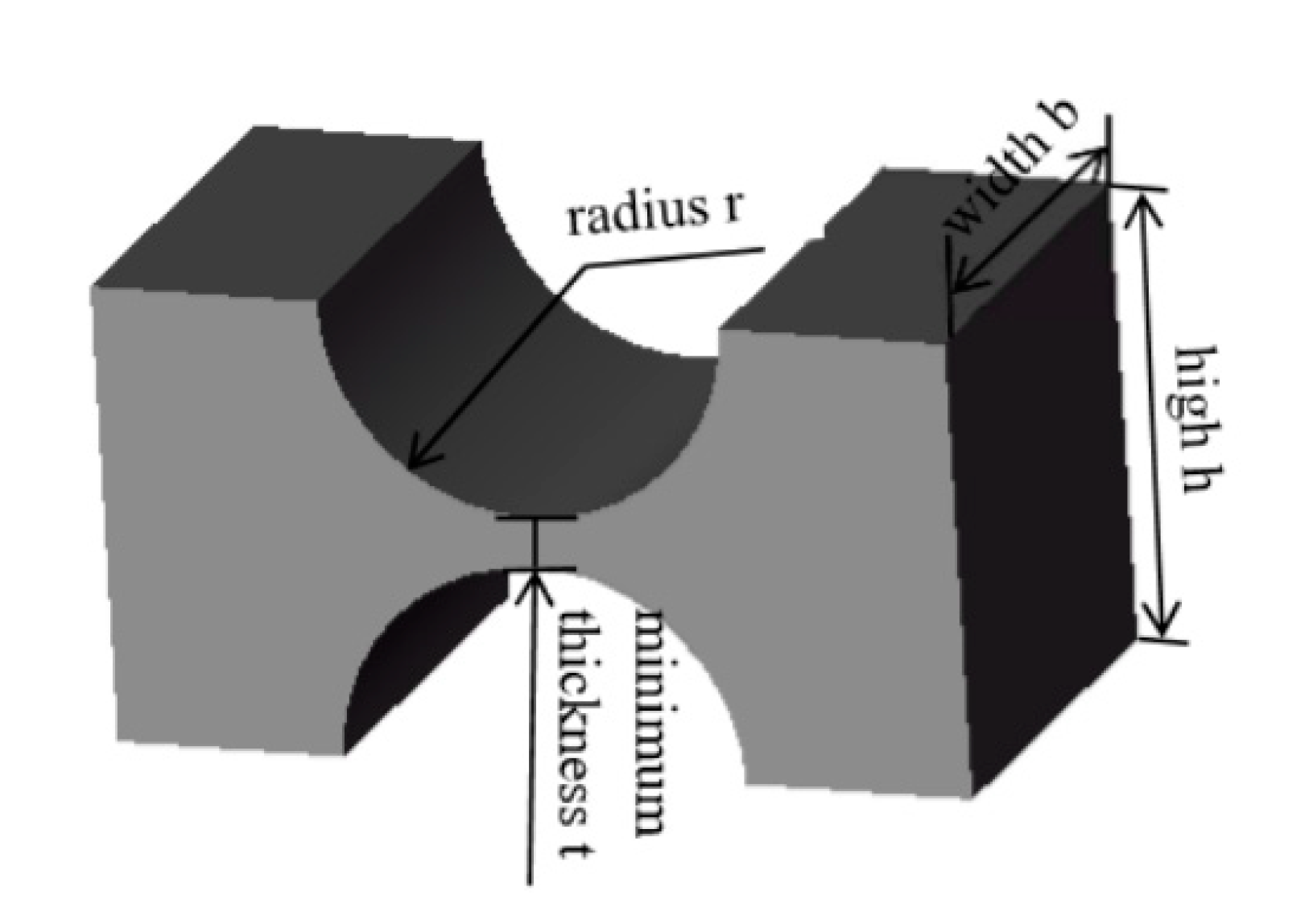

| Parameter | t | r | b | h |
|---|---|---|---|---|
| Value (mm) | 0.5 | 2.0 | 4.5 | 4.5 |
| No. | Natural Frequencies (Hz) | No. | Natural Frequencies (Hz) |
|---|---|---|---|
| 1 | 129.59 | 4 | 518.96 |
| 2 | 176.34 | 5 | 525.30 |
| 3 | 177.17 | 6 | 551.60 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, J.; Li, Y.; Zhuge, L. An Investigation on a Novel 3-RCU Flexible Micromanipulator. Micromachines 2020, 11, 423. https://doi.org/10.3390/mi11040423
Qian J, Li Y, Zhuge L. An Investigation on a Novel 3-RCU Flexible Micromanipulator. Micromachines. 2020; 11(4):423. https://doi.org/10.3390/mi11040423
Chicago/Turabian StyleQian, Junnan, Yangmin Li, and Lukai Zhuge. 2020. "An Investigation on a Novel 3-RCU Flexible Micromanipulator" Micromachines 11, no. 4: 423. https://doi.org/10.3390/mi11040423
APA StyleQian, J., Li, Y., & Zhuge, L. (2020). An Investigation on a Novel 3-RCU Flexible Micromanipulator. Micromachines, 11(4), 423. https://doi.org/10.3390/mi11040423






