A Multiparameter Gas-Monitoring System Combining Functionalized and Non-Functionalized Microcantilevers
Abstract
1. Introduction
2. Materials and Methods
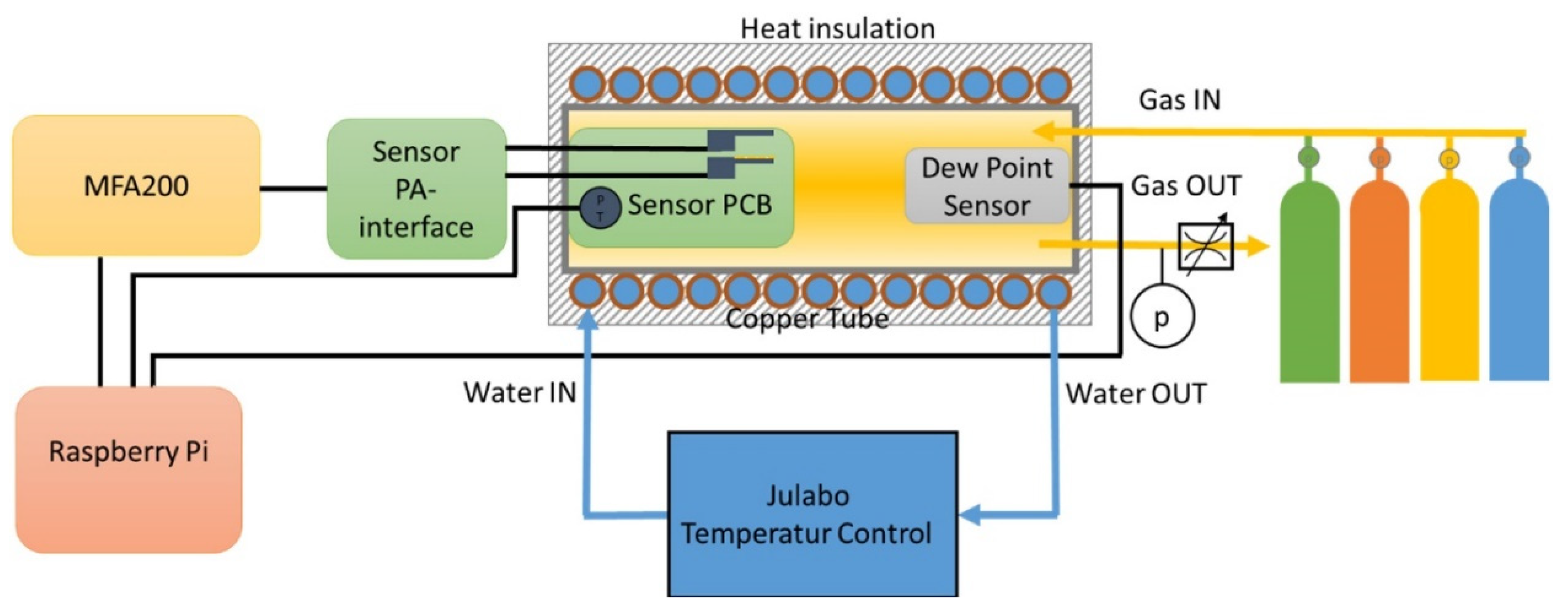
2.1. Experimental Setup
2.1.1. Sensor Printed Circuit Board (PCB) and Gas-Measuring Chamber
2.1.2. Signal Processing
2.1.3. Fluidic Measurements Setup
2.2. Cantilever Functionalization
2.2.1. Hydrophilic Nanoporous Materials
2.2.2. Functionalization Method 1: Oxygen Plasma and Incubation
2.2.3. Functionalization Method 2: Direct Spotting
- Ethanolic suspension 2% wt. of MCM-48 nanoparticles.
- Aqueous suspension 1% wt. of CBV100 crystals. A previous separation by centrifugation is carried out to reduce the particle size below 700 nm.
- Aqueous suspension of PDDA 0.2% wt. was eventually used as intermediate cationic polyelectrolyte to improve the coverage of the surface with MCM-48 spherical nanoparticles by electrostatic interactions.
3. Results
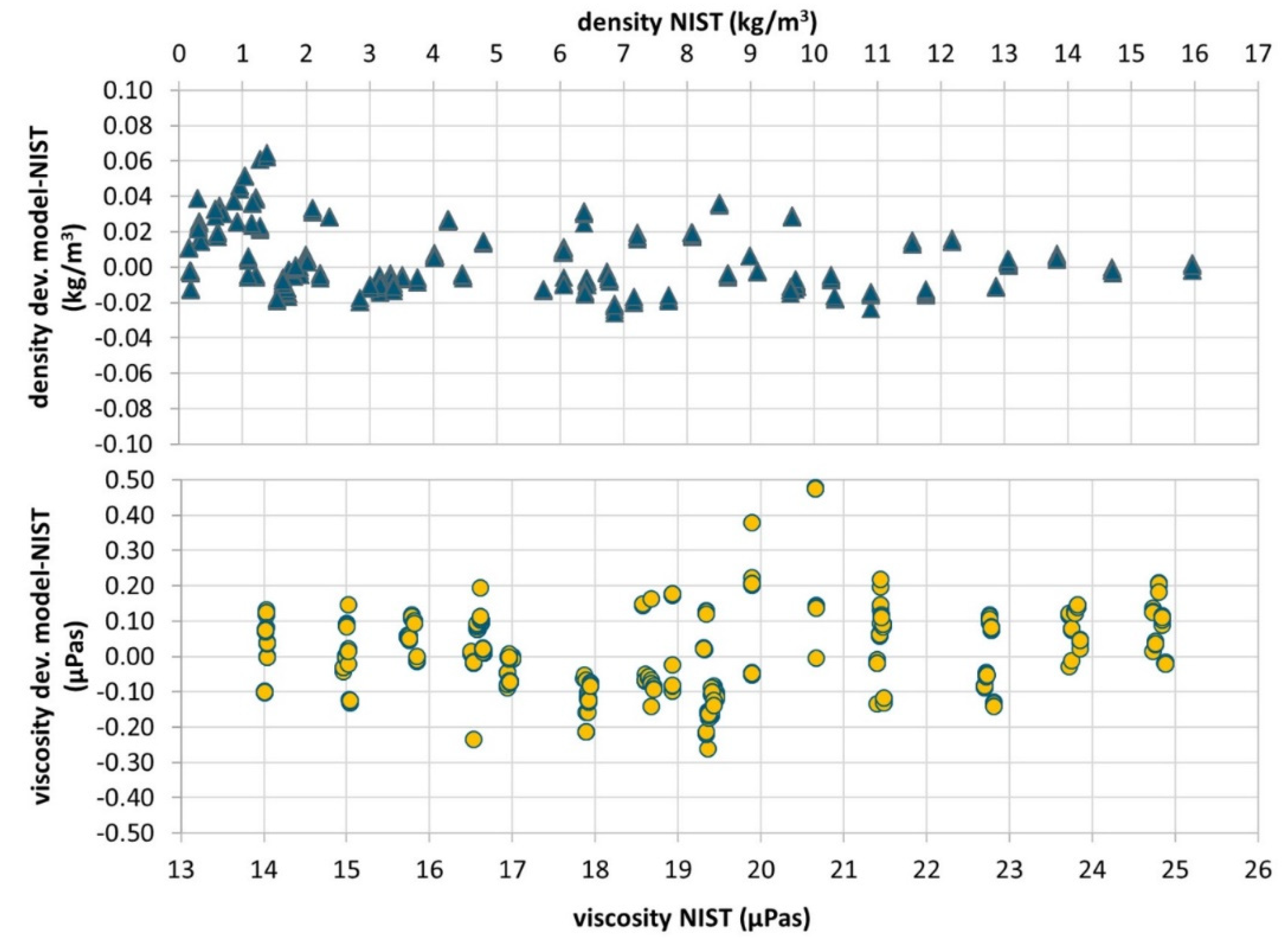
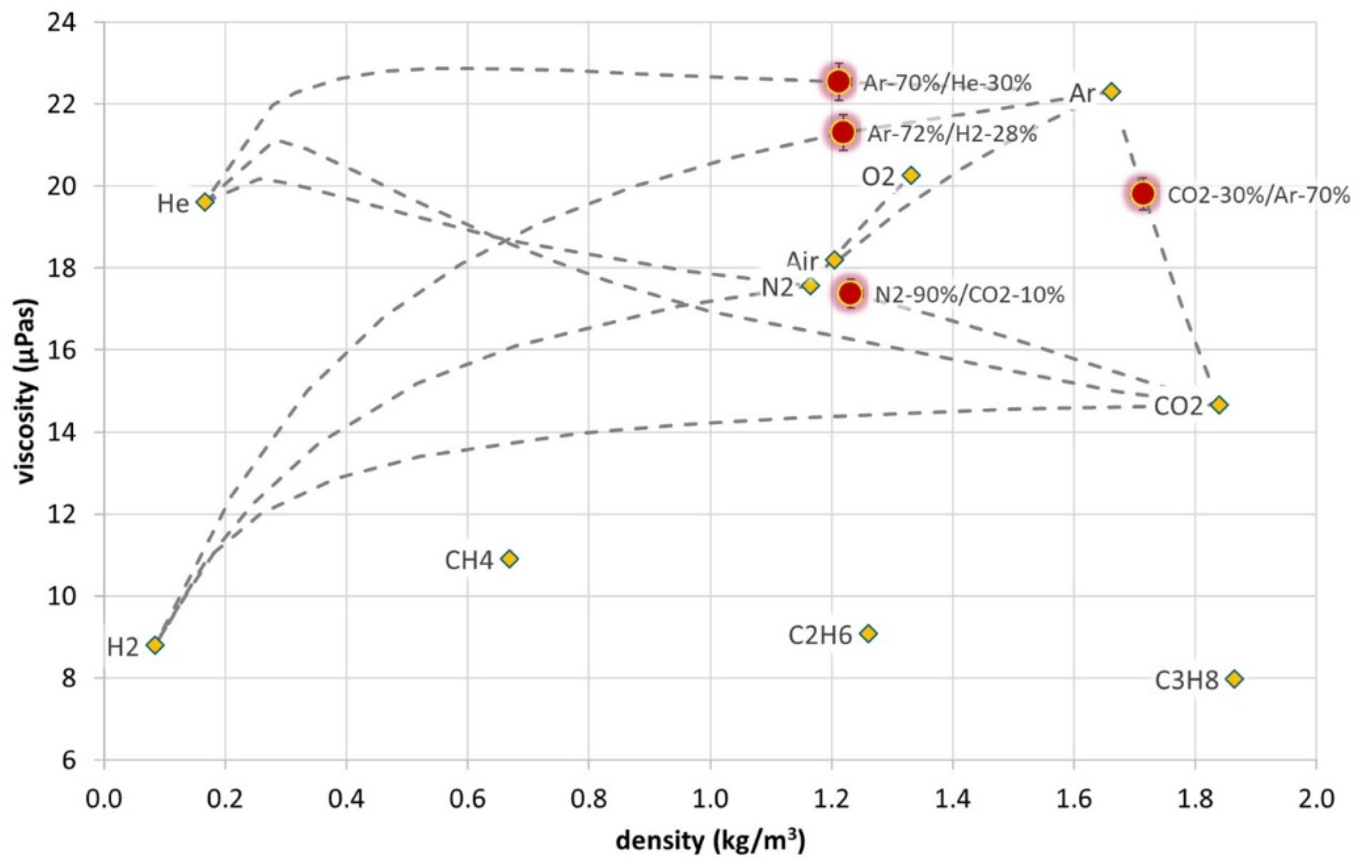
3.1. Density and Viscosity Measurement Results
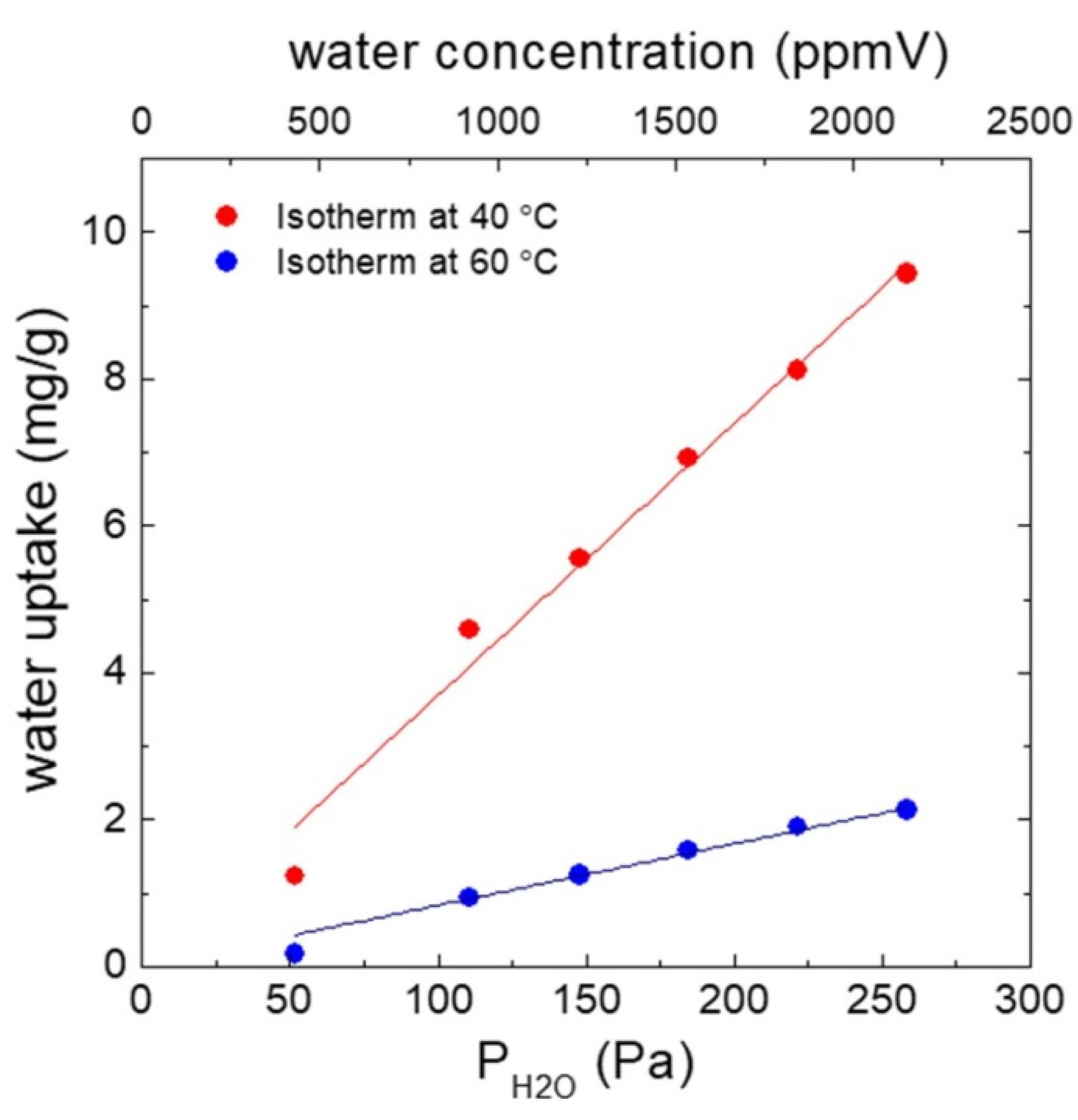
3.2. Humidity Measurement Results
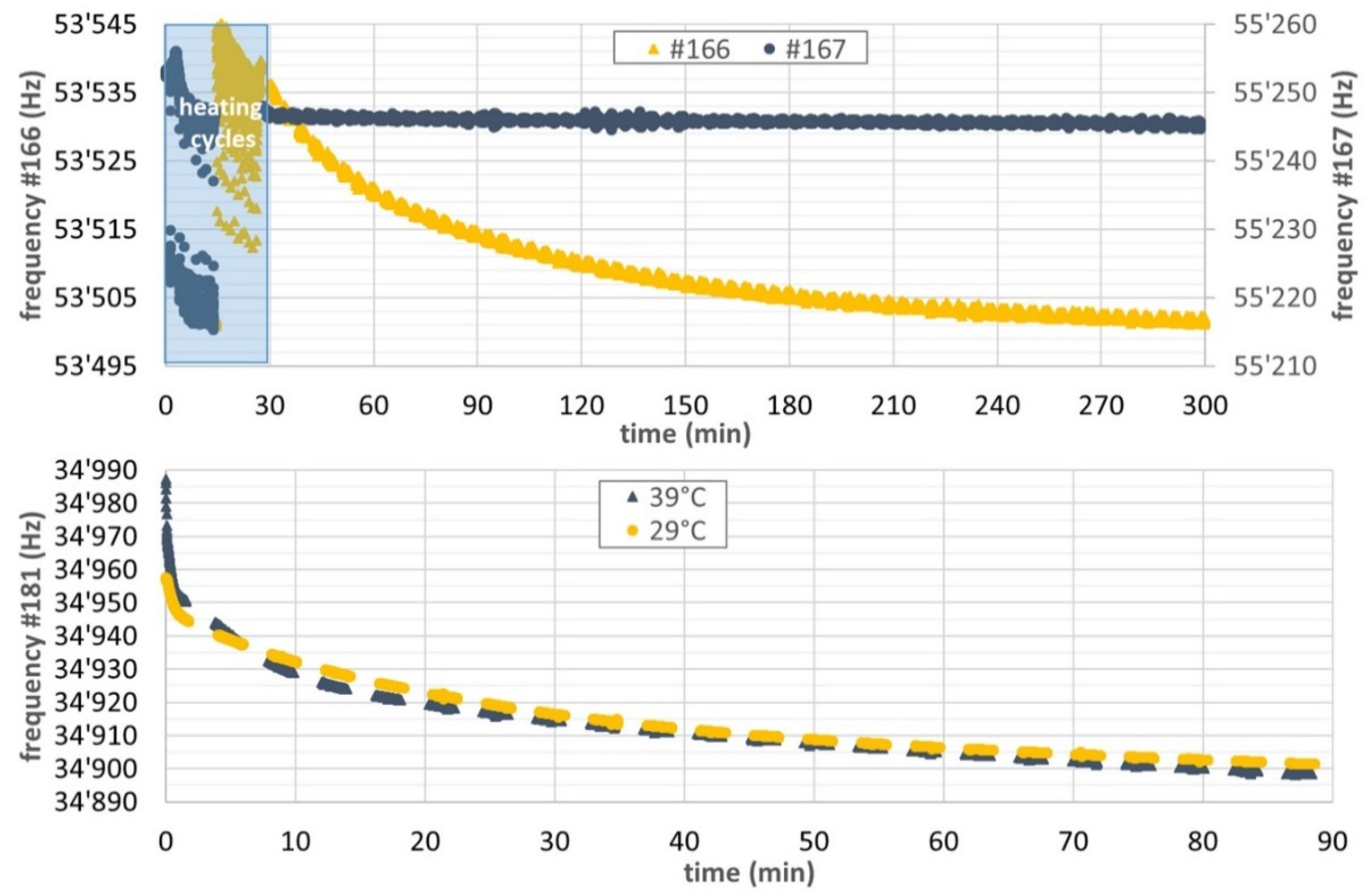
3.2.1. Typical Response of Cantilevers in the Presence of Humidity
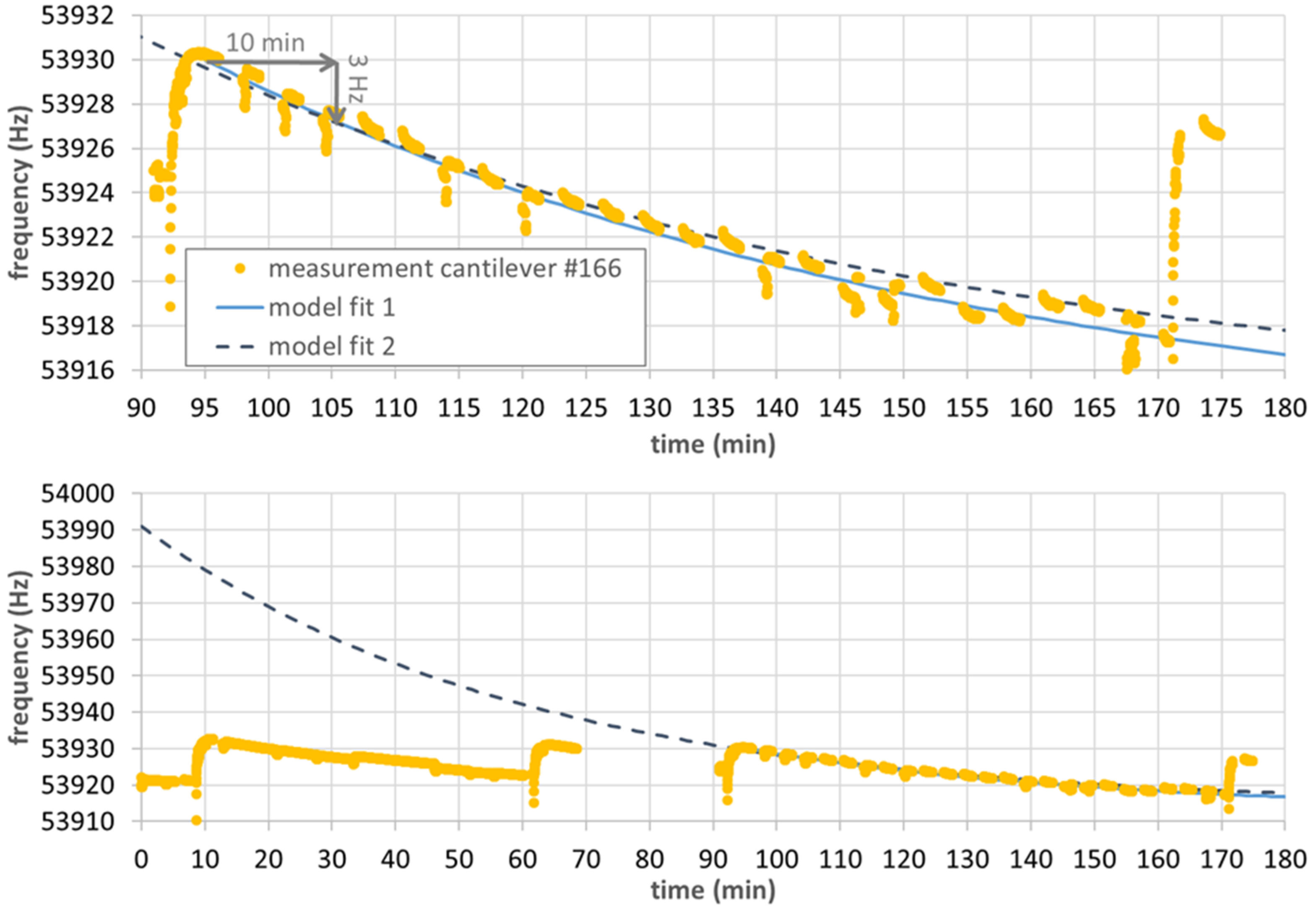
3.2.2. Sensing Approach 1: Dynamic Response after Degassing
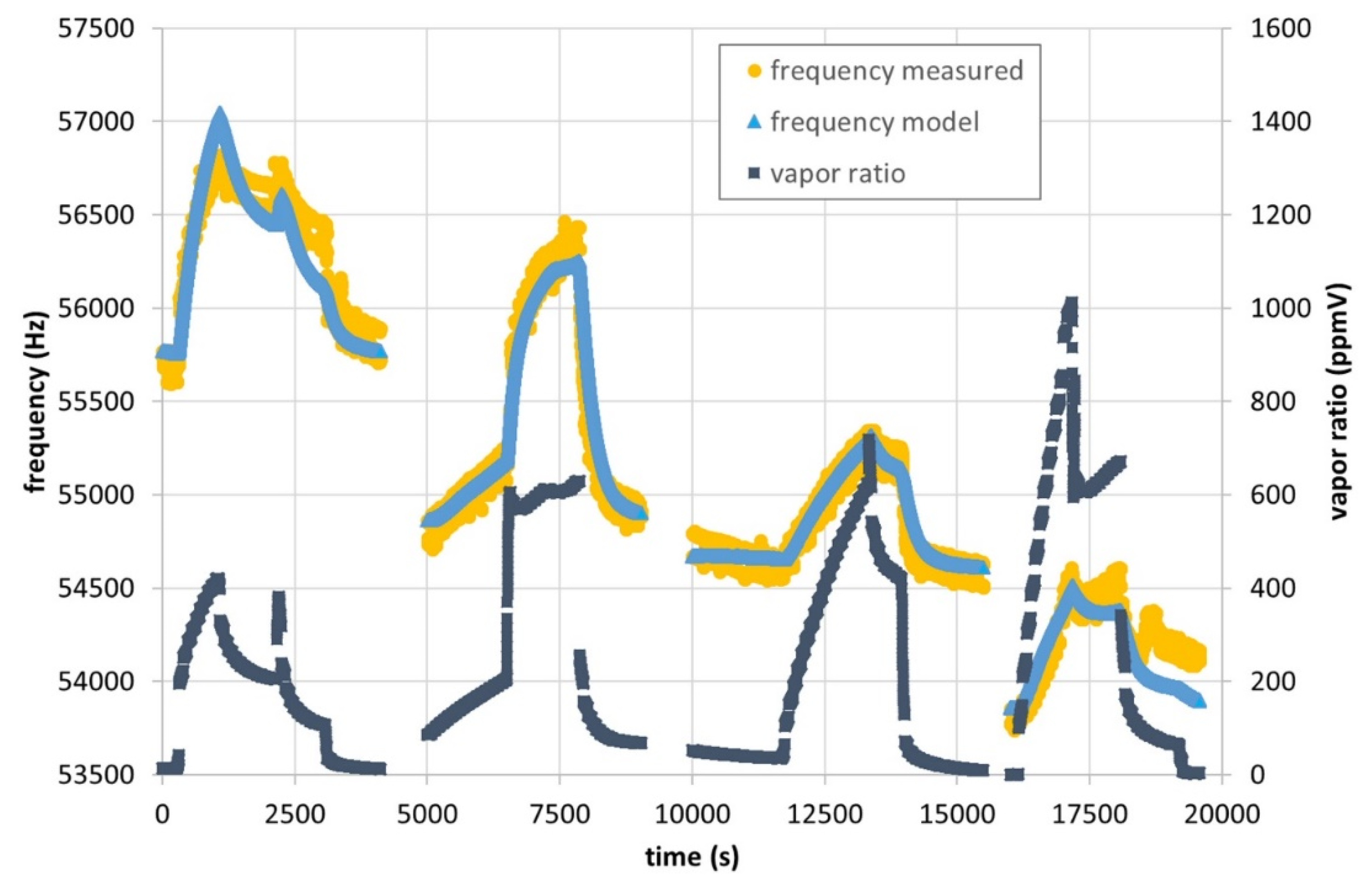
3.2.3. Sensing Approach 2: Instantaneous Response without Previous Degassing
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| silicon | |
| nanoparticles (sorbent) | |
| water molecule | |
| fluid | |
| mass (kg) | |
| volume (m3) | |
| molar mass (kg/mol) | |
| quality factor | |
| resonance frequency of the cantilever (Hz) | |
| with of the cantilever (m) | |
| length of the cantilever (m) | |
| height or thickness (m) | |
| time (s) | |
| density (kg/m3) | |
| η | viscosity (Pa·s) |
| Young’s modulus (Pa) | |
| temperature dependency of Young’s modulus(Pa/K) | |
| sorbate dependency of Young’s modulus per mass of sorbent (Pa) | |
| temperature dependency of the sorbate dependency of Young’s modulus (Pa/K) | |
| ; | constants |
| temperature (K) | |
| pressure (Pa) | |
| universal gas constant ( J/mol/K) | |
| partial pressure of water vapor (Pa) | |
| vapor ratio or vapor concentration (mol/mol = ppmV) | |
| Reynolds number | |
| net sorption rate constant (1/s) | |
| sorption enthalpy (J/mol) | |
| concentration of sorbate per m3 of the sorbent material (mol/m3) | |
| equilibrium concentration of sorbate per m3 of the sorbent material (mol/m3) | |
| adsorption rate constant (1/s) | |
| desorption rate constant (mol/m3/s) | |
| equilibrium adsorption constant (m3/mol) | |
| molecule (sorbate) concentration near surface in gas phase (mol/m3) | |
| concentration of free sorption sites per m3 of the sorbent material (mol/m3) | |
| concentration of sorption sites occupied by A per m3 of the sorbent material (mol/m3) | |
| total concentration of sorption sites per m3 of the sorbent material (mol/m3) | |
| fraction of occupied sites | |
| fraction of free sites | |
| number of gas molecules (1) | |
| number of moles (mol) | |
| Avogadro constant ( 6.02214076 × 1023/mol) | |
| alternative equilibrium adsorption constant (1/Pa) | |
| adsorption free energy (J/mol) | |
| isosteric isosteric heat of adsorption (J/mol) |
Appendix A
Appendix A.1. Density and Viscosity Determination from Resonating Microcantilevers
Appendix A.2. Adsorption Model (Linear Driving Force Model) on Nanoporous Solids
Appendix A.3. Modelling of the Mechanical Response of the Functionalized Microcantilever with Nanoporous Solids

Appendix B
Appendix B.1. Water Adsorption Heat on MCM-48
References
- ISO 14175:2008. Welding Consumables—Gases and Gas Mixtures for Fusion Welding and Allied Processes; International Organization for Standardization ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Huber, C.; Mehdaoui, A.; Pina, M.P.; Morales, J.J. A Multiparameter Gas Monitoring System Combining Functionalized and Non-functionalized Microcantilevers. In Proceedings of the 4th Conference on Microfluidic Handling Systems, Enschede, The Netherlands, 2–4 October 2019. [Google Scholar]
- Xu, J.; Bertke, M.; Wasisto, H.S.; Peiner, E. Piezoresistive microcantilevers for humidity Sensing. J. Micromech. Microeng. 2019, 29, 053003. [Google Scholar] [CrossRef]
- Ma, R.-H.; Lee, C.-Y.; Wang, Y.-H.; Chen, H.-J. Microcantilever-based weather station for temperature, humidity and flow rate measurement. Microsyst Technol. 2008, 14, 971–977. [Google Scholar] [CrossRef]
- Lee, D.; Shin, N.; Lee, K.-H.; Jeon, S. Microcantilevers with nanowells as moisture sensors. Sens. Actuators B Chem. 2009, 137, 561–565. [Google Scholar] [CrossRef]
- Scandella, L.; Binder, G.; Mezzacasa, T.; Gobrecht, J.; Berger, R.; Lang, H.P.; Gerber, C.; Gimzewski, J.K.; Koegler, J.H.; Jansen, J.C. Combination of single crystal zeolites and microfabrication: Two applications towards zeolite nanodevices. Microporous Mesoporous Mater. 1998, 21, 403–409. [Google Scholar] [CrossRef]
- SCL-Sensor.Tech. Available online: https://www.sclsensortech.com/self-sensing-cantilevers-tipless/ (accessed on 9 December 2019).
- Badarlis, A.; Pfau, A.; Kalfas, A. Measurement and Evaluation of the Gas Density and Viscosity of Pure Gases and Mixtures Using a Micro-Cantilever Beam. Sensors 2015, 15, 24318–24342. [Google Scholar] [CrossRef]
- Huber, C.; Reith, P.; Badarlis, A. Gas Density and Viscosity Measurement with a Micro-cantilever for Online Combustion Gas Monitoring. In Proceedings of the 19th GMA/ITG-Fachtagung Sensoren und Messsysteme, Nürnberg, Germany, 26–27 June 2018. [Google Scholar]
- Urbiztondo, M.A.; Peralta, A.; Pellejero, I.; Sesé, J.; Pina, M.P.; Dufour, I.; Santamaría, J. Detection of organic vapours with Si cantilevers coated with inorganic or organic layers. Sens. Actuators B Chem. 2012, 171, 822–831. [Google Scholar] [CrossRef]
- TE Connectivity, Digital Pressure and Temperature Sensor 0–14 Bar (MS5803 14BA). Available online: https://www.te.com/usa-en/product-CAT-BLPS0013.html (accessed on 20 December 2019).
- MicroResonant, O.G. Universal Resonance Analyzer MFA200. Available online: http://www.micro-resonant.at/cms/products_mfa_en/ (accessed on 9 December 2019).
- Sell, J.K.; Niedermayer, A.O.; Jakoby, B. A digital PLL circuit for resonator sensors. Sens. Actuators A Phys. 2011, 172, 69–74. [Google Scholar] [CrossRef]
- Voglhuber-Brunnmaier, T.; Reichel, E.K.; Niedermayer, A.O.; Feichtinger, F.; Sell, J.K.; Jakoby, B. Determination of particle distributions from sedimentation measurements using a piezoelectric tuning fork sensor. Sens. Actuators A Phys. 2018, 284, 266–275. [Google Scholar] [CrossRef]
- CS Instruments. FA 510/515—Dew Point Sensor for Adsorption Dryers. Available online: https://www.cs-instruments.com/products/d/dew-point/fa-510515-dew-point-sensor-80-to-20ctd/ (accessed on 31 December 2019).
- Nigar, H.; Garcia-Baños, B.; Peñarada-Foix, F.L.; Catalá-Civera, J.M.; Mallada, R.; Santamaría, J. Amine-Functionalized Mesoporous Silica: A Material Capable of CO2 Adsorption and Fast Regeneration by Microwave Heating. Am. Inst. Chem. Eng. 2015, 62, 547–555. [Google Scholar] [CrossRef]
- Nigar, H.; Navascuésa, N.; de la Iglesia, O.; Mallada, R.; Santamaría, J. Removal of VOCs at trace concentration levels from humid air by Microwave Swing Adsorption, kinetics and proper sorbent selection. Sep. Purif. Technol. 2015, 151, 193–200. [Google Scholar] [CrossRef]
- Yamamoto, T.; Kim, Y.H.; Kim, B.C.; Endo, A.; Thongprachan, N.; Ohmori, T. Adsorption characteristics of zeolites for dehydration of ethanol: Evaluation of diffusivity of water in porous structure. Chem. Eng. J. 2012, 181, 443–448. [Google Scholar] [CrossRef]
- NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP): Version 10. Available online: https://www.nist.gov/srd/refprop (accessed on 10 December 2019).
- García-Romeo, D.; Pellejero, I.; Urbiztondo, M.A.; Sesé, J.; Pina, M.P.; Martínez, P.A.; Calvo, B.; Medrano, N. Portable low-power electronic interface for explosive detection using microcantilevers. Sens. Actuators B Chem. 2014, 200, 31–38. [Google Scholar] [CrossRef]
- Pina, M.P.; Almazán, F.; Eguizábal, A.; Pellejero, I.; Urbiztondo, M.; Sesé, J.; Santamaría, J.; García-Romeo, D.; Calvo, B.; Medrano, N. Explosives Detection by array of Si µ-cantilevers coated with titanosilicate type nanoporous materials. IEEE Sens. J. 2016, 16, 3435–3443. [Google Scholar] [CrossRef]
- Gregg, S.J.; Sing, K.S.W. Adsorption, Surface Area and Porosity, 2nd ed.; Academic Press Inc.: London, UK, 1982; pp. 1–297. [Google Scholar]
- Hill, T.L. Statistical Mechanics of Adsorption. V. Thermodynamics and Heat of Adsorption. J. Chem. Phys. 1949, 17, 520. [Google Scholar] [CrossRef]
- Cortés, F.B.; Chejne, F.; Carrasco-Marín, F.; Moreno-Castilla, C.; Pérez-Cárdenas, A.F. Water adsorption on zeolite 13X: Comparison of the two methods based on mass spectrometry and thermogravimetry. Adsorption 2010, 16, 141–146. [Google Scholar] [CrossRef]
- Pellejero, I.; Agustí, J.; Urbiztondo, M.A.; Sesé, J.; Pina, M.P.; Santamaría, J.; Abadal, G. Nanoporous silicalite-only cantilevers as micromechanical sensors: Fabrication, resonance response and VOCs sensing performance. Sens. Actuators B Chem. 2012, 168, 74–82. [Google Scholar] [CrossRef]
- Baimpos, T.; Giannakopoulos, I.G.; Nikolakis, V.; Kouzoudis, D. Effect of gas adsorption on the elastic properties of faujasite films measured using magnetoelastic sensors. Chem. Mater. 2008, 20, 1470–1475. [Google Scholar] [CrossRef]
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64–76. [Google Scholar] [CrossRef]
- Hosaka, H.; Kuroda, S. Damping characteristics of beam-shaped-micro-oscillators. Sens. Actuators A Phys. 1995, 49, 87–95. [Google Scholar] [CrossRef]
- Maali, A.; Hurth, C.; Boisgard, R.; Jai, C.; Cohen-Bouhacina, T.; Aiméa, J.P. Hydrodynamics of oscillating atomic force microscopy cantilevers in viscous fluids. J. Appl. Phys. 2005, 97, 074907. [Google Scholar] [CrossRef]
- Sircar, S.; Hufton, J. Why does the Linear Driving Force Model for Adsorption Kinetics Work? Adsorption 2000, 6, 137–147. [Google Scholar] [CrossRef]


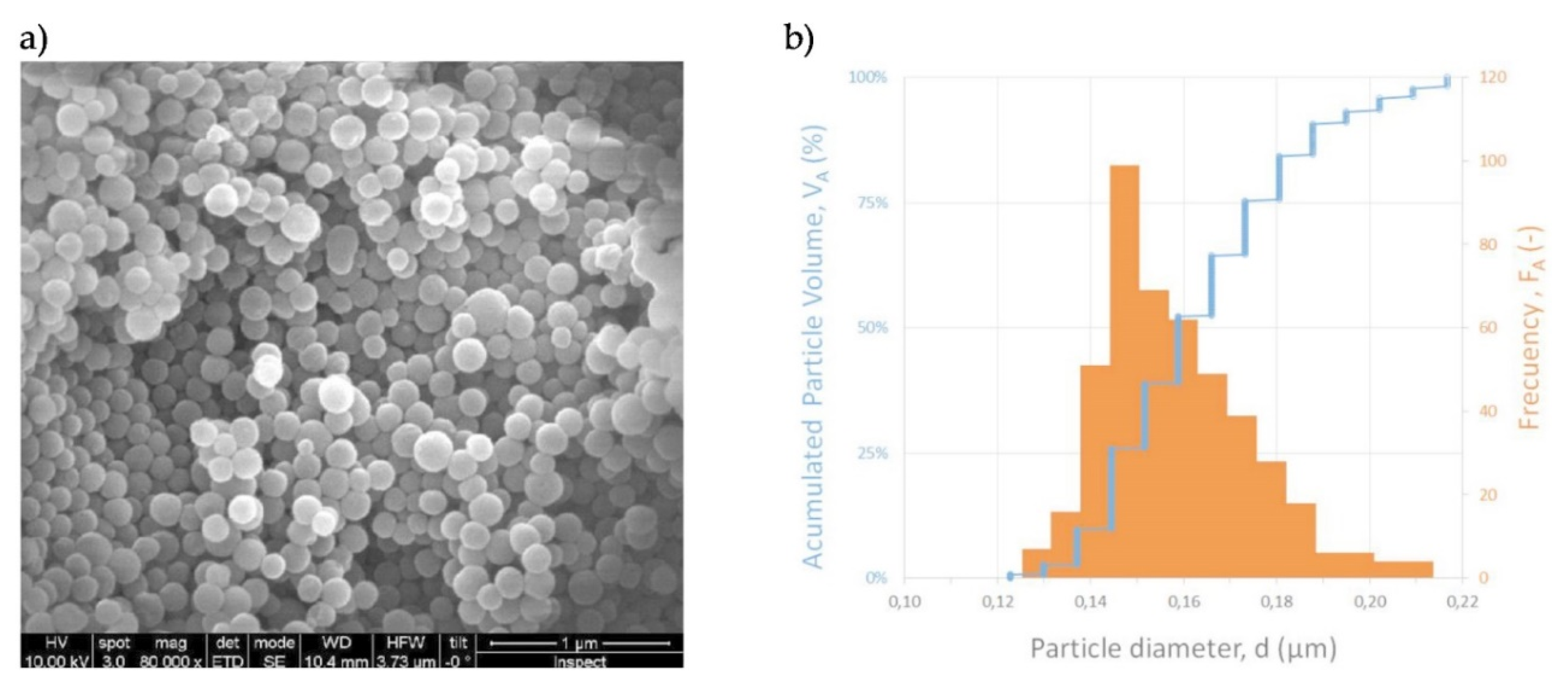




| Material | BET Surface Area | Pore Volume | Pore Size | Particle Size |
|---|---|---|---|---|
| m2/g | cm3/g | Å | nm | |
| CBV100 | 758 | 0.247 | 6.9 | <700 |
| MCM-48 | 1233 | 0.87 | 32 | 164 ± 18 |
| Chip# | Coating Material | Coating Method | Frequency in air before/after Coating (kHz) | Thickness of Cantilever Tip (µm) | Mass of Sorbent * (ng) | |
|---|---|---|---|---|---|---|
| 29 | bare chip | 35.02 | 2.6 | 0 | ||
| 125 | bare chip | 55.85 | 4.2 | 0 | ||
| 126 | bare chip | 59.93 | 4.5 | 0 | ||
| 149 | - | bare chip | 55.05 | 4.1 | 0 | |
| 167 | - | bare chip | 55.25 | 4.1 | 0 | |
| 190 | bare chip | 31.62 | 2.4 | 0 | ||
| 204 | bare chip | 30.45 | 2.3 | 0 | ||
| 166 | MCM-48 | Method 1 aqueous 2% wt. | 54.81 | 53.49 | 4.1 | 15 |
| 144 | MCM-48 | Method 2 ethanolic 2% wt. | 56.50 | 50.95 | 4.3 | 73 |
| 188 | MCM-48 | Method 2 ethanolic 2% wt. | 39.37 | 35.02 | 3.0 | 58 |
| 163 | MCM-48 on PDDA | Method 2 ethanolic 2% wt. with PDDA | 56.94 | 52.1 | 4.3 | 62 |
| 181 | CBV100 | Method 1 with PDDA | 38.03 | 34.37 | 2.9 | 48 |
| 162 | CBV100 | Method 2 aqueous 1% wt. | 55.22 | 53.30 | 4.1 | 23 |
| Chip# | Sensitivity ∆f/∆ρ | Density Deviation 1 | Viscosity Deviation 1,2 relative absolute | Qfactor_min | Qfactor_max | |
|---|---|---|---|---|---|---|
| Hz /(kg/m3) | kg/m3 | % | µPa·s | |||
| 29 | −191 | 0.038 | 2.0 | 0.38 | 40 | 230 |
| 125 | −189 | 0.023 | 1.4 | 0.25 | 90 | 500 |
| 126 | −195 | 0.035 | 1.0 | 0.18 | 90 | 550 |
| 149 | −192 | 0.028 | 1.1 | 0.20 | 70 | 490 |
| 190 | −191 | 0.039 | 1.5 | 0.28 | 30 | 200 |
| 204 | −183 | 0.056 | 1.4 | 0.27 | 30 | 200 |
| mean | −190 | 0.037 | 1.4 | 0.26 | 58 | 362 |
| min | −183 | 0.056 | 2.0 | 0.38 | 90 | 550 |
| max | −195 | 0.023 | 1.0 | 0.18 | 30 | 200 |
| Coefficient | Set 1 | Set 2 | Set 3 | Set 4 | Set 5 | Unit |
|---|---|---|---|---|---|---|
| 104 | 104 | 104 | 104 | 104 | Hz | |
| 311 | 311 | 311 | 311 | 311 | ng | |
| 170 | 170 | 170 | 170 | 170 | GPa | |
| 2330 | 2330 | 2330 | 2330 | 2330 | kg/m3 | |
| 4.16 | 4.16 | 4.16 | 4.16 | 4.16 | µm | |
| 2020 | 2020 | 2020 | 2020 | 2020 | kg/m3 | |
| 15 | 50 | 75 | 50 | 47 | ng | |
| 0.25 | 0.82 | 1.23 | 0.82 | 0.77 | µm | |
| 25 | 25 | 25 | 25 | 25 | °C | |
| Parameters calculated by the model | ||||||
| 4.89 × 10−3 | 4.89 × 10−3 | 4.89 × 10−3 | 4.86 × 10−3 | 4.85 × 10−3 | 1/s | |
| 61 | 74 | 67 | 102 | 161 | GPa | |
| 2.92 × 10−1 | 7.75 × 10−2 | 5.86 × 10−2 | 4.78 × 10−2 | 3.37 × 10−2 | 1/K | |
| 4.18 | 5.89 | 6.35 | 5.31 | 5.21 | GPa/(mg/g) | |
| −1.39 × 10−2 | −1.41 × 10−2 | −1.42 × 10−2 | 3.42 × 10−2 | 3.40 × 10−2 | 1/K | |
| 6.72 × 10−1 | 1.50 × 10−1 | 9.52 × 10−2 | 1.79× 10−1 | 2.03 × 10−1 | mg/g·Pa−1 | |
| 14.82 | 14.82 | 14.83 | 51.29 | 51.20 | kJ/mol | |
| −210 | −210 | −210 | −217 | −217 | Hz/(kg/m3) | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huber, C.; Pina, M.P.; Morales, J.J.; Mehdaoui, A. A Multiparameter Gas-Monitoring System Combining Functionalized and Non-Functionalized Microcantilevers. Micromachines 2020, 11, 283. https://doi.org/10.3390/mi11030283
Huber C, Pina MP, Morales JJ, Mehdaoui A. A Multiparameter Gas-Monitoring System Combining Functionalized and Non-Functionalized Microcantilevers. Micromachines. 2020; 11(3):283. https://doi.org/10.3390/mi11030283
Chicago/Turabian StyleHuber, Christof, Maria Pilar Pina, Juan José Morales, and Alexandre Mehdaoui. 2020. "A Multiparameter Gas-Monitoring System Combining Functionalized and Non-Functionalized Microcantilevers" Micromachines 11, no. 3: 283. https://doi.org/10.3390/mi11030283
APA StyleHuber, C., Pina, M. P., Morales, J. J., & Mehdaoui, A. (2020). A Multiparameter Gas-Monitoring System Combining Functionalized and Non-Functionalized Microcantilevers. Micromachines, 11(3), 283. https://doi.org/10.3390/mi11030283





