Cross-Sectional Dimension Dependence of Electroosmotic Flow in Fractal Treelike Rectangular Microchannel Network
Abstract
1. Introduction
2. Theoretical Modeling
3. Numerical Simulation
4. Results and Discussion
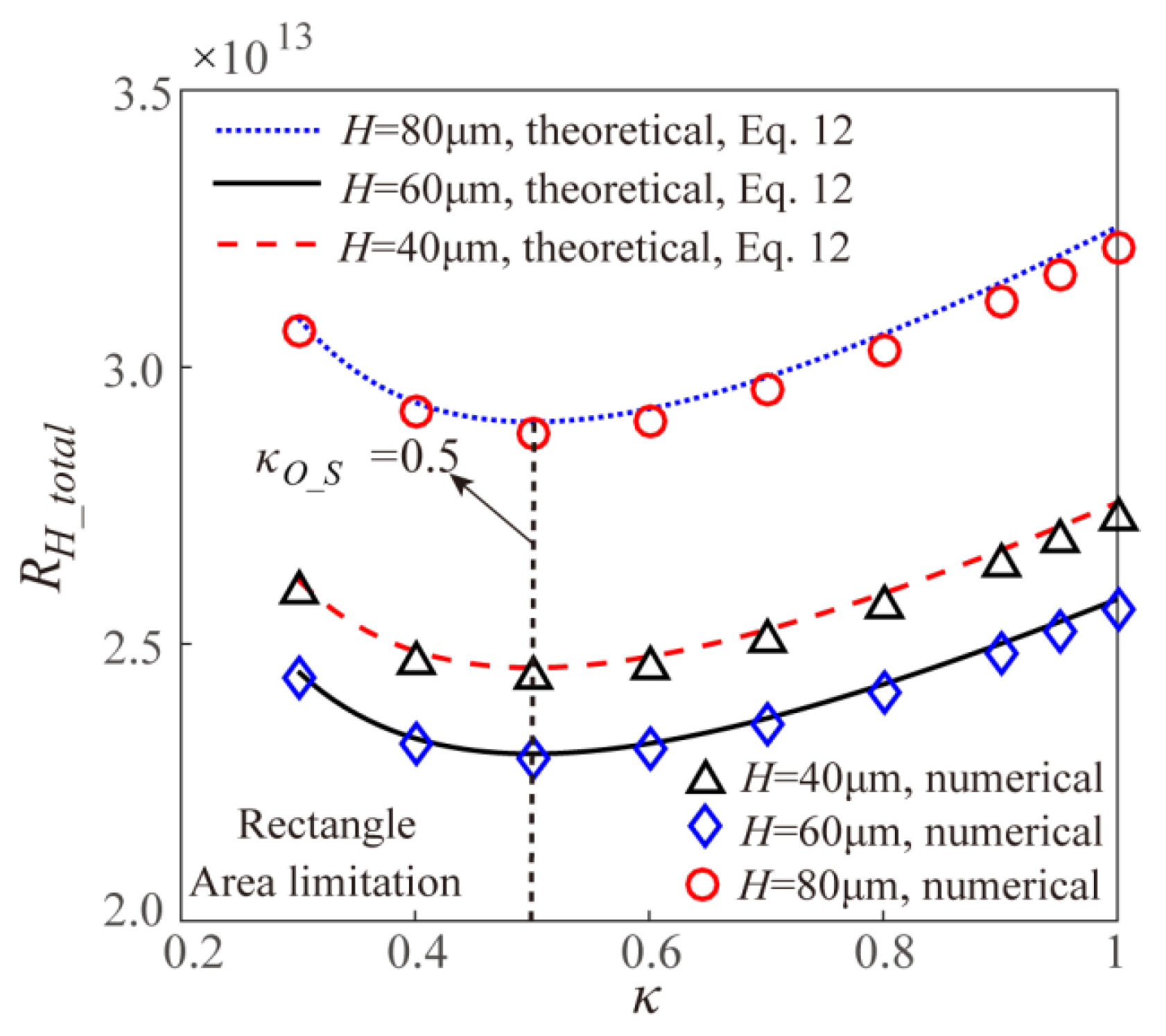
4.1. Models Validation
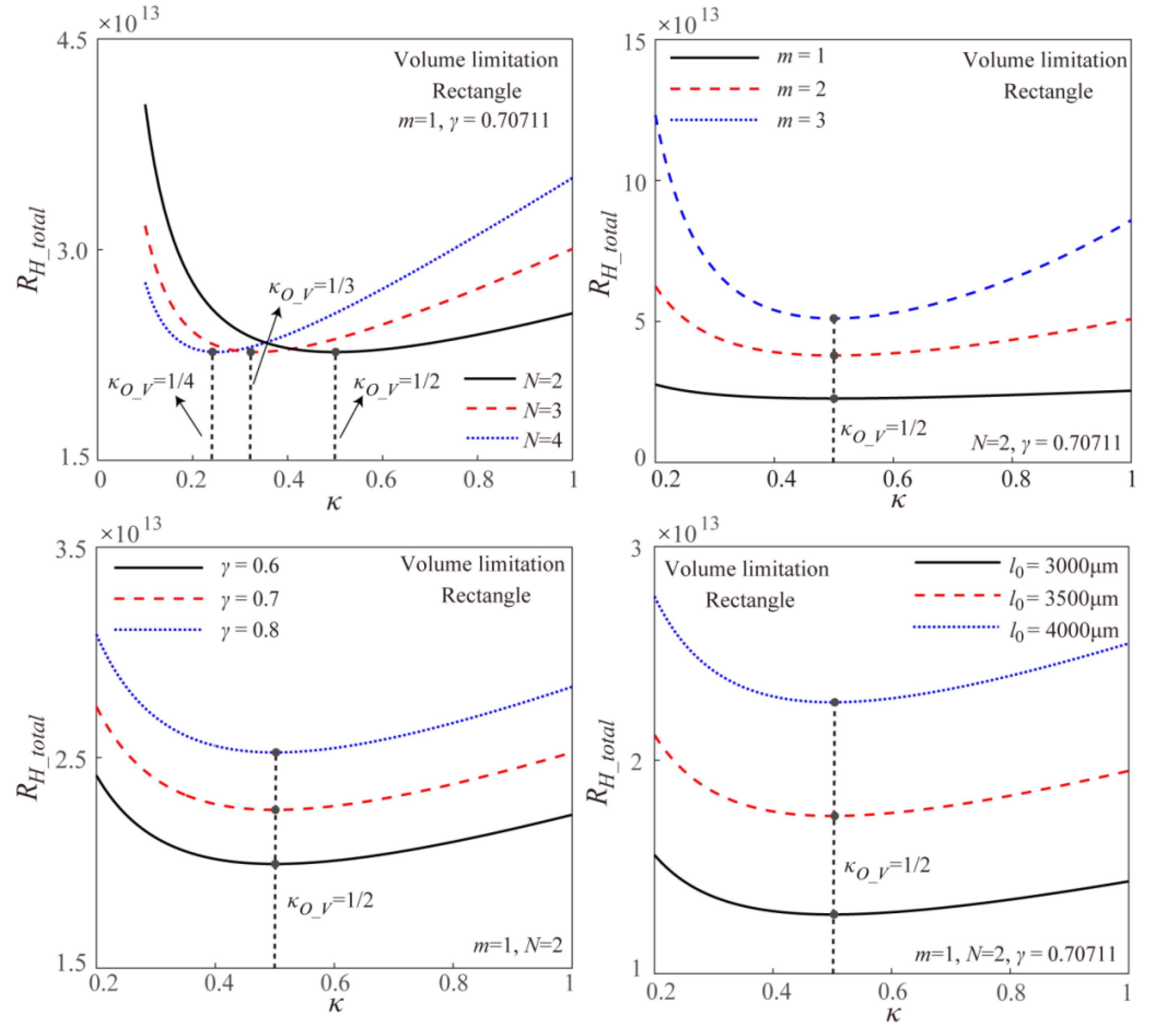
4.2. Volume Limitation
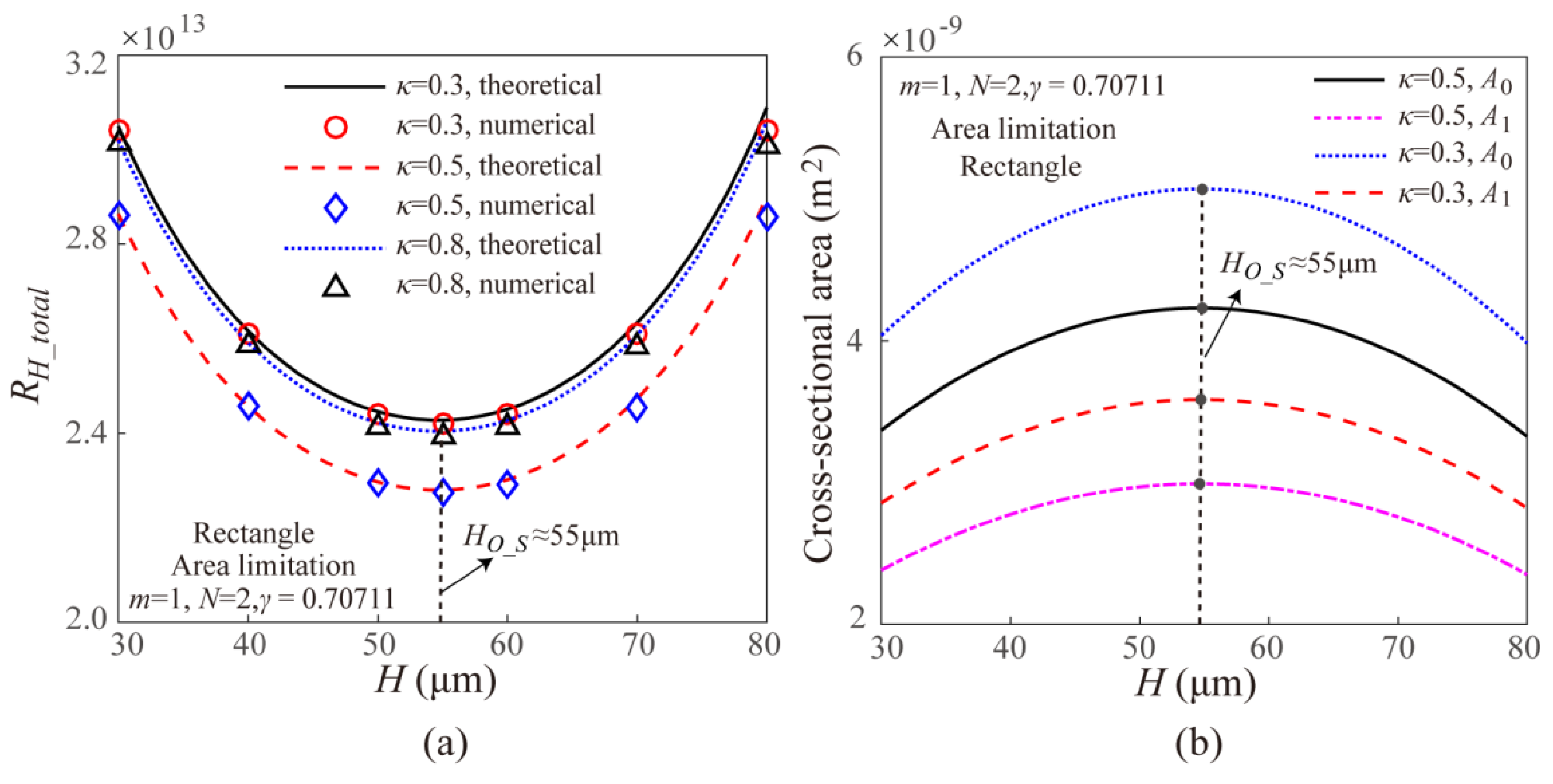
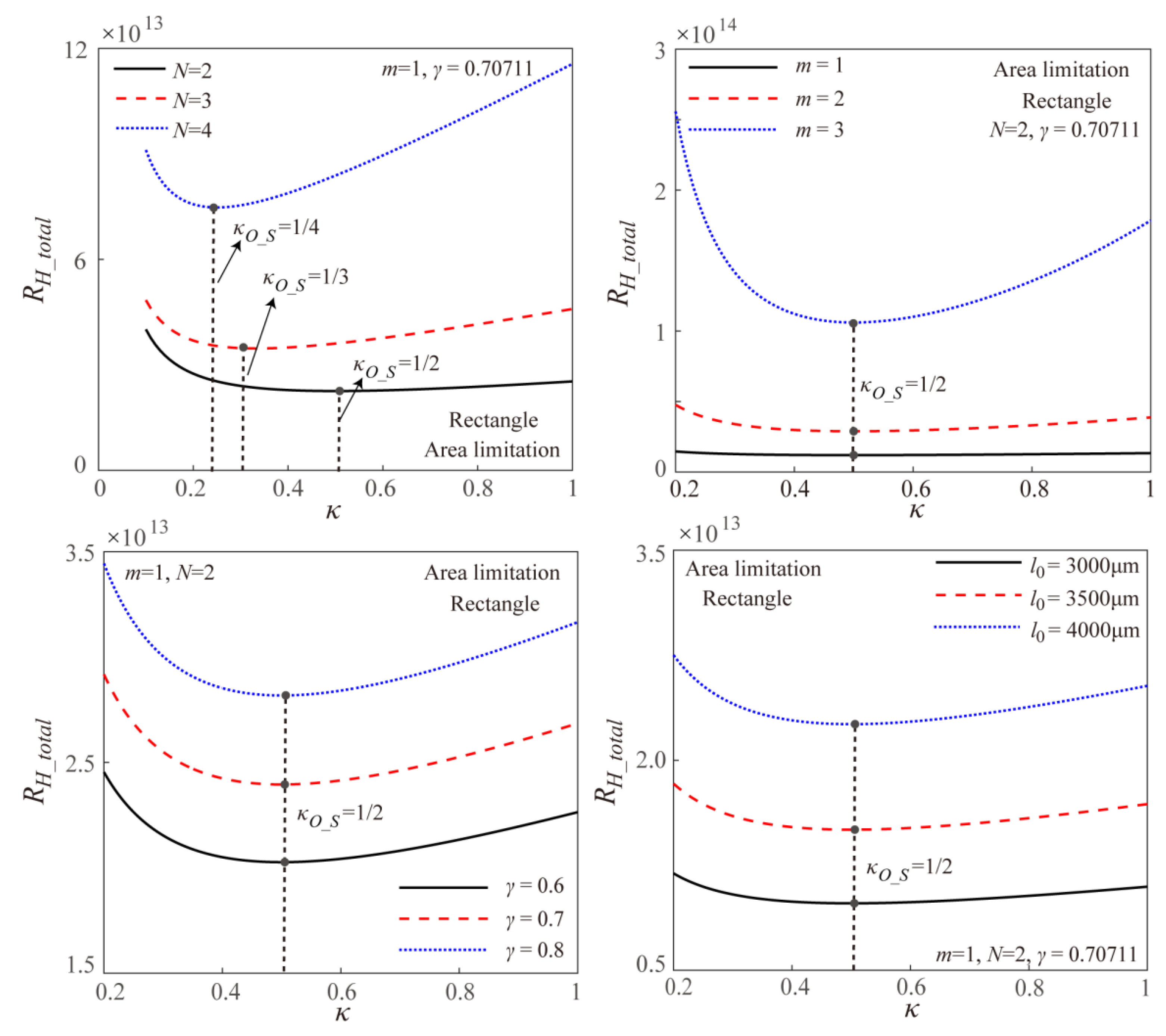
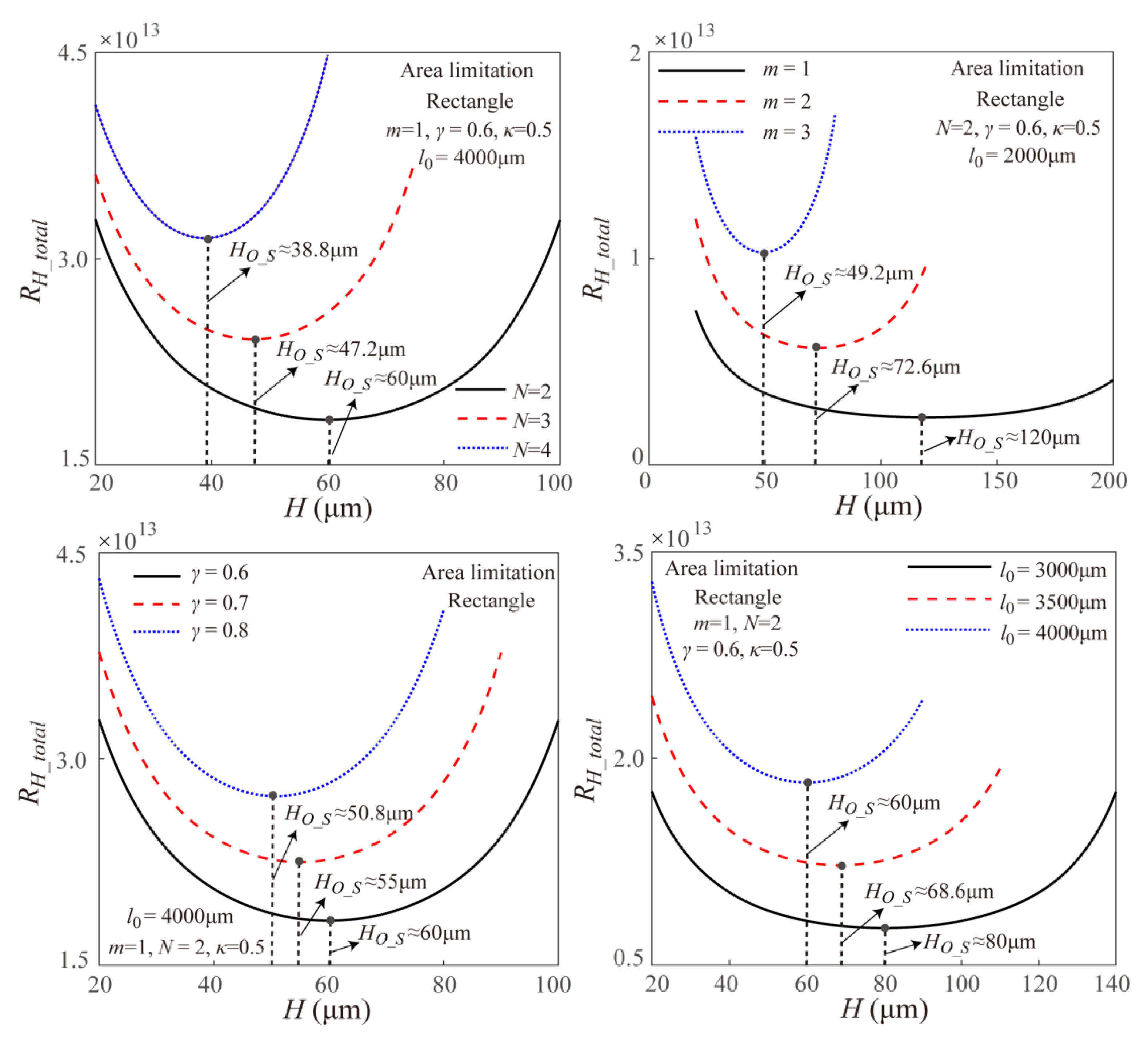
4.3. Surface Area Limitation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, D.Q. Encyclopedia of Microfluidics and Nanofluidics; Springer: New York, NY, USA, 2008. [Google Scholar]
- Lin, B. Microfluidics: Technologies and Applications; Springer: Berlin, Germany, 2011. [Google Scholar]
- Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering Flows in Small Devices: Microfluidics Toward a Lab-on-a-Chip. Annu. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef]
- Wong, P.K.; Wang, T.-H.; Deval, J.H.; Ho, C.-M. Electrokinetic in micro devices for biotechnology applications. IEEE/ASME Trans. Mechatron. 2004, 9, 366–376. [Google Scholar] [CrossRef]
- Jing, D.; Bhushan, B. The Coupling of Surface Charge and Boundary Slip at the Solid–liquid Interface and Their Combined Effect on Fluid drag: A Review. J. Colloid Interf. Sci. 2015, 454, 152–179. [Google Scholar] [CrossRef] [PubMed]
- Hunter, R.J. Zeta Potential in Colloid Science; Academic Press: London, UK, 1981. [Google Scholar]
- Israelachvili, J. Intermolecular and Surface Forces, 2nd ed.; Academic Press: London, UK, 1991. [Google Scholar]
- Hunter, R.J. Foundations of Colloid Science, 2nd ed.; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Jing, D.; Bhushan, B. Electroviscous effect on fluid drag in a microchannel with large zeta potential. Beilstein J. Nanotechnol. 2015, 6, 2207–2216. [Google Scholar] [CrossRef] [PubMed]
- Karniadakis, G.E.; Beskok, A. Micro Flows: Fundamentals and Simulation; Springer: Berlin, Germany, 2002. [Google Scholar]
- Burgreen, D.; Nakache, F.R. Eletrokinetic Flow in Ultrafine Capillary Silts. J. Phys. Chem. 1964, 68, 1084–1091. [Google Scholar] [CrossRef]
- Rice, C.L.; Whitehead, R. Electro Kinetic Flow in a Narrow Cylindrical Capillary. J. Phys. Chem. 1965, 69, 4017–4023. [Google Scholar] [CrossRef]
- Keh, H.J.; Liu, Y.C. Electroosmotic Flow in a Circular Capillary with a Surface Charge Layer. J. Colloid Interf. Surf. 1995, 172, 222–229. [Google Scholar] [CrossRef]
- Herr, A.; Molho, J.; Santiago, J.; Mungal, M.; Kenny, T.; Garguilo, M. Electroosmotic Capillary Flow With Nonuniform Zeta Potential. Anal. Chem. 2000, 72, 1053–1057. [Google Scholar] [CrossRef]
- Xuan, X.; Li, D. Electroosmotic flow in microchannels with arbitrary geometry and arbitrary distribution of wall charge. J. Colloid Interf. Surf. 2005, 289, 291–303. [Google Scholar] [CrossRef]
- Shamloo, A.; Merdasi, A.; Vatankhah, P. Numerical Simulation of Heat Transfer in Mixed Electroosmotic Pressure-Driven Flow in Straight Microchannels. J. Therm. Sci. Eng. App. 2016, 8, 021011. [Google Scholar] [CrossRef]
- Nosrati, R.; Hadigol, M.; Jafari, A.; Raisee, M.; Nourbakhsh, A. Numerical Investigation of Electroosmotic Mixing in Microchannels with Heterogeneous Zeta Potential. Adv. Sci. Eng. Med. 2011, 3, 1–9. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Hasanzadeh-Barforoushi, A.; Nejat, A.; Kowsary, F. Numerical study of mixing and heat transfer in mixed electroosmotic/pressure driven flow through T-shaped microchannels. Int. J. Heat Mass Transf. 2014, 75, 565–580. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, C.; Wang, S.; Liu, S. Electroosmotic Pumps and Their Applications in Microfluidic Systems. Microfluid. Nanofluid. 2009, 6, 145–162. [Google Scholar] [CrossRef] [PubMed]
- Gu, C.; Jia, Z.; Zhu, Z.; He, C.; Wang, W.; Morgan, A.; Lu, J.J.; Liu, S. Miniaturized Electroosmotic Pump Capable of Generating Pressures of More Than 1200 Bar. Anal. Chem. 2012, 84, 9609–9614. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1982. [Google Scholar]
- MacDonald, N. Trees and Networks in Biological Models; Wiley: Chichester, UK, 1983. [Google Scholar]
- Chen, Y.P.; Cheng, P. Heat transfer and pressure drop in fractal tree-like microchannel nets. Int. J. Heat Mass Transf. 2002, 45, 2643–2648. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B. The scaling laws of transport properties for fractal-like tree networks. J. Appl. Phys. 2006, 100, 104906. [Google Scholar] [CrossRef]
- Xu, P.; Sasmito, A.P.; Yu, B.; Mujumdar, A.S. Transport Phenomena and Properties in Treelike Networks. Appl. Mech. Rev. 2016, 68, 040802. [Google Scholar] [CrossRef]
- Jing, D.; Song, J.; Sui, Y. Hydraulic and thermal performances of laminar flow in fractal treelike branching microchannel network with wall velocity slip. Fractals 2019. [Google Scholar] [CrossRef]
- Jing, D.; He, L.; Wang, X. Optimization analysis of fractal tree-like microchannel network for electroviscous flow to realize minimum hydraulic resistance. Int. J. Heat Mass Transf. 2018, 125, 749–755. [Google Scholar] [CrossRef]
- Jing, D.; Song, S.; He, L. Reexamination of Murray’s law for tree-like rectangular microchannel network with constant channel height. Int. J. Heat Mass Transf. 2019, 128, 1344–1350. [Google Scholar] [CrossRef]
- Gosselin, L. Optimization of tree-shaped fluid networks with size limitations. Int. J. Therm. Sci. 2007, 46, 434–443. [Google Scholar] [CrossRef]
- Jing, D.; Song, J. Comparison on the hydraulic and thermal performances of two tree-like channel networks with different size constraints. Int. J. Heat Mass Transf. 2019, 130, 1070–1074. [Google Scholar] [CrossRef]
- Jing, D.; Yi, S. Electroosmotic flow in treelike branching microchannel network. Fractals 2019, 27, 1950095. [Google Scholar] [CrossRef]
- Oh, K.W.; Lee, K.; Ahn, B.; Furlani, E.P. Design of pressure-driven microfluidic networks using electric circuit analogy. Lab Chip 2011, 12, 515–545. [Google Scholar] [CrossRef] [PubMed]
- Patankar, N.A.; Hu, H.H. Numerical Simulation of Electroosmotic Flow. Anal. Chem. 1998, 70, 1870–1881. [Google Scholar] [CrossRef] [PubMed]
- Ren, L.Q.; Li, D.Q.; Qu, W.L. Electro-Viscous Effects on Liquid Flow in Microchannels. J. Colloid Interf. Sci. 2001, 233, 12–22. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, D.; Zhan, X. Cross-Sectional Dimension Dependence of Electroosmotic Flow in Fractal Treelike Rectangular Microchannel Network. Micromachines 2020, 11, 266. https://doi.org/10.3390/mi11030266
Jing D, Zhan X. Cross-Sectional Dimension Dependence of Electroosmotic Flow in Fractal Treelike Rectangular Microchannel Network. Micromachines. 2020; 11(3):266. https://doi.org/10.3390/mi11030266
Chicago/Turabian StyleJing, Dalei, and Xuekuan Zhan. 2020. "Cross-Sectional Dimension Dependence of Electroosmotic Flow in Fractal Treelike Rectangular Microchannel Network" Micromachines 11, no. 3: 266. https://doi.org/10.3390/mi11030266
APA StyleJing, D., & Zhan, X. (2020). Cross-Sectional Dimension Dependence of Electroosmotic Flow in Fractal Treelike Rectangular Microchannel Network. Micromachines, 11(3), 266. https://doi.org/10.3390/mi11030266



