Second-Harmonic Generation in Suspended AlGaAs Waveguides: A Comparative Study
Abstract
1. Introduction
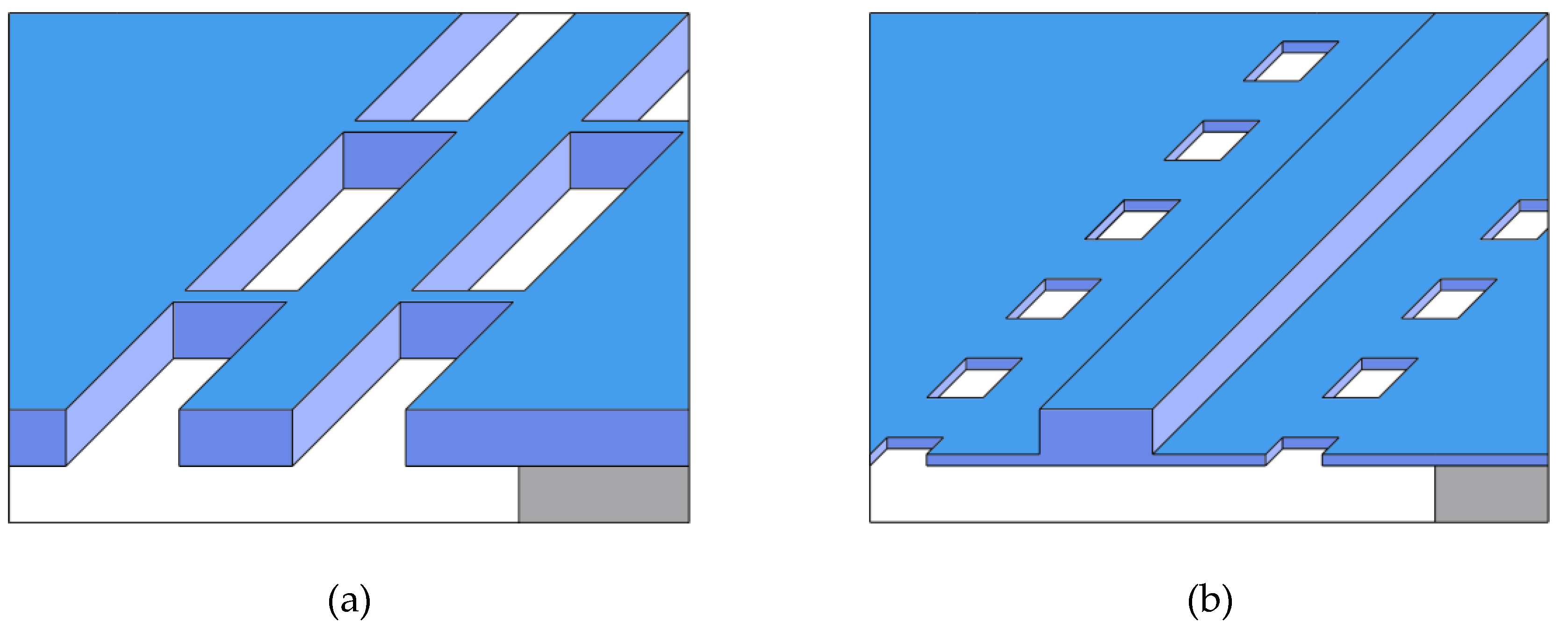
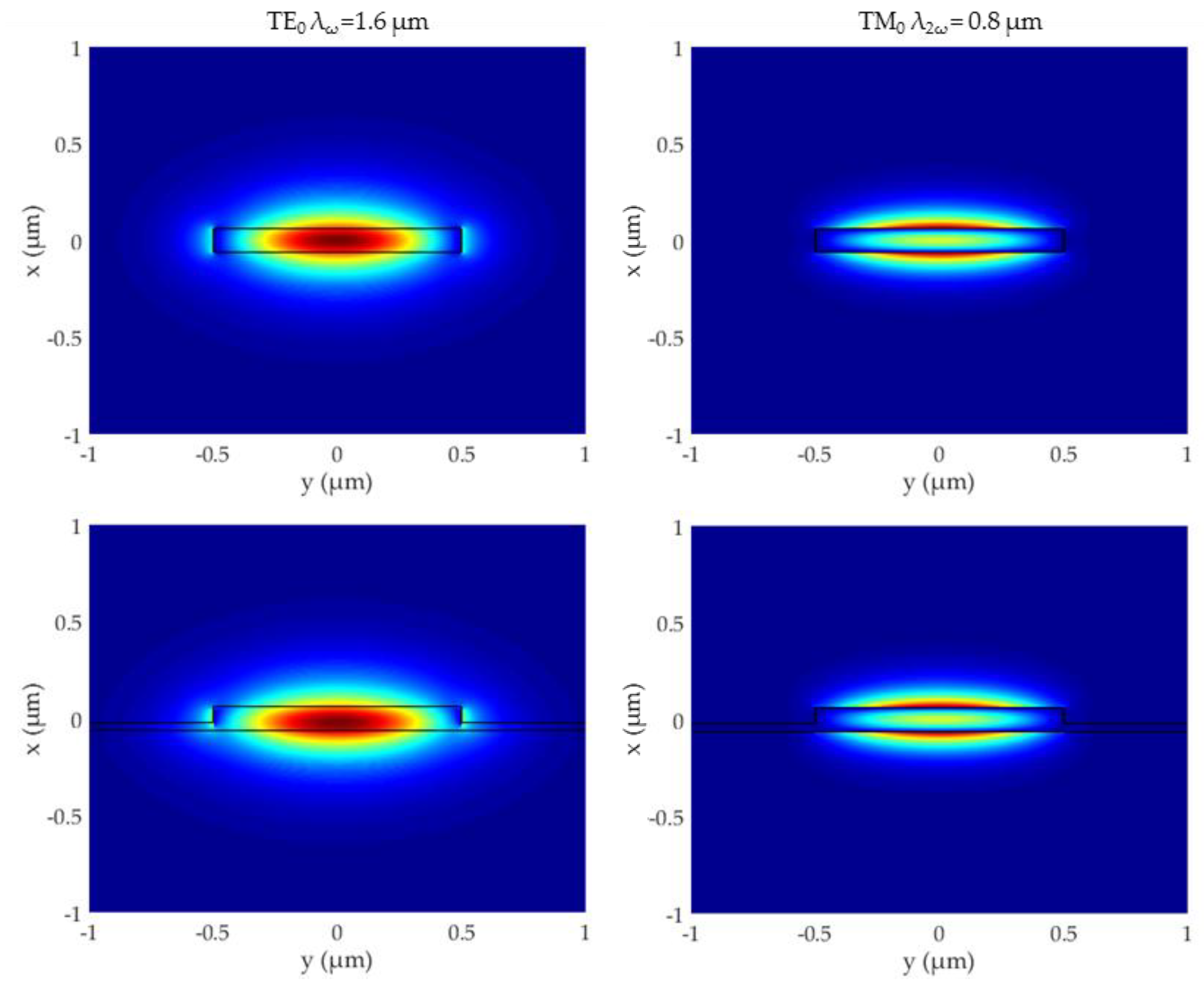
2. Materials and Methods
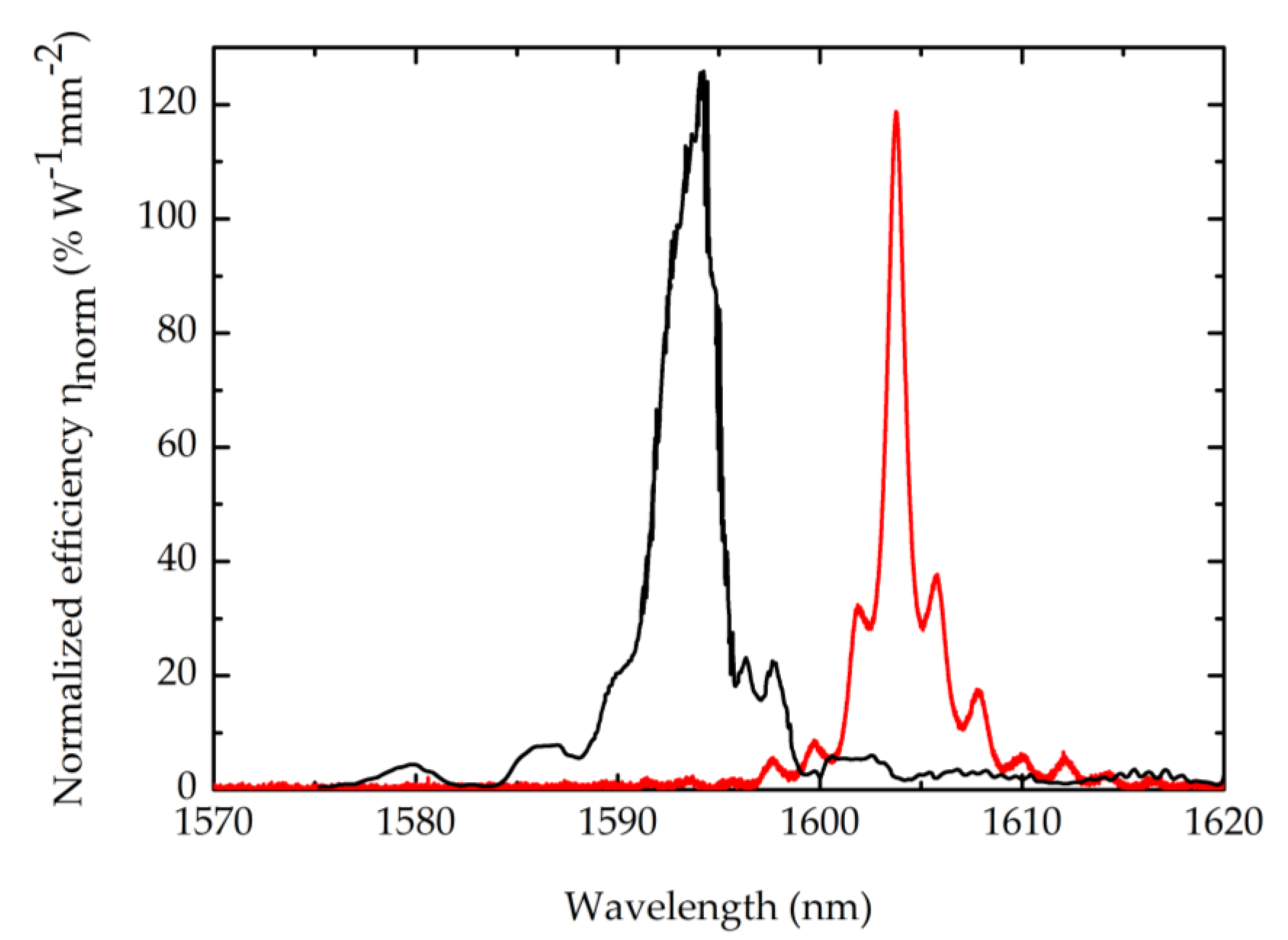
3. Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Monat, C.; Domachuk, P.; Eggleton, B. Integrated optofluidics: A new river of light. Nat. Photonics 2007, 1, 106–114. [Google Scholar] [CrossRef]
- Helmy, A.S.; Abolghasem, P.; Stewart Aitchison, J.; Bijlani, B.J.; Han, J.; Holmes, B.M.; Hutchings, D.C.; Younis, U.; Wagner, S.J. Recent advances in phase matching of second-order nonlinearities in monolithic semiconductor waveguides. Laser Photon. Rev. 2011, 5, 272. [Google Scholar] [CrossRef]
- Rodriguez-Ruiz, I.; Ackermann, T.N.; Muñoz-Berbel, X.; Llobera, A. Photonic Lab-on-a-Chip: Integration of Optical Spectroscopy in Microfluidic Systems. Anal. Chem. 2016, 88, 6630–6637. [Google Scholar] [CrossRef] [PubMed]
- Popa, D.; Udrea, F. Towards integrated Mid-Infrared Gas Sensors. Sensors 2019, 19, 2076. [Google Scholar] [CrossRef] [PubMed]
- Soler Penades, J.; Ortega-Moñux, A.; Nedeljkovic, M.; Wangüemert-Pérez, J.G.; Halir, R.; Khokhar, A.Z.; Alonso-Ramos, C.; Qu, Z.; Molina-Fernández, I.; Cheben, P.; et al. Suspended silicon mid-infrared waveguide devices with subwavelength grating metamaterial cladding. Opt. Express 2016, 24, 22908–22916. [Google Scholar] [CrossRef]
- Chiles, J.; Khan, S.; Ma, J.; Fathpour, S. High-contrast, all-silicon waveguiding platform for ultra-broadband mid-infrared photonics. Appl. Phys. Lett. 2013, 103, 151106. [Google Scholar] [CrossRef]
- Nedeljkovic, M.; Khokhar, A.Z.; Hu, Y.; Chen, X.; Soler Penadés, J.; Stankovic, S.; Chong, H.M.H.; Thomson, D.J.; Gardes, F.Y.; Reed, G.T.; et al. Silicon photonic devices and platforms for the mid-infrared. Opt. Mater. Express 2013, 3, 1205–1214. [Google Scholar] [CrossRef]
- Li, X.; Zhou, P.; He, S.; Gao, S. Dispersion engineering of suspended silicon photonic waveguides for broadband mid-infrared wavelength conversion. J. Opt. Soc. Am. B 2014, 31, 2295–2301. [Google Scholar] [CrossRef]
- Shoji, I.; Kondo, T.; Kitamoto, A.; Shirane, M.; Ito, R. Absolute scale of second-order nonlinear-optical coefficients. J. Opt. Soc. Am. B 1997, 14, 2268–2294. [Google Scholar] [CrossRef]
- Dolgaleva, K.; Ng, W.C.; Qian, L.; Aitchison, J.S. Compact highly-nonlinear AlGaAs waveguides for efficient wavelength conversion. Opt. Express 2011, 19, 12440–12455. [Google Scholar] [CrossRef]
- De Rossi, A.; Berger, V.; Calligaro, M.; Leo, G.; Ortiz, V.; Marcadet, X. Parametric fluorescence in oxidized aluminum gallium arsenide waveguides. Appl. Phys. Lett. 2001, 79, 3758–3760. [Google Scholar] [CrossRef]
- Savanier, M.; Ozanam, C.; Lanco, L.; Lafosse, X.; Andronico, A.; Favero, I.; Ducci, S.; Leo, G. Near-infrared optical parametric oscillator in a III-V semiconductor waveguide. Appl. Phys. Lett. 2013, 103, 261105. [Google Scholar] [CrossRef]
- Boitier, F.; Orieux, A.; Autebert, C.; Lemaître, A.; Galopin, E.; Manquest, C.; Sirtori, C.; Favero, I.; Leo, G.; Ducci, S. An electrically injected photon-pair source at room temperature. Phys. Rev. Lett. 2014, 112, 183901. [Google Scholar] [CrossRef] [PubMed]
- Caillet, X.; Berger, V.; Leo, G.; Ducci, S. A semiconductor source of counterpropagating twin photons: a versatile device allowing the control of the two-photon state. J. Mod. Opt. 2009, 56, 232–239. [Google Scholar] [CrossRef]
- Wathen, J.J.; Apiratikul, P.; Richardson, C.J.; Porkolab, G.A.; Carter, G.M.; Murphy, T.E. Efficient continuous-wave four-wave mixing in bandgap-engineered AlGaAs waveguides. Opt. Lett. 2014, 39, 3161–3164. [Google Scholar] [CrossRef] [PubMed]
- Gili, V.F.; Carletti, L.; Locatelli, A.; Rocco, D.; Finazzi, M.; Ghirardini, L.; Favero, I.; Gomez, C.; Lemaître, A.; Celebrano, M.; et al. Monolithic AlGaAs second-harmonic nanoantennas. Opt. Expr. 2016, 24, 15965–15971. [Google Scholar] [CrossRef]
- Liu, S.; Saravi, S.; Keeler, G.A.; Sinclair, M.B.; Yang, Y.; Reno, J.; Pertsch, T.; Brener, I. Resonantly Enhanced Second-Harmonic Generation Using III–V Semiconductor All-Dielectric Metasurfaces. Nano Lett. 2016, 16, 5426–5432. [Google Scholar] [CrossRef]
- Camacho-Morales, R.; Rahmani, M.; Kruk, S.; Wang, L.; Xu, L.; Smirnova, D.A.; Solntsev, A.S.; Miroshnichenko, A.; Tan, H.H.; Karouta, F.; et al. Nonlinear Generation of Vector Beams From AlGaAs Nanoantennas. ACS Nano Lett. 2016, 16, 7191–7197. [Google Scholar] [CrossRef]
- Marino, G.; Solntsev, A.S.; Xu, L.; Gili, V.F.; Carletti, L.; Poddubny, A.N.; Rahmani, M.; Smirnova, D.A.; Chen, H.; Lemaître, A.; et al. Spontaneous photon-pair generation from a dielectric nanoantenna. Optica 2019, 6, 1416–1422. [Google Scholar] [CrossRef]
- Marino, G.; Gigli, C.; Rocco, D.; Lemaître, A.; Favero, I.; De Angelis, C.; Leo, G. Zero-Order Second Harmonic Generation from AlGaAs-on-Insulator Metasurfaces. ACS Photonics 2019, 65, 1226–1232. [Google Scholar] [CrossRef]
- Gigli, C.; Marino, G.; Suffit, S.; Patriarche, G.; Beaudoin, G.; Pantzas, K.; Sagnes, I.; Favero, I.; Leo, G. Polarization- and diffraction-controlled second harmonic generation from semiconductor metasurfaces. J. Opt. Soc. Am. B 2019, 36, E55–E64. [Google Scholar] [CrossRef]
- Pu, M.; Ottaviano, L.; Semenova, E.; Yvind, K. Efficient frequency comb generation in AlGaAs-on-insulator. Optica 2016, 3, 823–826. [Google Scholar] [CrossRef]
- Chang, L.; Boes, A.; Guo, X.; Spencer, D.T.; Kennedy, M.J.; Peters, J.D.; Volet, N.; Chiles, J.; Kowligy, A.; Nader, N.; et al. Heterogeneously Integrated GaAs Waveguides on Insulator for Efficient Frequency Conversion. Laser Photonics Rev. 2018, 12, 1800149. [Google Scholar] [CrossRef]
- Chang, L.; Xie, W.; Shu, H.; Yang, Q.; Shen, B.; Boes, A.; Peters, J.D.; Jin, W.; Liu, S.; Moille, G.; et al. Ultra-efficient frequency comb generation in AlGaAs-on-insulator microresonators. Phys. Opt. 2019, submitted. arXiv:1909.09778. [Google Scholar]
- Guillotel, E.; Ravaro, M.; Ghiglieno, F.; Langlois, C.; Ricolleau, C.; Ducci, S.; Favero, I.; Leo, G. Parametric amplification in GaAs/AlOx waveguide. Appl. Phys. Lett. 2009, 94, 171110–171113. [Google Scholar] [CrossRef]
- Ozanam, C.; Savanier, M.; Lanco, L.; Lafosse, X.; Almuneau, G.; Andronico, A.; Favero, I.; Ducci, S.; Leo, G. Towards an AlGaAs/AlOx near-IR integrated optical parametric oscillator. J. Opt. Soc. Am. B 2014, 31, 542–550. [Google Scholar] [CrossRef]
- Shin, J.; Wu, S.; Dagli, N. Bulk Undoped GaAs–AlGaAs Substrate-Removed Electrooptic Modulators With 3.7-V-cm Drive Voltage at 1.55 µm. IEEE Photon. Technol. Lett. 2006, 18, 2251–2253. [Google Scholar] [CrossRef]
- Shin, J.; Chang, Y.-C.; Dagli, N. 0.3 V drive voltage GaAs∕AlGaAs substrate removed Mach–Zehnder intensity modulators. Appl. Phys. Lett. 2008, 92, 201103. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Baker, C.; Hease, W.; Sejil, S.; Senellart, P.; Lemaître, A.; Ducci, S.; Leo, G.; Favero, I. Ultrahigh Q-Frequency product for optomechanical disk resonators with a mechanical shield. Appl. Phys. Lett. 2013, 103, 241112. [Google Scholar] [CrossRef]
- Mariani, S.; Andronico, A.; Mauguin, O.; Lemaître, A.; Favero, I.; Ducci, S.; Leo, G. AlGaAs microdisk cavities for second-harmonic generation. Opt. Lett. 2013, 38, 3965–3968. [Google Scholar] [CrossRef]
- Kuo, P.S.; Bravo-Abad, J.; Solomon, G.S. Second-harmonic generation using 4bar-quasi-phasematching in a GaAs whispering-gallery-mode microcavity. Nat. Commun. 2014, 5, 3109–3115. [Google Scholar] [CrossRef] [PubMed]
- Mariani, S.; Andronico, A.; Lemaître, A.; Favero, I.; Ducci, S.; Leo, G. Second-harmonic generation in AlGaAs microdisks in the telecom range. Opt. Lett. 2014, 39, 3062–3065. [Google Scholar] [CrossRef] [PubMed]
- Morais, N.; Roland, I.; Ravaro, M.; Hease, W.; Lemaître, A.; Gomez, C.; Wabnitz, S.; De Rosa, M.; Favero, I.; Leo, G. Directionally induced quasi-phase matching in homogeneous AlGaAs waveguides. Opt. Lett. 2017, 42, 4287–4290. [Google Scholar] [CrossRef] [PubMed]
- Stievater, T.H.; Mahon, R.; Park, D.; Rabinovich, W.S.; Pruessner, M.W.; Khurgin, J.B.; Richardson, C.J.K. Mid-infrared difference-frequency generation in suspended GaAs waveguides. Opt. Lett. 2014, 39, 945–948. [Google Scholar] [CrossRef]
- Roland, I.; Borne, A.; Ravaro, M.; De Oliveira, R.; Lemaître, A.; Favero, I.; Leo, G. Frequency doubling and parametric fluorescence in a 4-port photonic chip. Opt. Lett. 2019. submitted. [Google Scholar]
- Sutherland, R.L. Handbook of Nonlinear Optics; Marcel Dekker: New York, NY, USA, 1996; p. 96. [Google Scholar]
- Scaccabarozzi, L.; Fejer, M.; Huo, Y.; Fan, S.; Yu, X.; Harris, J. Enhanced second-harmonic generation in AlGaAs⁄AlxOy tightly confining waveguides and resonant cavities. Opt. Lett. 2006, 31, 3626–3628. [Google Scholar] [CrossRef]
- Savanier, M.; Andronico, A.; Lemaître, A.; Galopin, E.; Manquest, C.; Favero, I.; Ducci, S.; Leo, G. Large Second-Harmonic Generation at 1.55 μm in oxidized AlGaAs waveguides. Opt. Lett. 2011, 36, 2955–2957. [Google Scholar] [CrossRef]

| Design | λ (nm) | R (%) | Ltrans (μm) | K (%) | Α (cm−1) | T (%) | κ (%) |
|---|---|---|---|---|---|---|---|
| Wire | 1600 | 16.7 | 200 | 30.3 ± 0.3 | 3.7 ± 0.5 | 34.0 ± 0.2 | 60.7 ± 0.3 |
| 800 | 24.3 | 200 | 23 ± 5 | 38 ± 12 | 0.50 ± 0.02 | 10.0 ± 1.0 | |
| Rib | 1600 | 16.7 | 200 | 30.1 ± 0.6 | 4.0 ± 1.0 | 5.0 ± 0.2 | 23.3 ± 0.7 |
| 800 | 24.3 | 200 | 22 ± 3 | 39 ± 7 | 0.50 ± 0.02 | 10.4 ± 0.7 |
| Design | LSHG (μm) | Pin (W) | PSHG (W) | η (% W−1) | ηnorm (% W−1 mm−2) |
|---|---|---|---|---|---|
| Wire | 1000 | 8.0 × 10−4 | 3.9 × 10−9 | 16 ± 2 | 128 ± 20 |
| Rib | 200 | 4.0 × 10−4 | 2.7 × 10−11 | 3.0 ± 0.5 | 119 ± 20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roland, I.; Ravaro, M.; Suffit, S.; Filloux, P.; Lemaître, A.; Favero, I.; Leo, G. Second-Harmonic Generation in Suspended AlGaAs Waveguides: A Comparative Study. Micromachines 2020, 11, 229. https://doi.org/10.3390/mi11020229
Roland I, Ravaro M, Suffit S, Filloux P, Lemaître A, Favero I, Leo G. Second-Harmonic Generation in Suspended AlGaAs Waveguides: A Comparative Study. Micromachines. 2020; 11(2):229. https://doi.org/10.3390/mi11020229
Chicago/Turabian StyleRoland, Iännis, Marco Ravaro, Stéphan Suffit, Pascal Filloux, Aristide Lemaître, Ivan Favero, and Giuseppe Leo. 2020. "Second-Harmonic Generation in Suspended AlGaAs Waveguides: A Comparative Study" Micromachines 11, no. 2: 229. https://doi.org/10.3390/mi11020229
APA StyleRoland, I., Ravaro, M., Suffit, S., Filloux, P., Lemaître, A., Favero, I., & Leo, G. (2020). Second-Harmonic Generation in Suspended AlGaAs Waveguides: A Comparative Study. Micromachines, 11(2), 229. https://doi.org/10.3390/mi11020229





