Long Carbon Fibers for Microwave Absorption: Effect of Fiber Length on Absorption Frequency Band
Abstract
1. Introduction
2. Materials and Methods
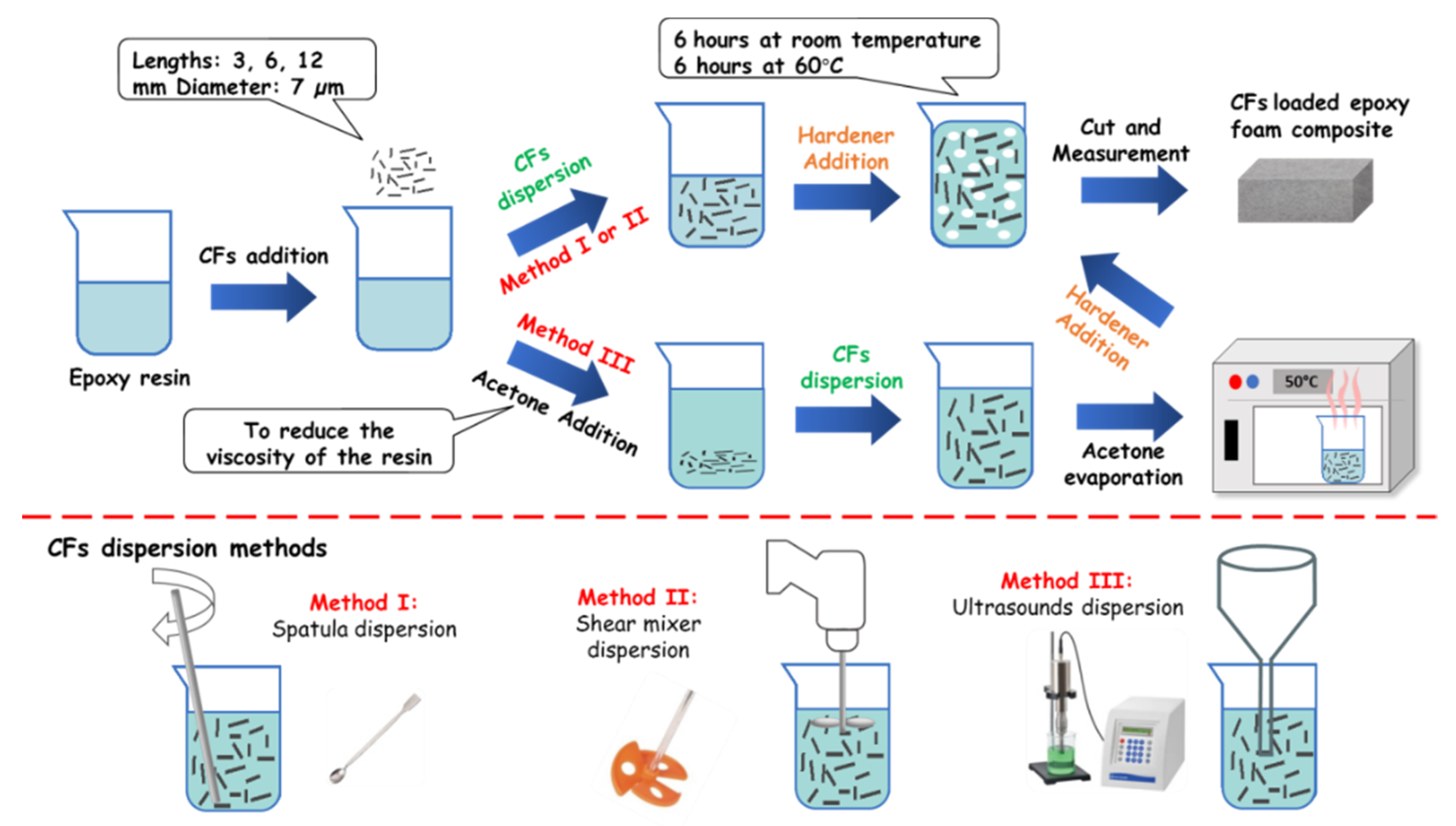
2.1. CFs/Epoxy Foam Composite Elaboration
2.2. Structural Characterization
2.3. Dielectric and EM Characterization
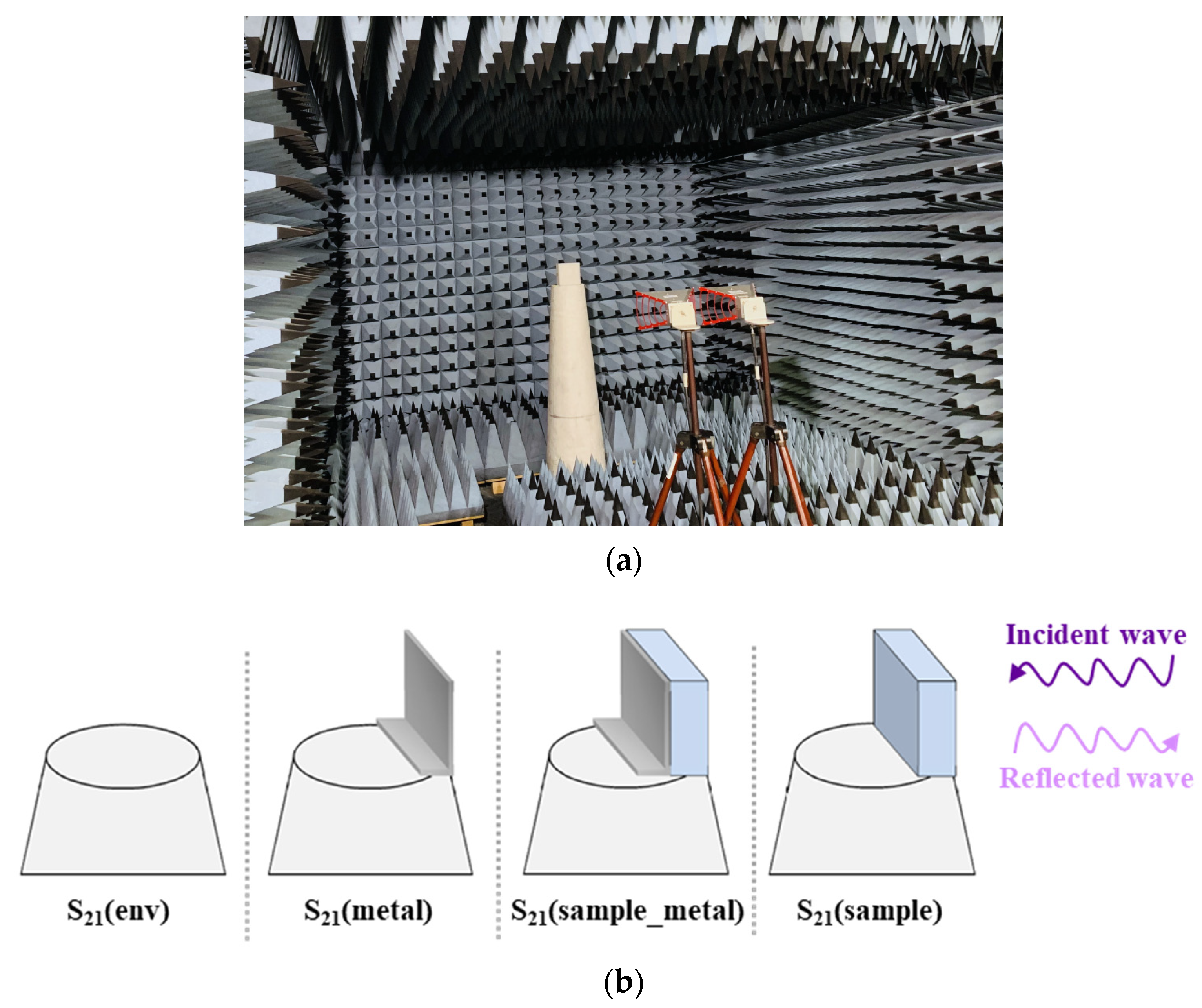
2.3.1. The Reflection Coefficient Measurement
2.3.2. Extraction of Dielectric Properties
2.3.3. Simulation of Absorption Performance of Pyramidal Absorber
3. Results and Discussions
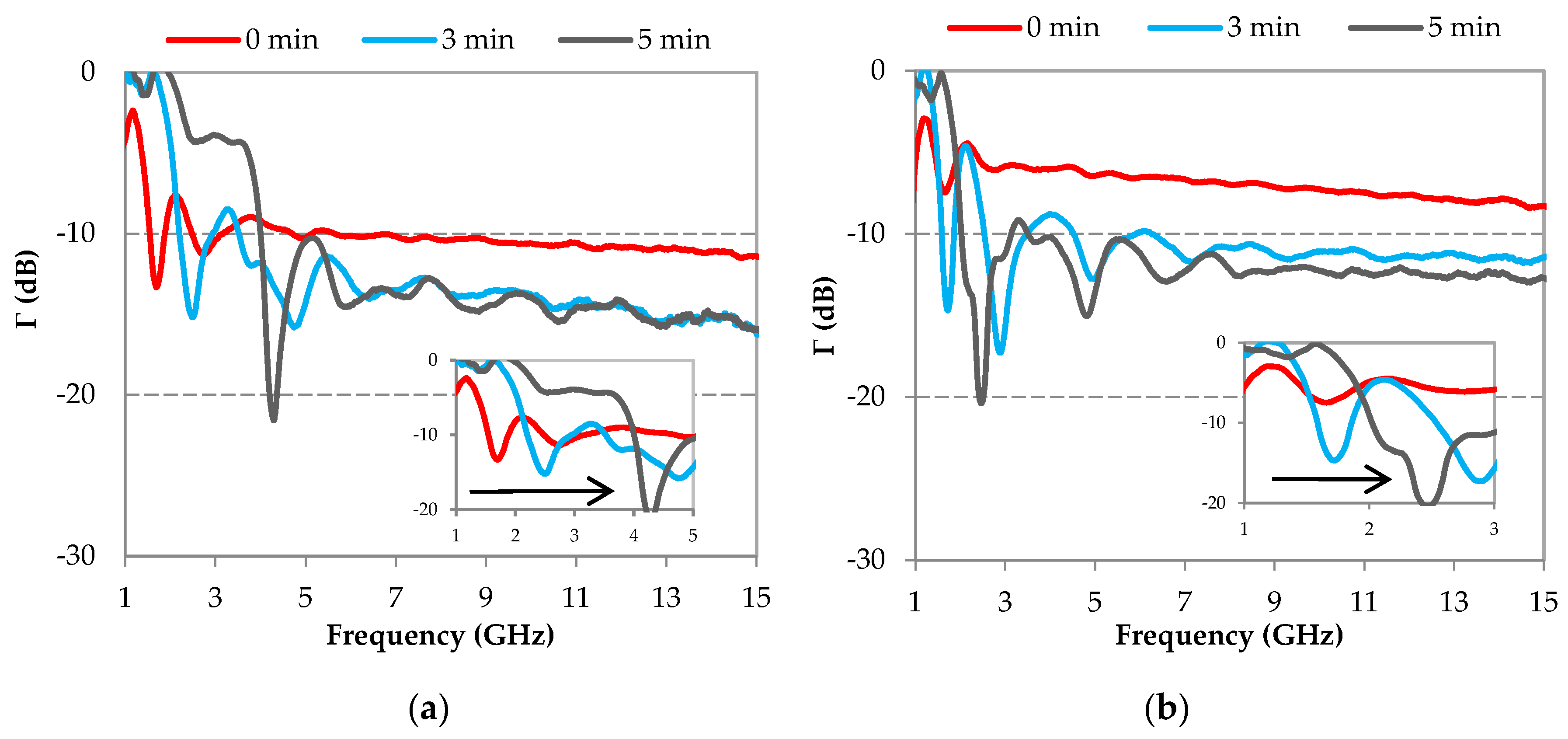
3.1. Effect of CFs Breakage on Reflection Coefficient of CFs Loaded Composites
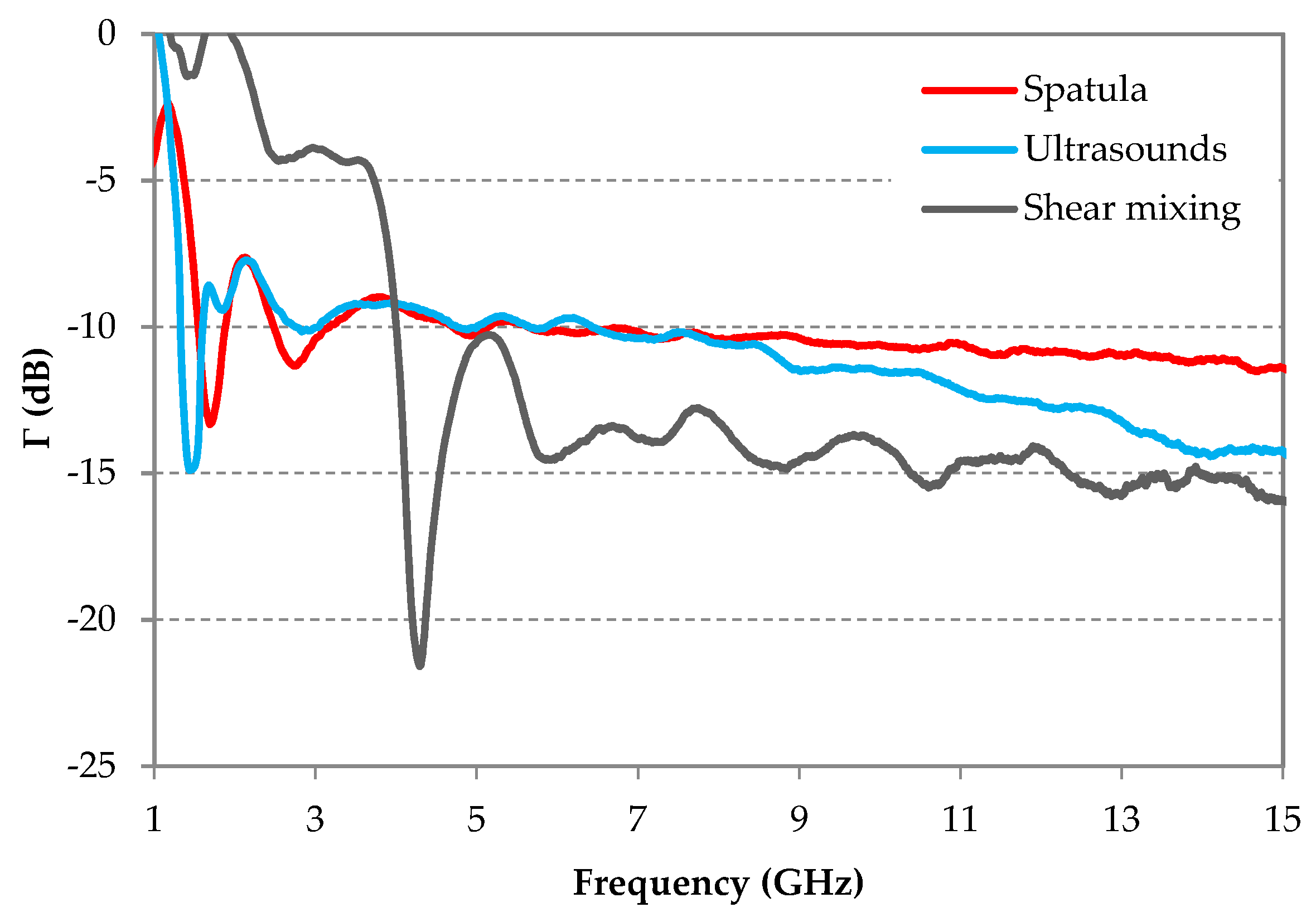
3.1.1. Effect of CFs Dispersing Method
3.1.2. Effect of CFs Shear Mixing Duration
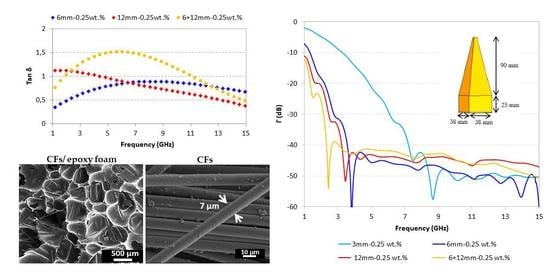
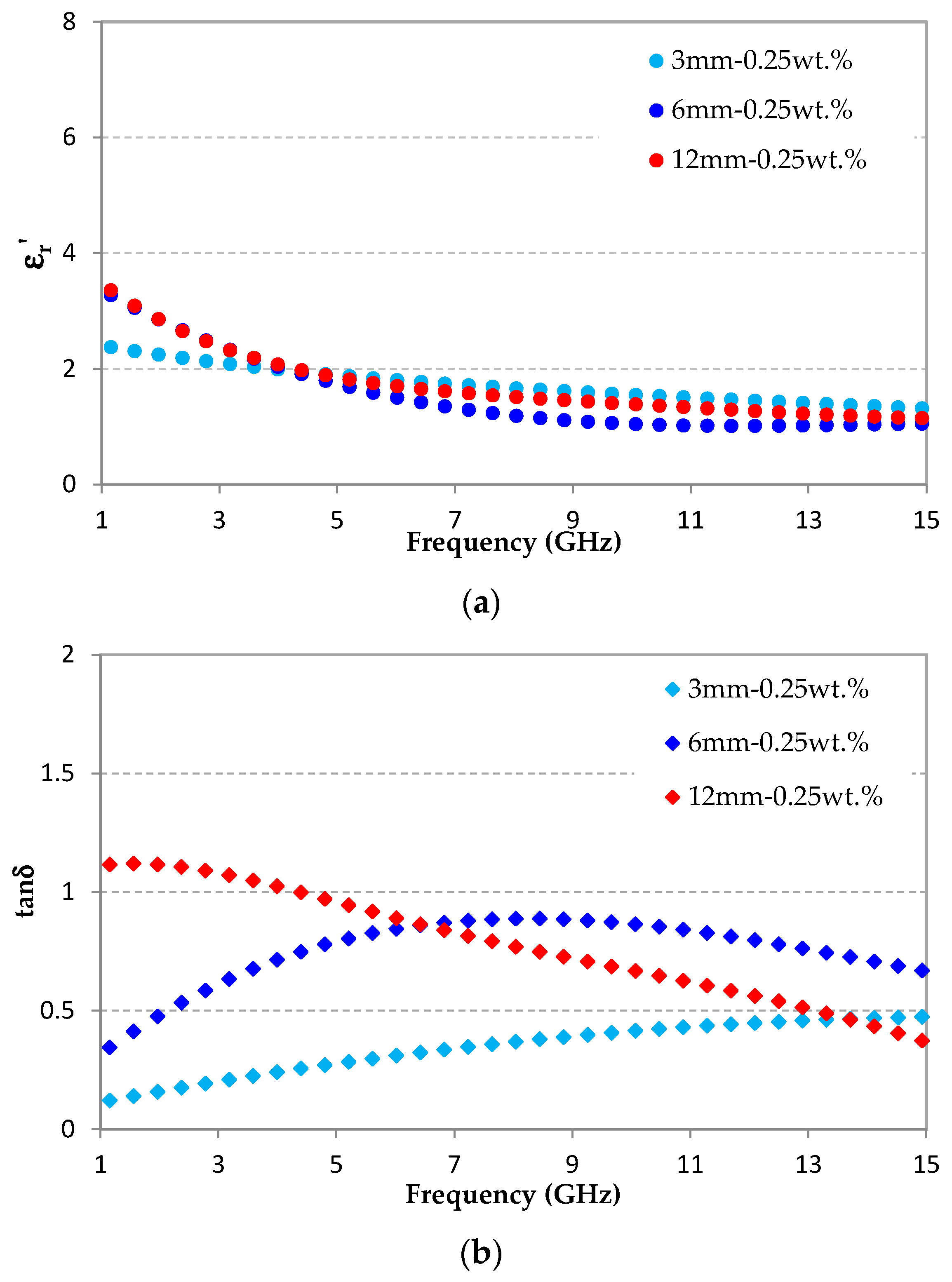
3.2. Effect of Carbon Fiber Lengths on Dielectric Properties of CF-Loaded Composites
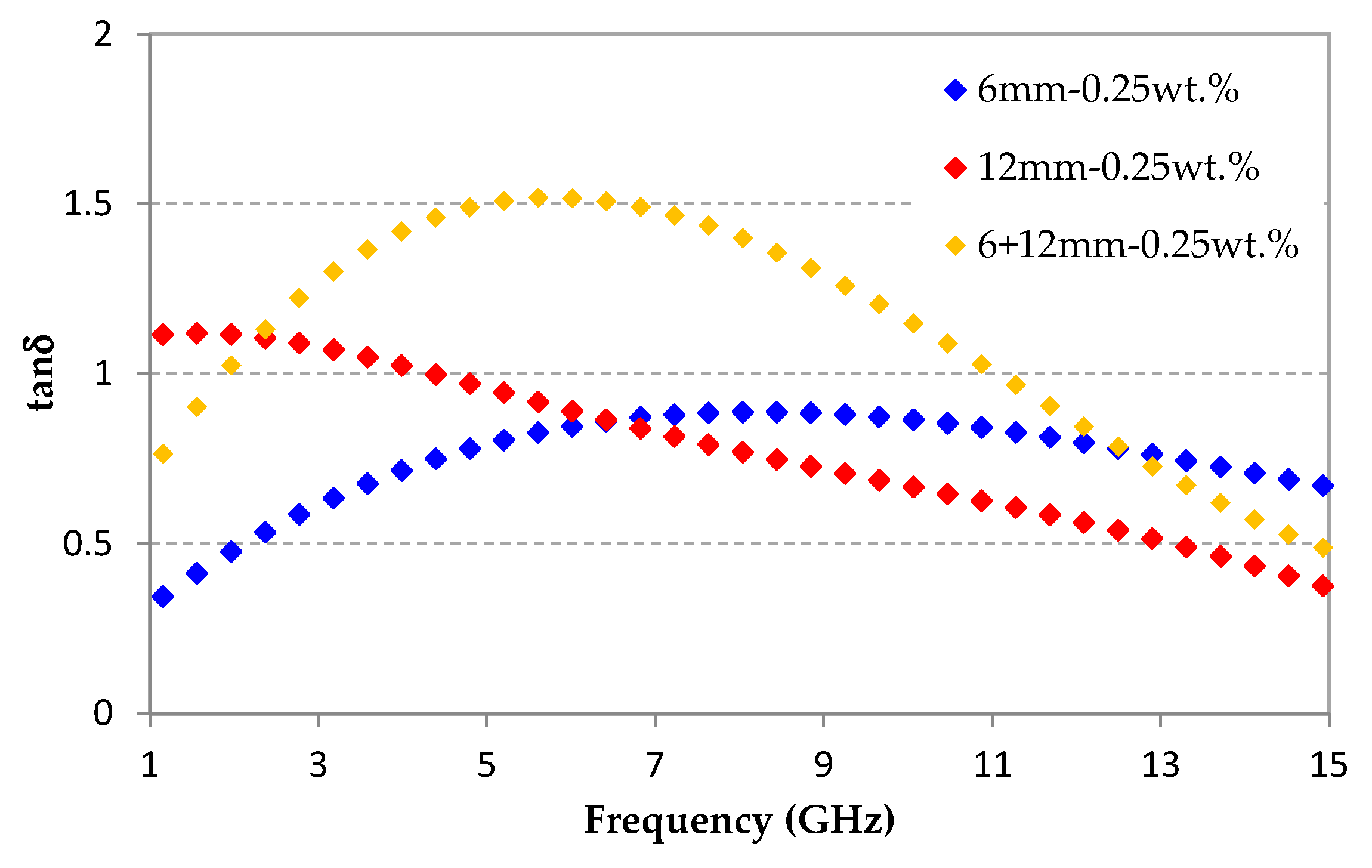
3.3. Towards a Hybrid Absorber Composite Material
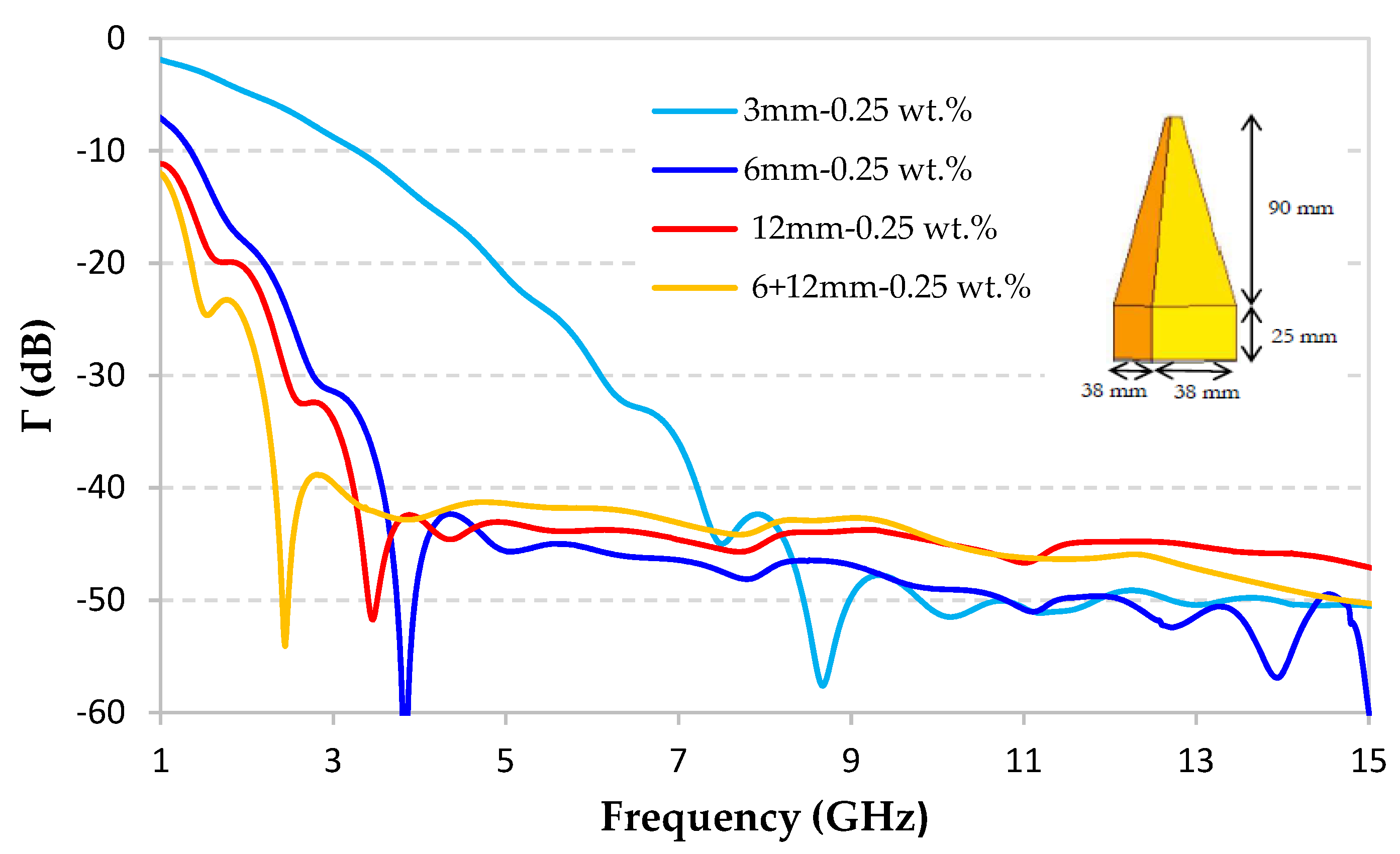
3.4. Simultaion of Absorption Performance of Pyramidal Absorber Based on Hybrid Composite
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Weller, G.C. Effects of electromagnetic radiation on equipment, with special reference to protection relays. In Proceedings of the IEE Colloquium on Electromagnetic Compatibility in the Electricity Supply Industry, London, UK, 9 November 1990; pp. 4/1–4/3. [Google Scholar]
- Paramonova, M.V.; Dyuba, E.K.Y. Study of the effet of electromagnetic fields on humans. Eur. J. Nat. Hist. 2020, 1, 24–27. [Google Scholar]
- Microwave Absorbers-Siepel. Available online: https://siepel.asia/products/rf-microwave/microwave-absorbers/ (accessed on 17 November 2020).
- Emerson & Cuming Anechoic Chambers. Available online: https://www.ecanechoicchambers.com/ (accessed on 17 November 2020).
- Top 10 Anechoic Absorber Considerations for RF and Microwave Applications. Available online: http://www.ets-lindgren.com/sites/etsauthor/General_Brochures/Top%2010%20Anechoic%20Absorber%20Considerations.pdf (accessed on 5 December 2020).
- Reijnders, L. Human health hazards of persistent inorganic and carbon nanoparticles. J. Mater. Sci. 2012, 47, 5061–5073. [Google Scholar] [CrossRef][Green Version]
- Pometcu, L.; Benzerga, R.; Sharaiha, A.; Pouliguen, P. Combination of artificial materials with conventional pyramidal absorbers for microwave absorption improvement. Mater. Res. Bull. 2017, 96, 86–93. [Google Scholar] [CrossRef]
- Holtby, D.G.; Ford, K.L.; Chambers, B. Genetic algorithm optimisation of dual polarised pyramidal absorbers loaded with a binary FSS. In Proceedings of the Loughborough Antennas & Propagation Conference, LAPC 2009, Loughborough, UK, 16–17 November 2009; pp. 217–220. [Google Scholar] [CrossRef]
- Yang, J.; Yang, Y.; Duan, H.; Zhao, G.; Liu, Y. Light-weight epoxy/nickel coated carbon fibers conductive foams for electromagnetic interference shielding. J. Mater. Sci. Mater. Electron. 2017, 28, 5925–5930. [Google Scholar] [CrossRef]
- Banerjee, P.; Bhattacharjee, Y. Lightweight Epoxy-Based Composites for EMI Shielding Applications. Electron. Mater. 2019. [Google Scholar] [CrossRef]
- Liu, S.; Chevali, V.S.; Xu, Z.; Hui, D.; Wang, H. A review of extending performance of epoxy resins using carbon nanomaterials. Compos. Part B Eng. 2018, 136, 197–214. [Google Scholar] [CrossRef]
- Wanasinghe, D.; Aslani, F. A review on recent advancement of electromagnetic interference shielding novel metallic materials and processes. Compos. Part B Eng. 2019, 176, 107207. [Google Scholar] [CrossRef]
- Chen, P.-W.; Chung, D.D.L. Concrete reinforced with up to 0.2 vol% of short carbon fibres. Composites 1993, 24, 33–52. [Google Scholar] [CrossRef]
- Méjean, C.; Pometcu, L.; Benzerga, R.; Sharaiha, A.; Le Paven-thivet, C.; Badard, M.; Pouliguen, P. Electromagnetic absorber composite made of carbon fibers loaded epoxy foam for anechoic chamber application. Mater. Sci. Eng. B 2017, 220, 59–65. [Google Scholar] [CrossRef]
- Pang, H.; Sahu, R.P.; Duan, Y.; Puri, I.K. MnFe2O4-coated carbon nanotubes with enhanced microwave absorption: Effect of CNT content and hydrothermal reaction time. Diam. Relat. Mater. 2019, 96, 31–43. [Google Scholar] [CrossRef]
- Wang, X.; Gong, R.; Li, P.; Liu, L.; Cheng, W. Effects of aspect ratio and particle size on the microwave properties of Fe-Cr-Si-Al alloy flakes. Mater. Sci. Eng. A 2007, 466, 178–182. [Google Scholar] [CrossRef]
- Zimmerman, D.T.; Cardellino, J.D.; Cravener, K.T.; Feather, K.R.; Miskovsky, N.M.; Weisel, G.J. Microwave absorption in percolating metal-insulator composites. Appl. Phys. Lett. 2008, 93, 1–4. [Google Scholar] [CrossRef]
- Duan, Y.; Gu, S.; Zhang, Z.; Wen, M. Characterization of structures and novel magnetic response of Fe 87.5Si 7Al 5.5 alloy processed by ball milling. J. Alloys Compd. 2012, 542, 90–96. [Google Scholar] [CrossRef]
- Liu, L.; Duan, Y.; Guo, J.; Chen, L.; Liu, S. Influence of particle size on the electromagnetic and microwave absorption properties of FeSi/paraffin composites. Phys. B Condens. Matter 2011, 406, 2261–2265. [Google Scholar] [CrossRef]
- Hong, W.; Xiao, P.; Luo, H.; Li, Z. Microwave axial dielectric properties of carbon fiber. Sci. Rep. 2015, 5, 1–8. [Google Scholar] [CrossRef]
- Song, W.; Konstantellos, G.; Li, D.; Lee, K.Y. Short carbon fibre-reinforced epoxy foams with isotropic cellular structure and anisotropic mechanical response produced from liquid foam templates. Compos. Sci. Technol. 2019, 184, 107871. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, H.; Hong, C.; Zhang, X.; Zeng, T. Lightweight chopped carbon fibre reinforced silica-phenolic resin aerogel nanocomposite: Facile preparation, properties and application to thermal protection. Compos. Part A Appl. Sci. Manuf. 2018, 112, 81–90. [Google Scholar] [CrossRef]
- Yamamoto, T.; Makino, Y.; Uematsu, K. Improved mechanical properties of PMMA composites: Dispersion, diffusion and surface adhesion of recycled carbon fiber fillers from CFRP with adsorbed particulate PMMA. Adv. Powder Technol. 2017, 28, 2774–2778. [Google Scholar] [CrossRef]
- Benzerga, R.; Badard, M.; Méjean, C.; El Assal, A.; Le Paven, C.; Sharaiha, A. Carbon Fibers Loaded Composites for Microwave Absorbing Application: Effect of Fiber Length and Dispersion Process on Dielectric Properties. J. Electron. Mater. 2020, 49, 2999–3008. [Google Scholar] [CrossRef]
- Nanni, F.; Travaglia, P.; Valentini, M. Effect of carbon nanofibres dispersion on the microwave absorbing properties of CNF/epoxy composites. Compos. Sci. Technol. 2009, 69, 485–490. [Google Scholar] [CrossRef]
- Chuang, W.; Geng-sheng, J.; Bing-liang, L.; Lei, P.; Ying, F.; Ni, G.; Ke-zhi, L. Dispersion of carbon fibers and conductivity of carbon fiber-reinforced cement-based composites. Ceram. Int. 2017, 43, 15122–15132. [Google Scholar] [CrossRef]
- Chuang, W.; Lei, P.; Bing-liang, L.; Ni, G.; Li-ping, Z.; Ke-zhi, L. Influences of molding processes and different dispersants on the dispersion of chopped carbon fibers in cement matrix. Heliyon 2018, 4. [Google Scholar] [CrossRef] [PubMed]
- Pometcu, L.; Méjean, C.; Benzerga, R.; Sharaiha, A.; Pouliguen, P.; Paven, C. Le On the choice of the dielectric characterization method for foam composite absorber material. Mater. Res. Bull. 2017, 96, 107–114. [Google Scholar] [CrossRef]
- Yadava, R.L. Antenna and Wave Propagation; Eastern ec.; PHI Learning Private Limited: New Delhi, India, 2012; ISBN 9788120342910. [Google Scholar]
- Fenner, R.A.; Rothwell, E.J.; Frasch, L.L. A comprehensive analysis of free-space and guided-wave techniques for extracting the permeability and permittivity of materials using reflection-only measurements. Radio Sci. 2012, 47. [Google Scholar] [CrossRef]
- Holloway, C.L.; DeLyser, R.R.; German, R.F.; McKenna, P.; Kanda, M. Comparison of electromagnetic absorber used in anechoic and semi-anechoic chambers for emissions and immunity testing of digital devices. IEEE Trans. Electromagn. Compat. 1997, 39, 33–47. [Google Scholar] [CrossRef]
- Inceoglu, F.; Ville, J.; Ghamri, N.; Durin, A.; Valette, R.; Vergnes, B. A Study of Fiber Breakage During Compounding of Glass Fiber Reinforced Composites. In Proceedings of the Polymer Processing Society 26th Annual Meeting, Banff, AB, Canada, 4–8 July 2010. [Google Scholar]
- Wang, J.; Geng, C.; Luo, F.; Liu, Y.; Wang, K.; Fu, Q.; He, B. Shear induced fiber orientation, fiber breakage and matrix molecular orientation in long glass fiber reinforced polypropylene composites. Mater. Sci. Eng. A 2011, 528, 3169–3176. [Google Scholar] [CrossRef]
- Dang, Z.M.; Shehzad, K.; Zha, J.W.; Mujahid, A.; Hussain, T.; Nie, J.; Shi, C.Y. Complementary percolation characteristics of carbon fillers based electrically percolative thermoplastic elastomer composites. Compos. Sci. Technol. 2011, 72, 28–35. [Google Scholar] [CrossRef]
- Duan, H.; Zhu, H.; Yang, J.; Gao, J.; Yang, Y.; Xu, L.; Zhao, G.; Liu, Y. Effect of carbon nanofiller dimension on synergistic EMI shielding network of epoxy/metal conductive foams. Compos. Part A Appl. Sci. Manuf. 2019, 118, 41–48. [Google Scholar] [CrossRef]
- Shehzad, K.; Dang, Z.M.; Ahmad, M.N.; Sagar, R.U.R.; Butt, S.; Farooq, M.U.; Wang, T.B. Effects of carbon nanotubes aspect ratio on the qualitative and quantitative aspects of frequency response of electrical conductivity and dielectric permittivity in the carbon nanotube/polymer composites. Carbon 2013, 54, 105–112. [Google Scholar] [CrossRef]
- Khosla, A.; Shah, S.; Shiblee, M.N.I.; Mir, S.H.; Nagahara, L.A.; Thundat, T.; Shekar, P.K.; Kawakami, M.; Furukawa, H. Carbon fiber doped thermosetting elastomer for flexible sensors: Physical properties and microfabrication. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef]
- Theravalappil, R.; Svoboda, P.; Vilcakova, J.; Poongavalappil, S.; Slobodian, P.; Svobodova, D. A comparative study on the electrical, thermal and mechanical properties of ethylene-octene copolymer based composites with carbon fillers. Mater. Des. 2014, 60, 458–467. [Google Scholar] [CrossRef]
- Méjean, C. Élaboration de Nouveaux Matériaux Absorbants: Application en Chambres Anéchoïques. Ph.D. Thesis, Université Bretagne Loire, Brest, France, 2017. [Google Scholar]
- Eddib, A.A.; Chung, D.D.L. Electric permittivity of carbon fiber. Carbon 2019, 143, 475–480. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Y.; Zhou, H.; Nie, M.; Wang, Q.; Hua, Z. Polyurethane/carbon fiber composite tubular electrode featuring three-dimensional interpenetrating conductive network. Carbon 2018, 139, 999–1009. [Google Scholar] [CrossRef]
- Hong, W.; Xiao, P.; Luo, H. Structural magnetic loss of vertical aligned carbon fibres. J. Appl. Phys. 2013, 113. [Google Scholar] [CrossRef]
- Cao, M.S.; Song, W.L.; Hou, Z.L.; Wen, B.; Yuan, J. The effects of temperature and frequency on the dielectric properties, electromagnetic interference shielding and microwave-absorption of short carbon fiber/silica composites. Carbon 2010, 48, 788–796. [Google Scholar] [CrossRef]
- Ling, J.; Zhai, W.; Feng, W.; Shen, B.; Zhang, J.; Zheng, W.G. Facile preparation of lightweight microcellular polyetherimide/graphene composite foams for electromagnetic interference shielding. ACS Appl. Mater. Interfaces 2013, 5, 2677–2684. [Google Scholar] [CrossRef]
- Zang, Y.; Xia, S.; Li, L.; Ren, G.; Chen, Q.; Quan, H.; Wu, Q. Microwave absorption enhancement of rectangular activated carbon fibers screen composites. Compos. Part. B Eng. 2015, 77, 371–378. [Google Scholar] [CrossRef]
- Pometcu, L. Matériaux et Formes Innovants Pour l’Atténuation en Hyper Fréquences. Ph.D. Thesis, Université Bretagne Loire, Brest, France, 8 September 2016. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Breiss, H.; El Assal, A.; Benzerga, R.; Méjean, C.; Sharaiha, A. Long Carbon Fibers for Microwave Absorption: Effect of Fiber Length on Absorption Frequency Band. Micromachines 2020, 11, 1081. https://doi.org/10.3390/mi11121081
Breiss H, El Assal A, Benzerga R, Méjean C, Sharaiha A. Long Carbon Fibers for Microwave Absorption: Effect of Fiber Length on Absorption Frequency Band. Micromachines. 2020; 11(12):1081. https://doi.org/10.3390/mi11121081
Chicago/Turabian StyleBreiss, Hanadi, Aicha El Assal, Ratiba Benzerga, Chloé Méjean, and Ala Sharaiha. 2020. "Long Carbon Fibers for Microwave Absorption: Effect of Fiber Length on Absorption Frequency Band" Micromachines 11, no. 12: 1081. https://doi.org/10.3390/mi11121081
APA StyleBreiss, H., El Assal, A., Benzerga, R., Méjean, C., & Sharaiha, A. (2020). Long Carbon Fibers for Microwave Absorption: Effect of Fiber Length on Absorption Frequency Band. Micromachines, 11(12), 1081. https://doi.org/10.3390/mi11121081