Electromechanical Analysis of Flexoelectric Nanosensors Based on Nonlocal Elasticity Theory
Abstract
1. Introduction
2. Nonlocal Elasticity Theory of Flexoelectric Materials
3. Theoretical Formulation of Flexoelectric Sensors with the Nonlocal Effect
4. Numerical Results and Discussion
4.1. Subjected to Uniformly Distributed Loads and a Concentrated Force
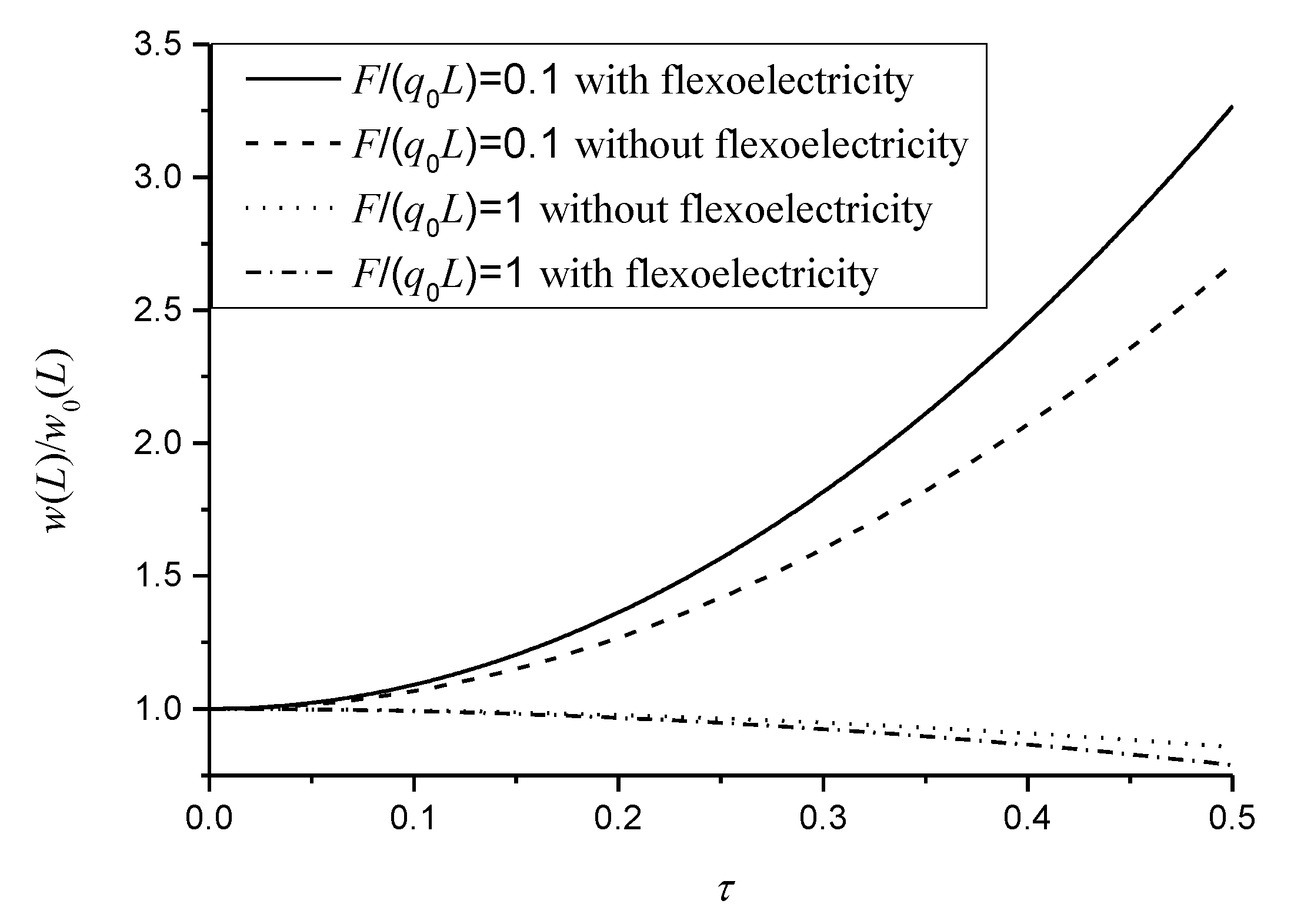
4.2. Subjected to Sinusoidal Distributed Loads and a Concentrated Force
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tagantsev, A.K. Piezoelectricity and flexoelectricity in crystalline dielectrics. Phys. Rev. B 1986, 34, 5883. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Large flexoelectric polarization in ceramic lead magnesium niobate. Appl. Phys. Lett. 2001, 79, 4420–4422. [Google Scholar] [CrossRef]
- Zubko, P.; Catalan, G.; Tagantsev, A.K. Flexoelectric effect in solids. Ann. Rev. Mater. Res. 2013, 43, 387–421. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Strain-gradient-induced electric polarization in lead zirconate titanate ceramics. Appl. Phys. Lett. 2003, 82, 3293–3295. [Google Scholar] [CrossRef]
- Shen, S.P.; Hu, S.L. A theory of flexoelectricity with surface effect for elastic dielectrics. J. Mech. Phys. Solids 2010, 58, 655–677. [Google Scholar] [CrossRef]
- Wang, B.; Gu, Y.; Zhang, S.; Chen, L.Q. Flexoelectricity in solids: Progress, challenges, and perspectives. Prog. Mater. Sci. 2019, 106, 100570. [Google Scholar] [CrossRef]
- Mashkevich, V.S.; Tolpygo, K.B. Electrical, optical and elastic properties of diamond type crystals: I. Sov. Phys. JETP 1957, 32, 435–439. [Google Scholar]
- Tagantsev, A.K. Electric polarization in crystals and its response to thermal and elastic perturbations. Phase Transit. 1991, 35, 119–203. [Google Scholar] [CrossRef]
- Majdoub, M.S.; Sharma, P.; Cagin, T. Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys. Rev. B 2008, 77, 125424. [Google Scholar] [CrossRef]
- Mohammadi, P.; Liu, L.P.; Sharma, P. A theory of flexoelectric membranes and effective properties of heterogeneous membranes. J Appl. Mech. 2014, 81, 011007. [Google Scholar] [CrossRef]
- Deng, Q.; Liu, L.; Sharma, P. Flexoelectricity in soft materials and biological membranes. J. Mech. Phys. Solids 2014, 62, 209–227. [Google Scholar] [CrossRef]
- Zhang, Z.; Yan, Z.; Jiang, L. Flexoelectric effect on the electroelastic responses and vibrational behaviors of a piezoelectric nanoplate. J. Appl. Phys. 2014, 116, 014307. [Google Scholar] [CrossRef]
- He, L.; Lou, J.; Zhang, A.; Wu, H.; Du, J.; Wang, J. On the coupling effects of piezoelectricity and flexoelectricity in piezoelectric nanostructures. AIP Adv. 2017, 7, 105106. [Google Scholar] [CrossRef]
- Liang, X.; Hu, S.; Shen, S. Effects of surface and flexoelectricity on a piezoelectric nanobeam. Smart Mater. Struct. 2014, 23, 035020. [Google Scholar] [CrossRef]
- Zhou, Z.D.; Yang, C.P.; Su, Y.X.; Huang, R.; Lin, X.H. Electromechanical coupling in piezoelectric nanobeams due to flexoelectric effect. Smart Mater. Struct. 2017, 26, 095025. [Google Scholar] [CrossRef]
- Deng, Q.; Kammoun, M.; Erturk, A.; Sharma, P. Nanoscale flexoelectric energy harvesting. Int. J. Solids Struct. 2014, 51, 3218–3225. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, R.; Hu, S.; Shen, S. Flexoelectric energy harvesters based on Timoshenko laminated beam theory. J. Intell. Mater. Syst. Struct. 2017, 28, 2064–2073. [Google Scholar] [CrossRef]
- Su, Y.; Lin, X.; Huang, R.; Zhou, Z. Analytical electromechanical modeling of nanoscale flexoelectric energy harvesting. Appl. Sci. 2019, 9, 2273. [Google Scholar] [CrossRef]
- Lu, Q.; Zhou, S.; Li, A. Size-dependent bending of an electro-elastic bilayer nanobeam due to flexoelectricity and strain gradient elastic effect. Compos. Struct. 2016, 135, 167–175. [Google Scholar]
- Su, Y.X.; Zhou, Z.D.; Yang, F.P. Electromechanical analysis of bilayer piezoelectric sensors due to flexoelectricity and strain gradient elasticity. AIP Adv. 2019, 9, 015207. [Google Scholar] [CrossRef]
- Chu, L.; Dui, G.; Ju, C. Flexoelectric effect on the bending and vibration responses of functionally graded piezoelectric nanobeams based on general modified strain gradient theory. Compos. Struct. 2018, 186, 39–49. [Google Scholar] [CrossRef]
- Xiang, S.; Lee, K.Y.; Li, X.F. Elasticity solution of functionally graded beams with consideration of the flexoelectric effect. J. Phys. D: Appl. Phys. 2020, 53, 105301. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface wave. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer Science & Business Media: New York, NY, USA, 2002. [Google Scholar]
- Reddy, J.N. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Wang, C.Y.; Murmu, T.; Adhikari, S. Mechanisms of nonlocal effect on the vibration of nanoplates. Appl. Phys. Lett. 2011, 98, 153101. [Google Scholar] [CrossRef]
- Bakhtiari-Nejad, F.; Nazemizadeh, M. Size-dependent dynamic modeling and vibration analysis of MEMS/NEMS-based nanomechanical beam based on the nonlocal elasticity theory. Acta Mech. 2016, 227, 1363–1379. [Google Scholar] [CrossRef]
- Li, L.; Li, X.; Hu, Y. Free vibration analysis of nonlocal strain gradient beams mode of functionally graded material. Int. J. Eng. Sci. 2016, 102, 77–92. [Google Scholar] [CrossRef]
- Li, C.; Yao, L.; Chen, W.; Li, S. Comments on nonlocal effects in nano-cantilever beams. Int. J. Eng. Sci. 2015, 87, 47–57. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Surface effects on the vibration behavior of flexoelectric nanobeams based on nonlocal elasticity theory. Eur. Phys. J. Plus 2017, 132, 19. [Google Scholar] [CrossRef]
- Barati, M.R. Closed-form nonlinear frequency of flexoelectric nanobeams with surface and nonlocal effects under closed circuit electric field. Mater. Res. Express 2018, 5, 025008. [Google Scholar] [CrossRef]
- Masoumi, A.; Amiri, A.; Talebitooti, R. Flexoelectric effects on wave propagation responses of piezoelectric nanobeams via nonlocal strain gradient higher order beam model. Mater. Res. Express 2019, 6, 1050d5. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and is applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Kleinert, H. Gauge Fields in Condensed Matter; World Scientific: Singapore, 1989; Volume 2, ISBN 9971-50-210-0. [Google Scholar]
- Abdollahi, A.; Peco, C.; Millan, D.; Arroyo, M.; Arias, I. Computational evaluation of the flexoelectric effect in dielectric solids. J. Appl. Phys. 2014, 116, 093502. [Google Scholar] [CrossRef]
- Kwon, S.; Huang, W.B.; Zhang, S.J.; Yuan, F.G.; Jiang, X.N. Flexoelectric sensing using a multilayered barium strontium titanate structure. Smart Mater. Struct. 2013, 22, 115017. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Zhou, Z. Electromechanical Analysis of Flexoelectric Nanosensors Based on Nonlocal Elasticity Theory. Micromachines 2020, 11, 1077. https://doi.org/10.3390/mi11121077
Su Y, Zhou Z. Electromechanical Analysis of Flexoelectric Nanosensors Based on Nonlocal Elasticity Theory. Micromachines. 2020; 11(12):1077. https://doi.org/10.3390/mi11121077
Chicago/Turabian StyleSu, Yaxuan, and Zhidong Zhou. 2020. "Electromechanical Analysis of Flexoelectric Nanosensors Based on Nonlocal Elasticity Theory" Micromachines 11, no. 12: 1077. https://doi.org/10.3390/mi11121077
APA StyleSu, Y., & Zhou, Z. (2020). Electromechanical Analysis of Flexoelectric Nanosensors Based on Nonlocal Elasticity Theory. Micromachines, 11(12), 1077. https://doi.org/10.3390/mi11121077




