Electroosmotic Flow of Non-Newtonian Fluid in Porous Polymer Membrane at High Zeta Potentials
Abstract
1. Introduction
2. Problem Formulation
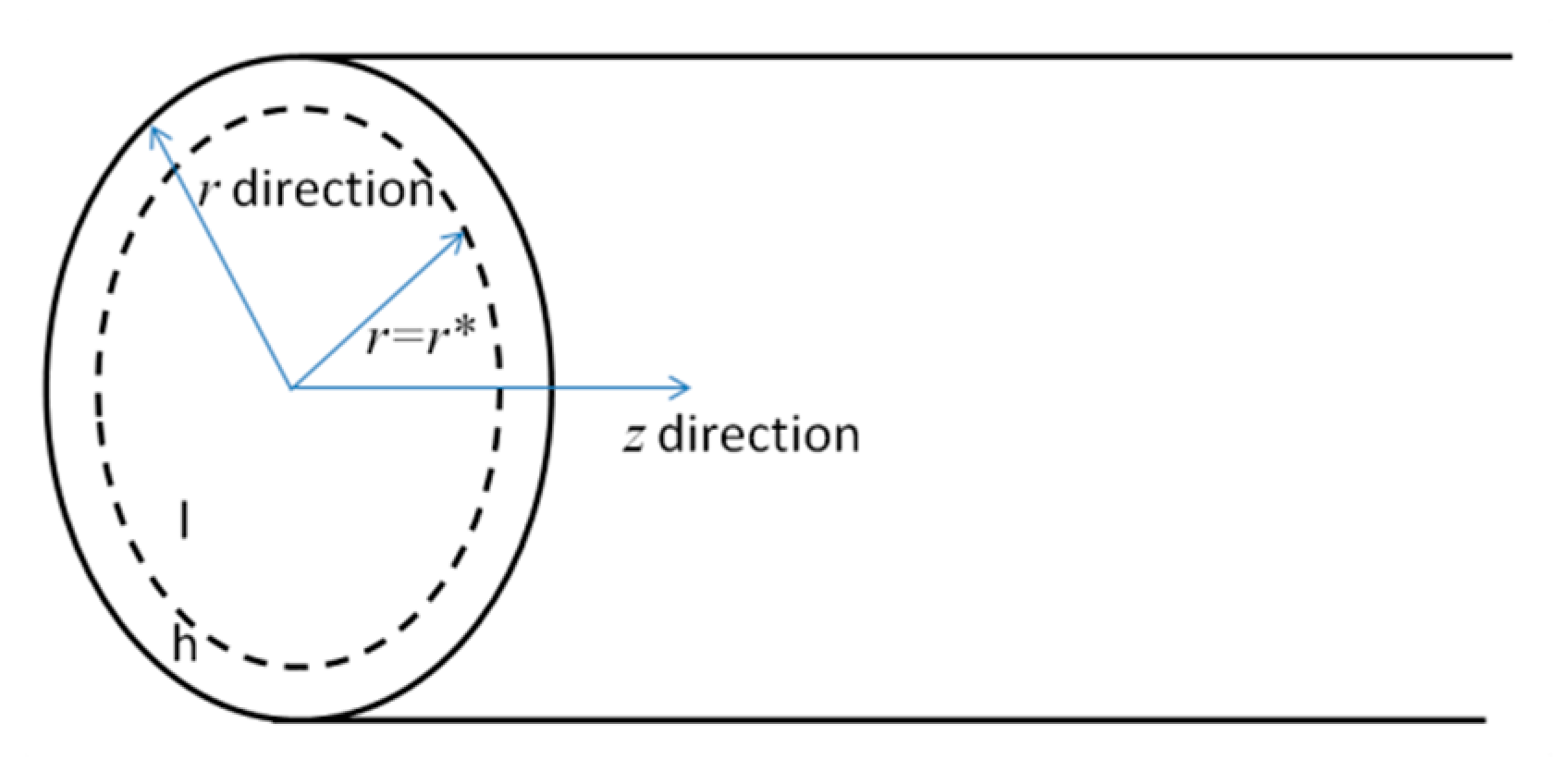
2.1. Mathematical Model for Electroosmotic Flow (EOF) of Power-Law Fluid in a Single Pore
- (1)
- According to microfluidic transport of liquid in microfluidic devices, the pore radius is much less than its length [1] and hence the flow velocity is assumed to be only along z-axis;
- (2)
- Each single pore is filled by ideal symmetric electrolyte solution with constant permittivity and no interaction between ions occurs [26];
- (3)
- The thickness of EDL is much less than the pore radius and EDLs will not overlap [26];
- (4)
- (5)
- Gravitational force is negligible [2], no external pressure gradient is imposed and an electric field is applied over the cross-section of microchannel;
- (6)
- An incompressible, laminar, and fully developed flow is assumed.
2.2. Mathematical Model for EOF of Power-Law Fluid through Porous Polymer Membrane
3. Results and Discussion
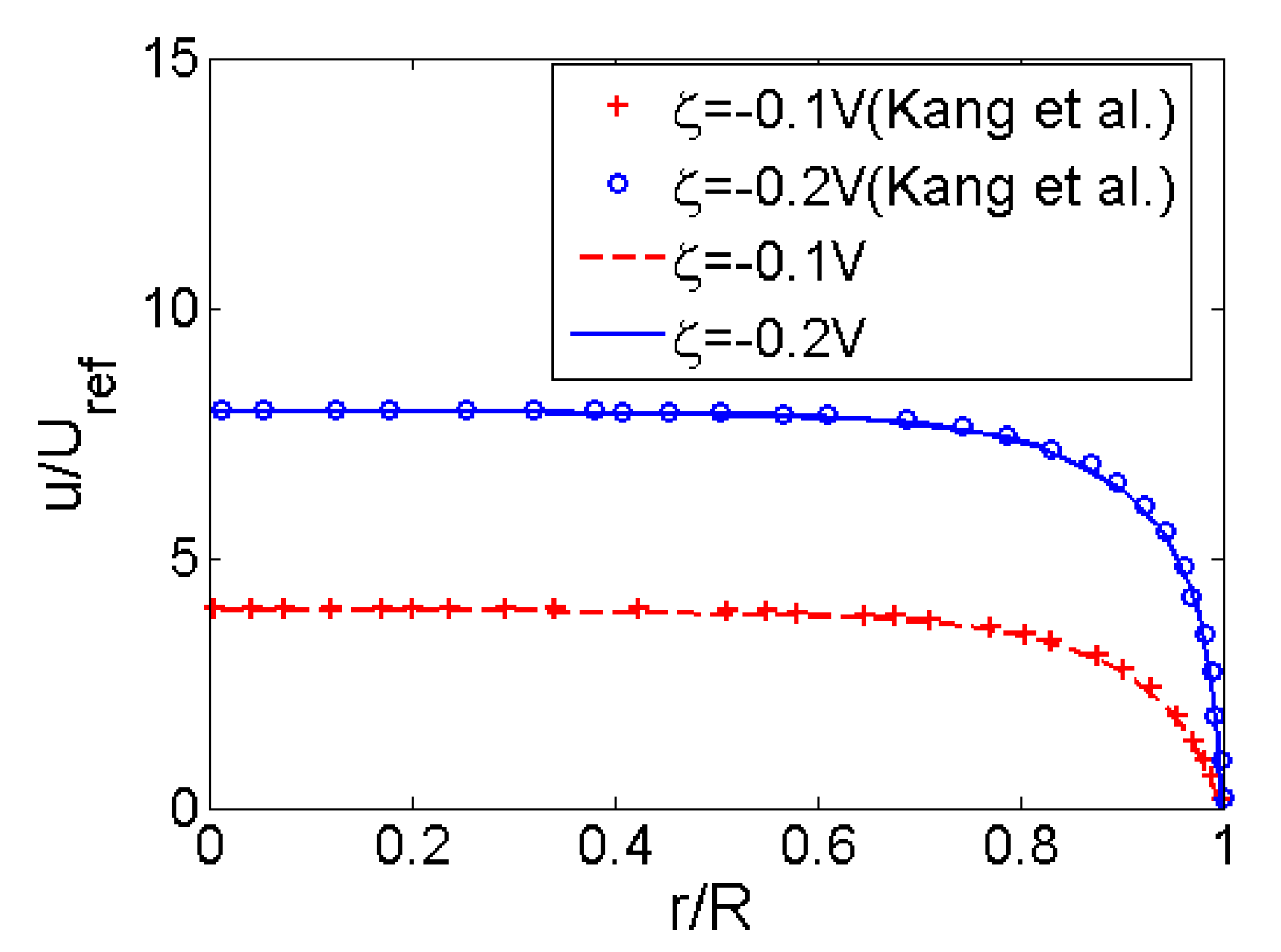
3.1. EOF of Power-Law Fluid in a Single Pore
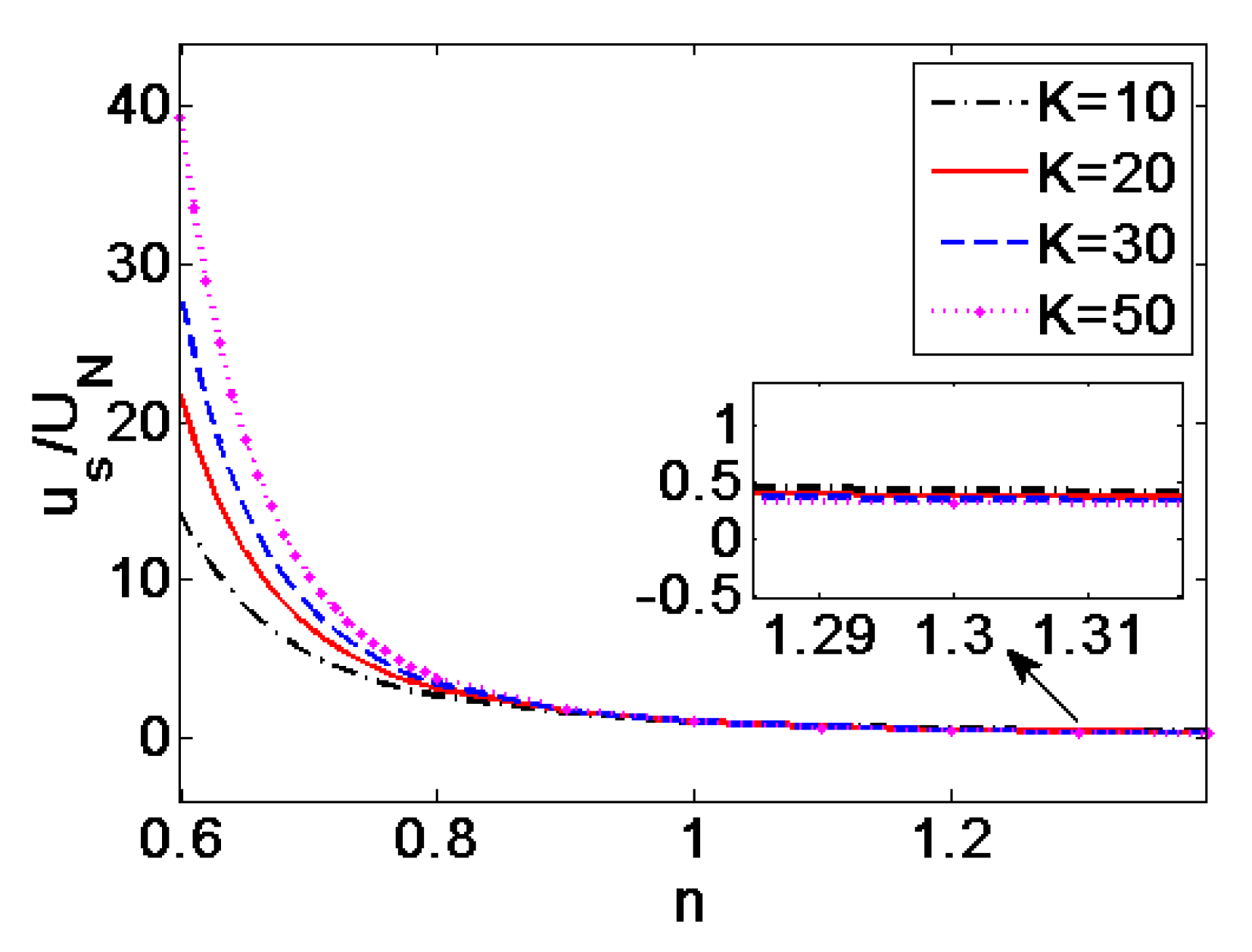
3.2. EOF of Power-Law Fluid through Porous Polymer Membrane
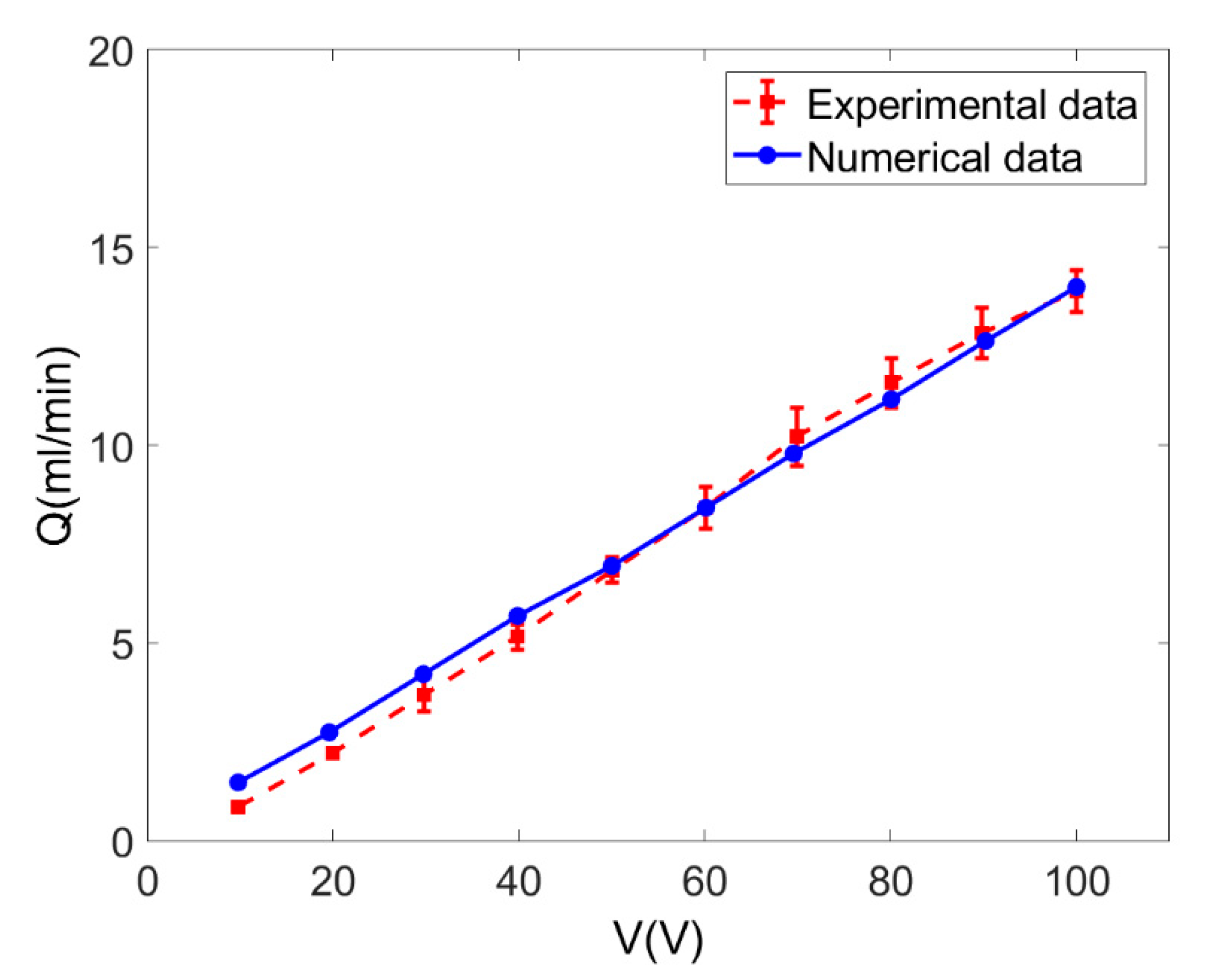
3.2.1. Effect of the Applied Electric Voltage
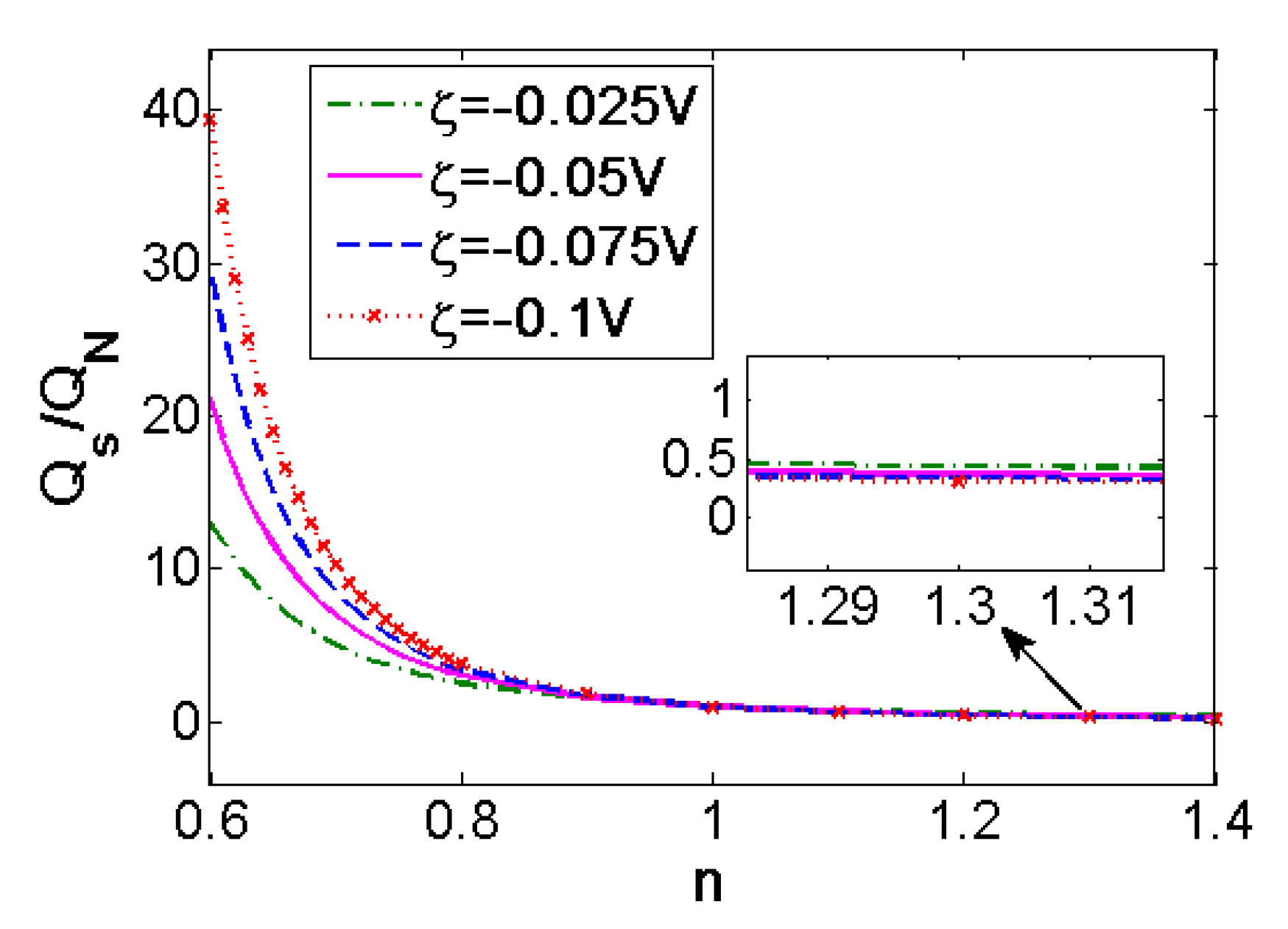
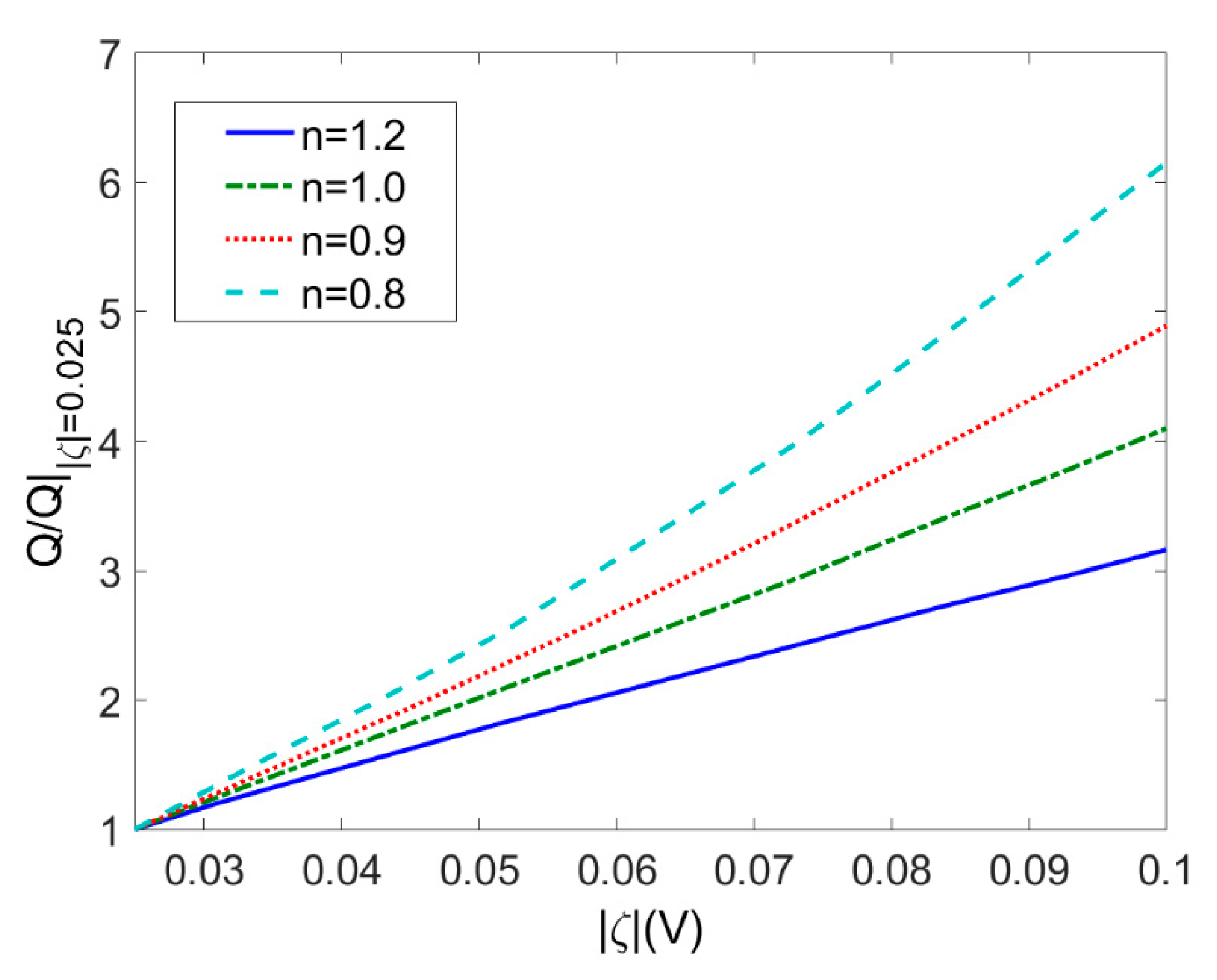
3.2.2. Effect of the Zeta Potential
3.2.3. Effect of the Geometric Properties of the Membrane
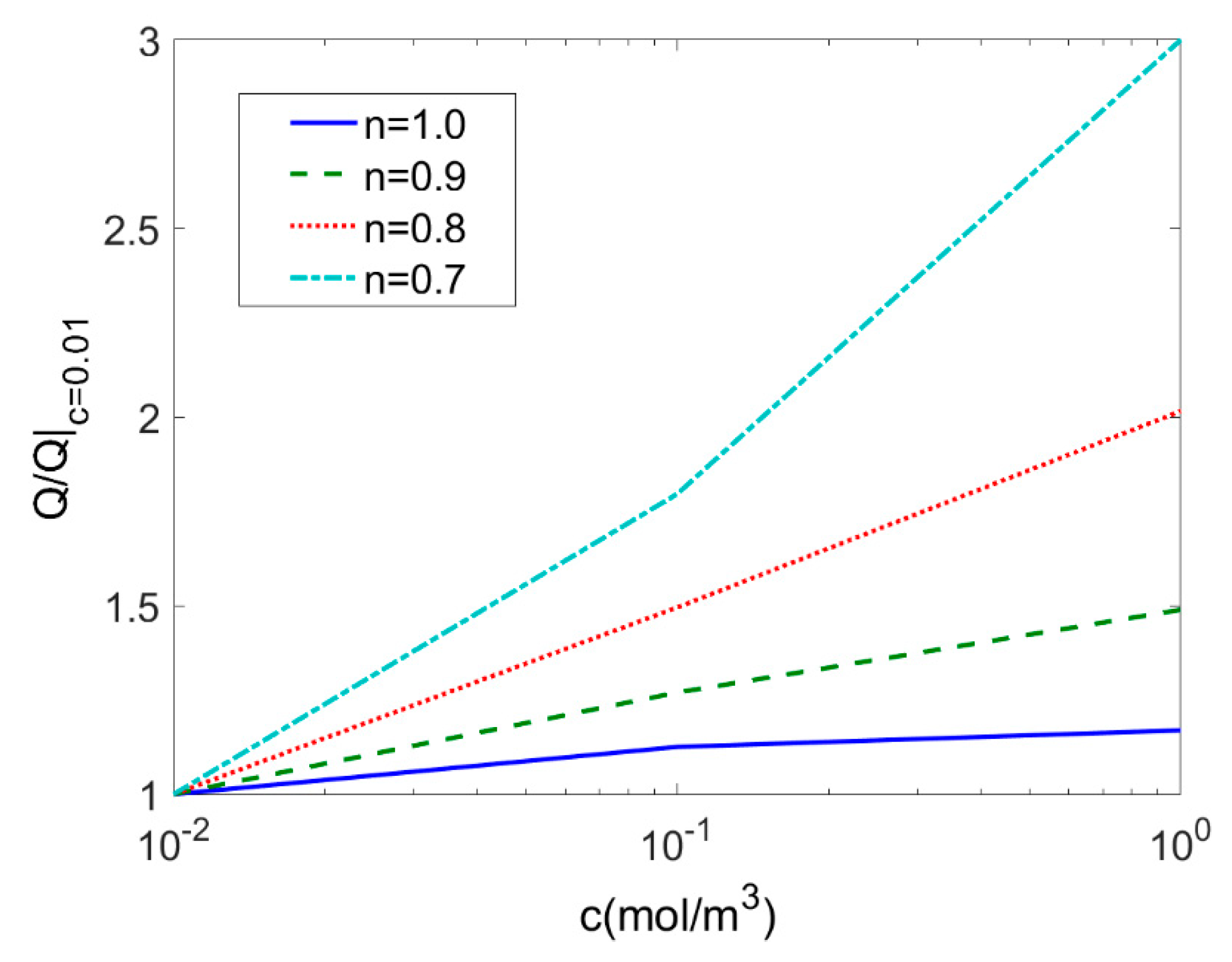
3.2.4. Effect of the Electrolyte Solution Concentration
4. Conclusions
- The characteristics of EOF for power-law fluids in a single pore is described in terms of velocity profile, average velocity and flow rate at first. The velocity profile shows more plug-like shape as the flow behavior index decreases (n < 1). A high zeta potential or a high dimensionless electrokinetic width can generate higher average velocity especially for shear thinning fluids in single pore.
- The mathematical model for EOF of power-law fluid through porous polymer membrane is presented by means of the assumption that porous polymer membrane has Gaussian distribution of pores. The performance of polymer porous membrane structure EO pump is evaluated from the perspective of the dependence of total flow rate on different parameters. The total flow rate of power-law fluid is increased with the increment of applied electric voltage, zeta potential, and concentration of solution. The influence of these parameters on total flow rate is much more evident for shear thinning fluids (n < 1) than that for shear thickening fluids (n > 1). Therefore, to attain high flow rate, high zeta potential, electrolyte solution with high ion density, thin membrane or shear thinning property of working liquid is desired in porous-structure EO pump applications.
Author Contributions
Funding
Conflicts of Interest
References
- Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering flows in small devices. Ann. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef]
- Bruus, H. Theoretical Microfluidics; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Bayraktar, T.; Pidugu, S.B. Characterization of liquid flows in microfluidic systems. Int. J. Heat Mass Transf. 2006, 49, 815–824. [Google Scholar] [CrossRef]
- Hunter, R.J. Zeta Potential in Colloid Science: Principles and Applications; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Karniadakis, G.E.; Beskok, A.; Aluru, N.R. Microflows and Nanoflows: Fundamentals and Simulation; Springer: New York, NY, USA, 2005; p. xxli. [Google Scholar]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, S.; Gendhar, B.; Chang, C.; Chang, K.B.; Li, G.; Zhao, M.; Liu, S.; Chang, K.B.; Zhao, M. Electroosmotic pumps for microflow analysis. Trac. Trend Anal. Chem. 2009, 28, 64–74. [Google Scholar] [CrossRef]
- Prakash, P.; Grissom, M.D.; Rahn, C.D.; Zydney, A.L. Development of an electroosmotic pump for high performance actuation. J. Membr. Sci. 2006, 286, 153–160. [Google Scholar] [CrossRef]
- Min, J.Y.; Kim, D.; Kim, S.J. A novel approach to analysis of electroosmotic pumping through rectangular-shaped microchannels. Sens. Actuators B Chem. 2006, 120, 305–312. [Google Scholar] [CrossRef]
- Yao, S.; Myers, A.M.; Posner, J.D.; Rose, K.A.; Santiago, J.G. Electroosmotic pumps fabricated from porous silicon membranes. J. Microelectromech. Syst. 2006, 15, 717–728. [Google Scholar] [CrossRef]
- Yao, S.; Hertzog, D.E.; Zeng, S.; Mikkelsen, J.C.; Santiago, J.G. Porous glass electroosmotic pumps: Design and experiments. J. Colloid Interface Sci. 2003, 268, 143–153. [Google Scholar] [CrossRef]
- Yao, S.; Santiago, J.G. Porous glass electroosmotic pumps: Theory. J. Colloid Interface Sci. 2003, 268, 133–142. [Google Scholar] [CrossRef]
- Kim, D.; Posner, J.D.; Santiago, J.G. High flow rate per power electroosmotic pumping using low ion density solvents. Sens. Actuators A Phys. 2008, 141, 201–212. [Google Scholar] [CrossRef]
- Ai, Y.; Yalcin, S.E.; Gu, D.; Baysal, O.; Baumgart, H.; Qian, S.; Beskok, A. A low-voltage nano-porous electroosmotic pump. J. Colloid Interface Sci. 2010, 350, 465–470. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Wang, L.; Xue, J. Low-voltage electroosmotic pumping using polyethylene terephthalate track-etched membrane. Nucl. Instrum. Mech. B 2012, 286, 223–228. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Zhu, X.; Wang, Y.; Xue, J. Low-voltage electroosmotic pumps fabricated from track-etched polymer membranes. Lab Chip 2012, 12, 1710–1716. [Google Scholar] [CrossRef] [PubMed]
- Kwon, K.; Park, C.-W.; Kim, D. High-flowrate, compact electroosmotic pumps with porous polymer track-etch membranes. Sens. Actuators A Phys. 2012, 175, 108–115. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, S. Analytical solutions for velocity, temperature and concentration distribution in electroosmotic microchannel flows of a non-newtonian bio-fluid. Anal. Chim. Acta 2006, 559, 15–24. [Google Scholar] [CrossRef]
- Chakraborty, S. Electroosmotically driven capillary transport of typical non-newtonian biofluids in rectangular microchannels. Anal. Chim. Acta 2007, 605, 175–184. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Zholkovskij, E.; Masliyah, J.H.; Yang, C. Analysis of electroosmotic flow of power-law fluids in a slit microchannel. J. Colloid Interface Sci. 2008, 326, 503–510. [Google Scholar] [CrossRef]
- Tang, G.H.; Li, X.F.; He, Y.L.; Tao, W.Q. Electroosmotic flow of non-newtonian fluid in microchannels. J. Non Newton. Fluid Mech. 2009, 157, 133–137. [Google Scholar] [CrossRef]
- Bharti, R.P.; Harvie, D.J.E.; Davidson, M.R. Electroviscous effects in steady fully developed flow of a power-law liquid through a cylindrical microchannel. Int. J. Heat Fluid Flow 2009, 30, 804–811. [Google Scholar] [CrossRef]
- Deng, S.Y.; Jian, Y.J.; Bi, Y.H.; Chang, L.; Wang, H.J.; Liu, Q.S. Unsteady electroosmotic flow of power-law fluid in a rectangular microchannel. Mech. Res. Commun. 2012, 39, 9–14. [Google Scholar] [CrossRef]
- Deng, S.Y. The parametric study of electroosmotically driven flow of power-law fluid in a cylindrical microcapillary at high zeta potential. Micromachines 2017, 8, 344. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.Y.; Deng, S.Y.; Chen, Y.Q. Periodical pressure-driven electrokinetic flow of power-law fluids through a rectangular microchannel. J. Non-Newton. Fluid Mech. 2014, 203, 38–50. [Google Scholar] [CrossRef]
- Vasu, N.; De, S. Electroosmotic flow of power-law fluids at high zeta potentials. Colloids Surf. A 2010, 368, 44–52. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. Nonlinear smoluchowski velocity for electroosmosis of power-law fluids over a surface with arbitrary zeta potentials. Electrophoresis 2010, 31, 973–979. [Google Scholar] [CrossRef] [PubMed]
- Philip, J.R.; Wooding, R.A. Solution of the poisson–boltzmann equation about a cylindrical particle. J. Chem. Phys. 1970, 52, 953–959. [Google Scholar] [CrossRef]
- Levine, S.; Marriott, J.R.; Robinson, K. Theory of electrokinetic flow in a narrow parallel-plate channel. J. Chem. Soc. Faraday Trans. 1975, 71, 1–11. [Google Scholar] [CrossRef]
- Kang, Y.J.; Yang, C.; Huang, X.Y. Dynamic aspects of electroosmotic flow in a cylindrical microcapillary. Int. J. Eng. Sci. 2002, 40, 2203–2221. [Google Scholar] [CrossRef]
- Wang, M.; Chen, S. Electroosmosis in homogeneously charged micro- and nanoscale random porous media. J. Colloid Interface Sci. 2007, 314, 264–273. [Google Scholar] [CrossRef]
- Hernández, A.; Calvo, J.I.; Prádanos, P.; Tejerina, F. Pore size distributions in microporous membranes. A critical analysis of the bubble point extended method. J. Membr. Sci. 1996, 112, 1–12. [Google Scholar] [CrossRef]
- Tripp, J.A.; Svec, F.; Fréchet, J.M.J.; Zeng, S.; Mikkelsen, J.C.; Santiago, J.G. High-pressure electroosmotic pumps based on porous polymer monoliths. Sens. Actuators B Chem. 2004, 99, 66–73. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, S.; Zeng, Y.; Li, M.; Liang, C. Electroosmotic Flow of Non-Newtonian Fluid in Porous Polymer Membrane at High Zeta Potentials. Micromachines 2020, 11, 1046. https://doi.org/10.3390/mi11121046
Deng S, Zeng Y, Li M, Liang C. Electroosmotic Flow of Non-Newtonian Fluid in Porous Polymer Membrane at High Zeta Potentials. Micromachines. 2020; 11(12):1046. https://doi.org/10.3390/mi11121046
Chicago/Turabian StyleDeng, Shuyan, Yukun Zeng, Mingying Li, and Cuixiang Liang. 2020. "Electroosmotic Flow of Non-Newtonian Fluid in Porous Polymer Membrane at High Zeta Potentials" Micromachines 11, no. 12: 1046. https://doi.org/10.3390/mi11121046
APA StyleDeng, S., Zeng, Y., Li, M., & Liang, C. (2020). Electroosmotic Flow of Non-Newtonian Fluid in Porous Polymer Membrane at High Zeta Potentials. Micromachines, 11(12), 1046. https://doi.org/10.3390/mi11121046



