Split-Band Interferometry-Assisted Phase Unwrapping for the Phase Ambiguities Correction
Abstract
:1. Introduction
2. Methods
2.1. Rationale of Split-Band Interferometry
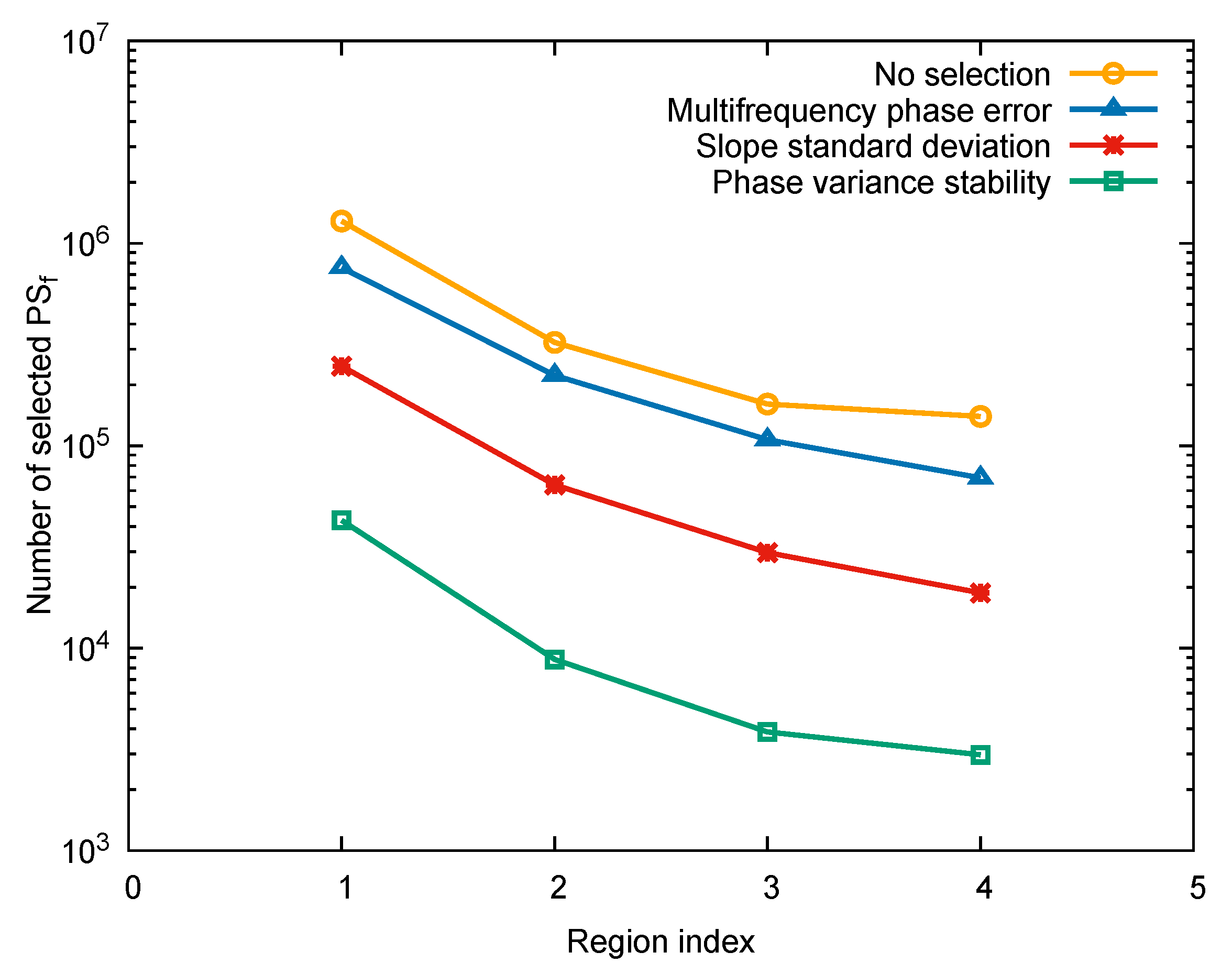
2.2. Detection of Frequency-Persistent Scatterers
2.2.1. Multifrequency Phase Error
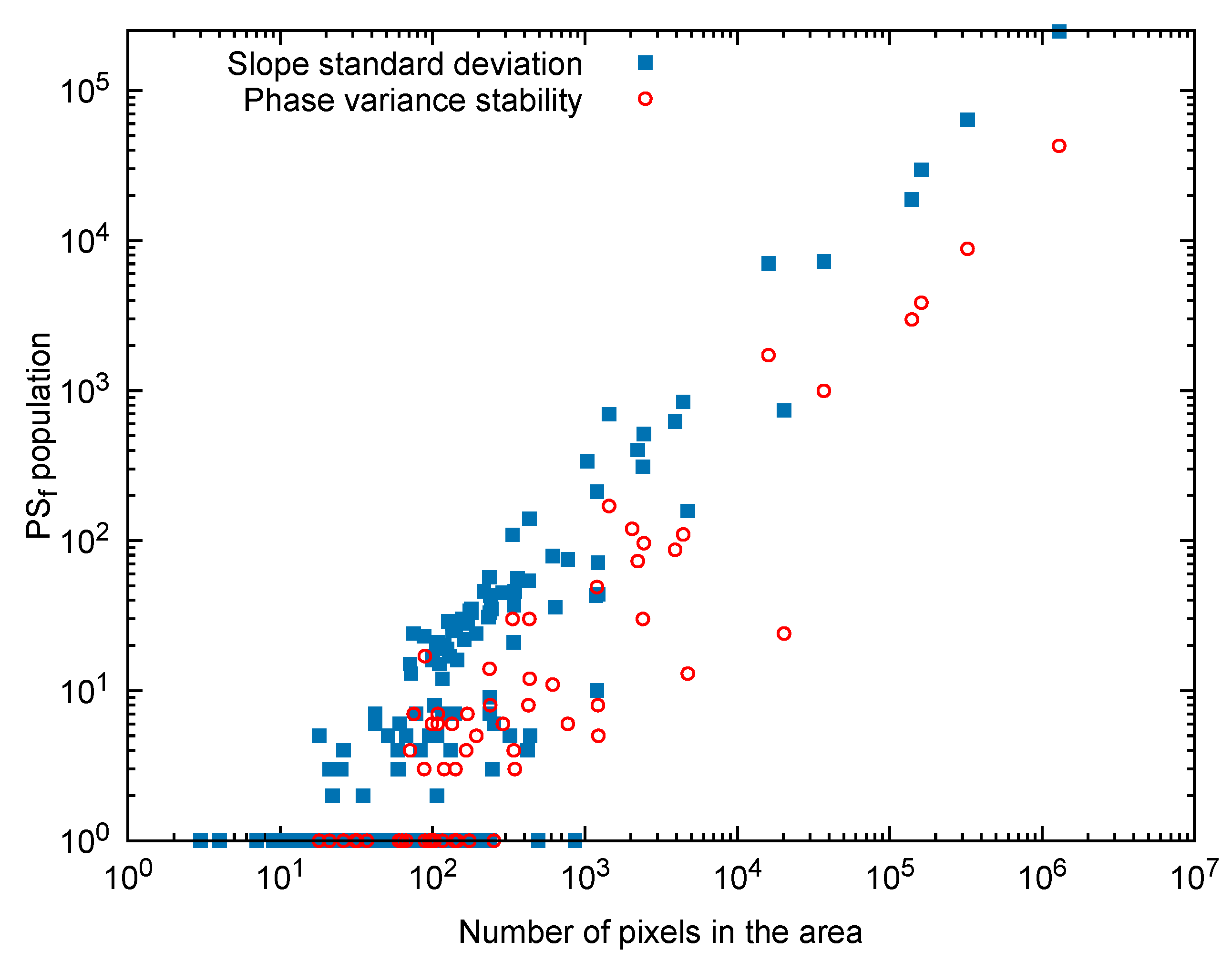
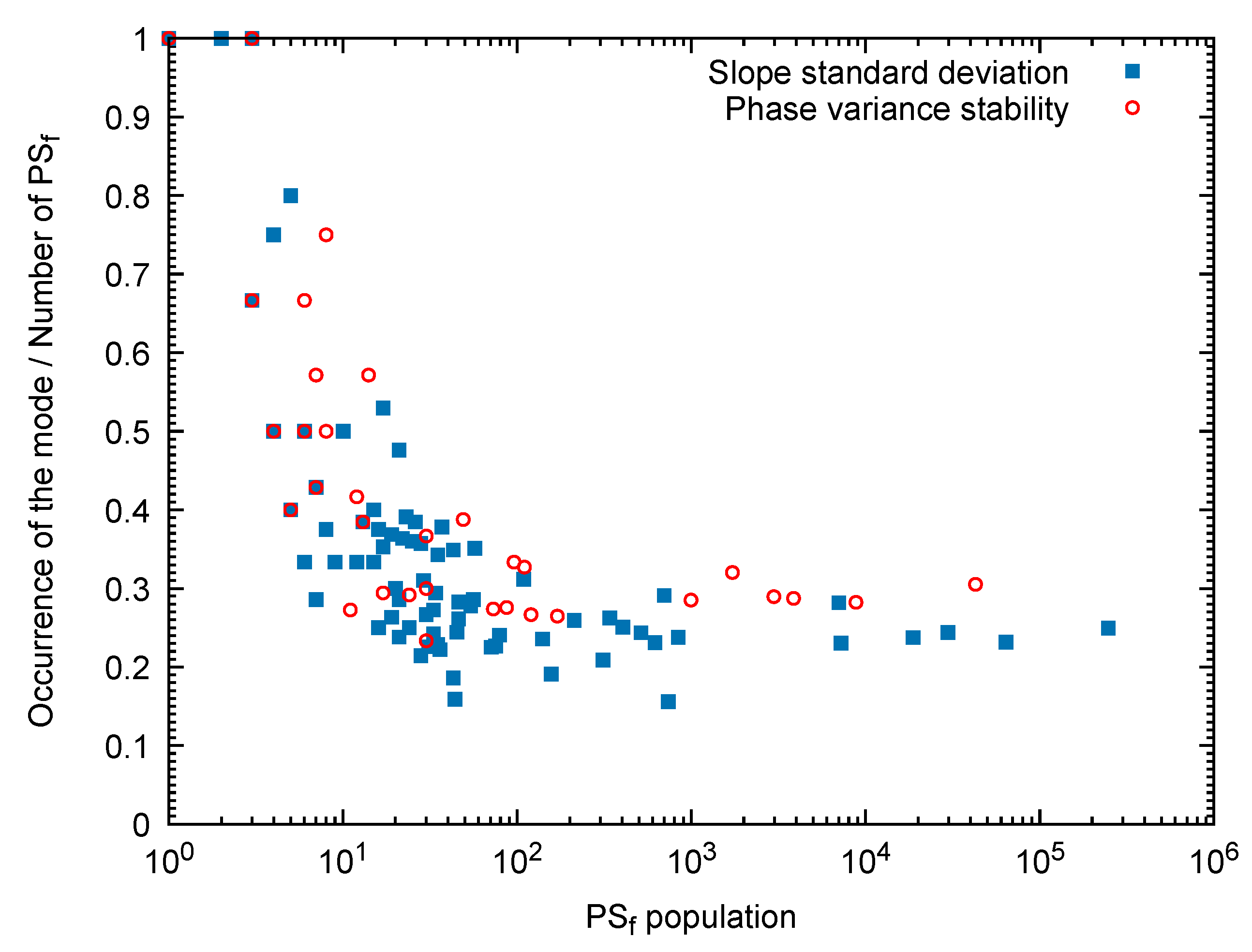
2.2.2. Slope Standard Deviation
2.2.3. Phase Variance Stability
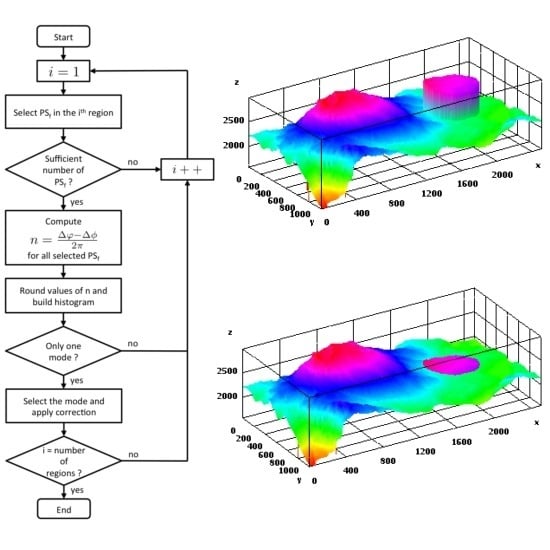
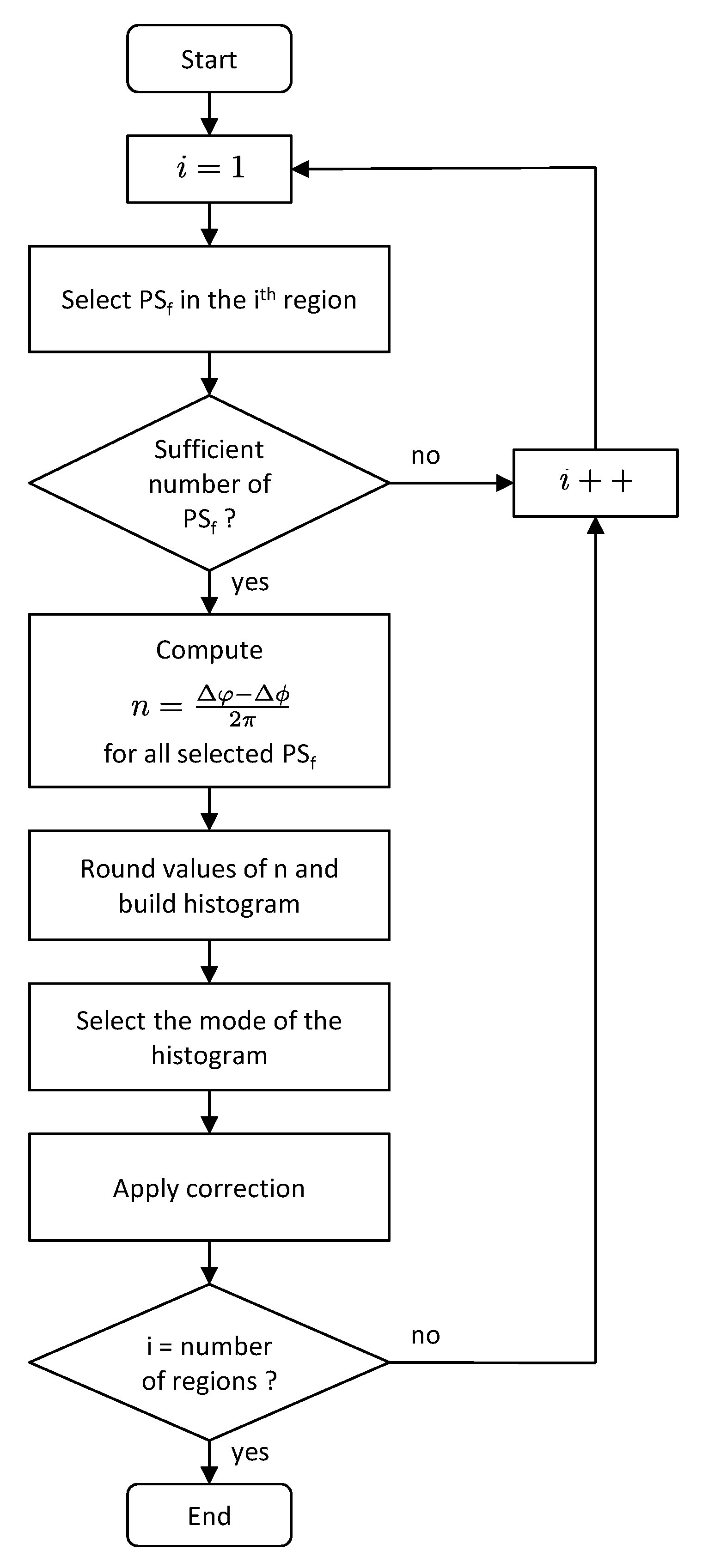
2.3. SBInSAR-Assisted Phase Unwrapping
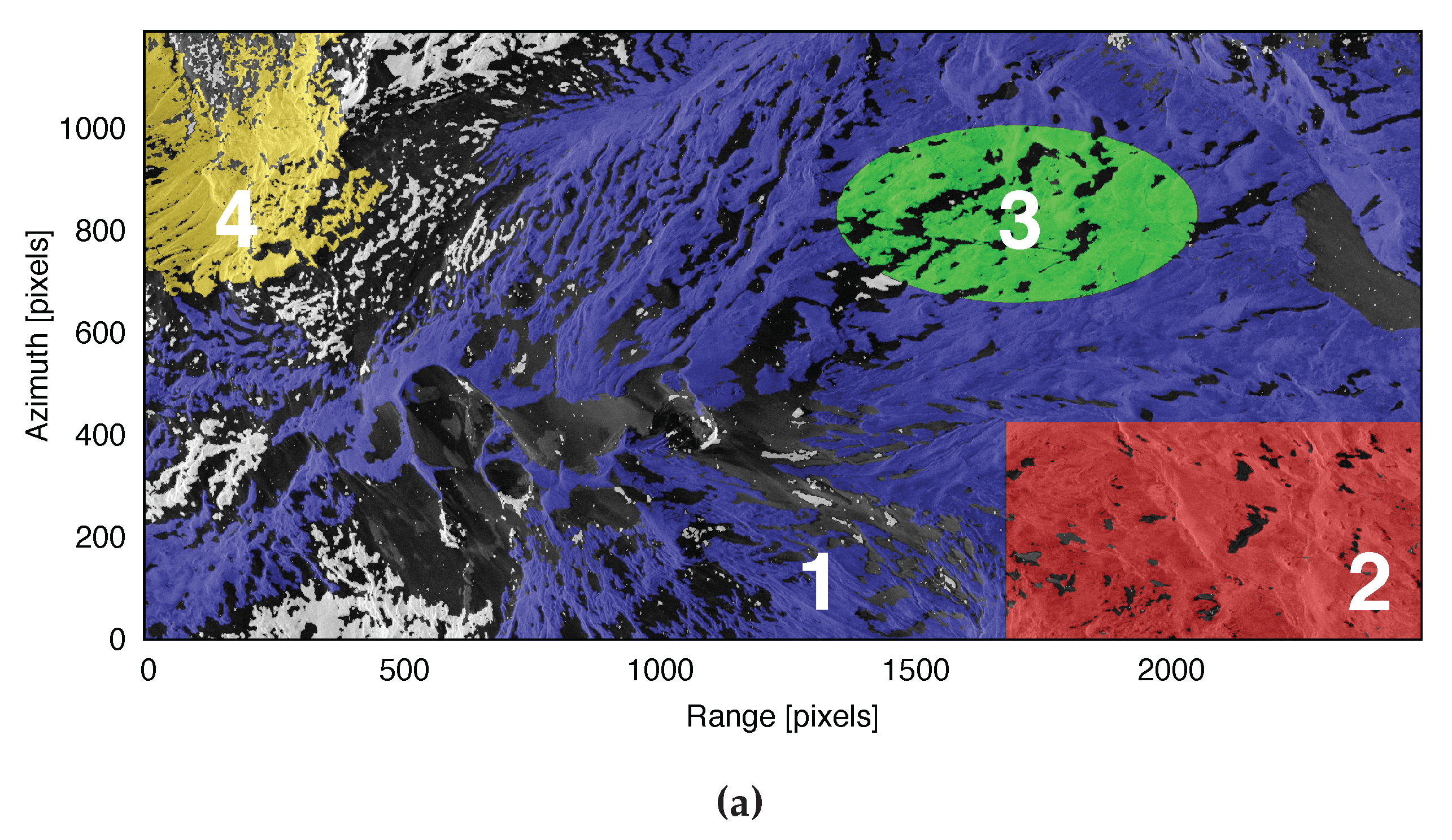
3. Copahue Test Case
3.1. Test Site
3.2. Data Set and Processing
3.3. Validation Procedure
3.4. Indicator of Quality
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PSf | Frequency-Persistent Scatterer(s) |
| SAR | Synthetic Aperture Radar |
| InSAR | Synthetic Aperture Radar Interferometry |
| SBInSAR | Split-Band Interferometry |
| DEM | Digital Elevation Model |
References
- Bovenga, F.; Giacovazzo, V.M.; Refice, A.; Nitti, D.O.; Veneziani, N.V. Interferometric Multi-Chromatic Analysis of High Resolution X-Band Data. In Proceedings of the Fringe 2011 Workshop, Frascati, Italy, 19–23 September 2011. [Google Scholar]
- Veneziani, N.; Bovenga, F.; Refice, A. A Wide-Band Approach to the Absolute Phase Retrieval in SAR Interferometry. Multidimens. Syst. Signal Process. 2003, 14, 183–205. [Google Scholar] [CrossRef]
- Bovenga, F.; Giacovazzo, V.M.; Refice, A.; Veneziani, N. Multichromatic Analysis of InSAR Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4790–4799. [Google Scholar] [CrossRef]
- Bovenga, F.; Rana, F.M.; Refice, A.; Veneziani, N. Multichromatic Analysis of Satellite Wideband SAR Data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1767–1771. [Google Scholar] [CrossRef]
- De Rauw, D.; Kervyn, F.; d’Oreye, N.; Albino, F.; Barbier, C. Split-Band Interferometric SAR Processing Using TanDEM-X Data. In Proceedings of the FRINGE’15: Advances in the Science and Applications of SAR Interferometry and Sentinel-1 InSAR Workshop, Frascati, Italy, 23–27 March 2015. [Google Scholar]
- Bovenga, F.; Giacovazzo, V.M.; Refice, A.; Veneziani, N.; Vitulli, R. Multi-Chromatic Analysis of InSAR Data: Validation and Potential. In Proceedings of the Fringe 2009, Frascati, Italy, 30 November–4 December 2009. [Google Scholar]
- Bovenga, F.; Derauw, D.; Rana, F.M.; Barbier, C.; Refice, A.; Veneziani, N.; Vitulli, R. Multi-Chromatic Analysis of SAR Images for Coherent Target Detection. Remote Sens. 2014, 6, 8822–8843. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Derauw, D.; Orban, A.; Barbier, C. Wide Band SAR Sub-Band Splitting and Inter-Band Coherence Meaurements. Remote Sens. Lett. 2010, 1, 133–140. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Chen, C. Measurement and mitigation of the ionosphere in L-band Interferometric SAR data. In Proceedings of the 2010 IEEE Radar Conference, Arlington, VA, USA, 10–14 May 2010; pp. 1459–1463. [Google Scholar]
- Furuya, M.; Suzuki, T.; Derauw, D. A step-by-step recipe of band splitting technique for isolation of ionospheric signal in L-band InSAR data. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Schreiber, R.; Moreira, A. Coregistration of Interferometric SAR Images Using Spectral Diversity. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2179–2191. [Google Scholar] [CrossRef]
- Jiang, H.; Feng, G.; Wang, T.; Bürgmann, R. Toward full exploitation of coherent and incoherent information in Sentinel-1 TOPS data for retrieving surface displacement: Application to the 2016 Kumamoto (Japan) earthquake. Geophys. Res. Lett. 2017, 44, 1758–1767. [Google Scholar] [CrossRef]
- Naranjo, J.A.; Polanco, E. The 2000 AD eruption of Copahue Volcano, Southern Andes. Rev. Geol. Chile 2004, 31, 279–292. [Google Scholar] [CrossRef]
- Tamburello, G.; Agusto, M.; Caselli, A.; Tassi, F.; Vaselli, O.; Calabrese, S.; Rouwet, D.; Capaccioni, B.; Napoli, R.D.; Cardellini, C.; et al. Intense magmatic degassing through the lake of Copahue volcano, 2013–2014. J. Geophys. Res. Solid Earth 2015, 120, 6071–6084. [Google Scholar] [CrossRef]
- Fournier, T.J.; Pritchard, M.E.; Riddick, S.N. Duration, magnitude, and frequency of subaerial volcano deformation events: New results from Latin America using InSAR and a global synthesis. Geochem. Geophys. Geosystems 2010, 11. [Google Scholar] [CrossRef]
- Velez, M.L.; Euillades, P.; Caselli, A.; Blanco, M.; Díaz, J.M. Deformation of Copahue volcano: Inversion of InSAR data using a genetic algorithm. J. Volcanol. Geotherm. Res. 2011, 202, 117–126. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Network approaches to two-dimensional phase unwrapping: intractability and two new algorithms. J. Opt. Soc. Am. A 2000, 17, 401–414. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. A 2001, 18, 338–351. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Phase unwrapping for large SAR interferograms: Statistical segmentation and generalized network models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef]


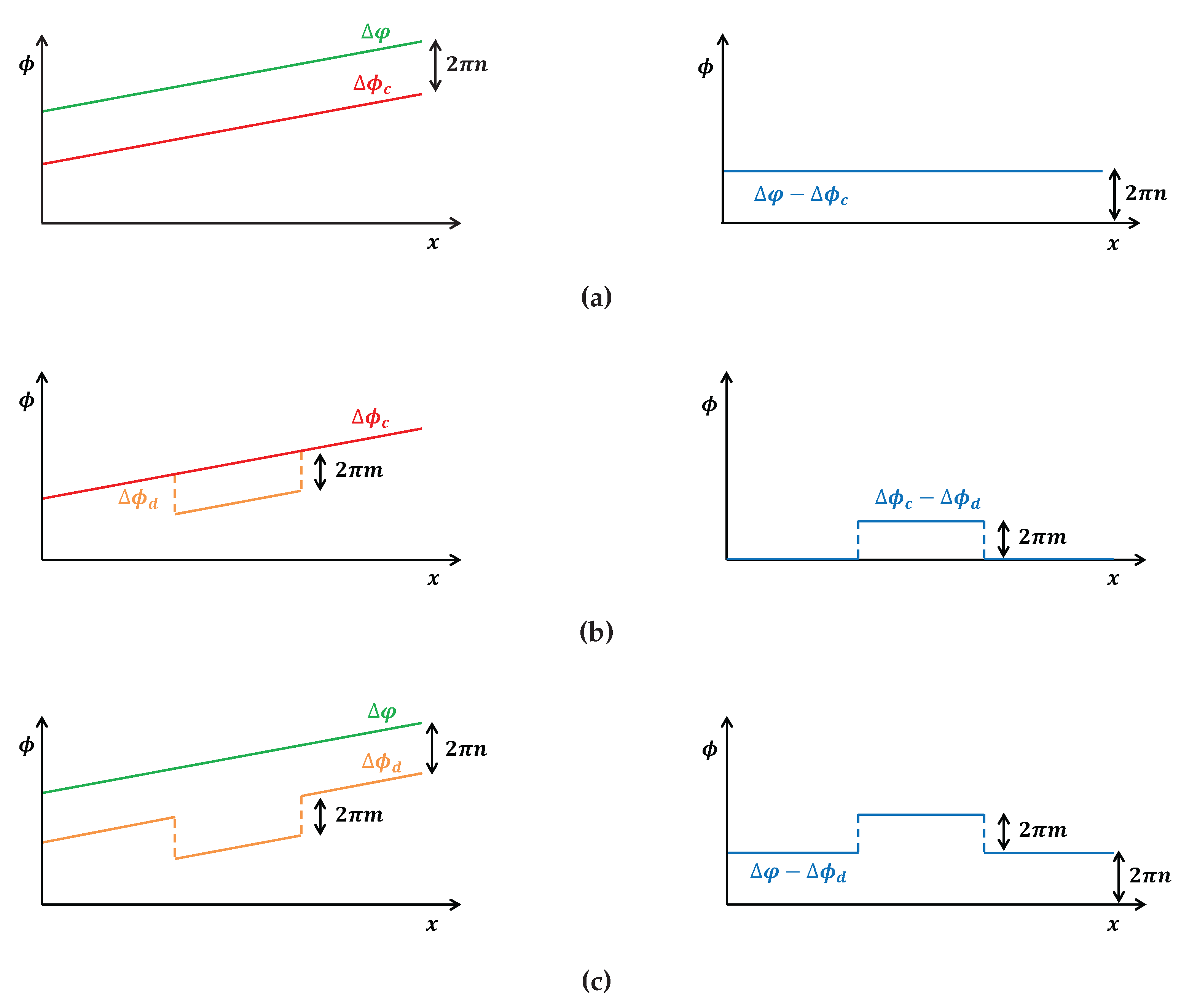


| Relative Phase-Offset | Cycles |
|---|---|
| -1 | |
| 0 | |
| -1 | |
| 1 | |
| 0 | |
| -1 |
| Computed Phase-Offset | Cycles |
|---|---|
| -3 | |
| -2 | |
| -3 | |
| -2 |
| PSf Selector | Region 1 | Region 2 | Region 3 | Region 4 |
|---|---|---|---|---|
| None | 54 | 43 | 43 | 85 |
| 25 | 26 | 25 | 30 | |
| 12 | 14 | 12 | 13 | |
| 8 | 9 | 8 | 9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Libert, L.; Derauw, D.; D’Oreye, N.; Barbier, C.; Orban, A. Split-Band Interferometry-Assisted Phase Unwrapping for the Phase Ambiguities Correction. Remote Sens. 2017, 9, 879. https://doi.org/10.3390/rs9090879
Libert L, Derauw D, D’Oreye N, Barbier C, Orban A. Split-Band Interferometry-Assisted Phase Unwrapping for the Phase Ambiguities Correction. Remote Sensing. 2017; 9(9):879. https://doi.org/10.3390/rs9090879
Chicago/Turabian StyleLibert, Ludivine, Dominique Derauw, Nicolas D’Oreye, Christian Barbier, and Anne Orban. 2017. "Split-Band Interferometry-Assisted Phase Unwrapping for the Phase Ambiguities Correction" Remote Sensing 9, no. 9: 879. https://doi.org/10.3390/rs9090879
APA StyleLibert, L., Derauw, D., D’Oreye, N., Barbier, C., & Orban, A. (2017). Split-Band Interferometry-Assisted Phase Unwrapping for the Phase Ambiguities Correction. Remote Sensing, 9(9), 879. https://doi.org/10.3390/rs9090879