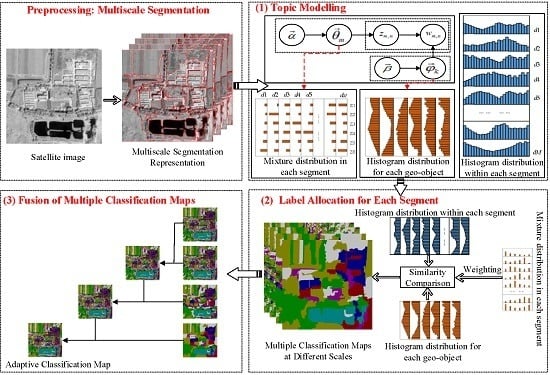
Topic Modelling for Object-Based Unsupervised Classification of VHR Panchromatic Satellite Images Based on Multiscale Image Segmentation
Abstract
1. Introduction
2. Methodology
2.1. Topic Modelling
2.1.1. Latent Dirichlet Allocation
- For the k-th element of K topics, sample the topic-specific term distribution according to the Dirichlet distribution, i.e., , where is the hyperparameter.
- Sample the topic mixture according to the Dirichlet distribution, i.e., , where is the hyperparameter.
- For each word , sample a topic according to the multinomial distribution, i.e., , and sample a word according to the multinomial distribution , i.e., .
2.1.2. Build an Analogue of Text-Related Terms in the Image Domain
- Word: a unique grayscale value of a pixel is defined as a word;
- Vocabulary: the unique grayscale values of the satellite image form the vocabulary;
- Document: each segment is regarded as a document, thus, all segments of multiple segmentation maps at different scales constitute the corpus;
- Topic: each topic corresponds to a specific geo-object category.
2.2. Label Allocation for Each Segment
2.3. Fusion of Multiple Classification Maps
3. Results and Discussion
3.1. Experiment Data
3.2. Experiment Setup
3.2.1. Methods for Comparison with the Proposed Approach
3.2.2. Evaluation Criteria
- Overall accuracy (OA): OA, which serves as a quantitative measurement of the agreement between the classification result and the ground truth map, is one of the most widely used statistics for evaluating the classification accuracy. OA can be calculated by dividing the total correctly-classified pixels by the total number of pixels checked by the ground truth map, and is given as , where is the total number of correct pixels, and is total number of pixels.
- Overall entropy (OE): entropy is an information theoretical criterion that is able to measure the homogeneity of the classification results. OE is defined as a linear combination of the class entropy, which describes how the pixels of the same geo-object are presented by the various clusters created, and the cluster entropy, which reflects the quality of the individual clusters in terms of the homogeneity of the pixels in a cluster. Generally speaking, a smaller overall entropy value corresponds to the classification map with a higher homogeneity. For details regarding, please refer to [27,35].
3.2.3. Parameter Setting
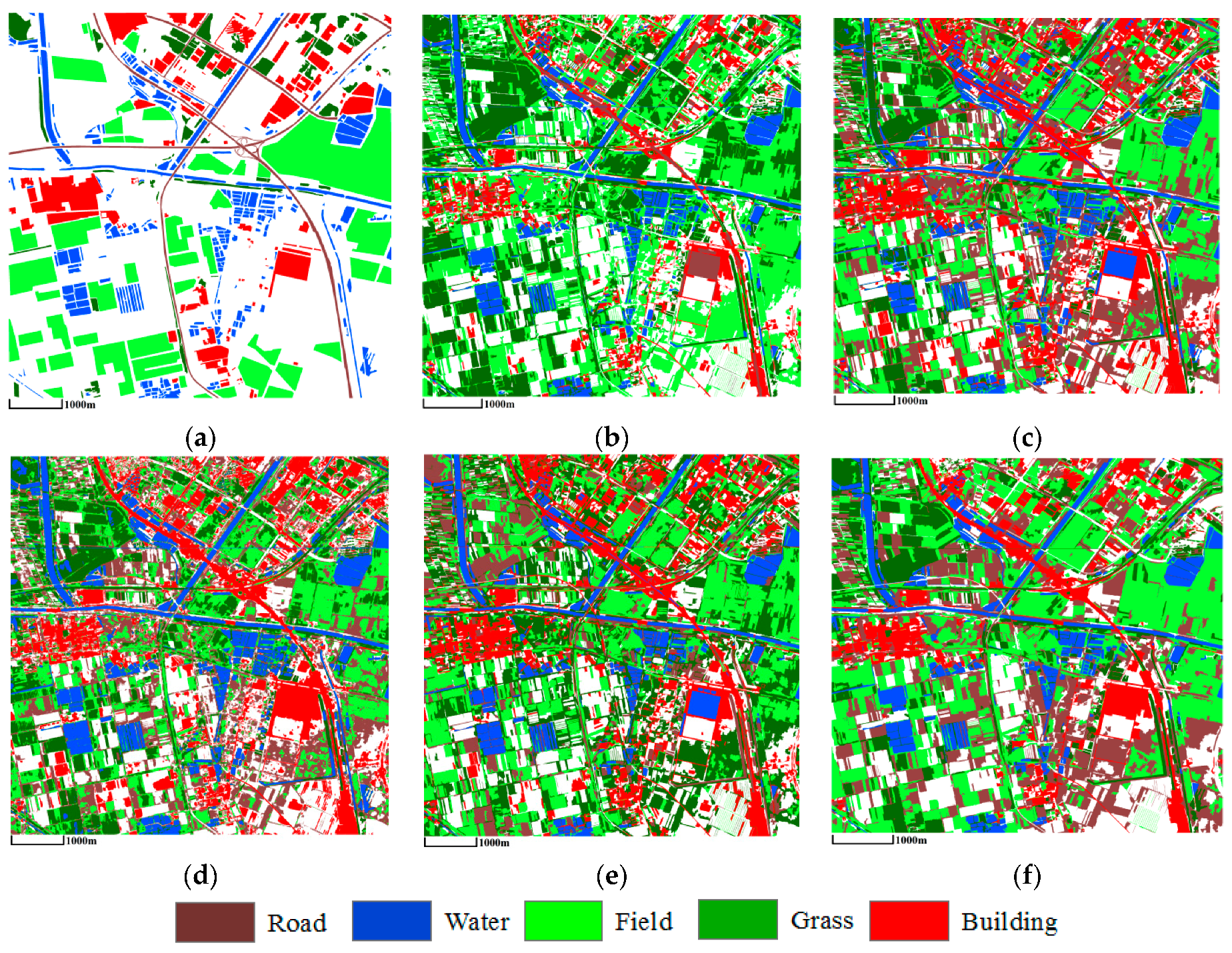
3.3. Comparison of Classification Results
3.3.1. Mapping Satellite-1 and QuickBird Images
3.3.2. ZY-3 Image
3.4. Analysis of Computational Efficiency
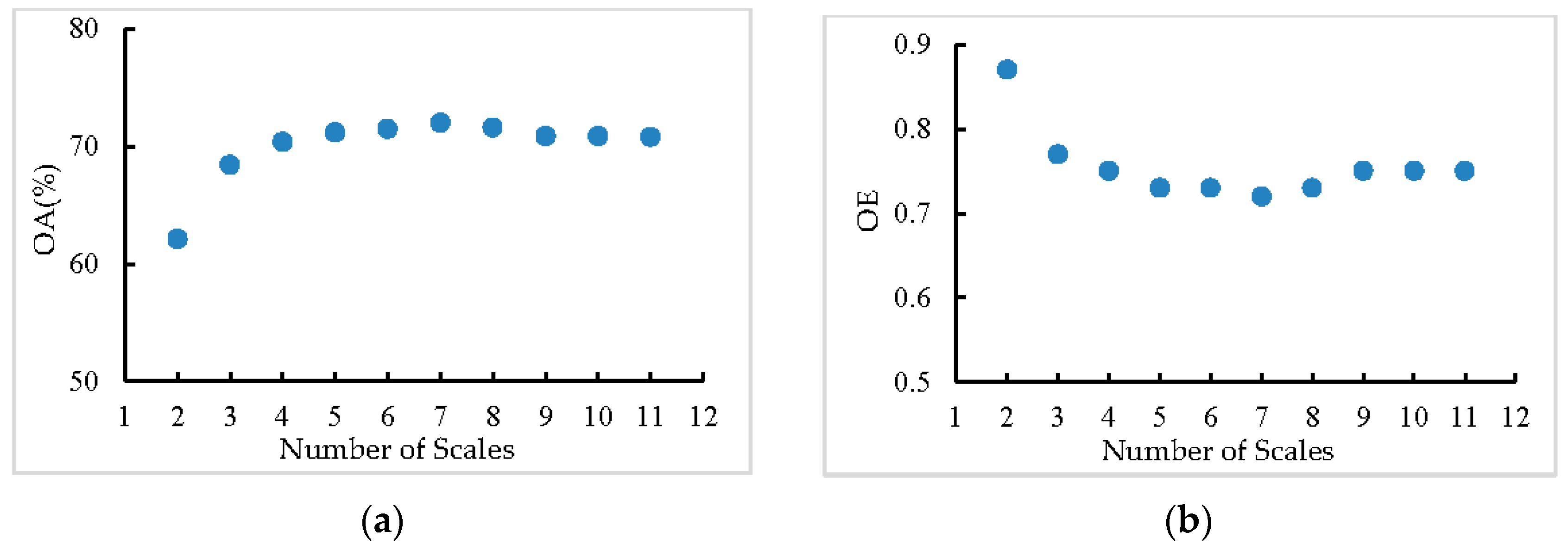
3.5. Analysis of Scale Setting
3.5.1. Influence of Different Settings on the Range of Scales
3.5.2. Special Cases of the mSegLDA
- Case #1: the mSegLDA based on a single-segmentation map with 100 segments;
- Case #2: the mSegLDA based on a single-segmentation map with 200 segments;
- Case #3: the mSegLDA based on a single-segmentation map with 500 segments;
- Case #4: the mSegLDA based on a single-segmentation map with 800 segments;
- Case #5: the mSegLDA based on a single-segmentation map with 1000 segments;
- Case #6: the mSegLDA based on a single-segmentation map with 1500 segments;
- Case #7: the mSegLDA based on a single-segmentation map with 2000 segments;
- Case #8: the mSegLDA based on a single-segmentation map with 2500 segments; and
- Case #9: the mSegLDA based on a single-segmentation map with 3000 segments.
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Benediktsson, J.A.; Chanussot, J.; Moon, W.M. Advances in very-high-resolution remote sensing. Proc. IEEE 2013, 101, 566–569. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Myint, S.W.; Gober, P.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Per-pixel vs. Object-based classification of urban land cover extraction using high spatial resolution imagery. Remote Sens. Environ. 2011, 115, 1145–1161. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; van der Meer, F.; van der Werff, H.; van Coillie, F.; et al. Geographic object-based image analysis-towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Judah, A.; Hu, B.; Wang, J. An algorithm for boundary adjustment toward multi-scale adaptive segmentation of remotely sensed imagery. Remote Sens. 2014, 6, 3583–3610. [Google Scholar] [CrossRef]
- Dragut, L.; Csillik, O.; Eisank, C.; Tiede, D. Automated parametrisation for multi-scale image segmentation on multiple layers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; He, Y.; Weng, Q. An automated method to parameterize segmentation scale by enhancing intrasegment homogeneity and intersegment heterogeneity. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1282–1286. [Google Scholar] [CrossRef]
- Zhang, L.; Jia, K.; Li, X.; Yuan, Q.; Zhao, X. Multi-scale segmentation appoach for object-based land-cover classification using high-resolution imagery. Remote Sens. Lett. 2014, 5, 73–82. [Google Scholar] [CrossRef]
- Malisiewicz, T.; Efros, A.A. Improving spatial support for objects via multiple segmentations. In Proceedings of the 18th British Machine Vision Conference, Warwick, UK, 10–13 September 2007. [Google Scholar]
- Russell, B.C.; Freeman, W.T.; Efros, A.A.; Sivic, J.; Zisserman, A. Using multiple segmentations to discover objects and their extent in image collections. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006. [Google Scholar]
- Pantofaru, C.; Schmid, C.; Hebert, M. Object recognition by integrating multiple image segmentations. In Proceedings of the 10th European Conference on Computer Vision, Marseille, France, 12–28 October 2008; pp. 481–494. [Google Scholar]
- Karadağ, Ö.Ö.; Senaras, C.; Vural, F.T.Y. Segmentation fusion for building detection using domain-specific information. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3305–3315. [Google Scholar] [CrossRef]
- Akcay, H.G.; Aksoy, S. Automatic detection of geospatial objects using multiple hierarchical segmentations. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2097–2111. [Google Scholar] [CrossRef]
- Santos, J.A.d.; Gosselin, P.-H.; Philipp-Foliguet, S.; Torres, R.d.S.; Falao, A.X. Multiscale classification of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3764–3775. [Google Scholar] [CrossRef]
- Syu, J.-H.; Wang, S.-J.; Wang, L.-C. Hierarchical image segmentation based on iterative contraction and merging. IEEE Trans. Image Process. 2017, 26, 2246–2260. [Google Scholar] [CrossRef] [PubMed]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Hofmann, T. Probabilistic latent semantic indexing. In Proceedings of the 22nd Annual International SIGIR Conference on Research and Development in Information, Retrieval Berkeley, CA, USA, 15–19 August 1999; pp. 50–57. [Google Scholar]
- Teh, Y.W.; Jordan, M.I.; Beal, M.J.; Blei, D.M. Hierarchical dirichlet processes. J. Am. Stat. Assoc. 2006, 101, 1566–1581. [Google Scholar] [CrossRef]
- Lienou, M.; Maitre, H.; Datcu, M. Semantic annotation of satellite images using latent dirichlet allocation. IEEE Geosci. Remote Sens. Lett. 2010, 7, 28–32. [Google Scholar] [CrossRef]
- Bratasanu, D.; Nedelcu, I.; Datcu, M. Bridging the semantic gap for satellite image annotation and automatic mapping applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 193–204. [Google Scholar] [CrossRef]
- Luo, W.; Li, H.; Liu, G.; Zeng, L. Semantic annotation of satellite images using author-genre-topic model. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1356–1368. [Google Scholar] [CrossRef]
- Li, S.; Tang, H.; He, S.; Shu, Y.; Mao, T.; Li, J.; Xu, Z. Unsupervised detection of earthquake-triggered roof-holes from uav images using joint color and shape features. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1823–1827. [Google Scholar]
- Zhao, B.; Zhong, Y.; Zhang, L. Scene classification via latent dirichlet allocation using a hybrid generative/discriminative strategy for high spatial resolution remote sensing imagery. Remote Sens. Lett. 2013, 4, 1204–1213. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhu, Q.; Zhang, L. Scene classification based on the multifeature fusion probabilistic topic model for high spatial resolution remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6207–6222. [Google Scholar] [CrossRef]
- Zhao, B.; Zhong, Y.; Xia, G.-S.; Zhang, L. Dirichlet-derived multiple topic scene classification model for high spatial resolution remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2108–2123. [Google Scholar] [CrossRef]
- Yi, W.; Tang, H.; Chen, Y. An object-oriented semantic clustering algorithm for high-resolution remote sensing images using the aspect model. IEEE Geosci. Remote Sens. Lett. 2011, 8, 522–526. [Google Scholar] [CrossRef]
- Tang, H.; Shen, L.; Qi, Y.; Chen, Y.; Shu, Y.; Li, J.; Clausi, D.A. A multiscale latent dirichlet allocation model for object-oriented clustering of vhr panchromatic satellite images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1680–1692. [Google Scholar] [CrossRef]
- Xu, K.; Yang, W.; Liu, G.; Sun, H. Unsupervised satellite image classification using markov field topic model. IEEE Geosci. Remote Sens. Lett. 2013, 10, 130–134. [Google Scholar] [CrossRef]
- Shen, L.; Tang, H.; Chen, Y.; Gong, A.; Li, J.; Yi, W. A semisupervised latent dirichlet allocation model for object-based classification of vhr panchromatic satellite images. IEEE Geosci. Remote Sens. Lett. 2014, 11, 863–867. [Google Scholar] [CrossRef]
- Shu, Y.; Tang, H.; Li, J.; Mao, T.; He, S.; Gong, A.; Chen, Y.; Du, H. Object-based unsupervised classification of vhr panchromatic satellite images by combining the hdp and ibp on multiple scenes. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6148–6162. [Google Scholar] [CrossRef]
- Shen, L.; Wu, L.; Li, Z. Topic modelling for object-based classification of VHR satellite images based on multiscale segmentations. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 359–363. [Google Scholar] [CrossRef]
- Barnard, K.; Duygulu, P.; Forsyth, D.; de Freitas, N.; Blei, D.M.; Jordan, M.I. Matching words and pictures. J. Mach. Learn. Res. 2003, 3, 1107–1135. [Google Scholar]
- Heinrich, G. Parameter Estimation for Text Analysis; Technical Note; Vsonix GmbH: Darmstadt, Germany; University of Leipzig: Leipzig, Germany, 2008. [Google Scholar]
- Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J. Spectral-spatial classification of hyperspectral imagery based on partitional clustering techniques. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2973–2987. [Google Scholar] [CrossRef]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. On clustering validation techniques. J. Intell. Inf. Syst. 2001, 17, 107–145. [Google Scholar] [CrossRef]
- Liu, M.-Y.; Tuzel, O.; Ramalingam, S.; Chellappa, R. Entropy rate superpixel segmentation. In Proceedings of the 13rd IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2097–2104. [Google Scholar]


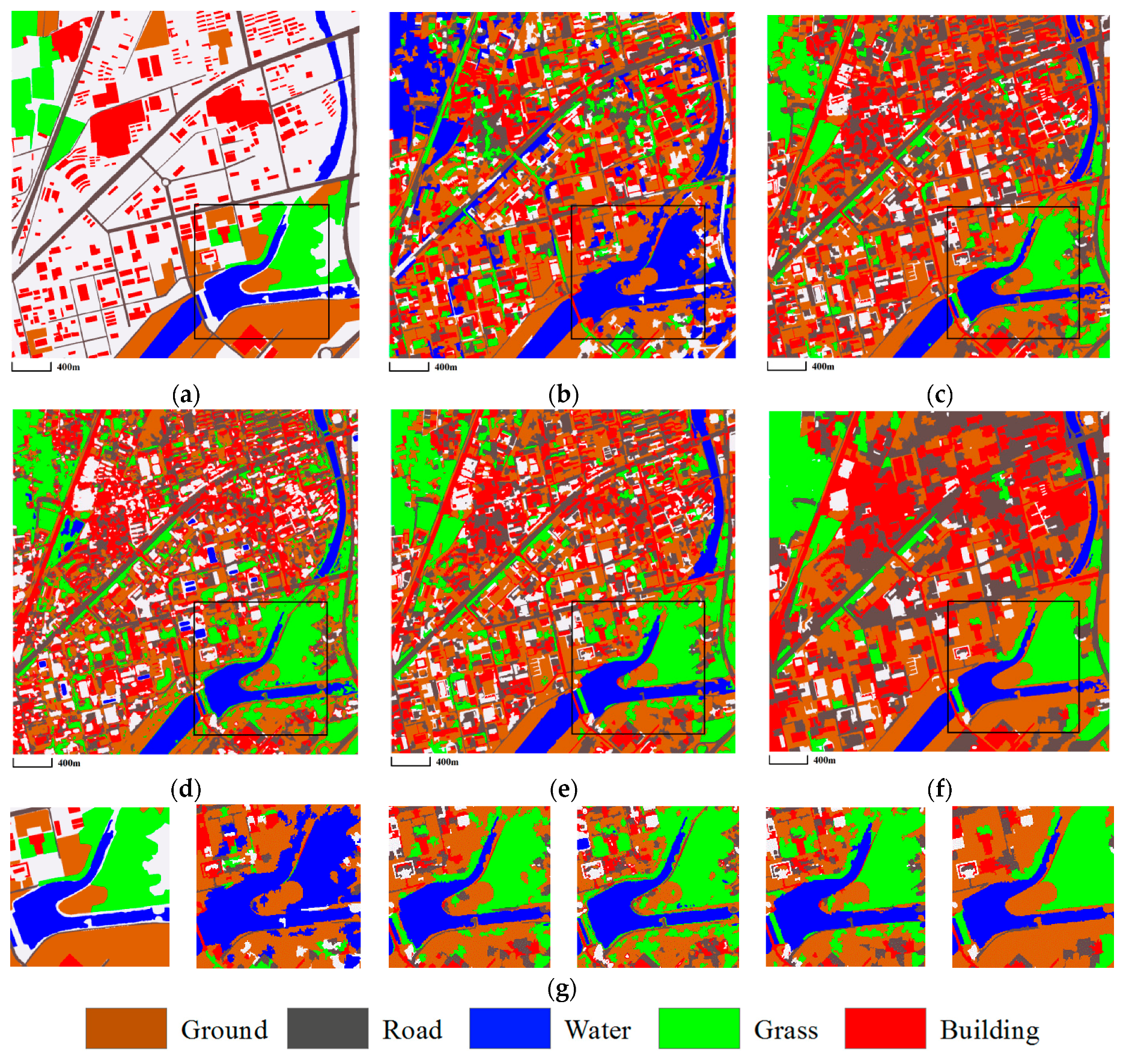


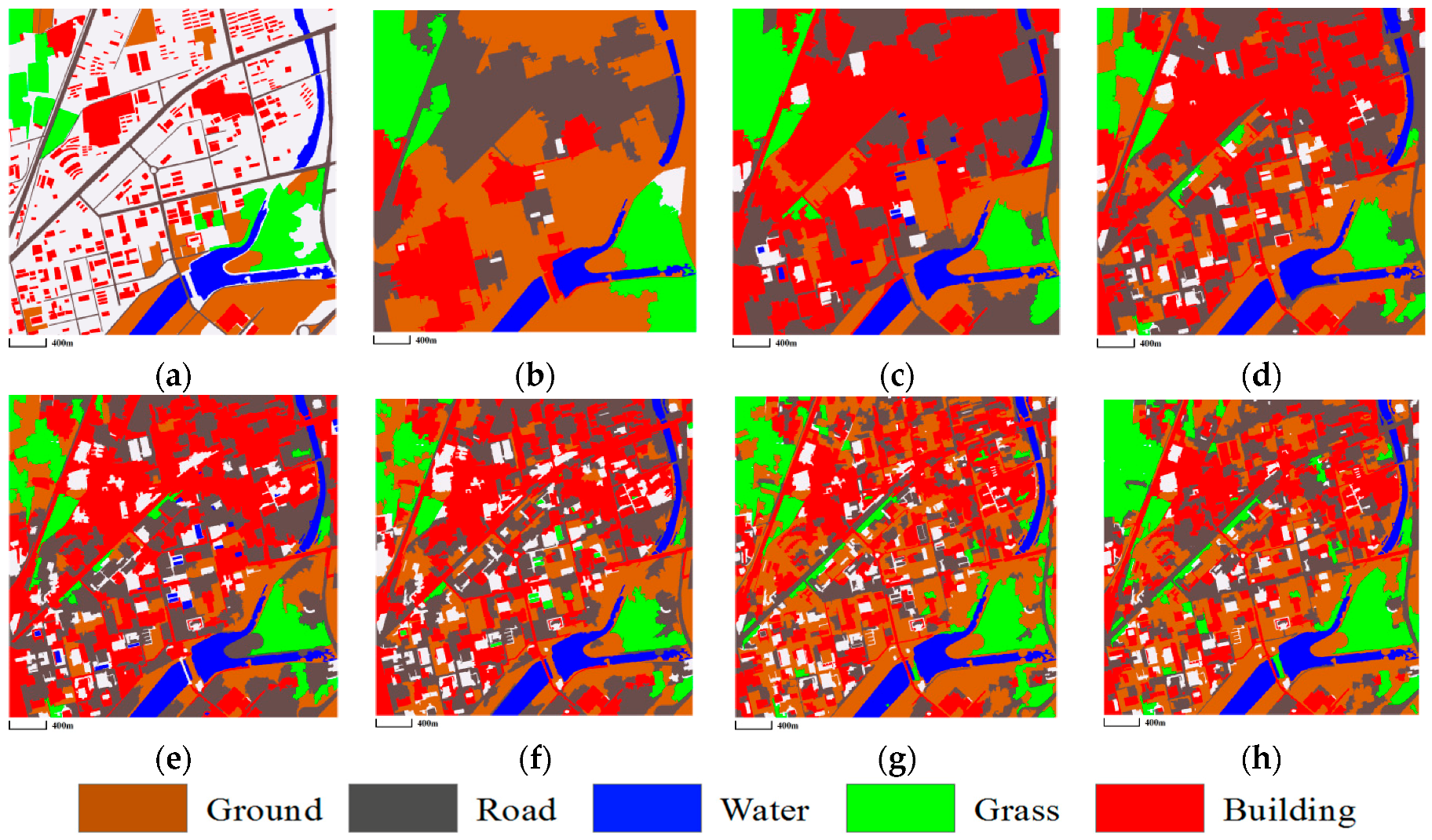
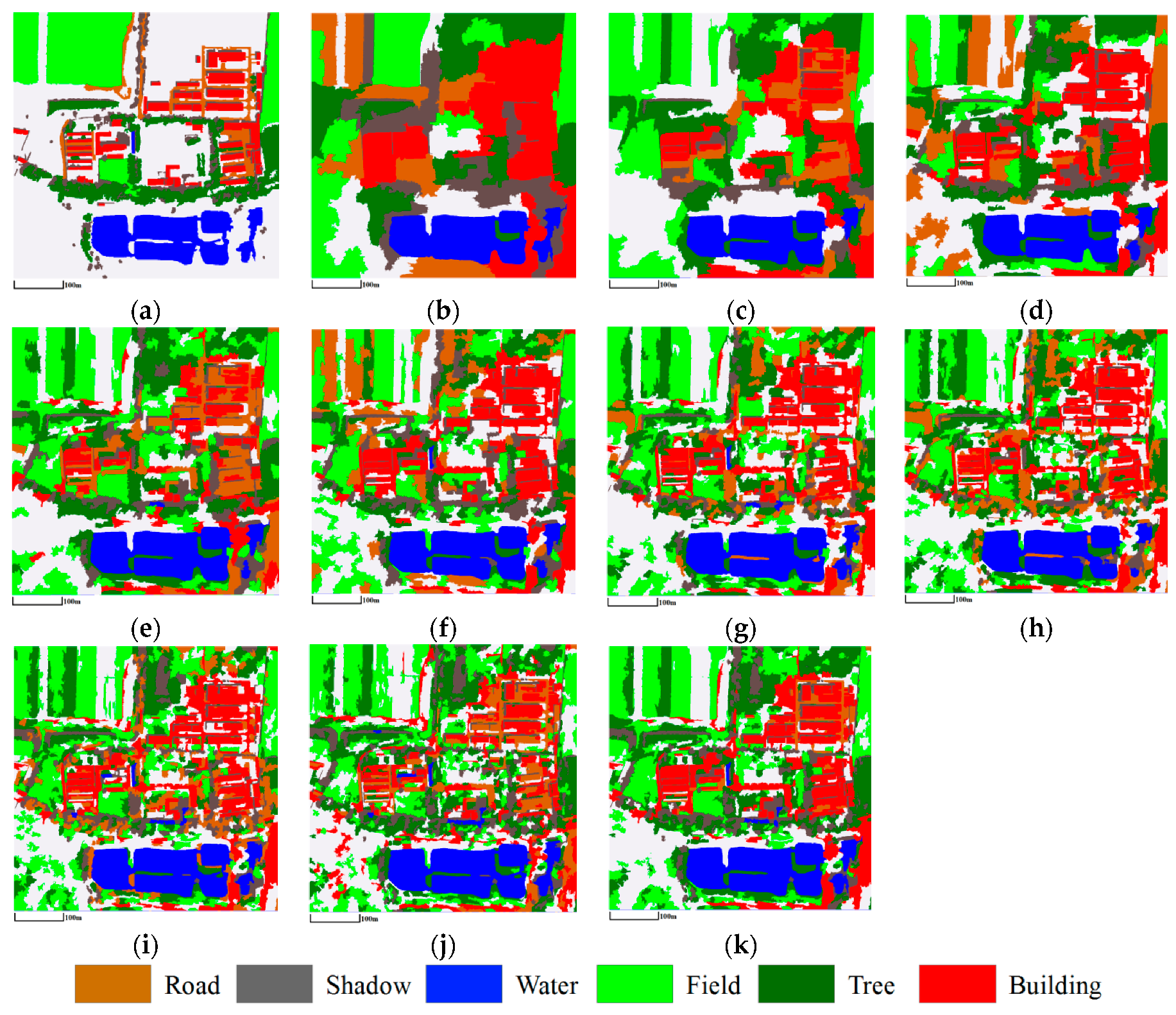
| O_ISODATA | O_LDA | msLDA | HDP_IBP | mSegLDA | |
|---|---|---|---|---|---|
| OA | 48.6 | 69.3 | 68.4 | 70.1 | 72.0 |
| OE | 0.89 | 0.79 | 0.84 | 0.76 | 0.72 |
| O_ISODATA | O_LDA | msLDA | HDP_IBP | mSegLDA | |
|---|---|---|---|---|---|
| OA | 49.8 | 65.1 | 68.2 | 65.5 | 74.3 |
| OE | 0.96 | 0.84 | 0.80 | 0.84 | 0.71 |
| O_ISODATA | O_LDA | msLDA | HDP_IBP | mSegLDA | |
|---|---|---|---|---|---|
| OA | 63.0 | 58.9 | 61.6 | 59.2 | 65.7 |
| OE | 0.78 | 0.93 | 0.85 | 0.87 | 0.74 |
| Methods | Running Time (in Seconds) |
|---|---|
| O_LDA | 797 |
| msLDA | 5056 |
| HDP_IBP | 766 |
| mSegLDA | 2413 |
| Case #1 | Case #2 | Case #3 | Case #4 | Case #5 | Case #6 | mSegLDA | |
|---|---|---|---|---|---|---|---|
| OA | 64.1 | 62.6 | 66.2 | 66.1 | 68.1 | 66.0 | 72.0 |
| OE | 0.87 | 0.89 | 0.83 | 0.83 | 0.81 | 0.81 | 0.72 |
| Case #1 | Case #2 | Case #3 | Case #4 | Case #5 | Case #6 | Case #7 | Case #8 | Case #9 | mSegLDA | |
|---|---|---|---|---|---|---|---|---|---|---|
| OA | 57.8 | 67.7 | 59.7 | 60.1 | 65.4 | 67.1 | 63.7 | 66.5 | 0.71 | 74.3 |
| OE | 0.87 | 0.87 | 0.76 | 0.75 | 0.85 | 0.74 | 0.74 | 0.79 | 0.78 | 0.72 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, L.; Wu, L.; Dai, Y.; Qiao, W.; Wang, Y. Topic Modelling for Object-Based Unsupervised Classification of VHR Panchromatic Satellite Images Based on Multiscale Image Segmentation. Remote Sens. 2017, 9, 840. https://doi.org/10.3390/rs9080840
Shen L, Wu L, Dai Y, Qiao W, Wang Y. Topic Modelling for Object-Based Unsupervised Classification of VHR Panchromatic Satellite Images Based on Multiscale Image Segmentation. Remote Sensing. 2017; 9(8):840. https://doi.org/10.3390/rs9080840
Chicago/Turabian StyleShen, Li, Linmei Wu, Yanshuai Dai, Wenfan Qiao, and Ying Wang. 2017. "Topic Modelling for Object-Based Unsupervised Classification of VHR Panchromatic Satellite Images Based on Multiscale Image Segmentation" Remote Sensing 9, no. 8: 840. https://doi.org/10.3390/rs9080840
APA StyleShen, L., Wu, L., Dai, Y., Qiao, W., & Wang, Y. (2017). Topic Modelling for Object-Based Unsupervised Classification of VHR Panchromatic Satellite Images Based on Multiscale Image Segmentation. Remote Sensing, 9(8), 840. https://doi.org/10.3390/rs9080840