Evaluation of Satellite-Altimetry-Derived Pycnocline Depth Products in the South China Sea
Abstract
1. Introduction
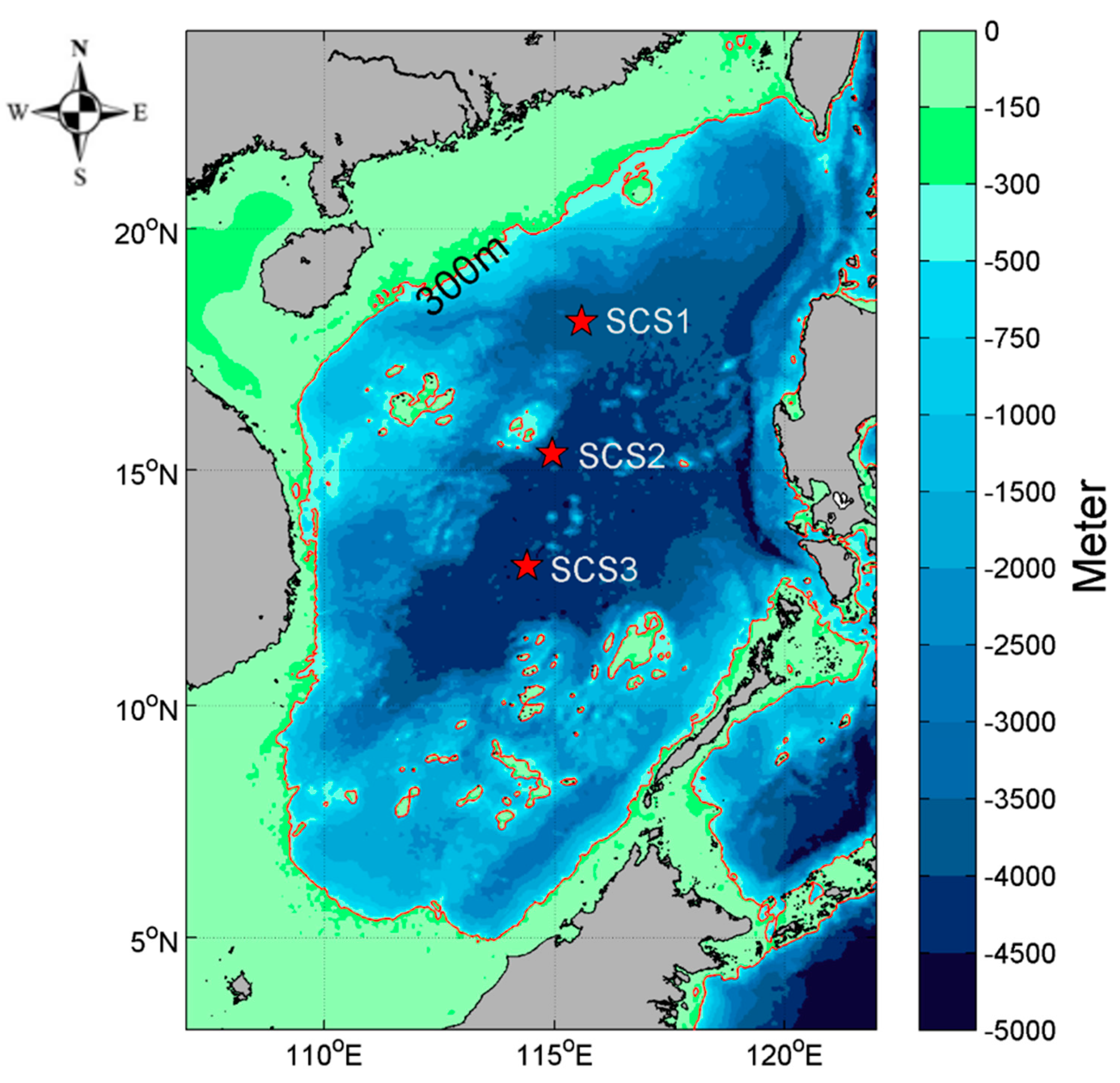
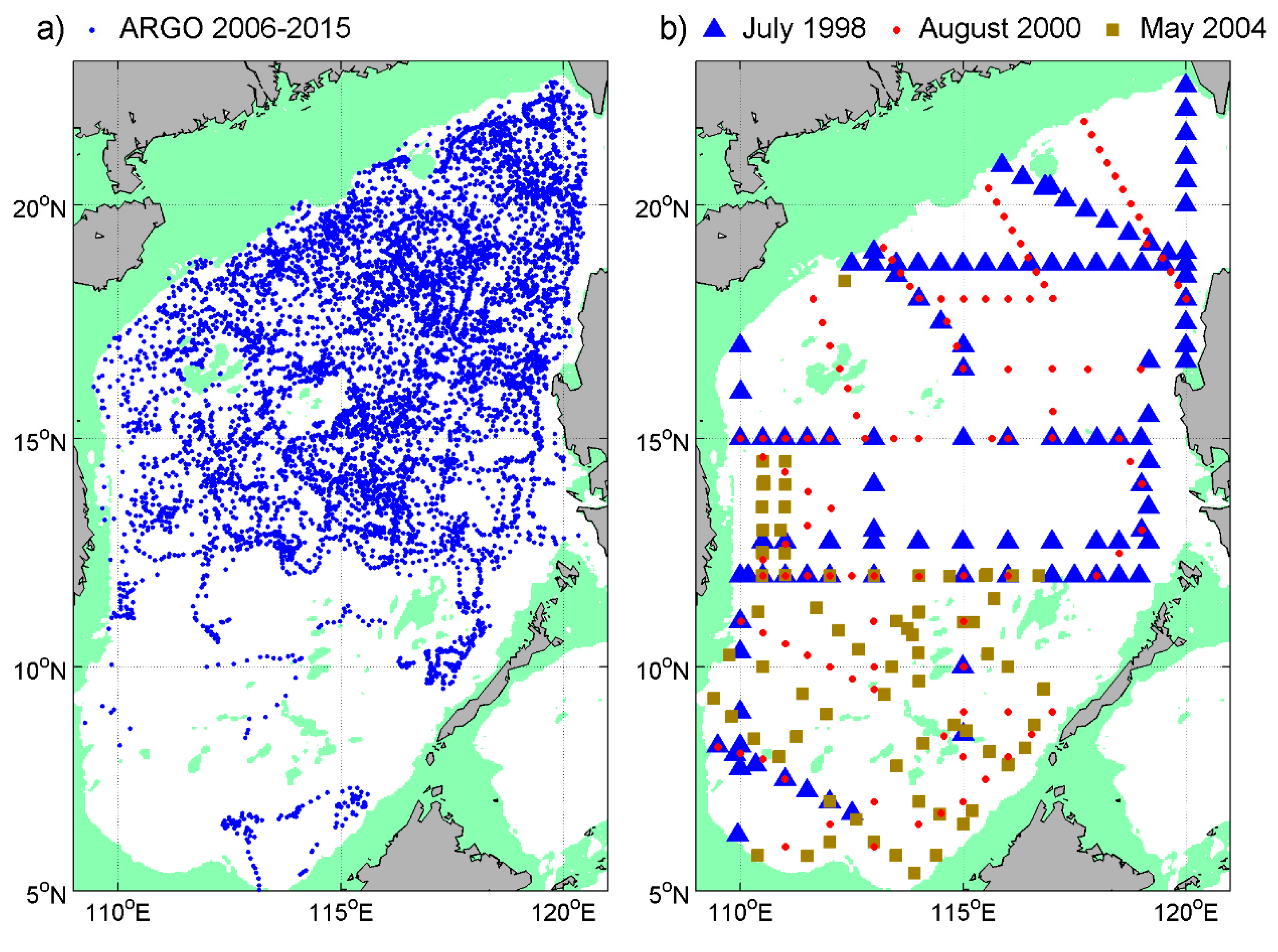
2. Data
3. Methods
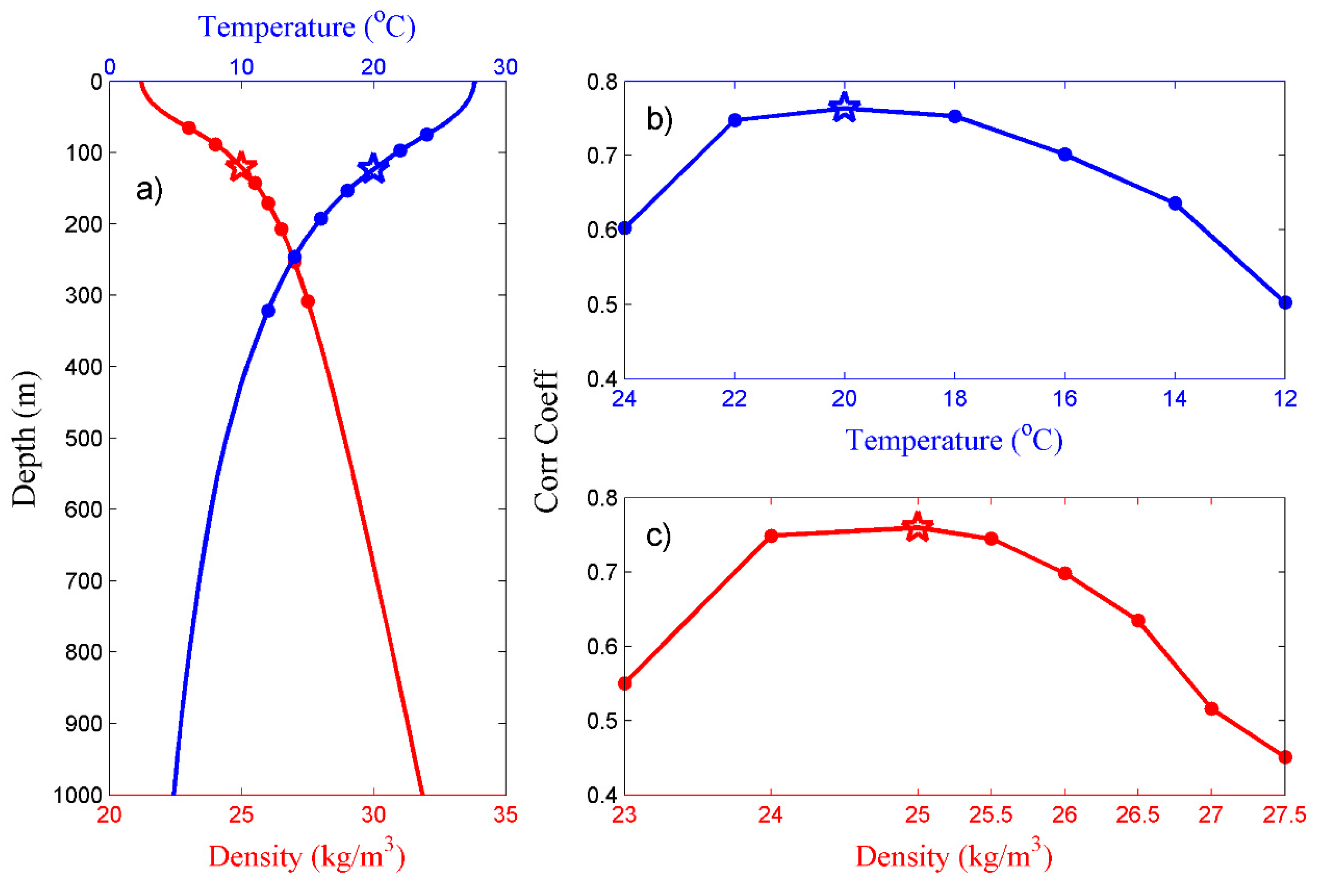
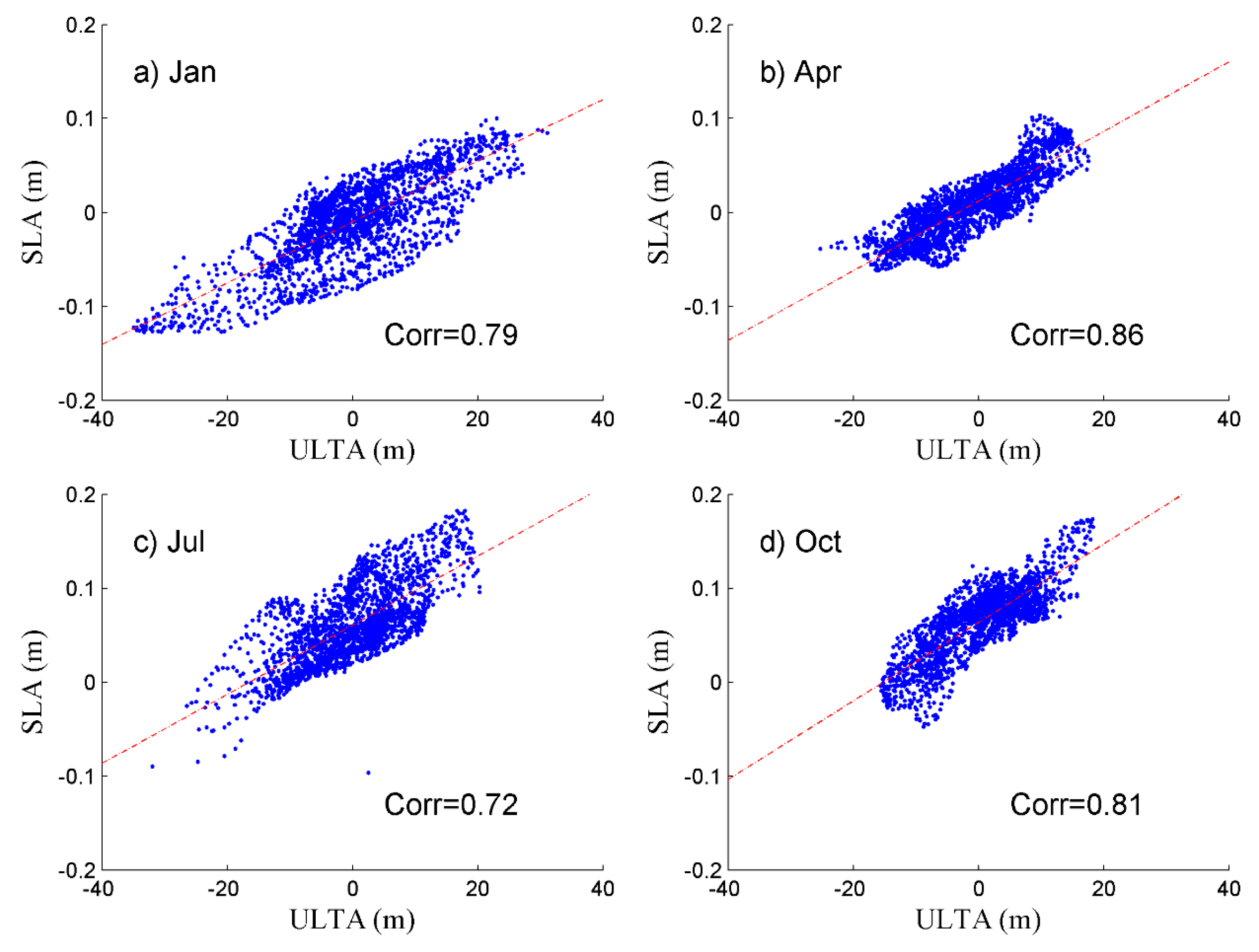
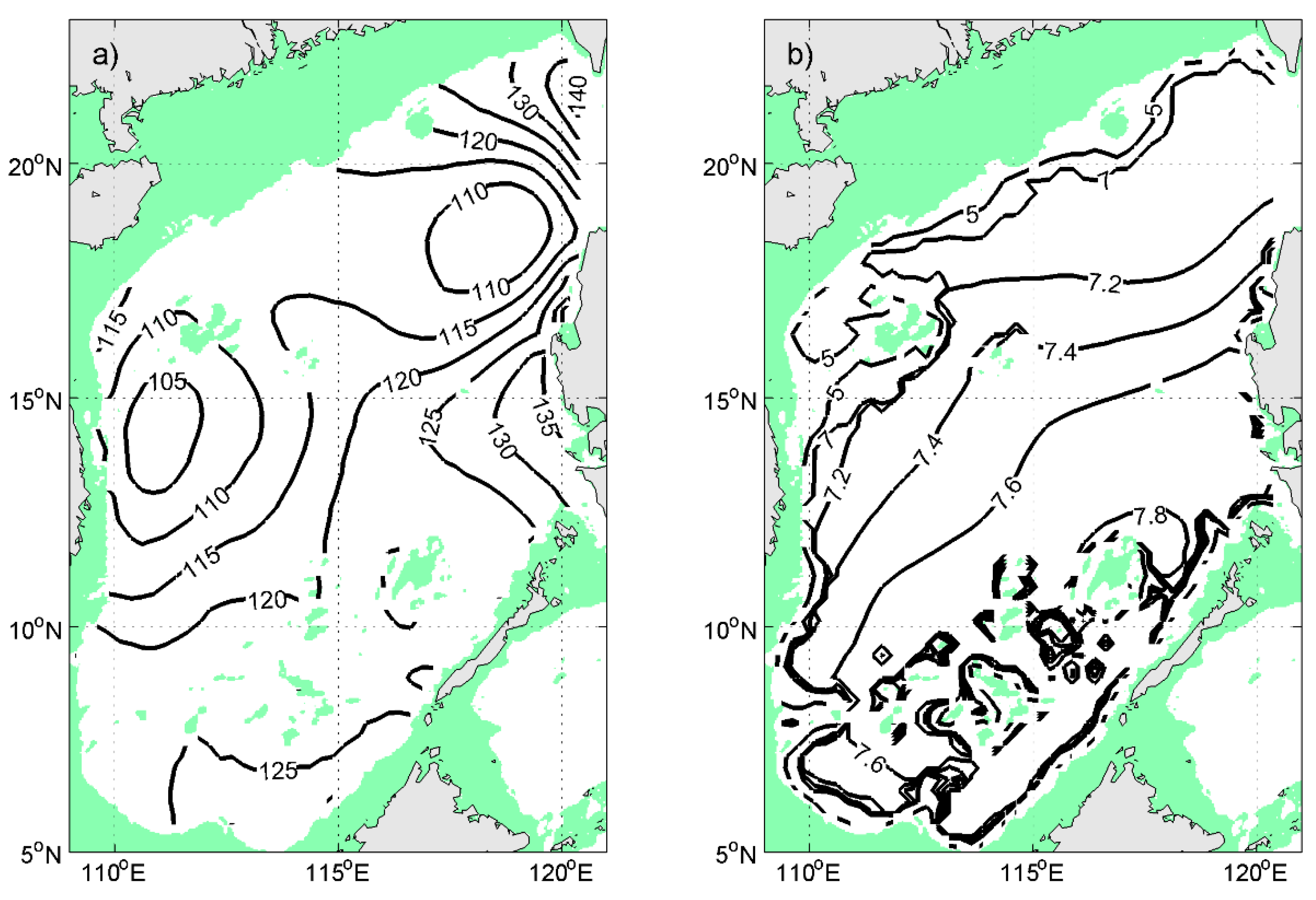
4. Parameter Determination
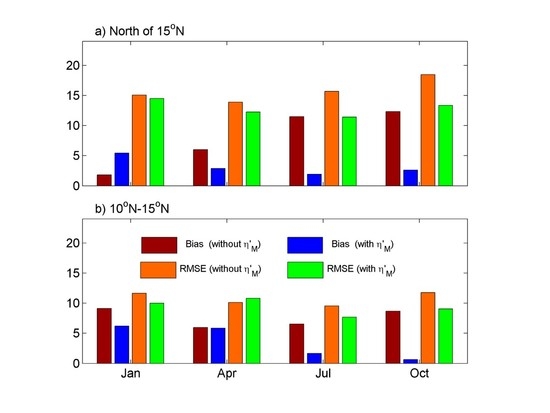
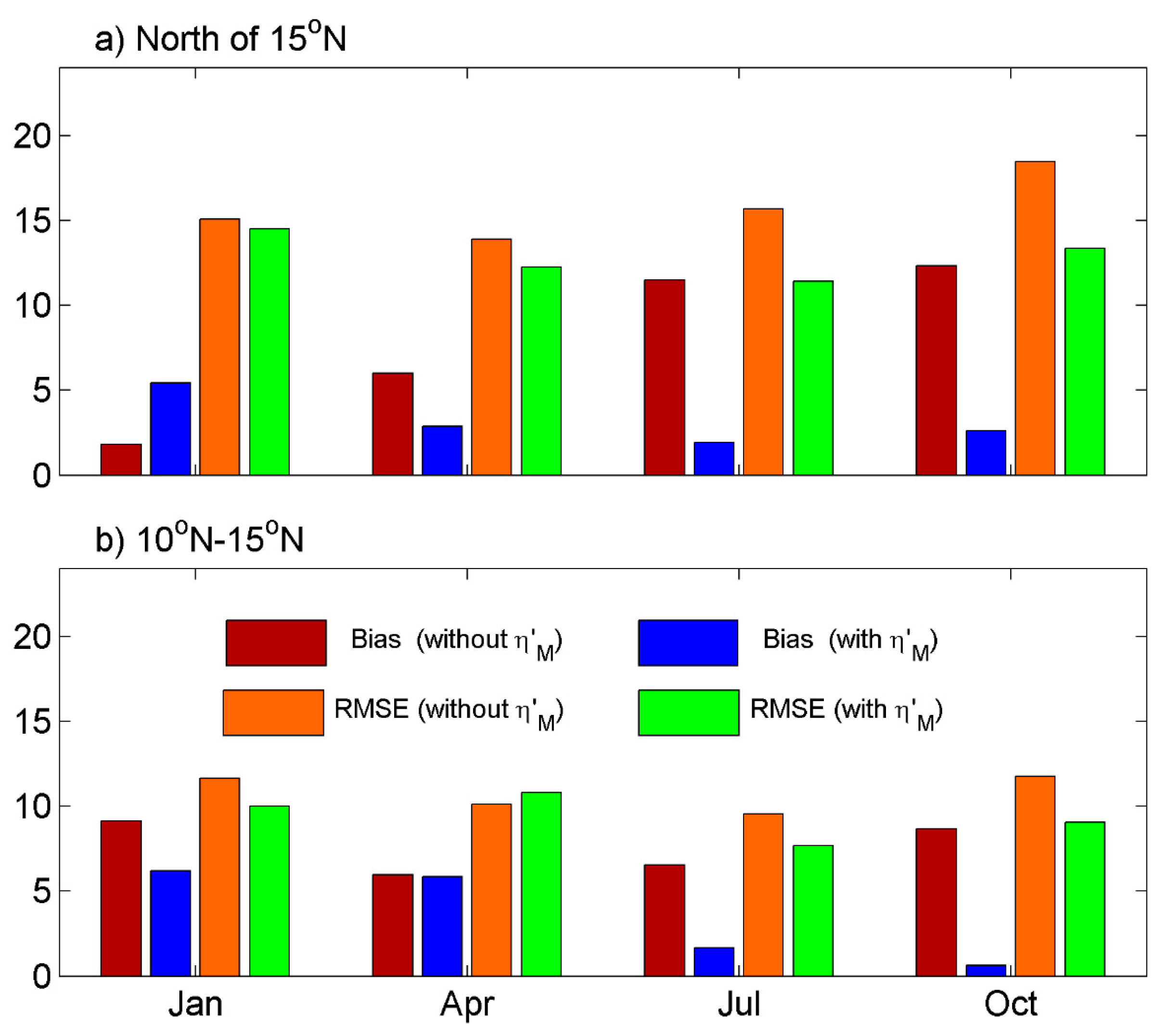
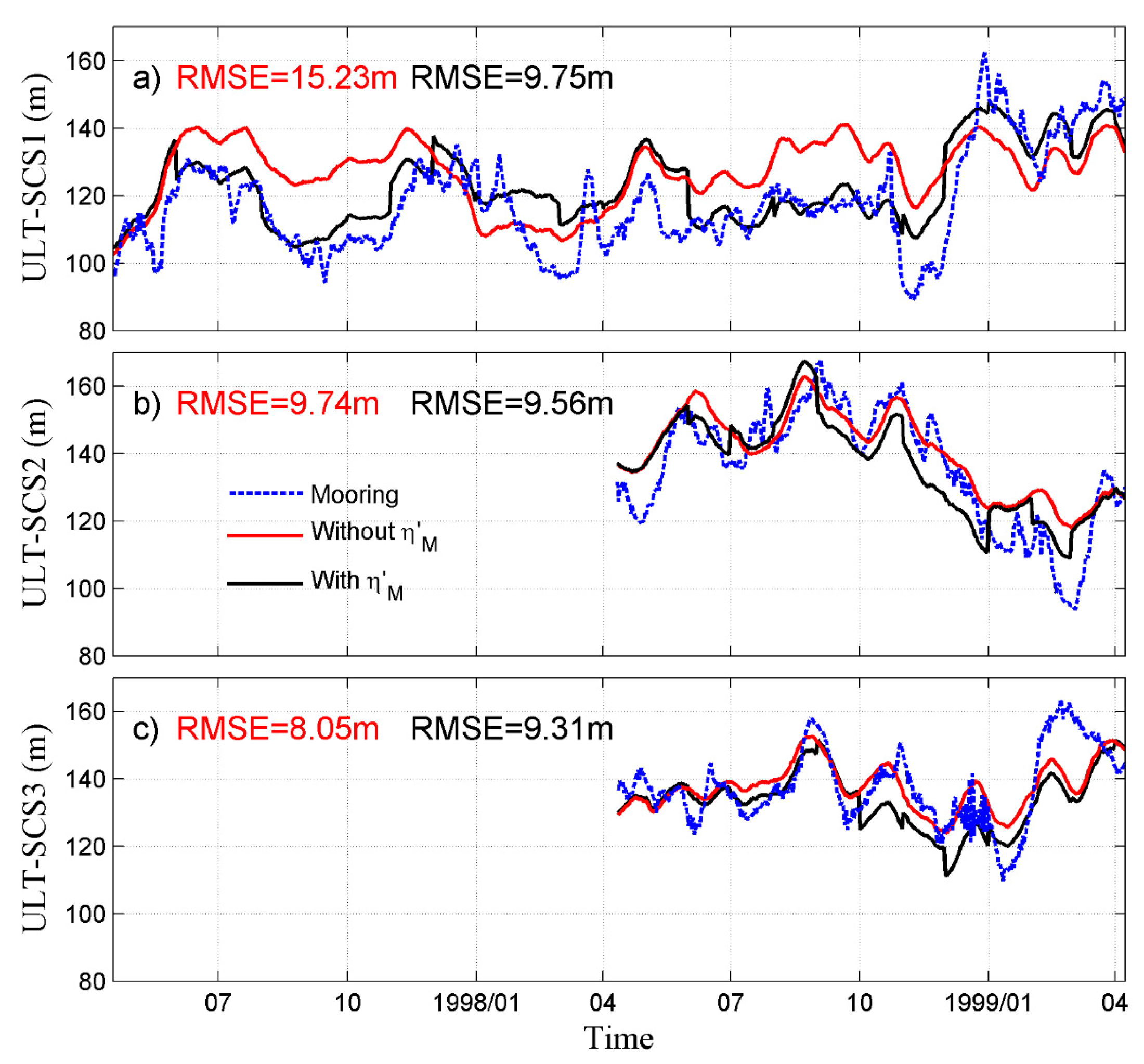
5. Product Evaluation
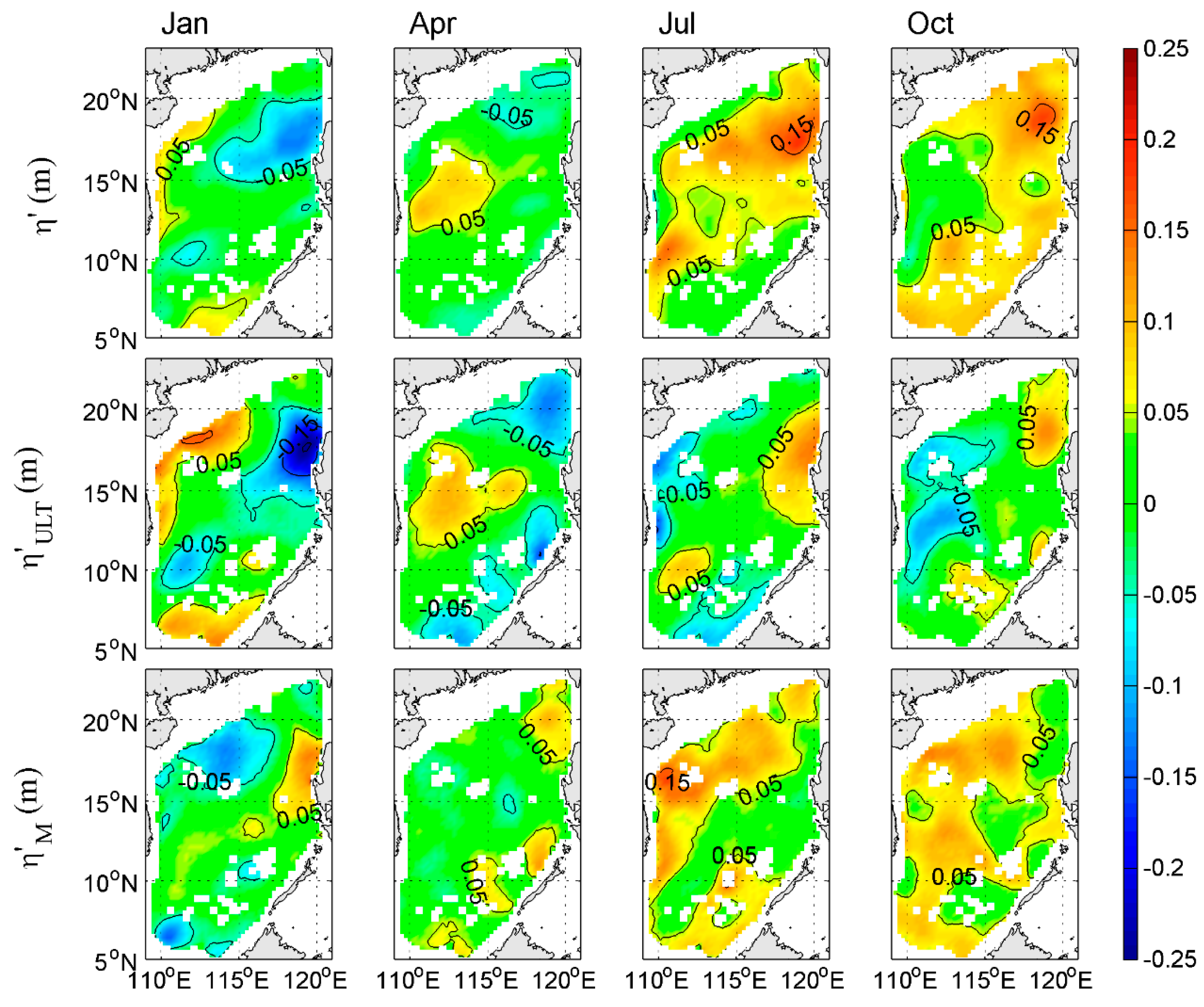
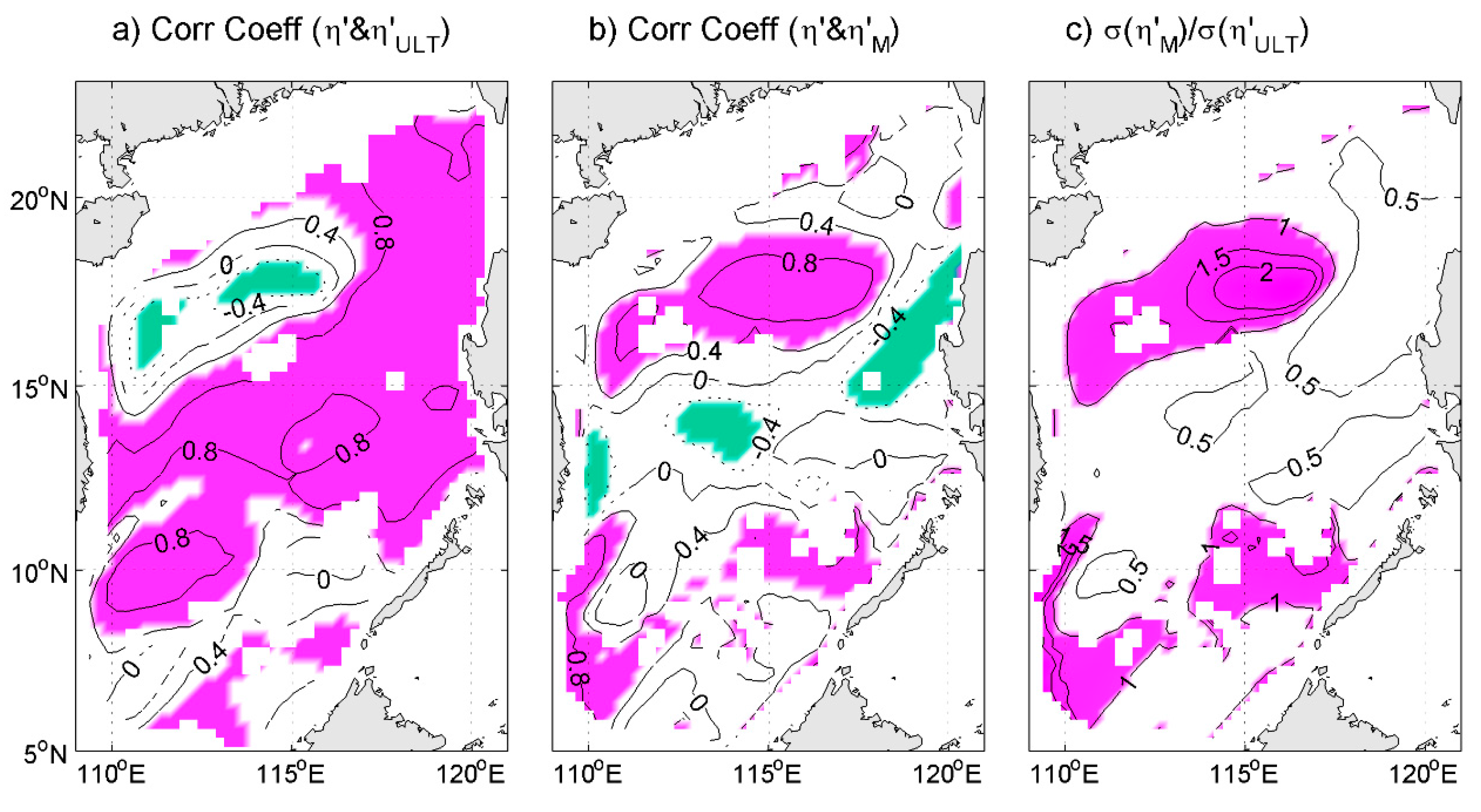
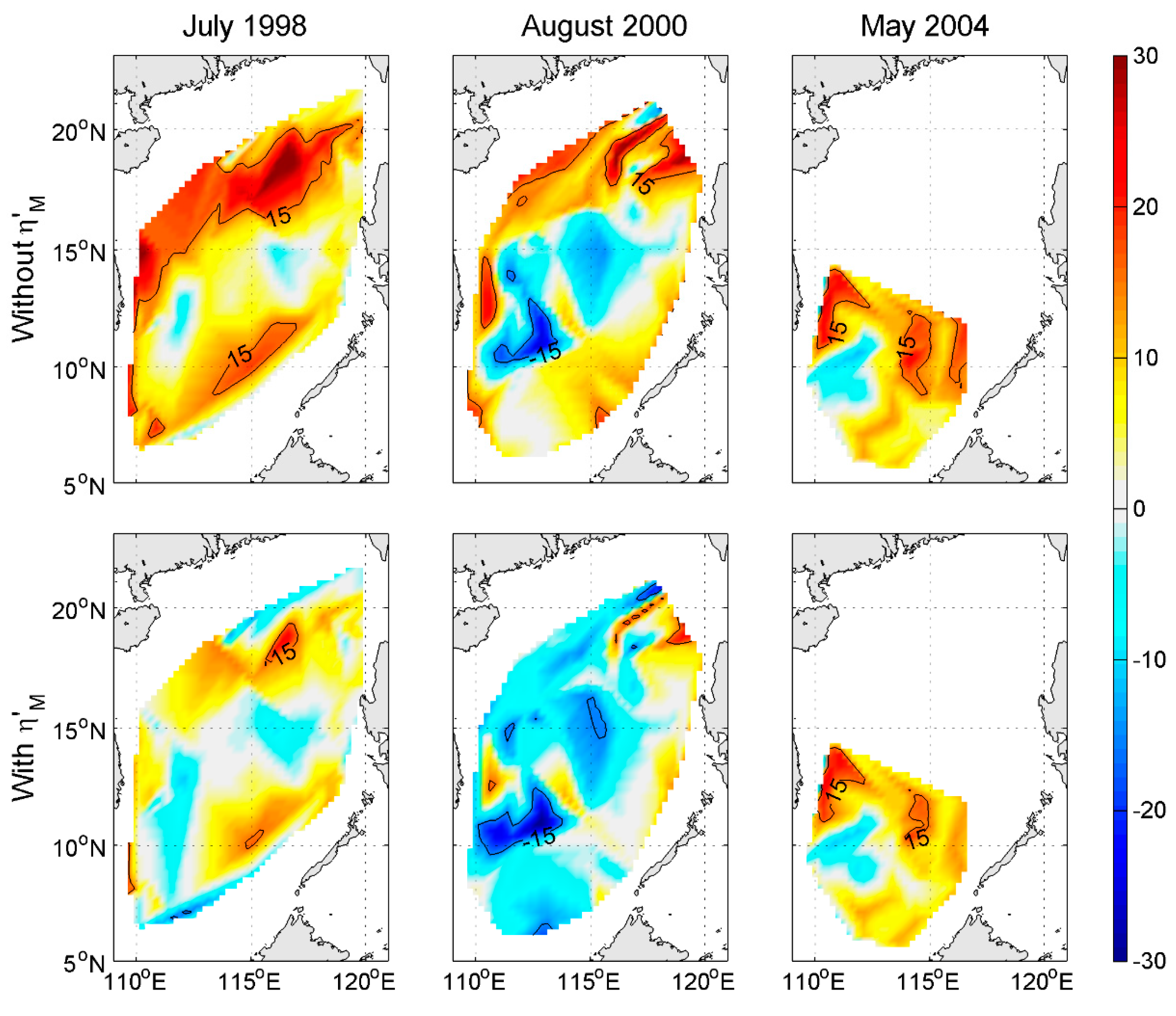
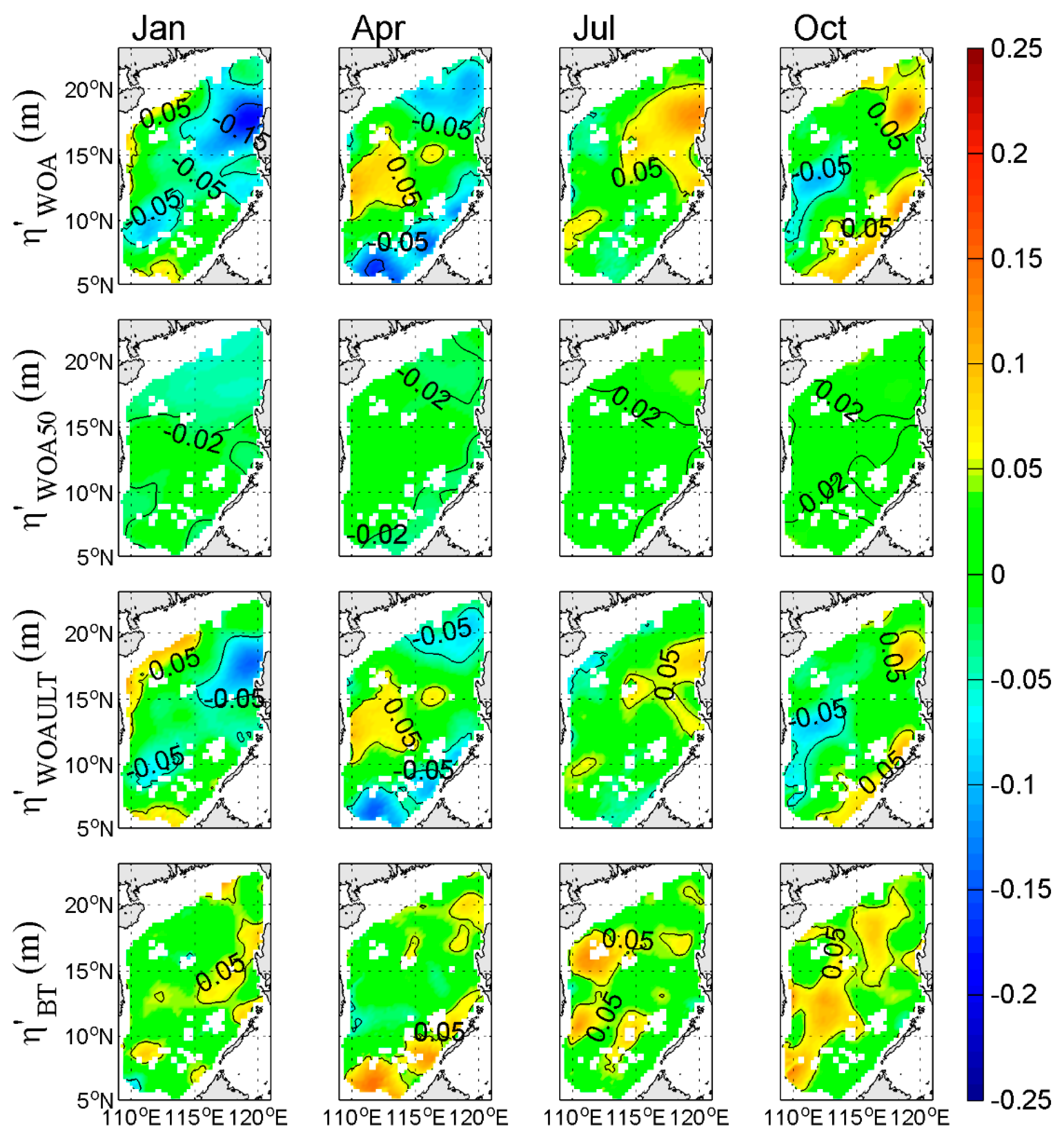
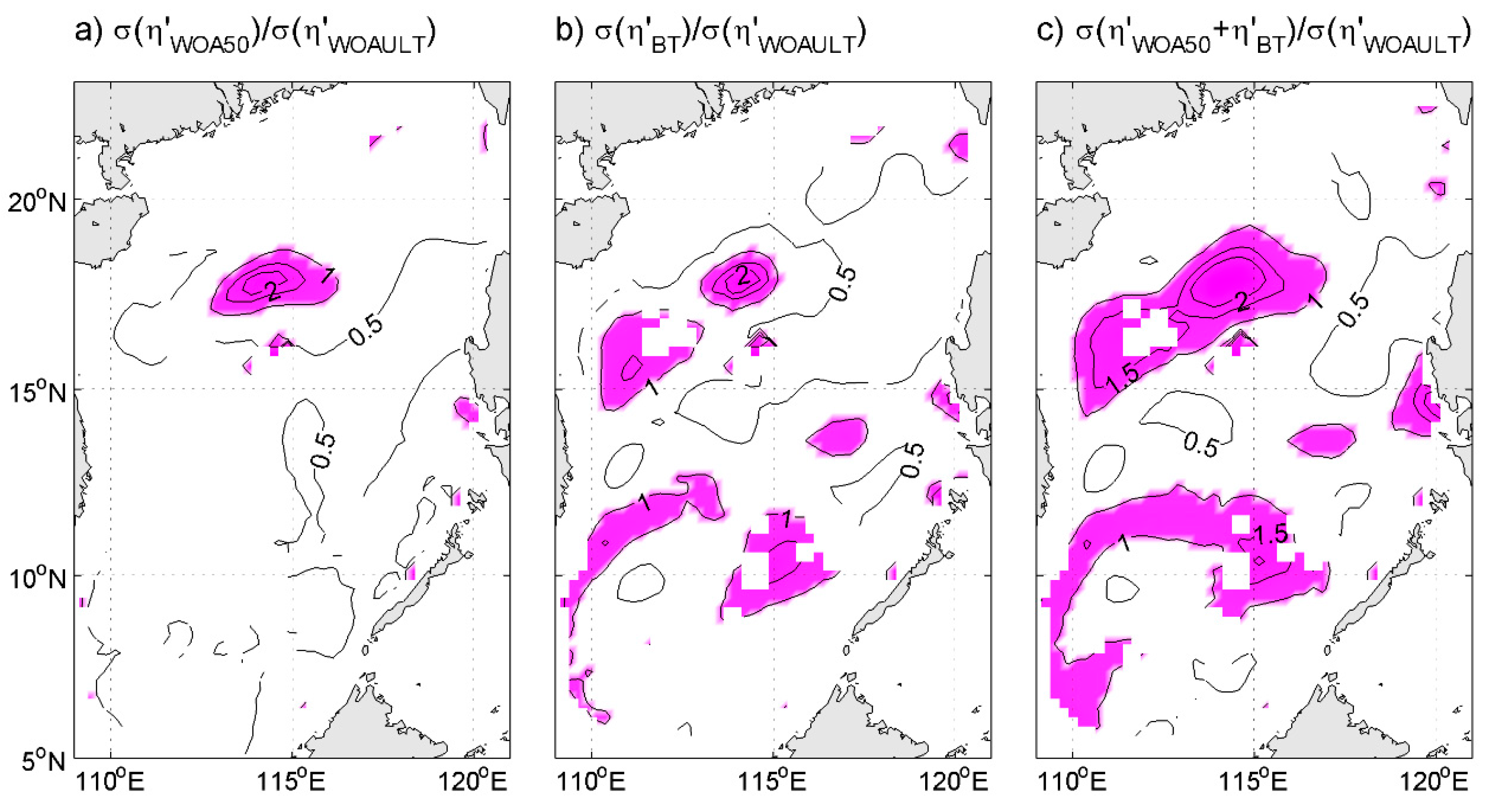
6. Physical Mechanisms of the Modified Component
7. Conclusions and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Goni, G.J.; Kamholz, S.; Garzoli, S.L.; Olson, D.B. Dynamics of the Brazil-Malvinas confluence based on inverted echo sounders and altimetry. J. Geophys. Res. 1996, 101, 16273–16289. [Google Scholar] [CrossRef]
- Garzoli, S.L.; Goni, G.J.; Mariano, A.J.; Olson, D.B. Monitoring the upper southeastern Atlantic transports using altimeter data. J. Mar. Res. 1997, 55, 453–481. [Google Scholar] [CrossRef]
- Sainz-Trapaga, S.; Goni, G.J.; Sugimoto, T. Identification of the Kuroshio Extension, its bifurcation and Northern Branch from altimetry and hydrographic data during October 1992–August 1999: Spatial and temporal variability. Geophys. Res. Lett. 2001, 28, 1759–1762. [Google Scholar] [CrossRef]
- Goni, G.J.; Wainer, I. Investigation of the Brazil current front variability from altimeter data. J. Geophys. Res. 2001, 106, 31117–31128. [Google Scholar] [CrossRef]
- Shay, L.K.; Goni, G.J.; Black, P.G. Effects of a warm oceanic feature on Hurricane Opal. Mon. Weather Rev. 2000, 128, 1366–1383. [Google Scholar] [CrossRef]
- Pun, I.F.; Lin, I.I.; Wu, C.R.; Ko, D.S.; Liu, W.T. Validation and application of altimetry derived upper ocean thermal structure in the western North Pacific Ocean for typhoon intensity forecast. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1616–1630. [Google Scholar] [CrossRef]
- Polito, P.S.; Sato, O.T. Patterns of sea surface height and heat storage associated to intraseasonal Rossby waves in the tropics. J. Geophys. Res. 2003, 34, L09603. [Google Scholar] [CrossRef]
- Lentini, C.A.D.; Goni, G.J.; Olson, D.B. Investigation of Brazil current rings in the confluence region. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Momin, I.M.; Sharma, R.; Basu, S. Satellite-derived heat content in the tropical Indian Ocean. Remote Sens. Lett. 2011, 2, 269–277. [Google Scholar] [CrossRef]
- Lin, C.Y.; Ho, C.R.; Zheng, Z.W.; Kuo, N.J. Validation and variation of upper layer thickness in South China Sea from satellite altimeter data. Sensors 2008, 8, 3802–3818. [Google Scholar] [CrossRef] [PubMed]
- Gill, A.E.; Niiler, P.P. The theory of seasonal variability in the ocean. Deep Sea Res. 1973, 20, 141–177. [Google Scholar] [CrossRef]
- Wyrtki, K. Scientific Results of Marine Investigations of the South China Sea and the Gulf of Thailand. In Physical Oceanography of the Southeast Asian Waters; Scripps Institution of Oceanography: La Jolla, CA, USA, 1961; Volume 2, p. 195. [Google Scholar]
- Qu, T. Upper-Layer Circulation in the South China Sea. J. Phys. Oceanogr. 2000, 30, 1450–1460. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Yuan, Y. Patterns of upper layer circulation variability in the South China Sea from satellite altimetry using the self-organizing map. Acta Oceanol. Sin. 2008, 27, 129–144. [Google Scholar] [CrossRef]
- Amiruddin, A.; Haigh, I.; Tsimplis, M.; Calafat, F.; Dangendorf, S. The seasonal cycle and variability of sea level in the South China Sea. J. Geophys. Res. 2015, 120, 5490–5513. [Google Scholar] [CrossRef]
- Cheng, Y.; Hamlington, B.; Plag, H.-P.; Xu, Q. Influence of ENSO on the variation of annual sea level cycle in the South China Sea. Ocean Eng. 2016, 126, 343–352. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, H.; Liu, Q. Regional dynamics of seasonal variability in the South China Sea. J. Phys. Oceanogr. 2001, 31, 272–284. [Google Scholar] [CrossRef]
- Cheng, X.; Qi, Y. On steric and mass-induced contributions to the annual sea-level variations in the South China Sea. Glob. Planet Chang. 2010, 72, 227–233. [Google Scholar] [CrossRef]
- World Ocean Atlas 2013. Available online: http://apdrc.soest.hawaii.edu (accessed on 4 March 2017).
- Archiving, Validation and Interpretation of Satellite Oceanographic Data. Available online: ftp.aviso.altimetry.fr (accessed on 4 March 2017).
- Le Traon, P.Y.; Ogor, F. ERS-1/2 orbit improvement using TOPEX/POSEIDON: The 2 cm challenge. J. Geophys. Res. 1998, 103, 8045–8057. [Google Scholar] [CrossRef]
- Le Traon, P.Y.; Nadal, F.; Ducet, N. An improved mapping method of multisatellite altimeter data. J. Atmos. Ocean. Technol. 1998, 15, 522–534. [Google Scholar] [CrossRef]
- US Global Ocean Data Assimilation Experiment. Available online: http://www.usgodae.org/cgi-bin/argo_select.pl (accessed on 4 March 2017).
- Liu, Y.; Yuan, Y.; Su, J.; Jiang, J. Circulation in the South China Sea in summer of 1998. Chin. Sci. Bull. 2000, 45, 1648–1655. [Google Scholar] [CrossRef]
- Zeng, L.; Wang, D.; Chen, J.; Wang, W.; Chen, R. SCSPOD14, a South China Sea physical oceanographic dataset derived from in situ measurements during 1919–2014. Sci. Data 2016, 3, 160029. [Google Scholar] [CrossRef] [PubMed]
- Metzger, E.J.; Hurlburt, H. Coupled dynamics of the South China Sea, the Sulu Sea, and the Pacific Ocean. J. Geophys. Res. 1996, 101, 12331–12352. [Google Scholar] [CrossRef]
- Wang, G.; Chen, D.; Su, J. Generation and life cycle of the dipole in the South China Sea summer circulation. J. Geophys. Res. 2006, 111, C06002. [Google Scholar] [CrossRef]
- Zhuang, W.; Qiu, B.; Du, Y. Low-frequency western Pacific Ocean sea level and circulation changes due to the connectivity of the Philippine Archipelago. J. Geophys. Res. 2013, 118, 6759–6773. [Google Scholar] [CrossRef]
- He, Y.; Cai, S.; Wang, D.; He, J. A model study of Luzon cold eddies in the northern South China Sea. Deep Sea Res. Part I 2015, 97, 107–123. [Google Scholar] [CrossRef]
- Gan, J.; Qu, T. Coastal jet separation and associated flow variability in the southwest South China Sea. Deep Sea Res. Part I 2008, 55, 1–19. [Google Scholar] [CrossRef]
- Wu, C.R.; Shaw, P.T.; Chao, S.Y. Assimilating altimetric data into a South China Sea model. J. Geophys. Res. 1999, 104, 29987–30005. [Google Scholar] [CrossRef]
- Chu, X.; Xue, H.; Qi, Y.; Chen, G.; Mao, Q.; Wang, D.; Chai, F. An exceptional anticyclonic eddy in the South China Sea in 2010. J. Geophys. Res. 2014, 119, 881–897. [Google Scholar] [CrossRef]
- Chambers, D.P.; Bonin, J.A. Evaluation of Release 05 time-variable gravity coefficients over the ocean. Ocean Sci. 2012, 8, 859–868. [Google Scholar] [CrossRef]
- Chambers, D.P.; Willis, J.K. A Global Evaluation of Ocean Bottom Pressure from GRACE, OMCT, and Steric-Corrected Altimetry. J. Atmos. Ocean Technol. 2010, 27, 1395–1402. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Yu, K.; Dong, C.; He, Z.; Yan, Y.; Wang, D. Evaluation of Satellite-Altimetry-Derived Pycnocline Depth Products in the South China Sea. Remote Sens. 2017, 9, 822. https://doi.org/10.3390/rs9080822
Chen Y, Yu K, Dong C, He Z, Yan Y, Wang D. Evaluation of Satellite-Altimetry-Derived Pycnocline Depth Products in the South China Sea. Remote Sensing. 2017; 9(8):822. https://doi.org/10.3390/rs9080822
Chicago/Turabian StyleChen, Yingying, Kai Yu, Changming Dong, Zhigang He, Yunwei Yan, and Dongxiao Wang. 2017. "Evaluation of Satellite-Altimetry-Derived Pycnocline Depth Products in the South China Sea" Remote Sensing 9, no. 8: 822. https://doi.org/10.3390/rs9080822
APA StyleChen, Y., Yu, K., Dong, C., He, Z., Yan, Y., & Wang, D. (2017). Evaluation of Satellite-Altimetry-Derived Pycnocline Depth Products in the South China Sea. Remote Sensing, 9(8), 822. https://doi.org/10.3390/rs9080822