Feasibility of GNSS-R Ice Sheet Altimetry in Greenland Using TDS-1
Abstract
1. Introduction
2. GNSS-R and the TDS-1 Reflectometry Instrument
3. Data Set and Models Used in This Study
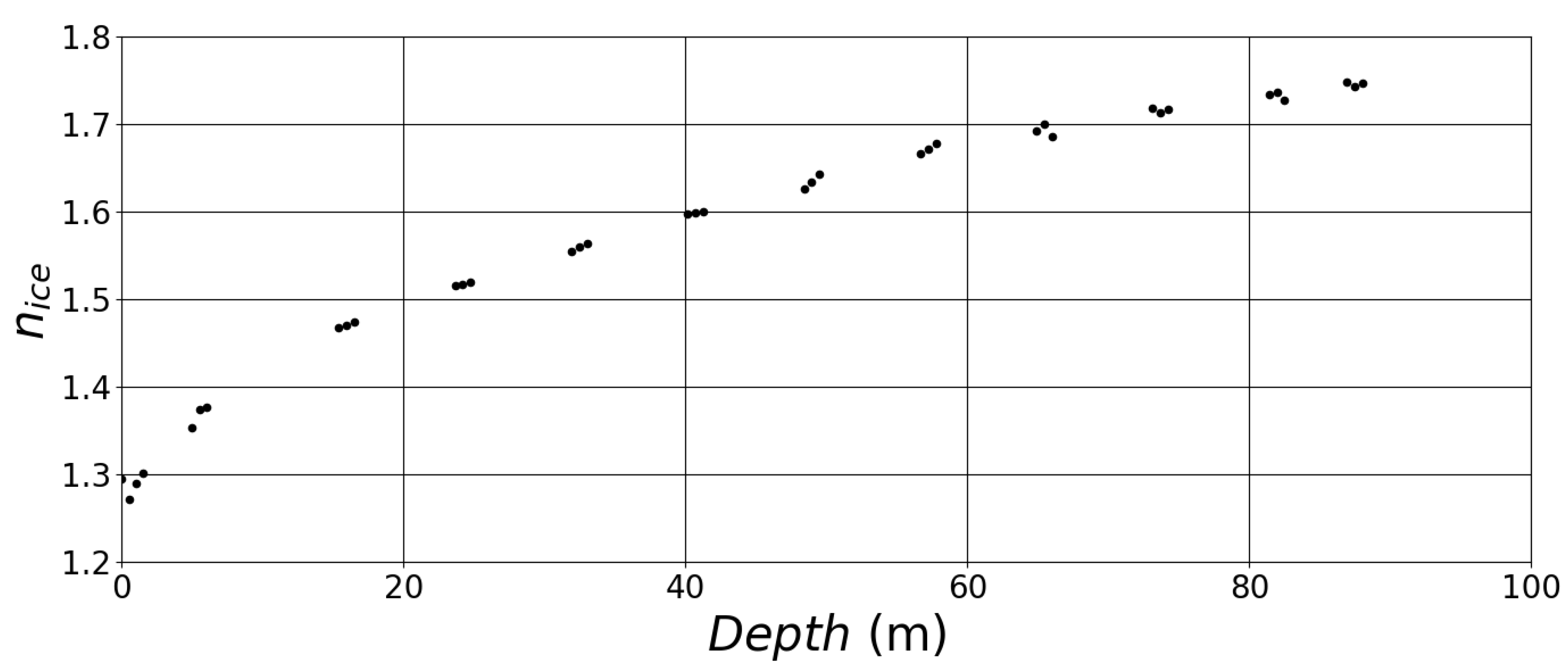
3.1. Additional Model Components
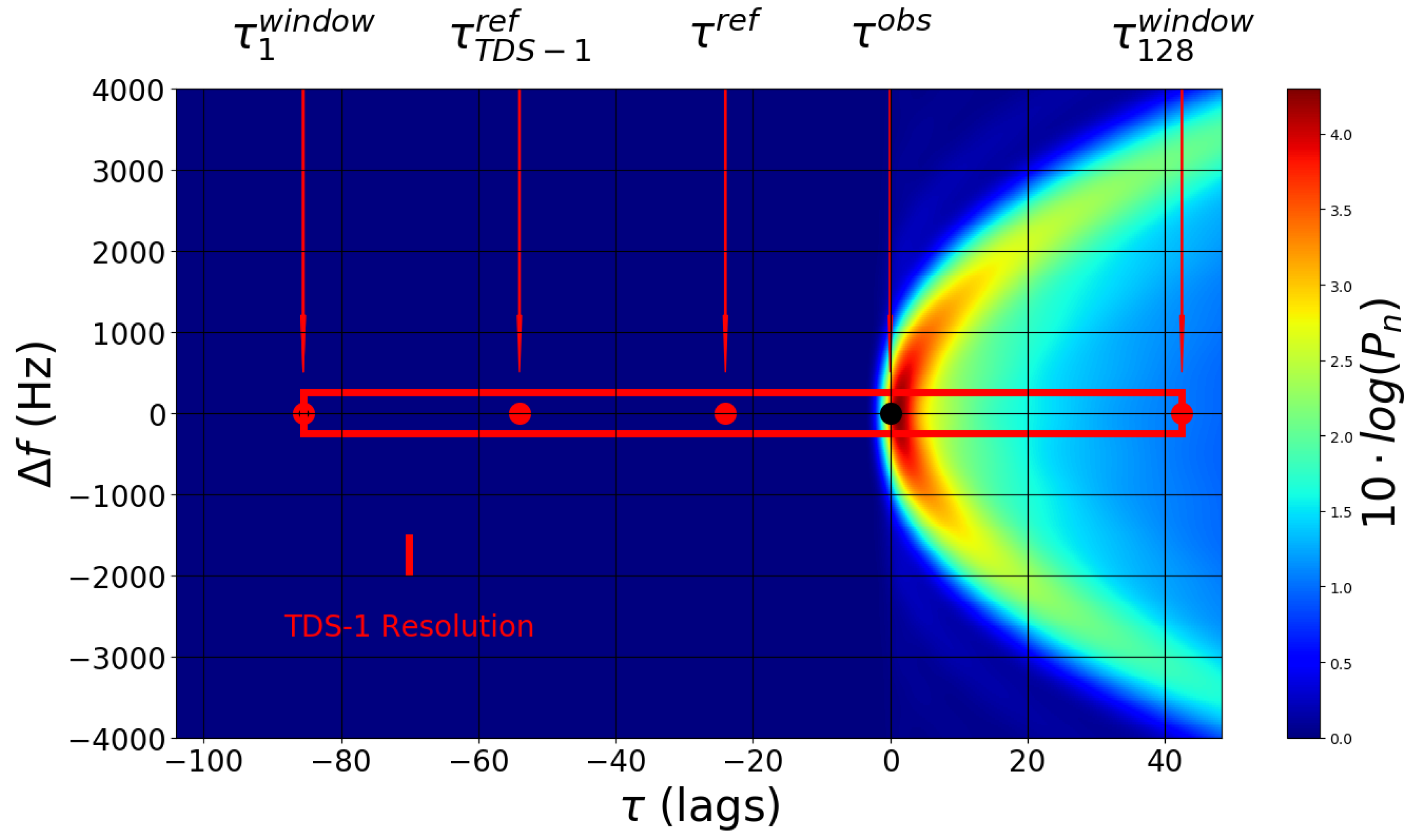
3.2. Expected Delay Precision
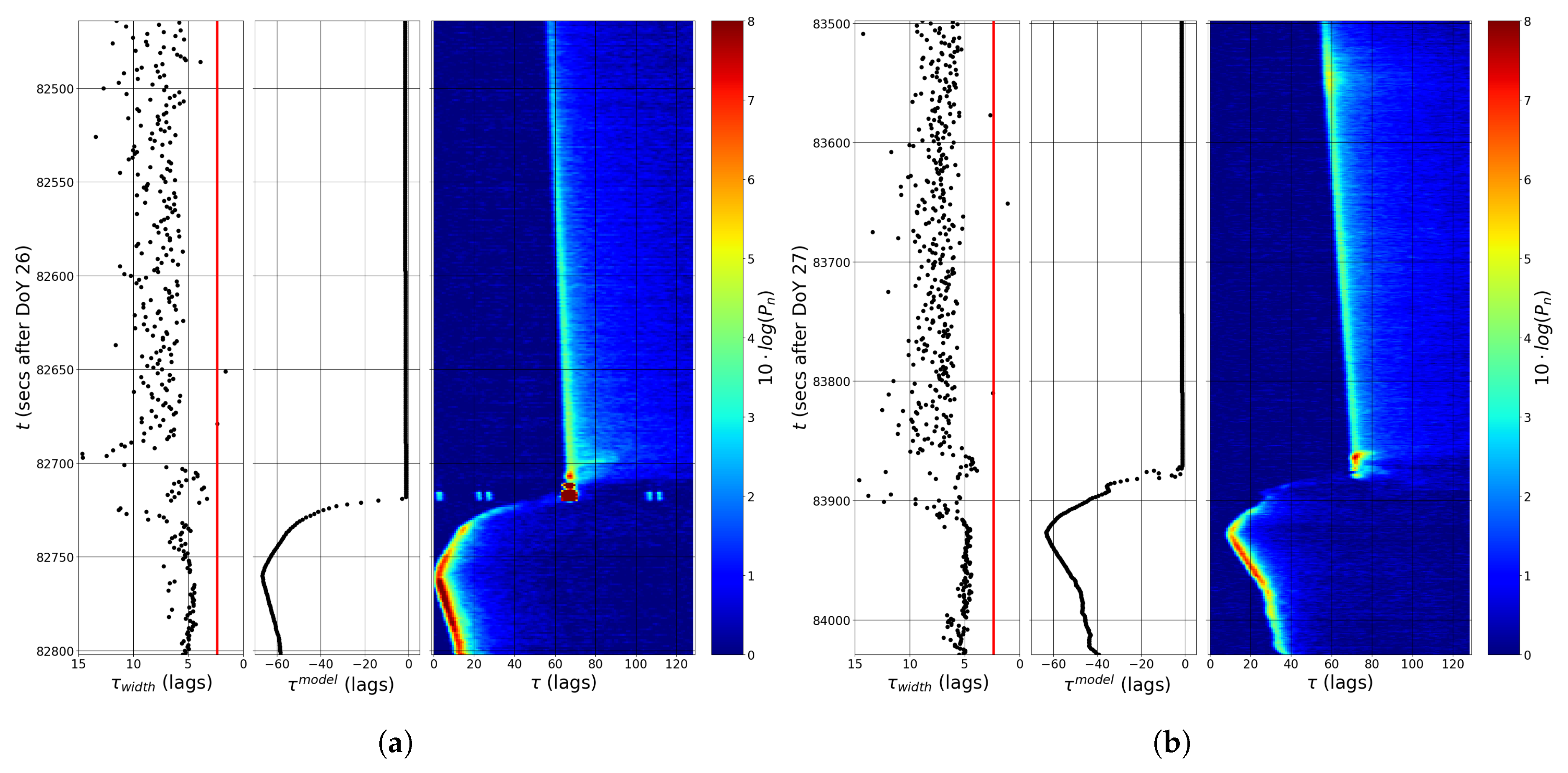
3.3. Selected Waveforms over Greenland
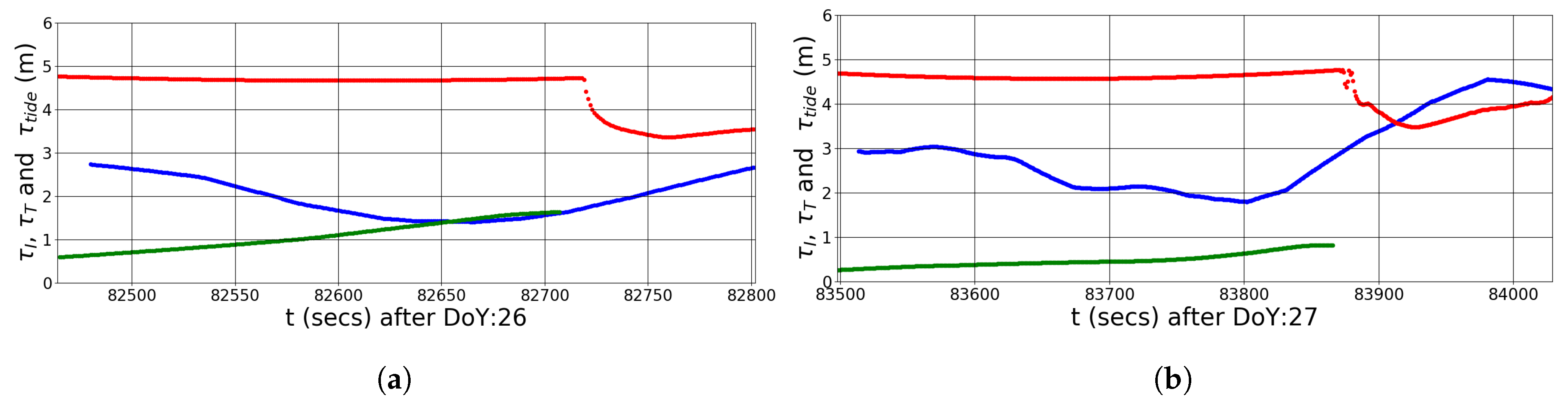
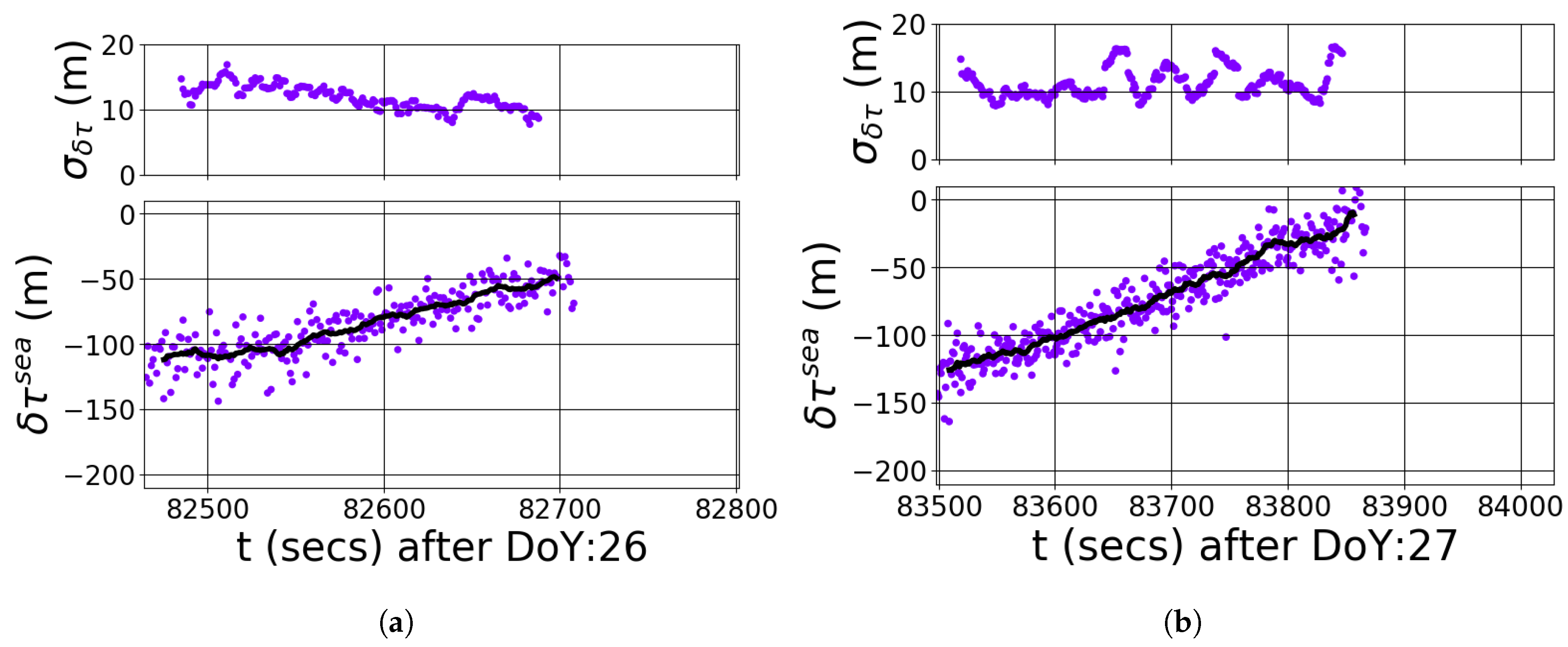
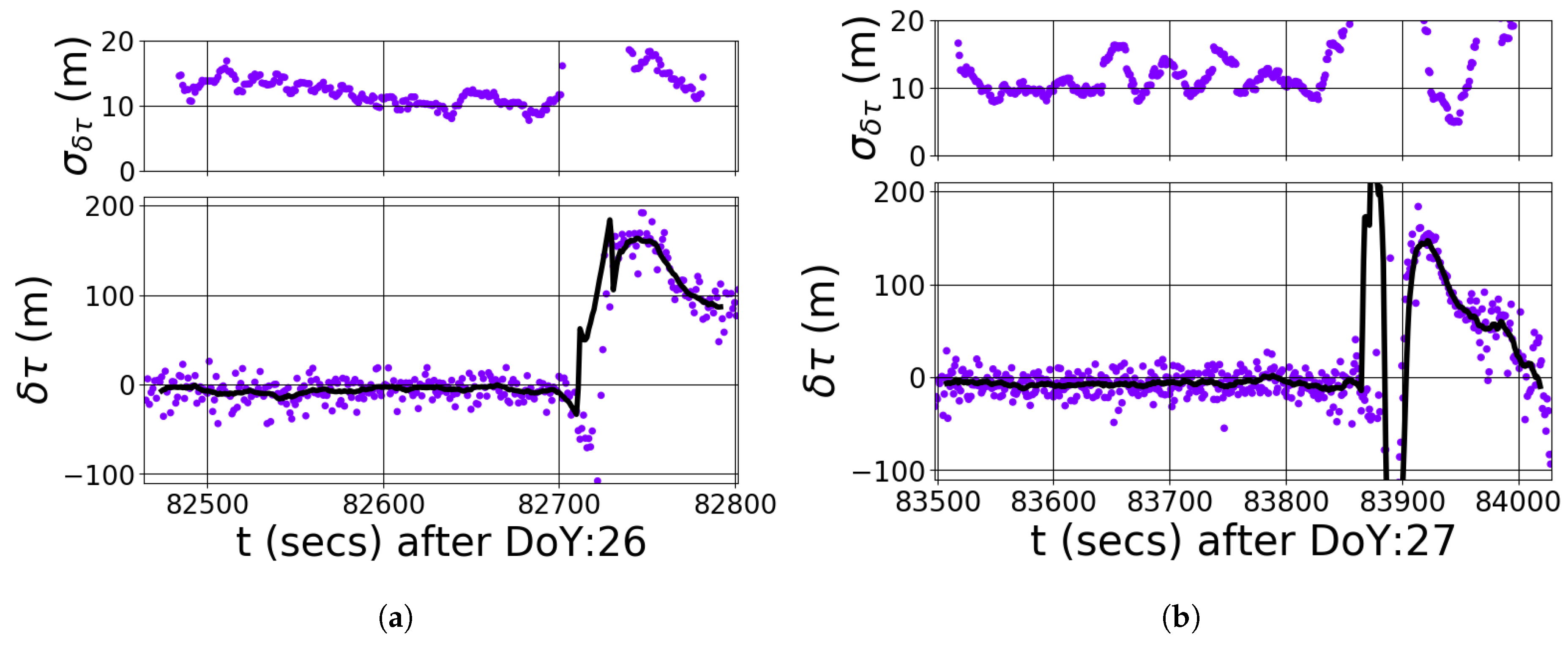
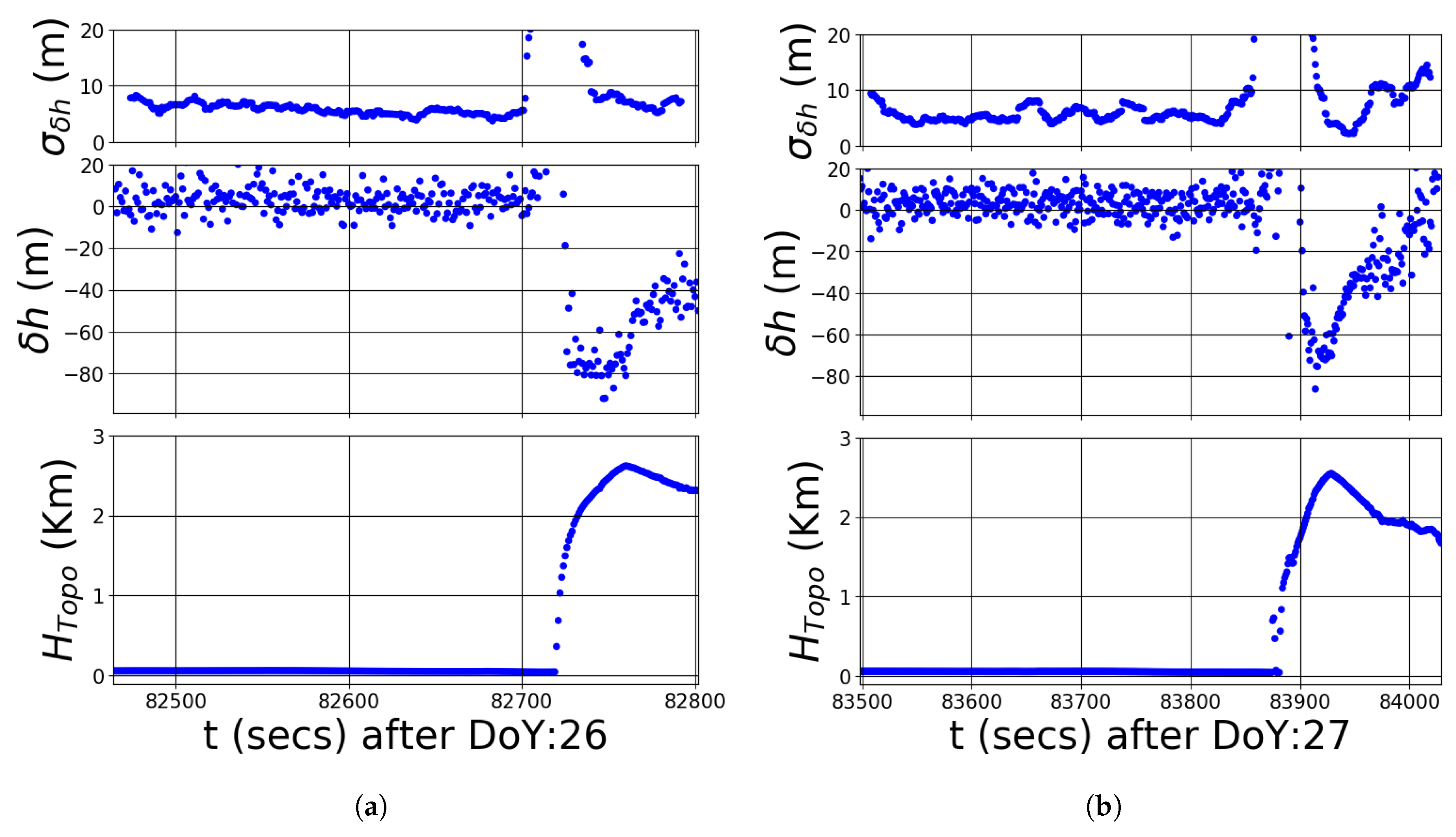
4. Results
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CYGNSS | Cyclone Global Navigation Satellite System |
| DDM | Delay-Doppler Map |
| DEM | Digital Elevation Model |
| EGM | Earth Gravitational Model |
| GCM | Greenland Cumulative Melt |
| GIM | Global Ionospheric Maps |
| GNSS | Global Navigation Satellite System |
| GNSS-R | GNSS Reflectometry |
| cGNSS-R | Conventional GNSS-R |
| iGNSS-R | Interferometric GNSS-R |
| GPS | Global Positioning System |
| IGS | International GNSS Service |
| NEEM | North Greenland Eemian Ice Drilling |
| NSIDC | National Snow and Ice Data Center |
| Signal-to-Noise Ratio | |
| TDS | TechDemoSat |
| TDX | Tandem-X Mission |
| VTEC | Vertical Total Electron Content |
| WGS | World Geodetic System |
References
- Gregory, J.M.; Huybrechts, P.; Raper, S.C.B. Climatology: Threatened loss of the Greenland ice-sheet. Nature 2004, 428, 616. [Google Scholar] [CrossRef] [PubMed]
- Lythe, M.B.; Vaughan, D.G. BEDMAP: A new ice thickness and subglacial topographic model of Antarctica. J. Geophys. Res. Solid Earth 2001, 106, 11335–11351. [Google Scholar] [CrossRef]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Leverman, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D.; et al. Sea Level Change. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Mouginot, J.; Rignot, E.; Scheuchl, B.; Fenty, I.; Khazendar, A.; Morlighem, M.; Buzzi, A.; Paden, J. Fast retreat of Zachariæ Isstrøm, northeast Greenland. Science 2015, 350, 1357–1361. [Google Scholar] [CrossRef] [PubMed]
- McMillan, M.; Shepherd, A.; Sundal, A.; Briggs, K.; Muir, A.; Ridout, A.; Hogg, A.; Wingham, D. Increased ice losses from Antarctica detected by CryoSat-2. Geophys. Res. Lett. 2014, 41, 3899–3905. [Google Scholar] [CrossRef]
- Nghiem, S.V.; Hall, D.K.; Mote, T.L.; Tedesco, M.; Albert, M.R.; Keegan, K.; Shuman, C.A.; DiGirolamo, N.E.; Neumann, G. The extreme melt across the Greenland ice sheet in 2012. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Zwally, H.J.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D.; et al. ICESat’s laser measurements of polar ice, atmosphere, ocean, and land. J. Geodyn. 2002, 34, 405–445. [Google Scholar] [CrossRef]
- Wingham, D.J.; Francis, C.R.; Baker, S.; Bouzinac, C.; Brockley, D.; Cullen, R.; de Chateau-Thierry, P.; Laxon, S.W.; Mallow, U.; Mavrocordatos, C.; et al. CryoSat: A mission to determine the fluctuations in Earth’s land and marine ice fields. Adv. Space Res. 2006, 37, 841–871. [Google Scholar] [CrossRef]
- Brenner, A.C.; DiMarzio, J.P.; Zwally, H.J. Precision and Accuracy of Satellite Radar and Laser Altimeter Data Over the Continental Ice Sheets. IEEE Trans. Geosci. Remote Sens. 2007, 45, 321–331. [Google Scholar] [CrossRef]
- Martin-Neira, M.; D’Addio, S.; Buck, C.; Floury, N.; Prieto-Cerdeira, R. The PARIS Ocean Altimeter In-Orbit Demonstrator. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2209–2237. [Google Scholar] [CrossRef]
- Ruf, C.; Unwin, M.; Dickinson, J.; Rose, R.; Rose, D.; Vincent, M.; Lyons, A. CYGNSS: Enabling the Future of Hurricane Prediction [Remote Sensing Satellites]. IEEE Geosci. Remote Sens. Mag. 2013, 1, 52–67. [Google Scholar] [CrossRef]
- Cardellach, E.; Rius, A.; Martin-Neira, M.; Fabra, F.; Nogués-Correig, O.; Ribó, S.; Kainulainen, J.; Camps, A.; D’Addio, S. Consolidating the Precision of Interferometric GNSS-R Ocean Altimetry Using Airborne Experimental Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4992–5004. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Domènech, E.V.i.; Pascual, D.; Martin, F.; Rius, A.; Ribó, S.; Benito, J.; Andrés-Beivide, A.; Saameno, P.; et al. Optimization and Performance Analysis of Interferometric GNSS-R Altimeters: Application to the PARIS IoD Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1436–1451. [Google Scholar] [CrossRef]
- Wickert, J.; Cardellach, E.; Martín-Neira, M.; Bandeiras, J.; Bertino, L.; Andersen, O.B.; Camps, A.; Catarino, N.; Chapron, B.; Fabra, F.; et al. GEROS-ISS: GNSS REflectometry, Radio Occultation, and Scatterometry Onboard the International Space Station. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4552–4581. [Google Scholar] [CrossRef]
- Unwin, M.; Jales, P.; Tye, J.; Gommenginger, C.; Foti, G.; Rosello, J. Spaceborne GNSS-Reflectometry on TechDemoSat-1: Early Mission Operations and Exploitation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4525–4539. [Google Scholar] [CrossRef]
- Cardellach, E.; Ao, C.O.; de la Torre Juárez, M.; Hajj, G.A. Carrier phase delay altimetry with GPS-reflection/occultation interferometry from low Earth orbiters. Geophys. Res. Lett. 2004, 31, 377–393. [Google Scholar] [CrossRef]
- Cardellach, E.; Fabra, F.; Rius, A.; Pettinato, S.; D’Addio, S. Characterization of dry-snow sub-structure using GNSS reflected signals. Remote Sens. Environ. 2012, 124, 122–134. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, B04406. [Google Scholar] [CrossRef]
- Benson, C. Stratigraphic Studies in the Snow and Firn of the Greenland Ice Sheet; Cold Regions Research and Engineering Lab: Hanover, NH, USA, 1962. [Google Scholar]
- Jales, P.; Unwin, M. MERRByS Product Manual: GNSS-Reflectometry on TDS-1 with the SGR-ReSI; Surrey Satellite Technol. Ltd.: Guildford, UK, 2015. [Google Scholar]
- Jales, P. Spaceborne Receiver Design for Scatterometric GNSS Reflectometr. Ph.D. Thesis, University of Surrey, Guildford, UK, 2012. [Google Scholar]
- Schiavulli, D.; Nunziata, F.; Migliaccio, M.; Frappart, F.; Ramilien, G.; Darrozes, J. Reconstruction of the Radar Image From Actual DDMs Collected by TechDemoSat-1 GNSS-R Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4700–4708. [Google Scholar] [CrossRef]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Roselló, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Pablos, M.; Foti, G.; Gommenginger, C.; Liu, P.W.; Judge, J. Soil moisture and vegetation impact in GNSS-R TechDemosat-1 observations. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1982–1984. [Google Scholar]
- Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A.J. Demonstrating soil moisture remote sensing with observations from the UK TechDemoSat-1 satellite mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Foti, G.; Gommenginger, C. Ionospheric Effects in GNSS-Reflectometry From Space. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5851–5861. [Google Scholar] [CrossRef]
- Hu, C.; Benson, C.; Rizos, C.; Qiao, L. Single-Pass Sub-Meter Space-Based GNSS-R Ice Altimetry: Results From TDS-1. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 1–7. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.; Cipollini, P.; Zuffada, C. First spaceborne observation of sea surface height using GPS-Reflectometry. Geophys. Res. Lett. 2016, 43, 767–774. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Spaceborne GNSS-R Sea Ice Detection Using Delay-Doppler Maps: First Results From the U.K. TechDemoSat-1 Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4795–4801. [Google Scholar] [CrossRef]
- AlonsoArroyo, A.; Zavorotny, V.U.; Camps, A. Sea ice detection using GNSS-R data from UK TDS-1. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 2001–2004. [Google Scholar]
- Yan, Q.; Huang, W.; Moloney, C. Neural Networks Based Sea Ice Detection and Concentration Retrieval From GNSS-R Delay-Doppler Maps. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 1–10. [Google Scholar] [CrossRef]
- Schiavulli, D.; Frappart, F.; Ramillien, G.; Darrozes, J.; Nunziata, F.; Migliaccio, M. Observing Sea/Ice Transition Using Radar Images Generated From TechDemoSat-1 Delay Doppler Maps. IEEE Geosci. Remote Sens. Lett. 2017, 14, 734–738. [Google Scholar] [CrossRef]
- Elachi, C. Spaceborne Radar Remote Sensing: Applications and Techniques; IEEE Press: New York, NY, USA, 1988. [Google Scholar]
- Hajj, G.A.; Zuffada, C. Theoretical description of a bistatic system for ocean altimetry using the GPS signal. Radio Sci. 2003, 38, 1089. [Google Scholar] [CrossRef]
- Rius, A.; Cardellach, E.; Martin-Neira, M. Altimetric Analysis of the Sea-Surface GPS-Reflected Signals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2119–2127. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef]
- Wiehl, M.; Legresy, B.; Dietrich, R. Potential of reflected GNSS signals for ice sheet remote sensing. Prog. Electromagn. Res. 2003, 40, 177–205. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2006. [Google Scholar]
- Hernández Pajares, M.; Roma Dollase, D.; Krankowski, A.; García Rigo, A.; Orús Pérez, R. Comparing performances of seven different global VTEC ionospheric models in the IGS context. In Proceedings of the International GNSS Service Workshop (IGS 2016), Sydney, Australia, 8–12 February 2016; pp. 1–13. [Google Scholar]
- Gleason, S.; Hodgart, S.; Sun, Y.; Gommenginger, C.; Mackin, S.; Adjrad, M.; Unwin, M. Detection and Processing of bistatically reflected GPS signals from low Earth orbit for the purpose of ocean remote sensing. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1229–1241. [Google Scholar] [CrossRef]
- Bracewell, R. The Fourier Transform and Its Applications; Electrical and Electronic Engineering; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Hoen, E.W.; Zebker, H.A. Penetration depths inferred from interferometric volume decorrelation observed over the Greenland ice sheet. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2571–2583. [Google Scholar]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Volume 2—Radar remote sensing and surface scattering and emission theory. In Microwave Remote Sensing: Active and Passive; Artech House: Norwood, MA, USA, 1982. [Google Scholar]
- Fujita, S.; Hirabayashi, M.; Goto-Azuma, K.; Dallmayr, R.; Satow, K.; Zheng, J.; Dahl-Jensen, D. Densification of layered firn of the ice sheet at NEEM, Greenland. J. Glaciol. 2014, 60, 905–921. [Google Scholar] [CrossRef]
- Simonsen, S.B.; Stenseng, L.; Aðalgeirsdóttir, G.; Fausto, R.S.; Hvidberg, C.S.; Lucas-Pichery, P. Assessing a multilayered dynamic firn-compaction model for Greenland with ASIRAS radar measurements. J. Glaciol. 2013, 59, 545–558. [Google Scholar] [CrossRef]
- Rignot, E.; Echelmeyer, K.; Krabill, W. Penetration depth of interferometric synthetic-aperture radar signals in snow and ice. Geophys. Res. Lett. 2001, 28, 3501–3504. [Google Scholar] [CrossRef]
- Mote, T.L.; Anderson, M.R. Variations in snowpack melt on the Greenland ice sheet based on passive-microwave measurements. J. Glaciol. 1995, 41, 51–60. [Google Scholar] [CrossRef]
- Overly, T.B.; Hawley, R.L.; Helm, V.; Morris, E.M.; Chaudhary, R.N. Greenland annual accumulation along the EGIG line, 1959–2004, from ASIRAS airborne radar and neutron-probe density measurements. Cryosphere 2016, 10, 1679–1694. [Google Scholar] [CrossRef]
- Forster, R.R.; van den Broeke, M.R.; Miège, C.; Burgess, E.W.; van Angelen, J.H.; Lenaerts, J.T.; Koenig, L.S.; Paden, J.; Lewis, C.; Gogineni, S.P.; et al. Extensive liquid meltwater storage in firn within the Greenland ice sheet. Nat. Geosci. 2014, 7, 95–98. [Google Scholar] [CrossRef]
- Koenig, L.S.; Alexander, P.M.; MacGregor, J.A.; Paden, J.D.; Forster, R.R.; McConnell, J.R. Annual Greenland accumulation rates (2009–2012) from airborne snow radar. Cryosphere 2016, 10, 1739. [Google Scholar] [CrossRef]
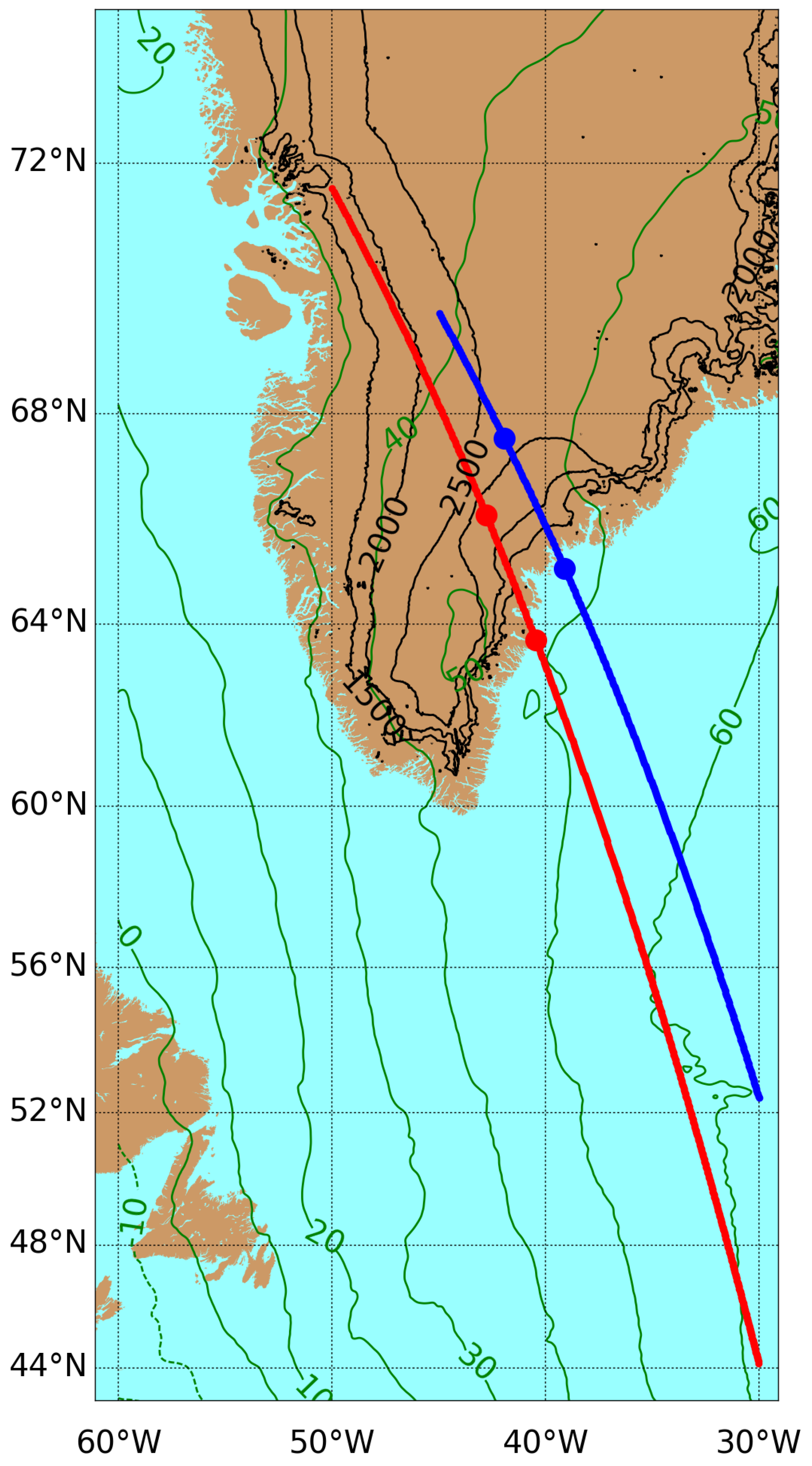
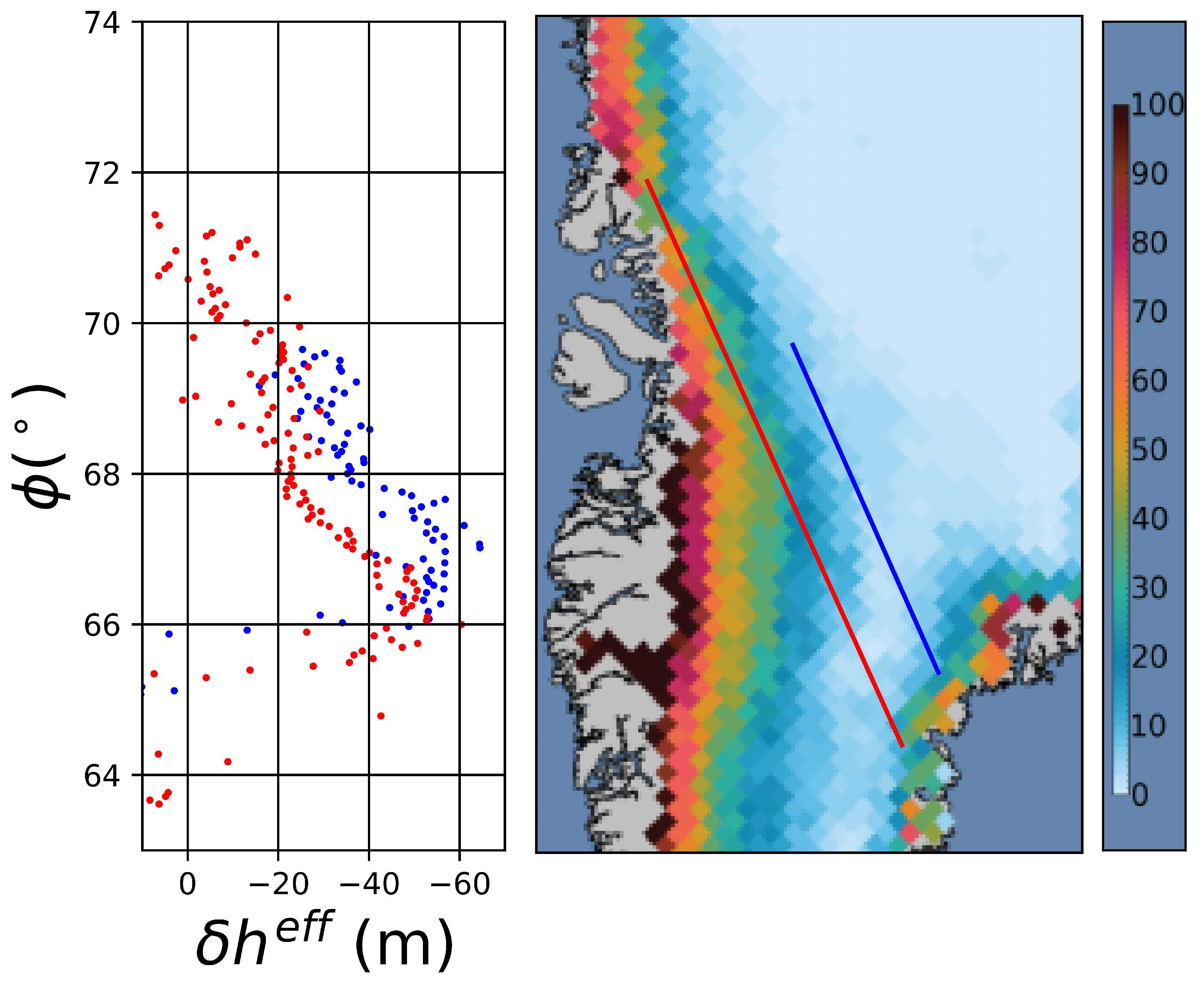
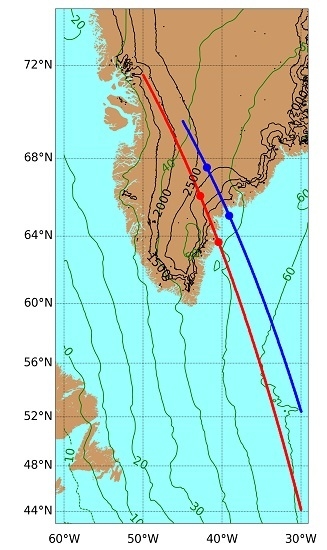
| First Transect | Second Transect | |
|---|---|---|
| TDS-1 RD ID | 16 | 16 |
| TDS-1 Track ID | 120 | 765 |
| Date | 26 January 2015 | 27 January 2015 |
| Second of Day | 82,470–82,800 (s) | 83,505–84,200 (s) |
| GPS PRN | 31 | 31 |
| SP Lat&Lon (Start) | [52.775N, 30.164W] | [43.687N, 25.605W] |
| SP Lat&Lon (End) | [69.574N, 44.747W] | [78.828N, 71.880W] |
| Incidence angle i | 3–19 () | 4–28 () |
| Gain | 8–12 (dBi) | 8–13 (dBi) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rius, A.; Cardellach, E.; Fabra, F.; Li, W.; Ribó, S.; Hernández-Pajares, M. Feasibility of GNSS-R Ice Sheet Altimetry in Greenland Using TDS-1. Remote Sens. 2017, 9, 742. https://doi.org/10.3390/rs9070742
Rius A, Cardellach E, Fabra F, Li W, Ribó S, Hernández-Pajares M. Feasibility of GNSS-R Ice Sheet Altimetry in Greenland Using TDS-1. Remote Sensing. 2017; 9(7):742. https://doi.org/10.3390/rs9070742
Chicago/Turabian StyleRius, Antonio, Estel Cardellach, Fran Fabra, Weiqiang Li, Serni Ribó, and Manuel Hernández-Pajares. 2017. "Feasibility of GNSS-R Ice Sheet Altimetry in Greenland Using TDS-1" Remote Sensing 9, no. 7: 742. https://doi.org/10.3390/rs9070742
APA StyleRius, A., Cardellach, E., Fabra, F., Li, W., Ribó, S., & Hernández-Pajares, M. (2017). Feasibility of GNSS-R Ice Sheet Altimetry in Greenland Using TDS-1. Remote Sensing, 9(7), 742. https://doi.org/10.3390/rs9070742