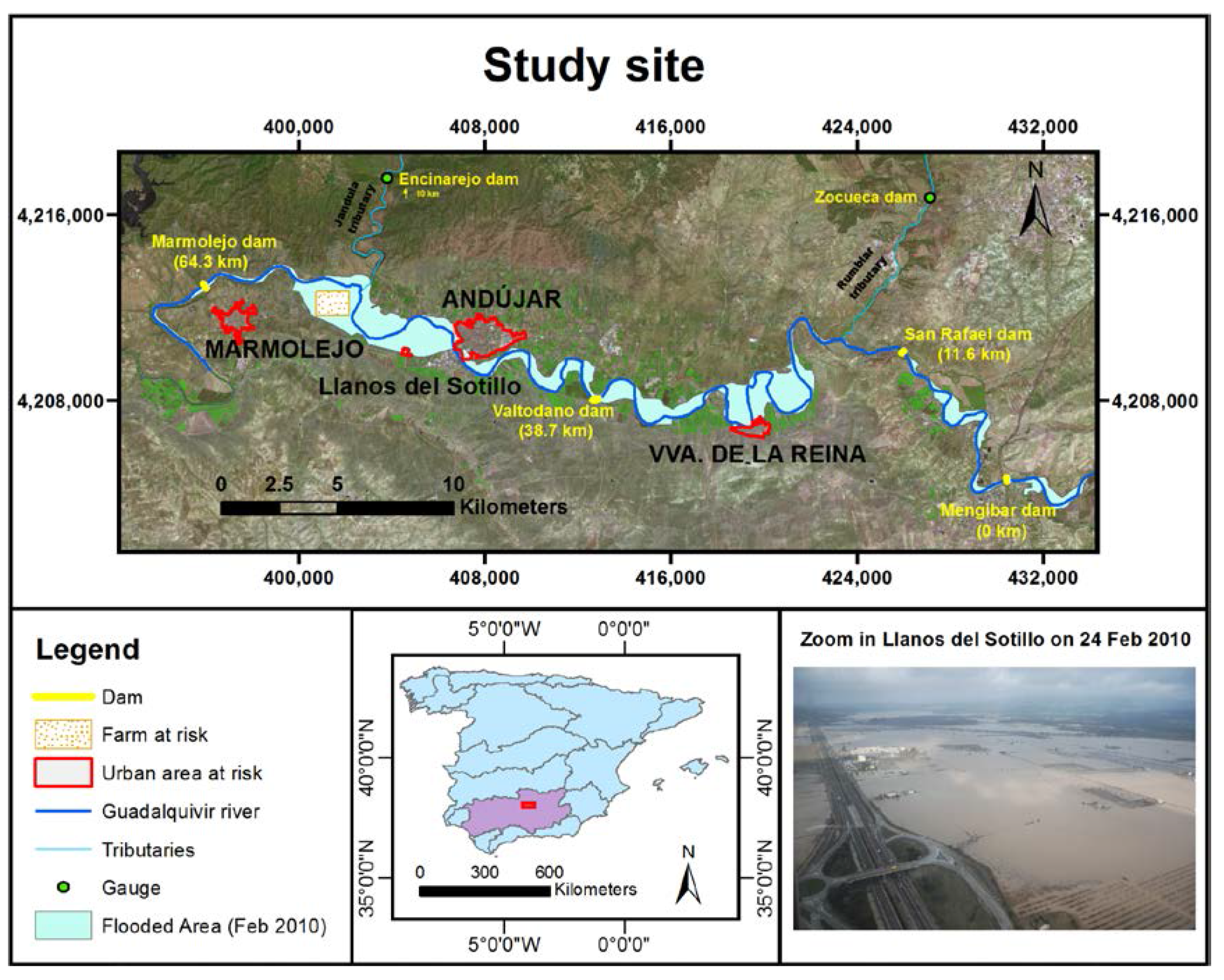
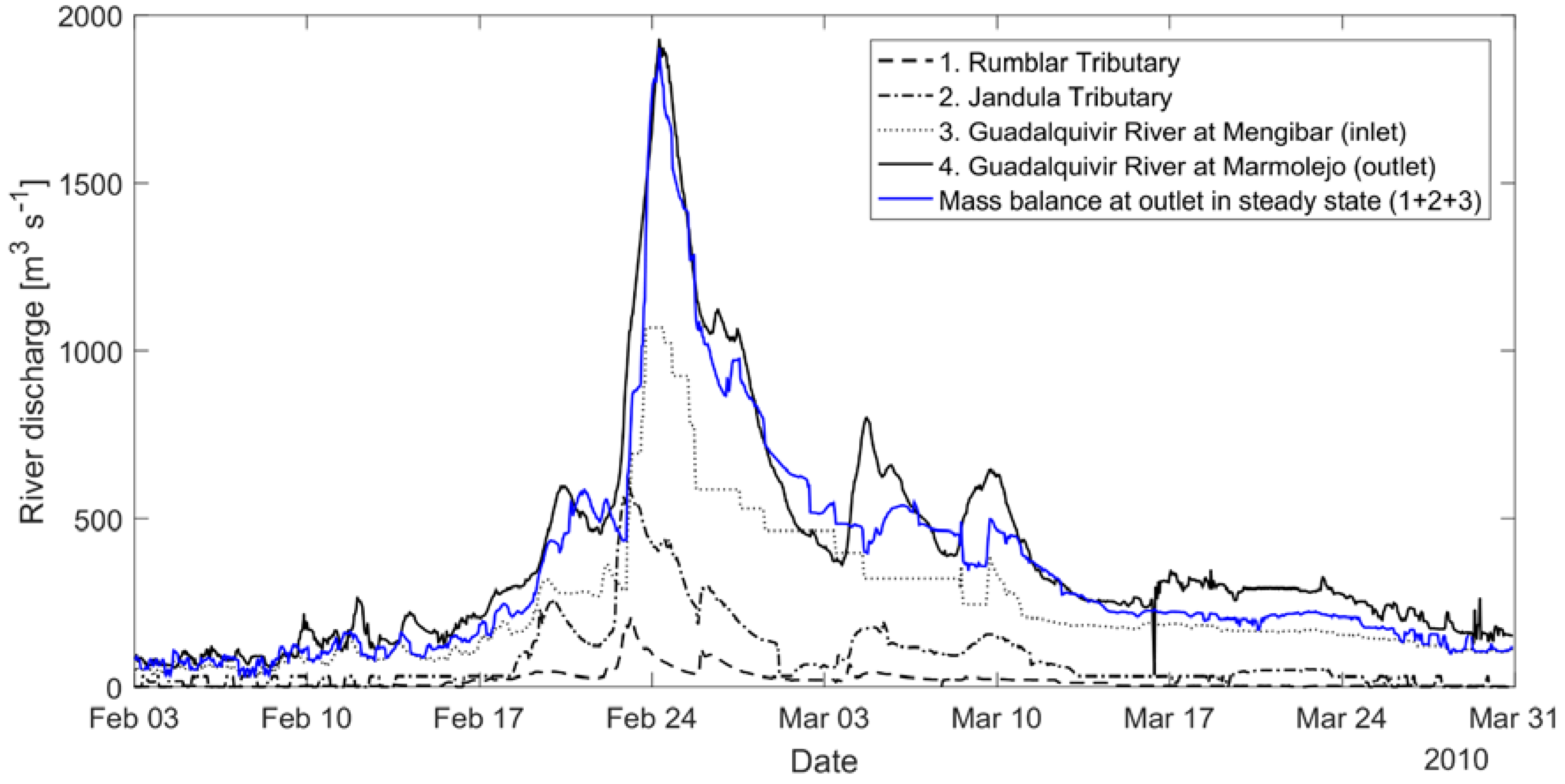
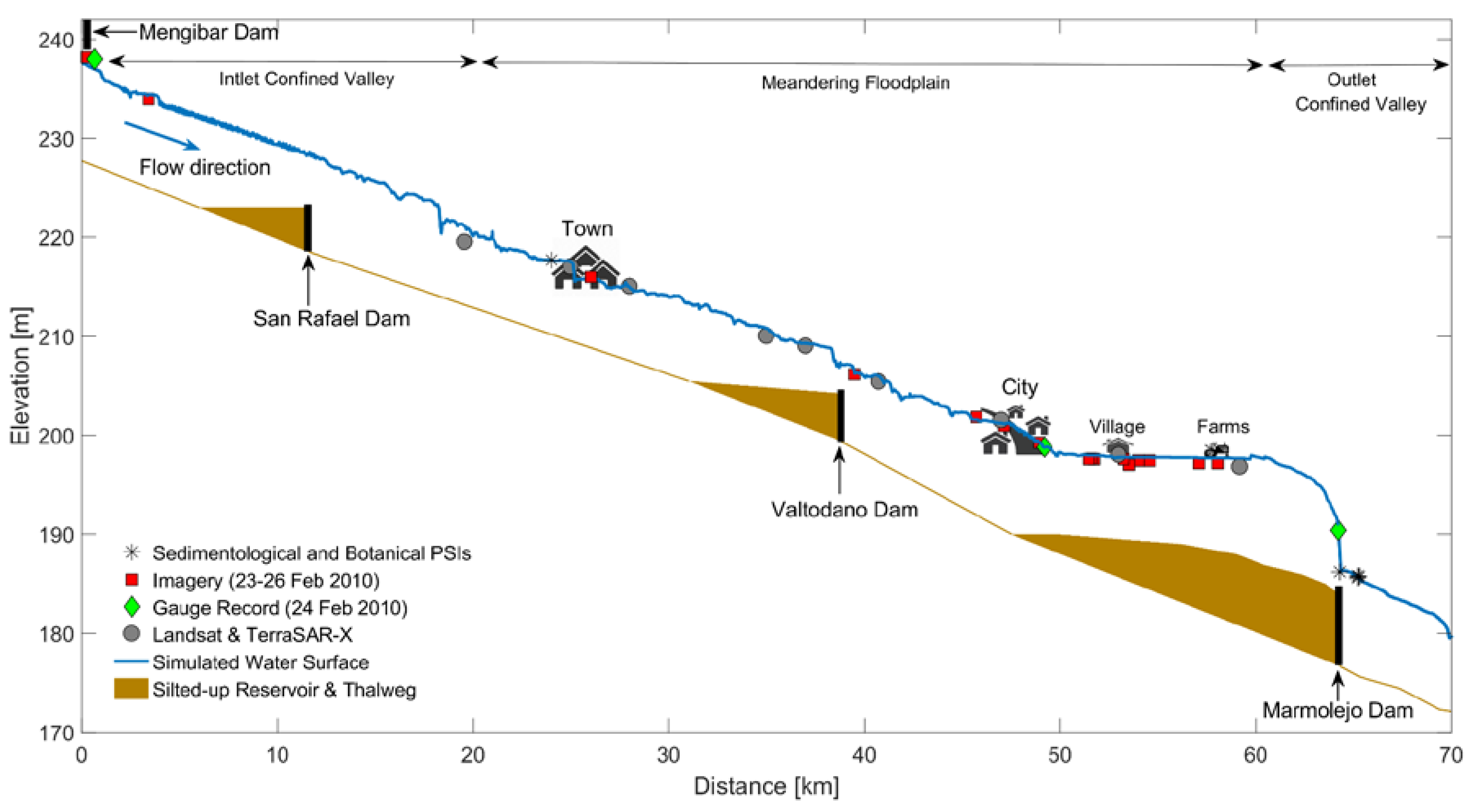
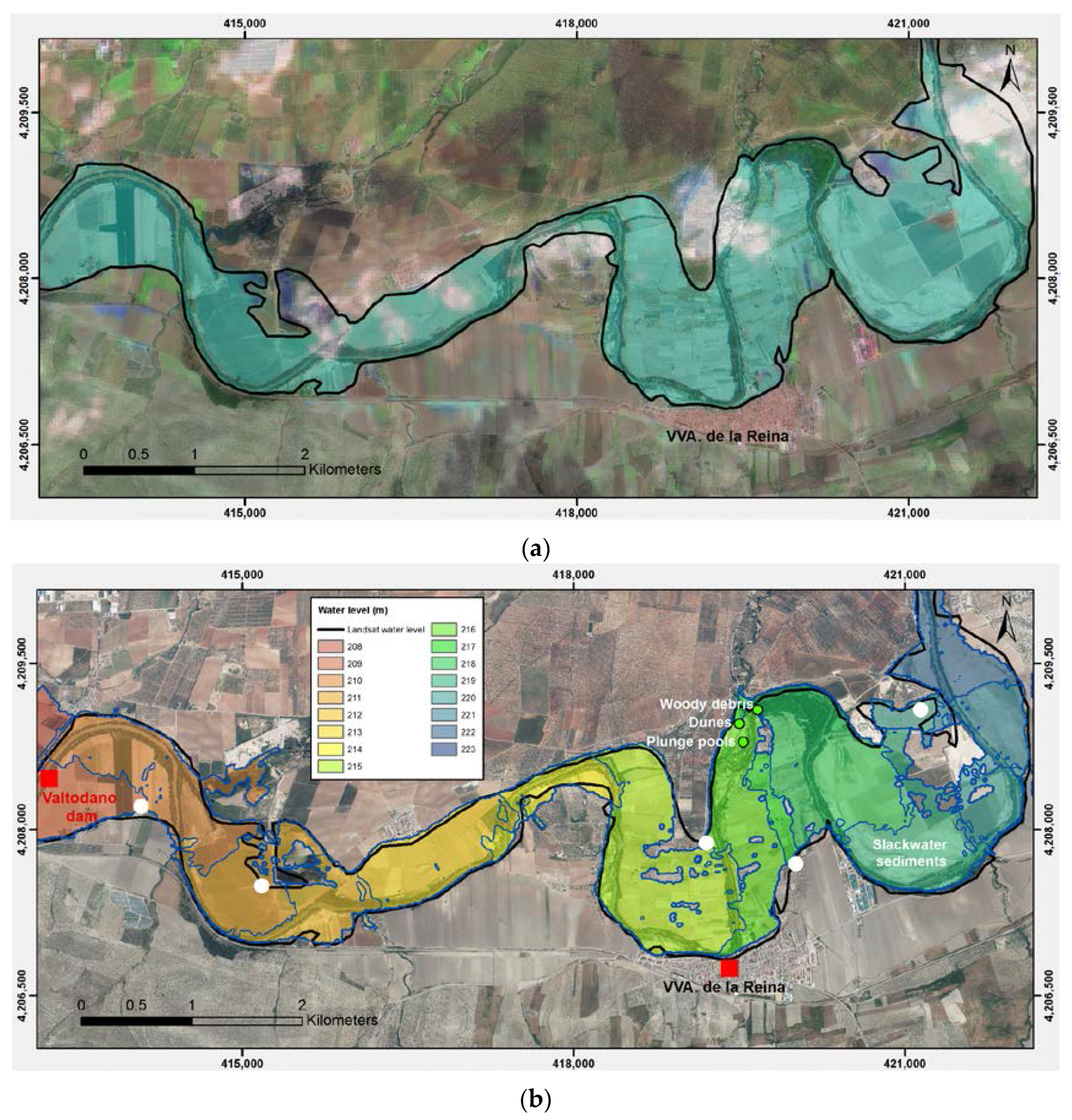
4.1. Trend in Streamflow over Time
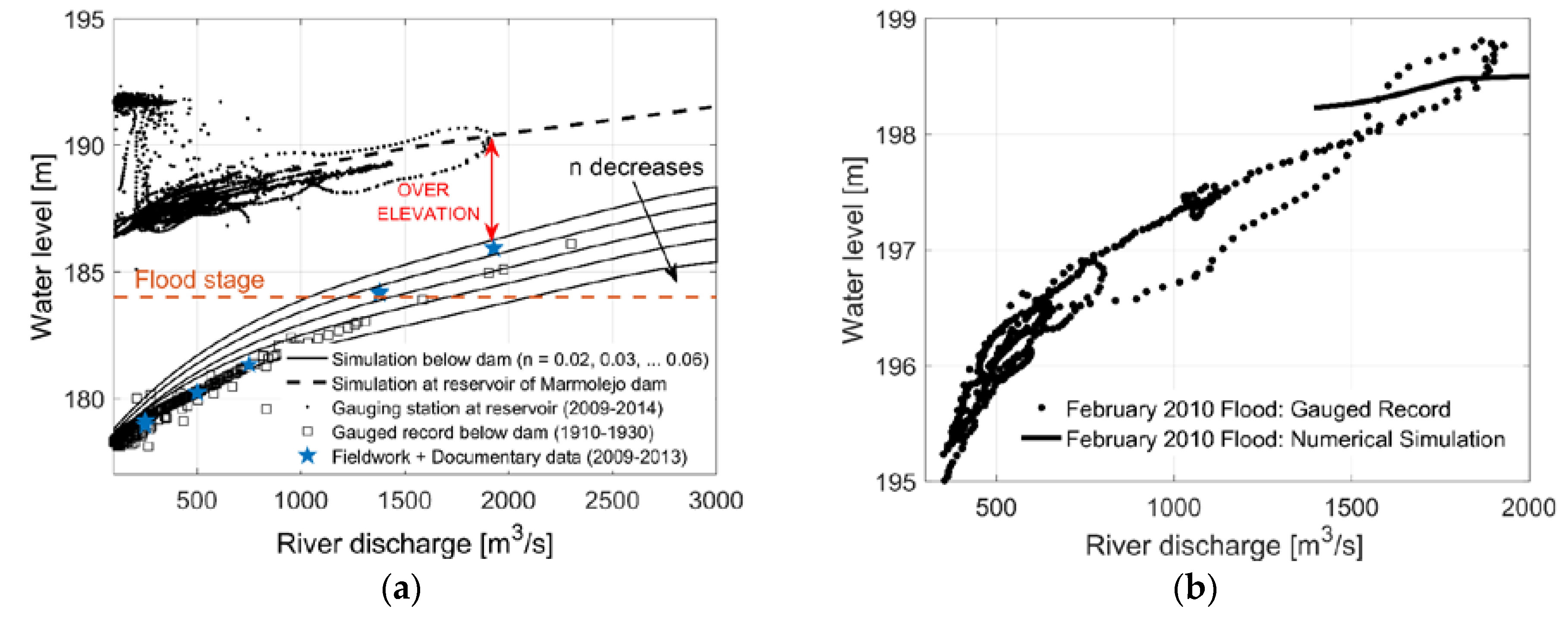
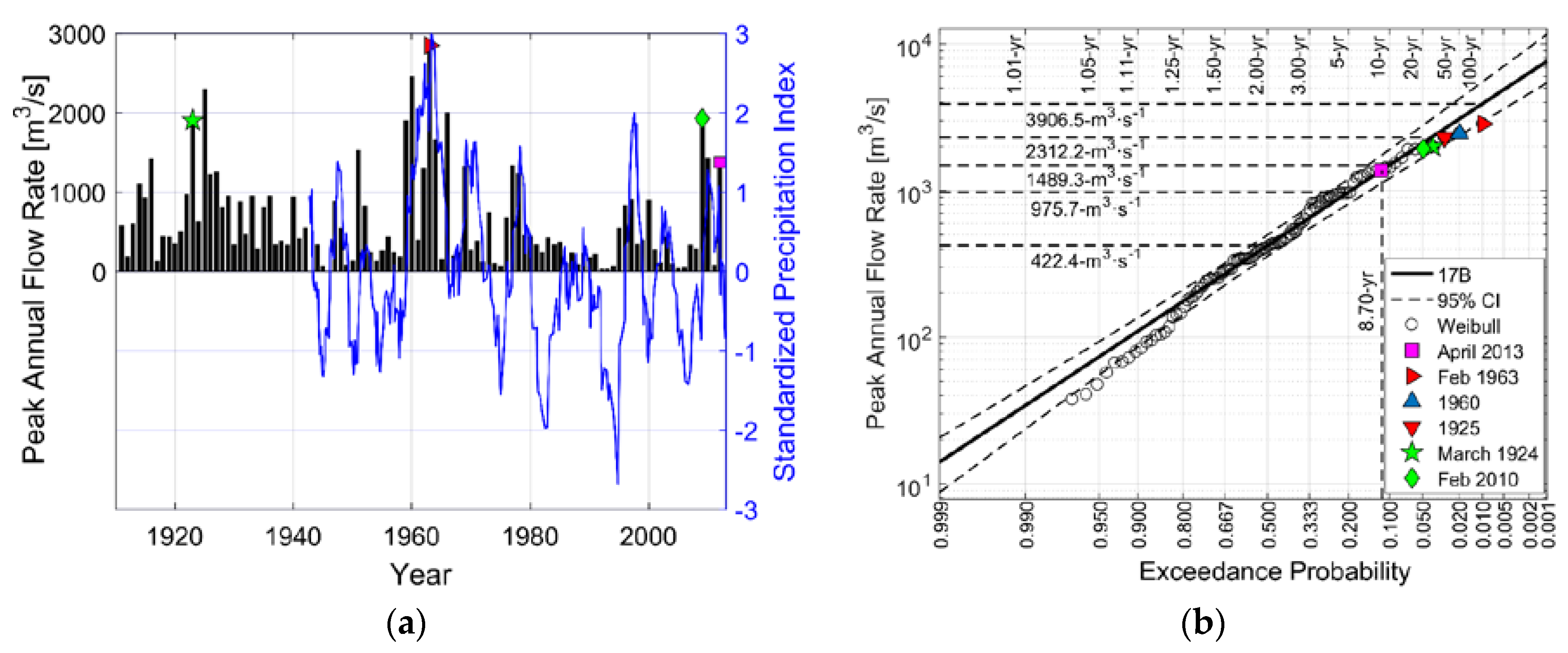
Figure 10a shows maximum annual river discharge values at the study site aiming to provide an idea of the severity and frequency of flooding since the year 1910. Climatically, the first half of the twentieth century registered periods of high flood recurrence (1910–1930) with discharges on the order of 1000–2300 m
3·s
−1, but also of moderate events (1930–1950) lower than 1000 m
3·s
−1. Unusually high flood frequencies occurred in the period 1951–1980. The most catastrophic flood developed in winter of 1963 with a peak water discharge as high as 2850 m
3·s
−1. Persistently drier conditions with scarce hydrological events were observed between 1980 and 1996. In the 21st century, flood frequency and magnitude decrease, with peak annual flow rates of approximately 1300–2000 m
3·s
−1 in the period 2009–2013. Since then, we are suffering a period of drought. Subsequently, the recurrence intervals of maximum flood magnitudes were evaluated using the Bulletin 17B and Expected Moments Algorithm procedures implemented in PeakFQ [
43].
Figure 10b shows the exceedance probabilities and return periods of both systematic and historical (high outliers) floods. Floods highlighted with a green pentagram, and diamond symbols correspond with March 1924 and February 2010 extreme events, respectively, and an associated return period of about 20 years. Rare hydrological events with larger return periods occurred in 1960 (50 years) and 1963 (100 years).
It is worth proving that the observed decrease in peak streamflows in the post-impoundment era (i.e., since approximately 1950) is due to less frequent precipitation in the Guadalquivir River Basin, as established in climate change reports [
3,
4]. The climate component shows the decrease in time of the annual precipitation across the Guadalquivir Basin [
13,
14]. Here, we adopt the standardised precipitation index (SPI), which is based on a proper statistical distribution of the precipitation [
44]. Originally, it was developed for drought detection. Later, it was used with success as a regional system for climate risk monitoring and to detect the potential threat of possible flood events.
Figure 10a compares the peak annual streamflow and the 36 months SPI curve. Interestingly, we got positive values of SPI during the periods of high flood recurrence commented beforehand. The largest value of 3.01 occurs in the hydrological year 1963 when the largest flood occurred. Other local maximums, with SPI values of 1.63, 1.57, 1.99 and 1.28, are well correlated with extreme floods in 1970, 1979, 1997 and 2010. Interestingly, reservoirs attenuated the hydrological event of 1996 because of their nearly empty states after the drought period 1980–1996, when SPI reached −2.68 (values lower than −1.65 correspond to extreme drought [
45]). Unfortunately, all the reservoirs attained the top water level in the rest of extreme rainfall events, and could not regulate the peak streamflow.
4.2. Effects of Vegetation Encroachment and Aggradation on Channel Capacity
The term
channel capacity has two senses according with the existing literature: originally, it represents the cross-sectional channel area at flood stage
AFS [
46,
47]; a broader meaning refers to the average cross-sectional discharge at flood stage
QFS which is evaluated as the product of
AFS and the cross-sectional average flow velocity
VFS [
5,
48]. In the first case, the unique cause of changes in channel capacity can be bed aggradation/degradation or channel narrowing/widening. In the second case, channel capacity can be controlled not only by depth and width at flood stage but also bed slope and boundary roughness (e.g., grain size and bank vegetation). Hence, we refer to channel capacity at flood stage as the volume of flow that can be carried within the channel at flood stage
QFS. To close the concept, we define the flood stage as an established gauge height for a given location above which a rise in water surface level begins to create a hazard [
5]. We identified it with the bankfull stage from the proto-floodplain (top of the point bar surface) that supports woody vegetation [
49].
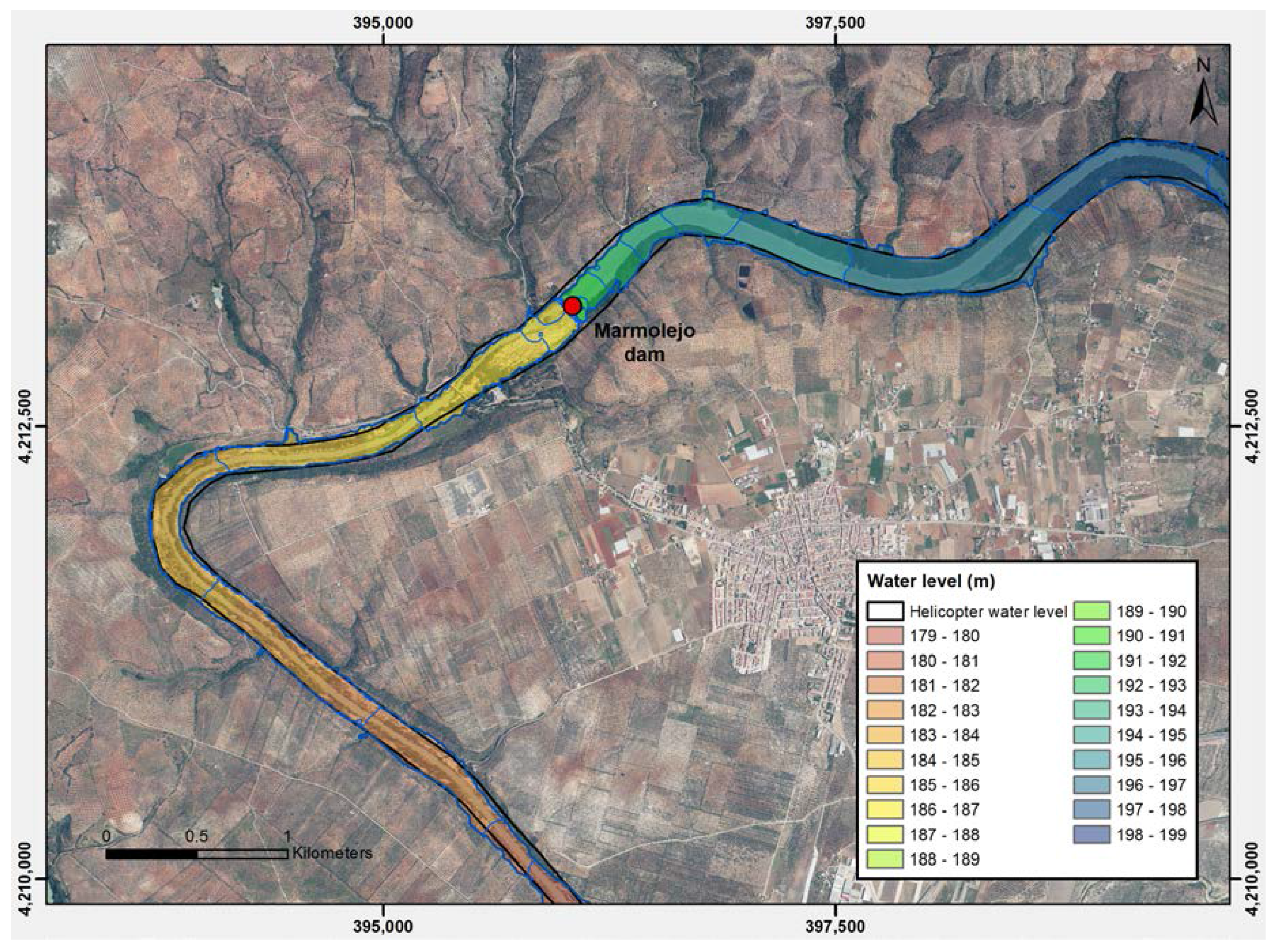
Widespread flood-level rise occurred all over the studied area after impoundment, which reflects a change in channel capacity (denoted from now on by ∆
QFS). In the confined valley setting, we inferred the accumulated change in channel capacity from the rating curve at flood stage. In the inlet valley (
Figure 6), the accumulated reduction in channel capacity amounts to ∆
QFS = 568 m
3·s
−1 since 1910 and represents the 56% of the original capacity
QFS = 1010 m
3·s
−1 for a 8 m flood depth (see
Figure 5a). The major alteration process was the development of a shallow island in the middle of the channel. It was colonized by non-flexible riparian vegetation (recall
Figure 5b) that reduces the mean flow velocity
VFS. In the outlet valley (
Figure 7), downstream of the dam, the influence of bank vegetation on channel capacity was moderate (
Figure 8a). Setting a flood depth of 7.2 m yields ∆
QFS = 188 m
3·s
−1 for
QFS = 1565 m
3·s
−1. In the floodplain downstream of Andújar city (
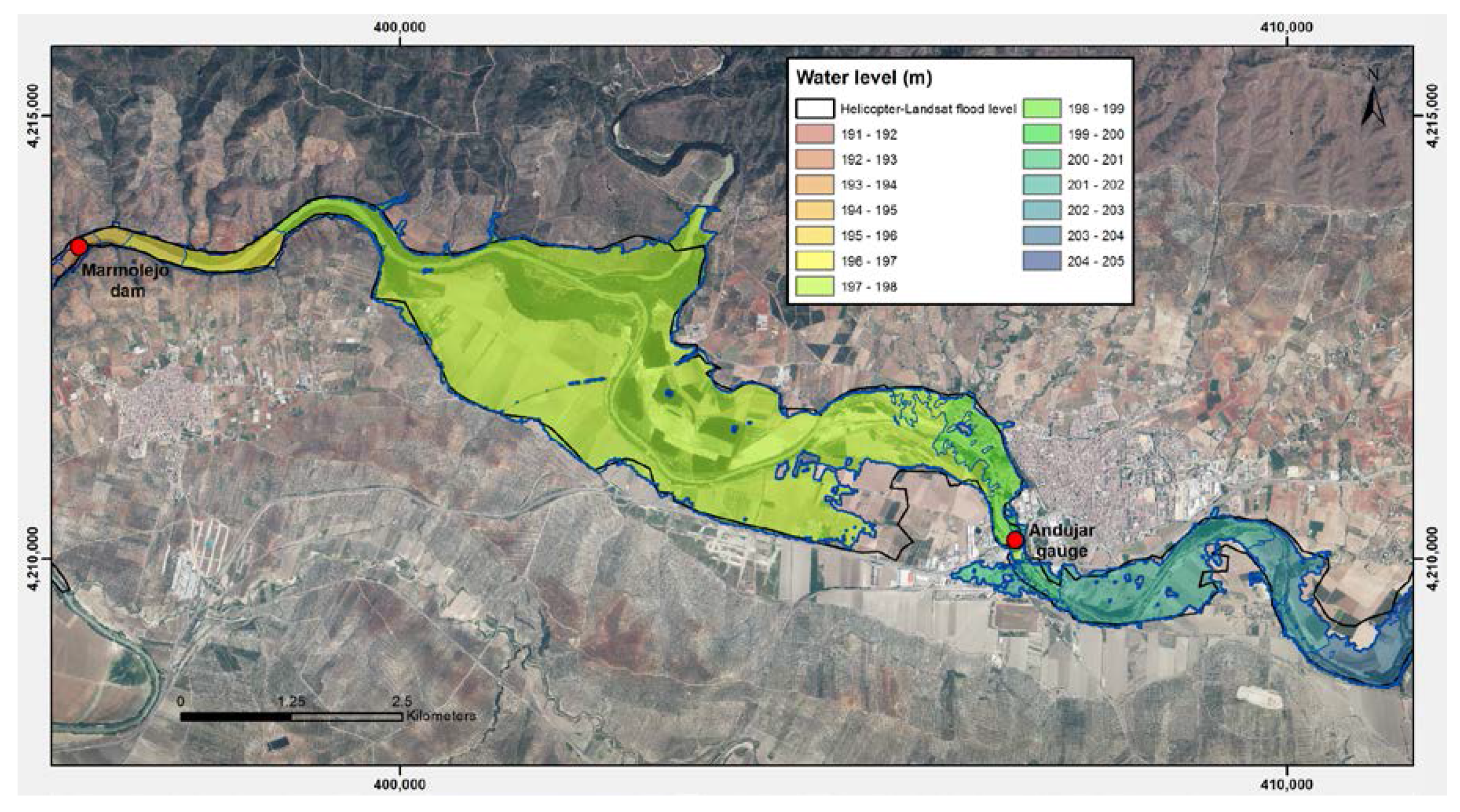
Figure 9), the base-level rise upstream of the silted-up reservoir exacerbated flooding in the period 2009–2013 with respect to the middle of the twentieth century, but the lack of documentary records during the Spanish civil war and the dictatorial regime prevented their analysis.
Alternatively, we followed the original approach by Fergus [
47] and characterised ∆
QFS in terms of the change in cross-sectional channel area at flood stage ∆
AFS.
Table 5 summarises channel change statistics in twenty cross profiles uniformly distributed from the city to the entrance of the outlet valley with a distance of 400 m between each profile. In the river stretch between the city and the confluence, the channel width (flow depth) at flood stage decreased from 121 (6.2) to 111 (4.3) m during the study period. Downstream of the confluence, the decrease from 138 (9) to 100 and (4.2) m was more pronounced than upstream. Hence, the mean cross-sectional channel area at flood stage
AFS in 1900 was 1249 and 448 m
2 in the river stretch upstream and downstream of the Guadalquivir-Jándula river confluence. This makes a difference with respect to present days as the actual channel area in each river reach is 448 and 506 m
2, which amounts to the relative reduction in cross-sectional channel area ∆
AFS/
AFS = 64% and 28%.
In the meandering floodplain (
Figure 4), we proceeded to analyse the channel form, a procedure that provides a context for interpretation of past changes in the fluvial environment (
Appendix B). We adopted the following two methods to quantify the original channel capacity in the early twentieth century. First, Dury’s algebraic equation was selected from available equations in the paleohydrology literature to estimate pre-impoundment channel capacity using geometrical data of the meanders into the lowest sand-mud terrace [
50]. Second, results from regime based equations by Yalin and da Silva [
51] linking the bankfull dimensions of the channel and the water discharge served not only to estimate channel capacity pre-impoundment but also to account for changes in channel roughness due to post-impoundment vegetation encroachment.
Substituting the mean wavelength value given in
Appendix A into Dury’s correlation (A1), one obtains the pre-impoundment channel capacity
QFS = 2023 m
3·s
−1 in the meandering setting. Streamflows larger than 2000 m
3·s
−1 were required to overtop the river banks and inundate the current floodplain in years previous to flow regulation. A similar result was obtained using equations by Yalin and da Silva [
51], who reviewed all the available regime-data before the year 1990 and correlated the bankfull dimensions of the collected rivers and the river discharge. The main advantage of the second approach is that it incorporates the dependency on the roughness coefficient explicitly. In the situation of pre-vegetation encroachment,
n = 0.035 s·m
−1/3 [
1]. Evaluating (A3) with the mean thalweg slope
S0 = 0.076%, the mean bankfull width
B = 184 m and flow depth in the range of 4–5 m, yields 1460 ≤
QFS ≤2118 m
3·s
−1. Note that the upper bound is in close agreement with Dury’s solution
QFS = 2023 m
3·s
−1 and the National Database of Historical Floods [
29,
30], which reported flood episodes only in the years 1963 and 1945 with river discharges in the range of 2500–3000 m
3·s
−1.
In the current situation of channel infilling and vegetation encroachment, the mean Manning’s roughness increases up to 0.06 s·m
−1/3 (
Figure 8a). Such an increase in roughness leads to an overall reduction in channel capacity from 1460 to 852 m
3·s
−1 for the bankfull flow depth of 4 m. As a matter of fact, inundations of the meandering stretch occurred during the years 2009–2013 at the water discharges of 800–1070 m
3·s
−1, which is consistent with the prediction of the hydraulic model.
The unexpected increase in inundated areas in the Upper River Basin during extreme rainfall events in 2010–2013 (
Figure 4,
Figure 6,
Figure 7 and
Figure 9) contrasts with historical records of inundations before river flow regulation and trends in both precipitation and streamflow during the twentieth century (recall
Figure 10). In the inlet valley of the study site, we found flows as deep as 12.3 m with a local streamflow of, approximately, 2000 m
3·s
−1 in the inundation of the year 1963 (
Figure 5a). The rest of floods in the period 1912–2009 were less severe and exhibited flow depths lower than 10.6 m with local river discharges smaller than 1577 m
3·s
−1 at the same location. Surprisingly, maximum stages in the period 2010–2013 varied in the range of 9.7–10.4 m for streamflows in the range of 670–1024 m
3·s
−1. Such flow depths are similar in magnitude than in 1924 when the river discharge achieved 1577 m
3·s
−1. Furthermore, flow depths corresponding with a 670 m
3·s
−1 river discharge increased from 6.7–7.5 m to 9.7 m over the studied period. In the outlet valley, the deepest historical flood developed a flow depth of 8 m for 2300 m
3·s
−1 that nearly equals the stage of a modern flood with the lower discharge of 1950 m
3·s
−1. Nonetheless, the observed increase in flood risk during modern floods is due to the decrease in channel capacity post-impoundment.