Abstract
The Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) system on board the Terra (EOS AM-1) satellite has been a source of stereoscopic images covering the whole globe at 15-m resolution with consistent quality for over 16 years. The potential of these data in terms of geomorphological analysis and change detection in three dimensions is unrivaled and should be exploited more. Due to uncorrected errors in the image geometry due to sensor motion (“jitter”), however, the quality of the DEMs and orthoimages currently available is often insufficient for a number of applications, including surface change detection. We have therefore developed a series of algorithms packaged under the name MicMac ASTER (MMASTER). It is composed of a tool to compute Rational Polynomial Coefficient (RPC) models from the ASTER metadata, a method that improves the quality of the matching by identifying and correcting jitter-induced cross-track parallax errors and a correction for along-track jitter when computing differences between DEMs (either with another MMASTER DEM or with another data source). Our method outputs more precise DEMs with less unmatched areas and reduced overall noise compared to NASA’s standard AST14DMO product. The algorithms were implemented in the open source photogrammetric library and software suite MicMac. Here, we briefly examine the potential of MMASTER-produced DEMs to investigate a variety of geomorphological changes, including river erosion, seismic deformation, changes in biomass, volcanic deformation and glacier mass balance.
Keywords:
ASTER; jitter; orbit; attitude correction; DEM generation; RPC; geoscience; glacier; volcano; deforestation; earthquake 1. Introduction
The analysis of the change of the Earth’s surface relies on time series of DEMs, which in turn rely on the high quality acquisition and processing of data. The last few years have seen an impressive expansion of the operating satellite systems—both optical, such as Pleiades or Worldview, or microwave, such as TerraSar-X—that are able to produce very high resolution products with minimal errors, but whose spatial and/or temporal cover is limited [1]. The Terra (EOS AM-1) satellite was launched in December 1999 on a Sun-synchronous orbit with the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) system on board. For more than 17 years, pairs of stereo images were collected by ASTER globally at a 15-m resolution in the near infra-red band, making its data the largest consistent multi-temporal dataset of stereo images available worldwide. The pairs consist of a nadir-pointing image (Band 3N) and a back-looking image (Band 3B) with an effective 30.6° parallax angle. However, the data are plagued with a high frequency satellite jitter that induces an attitude perturbation. This jitter yields at least three superimposed sinusoidal signals in both cross-track and along-track directions in the DEM comparison between the standard DEM product (AST14DMO) and the ground truth [2], or between ASTER and QuickBird images [3]. The low acquisition frequency and limited precision of the GNSS/IMU platform and star camera prevent the on-board estimation of jitter using the metadata alone. The jitter-induced waves were estimated by [4] as a combination of waves of 4.6-km and 34-km frequency in both cross-track and along-track directions. The nadir axis jitter (yaw) is described as not having a significant influence (millimeters). Proposed causes for this disturbance include the mechanical cooling system, the rotation of mirrors and movements of the high gain antenna, but a source is yet to be formally identified.
A solution to correct the jitter in the SWIR system (pseudo-nadir, short wave infra-red band) was proposed by [5] using the very short time delay between the acquisition of Bands S4–S9. A similar approach was demonstrated in [6] and tested by [7] for the ZY-3 (Ziyuan 3) system. However, it cannot be applied to correct the ASTER VNIR system (pseudo-nadir and back-looking, green, red and near infra-red band) since “The VNIR subsystem is free from [band to band] parallax error because a dichroic filter divides incident light into each VNIR band.” [5]. Furthermore, only one band (near infra-red) is captured by the back-looking telescope. More recently, [8] presented a method to correct jitter perturbations in the data acquired by the ZY-3 satellite, relying on a much more modern IMU system that provides enough information to directly estimate jitter.
Today’s standard DEM product from ASTER is generated by NASA with the SilcAst (http://www.silc.co.jp/en/products.html) software and is packaged in the AST14DMO product. Other available commercial software such as PCI Geomatica or ENVI can also produce ASTER DEMs. However, none of these products provide a sufficient geometric quality for a number of applications such as glacier volume change estimation over short periods, the expected change being significantly smaller than the accuracy of the product (a few meters against m [9]; see Figure 1 for the DMO over a sea ice (flat) scene).
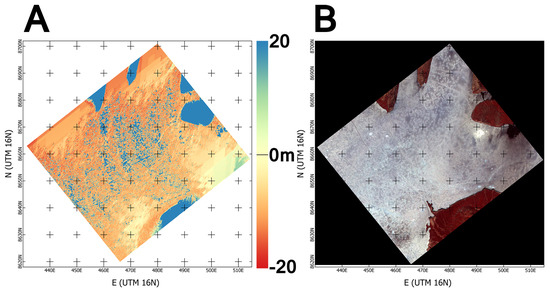
Figure 1.
AST14DMO product over a fast sea ice scene (AST_L1A_00307072008194108_02012009125352.hdf). The DEM (A) should be uniformly flat in the sea ice area, but presents large, clearly interpolated areas and high noise; the data peaks are at several hundred meters; (B) The orthorectified image (contrast enhanced).
Our objective is to offer a processing workflow that can produce higher quality products for any ASTER scene. This means that the method cannot rely on the use of Ground Control Points (GCPs) as suggested by [10,11,12] or on a ground truth obtained by other methods on stable terrain because such a ground truth is not consistently available or of sufficient quality (the SRTM mission only covering 60° N–56° S, for instance). To this aim, we have developed MMASTER (where MM stands for MicMac, the photogrammetric processing library in which we implemented our work), a DEM processing tool that does not rely on external data sources, takes into account and corrects the jitter and improves the quality and completeness of ASTER DEMs compared to the data included in the AST14DMO product. The main scientific objective of MMASTER is to provide better and unbiased differences between DEMs (dDEMs) for topographic change analysis.
In this paper, we first present the MMASTER processing chain in depth, then a number of examples showcasing the relevance of improved topographic change measurements for a number of scientific fields, such as landslide and soil erosion, forestry, volcanology and glaciology.
2. Methodology
2.1. General Description
Our aim here is two-fold: first, to produce the best possible DEM from a single stereo pair (one ASTER L1A scene), then to produce the best possible difference of DEMs (one MMASTER and another DEM, possibly MMASTER). We start by applying the radiometric corrections provided in the image metadata. We then estimate Rational Polynomial Coefficient (RPC) models for both images of the stereo pair. Using the RPC models and the images, we compute the parallax error in the cross-track direction and estimate the effect of the composition of the jitters of the nadir and back-looking bands (3N and 3B). We then correct the 3B band so that it is coherent with the 3N band and use the RPC model and the corrected images to compute the DEM.
For the DEM differencing, the relative offset between the two DEMs and the exact parameters of the combined jitter effect (frequencies, phase and variation in amplitude) on the DEM are estimated using the stable terrain and removed from the DEM difference. The final product is a DEM difference that has low high-frequency noise and is mostly free of the jitter-induced elevation bias. An outline of this overall method is shown in Figure 2.
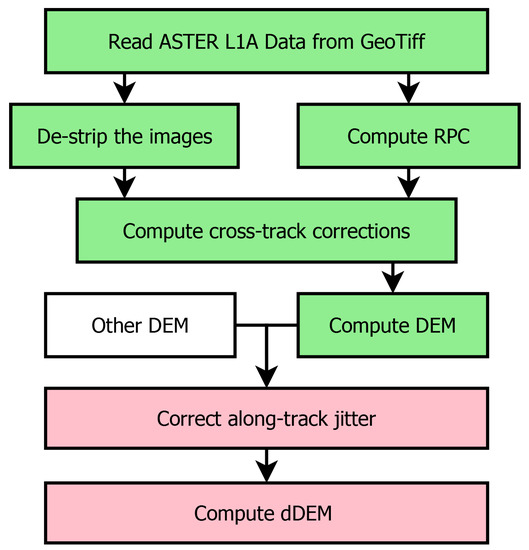
Figure 2.
General diagram of the process from the raw data to the DEM difference. Green is the DEM production and red the DEM differencing. Outlined in red are the key novelties.
Throughout this section, we use the scene AST_L1A_00307072008194108_02012009125352 to illustrate the different steps of the process. We chose this scene because it is over fast sea ice, as it is a virtually flat type of surface ([13] reports topography reaching 3 m at most) and has high contrasts for correlation, thus being a scenario having a perfect built-in ground truth over most of the scene and not requiring post-processing to display the different improvements.
2.2. From the Raw Data to Images and RPCs
2.2.1. Radiometric Correction and De-Striping of the Images
Each ASTER band is delivered with a calibration of the sensors’ response that is applied to correct the striping effect created by inconsistent sensitivity of each cell of the line arrays. The calibration consists of three coefficients per column of each band, describing a linear function to be applied (see Equation (1)):
where the parameters are regularly calibrated in-flight using a halogen lamp that uniformly radiates light to the sensors [14]. The application of the calibration data is straightforward and greatly reduces the striping in the images (see an example in Figure 3).
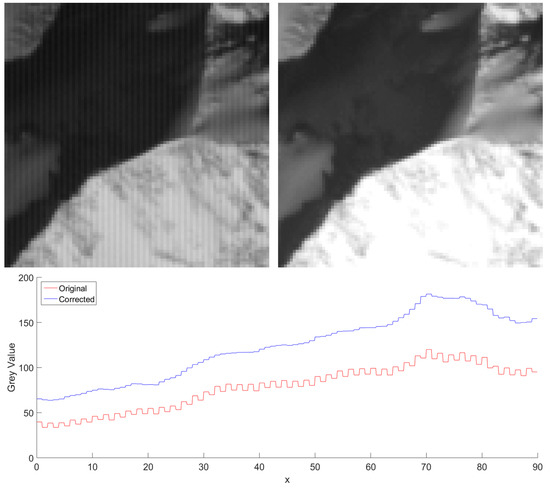
Figure 3.
Extract of the VNIR Band 3N of an ASTER scene. (Top left) Original image. (Top right) After destriping. (Bottom) Mean profile across the x axis for both extracts.
This process is not perfect, however, as the sensors’ response is not perfectly linear and their aging is degrading the linearity of the response even further. Some residual striping is still present after correction. A more pressing problem caused by these corrections is the further reduction of the already limited 8-bit dynamic range, resulting in important posterization in the highlights and shadows. Many images do not use the entire available dynamic range (see Figure 4).
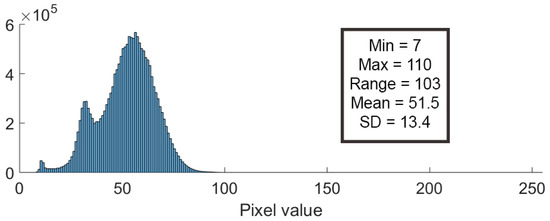
Figure 4.
Histogram of Band 3N of the Sea Ice scene AST_L1A_00307072008194108_02012009125352.hdf. Half of the available dynamic range is not used, making the image essentially “7 bits” rather than the nominal 8 bits.
2.2.2. Computing the RPC
Rational Polynomial Coefficient (RPC) models [15] are functions that replace both the internal orientation (sensor and optic calibration) and the external orientation (orbit determination and pointing angles). When provided, they can be used by any software without the need to know any information about the underlying acquisition system, which made them popular with both satellite system providers keen on keeping the specification of their system private, as well as software manufacturers keen on having a multipurpose tool.
The metadata attached to the images contains a number of records for each band of the satellite position (from 12–16 depending on the scene and the band considered, usually more for the back-looking image than for the nadir image), to each of which is attached a line of 11 lattice points in image coordinates (column, row) and geographical coordinates (geocentric longitude and latitude on the ellipsoid; see Figure 5). In order to be compatible with the coordinate transformation system and to be able to compute the DEM in cartographic projection systems (such as UTM), the geocentric coordinates are converted to geocentric Cartesian coordinates, then to geodetic through the algorithm ALG0012 in [16].
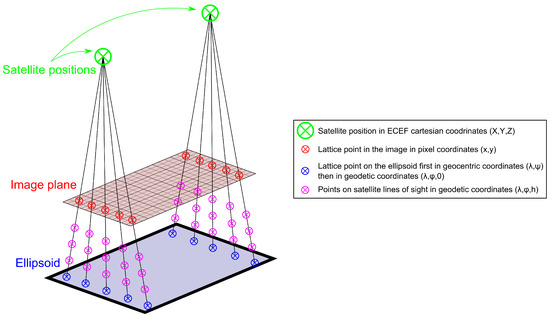
Figure 5.
Satellite positions and associated lattice points in the image and the geographical coordinates and 3D GRID created from the lattice points.
The method used to compute RPCs is similar to the one described in [15,17]. For each line of sight defined by the association of a satellite position and one of its lattice points in geographical coordinates, we can define a collection of points at regularly-spaced altitudes. This allows for the creation of layers of points, forming a 3D grid of points in geographical coordinates (geodetic longitude, latitude, ellipsoid height), which are linked to points in the image (see Figure 5). Because the terrain is unknown beforehand and the system must be defined in a first pass for all possible altitudes, grids must be defined between −500 m (altitude of the shores of the Dead Sea) and +8850 m (summit of Mount Everest). Grids spaced every 200 m proved to offer a reasonable vertical density. In order to optimize these parameters, a very rough DEM is first computed to extract the minimum and maximum values (after filtering by correlation score to remove sea and clouds) in order to define a vertical grid with a smaller elevation range to refine and improve the RPC model fit. In the case where the maximum and minimum altitudes are (even approximately) known a priori, these parameters can of course be optimized directly.
These grids are then used to estimate the direct (from the image to geographical coordinates; see Equations (2), (3) and (6)) and inverse RPC (from geographical to image coordinates; see Equations (4)–(6)) models for the image through least square matching, associated with a regularization factor as suggested by [15]; they are rational function polynomial equations of the normalized image and geographical coordinates (scaled to a unit cube), defined as:
with:
The number of original lattice points (a minimum of 146) ensures that the system is solvable, granting that the constant component in is fixed (). The 3D density of points feeding the equations in the defined grids makes the solution robust, with residuals on the order of in the unitary cube unit ( × , equivalent to degrees (<0.12 m) or pixels) for both the direct and inverse RPC.
2.3. Computing the Cross-Track Corrections
The jitter of the satellite can be divided into three components: the cross-track (roll), the along-track (pitch) and the rotation along the nadir axis (yaw). Since the two images of each set are taken in the same orbit, the epipolar lines are almost parallel to the along track direction ( × degrees away from the y axis of the images). This results in a nearly perfect separation of the cross- and along-track components of jitter in image space, while the yaw component can be seen as a very small perturbation. In Figure 6, we can see that the perspective ray from the nadir image can only cross the one from the back-looking image if the cross-track attitude of the satellite is known (i.e., the ray does not intersect with the rest of the red triangle).
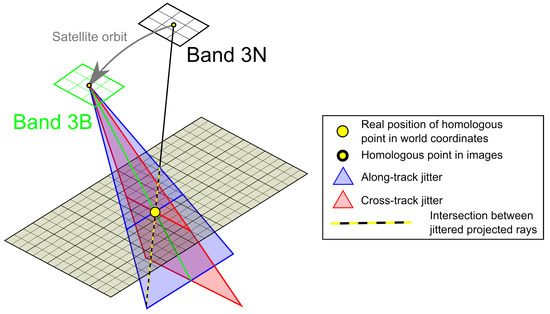
Figure 6.
Effect of the jitters on the direction of the perspective ray of the back-looking image (nadir image considered stable). We can see that the along-track jitter (blue) allows for the intersection of the projected rays whatever its amplitude, while the across track jitter immediately creates an absence of intersection.
The effect of the combination of cross-track components of the jitter is directly observable by performing a bi-dimensional correlation around the theoretical epipolar lines (see Figure 7), with the potency of the vibration in pixels equal to the distance between the point of maximum correlation (the homologous point) and the epipolar line.
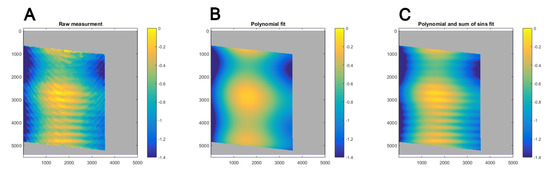
Figure 7.
(A) Measure of the combined across-track vibration visible in the back-looking image through bi-dimensional correlation (sea ice scene AST_L1A_00307072008194108_02012009125352.hdf) in image space coordinates. (B) Polynomial fit of the general pattern. (C) Added sinusoidal fit of the higher frequency jitter (i.e., (C) is the model of the true distortion pattern in (A)). The gray area on the edge corresponds to the area of the back-looking image where there is no corresponding nadir looking image or no data in the back-looking image.
The effect of the along-track jitter component does not degrade correlation, but rather biases the individual parallax measurements and is therefore not measurable in the raw line-of-site data. In Figure 6, we can see that the perspective rays from both images are crossing for all of the possible along-track attitudes represented by the blue triangle.
The cross-track parallax errors are exported as a grid (see Figure 7A), representing correction factors for each pixel in the back-looking image. This computed grid is sensitive to correlation noise, errors and a potential lack of correlation. Therefore, it is necessary to model the parallax errors to generate a cross-track jitter correction to be applied to the back-looking image so that the real and theoretical epipolar lines match up.
First, the data are filtered to remove areas that returned low bi-dimensional correlation (and hence, are dubious). The rejection mask is dilated by a 21 pixel-wide square structuring element to ensure that lower correlation regions are not affecting our jitter model. This latter step simply improves the robustness of the model while reducing the processing time required. The large-scale error pattern is solved using a 7th degree polynomial in both the x and y directions (see Figure 7B and Equation (7)). The choice of the 7th degree polynomial compared to a more gradual increase of the polynomial degrees, stopping when the residual value stops evolving, is motivated by both an improved computational speed and by the extensive testing showing that this value was generally the best.
After solving for the lower frequency errors, the smaller jitter vibration is estimated by fitting a sum of 8 sines sliding along the y axis (see Equation (8)) on 90% overlapping 1000 pixel-wide columns (the choice of fitting 8 sines is a result of extensive testing and ensures the robustness of the solution).
Finally, the median solution for each pixel of the stack of 10 values created by the overlaps is selected (see Figure 7C and Equation (9)). The sliding window for the jitter estimate is necessary to deal with extra perturbations in the data, in particular caused by a slight variation between the jitter angle and the satellite trajectory. The corrections therein computed are then applied to the back-looking image (see Equation (9)), warping it using bilinear interpolation.
2.4. Computing the DEM
To compute the DEM, a target grid covering the scene’s coverage is first determined. The spacing of the grid starts very large and iteratively reaches the desired value. For each point of the grid, the RPC models are used to determine the image coordinates for different candidate altitudes (or in other words, describing the epipolar lines). For each candidate altitude (see Figure 8), the normalized cross-correlation score using a 5 × 5 window on both images is computed, and the best candidate is kept. Without correction, this yields DEMs of similar quality as the AST14DMO product, with significant noise and areas that could be filtered out based on the correlation score (see the example in Figure 9A). Since MMASTER is relying on MicMac for correlation, it is using the semi-global matching algorithm implemented therein [18] to compute the DEM.
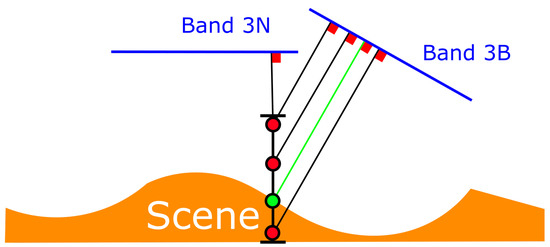
Figure 8.
Search for the altitude yielding the best correlation for a given position.
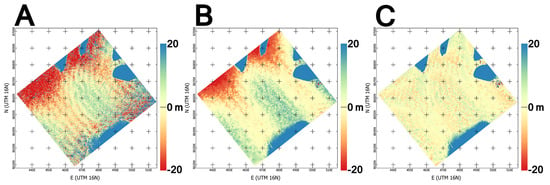
Figure 9.
DEM product over the sea ice scene AST_L1A_00307072008194108_02012009125352.hdf. (A) Using only the metadata; (B) After correcting the cross-track parallax; (C) After fitting cross- and along-track corrections using a flat DEM over the sea ice area.
Correcting the back-looking image through the method described in Section 2.3 significantly improves correlation scores over the entire area, reduces noise in the final DEM produced and, in most cases, provides greater coverage compared to the DEM obtained from the uncorrected images (see Figure 9B).
The standard approach is to compute the DEM on a grid with a 30-m spacing, but the user can choose to compute the DEM at a higher resolution. A higher resolution gives some finer details, but may also increase the noise in the data. We found that computing the DEM on a 10-m spacing grid, then sub-sampling it down to 30 m is a good compromise between noise and detail, but the user can choose other parameters better suiting their needs.
2.5. Correction of the Along-Track Jitter
After correcting the cross-track component of the jitter, the along-track component is still present in the DEMs. Because of its relatively low amplitude compared to the terrain variation in most scenes, it is not easy to detect the along-track jitter effect from the single DEM produced alone. However, when computing dDEMs for estimating elevation change, computing the elevation difference between two scenes largely removes the terrain signal and shows the superposition of the jitter effects from both DEMs (if both are from ASTER data). Actual terrain change (such as glacier elevation change, erosion or similar processes) is also added to the signal. Figure 9B shows the difference between the DEM after a 3D co-registration using the method described in [2] and a flat DEM at 0-m elevation over the sea ice area.
To remove this remaining effect composed of the along-track jitters of the two ASTER DEMs, we first need to filter out the part of the terrain that cannot be assumed stable because of natural or anthropogenic change. This can be done by thresholding (in the case of very large change), or by masking changing terrain manually. If the changing terrain is of a known type, like glaciers, filtering can be done by using a database of glacier areas and a buffer to account for possible glacier changes over time or database inaccuracies, or by detecting glaciers using multispectral methods such as band ratios [19]. This last method, while being automated, as well as not requiring external data, works on clean-ice glaciers, but might fall short on debris-covered glaciers and other non-glacier phenomena such as landslides [20]. Note also that due to sensor degradation, ASTER SWIR data are no longer available for multispectral analysis in images acquired in recent years.
With only the stable terrain remaining, post-processing corrections are made by first co-registering [2] and then differencing the two DEMs. Three corrections are then applied stepwise. The first is removal of a remaining bias pattern apparent in the across-track direction of the ASTER scenes, which, in our experience, is apparent in all scenes. We also noticed that the pattern of this bias seems to be somehow linked with latitude. To remove this bias, we fit a polynomial in the across-track direction to solve for the bias. The order of this polynomial is chosen based on iteratively fitting until further improvement in the Root Mean Square Error (RMSE) is not apparent. Similarly to the across-track biases, along-track biases are apparent at two distinct frequencies [4]. We automatically check for the best fit (lowest RMSE) between a polynomial fit and a sum of up to six sines. Often, two sums of sines are iteratively fit in the along-track direction to remove first the long wavelength (∼34 km), larger amplitude(–15 m) signal and then the short jitter wavelength (with known bounds on wavelength ( km) and amplitude ( m)). Depending on the amount and distribution of stable terrain in the scene available for fitting, the signal might be difficult to identify and therefore only partially corrected. Figure 9C shows the DEM after the application of these above corrections.
After all of these corrections are applied to a “best case scenario” scene, fast sea ice (a completely flat area with good contrast), the standard deviation of the error is significantly improved to under 3 m as compared to over 20 m in the AST14DMO product (see Table 1), and the completeness reaches 100% (see Figure 1 vs. Figure 9C). Over more challenging scenes, both of these values can be worse (see Section 3.1, Section 3.4 and Section 3.5).

Table 1.
Statistics of the elevation of the fast sea ice depending on the data processing. All DEMs were co-referenced to a flat DEM at 0-m elevation on the ice area (so mean elevation of the sea ice is 0 m for all DEMs). MicMac ASTER (MMASTER) versions are: (a) without corrections; (b) with cross-track correction from Section 2.3; (c) with cross- and along-track correction from Section 2.5. The standard deviations are computed without cropping the outliers. Cropping the outliers at SD returns respectively for the DMO and the MMASTER c 15.37 m and 2.70 m.
2.6. Implementation
Most of our workflow is implemented in the free open source MicMac photogrammetric library (developed at the French National Institute of Geographic and Forest Information (IGN) [18]), except for the post-processing steps described in Section 2.5 (correction of the DEM by analysis of dDEM), which is currently implemented as a MATLAB script. Hence, we can offer a ready-to-use software package to produce DEMs and orthoimages from Level 1A ASTER products.
A bash script (WorkFlowMMASTER.sh) that runs the necessary MicMac and GDAL (http://www.gdal.org/) commands to compute an MMASTER DEM and orthoimage is available on the MicMac wiki page (http://micmac.ensg.eu/index.php/MMASTER).
Note that to compute an MMASTER DEM, it is necessary to compile MicMac from the IncludeALGLIB branch from https://github.com/micmacIGN/micmac/tree/IncludeALGLIB. GDAL is also used as an automation tool in the workflow linked above.
3. Use Cases and Applications
In the following sections, we assess how MMASTER performs under different scene conditions and demonstrate some examples of how the data created through the MMASTER process can be used for different scientific applications. We use different external data for validation, comparison and quality qualification. In our assessment studies and application scenarios, the focus is on investigating MMASTER performance and not on in-depth analysis of the geophysical phenomena shown.
3.1. Mountainous Terrain and River Landforms in Alaska: MMASTER vs. DMO vs. Alaska IFSAR
Our goal for the first scenario was to test our processing in a more challenging topographic environment, so we chose a mountainous area in northwestern Alaska where a high-quality IFSAR DEM flown in summer 2012 was available for quality assessment (data available from the U.S. Geological Survey; see https://lta.cr.usgs.gov/IFSARAlaska). The area includes neither glaciers, nor large unstable features, so we considered the whole scene to represent stable terrain. However, the improvement in DEM quality offered by MMASTER revealed very clear patterns of elevation differences around the river beds.
The ASTER L1A scenes (dataset reference in Table 2) were processed as described above, using the IFSAR (InterFerometric Synthetic Aperture Radar) DEM as the ground truth for the along-track bias removal. Figure 10 shows the elevation change derived from a co-referenced DMO (A) and from a processed MMASTER scene (B). The statistical distribution of the elevation change is quite similar for both scenes ( m for the DMO and m for the MMASTER), because the amplitude of the corrections made through the MMASTER process is in the same range as the remaining noise.

Table 2.
Dataset references for the Mountainous Terrain and River Landforms in Alaska example.
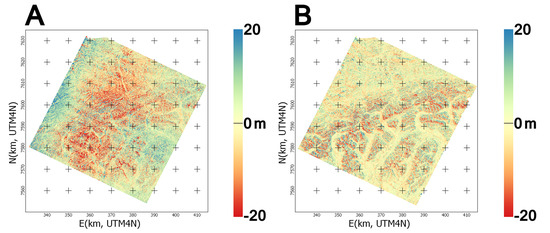
Figure 10.
Elevation difference after co-registration over the Alaska scene (AST_L1A#00307082010224323_07132010140226.hdf) for the DMO (A) and the MMASTER (B) products.
Nonetheless, the elevation change/error map reveals that MMASTER offers a better spatially-spread distribution with reduced local bias and noise. In the MMASTER-IFSAR difference, local patterns of elevation differences around the river beds are apparent, which are not visible in the DMO-IFSAR difference as they are hidden by the high frequency noise (see Figure 11).
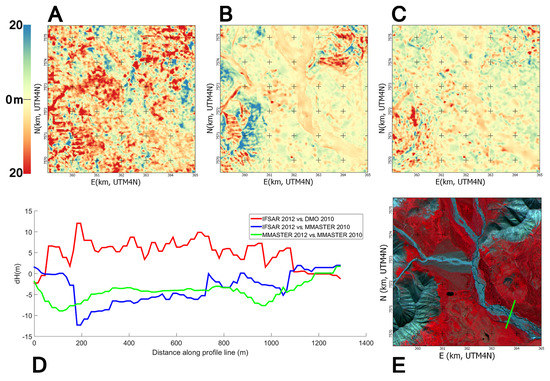
Figure 11.
Zooms from Figure 10 on an area showing river bank elevation change patterns. (A) DMO 2010 vs. IFSAR; (B) MMASTER 2010 vs. IFSAR; (C) MMASTER 2010 vs. MMASTER 2012; (D) profile line over a river; (E) MMASTER 2010 orthoimage of the area with the position of the profile line (green).
The patterns visible around the river beds seem at first sight to be related to river erosion; however, both their magnitude (that would reach extreme values of up to m·y of elevation lost) and their distribution (sometimes far away from the actual position of the rivers between 2010 and 2012) leads us to conclude that river erosion may not be the main source of elevation differences between the two datasets. Further inspection of the processing of the IFSAR data (described in [21]) and a look at higher resolution pictures of the area (taken from the ground) reveal that the patterns of elevation change are actually somehow correlated with the presence of trees close to the river banks. Such trees are less commonly found further away from the rivers, where the vegetation is mainly bushes and grass, typical for the tundra environment. The dual-band IFSAR is indeed processed so as to reveal the bare earth, while MMASTER captures the top of the canopy (up to ≈10 m high trees). It is quite impressive to be able to detect such a clear pattern of radar penetration when the amplitude of the phenomena is only in the order of 5 m, showing that the MMASTER DEM precision is even better. Another factor explaining the elevation-difference pattern is that the sharpness of the terrain is much better resolved in the 5-m posting IFSAR data than in the MMASTER, where cliffs and other steep slopes tend to be softer, as we can see in the thin red patterns of elevation difference for very narrow valleys (<200 m).
Comparison with an ASTER scene from 2012 does not reveal such clear patterns (see Figure 11C), but we can still see some elevation difference around the river that correlates with visible meandering. These patterns of a few meters of elevation change, which seem to superimpose on the apparent elevation change measured with the IFSAR, in the actual river bed (or in what became palaeochannels) can only be attributed to actual erosion.
Errors in steep terrain are well visible because the resulting ASTER-derived DEMs are somehow softer (and of lower resolution) than the IFSAR DEM. Steep terrain is also affected by the stereo configuration of the ASTER system with a large back-looking angle that creates images with limited view on north-facing slopes (completely hidden for slopes over 60°) and stretched out south-facing slopes. To counteract this effect, more modern satellites designed with fixed stereo configurations use(d) either aft and back-looking images (for example, the SPOT5 HRS system had −20° and +20° telescopes) or even three telescopes (aft, nadir and back-looking) like ALOS PRISM (−24°, 0°, +24°). A third factor affecting the elevation of steep terrain is that at high north (resp. south) latitude, the Sun angles (particularly in winter) are such that north-facing (resp. south) slopes are in the shadow and therefore present very low contrast for the correlator to grasp (see Figure 12).

Figure 12.
Extract from the bands 3N (left) and 3B (right) of AST_L1A#00307082010224323_07132010140226.hdf. Differences in appearance of steep terrain are well visible: north-facing slopes are much less visible because of the Sun angle (both bands) and the view angle (Band 3B). In red, a north-facing slope (compacted in Band 3B) and in green a south-facing slope (stretched in Band 3B).
Through this example we show the accuracy on stable terrain, the ability to detect river erosion of about 2 m (which was impossible with AST14DMO data), the ability to evaluate vegetation penetration compared to a radar-interferometry DTM (here, IFSAR) and the limits of the stereo configuration of the ASTER system to evaluate north-facing slopes.
3.2. Earthquake 2D Displacement Estimation
In this scenario, the higher precision orthorectified imagery provided by MMASTER (dataset reference in Table 3) is used to identify the position and quantify the magnitude of co-seismic slips caused by an earthquake. The improvement of the quality of the DEM compared to the DMO product results in better orthorectification as vertical DEM errors propagate into lateral displacement in the orthoimages [22]. Measurement of seismic displacement using ASTER images has been attempted previously, with varying degrees of success, for instance by [23,24].

Table 3.
Dataset references for the New Zealand earthquake example.
On 14 November 2016, New Zealand experienced a earthquake near Kaikoura. This fault slipped by up to 10 m in certain areas, two thirds of an ASTER pixel. Subpixel displacement estimation is not a challenge with modern software, and we exploited the integrated tool MM2DPosSism of MicMac [25] to perform the measurements. Such displacements are easier to measure with the more modern Landsat-8 and Sentinel-2 data, but these products have not been available for very long. Selecting such a modern earthquake provides the ability to use them as a ground truth (data processing and analysis was done in the studies of [26]). The vertical displacement is not of high enough magnitude and either too spread or too local to be identified with the MMASTER product on a point-by-point basis.
In Figure 13, we display the measurement of the movement in an Euclidean system rotated by 45°, where the Kekerengu fault lies roughly along one axis and the Papatea fault on the other, in order to emphasize the faults. On the southwest to northeast axis (Figure 13A), the displacement at the Kekerengu fault line is measured as m or pixels. On the northwest to southeast axis (Figure 13B), the displacement at the Papatea fault line is measured as m or pixels. These displacements are in accordance with the values measured from the much more accurate and modern Sentinel-2 and Landsat-8 data by [26] (respectively, 9 m and 6.5 m for the Kekerengu and Papatea faults).
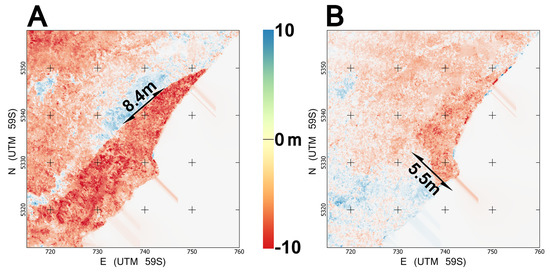
Figure 13.
Cumulative seismic horizontal displacements. (A) SW-NE, the Kekerengu fault is highlighted; (B) NW-SE, the Papatea fault is highlighted.
Another validation source could be data from GNSS networks (available from http://www.geonet.org.nz/data/types/geodetic). Data from the stations in the general area of the faults for the period surrounding the earthquake event validate the directions of the displacements, but the density and location of the GNSS stations do not permit one to see the fine details of the displacements, nor their magnitude in the immediate vicinity of the fault lines. Indeed, only one station is in the area depicted in Figure 13 and Figure 14.
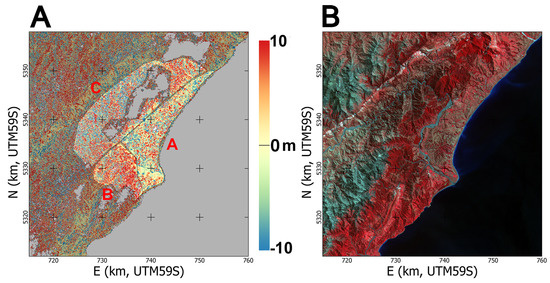
Figure 14.
(A) Post seismic vertical displacement. The three highlighted Zones A, B and C are separated by the Kekerengu and Papatea faults. Grey areas are where the elevation change was over 30 m or not computed because of the sea or the presence of clouds (mostly in the 2016 scene); (B) Orthoimage from the 2011 scene.
Using the position of the faults identified from the horizontal displacement, three zones can be defined to compute statistics of the vertical displacement (see Zones A, B and C in Figure 14A). Taking Zone C as the reference, Zone B was subject to an uplift in the order of m, while Zone A shows a m settlement. The zonal-statistical approach is necessary here because the signal is close to the accuracy limit of the product, and the DEMs are fairly noisy over rugged terrain.
Through this example, we show that MMASTER data can be used for sub-pixel scale (≈5 m) displacement analysis in both planar and vertical directions. Even if the more modern systems can provide more accurate information (at least in 2D), this opens the possibility to measure such displacement for events that have happened further in the past ≈15 years.
3.3. MMASTER on Volcanic Processes
Active volcanic areas are known to experience significant topographic changes due to numerous surface and subsurface processes. We generate MMASTER DEMs over the Puyehue-Cordón Caulle volcanic complex, southern Chile, where a voluminous explosive eruption occurred in June 2011. The eruption resulted in a number of substantial topographic changes: (1) the effusion of a massive, 30–45 m-thick rhyolite lava flow that emanated from an effusive vent on the NNW flank of the volcano [27], (2) the shallow emplacement of a laccolithic intrusion that triggered a >200-m bulge of the Earth’s surface and (3) the thick deposition of explosive material as a result of pyroclastic flows. In addition, the eastward transport of the eruptive column led to thick ash and tephra deposits [28], which considerably affected the ecosystems of the regions east of the volcano [29], including killing the vegetation due to the toxic ash concentration. The Puyehue-Cordón Caulle volcanic complex is thus an ideal case study for assessing the relevance of our method to quantify topography changes resulting from volcanic activity.
For this scenario, we differenced the MMASTER DEMs from two scenes 10 years apart (dataset reference in Table 4), the first one in 2003 (i.e., before the 2011 eruption) and the second in 2013 (i.e., after the end of the 2011 eruption). The comparison between both images (Figure 15A,B) clearly highlights (1) the dark rhyolitic lava flow NNW of the summit Puyehue caldera and (2) the distribution of thick pyroclastic deposits, in light grey. The 2013 image also displays a dark aureole surrounding the main volcanic edifice to the north, east and south. In the 2003 image, this area corresponds to vegetation; therefore, we interpret this dark aureole as regions where the forest was killed by the ash deposited during the main eruption.

Table 4.
Dataset references for the Cordón-Caulle volcano.
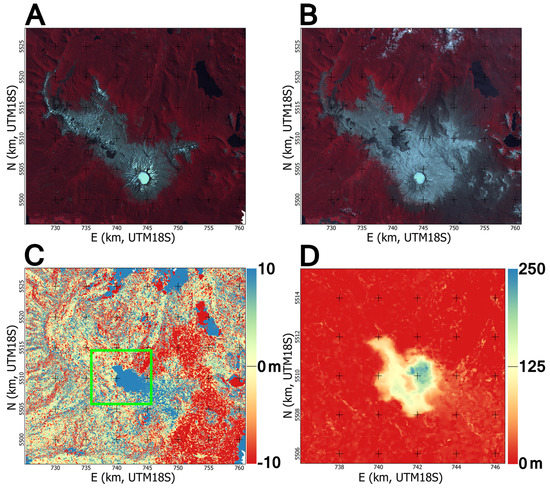
Figure 15.
(A) Orthoimage in 2003; (B) Orthoimage in 2013; (C) Elevation change 2003–2013 for the area covered by the upper row orthoimages; (D) Zoomed-in and adjusted color scale on the elevation change around the laccolith intrusion (area highlighted in (C)).
Figure 15 displays two dDEM maps with distinct color scales. In the right map, the color scale spans from 0–250 m to highlight substantial topography change at the vicinity of the main eruptive vent. The topographic pattern displays: (1) a sub-circular feature of 200–250 m in amplitude, which corresponds to a combination of surface bulging due to the shallow laccolith emplacement and deposition of erupted materials, and (2) an elongated, relatively flat feature of 125 m in amplitude, which corresponds to the rhyolitic lava flow. The topography difference calculated with MMASTER shows the same patterns as that described by [30], computed using the ASTER GDEMv2 and a Pleiades DEM.
Other interesting results are given by the other dDEM map, with color scale ranging from −10 m–10 m. This map displays an aureole to the north, east and south of the volcano with average elevation difference of −10 m. This aureole exactly correlates with the dark gray aureole in the 2013 image, interpreted as the forest (appearing red in the 2003 G-R-IR orthoimage) killed by the ash deposits. We thus infer that this aureole of apparent subsidence is not an artifact, and the topography difference corresponds to the overall thickness of the vegetation cover that died after the eruption. The map also displays a slightly more elevated (<+10 m) zone close to the summit caldera. This zone exactly correlates with the visible light gray areas corresponding to thick ash deposits. Our product is therefore able to detect the local, thick pyroclastic deposits produced during the eruption, though it is not able to detect tephra deposits of a few tens of centimeter thickness observed far away from the volcano [29].
3.4. MMASTER on Tree Surface and dDEM
Large parts of the Earth are covered by forest, so we also aimed at assessing MMASTER performance over forested areas. For this scenario, we show that MMASTER products can be successfully computed over vegetated areas (using the dataset referenced in Table 5). Such data can be used to evaluate the biomass loss by clear-cuts in the Amazonian forest since tree height is well correlated with biomass and so is biomass change [31]. The aim of this application scenario is two-fold: (1) to detect the clear-cut areas and (2) to provide an estimate for the average tree height. Since no penetration of the signal is expected here, contrary to some radar-based altimeter products [32], the data can be used as a complement or data validation.

Table 5.
Dataset references for the Amazonian forest clear-cut scene.
In this scenario, an extra processing step is necessary to mask the area of clear-cut that cannot be filtered using pre-existing data. First, a dDEM needs to be produced to create a mask that can then be applied before removing the along-track jitter and computing the final dDEM. The mask is created by a thresholding of the uncorrected dDEM (in this case, the threshold is set at m) and then a morphological opening and dilating (5 × 5 square structuring element for both) of the result to obtain a binary mask of the clear-cut areas to be filtered out for the along-track correction. A similar approach is then followed to create the mask identifying clear-cut areas from the final dDEM. The final mask is shown in Figure 16B.
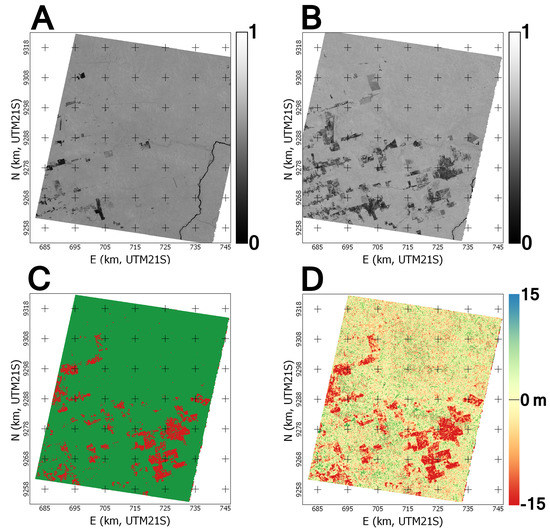
Figure 16.
Top row: NDVI in 2003 (A) and 2010 (B). Bottom row: MMASTER clear-cut mask (C) (red is clear-cut area) and elevation change 2003–2010 (D).
Masking could also be done by identifying the clear-cut areas in the NDVI product that can be derived from the orthorectified data (see Figure 16A,C, dark is low NDVI indicating no vegetation, while light is high NDVI indicating the presence of vegetation), since we can expect that the NDVI value would have dropped significantly (see for instance, the method discussed in [33]). However, in the case of re-exploited clear-cut areas (by soybean plantations, for instance), the NDVI-based method would fail.
A statistical analysis of the final dDEM (shown in Figure 16D) over the areas that have been clear-cut (representing 276.9 km or of the total scene) yields a mean elevation change of m, while the areas not showing any cuts (2946.6 km or ) yield m. If the standard deviation is not insignificant, it is in both cases within the expected range for soft terrain, showing that the DEM accuracy is not significantly degraded in tree-covered areas.
Our example over the Amazonian forest suggests that tree heights, or their strong changes (here: man-made clear-cuts) can be extracted from MMASTER DEMs. DEM extraction of the forest was surprisingly unproblematic given the repetitive structure of forest that may lead to confusion of the correlator. Extracting tree heights or their changes over time over large areas from ASTER scenes might be useful for spatio-temporal combination with radar DEMs or radar/laser altimetry due to their different penetration into the canopy or different spatial or temporal coverage.
3.5. MMASTER for Large Glacier Elevation Change
For our fifth and final scenario, we wanted to demonstrate the use of MMASTER DEM differencing over a glacier and compare it with independent validation data. We thus needed an area with two ASTER scenes acquired at timestamps corresponding to the acquisition of independent data. We found such an area around Daugard-Jensen glacier in eastern Greenland. It was covered by data from the SPIRIT project (SPOT 5 HRS stereoscopic survey of Polar Ice: Reference Images and Topographies [34]) and by ASTER in 2007 and 2014 nearly simultaneously (with respectively four- and 10- day delays between the two systems. The references and exact dates of the acquisitions are listed in Table 6).

Table 6.
Dataset references for the Daugaard-Jensen glacier.
The SPIRIT project used SPOT 5 HRS stereo pairs to create DEMs over selected important polar regions at a 40-m GSD in UTM projection. The accuracy of the DEMs produced by the SPOT 5 HRS system has been assessed at around 5 m (relative) and 10/15 m (absolute) [35]. After co-registration of two of these products, we can therefore expect an accuracy of the elevation difference of around 7 m.
Elevation change grids were computed for each dataset with co-registered products (the SPIRIT scenes together, on the one hand (see Figure 17B) and the two DMO scenes together, on the other hand (see Figure 17C)), or for the MMASTER product, after application of our method (see Figure 17D). Our analysis focuses on the part of Daugaard-Jensen glacier that is visible in both ASTER scenes. The approximate centerline and the selected area are shown in Figure 17A.
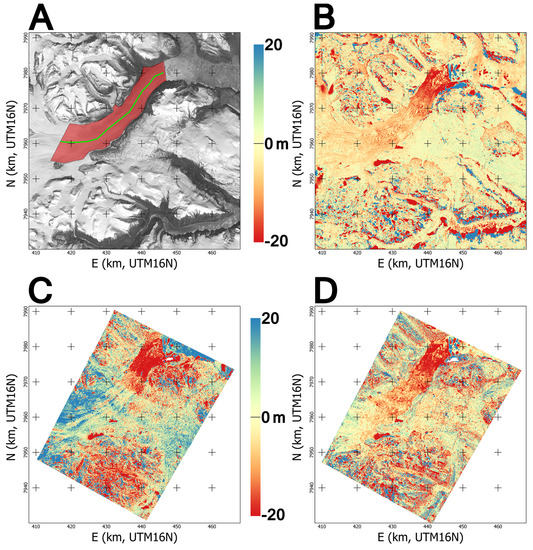
Figure 17.
(A) Centerline (green) and area (red) considered for the quantitative analysis, overlaying the SPIRIT 2014 orthoimage. Others: Measured elevation change from co-registered 2007 and 2014 DEMs ((B) SPIRIT DEMs; (C) AST14DMO DEMs; (D) MMASTER DEMs).
We first extracted the 2007–2014 elevation change values over the centerline for each dataset. The difference between the SPIRIT elevation change values (considered ground truth with a m accuracy) and both the DMO and MMASTER values are plotted in Figure 18. The MMASTER values are for the most part (82%) inside of the m accuracy band given by the SPIRIT data (agreement of m), while the DMO is significantly off (agreement of m, with only 30% in the accuracy band). The DMO data show both error trends and sharp error peaks reaching 175 m, while the MMASTER is fairly contained (max. error of 24 m). While the error trend should stem from the long-wavelength jitter effects not accounted for in the DMO in contrast to the MMASTER DEM, we assume that the sharp error peaks could in parts be due to the cross-track jitter not accounted for in the DMO processing. Corresponding points in the ASTER stereo data can have a cross-track offset from the (approximately along-track) epipolar line that is too large to match between them when using a directional (i.e., along-track) correlation algorithm with insufficient cross-track margin.
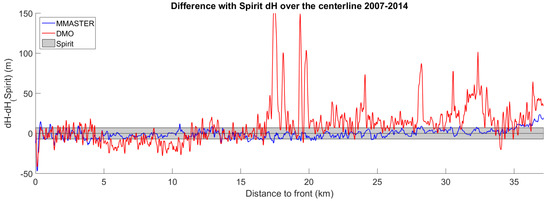
Figure 18.
Difference along the centerline (shown in Figure 17A) between the 2007–2014 elevation change from the SPIRIT data (set as the reference data and thus zero; the error bar shown in grey; see Figure 17B) and the elevation change from our product (MMASTER, see Figure 17D) and the DMO product (see Figure 17C).
We then compared the volume change computed for the selected area of the main glacier (see Table 7). For the Daugaard-Jensen outlet glacier section, it appears that while the MMASTER and the SPIRIT data are in relative accordance with a -m difference in estimation of the mean elevation change from the MMASTER data compared to the SPIRIT data, the DMO data show significantly different values, as well as a -m difference in estimation of the mean elevation change, hence concluding that the glacier is experiencing volume gain.

Table 7.
Mean elevation change and volume change in the glacier tongue according to each dataset.
With this example, we show that it is possible to fit corrections to the bias observed on stable ground and produce MMASTER dDEMs that are suitable to survey glacier elevation change with an accuracy better than m, whereas it proved challenging to obtain good data with the DMO products. MMASTER products show good accordance with SPIRIT products (that have themselves been proven to be adequate for mapping glacier elevation change by [34]). It must however be noted that the glacier surface is a type of surface at risk of being contrast-free if fresh, soft snow is present, or if the ASTER gain settings are not setup for glacier brightness (then the white surface is saturated, and no data can be extracted).
4. Discussion
With MMASTER, a new and modernized method to produce DEMs from ASTER L1A data is available to users. We have shown that the potential applications for the ASTER data, which were already numerous with the AST14DMO product, are now even more varied. The increased data quality (accuracy and coverage) also offers the ability to extract more accurate surface difference data (reducing the error bars in dDEMs), thereby enabling applications that were previously not possible.
The main improvements of MMASTER compared to the AST14DMO are significantly reduced local noise as a result of (1) the cross-track parallax corrections, leading to better correlation, and (2) a more modern correlator, as well as the large-scale bias removal from both the cross- and along-track corrections. The latter bias removal is important for a number of applications where the actual elevation change patterns resemble in parts the typical elevation pattern caused by the jitter. For example, elevation changes by glacier surges may look in parts similar to the elevation changes induced jitter and, thus, lead to incorrect interpretations [36]. As a further advantage, the improved MMASTER DEMs lead to orthoimages with reduced distortions and enable thus improved displacement matches.
Determining the quality of either a single MMASTER DEM or of an MMASTER dDEM is difficult to reduce into a single number. Indeed, terrain characteristics such as terrain ruggedness, texture or even orientation can lead to abnormally noisy data. A bad gain setting of the ASTER system during image acquisition might also reduce the contrast in the scene dramatically, leading to substandard products. As shown in Figure 9 and Table 1, in an ideal scenario, the standard deviation of an MMASTER DEM can fall down to better than m (compared to the m of the DMO product for the same scene, coherent with the number given by [9]). Examples in Section 3.3, Section 3.4 and Section 3.5 show that a standard deviation of m can be expected over terrain that is not too rugged, even with soft ash deposits, tree cover or mostly bright glacier surfaces.
However, even with the improved processing, ASTER DEMs are still quite imperfect, and some precautions are needed when using these data. Indeed, the accuracy reduces to m when a significant part of the scene is very rugged terrain (see Section 3.1), because (1) MMASTER DEMs are fairly smooth, the correlation being done on 45 m-wide windows (three pixels) and the final product being a DEM at 30-m GSD, and (2) north-facing slopes are badly imaged by the nadir- and back-looking (northward looking) telescopes (see Figure 12).
Low-contrast surfaces can also be a problem, as ASTER’s VNIR sensor does not deliver very high dynamic images (nominal bit depth is eight bits, but the histograms are rarely well distributed; see Figure 4). Bright (like snow, ice (see, for instance, the noise over the small ice cap area just east of the bottom of Daugaard-Jensen glacier’s tongue in Figure 17D) or sand) and dark (mostly shadowed area) areas are often contrast-free and therefore do not provide data from correlation. In order to help the end users to quantify the quality of the data they are using, MMASTER outputs a correlation score map, advising to a degree on the dubiousness of the data. It is however important to notice that good correlation is not a guarantee of good data, as even clouds sometimes yield great correlation.
Larger scale effects (jitter) are also still visible in the output DEM before either a correction with a reference DEM or a comparison with another DEM (MMASTER or other) in order to get dDEMs (the actual aim of the MMASTER method). Absolute accuracy is also not guaranteed as navigation data are imperfect; it is often off by up to 50 m in XYZ (a value also reported in [9]). Thus, coregistration is necessary for any application using the DEMs as a reference surface.
Because of the way the corrections are fitted, the fit is best when the whole scene can provide data, which is not the case if large parts of the scene are covered by water or clouds, or are saturated or else result in bad correlation. In these cases, the correction fit might be of lower quality and even largely wrong over the areas where no or few data are available, leading to unrestrained behavior in the polynomial fit. However, this is in practice not of much concern, as bad corrections over areas that would not produce data anyways are less of a problem. Furthermore, in our testing, even scenes with up to 70% data gaps were still processed successfully, especially if the gaps are located in a single part of the scene (the 2016 New Zealand scene from Section 3.2 is half ocean on the east side and has some important cloud cover over land), but the success rate may vary for other applications and scene conditions.
The main reason behind the polynomial fit of the measured signals is that the corrections are different from scene to scene. However, we noticed some consistencies. The main one we find is a latitude dependency on the cross-track elevation bias (for both the DMO product and the MMASTER product before comparison with another DEM), with the edge of the images presenting a varying pattern: at high latitudes, the part of the DEM related to the left edge of the images bends down (as seen in Figure 1A, Figure 9A,B and Figure 10A), while, close to the Equator, the right edge bends up. Close to 45° N/S, this pattern is absent. We have no clear idea about the underlying reason for this latitude-dependent scene deformation (it could, for example, be due to atmospheric refraction, orbit determination or some other process), but once understood, MMASTER could be improved accordingly.
5. Conclusions
The ASTER data archive is a goldmine for the analysis of changes on the surface of the Earth since 2000, including elevation change. However, previously available DEM products from ASTER, e.g., the AST14DMO product or personally-generated DEMs from commercial software (e.g., PCI Geomatica, ENVI, etc.), were not high enough quality for a number of applications. We have therefore developed the open source processing chain MMASTER that takes ASTER L1A scenes in GeoTiff format, extracts the images from the VNIR Bands 3N and 3B, as well as the necessary meta-data and computes a DEM and orthoimage of the scene. From this baseline, we can conduct fine analysis of the raw data and apply corrections to it.
The data produced by the MMASTER system are a significant improvement on the AST14DMO product with the precision increasing from 20 m to 5 m. This opens up a new realm of potential applications in a wide variety of fields as demonstrated in the second part of this paper: glacier volume change can be estimated with a higher confidence; the effects of a volcanic eruption on its local environment can be better quantified; and the former tree height of a clear-cut forest can be well estimated. The increase in quality can also help estimating radar penetration in vegetation (as seen in Section 3.1), but also on snow and ice when compared to radar-interferometric DEMs, a still ill-resolved issue. In addition, the quality of the orthoimages that can be computed is improved, opening up the opportunity for better assessment of horizontal shift in terrain, as demonstrated in the New Zealand earthquake example in Section 3.2.
MMASTER opens a range of new perspectives for the community in view of the large and over 16 year-long global-scale archive of ASTER stereo data, its recent free availability and the fact that the ASTER stereo sensor is still operational and will continue to acquire new data in the foreseeable future. The immediate availability of the processing chain will hopefully put this new data in the hands of experts in a number of fields that we may not even have considered in this paper.
Acknowledgments
Acquisition of the ASTER images was guided by NASA JPL, through the ASTER science team and the Global Land Ice Measurements from Space (GLIMS) initiative. The study was funded by the European Research Council under the European Union’s Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement No. 320816 and the ESA project Glaciers_cci (4000109873/14/I-NB). We also acknowledge the help from Marc Pierrot-Deseilligny, Ewelina Rupnik and the rest of the MicMac team at IGN/ENSG (Ecole Nationnale des Sciences Géographiques). for their help in the development of the software.
Author Contributions
Luc Girod designed and implemented the MMASTER processing chain, chose the datasets, processed the data and wrote the paper. Christopher Nuth helped with the design of MMASTER, implemented the MATLAB post-processing and wrote the paper. Andreas Kääb provided essential insights into the ASTER system early in the development of the method, helped with the evaluation and edited the paper. Robert McNabb preformed extensive testing of the method and provided critical feedback that helped make the process streamlined and consistent, as well as edited the paper. Olivier Galland contributed the analysis of the volcanic example and edited the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dewez, T.J.; Akkari, H.; Kaab, A.M.; Lamare, M.L.; Doyon, G.; Costeraste, J. Z-Earth: 4D topography from space combining short-baseline stereo and lidar. In AGU Fall Meeting Abstracts; American Geophysical Union: San Francisco, CA, USA, 2013. [Google Scholar]
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef]
- Ayoub, F.; Leprince, S.; Binety, R.; Lewis, K.W.; Aharonson, O.; Avouac, J.P. Influence of camera distortions on satellite image registration and change detection applications. In Proceedings of the Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008. [Google Scholar]
- Kääb, A.; Lamare, M.; Abrams, M. River ice flux and water velocities along a 600 km-long reach of Lena River, Siberia, from satellite stereo. Hydrol. Earth Syst. Sci. 2013, 17, 4671–4683. [Google Scholar] [CrossRef]
- Iwasaki, A. Detection and estimation satellite attitude jitter using remote sensing imagery. Adv. Spacecr. Technol. 2011, 13, 257–272. [Google Scholar]
- Ye, Z.; Xu, Y.; Wang, F.; Liu, S.; Tang, X.; Li, L.; Xie, J.; Tong, X. Estimation of the Attitude Perturbance Using Parallax Imagery-Application to ZY-3 Satellite. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 1, 279–283. [Google Scholar] [CrossRef]
- Pan, J.; Che, C.; Zhu, Y.; Wang, M. Satellite Jitter Estimation and Validation Using Parallax Images. Sensors 2017, 17, 83. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Zhu, Y.; Jin, S.; Pan, J.; Zhu, Q. Correction of ZY-3 image distortion caused by satellite jitter via virtual steady reimaging using attitude data. ISPRS J. Photogramm. Remote Sens. 2016, 119, 108–123. [Google Scholar] [CrossRef]
- Fujisada, H.; Bailey, G.B.; Kelly, G.G.; Hara, S.; Abrams, M.J. ASTER DEM performance. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2707–2714. [Google Scholar] [CrossRef]
- Toutin, T. Three-dimensional topographic mapping with ASTER stereo data in rugged topography. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2241–2247. [Google Scholar] [CrossRef]
- Deilami, K.; Mohd, M.I.B.S.; Atashpareh, N. An accuracy assessment of ASTER stereo images-derived digital elevation model by using rational polynomial coefficient model. Am. J. Sci. Res. 2012, 55, 128–135. [Google Scholar]
- Liu, S.; Tong, X.; Wang, F.; Sun, W.; Guo, C.; Ye, Z.; Jin, Y.; Xie, H.; Chen, P. Attitude Jitter Detection Based on Remotely Sensed Images and Dense Ground Controls: A Case Study for Chinese ZY-3 Satellite. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 5760–5766. [Google Scholar] [CrossRef]
- Divine, D.V.; Pedersen, C.A.; Karlsen, T.I.; Aas, H.F.; Granskog, M.A.; Hudson, S.R.; Gerland, S. Photogrammetric retrieval and analysis of small scale sea ice topography during summer melt. Cold Reg. Sci. Technol. 2016, 129, 77–84. [Google Scholar] [CrossRef]
- Abrams, M.; Hook, S.; Ramachandran, B. ASTER User Handbook, 2nd ed.; Jet Propulsion Laboratory: Pasadena, CA, USA, 2002. [Google Scholar]
- Tao, C.V.; Hu, Y. A comprehensive study of the rational function model for photogrammetric processing. Photogramm. Eng. Remote Sens. 2001, 67, 1347–1358. [Google Scholar]
- L’information Grandeur Nature (IGN). Algorithmes Nécessaires au Changement de Système géodésique; Technical Report; Institut Géographique National—Service de Géodésie et Nivellement: Vincennes, France, 1995. [Google Scholar]
- Lutes, J.A.; Grodecki, J.F. Estimation of Coefficients for a Rational Polynomial Camera Model. U.S. Patent 7,421,151, 2 September 2008. [Google Scholar]
- Rupnik, E.; Daakir, M.; Pierrot Deseilligny, M. MicMac—A free, open-source solution for photogrammetry. Open Geospat. Data Softw. Stand. 2017, 2, 1–9. [Google Scholar] [CrossRef]
- Winsvold, S.H.; Kääb, A.; Nuth, C. Regional Glacier Mapping Using Optical Satellite Data Time Series. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016. [Google Scholar] [CrossRef]
- Robson, B.A.; Nuth, C.; Dahl, S.O.; Hölbling, D.; Strozzi, T.; Nielsen, P.R. Automated classification of debris-covered glaciers combining optical, SAR and topographic data in an object-based environment. Remote Sens. Environ. 2015, 170, 372–387. [Google Scholar] [CrossRef]
- Kampes, B.; Blaskovich, M.; Reis, J.J.; Sanford, M.; Morgan, K. Fugro Geosar Airborne Dual-Band Ifsar Dtm Processing. In Proceedings of the ASPRS 2011 Annual Conference, Milwaukee, WI, USA, 1–5 May 2011. [Google Scholar]
- Altena, B.; Kääb, A. Elevation Change and Improved Velocity Retrieval Using Orthorectified Optical Satellite Data from Different Orbits. Remote Sens. 2017, 9, 300. [Google Scholar] [CrossRef]
- Schiek, C.G.; Hurtado, J.M. Slip analysis of the Kokoxili earthquake using terrain-change detection and regional earthquake data. Geosphere 2006, 2, 187–194. [Google Scholar] [CrossRef]
- Avouac, J.P.; Ayoub, F.; Leprince, S.; Konca, O.; Helmberger, D.V. The 2005, M w 7.6 Kashmir earthquake: Sub-pixel correlation of ASTER images and seismic waveforms analysis. Earth Planet. Sci. Lett. 2006, 249, 514–528. [Google Scholar] [CrossRef]
- Rosu, A.M.; Pierrot-Deseilligny, M.; Delorme, A.; Binet, R.; Klinger, Y. Measurement of ground displacement from optical satellite image correlation using the free open-source software MicMac. ISPRS J. Photogramm. Remote Sens. 2015, 100, 48–59. [Google Scholar] [CrossRef]
- Kääb, A.; Altena, B.; Mascaro, J. Coseismic displacements of the 14 November 2016 Mw 7.8 Kaikoura, New Zealand, earthquake using the Planet optical cubesat constellation. Nat. Hazards Earth Syst. Sci. 2017, 17, 627–639. [Google Scholar] [CrossRef]
- Farquharson, J.; James, M.; Tuffen, H. Examining rhyolite lava flow dynamics through photo-based 3D reconstructions of the 2011–2012 lava flowfield at Cordón-Caulle, Chile. J. Volcanol. Geotherm. Res. 2015, 304, 336–348. [Google Scholar] [CrossRef]
- Bonadonna, C.; Cioni, R.; Pistolesi, M.; Elissondo, M.; Baumann, V. Sedimentation of long-lasting wind-affected volcanic plumes: The example of the 2011 rhyolitic Cordón Caulle eruption, Chile. Bull. Volcanol. 2015, 77, 13. [Google Scholar] [CrossRef]
- Masciocchi, M.; Pereira, A.; Lantschner, M.; Corley, J. Of volcanoes and insects: The impact of the Puyehue—Cordon Caulle ash fall on populations of invasive social wasps, Vespula spp. Ecol. Res. 2013, 28, 199–205. [Google Scholar] [CrossRef]
- Castro, J.M.; Cordonnier, B.; Schipper, C.I.; Tuffen, H.; Baumann, T.S.; Feisel, Y. Rapid laccolith intrusion driven by explosive volcanic eruption. Nat. Commun. 2016, 7, 13585. [Google Scholar] [CrossRef] [PubMed]
- Solberg, S.; Riegler, G.; Nonin, P. Estimating Forest Biomass From TerraSAR-X Stripmap Radargrammetry. IEEE Trans. Geosci. Remote Sens. 2015, 53, 154–161. [Google Scholar] [CrossRef]
- Imhoff, M.; Story, M.; Vermillion, C.; Khan, F.; Polcyn, F. Forest Canopy Characterization and Vegetation Penetration Assessment with Space-Borne Radar. IEEE Trans. Geosci. Remote Sens. 1986, 4, 535–542. [Google Scholar] [CrossRef]
- Heiskanen, J. Estimating aboveground tree biomass and leaf area index in a mountain birch forest using ASTER satellite data. Int. J. Remote Sens. 2006, 27, 1135–1158. [Google Scholar] [CrossRef]
- Korona, J.; Berthier, E.; Bernard, M.; Rémy, F.; Thouvenot, E. SPIRIT. SPOT 5 stereoscopic survey of Polar Ice: Reference images and topographies during the fourth International Polar Year (2007–2009). ISPRS J. Photogramm. Remote Sens. 2009, 64, 204–212. [Google Scholar] [CrossRef]
- Baudoin, A.; Schroeder, M.; Valorge, C.; Bernard, M.; Rudowski, V. The HRS-SAP initiative: A scientific assessment of the High Resolution Stereoscopic instrument on board of SPOT-5 by ISPRS investigators. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 372–378. [Google Scholar]
- Berthier, E. Volume loss from Bering Glacier (Alaska), 1972–2003: Comment on Muskett and others (2009). J. Glaciol. 2010, 56, 555–557. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).