1. Introduction
Digital orthophoto map (DOM) is one of the most popularly used products in the field of photogrammetry, and it can provide both pleasant textures and accurate geometric properties of maps. However, to produce a large-scale orthophoto, we need to stitch a large set of orthoimages into the single composite image due to fact that the covered region of a single orthoimage is limited. Therefore, image mosaicking is one of the key technologies to generate a large-scale DOM. It also is an important and classical problem in the fields of photogrammetry [
1,
2,
3,
4,
5], remote sensing [
6,
7] and computer vision [
8,
9,
10], which is used to merge a set of geometrically aligned images into a single composite image as seamlessly as possible. In an ideally static scene in which both the photometric inconsistencies and the geometric misalignments are not existing or not obviously visible in overlap regions, the mosaicked image always looks perfect only when the geometric distance criterion is used. However, in some cases, there exist photometric inconsistencies to different extents in overlap regions between images due to illumination variations and different exposure settings. This problem can be solved well by a series of color correction and image blending approaches [
11,
12]. In addition, in orthoimages, the geometric positions of corresponding pixels on obvious ground objects from different images may be different if they are not included in the digital terrain model (DTM) or wrongly modeled [
6]. Therefore, the visible seams in those object regions may appear if the seamlines cross them. The effective way to solve this problem is to detect the optimal seamlines to avoid crossing majority of visually obvious objects and most of the overlap regions with low image similarity and large object dislocation. In this paper, our work focuses on detecting the optimal seamlines between overlapped images to eliminate the influences of geometric misalignments.
Optimal seamline detection methods search for the seamlines in overlap regions between adjacent images where their intensity or gradient differences are minimal, especially avoiding crossing the obvious ground objects like buildings and cars. Most of the optimal seamline detection methods formulated it as an energy minimization problem. Generally, those methods can be implemented in two stages. In the first stage, the cost images are defined to represent the differences between the original images. In the second stage, the optimal seamlines are further found based on the cost images via different optimization algorithms, e.g., snake model [
13], Dijkstra’s algorithm [
14], dynamic programming [
15], and graph cuts [
16]. The major issues of optimal seamline detection focus on how to define the cost images more reasonably and how to find the seamlines more efficiently and effectively. According to the used optimization algorithms, we simply review recently proposed seamline detection approaches in the following.
Kerschner [
6] proposed an automated seamline detection method using twin snake based on the energy function defined on the similarity of color and texture. The energy optimization started from two snakes on the opposite borders of the overlap region, which moved closer during the energy minimization process, and the optimal seamline was found when two twin snakes coincided. However, this algorithm requires a high computation cost and cannot overcome the local minimum problem. Wang et al. [
17] proposed an improved snake model to detect the seamline. In this algorithm, the sum of the mismatched values on the seamline was defined as the energy function, and then the seamline with the lowest energy was regarded as the final optimal seamline. This improved snake model solves the local optimum problem existed in the snake model to some extent, but not completely.
Besides the snake model, the Dijkstra’s algorithm is also popularly used for detecting the optimal seamlines. Chon et al. [
1] designed a novel objective function to evaluate the mismatching between two images based on the normalized cross correlation (NCC). Their proposed method first determined the desired level of maximum difference along the seamline and then applied the Dijkstra’s algorithm to find the best seamline with the minimal objective function. Compared with the simple Dijkstra’s algorithm, their method could find a longer seamline with less pixels with high energy costs. Pan et al. [
4] proposed a new method for seamline detection based on segmentation. It first determined the preferred regions based on the spans of segments generated by the meanshift algorithm. Then, the last pixel-level seamline was detected by using the Dijkstra’s algorithm on the cost image defined by intensity differences. After that, several object-based algorithms [
18,
19] were proposed to detect high-quality seamlines. In addition, Chen et al. [
20] proposed a new automatic seamline selection algorithm by using the digital surface model (DSM). It found the optimal seamline via the Dijkstra’s algorithm under the guide of the elevation information extracted from DSM. Similarly, Pang et al. [
21] guided the seamline with the corresponding pixel-wise disparity generated by a semi-global matching (SGM) algorithm. Similar with the Dijkstra’s algorithm, the Floyd–Warshall shortest path algorithm [
22] can also be used to find the optimal seamline. Wan et al. [
3] proposed a vector road-based seamline determination algorithm ensuring that the seamline follows the centerlines of wide streets and avoids crossing foreground objects. This algorithm firstly built a weighted graph by overlapping the extracted skeleton of the overlap regions and vector roads, and then found the lowest cost path between two intersections of adjacent image polygons by applying the Floyd–Warshall algorithm.
The dynamic-programming-based optimal seamline detection strategy can also be used for optimal seamline detection, which is less time-consuming than the Dijkstra’s algorithm. Yu et al. [
2] proposed to combine the pixel-based similarity defined by color, edge and texture informations with the region-based saliency map based on the human attention model to guide the optimal seamline searching process of the dynamic programming (DP) algorithm. Zeng et al. [
23] proposed a new optimal searching criterion that combines the gradient difference and the edge-enhanced weighting intensity one, which provides an effective mechanism for avoiding problems caused by moving objects and geometric misalignments. Then, this algorithm applied dynamic programming to find the optimal seamline.
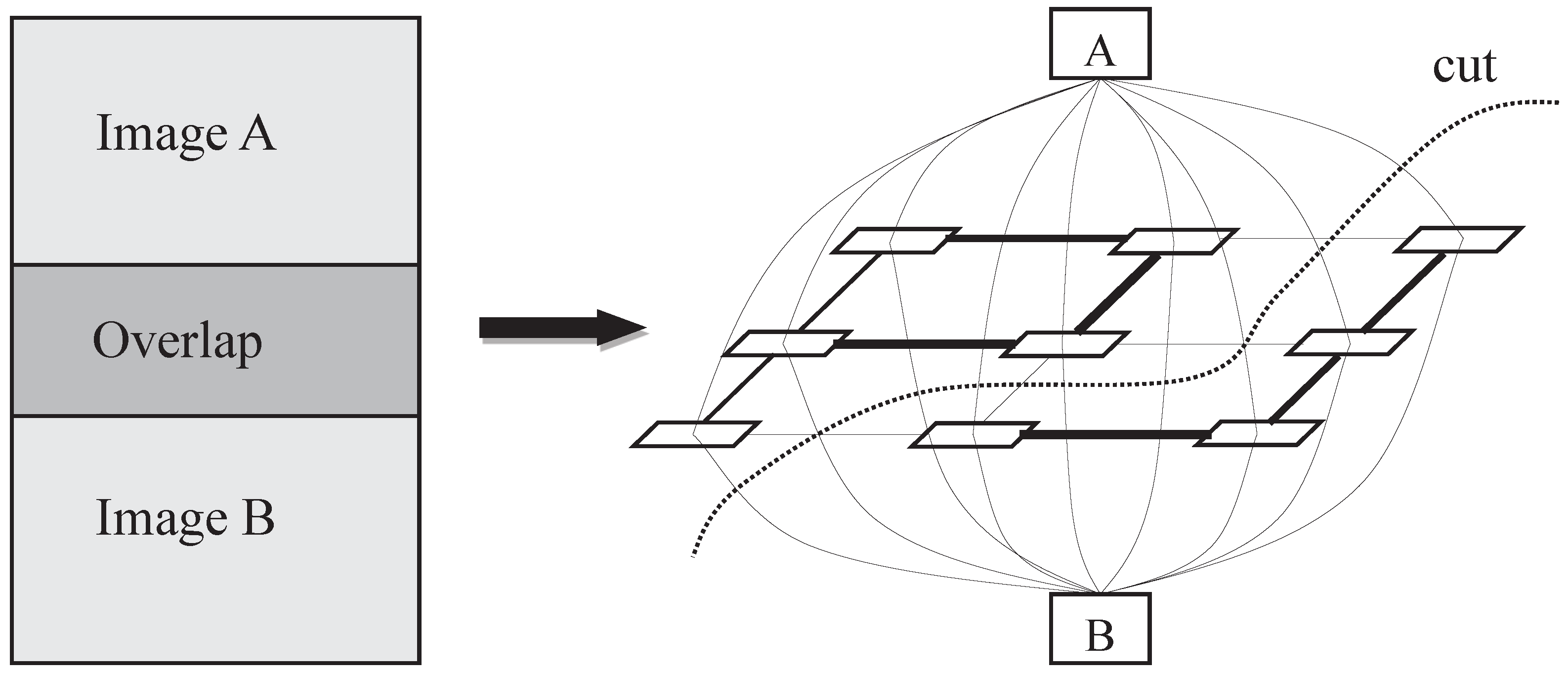
In addition, graph cuts has also been popularly applied to find the optimal seamlines. Graph cuts [
16] is an efficient energy optimization algorithm to solve labeling problems and has been widely utilized in many applications of image processing and computer vision, such as image segmentation, stereo matching, and image blending [
5,
9,
10,
24]. The basic idea of graph cuts is to first construct a weighted graph where each edge weight cost represents the corresponding cost energy value, and then to find the minimum cut in this graph based on the max-flow or min-cut algorithm [
25]. To some extent, the optimal seamline detection problem can be regarded as the inverse process of image segmentation. The aim of image segmentation is to separate the segments in the positions with large differences between adjacent pixels. In contrast, the optimal seamline locates on the positions with small differences between adjacent images. Therefore, the optimal seamline can be detected via graph cuts as image segmentation does. Kwatra et al. [
24] first applied the graph cuts algorithm to find the seamline for image and video synthesis. Their proposed method defined an energy function based on the difference of color intensities and gradient magnitudes along horizontal and vertical directions and then applied graph cuts to find optimal seamlines. Agarwala et al. [
10] provided a framework to easily create a single composite image using graph cuts to choose good seamlines within the constituent images, which needs an intuitive human–computer interaction for defining local and global objectives. Gracias et al. [
9] combined the watershed segmentation and the graph cuts algorithm to detect the optimal seamlines. Their algorithm began with creating a set of watershed segments on the difference image of overlap regions followed by finding the solution via graph cuts between those segments instead of the entire set of pixels. Li et al. [
5] first defined the cost image by combining the informations of image color, gradient and texture complexity, and then found the optimal seamline via graph cuts.
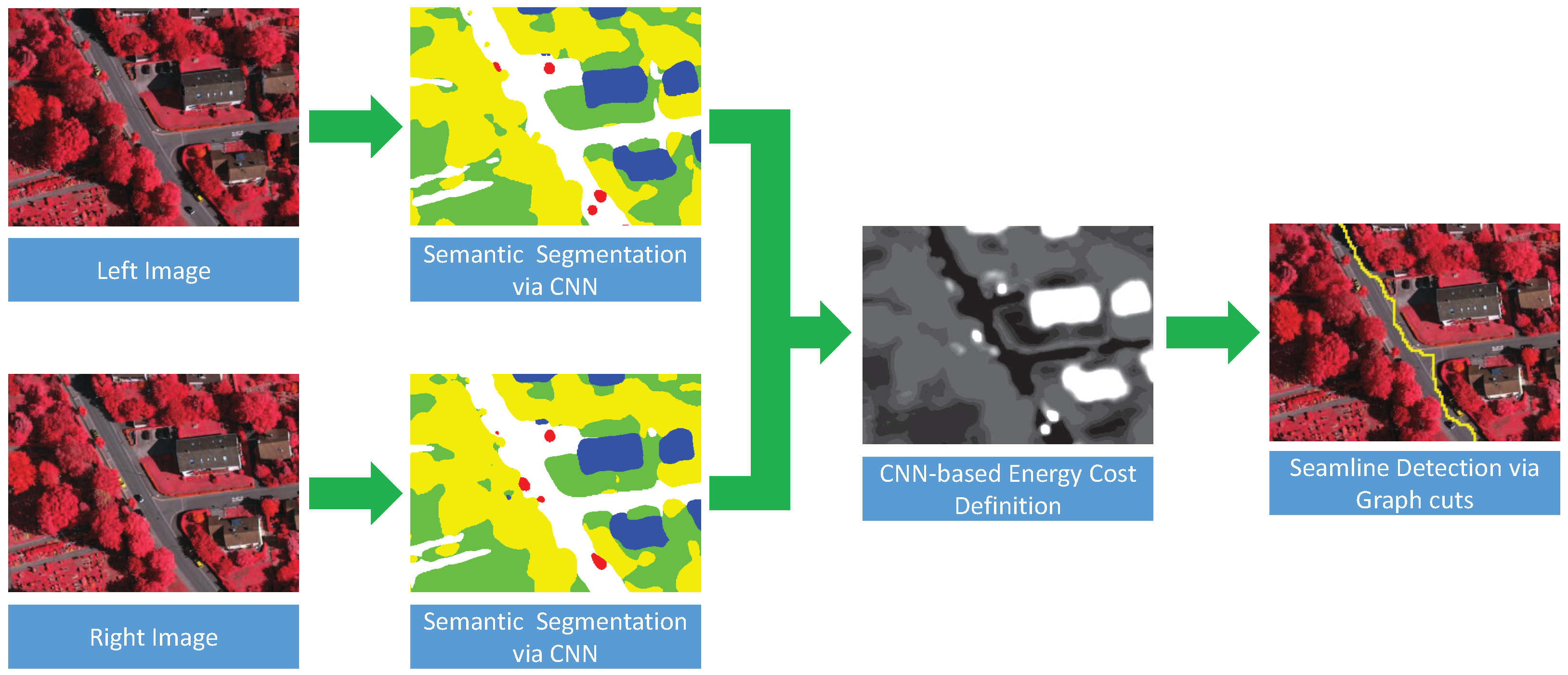
By the review of the above-mentioned optimal seamline detection methods, we can find that many features (intensity, color, gradient, texture, road vector, saliency, segments, disparity and DSM, and so on) have been used to guide the optimal seamline searching process. However, those features cannot completely describe the differences between overlapped images independently, and it is also difficult to find the best combination of several features to represent the differences. Therefore, in this paper, we propose a new optimal seamline detection method based on the scene semantic segmentation using convolutional neural network (CNN). The energy costs are defined based on the classification results of CNN, instead of combining many different hand-designed features. The workflow of our method is presented in
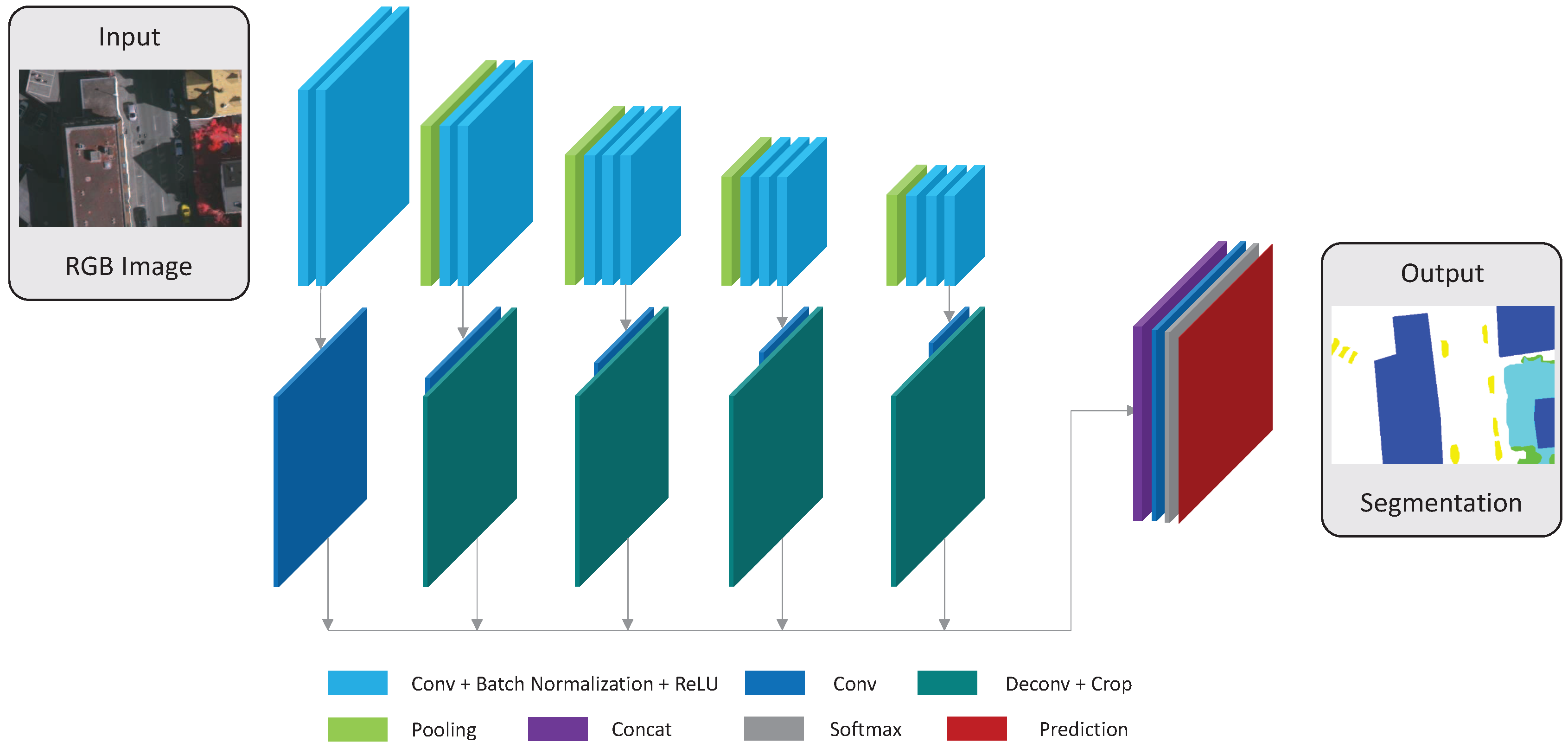
Figure 1. Firstly, we manually label the remote sensing image data into several most cover classes as the training data, which is then used to train our proposed fully convolutional network for semantic segmentation. Secondly, the overlap regions of the left and right images are classified via the trained network independently, and we can obtain the probabilities of each pixel belonging to each of the specified classes. Finally, we define the energy costs based on those classification probabilities, and find the optimal seamlines via graph cuts. In addition, the detected seamlines are evaluated quantitatively based on the defined quality measurements. The main contributions of our proposed approach are summarized as follows:
We design a novel energy function to guide the searching process of optimal seamlines between two input geometrical aligned images. This energy function is defined by using the semantic segmentation results generated by CNN. Thus, we do not need to design the features for optimal seamline detection anymore. The experiments proved that this energy function performs well in avoiding crossing obvious objects because it can distinguish the whole regions of obvious objects from the images.
We fuse the defined energy function into the graph cuts optimization framework to find the optimal seamlines with minimum energy cost, and we propose using the structural similarity (SSIM) index to quantitatively evaluate the qualities of detected seamlines. We test our proposed approach in several groups of images captured from different places and prove that our proposed approach outperforms the state-of-the-art approaches and commercial software.
The remaining part of this paper is organized as follows.
Section 2 introduces the training data and the convolutional neural network for semantic image segmentation used in our paper.
Section 3 introduces the graph cuts energy minimization framework for finding the optimal seamline between two images based on the CNN-based energy costs, and the method for quality assessment of mosaicked images is presented in
Section 4. Experimental results on several groups of challenging orthoimages are presented in
Section 5 followed by the conclusions drawn in
Section 6.
4. Quality Assessment
After the optimal seamline detection, we need to evaluate the quality of detected seamline. The traditional and popularly used method is to count the number of obvious objects crossed by the detected seamline [
4,
5,
21]. However, this method has two disadvantages. One problem is that this measurement is subjective, and different people may give different results. For example, one bad seamline locates on a region with many buildings, and crosses most of them. In this region, many buildings are connected together, and we can not accurately distinguish them one by one. One people may think that this seamline crosses 10 buildings, but another people may think that this seamline only crosses five buildings. Another problem is that this measurement is not fair enough in some cases. For example, one seamline crosses a small building, and the artifacts caused by this seamline are almost invisible. Another seamline crosses a tall building, and the artifacts caused by this seamline are visible. However, according to this measurement, the qualities of these two seamlines are the same, and both of them cross one building. Obviously, this is not reasonable.
Therefore, to evaluate the quality of detected seamline more reasonable, the quality measurement should be objective, fair, and quantitative. In this paper, we propose to apply the structural similarity (SSIM) index [
34] to quantitatively evaluate the qualities of detected seamlines, and compare our method with other state-of-the-art algorithms based on this measurement. In the last several decades, a great deal of effort has gone into the development of quality assessment methods that take advantage of known characteristics of the human visual system (HVS). Wang et al. [
34] proposed a noticeable quality metric named the structural similarity (SSIM) index. In the last several years, the SSIM index has been widely used to evaluate the qualities of color correction [
35] and image mosaicking methods [
36,
37]. Here, we apply the SSIM index to evaluate the quality of the detected seamlines. Let
be the seamline between image pair
and
, and
is the last image mosaicked from
and
based on the seamline
. The quality measurement
is defined as:
where
denotes the SSIM index between two blocks
and
from two images
and
, respectively, and
and
are the image contents at the
j-th local window center at the
j-th point
of
.
is the point number of the seamline
. In addition, the SSIM index is computed independently in each channel of the image in RGB color space, and then the last SSIM index
is computed by averaging them. The SSIM index itself is defined as a combination of luminance, contrast and structure components as:
where
,
, and
, where
and
are the mean luminance values of the windows
a and
b, respectively, and
and
are the standard variances of the windows
a and
b, respectively.
is the covariance between the blocks
a and
b. Here, the small constants
,
and
are included to avoid the divide-by-zero error, and the balancing parameters
,
and
are applied to adjust the relative importance of three components. According to the method presented in [
34], we use the default settings:
,
,
,
for images of dynamic range
and
. The higher the value of
, the higher quality of detected seamline, and the maximum value of
is 1.
5. Experiments and Evaluation
Extensive experiments on three sets of aerial images were conducted to comprehensively evaluate the performance of our proposed CNN-based optimal seamline detection algorithm. The proposed CNN-based semantic image segmentation network was trained and tested with a single NVIDIA TITAN X using the Caffe library. The optimal seamline detection and quality measurement stages were implemented with C++ under Windows and tested in a desktop computer with an Intel Core i7-4770 at 3.4 GHz and the 16 GB RAM memory. The semantic segmentation was implemented in a single NVIDIA TITAN X with the Caffe library. For a 544 × 384 image, our network took about 0.58 seconds to make a pixel-wise segmentation.
The details of used three sets of images are presented in
Table 2. For the third dataset, we only know that those images are captured from a small town of China, but we don’t know the detailed name of this town. The images of each dataset are firstly geometrically aligned into the same coordinate according to the digital terrain model (DTM). However, there always exist geometric misalignments in the regions of obvious objects, e.g., buildings, cars and trees, since those regions are not included in the DTM in general. In contrast, the geometric misalignments in the regions of earth are almost invisible, e.g., roads, grass, water and impervious surface. Because they are planar and do not have altitude with respect to the local earth, they are included in the DTM. This is the main reason why the optimal seamlines should avoid crossing the obvious objects. In our used datasets, the geometric misalignments are only existed in the regions of obvious objects, and there are no geometric misalignments in the regions of planar earth.
The experiments are consisted of three parts. In the first experiment, we verified the effectiveness and superiority of our defined CNN-based energy cost function by using the first set of images. In the second experiment, we also used the first set of images. We compared our proposed approach with the Li et al. algorithm step by step. We proved that our proposed approach outperforms the Li et al. algorithm, and illustrated why our approach is better. In addition, we also compared our proposed approach with Dijkstra’s approach and
OrthoVista. In the last experiment, we conducted our approach on the rest two sets of images captured form different areas to prove that our proposed approach can handle different types of images. In addition, we also compared our proposed approach with the Li et al. algorithm, Dijkstra’s approach and
OrthoVista to prove the superiority of our proposed approach. Noticeably, our proposed approach is semi-automatic, and we need to prepare training data for semantic images segmentation. However, after the model has been trained, we can automatically detect the seamline between the images as Li et al. algorithm, Dijkstra’s approach and
OrthoVista do. For the first dataset, according to the method presented in the
Section 2.2, we prepared 482 training images from the ground truth provided by International Society for Photogrammetry and Remote Sensing (ISPRS). For the second dataset, we prepared 221 training images from the ground truth generated by manually classifying. For the third dataset, due to those images being captured from a non-urban area, and this area is relatively simple, so the training images for this dataset are not prepared, and we directly use the trained model of the second dataset to test this dataset. The prepared training images are relatively small in this work, and the models trained by us may be not common. However, in those experiments, we just want to prove that the key idea of our proposed approach is effective, namely, the results of semantic segmentation generated by CNN can be used to guide the searching process of optimal seamlines and can generate better seamlines than state-of-the-art approaches and software.
5.1. Evaluation on CNN-Based Energy Definition
To verify the effectiveness and superiority of our proposed CNN-based optimal seamline detection algorithm, the images provided by ISPRS [
38] were used to conduct our first experiment, namely, the first dataset. Those images were captured from Vaihingen, Germany, with the size of
. In addition, for some regions, ISPRS also provides the ground truth images, which can be used to train our semantic segmentation network. This dataset is comprised of three strips, and there are no overlap regions between the first strip and the third strip. Therefore, we used the regions with ground truth in the third strip to train our network, and conducted our experiments in the first strip.
In this experiment, to illustrate the effectiveness of our defined CNN-based energy cost, we conducted this experiment between two adjacent images. In Equation (
6), we define the energy cost
of
only based on the classification results of semantic segmentation. In this experiment, we modified
as follows:
where
is the coefficient to balance two energy cost terms,
represents the CNN-based energy cost defined according to Equation (
6), and
denotes the intensity difference cost, which is one of the most widely used energy costs to detect the optimal seamlines for image mosaicking, which is defined as follows:
where
and
denote the intensity values of
in
and
, respectively. Obviously, if we set
, only the CNN-based energy cost term is used to detect the seamlines, and if we set
, only the intensity difference term is applied to detect the seamlines. In this experiment, we modified the value of this balancing coefficient to illustrate the effectiveness of our defined CNN-based energy cost term. Of course, when we set
, our proposed approach is used to detect the seamlines. In
Figure 7, we present the seamline detection results generated by different weight settings as
,
, and
. From the whole seamline detection results and especially the detailed local regions shown in
Figure 7, we observed that the seamlines detected with the use of CNN-based energy terms are much better than the seamline detected without its use. Noticeably, in the enlarged region, the seamline crosses two buildings instead of nearby roads when the weight was set as
, as shown in the left column of
Figure 7, due to the fact that the roofs of these two buildings are smooth as well as nearby roads. However, when we set the weight as
or
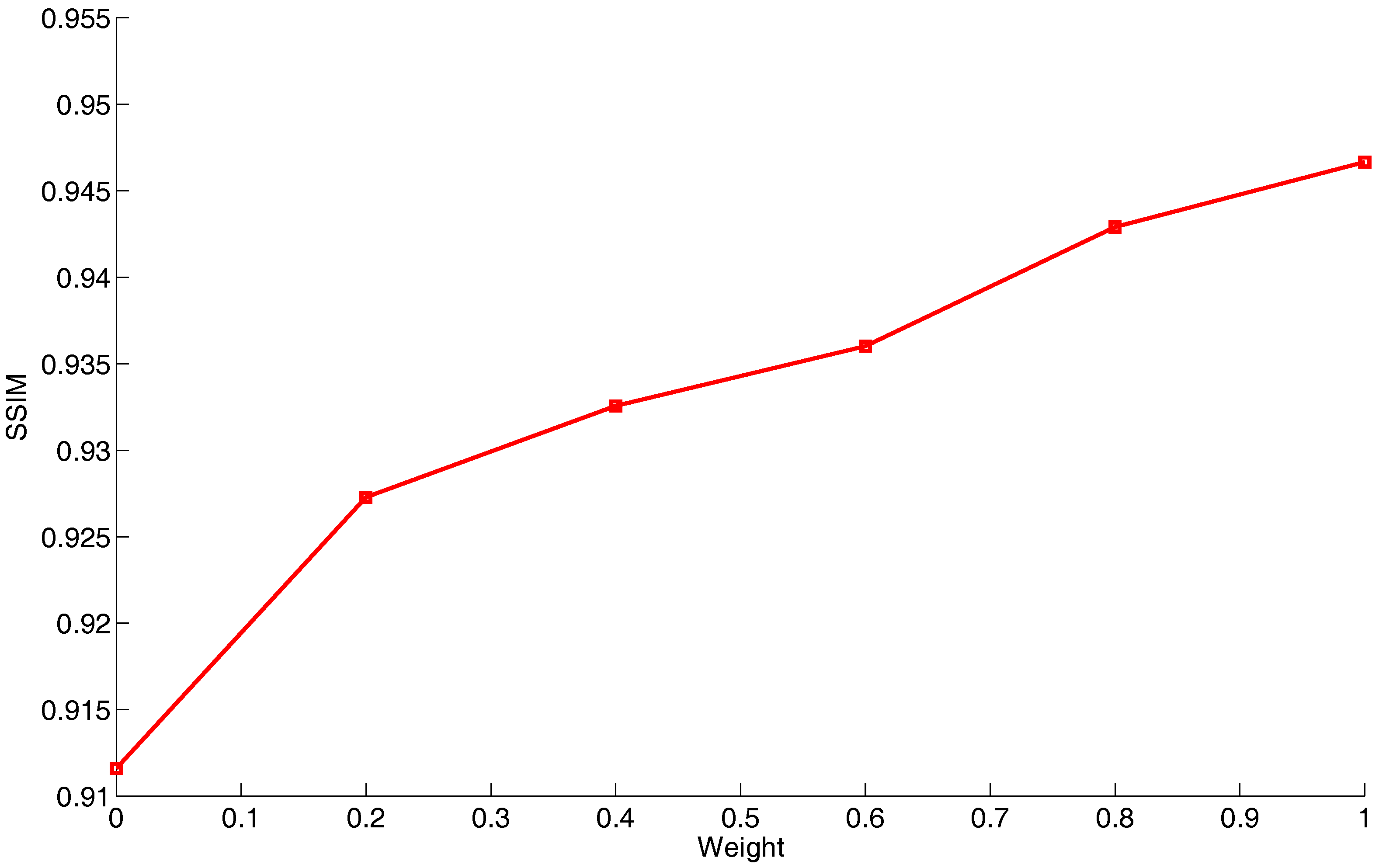
, the seamlines successfully rounded these two buildings as expected and chose to cross nearby roads when the CNN-based energy term was considered. In addition, we also applied the SSIM index to quantitatively measure the qualities of seamlines detected by using different weights, and the quality curve is demonstrated in
Figure 8. From this quality curve, we observed that, as the value of the weight
w increased, the quality of the detected seamline becomes more higher. From this experiment, we convincingly proved that our proposed CNN-based energy cost is effective.
5.2. Comparative Evaluation
In this section, to illustrate the difference between our proposed approach and the state-of-the-art one proposed by Li et al. [
5] more clearly, we conducted the experiment on four adjacent images in the first strip of the Vaihingen dataset. We compared these two approaches to prove the superiority of our proposed approach, and illustrated why our approach outperforms the approach proposed by [
5]. Then, we also give the quality evaluations of the seamlines detected by two approaches by using both the traditional measurement and the quantitative one. In addition, we also compared our proposed approach with Dijkstra’s approach [
39] and
OrthoVista [
40].
OrthoVista is one of the most popularly used commercial software programs.
The seamline detection results generated by Li et al. [
5] and our proposed approach are shown in
Figure 9a,b, respectively. From the whole seamline detection results and especially the detailed local regions, we observed that the seamlines detected by our proposed approach is much better than the seamlines detected by Li et al. [
5]. For example, in three local regions, the seamlines detected by our proposed approach all avoid crossing the buildings, and choose to pass through nearby roads, but the seamlines detected by Li et al. [
5] fail to bypass those obvious objects. To illustrate the reason of this problem more clear, we also presented the corresponding normalized energy cost maps of local enlarged regions in the middle column of
Figure 9a,b. We found that the energy cost maps generated by our approach are more reasonable, which can distinguish the obvious objects from the background more better. In addition, we can find out why the seamlines presented in
Figure 9a cross those buildings. For example, in the first local region, the energy costs of two buildings crossed by the seamlines are very small due to the fact that the roofs of these two buildings are very smooth. However, in the energy cost map generated by our proposed semantic-based approach, the energy costs of those two buildings are so large that the seamlines would avoid crossing them. For the second and third local regions, the similar reason can be used to illustrate why the seamlines detected by Li et al. [
5] fail to bypass those buildings, but our seamlines avoid crossing them.
In addition, we present the seamline detection results generated by Dijkstra’s approach [
39] and
OrthoVista in
Figure 10. We can find that our proposed approach also outperforms Dijkstra’s approach and
OrthoVista. From the local enlarged regions, we observed that the seamlines detected by
OrthoVista cannot avoid crossing obvious objects in some cases. In total, those seamlines cross 21 buildings and 17 cars, but the seamlines detected by our approach only cross two cars. We also observed that the seamlines generated by Dijkstra’s approach can avoid crossing major obvious objects as our approach does. However, they also cross two buildings and two cars.
In addition, to prove the superiority of our proposed approach more powerful, some statistical results of those seamlines generated by four approaches are presented in
Table 3. In the second column, we presented the results of the traditional quality measurement, namely, the numbers of obvious objects passed through, and we found that the seamlines generated by Li et al.’s approach cross 15 buildings and two cars, but the seamlines detected by our proposed approach successfully avoid crossing the buildings, and only cross two cars. In addition, we also evaluated those seamlines by using the quantitative quality measurement defined in
Section 4, which can provide an objective evaluation, as shown in the third column of
Table 3. We found that the score of our seamlines is 0.9585, which is much larger than the scores of the seamlines generated by the rest three approaches. From those two quality measurements, we proved that our proposed optimal seamline detection approach outperforms the state-of-the-art approaches and commercial software.
In the aspect of computational time, as shown in the last column of
Table 3, the approach proposed by Li et al. [
5] took around 65.31 s, consisting of all the elapsed times in energy computation and graph cuts optimization. Our proposed approach took around 80.89 s, not only including energy definition and graph cuts optimization, but also including semantic segmentation (27.19 s). Therefore, the time of seamline detection via graph cuts is just 53.70 s. Dijkstra’s approach took around 96.281 s, which is the longest one. In addition,
OrthoVista took around 50 s.
In conclusion, in this experiment, we firstly made the comparison between two approaches step-by-step: one is our approach, and the other is one of the state-of-the-art approaches [
5]. From the comparative experimental results, we found that our approach can generate more better seamlines than this state-of-the-art approach, and just a little time-consuming than this approach due to the fact that we need to do semantic segmentation in advance. From this visual comparison, we also can find that the energy cost map defined by our proposed CNN-based approach is more reasonable than the energy map defined by [
5], which is the main reason why our approach performs better than [
5]. In addition, we also proved that our proposed approach is better than Dijkstra’s approach and
OrthoVista too.
5.3. More Comparative Experiments
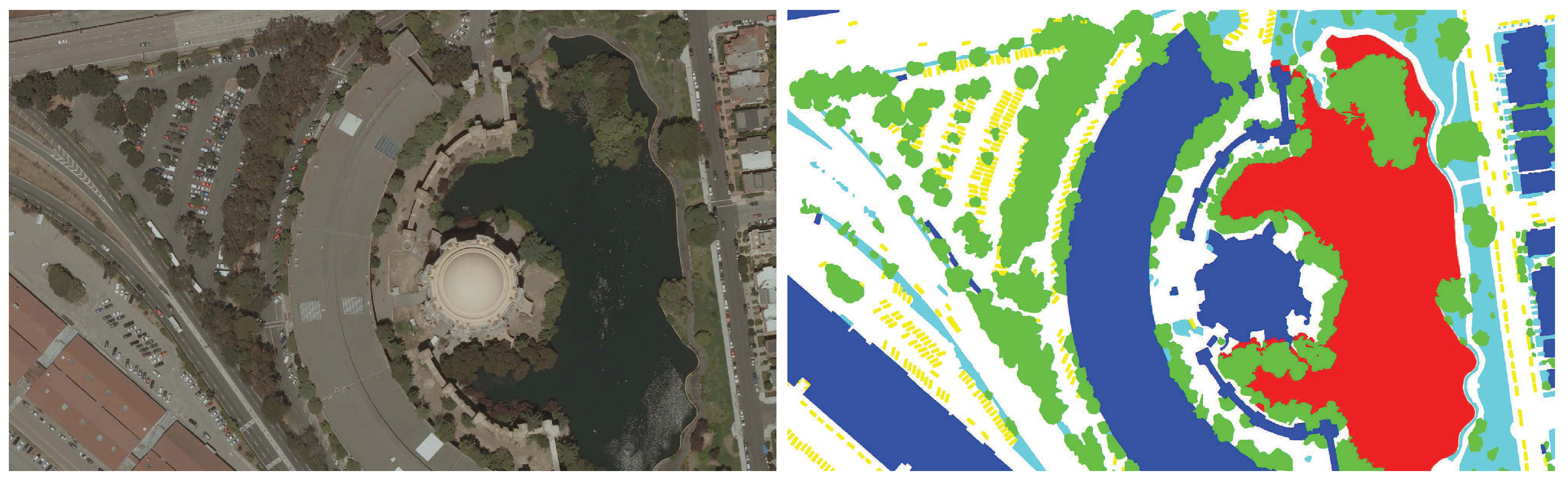
To prove that our proposed approach can handle more types of aerial images, we firstly tested our proposed approach on the images captured from San Francisco, namely, the second dataset. In this dataset, we manually classified those training images into six object classes as a typical example shown in
Figure 11. We selected two groups of images from this dataset to test our proposed approach and compared it with Li et al.’ approach, Dijkstra’s approach [
39] and
OrthoVista. The first group is comprised of three adjacent images, and the second group is comprised of four adjacent images.
Figure 12 shows the seamline detection results of the first group of images. We found that the seamlines detected by Li et al., approach, Dijkstra’s approach and
OrthoVista all cross many buildings, as shown in
Figure 12b–d, especially in the enlarged detailed regions. However, the seamlines detected by our proposed approach successfully avoid crossing those buildings and choose to cross the nearby roads, as shown in
Figure 12a. The seamlines detected by our approach also cross some buildings, but all of them are located on the endpoint regions of the seamlines whose endpoints are formed by the overlapped intersection. Those buildings are also crossed by the seamlines detected by those three approaches and software. The seamline detection results of the second group of images are shown in
Figure 13. Similar conclusions can be drawn. Namely, our proposed approach outperforms the Li et al. approach, Dijkstra’s approach and
OrthoVista, and the seamlines detected by our approach can round most buildings crossed by the seamlines detected by those state-of-the-art approaches and software.
In addition, we also tested our proposed approach on the images captured from one non-urban area. We selected three adjacent images from this dataset to test our proposed approach. Noticeably, we have not generated the ground truth images for this dataset. In addition, we applied the trained model of the second dataset to do semantic segmentation for this non-urban dataset. In addition, we found that our proposed approach also can generate high-quality seamlines for non-urban area, as shown in
Figure 14a. In addition, we also can find that the rest of the three approaches can also detect high-quality seamlines, as shown in
Figure 14b–d, because only a few obvious objects exist in this non-urban area.
At last, we present the detailed statical results of those seamlines generated by four approaches in
Table 4. From
Table 4, we can easily find that the seamlines generated by our approach cross the least obvious objects in all experiments by comparing with Li et al.’s approach, Dijkstra’s approach and
OrthoVista. In addition, the buildings crossed by our approach are located on the endpoint regions. Those buildings are very difficult to bypass. We also applied the SSIM index to evaluate the qualities of detected seamlines. The results of quantitative evaluation also show that our seamlines have highest scores in all experiments, as shown in the third column of
Table 4. In the aspect of computation time, the computational times of four approaches are almost the same, and they are all at the same level, as shown in the last column of
Table 4.