Power Sensitivity Analysis of Multi-Frequency, Multi-Polarized, Multi-Temporal SAR Data for Soil-Vegetation System Variables Characterization

Abstract

The knowledge of spatial and temporal variability of soil water content and others soil-vegetation variables (leaf area index, fractional cover) assumes high importance in crop management. Where and when the cloudiness limits the use of optical and thermal remote sensing techniques, synthetic aperture radar (SAR) imagery has proven to have several advantages (cloud penetration, day/night acquisitions and high spatial resolution). However, measured backscattering is controlled by several factors including SAR configuration (acquisition geometry, frequency and polarization), and target dielectric and geometric properties. Thus, uncertainties arise about the more suitable configuration to be used. With the launch of the ALOS Palsar, Cosmo-Skymed and Sentinel 1 sensors, a dataset of multi-frequency (X, C, L) and multi-polarization (co- and cross-polarizations) images are now available from a virtual constellation; thus, significant issues concerning the retrieval of soil-vegetation variables using SAR are: (i) identifying the more suitable SAR configuration; (ii) understanding the affordability of a multi-frequency approach. In 2006, a vast dataset of both remotely sensed images (SAR and optical/thermal) and in situ data was collected in the framework of the AgriSAR 2006 project funded by ESA and DLR. Flights and sampling have taken place weekly from April to August. In situ data included soil water content, soil roughness, fractional coverage and Leaf Area Index (LAI). SAR airborne data consisted of multi-frequency and multi-polarized SAR images (X, C and L frequencies and HH, HV, VH and VV polarizations). By exploiting this very wide dataset, this paper, explores the capabilities of SAR in describing four of the main soil-vegetation variables (SVV). As a first attempt, backscattering and SVV temporal behaviors are compared (dynamic analysis) and single-channel regressions between backscattering and SVV are analyzed. Remarkably, no significant correlations were found between backscattering and soil roughness (over both bare and vegetated plots), whereas it has been noticed that the contributions of water content of soil underlying the vegetation often did not influence the backscattering (depending on canopy structure and SAR configuration). Most significant regressions were found between backscattering and SVV characterizing the vegetation biomass (fractional cover and LAI). Secondly, the effect of SVV changes on the spatial correlation among SAR channels (accounting for different polarization and/or frequencies) was explored. An inter-channel spatial/temporal correlation analysis is proposed by temporally correlating two-channel spatial correlation and SVV. This novel approach allowed a widening in the number of significant correlations and their strengths by also encompassing the use of SAR data acquired at two different frequencies.

1. Introduction

A positive impact on hydrology as well as on modern agricultural practices can be achieved by monitoring spatial and temporal dynamics of some land surface variables such as soil water content, m_v, and vegetation. Despite the fact that synthetic aperture radar (SAR) allows acquiring in all weather conditions, unassessed strengthenings of the relations among backscattering, σ°, at different frequencies and polarizations and soil-vegetation variables (SVV) are limiting the operational application of SAR. Indeed, SAR configuration controls the wave-target interactions [1,2] and, thus, affects models’ assessments depending on its frequency, polarization and acquisition geometry.

The dependence of bare soils σ°, σ°_S, on both water content and surface roughness was modeled by several authors [1,2,3,4,5]. However, the need of a prior knowledge of the soil surface roughness could reduce the feasibility of SAR techniques [4,6,7,8]. Indeed, reliable roughness measures are hardly achievable: (i) in situ measurements with contact methods (e.g., grid board [9]) are point based and usually not representative at plot scale; (ii) innovative methodologies (e.g., non-contact ultrasonic profiling) are capable of describing wide areas but still economically expensive (i.e., requiring airborne acquisitions).

Over vegetated areas an additional σ° contribution, σ°_V, needs to be taken into account. Several authors, investigated σ°_V by setting up theoretical models [10,11,12] schematizing the vegetation as simple targets of known geometry (such as plates and cylinders). Simple empirical models, avoiding a rigorous mathematical and geometrical simulation of the canopy, are often based on ratios of bands acquired at different polarizations [13,14,15,16]. The need of a priori characterization of vegetation structure (hardly achievable through in situ campaigns) reduces the operational use of SAR in agriculture.

In recent years, several researches focused on m_v quantification (over both bare, B, and vegetated, V, soils) explored different SAR configurations and approaches by testing (

Table 1. m_v retrieval using SAR: overview table on previous studies. Accuracy is reported in terms of: determination coefficient, r²; correlation, r; root mean square error, rmse; average absolute deviation, aad; and mean square error, mse. For detailed notes please refer to Appendix A.

			SAR configuration			Approach
Reference	Sensor	Bare or Vegetated	Freq.	Polarizations	Angles	Multi Freq.	Mult Pol.	Multi Angles	Temporal Index	Passive Data	In Situ Data	σ° Model	Statistical	Empirical Fitting	Polarimetric	Ratio Method	Performance Index	Notes
[19]	TSX	B	X	HH	Multi						•	IEM		•			r2 = 0.8; rmse = 1.32 (a) and 1.14 (b)	i
[20]	TSX, CSK	B	X	HH VV	Dual		•				•	IEM Dubois		•			r2 = 0.64 (a); 0.07 (b); 0.77 (c); 0.06 (d)	ii
[21]	CSK	B V	X	HH HV VV	Single		•				•	Oh RTM						*
[22]	ERS-2	B	C	VV	Single						•	IEM	•				rmse ~ 6%
[23]	ERS-2	B V	C	VV	Single				•	•	•			•		•	r2 ~ 0.93
[24]	Radarsat-1	B V	C	HH	Single					•	•	IEM WC		•			rmse ~ 0.1–0.25
[25]	Radarsat-1	B V	C	HH	Single					•	•		•				r ~ 0.7
[26]	ERS-2	B V	C	VV	Single						•		•				r2 ~ 0.9
[27]	ASAR	B V	C	HH	Single				•				•				r ~ 0.7
[28]	Radarsat-1	B	C	HH	Dual			•			•			•			r2 ~ 0.93
[29]	Radarsat-1	B V	C	HH	Dual			•			•			•			r2 = 0.79 (a); 0.93 (b)	iii
[30]	ASAR	B V	C	HH VV	Single		•				•	IEM GO	•	•	•		rmse 1.5–8.5%
[31]	ASAR	B V	C	VV VH	Single		•			•	•	MIMICS WC					aad ~ 0.051
[32]	ASAR	B V	C	HH VV	Dual		•	•			•	IEM		•				*
[33]	Radarsat-2	B V	C	HH VV HV	Single		•				•	WC		•			r2 = 0.61 (a); r2 = 0.73 (b)	iv
[34]	Radarsat-2	B V	C	HH HV VV	Single		•		•		•			•	•		rmse < 0.07
[35]	ASAR	B V	C	HH HV VH VV	Single		•			•	•		•	•			r2 ~ 0.87 rmse = 2.83%	v
[36]	PALSAR	B V	L	HH HV	Single		•				•			•	•		rmse 4–14%
[37]	SIR-C	B V	L	HH HV VV	Single		•					Dubois						*
[38]	PALSAR	B V	L	HH HV VV	Single		•			•		Dubois			•		rmse ~ 0.041
[39]	PALSAR	B V	L	HH HV VV	Single		•				•	IEM OH Dubois					rmse 4–14%
[40]	E-SAR	B V	L	HH HV VV	Single		•					Oh Dubois					r2 ~ 0.85 (a); r2 ~ 0.4 (b)	vi
[41]	E-SAR	B V	L	HH HV VH VV	Single		•									•	rmse ~ 4.5%
[42]	Proximity sensing	B	C S	HH VV	Single	•	•			•	•	IEM	•				MRE ~ 12–20% (a) ~ 9–36% (b)	vii
[43]	AirSAR	B V	C L	HH VV	Single		•			•	•	IEM	•				r = 0.68 (a); 0.60 (b)	viii
[44]	Proximity sensing	B V	C L	HH VV	Dual						•	IEM WC				•	0.72 ≤ r ≤ 0.79 (a); 0.08 ≤ r ≤ 0.80 (b)	ix
[45]	SIR-C, X-SAR	B V	C L	HH HV VV	Single						•	IEM WC		•			r ~ 0.83 (a), ~ 0.95 (b)	x
[46]	SIR-C	B V	C L	HH HV VV	Single		•				•			•			r2 = 0.743 (a); r2 = 0.840 (b)	xi
[47]	TSX, ASAR, PALSAR	B	X C L	HH VV	Multi						•			•		•		*

): (i) the use of temporal indices; (ii) the integration of passive microwaves and in situ data; (iii) different σ° models; (iv) the conjunct use of complex statistical models (such as Bayesian approach); (v) empirical fitting and ratio methods (refer to the Appendix A for symbols and acronyms). There were several approaches: empirical, EA; semi-empirical, SEA; theoretical, TA; polarimetric, PA; statistical SA, these latter employing Neural Networks, polarimetric indices or, channels ratio. Some authors calibrated σ° models such as: IEM (Integral Equation Model [4]), WC (Water-Cloud model [17]); GO (Geometrical Optics [4]); Dubois [1]; Oh [2,3]; RTM (Radiative Transfer Model); MIMICS (Michigan Microwave Canopy Scattering model [18]). Several authors separated soil and vegetation contributions by exploiting more than two polarizations (single frequency), by parameterizing the WC through in situ data.

All these approaches are usually based on regression analyses among σ° and SVV (i.e., soil roughness, water content, fractional cover and leaf area index). It is well known that SAR configuration (acquisition geometry, frequency and polarization) plays a fundamental role in the σ° vs. SVV relationship; thus it is expected that modifications of some SVV change also the spatial correlation between data acquired with different configurations.

Based on this evidence, this paper firstly aims to quantify the strength of the relation among σ° and four SVV (dynamic and single regression analyses) over bare and vegetated soils, over a wide range of cultivars and for different SAR configurations. These first sections are tailored to address: (i) frequencies and polarizations showing the highest sensitivities of σ° to the dynamic of the selected SVV; (ii) SAR configurations suitable to estimate SVV changes; (iii) frequencies and polarizations carrying redundant information.

Afterwards, the paper shows the effect of SVV changes on the spatial correlation among SAR channels and proposes, as novel approach, the use of temporal regressions of two-channel spatial correlations vs. SVV to explore any improvement achievable compared to the single-channel regression approach.

2. Study Area

In situ and SAR data have been collected on the 24 km² DEMMIN (Durable Environmental Multidisciplinary Monitoring Information Network) test site (Figure 1). The site is hosted by a farm located in Mecklenburg-Western Pomerania in North-Eastern Germany (Görmin farm, 53°59′33′′N–13°16′40′′E, EPSG 4326).

Nine crops were monitored over one or more plots (the plot identifier is reported between brackets): wheat (IDs 230 and 250), rape (IDs 101 and 140), barley (IDs 440 and 450), maize (ID 222) and sugar beet (IDs 102, 460). Sowing and harvesting dates are reported in

Table 2. Sowing and harvesting dates for main crops during the investigation period; plots IDs are reported within brackets.

Crop (ID)	Sowing Dates	Harvest Dates
Wheat (230, 250)	5 September–31 October	15–31 August
Barley (440, 450)	12–25 September	15–25 July
Rape (101, 140)	8 August–5 September	28 July–10 August
Maize (222)	20 April–5 May	25 September–10 October
Sugar beet (102, 460)	25 March–20 April	25 September–31 October

. Noticeable, these cultivars are characterized by different vegetation architecture. Main soil textures in the Görrmin area were loamy sand and sandy loam. Within this area, the 9 monitored plots are characterized by loamy sand texture. In particular, the soil texture of plots 222, 450 and 140 is predominantly loamy sand; plot 460 is characterized by loamy sand and slightly loamy sand soil; whereas the other plots are characterized by both loamy sand and strong loamy sand soils.

3. Materials

Data have been collected between April and August 2006 in the framework of the AgriSAR 2006 project (funded by the European Space Agency, ESA) primarily planned to address programmatic needs of Sentinel-1 two-satellite constellation. AgriSAR 2006 campaign was specifically tailored to investigate σ° dynamic throughout the crop-growing season. The dataset includes weekly in situ measures and airborne SAR and optical images.

In particular, in situ data have been collected by the Leibnitz-Zentrum für Agrarlandschaftsforschung (ZALF) and the University of Kiel (Christian-Albrechts-Universität, Department of Geography) almost simultaneously to SAR and optical flights. Measurements of m_v (at 0–5 and 5–10 cm below ground level, b.g.l.), soil surface roughness, fractional cover, F_v, and LAI were acquired by the research teams along 16 campaigns. In situ LAI and m_v were measured using a LICOR-2000 and a portable IMKO TRIME-FM TDR respectively, root mean square of roughness height, h’, was characterized with a laser profiler and a Rollei d7 metric digital stereoscopic system [48]. 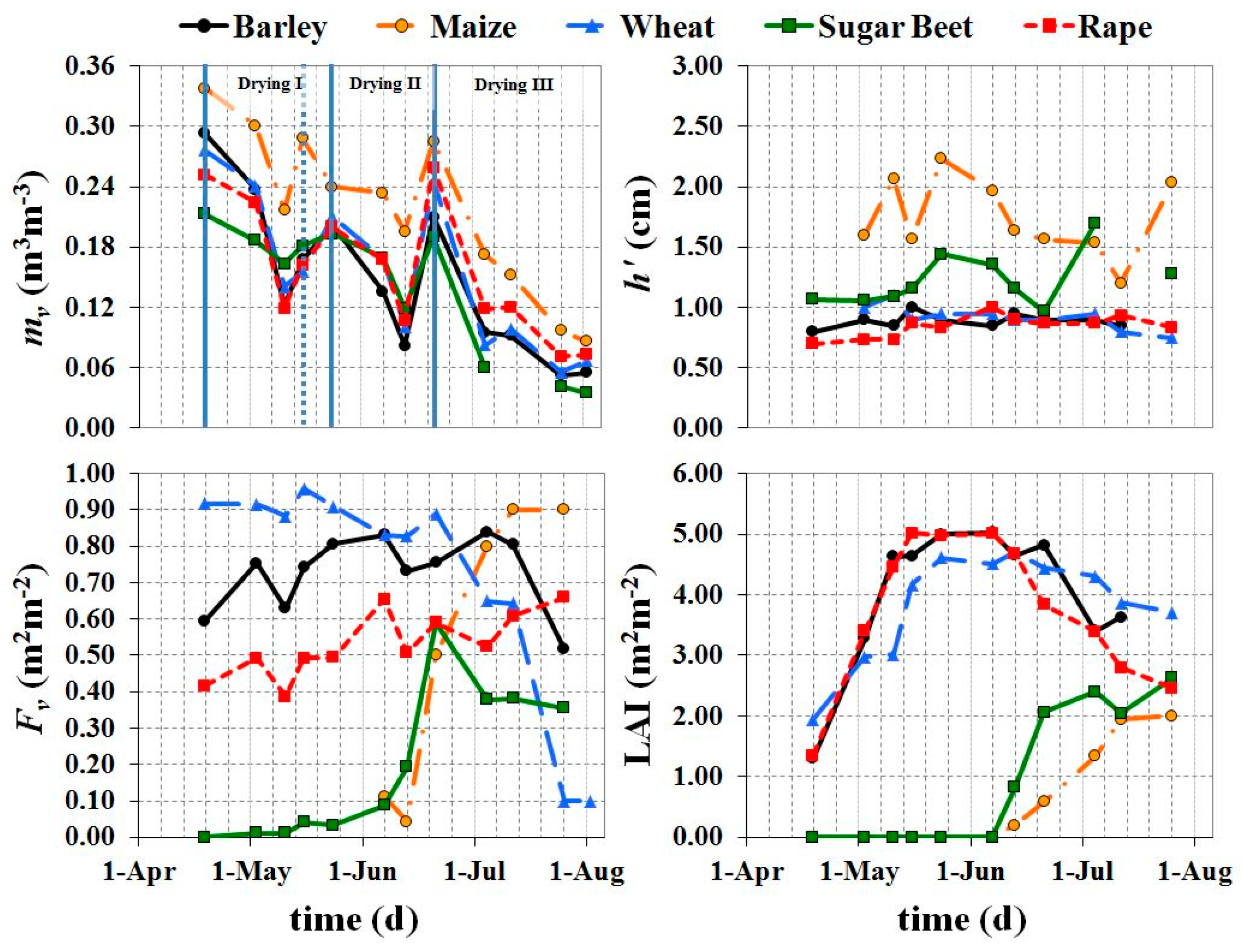A TDR probe (IMKO TRIME-ES, theoretical accuracy of ±0.01–±0.03 m³m⁻³) was installed from the Ludwig-Maximilians Universitat München (LMU) and the University of Kiel on fields 102 (sugar beet) and 250 (wheat) providing measures of m_v at 5 depths (5, 9, 15, 25 and 47 cm b.g.l.) with a temporal resolution of half an hour. Approximately 1150 measurements were executed, equally spread among plots and acquisition times. In particular, ~24 measurements were carried out for each in situ campaign; for each plot, always the same locations were taken into account; ~36 measurements per plot was carried out during the whole in situ campaign for each SVV. The sugar beet field was completely bare from the first campaign in 19 April until 11 May (F_v reached 10% in 7 June); maize field was completely bare until the end of May. Other fields were vegetated until July; rape and barley were harvested during the airborne SAR campaign (Figure 2).

During the investigation three drying periods occurred; m_v varies in the range [0.34–0.06 m³m⁻³] with some differences among fields. In maize crop, m_v was higher than in other fields, probably only due to the root-zone water dynamics of this cultivar (the soil texture was similar to the other monitored plots); m_v in barley, wheat, sugar beet and rape fields behaves similarly during the whole period. Finally, temporal trends of h’ over barley, rape and wheat fields are quite similar; whereas h’ exhibits higher values and different temporal behavior over maize and sugar beet (Figure 3).

The SAR dataset includes 120 images acquired in X, C and L bands (central wavelengths: 2, 5, and 21 cm respectively) in dual polarization (HH and VV for X band) and in quad-polarization (HH, VV, VH and HV for C and L bands). Flights were weekly carried out from the 9th of April to the 2nd of August by an airborne E-SAR (Experimental SAR), operated by the German Aerospace Center (Deutsches Zentrum für Luft- und Raumfahrt—DLR). The E-SAR sensor was on board a Do228 aircraft; although a total of 16 radar flights were executed during the AgriSAR 2006 campaign, the 12 performed in the E-W direction were considered in this research. The deployment of corner reflectors of 20 cm × 20 cm during one of the in situ campaigns allowed obtaining multi-look, geo-coded and calibrated σ° products at a raw spatial resolution, R_S, of 2 m.

During the airborne SAR acquisitions, high variability of m_v, F_v and LAI occurred over both bare and vegetated soils, including different cultivars. Thus, AgriSAR 2006 dataset allows investigating (i) how σ° is controlled by changes of SVV and, (ii) how SAR configuration (acquisition geometry, frequency and polarization) rules the relationships between σ° and SVV.

4. Methods

For bare soils, h’ and m_v were included in the analysis; whereas, over vegetation the behavior of σ° was assessed under a wide range of m_v for different cultivars with varying h’, LAI, and F_v.

Different data analyses were carried out: (i) dynamic analysis of both σ° and SVV over all fields and over a selected plot; (ii) single regressions between σ° and SVV; (iii) single regression analysis between inter-channel spatial correlation and SVV at plot scale.

4.1. Data Aggregation

As a preliminary step, images were spatially averaged to reduce the speckle. Although several filters have been proposed to this aim [49,50,51,52,53] a simple spatial averaging technique was preferred. Indeed, the spatial aggregation limits inaccuracies in the comparison between σ° and in situ data due to georeferencing errors and GPS positioning uncertainties, respectively. The more appropriated R_S was selected based on the values assumed by the Moran index I_M [54] and the speckle index, I_S [55].

4.2. Dynamic Analyses

This section is focused on the investigation of σ° temporal behavior. In the first subsection, σ° dynamic was evaluated at different frequencies and polarizations during the whole period for varying SVV. Subsequently, the σ° temporal dynamic is qualitatively compared to SVV changes for two selected plots.

4.2.1. Dynamic Analysis: All Plots

Firstly, it was analyzed the σ° dynamic at different frequencies and polarizations (hereinafter referred to as channel) during the whole period, in which variations of m_v, h’, LAI and F_v occurred.

For each plot the σ° range of variability, ∆σ°_plot, was evaluated. Then, for each channel, metrics such us the average of ∆σ°_plot, ∆σ°_avg, and standard deviation of ∆σ°_plot, ∆σ°_stdev, were quantified. The higher ∆σ°_avg the more the channel sensitivity to SVV changes, the higher ∆σ°_stdev the more heterogeneity among plots. The corresponding metrics computed on ∆h’, ∆m_v, ∆F_v and ∆LAI are discussed within the corresponding result Section 5.2.1. Backscattering varies with the dielectric and geometric properties of the soil-vegetation system. In particular, dielectric properties are ruled by m_v (for the soil layer) and canopy water content; whereas, the geometric properties are ruled by h’ (for the soil layer) and by both vegetation biomass (F_v and LAI) and canopy structure (this latter has not been parameterized during the campaign).

4.2.2. Dynamic Analysis: Two Selected Plots

This analysis was performed for two selected plots: the first displayed soil drying over both bare and vegetated stages (plot 460, sugar beet); the second (plot 450, barley) was fully vegetated from April to July, then, it was harvested and thus, was bare during the last two SAR acquisitions. The analysis allows understanding how σ° behaves with m_v over changing SVV. Outcomes over the first plot allow evaluating which channels have the higher sensitivity to vegetation growth. The dynamic of σ° over the second selected plot allows evaluating which channels have higher sensitivity to m_v when the soil is beneath a vegetation canopy.

4.3. Temporal Single Regression Analysis

Because of the speckle noise affecting SAR images at raw resolution, operational applications are to be preferred using spatially aggregated images by averaging both in situ measures and the corresponding aggregated σ° values. Thus, temporal single regressions among σ° and SVV were analyzed to address the application of semi-empirical models over bare and vegetated plots; m_v and h’ were analyzed over bare soil, whereas, F_v and LAI were also explored over vegetated areas.

4.4. Inter-Channel Spatial/Temporal Correlation

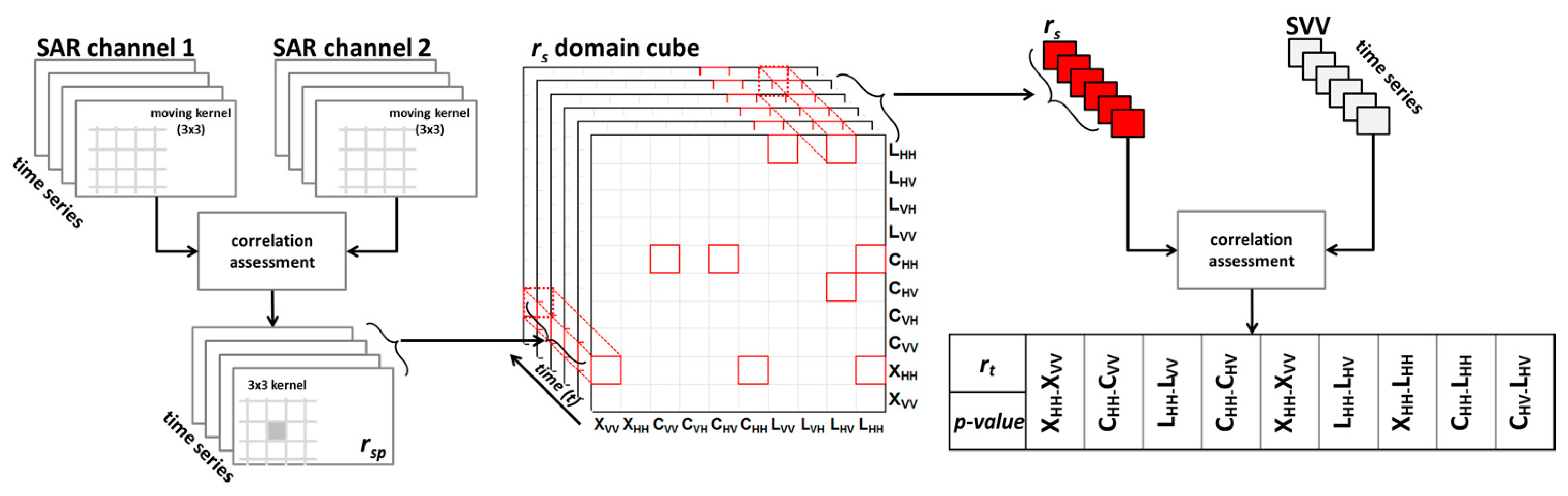
A target is expected exhibiting different dielectric and geometrical properties if sensed with distinct SAR configurations. Thus, a pixel based spatial correlation image, r_sp, was evaluated for each plot using a moving kernel. A plot representative spatial correlation, r_s, was obtained by averaging values of r_sp co-localized to in situ measures. The calculation is extended to all available channel pairs and acquisition times, thus, generating an r_s domain cube. Because the moving kernel is applied on spatially aggregated images, a minimum kernel size (3 × 3) was chosen to avoid exceeding plots’ dimensions. A total of 45 channel pairs were analyzed; the r_s cube was evaluated for each of the 9 monitored plots.

The dynamic between r_s and SVV was analyzed via a single regression over 9 selected pairs of channels. The analysis determines in what extent r_s could be useful to assess SVV changes; thus, results are shown in terms of plot temporal correlation coefficients, r_t, out-coming from the r_s vs. SVV regressions (Figure 4).

Finally, errors associated to best regressions (both σ° vs. SVV and r_s vs. SVV) are computed in terms of mean absolute errors (MAE).

5. Results

5.1. Data Aggregation

The I_M first derivative suggests almost the same aggregation level for co-polarized, σ°_pp, and cross-polarized, σ°_pq, channels. Whereas, R_S suggested by the I_S analysis are higher at σ°_pp than those at σ°_pq with highest values shown by X_HH, and lowest value exhibited by L_HV. The R_S equal to 20 m, as suggested by I_S analysis, although even coarser then the value suggested by I_M analysis (≈10 m), remains suitable to characterize the average plot size (~280 m).

5.2. Dynamic Analyses

5.2.1. Dynamic Analysis: All Plots

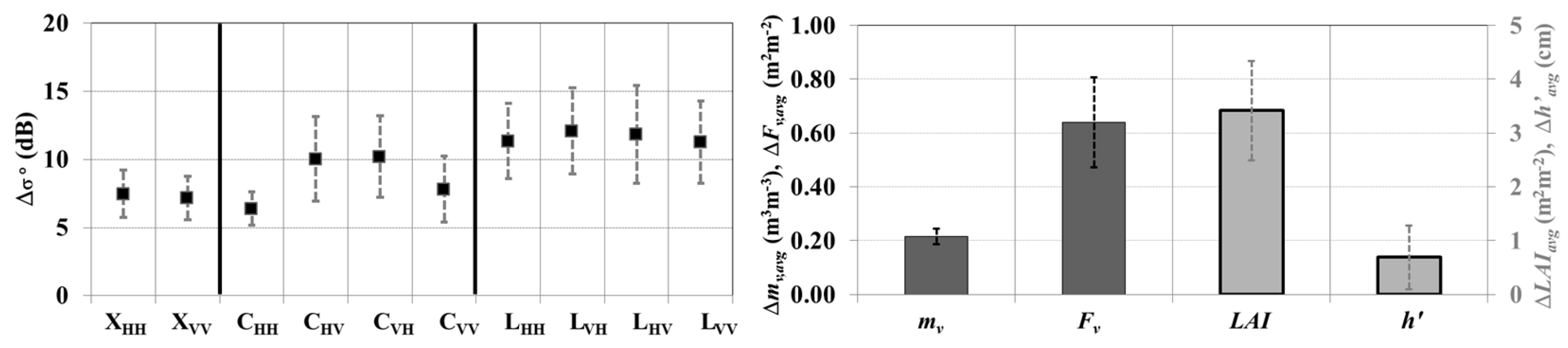
L bands show the highest ∆σ°_avg values especially at cross-polarized channels. This suggests that σ° at L band could be highly influenced by SVV dynamics. The higher values of ∆σ°_stdev also highlight that σ° is influenced by SVV depending on the cultivar; contrarily, lower ∆σ°_stdev exhibited by X_pp and C_pp bands implies a weaker influence of the cultivar (Figure 5, left panel).

Numerically, the highest dynamic (∆σ°_avg = 12 dB and ∆σ°_stdev = 3.2 dB) is exhibited by L_HV whereas the lowest is observed for C_HH (∆σ°_avg = 6.4 dB and ∆σ°_stdev = 1.2 dB). SVV variations are responsible of changes of dielectric and geometric properties of the soil-vegetation system (Figure 5, right panel). The variations of m_v was on average ≈0.2 m³m⁻³ (with standard deviation ∆m_v,stdev = 0.03 m³m⁻³), whereas ∆F_v,avg = 0.64 (∆F_v,stdev = 0.17), ∆LAI_avg = 3.42 m³m⁻² (∆LAI_stdev = 0.92 m³m⁻²) and ∆h’_avg = 0.7 cm (∆h’_stdev = 0.6 cm). To describe the differences observed in distinct channels as resulting from SVV changes, the dynamic analysis was applied to bare plots (plots 460 and 222).

Bare soils exhibited lower ∆σ°_avg (particularly at L frequency) compared with those observable during the whole investigation period (where both bare and vegetated conditions occurred).

Over vegetation, the highest ∆σ°_avg at L frequency was found for sugar beet, which is characterized by a broad-leaf structure; whereas X channels exhibited highest ∆σ°_avg for barley and wheat; finally C channels exhibited highest ∆σ°_avg for rape, barley and wheat. These differences confirm that vegetation structure determines the geometric properties of the target.

5.2.2. Dynamic Analysis: Two Selected Plots

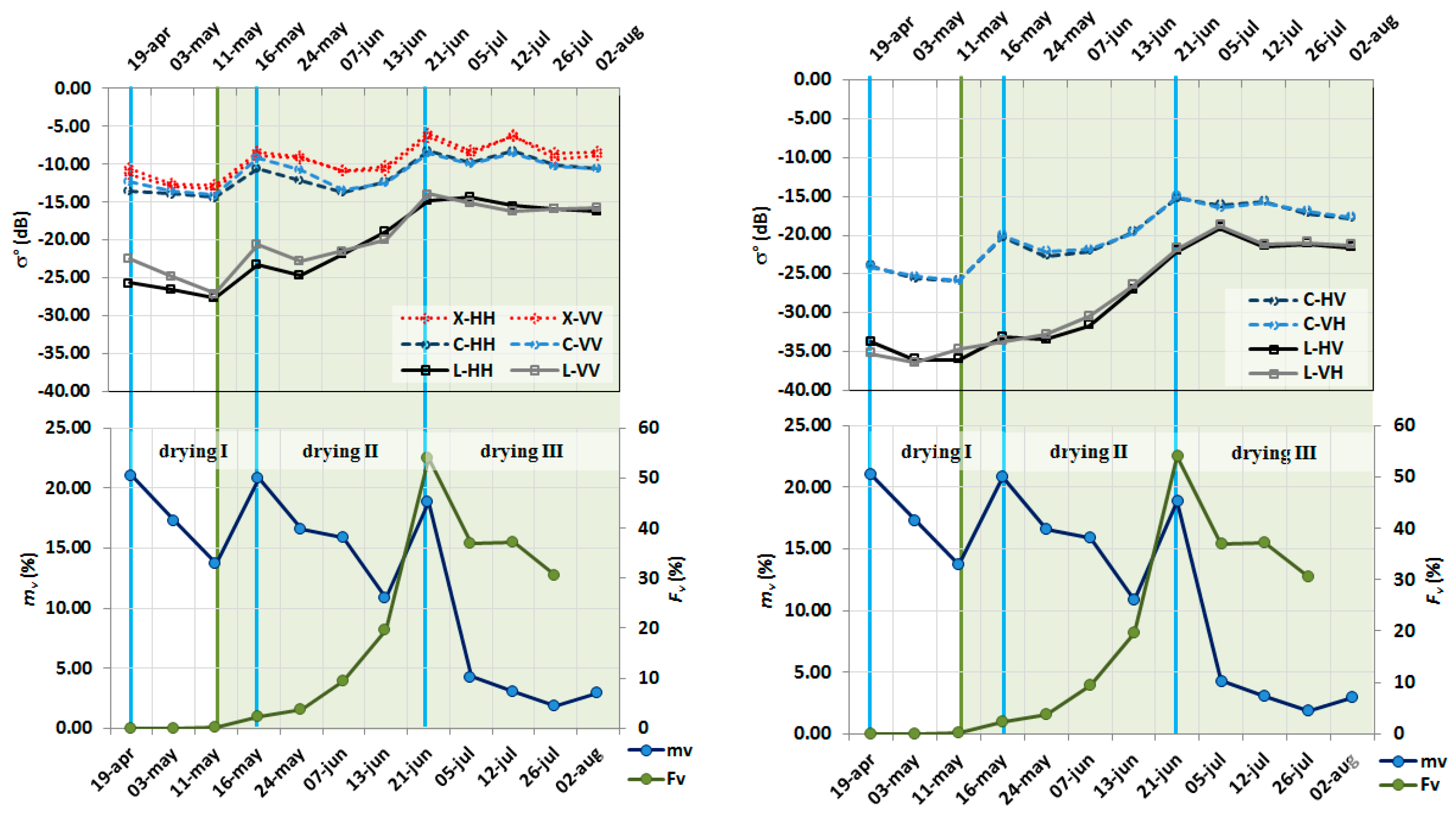
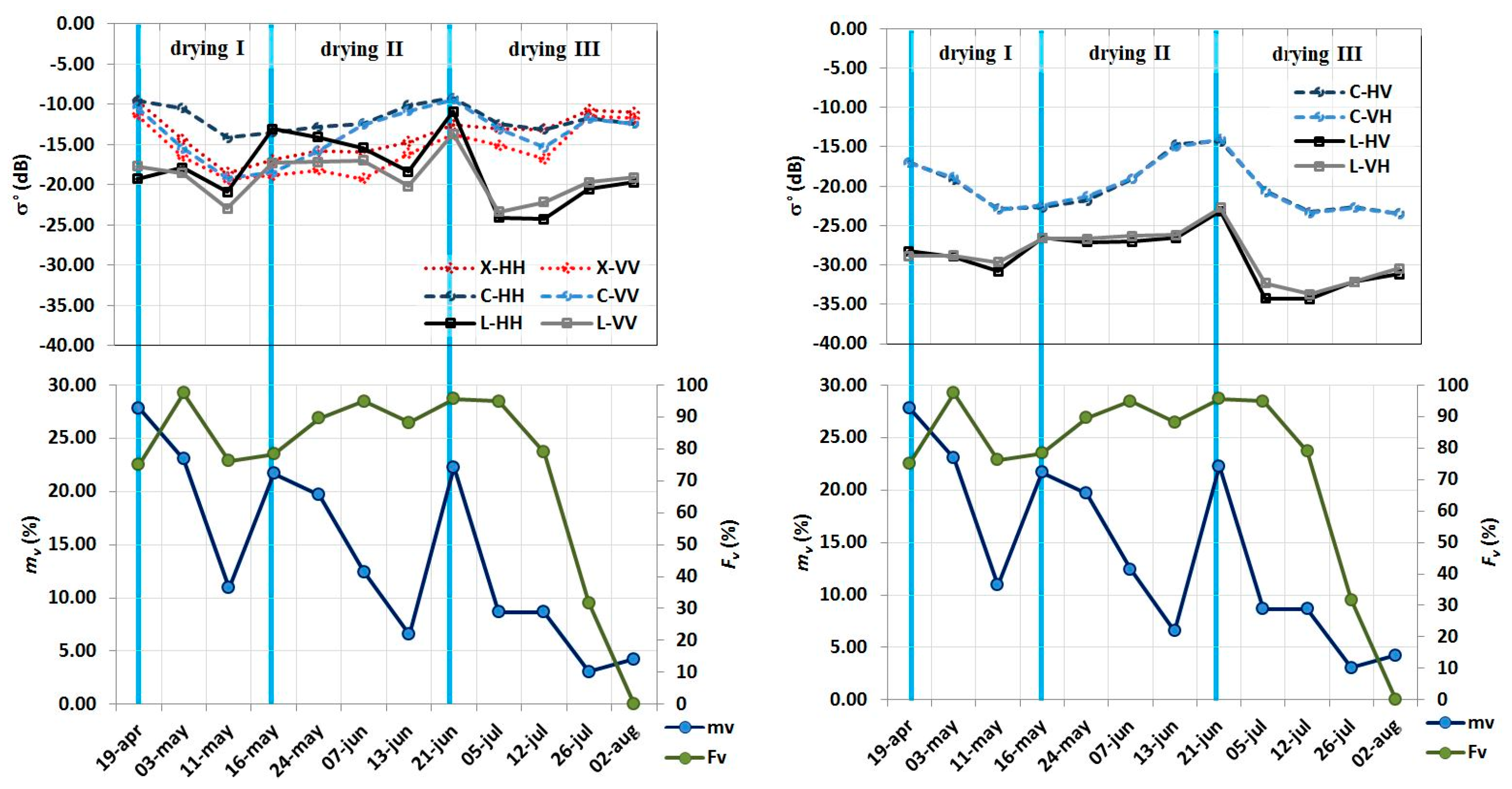
The dynamic analysis for the plot 460 revealed that σ°_pq exhibits lower values if compared to σ°_pp at the same frequency. Peaks of σ° occur contextually to m_v maxima (Figure 6, drying period I). As expected, σ° over bare soil (until the 11th of May) is linearly correlated to m_v at all channels. With the growth of the vegetation two different σ° behaviors were observed: σ° at L (both σ°_pp and σ°_pq) and C (σ°_pq only) is highly related to m_v until F_v is lower than 3%. Whereas σ°_pp at X and C frequencies were still influenced by m_v dynamics until F_v is lower than 10% (Figure 6, drying period II).

The difference between σ° collected on 19 April and 21 June is prevalently a measure of the vegetation biomass change; indeed, σ° at these two times were acquired at almost similar h’ and m_v conditions. It is noticeable that high positive σ° differences occur at cross-polarization, thus confirming outcomes of several other studies (e.g., [56]).

The dynamic analysis for the plot 450 (barley) revealed that all σ° at L frequency behave similarly to m_v; σ° at C and X frequencies is less influenced by m_v dynamics, thus highlighting that σ° at L frequency partially penetrated the canopy cover (Figure 7, drying periods I to III). In particular, σ°_L,HH vs. m_v was characterized by r² ≈ 0.27, whereas lower r² characterized regressions with other frequencies (r² ~ 10⁻⁴ for both σ°_C,HH and σ°_X,HH vs. m_v). Conversely, L frequencies were not linked to F_v (r² ~ 0.05); whereas, slightly higher r² (~0.15) characterized σ° vs. F_v at C frequency; finally, X channels were completely uncorrelated with F_v (r² ~ 10⁻⁶).

5.3. Temporal Single Regression Analysis

A first analysis was applied on bare soils having different h’. Single regressions among σ° vs. m_v and h’ were calculated separately for two plots (IDs 460 and 222) that remained bare until the first week of May; h’ values ranged between 0.93–1.77 and 1.42–2.05 cm, for plots 460 and 222 respectively (

Table 3. σ° vs. m_v over bare soil for plot 460 (left panel) and plot 222 (right panel). Significant and very strong correlations (i.e., p-value less than 0.05 and r > 0.8) are highlighted in dark-grey with values in bold: quasi-significant correlations (i.e., 0.05 < p-value < 0.1) are underlined.

σ° vs. mv	r	m	q	p-Value	σ° vs. mv	r	m	q	p-Value
XHH	0.79	1.00	−30.12	6.0 × 10−2	XHH	0.62	0.46	−22.89	2.6 × 10−1
XVV	0.83	1.01	−29.98	4.0 × 10−2	XVV	0.61	0.43	−22.40	2.8 × 10−1
CHH	0.60	0.59	−24.29	2.1 × 10−1	CHH	0.83	0.56	−25.79	8.0 × 10−2
CHV	0.63	0.94	−41.30	1.8 × 10−1	CHV	0.71	0.54	−34.42	1.8 × 10−1
CVV	0.71	0.91	−29.61	1.2 × 10−1	CVV	0.77	0.52	−24.14	1.3 × 10−1
LHH	0.46	0.67	−37.84	3.6 × 10−1	LHH	0.99	1.12	−51.45	6.2 × 10−4
LHV	0.65	0.78	−48.88	1.6 × 10−1	LHV	0.99	0.98	−54.99	2.8 × 10−4
LVV	0.74	1.20	−46.16	9.6 × 10−2	LVV	0.99	1.34	−56.59	4.2 × 10−4

). Correlations, r, are classified according to Evans, 1996 [57]; slopes, m, and intercepts, q, values could be employed to apply empirical or semi-empirical models (e.g., the WC model [17]). No significant correlations characterized the σ° vs. h’ regressions (not shown).

Noticeable, very strong and significant σ° vs. m_v correlations were found for X_VV (plot 460), C_HH and for L frequencies (plot 222); while, strong (i.e., 0.6 < r < 0.8) correlations were not significant (p-value > 0.1).

For plot 460 two quasi-significant correlations were found at X_HH and L_VV, respectively. The highest σ° vs. m_v correlations were found at L frequency (≈0.99).

A second analysis was applied on vegetated plots (

Table 4. r of σ° vs. m_v for plots covered by vegetation. Quasi-significant correlations (i.e., 0.05 < p-value < 0.1) are outlined; significant correlations (i.e., p-value < 0.05) are highlighted in light-grey; strong and significant correlations are also bolded; very weak correlations (r < 0.19) are not reported.

σ° vs. mv	Sugar		Barley		Maize		Rape		Wheat
	r	p-Value	r	p-Value	r	p-Value	r	p-Value	r	p-Value
XHH	0.32	5.9 × 10−1	-	-	0.54	2.7 × 10−1	0.37	8.4 × 10−2	0.25	2.6 × 10−1
XVV	0.34	5.7 × 10−1	-	-	0.55	2.6 × 10−1	0.46	2.7 × 10−2	-	-
CHH	0.23	7.2 × 10−1	0.38	7.4 × 10−2	0.39	4.4 × 10−1	0.19	4.0 × 10−1	0.32	1.3 × 10−1
CHV	-	-	0.35	9.8 × 10−2	-	-	-	-	0.46	2.6 × 10−2
CVV	-	-	-	-	0.59	2.1 × 10−1	0.27	2.1 × 10−1	-	-
LHH	-	-	0.46	2.8 × 10−2	0.75	8.4 × 10−2	0.46	2.6 × 10−2	0.51	1.3 × 10−2
LHV	-0.52	3.7 × 10−1	0.52	1.2 × 10−2	0.72	1.1 × 10−1	0.39	6.6 × 10−2	0.66	6.6 × 10−4
LVV	-	-	0.53	9.4 × 10−3	0.28	5.9 × 10−1	0.40	5.0 × 10−2	0.55	7.0 × 10−3

). Noticeable, σ° vs. h’ returned no significant correlations (not shown). Regarding σ° vs. m_v, only moderate to strong correlations (0.4 < r < 0.8) were found as the capability of the signal of perceiving the m_v is attenuated by the vegetation cover. Most significant σ° vs. m_v correlations were found at L frequency, highlighting that the longer the wave the better the canopy penetration. A limited number of quasi- and significant correlations were found at C and X frequencies even if these were characterized by lower r values.

Several very strong and significant σ° vs. F_v correlations (

Table 5. r of σ° vs. F_v for plots covered by vegetation. Quasi-significant correlations are outlined; significant correlations are highlighted in light-grey; very strong and significant correlations are highlighted in dark-gray with values in bold; very weak correlations are not reported.

σ° vs. Fv	Sugar		Barley		Maize		Rape		Wheat
	r	p-Value	r	p-Value	r	p-Value	r	p-Value	r	p-Value
XHH	0.90	3.8 × 10−2	0.19	3.9 × 10−1	0.30	6.3 × 10−1	0.39	7.2 × 10−2	-	-
XVV	0.85	7.0 × 10−2	0.27	2.2 × 10−1	0.22	7.3 × 10−1	0.32	1.5 × 10−1	-	-
CHH	0.87	5.0 × 10−2	-	-	0.52	3.7 × 10−1	0.33	1.3 × 10−1	-	-
CHV	0.90	3.7 × 10−2	-	-	0.81	9.6 × 10−2	-	-	-	-
CVV	0.87	5.8 × 10−2	-	-	0.21	7.3 × 10−1	0.37	9.3 × 10−2	0.29	1.9 × 10−1
LHH	0.79	1.1 × 10−1	-	-	0.87	5.0 × 10−2	0.39	7.6 × 10−2	0.28	2.1 × 10−1
LHV	0.53	3.6 × 10−1	-	-	0.95	1.2 × 10−2	0.48	2.3 × 10−2	0.33	1.3 × 10−1
LVV	0.90	3.9 × 10−2	-	-	0.69	1.9 × 10−1	0.54	9.3 × 10−3	-	-

) were found over maize (at C_HV, L_HH and L_HV) and sugar (all channels except L_HH and L_HV). These plants are both characterized by bigger leaf dimensions compared to those characterizing other cultivars. Noticeable, σ° vs. F_v regressions showed higher r than those characterizing σ° vs. m_v (best r ~ 0.95 for σ° vs. F_v at L_HV over maize plot), thus confirming that: (i) σ° is mainly controlled by geometric and dielectric properties of the vegetation; (ii) the canopy limits the assessment of the properties of the underlying soil. Although several significant correlations were found for other cultivars, these were characterized by weak (0.2 < r < 0.4) or moderate (0.4 < r < 0.6) r values.

The highest and significant σ° vs. LAI correlations were found again for sugar beet and maize; whereas, no significant correlations were found at X and C_HH channels. Several significant correlations were found for other cultivars; diversely than σ° vs. F_v, most of these exhibited a strong correlation (

Table 6. r of σ° vs. LAI for plots covered by vegetation. Significant correlations are highlighted in light-grey; strong and significant correlations are also bolded; very strong and significant correlations are highlighted in dark-grey with values in bold; very weak correlations are not reported.

σ° vs. LAI	Sugar		Barley		Maize		Rape		Wheat
	r	p-Value	r	p-Value	r	p-Value	r	p-Value	r	p-Value
XHH	0.72	0.17	0.63	4.7 × 10−3	-	-	-	-	0.50	2.5 × 10−2
XVV	0.70	0.19	0.61	6.7 × 10−3	-	-	-	-	0.51	2.2 × 10−2
CHH	0.80	1.0 × 10−1	0.32	1.9 × 10−1	0.31	6.2 × 10−1	0.31	1.8 × 10−1	0.64	2.4 × 10−3
CHV	0.91	3.1 × 10−2	-	-	0.64	2.5 × 10−1	-	-	0.49	2.7 × 10−2
CVV	0.80	1.0 × 10−1	0.19	4.5 × 10−1	-	-	0.21	3.8 × 10−1	0.19	4.3 × 10−1
LHH	0.98	2.7 × 10−3	0.53	2.2 × 10−2	0.94	1.9 × 10−2	0.44	5.0 × 10−2	0.38	9.8 × 10−2
LHV	0.93	2.1 × 10−2	0.60	7.9 × 10−3	0.95	1.2 × 10−2	0.60	4.7 × 10−3	0.25	3.0 × 10−1
LVV	0.89	4.5 × 10−2	0.32	1.9 × 10−1	0.59	2.9 × 10−1	0.28	2.3 × 10−1	-	-

). For some channels, σ° resulted significantly correlated with both LAI and F_v. Although σ° at L_HH resulted also correlated to m_v the higher p-value indicates a weaker significance of this correlation.

5.4. Inter-Channel Spatial/Temporal Correlation at Plot Scale

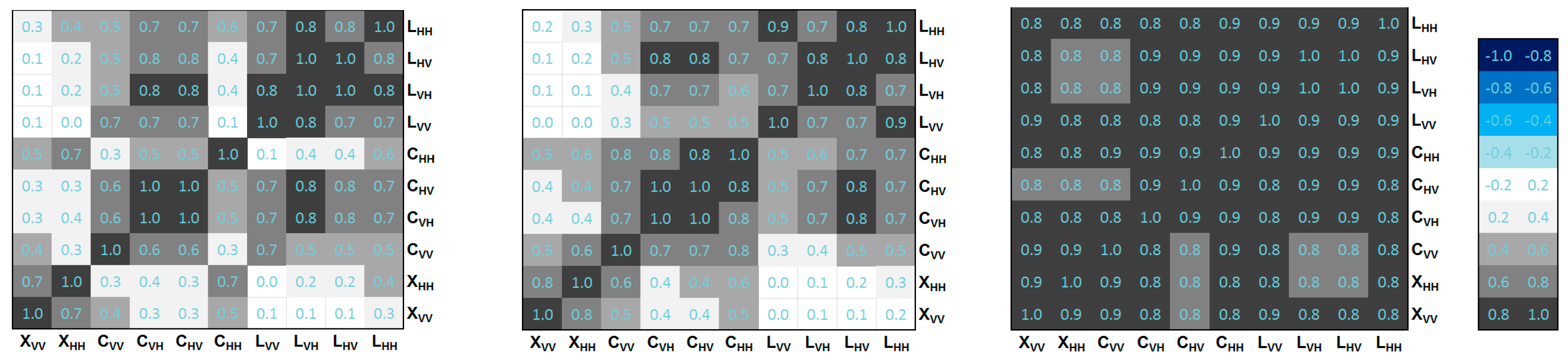
This section discusses and analyzes r_s domains for the two selected plots (see Section 4.2.2 and Section 5.2.2). For the plot 460, r_s domains were analyzed for increasing vegetation cover (for bare to vegetated) and decreasing m_v (Figure 8). In particular, three different dates were selected: (i) 19 April, when field was bare and m_v ~ 0.21 m³m⁻³; (ii) 7 June, when field was slightly vegetated (F_v ~ 0.1) and m_v decreased to ~0.16 m³m⁻³; and, (iii) 26 July, when F_v increased up to (~0.35) and the m_v decreased to ~0.02 m³m⁻³.

On 19 April the r_s domain highlights that strong to very strong correlation occurred among σ° at L and X channels, weak to very strong correlations were observed among σ° at C channels. On 7 June, when m_v slightly decreased and sugar beet started growing (F_v ~ 0.1); r_s between σ° at some channels slightly increased (e.g., σ° at C_HH and C_VV). Finally, on the 26th of July σ° of most of the bands were strongly correlated (r_s > 0.8). Whereas, lower correlations were observed among some σ° at C_HV and σ°_pq at L frequency (r_s ~ 0.8). The decreasing of m_v caused a noticeable increasing of r_s for all channel pairs.

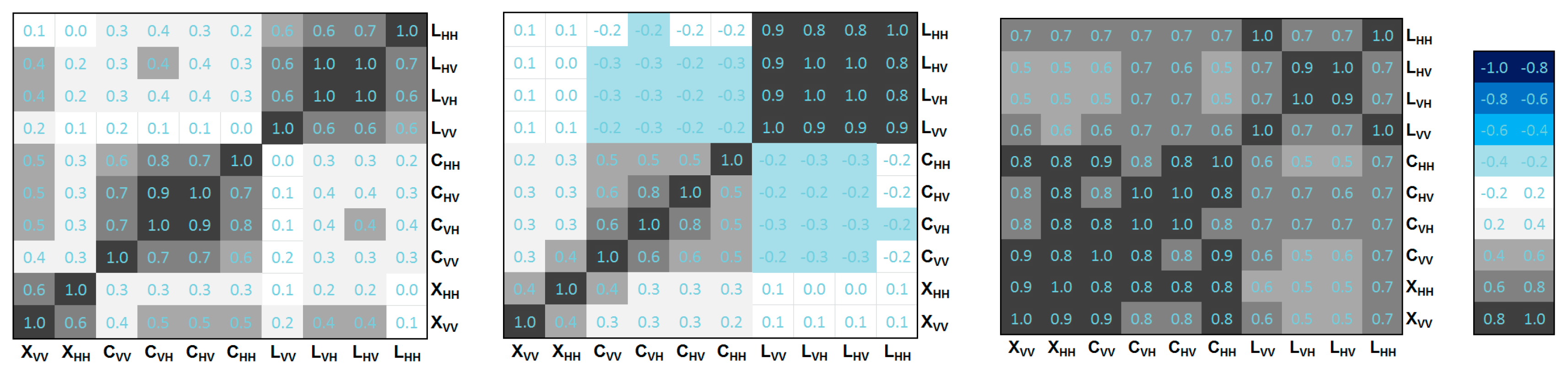
For the field 450 (Figure 9) r_s domains were analyzed at three selected times: (i) on 13 June, when F_v ~ 0.9 and m_v ~ 0.06 m³m⁻³; (ii) on 21 June, when F_v slightly increased (F_v ~ 0.95) and m_v considerably increased to ~0.22 m³m⁻³; and, (iii) on 26 July, when both F_v and m_v considerably decreased to ~0.3 and ~0.06 m³m⁻³ respectively.

On 13 June, the higher correlations among channels of the same frequency are observable. More specifically, moderate to very strong correlations occur among X, C and L frequency channels. Conversely, very weak to weak correlations characterized inter-frequency channels (e.g., C vs. L frequencies). On 21 June, m_v considerably increased (with almost constant F_v) causing a radical change in the C vs. L region; indeed, positive weak became negative weak correlations. On 26 July the m_v and F_v decreased to their minimum values causing the considerably increase of all r_s values.

Based on the above mentioned evidences, it could be hypnotized that r_s and SVV time series are correlated (temporal).

Thus, for 9 selected channel pairs the r_s vs. SVV were computed over both bare soil (

Table 7. r_t, over bare soils occurring during the study period; quasi-significant correlations (i.e., characterized by 0.05 < p-value < 0.1) are outlined; very weak correlations (r < 0.19) are not reported.

rs	rt (-)
	rs vs. mv				rs vs. h'
	Sugar Crop		Maize Crop		Sugar Crop		Maize Crop
	r	p-Value	r	p-Value	r	p-Value	r	p-Value
σ°X,HH vs. σ°X,VV	−0.22	7.2 × 10−1	0.65	2.4 × 10−1	0.88	5.1 × 10−2	-	-
σ°C,HH vs. σ°C,VV	−0.57	3.2 × 10−1	−0.51	3.8 × 10−1	0.65	2.4 × 10−1	0.29	7.1 × 10−1
σ°L,HH vs. σ°L,VV	−0.64	2.5 × 10−1	−0.66	2.2 × 10−1	0.56	3.2 × 10−1	-	-
σ°C,HH vs. σ°C,HV	−0.33	5.9 × 10−1	-	-	−0.62	2.6 × 10−1	-	-
σ°L,HH vs. σ°L,HV	0.77	1.3 × 10−1	−0.27	6.7 × 10−1	−0.21	7.3 × 10−1	0.49	5.1 × 10−1
σ°X,HH vs. σ°C,HH	0.78	1.2 × 10−1	0.78	1.2 × 10−1	0.29	6.4 × 10−1	−0.78	2.2 × 10−1
σ°C,HH vs. σ°L,HH	-	-	0.24	7.0 × 10−1	−0.85	6.8 × 10−2	−0.32	6.8 × 10−1
σ°X,HH vs. σ°L,HH	-	-	-	-	−0.83	8.0 × 10−2	−0.32	6.8 × 10−1
σ°C,HV vs. σ°L,HV	−0.35	5.6 × 10−1	0.58	3.1 × 10−1	−0.80	1.1 × 10−1	−0.29	7.0 × 10−1

) and vegetated plots (

Table 8. r_t vs. h’ temporal correlations, r_t, over the whole period for different crops; significant strong correlations (p-value < 0.05, 0.6 < r < 0.8) are in light-gray highlighted with values in bold; quasi-significant correlations (0.05 < p-value < 0.1) are outlined; very weak correlations (r < 0.19) are not reported.

rs	rt between rs and h'
	Sugar Beet		Barley		Maize		Rape		Wheat
	r	p-Value	r	p-Value	r	p-Value	r	p-Value	r	p-Value
σ°X,HH vs. σ°X,VV	−0.35	6.5 × 10−1	0.26	4.6 × 10−1	0.56	2.4 × 10−1	0.27	4.2 × 10−1	-	-
σ°C,HH vs. σ°C,VV	−0.88	1.2 × 10−1	-	-	0.29	5.8 × 10−1	0.34	3.1 × 10−1	0.47	2.1 × 10−1
σ°L,HH vs. σ°L,VV	0.31	6.9 × 10−1	0.55	1.0 × 10−1	-	-	−0.35	2.9 × 10−1	-	-
σ°C,HH vs. σ°C,HV	−0.70	3.0 × 10−1	0.51	1.3 × 10−1	0.48	3.4 × 10−1	0.49	1.2 × 10−1	0.52	1.5 × 10−1
σ°L,HH vs. σ°L,HV	0.55	4.5 × 10−1	−0.49	1.5 × 10−1	0.28	6.0 × 10−1	−0.35	2.9 × 10−1	0.53	1.4 × 10−1
σ°X,HH vs. σ°C,HH	−0.70	3.0 × 10−1	-	-	0.25	6.4 × 10−1	0.44	1.7 × 10−1	0.45	2.2 × 10−1
σ°C,HH vs. σ°L,HH	−0.66	3.4 × 10−1	0.54	1.1 × 10−1	−0.24	6.5 × 10−1	-	-	0.69	3.9 × 10−2
σ°X,HH vs. σ°L,HH	0.32	6.8 × 10−1	−0.68	3.1 × 10−2	-	-	0.43	1.9 × 10−1	0.45	2.2 × 10−1
σ°C,HV vs. σ°L,HV	−0.91	9.4 × 10−2	-	-	−0.31	5.5 × 10−1	−0.31	3.5 × 10−1	0.28	4.5 × 10−1

,

Table 9. r_t vs. m_v temporal correlations, r_t, over the whole period for different crops; significant correlations (p-value < 0.05) are in light-gray highlighted; strong (0.6 < r < 0.8) significant correlations are also bolded; very strong (r > 0.8) significant correlations are also highlighted in dark-gray; quasi-significant correlations (0.05 < p-value < 0.1) are outlined; very weak correlations (r < 0.19) are not reported.

rs	rt between rs and mv
	Sugar Beet		Barley		Maize		Rape		Wheat
	r	p-Value	r	p-Value	r	p-Value	r	p-Value	r	p-Value
σ°X,HH vs. σ°X,VV	0.24	7.6 × 10−1	-	-	-	-	-	-	−0.65	2.0 × 10−3
σ°C,HH vs. σ°C,VV	-	-	-	-	0.31	5.5 × 10−1	-	-	-	-
σ°L,HH vs. σ°L,VV	−0.98	2.1 × 10−2	-	-	0.61	2.0 × 10−1	−0.26	2.4 × 10−1	−0.38	9.7 × 10−2
σ°C,HH vs. σ°C,HV	-	-	−0.48	3.2 × 10−2	−0.50	3.1 × 10−1	−0.23	2.9 × 10−1	-	-
σ°L,HH vs. σ°L,HV	−0.97	2.9 × 10−2	−0.27	2.5 × 10−1	−0.67	1.5 × 10−1	−0.36	1.0 × 10−1	−0.33	1.5 × 10−1
σ°X,HH vs. σ°C,HH	-	-	0.26	2.7 × 10−1	−0.19	7.3 × 10−1	−0.20	3.6 × 10−1	-	-
σ°C,HH vs. σ°L,HH	−0.33	6.7 × 10−1	-	-	−0.67	1.5 × 10−1	0.20	3.8 × 10−1	-	-
σ°X,HH vs. σ°L,HH	−0.88	1.2 × 10−1	−0.23	3.3 × 10−1	−0.67	1.5 × 10−1	-	-	−0.49	2.8 × 10−2
σ°C,HV vs. σ°L,HV	-	-	−0.28	2.3 × 10−1	−0.68	1.4 × 10−1	0.24	2.8 × 10−1	−0.53	1.6 × 10−2

,

Table 10. r_t vs. F_v temporal correlations, r_t, over the whole period for different crops; significant correlations (p-value < 0.05) are in light-gray highlighted; strong (0.6 < r < 0.8) significant correlations are also bolded; very strong (r > 0.8) significant correlations are also highlighted in dark-gray; quasi-significant correlations (0.05 < p-value < 0.1) are outlined; very weak correlations (r < 0.19) are not reported.

rs	rt between rs and Fv
	Sugar Beet		Barley		Maize		Rape		Wheat
	r	p-Value	r	p-Value	r	p-Value	r	p-Value	r	p-Value
σ°X,HH vs. σ°X,VV	0.72	1.7 × 10−1	−0.41	7.3 × 10−2	−0.83	4.2 × 10−2	−0.21	3.5 × 10−1	-	-
σ°C,HH vs. σ°C,VV	−0.44	4.6 × 10−1	−0.41	7.0 × 10−2	−0.91	1.3 × 10−2	−0.33	1.3 × 10−1	0.78	4.4 × 10−5
σ°L,HH vs. σ°L,VV	−0.55	3.3 × 10−1	0.28	2.4 × 10−1	−0.83	4.1 × 10−2	−0.46	2.9 × 10−2	-	-
σ°C,HH vs. σ°C,HV	−0.65	2.3 × 10−1	-	-	−0.20	7.1 × 10−1	0.23	3.0 × 10−1	0.79	3.6 × 10−5
σ°L,HH vs. σ°L,HV	−0.66	2.2 × 10−1	-	-	0.42	4.1 × 10−1	-	-	-	-
σ°X,HH vs. σ°C,HH	0.30	6.2 × 10−1	−0.76	1.1 × 10−4	−0.57	2.4 × 10−1	−0.41	6.0 × 10−2	0.74	2.1 × 10−4
σ°C,HH vs. σ°L,HH	−0.46	4.3 × 10−1	-	-	0.29	5.8 × 10−1	−0.36	9.8 × 10−2	0.45	4.5 × 10−2
σ°X,HH vs. σ°L,HH	-	-	-	-	0.31	5.5 × 10−1	−0.35	1.1 × 10−1	-	-
σ°C,HV vs. σ°L,HV	0.32	5.9 × 10−1	-	-	-	-	−0.25	2.6 × 10−1	0.25	2.9 × 10−1

and

Table 11. r_t vs. LAI temporal correlations, r_t, over the whole period for different crops; significant correlations (p-value < 0.05) are in light-gray highlighted; strong (0.6 < r < 0.8) significant correlations are also bolded; quasi-significant correlations (0.05 < p-value < 0.1) are outlined; very weak correlations (r < 0.19) are not reported.

rs	rt between rs and LAI
	Sugar Beet		Barley		Maize		Rape		Wheat
	r	p-Value	r	p-Value	r	p-Value	r	p-Value	r	p-Value
σ°X,HH vs. σ°X,VV	0.55	3.3 × 10−1	0.52	2.6 × 10−2	−0.49	4.0 × 10−1	-	-	0.76	2.4 × 10−4
σ°C,HH vs. σ°C,VV	−0.83	8.2 × 10−2	−0.26	2.9 × 10−1	−0.81	1.0 × 10−1	-	-	-	-
σ°L,HH vs. σ°L,VV	-	-	−0.57	1.3 × 10−2	−0.83	8.2 × 10−2	-	-	-	-
σ°C,HH vs. σ°C,HV	−0.86	6.1 × 10−2	0.42	8.3 × 10−2	0.27	6.6 × 10−1	0.32	1.7 × 10−1	0.25	3.2 × 10−1
σ°L,HH vs. σ°L,HV	-	-	−0.48	4.2 × 10−2	0.84	7.3 × 10−2	-	-	−0.30	2.3 × 10−1
σ°X,HH vs. σ°C,HH	-	-	0.39	1.1 × 10−1	-	-	-	-	0.21	4.0 × 10−1
σ°C,HH vs. σ°L,HH	−0.54	3.5 × 10−1	−0.69	1.4 × 10−3	0.20	7.5 × 10−1	0.19	4.1 × 10−1	-	-
σ°X,HH vs. σ°L,HH	0.40	5.1 × 10−1	−0.24	3.3 × 10−1	0.25	6.9 × 10−1	-	-	-	-
σ°C,HV vs. σ°L,HV	−0.74	1.5 × 10−1	−0.22	3.9 × 10−1	-	-	0.46	3.9 × 10−2	0.42	8.3 × 10−2

) to explore the determinability of SVV through r_s. Results are shown in terms of correlation coefficients, r_t.

Over bare soils, a total of 36 correlations (9 band pairs, 2 soil variables, 2 crops) were evaluated. Only 13 (≈30%) r_t are moderate (>|0.6|); most of them (6 cases) involve multi-frequency pairs. Conversely to the single regression approach, the inter-channel spatial/temporal correlation analysis pointed out three quasi-significant and very strong r_s vs. h’ correlations (involving X_HH-X_VV, C_HH-L_HH, X_HH-L_HH pairs). Best correlations will be further analyzed within the discussion section (

Table 12. Best results achieved through the dynamic and correlation analyses; significant correlations are highlighted in light-grey, quasi-significant correlations are underlined; other correlations are not reported; for each correlation MAE is also reported.

Channel	σ° Dynamic Analysis—∆σ° (dB)		σ° vs. SVV Analysis
	Whole Dataset		Bare Soils				Vegetated
			σ° vs. h'		σ° vs. mv		σ° vs. h'		σ° vs. mv		σ° vs. Fv		σ° vs. LAI
	Varying h', mv, Fv and LAI (∆σ°avg)	Varying LAI (∆σ°)	r (-)	MAE (dB)	r (-)	MAE (dB)	r (-)	MAE (dB)	r (-)	MAE (dB)	r (-)	MAE (dB)	r (-)	MAE (dB)
XHH	7.50	6.99	-	-	0.79	0.81	-	-	0.37	1.03	0.90	0.54	0.63	1.28
XVV	7.20	6.16	-	-	0.82	0.66	-	-	0.46	1.05	0.85	0.74	0.62	1.48
CHH	6.40	5.79	-	-	0.83	0.71	-	-	0.38	1.22	0.87	0.75	0.64	0.90
CHV	10.00	10.39	-	-	-	-	-	-	0.46	1.41	0.90	0.62	0.91	0.54
CVV	7.80	5.02	-	-	-	-	-	-	-	-	0.87	0.61	-	-
LHH	11.40	11.72	-	-	0.99	0.24	-	-	0.51	2.44	0.87	0.76	0.98	0.29
LHV	12.10	13.96	-	-	0.99	0.15	-	-	0.66	1.79	0.95	0.67	0.95	0.83
LVV	11.30	10.95	-	-	0.99	0.22	-	-	0.55	1.61	0.90	0.83	0.89	0.88

and

Table 13. Best results achieved through the inter-channel correlation analysis. Additionally, to the key legend of Table 12, improvements, with respect to the single regression approach, are highlighted in blue; bolded blue values refer to improvements achieved through the multi-frequency approach.

	Channel Pairs	rs vs. SVV Analysis
		Bare				Vegetated
		rs vs. h'	MAE (-)	rs vs. mv	MAE (-)	rs vs. h'	MAE (-)	rs vs. mv	MAE (-)	rs vs. Fv	MAE (-)	rs vs. LAI	MAE (-)
rs single Freq.	XHH vs. XVV	0.88	0.02	-	-	-	-	−0.65	0.05	−0.83	0.02	0.76	0.04
	CHH vs. CVV	-	-	-	-	-	-	-	-	−0.91	0.02	−0.83	0.03
	LHH vs. LVV	-	-	-	-	-	-	−0.98	0.01	−0.83	0.03	−0.57	0.13
	CHH vs. CHV	-	-	-	-	-	-	−0.48	0.05	0.79	0.07	−0.86	0.07
	LHH vs. LHV	-	-	-	-	-	-	−0.97	0.04	-	-	−0.48	0.18
rs dual Freq.	XHH vs. CHH	-	-	-	-	-	-	-	-	−0.76	0.08	-	-
	CHH vs. LHH	−0.85	0.05	-	-	0.69	0.09	-	-	0.45	0.13	−0.69	0.18
	XHH vs. LHH	−0.83	0.08	-	-	−0.68	0.07	−0.49	0.16	-	-	-	-
	CHV vs. LHV	-	-	-	-	−0.91	0.07	−0.53	0.09	-	-	0.46	0.10

).

Over vegetated areas, among 180 correlations (9 band couples, 4 soil-vegetation variables, 5 crops), only 34 (≈18%) r_t were higher than |0.6|; 14 are strong and very strong significant correlations and 5 of these involve multi-frequency combinations (Table 8, Table 9, Table 10 and Table 11).

Over vegetated areas, r_s vs. h’ produces the lowest number of significant correlations as, in this case, σ° is mainly ruled by canopy dielectric (plant water content) and geometric properties (LAI, F_v and vegetation structure).

However, conversely to the single regression analysis, the dual-frequencies inter-channel spatial/temporal approach pointed out some strong significant correlations. Despite r_t were computed over vegetated plots, some negative strong and very strong significant r_t were observed between r_s and m_v for pairs of σ° at L and X frequencies. These results partially confirm the suitability of dual frequency approach to quantify m_v and biomass (F_v particularly), as already reported by other authors [16,58]; further discussion about the improvements achievable through the multi-channel approach and the multi-frequency correlation will be provided in the next section.

6. Discussion on Best Results Achieved

This section summarizes best results achieved from the dynamic and single regression analyses (Table 12). Due to the reciprocity property of cross-polarizations, only outcomes achieved by using σ°_HV and σ°_pp channels are further discussed. In addition, this part will be focused on the quasi- and significant correlations only.

The dynamic analysis highlighted that ∆σ° at C_HV and L frequency generally showed the highest ∆σ° (≈10–12 dB); however, individual contributions of h’, m_v, F_v and LAI were not definitely distinguishable.

By observing ∆σ° due to vegetation variations (i.e., changes in LAI and F_v) ∆σ°_pq are higher at L (~14 dB) rather than at C frequency (~10 dB); this is probably due to the structure of sugar beet characterized by very large leaves. Moreover, as confirmed by other studies, σ°_HV and σ°_VH (not shown here) behave quite similarly according to the reciprocity principle, which for most natural media assumes a symmetric scattering matrix [59].

The correlation analysis highlights that over bare soils, σ° vs. m_v are significant and characterized by high r at all channels with exceptions of C_HV and C_VV. The highest r and the lowest MAE were found at L frequency. Whereas no significant σ° vs. h’ correlations were achieved.

Over vegetated areas, since h’ was measured below canopy, no significant r values have been found as σ° over dense vegetation is mainly ruled by: (i) surface water contents (m_v and canopy water content) and (ii) surface roughness (correlated with biomass variables, including LAI and F_v, and vegetation structure). Quasi-significant and significant moderate to strong correlations (i.e., 0.4 < r < 0.8) characterized σ° vs. m_v at all channels with the exception of C_VV. The highest r values were found at L frequency probably due to the higher ability of longer waves to penetrate the canopy layer.

Very strong correlations (i.e., r > 0.8) were found for σ° vs. F_v at all frequencies and polarizations; highest r characterized σ° vs. F_v at X_HH, C_HV and L_HV comparisons. Strong to very strong r characterized σ° vs. LAI comparisons with the highest values at C_HV and L frequencies.

All these results highlight that, on the average, σ° at L bands are more suitable than others to infer SVV over both bare and vegetated areas.

It has been observed that, usually, correlations showing the highest r were also characterized by the lower MAE (although this is not a general rule). Over bare soils and for all channels, lower MAE were found for σ° vs. m_v (MAE was ≈0.6 dB on average) with respect to the vegetated soils (≈1.3 dB). Lower MAE characterized both σ° vs. F_v and σ° vs. LAI (on average ≈0.7 dB and ≈1 dB, respectively) if compared to σ° vs. m_v. Finally, lowest MAE were found at L frequency for σ° vs. m_v (bare soils) and for σ° vs. F_v and σ° vs. LAI (vegetated plots).

Over bare soils, the inter-channel correlation analysis (Table 13) revealed three quasi-significant and very strong r_s vs. h’ correlations; thus, it was observed a remarkable improvement with respect to the single frequency approach. However, no significant r_s vs. m_v correlations were found, meaning that all channel pairs were useless to assess m_v by means of this approach.

Improvements with regards to the single regression approach (Table 13, highlighted in red) were observed in several cases; the dual-frequency approach allowed pointing out higher correlations (Table 13, bolded red values) if compared to the single-frequency approach. Remarkably, r_s seems to be negatively correlated with SVV with some exceptions (see Table 7, Table 8, Table 9, Table 10 and Table 11). These exceptions are probably linked to the vegetation structure (as most of them were found for F_v and LAI for the wheat plot); however, further analyses are required to corroborate this hypothesis. Further investigations could be carried out by employing multi-mission satellite data (e.g., using nowadays imagery acquired by Cosmo-SkyMed, TerraSAR-X, Palsar and Sentinel 1).

Over vegetated plots in particular, the more suitable band pairs to assess m_v were L_HH-L_VV and L_HH-L_HV (r_t > |0.97|); however, the inter-channel approach opens the possibility to assess m_v for all pairs except C_HH-C_VV, X_HH-C_HH and C_HH-L_HH.

As for the m_v, several channel pairs are suitable to assess F_v (strong to very strong significant correlations) with the exception of the C_HH-L_HH pair. Channel pairs more suitable to assess LAI are: X_HH-X_VV, C_HH-L_HH, C_HV-L_HV.

7. Conclusions

The paper reports a detailed analysis on the influence of main SVV on σ°. Statistical analyses have been carried out to define suitable frequencies/polarimetry configuration to characterize the main SVV over bare and vegetated plots. Dataset includes X, C and L SAR bands with HH, VV, VH and HV polarizations and in situ measurements.

The dynamic and correlation analyses investigate the behavior of single bands with changing SVV. The inter-channel correlation analysis explores the behavior of band pairs with SVV changing over time.

The dynamic analysis revealed that cross-polarized channels exhibit higher sensitiveness to SVV, in particular to LAI and F_v.

The single correlation analysis revealed that: (i) over bare soil, σ° vs. m_v exhibits strong and very strong correlation at all channels; best r characterizes σ° vs. m_v at L channels (r ~ 1); (ii) over vegetated areas, highest r characterizes σ° vs. F_v and σ° vs. LAI with best suitable channels at L frequency.

The inter-channel correlation (using a single frequency) displayed significant r_s vs. h’ correlations over both bare and vegetated plots (unachievable by means of the single regression approach). The inter-channel spatial/temporal regression analysis is more suitable than the single channel approach in several cases. Thus, the inter-channel correlation analyses promise to retrieve other SVV with good accuracies even over vegetated plots. In some cases, best correlations are found by adopting the dual frequency approach compared to the use of a single frequency.

Despite all the analyses confirming that L bands are more suitable than others to infer SVV over both bare and vegetated plots, few satellite sensors provide SAR data at L frequency (PALSAR 1 and 2); as a consequence, in the past, most of the models (see Table 1) have been implemented on C and X bands only (widely available). In addition, the NASA JPL’s Soil Moisture Active Passive (SMAP), a mission launched at the end of 2015, partially failed after collecting just two months of data because of the malfunctioning of the SAR (L_VV, L_HH, and L_HV).

Based on the results achieved by means of the inter-channel analysis, it could be interesting to perform further experiments exploiting data collected also by the near future SAR sensors; including: (i) SAOCOM-CONAE 1A/1B (Argentina) an L band two-satellite flying in constellation with COSMO-SkyMed; (ii) Tandem-L (DLR-Germany) a two formation-flying radar satellites operating in L band (planned to be launched at the end of 2022), and (iii) NISAR (NASA JPL-United States, 2020) that will include both L and S band polarimetry SAR sensors. These new experiments could be carried out coupling SAR to optical retrieved vegetation biomass (e.g., by means of Sentinel 2 or Landsat 8) and soil water content (e.g., through the use of passive microwave) maps. Thus, widening the study area these new researches could point out expected limitations in the relationship’s inversion.