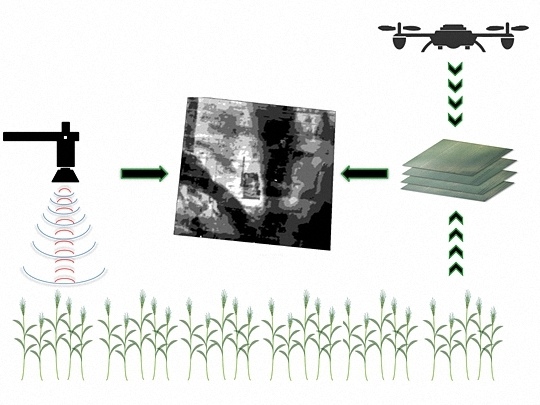
Regression Kriging for Improving Crop Height Models Fusing Ultra-Sonic Sensing with UAV Imagery
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Sensor and Sensor Platform Specifications
2.3. Field Measurements
2.4. Generating the Crop Height and Orthoimage Data from the UAV Images
2.5. Kriging Interpolation
2.6. Data Analysis
3. Results
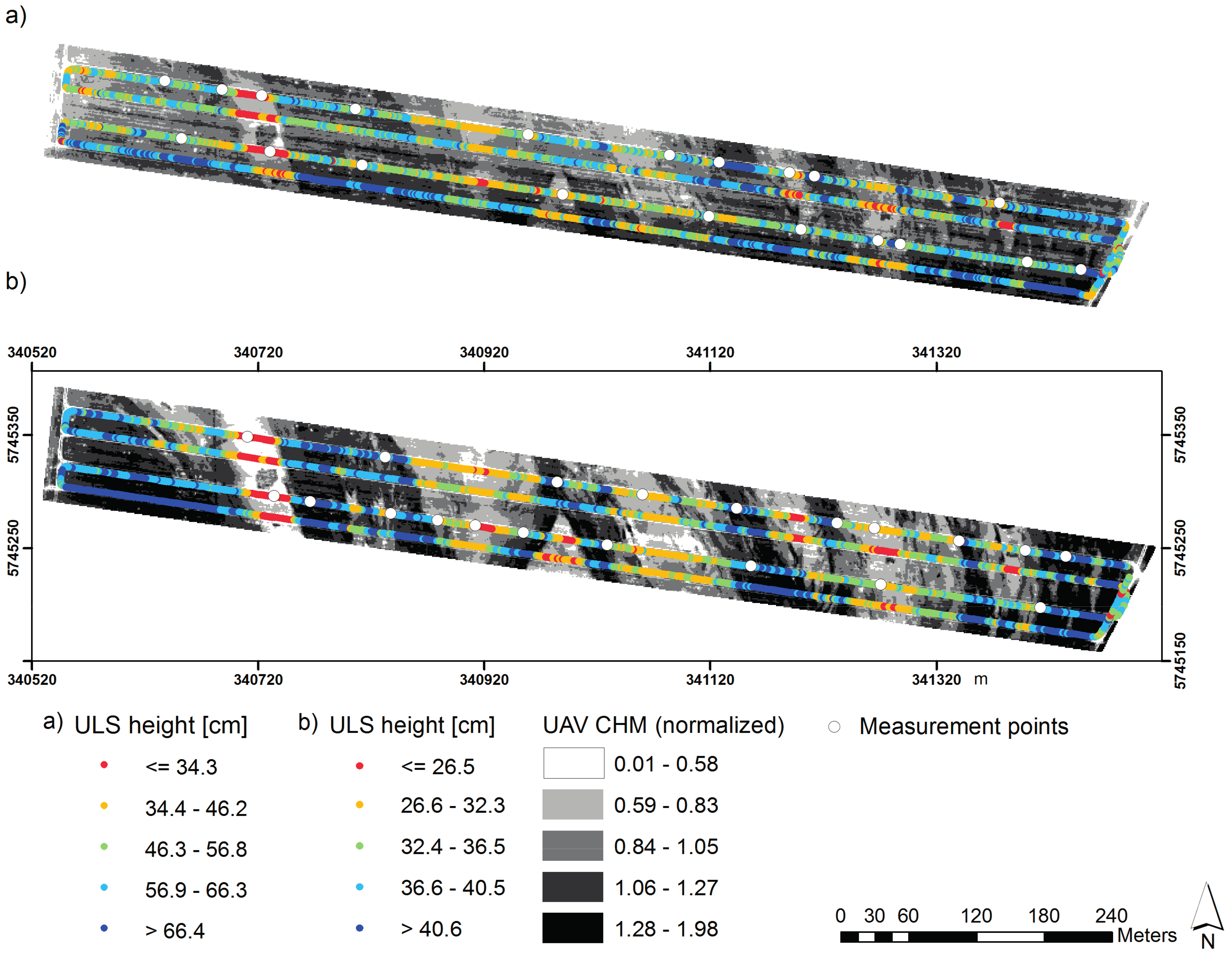
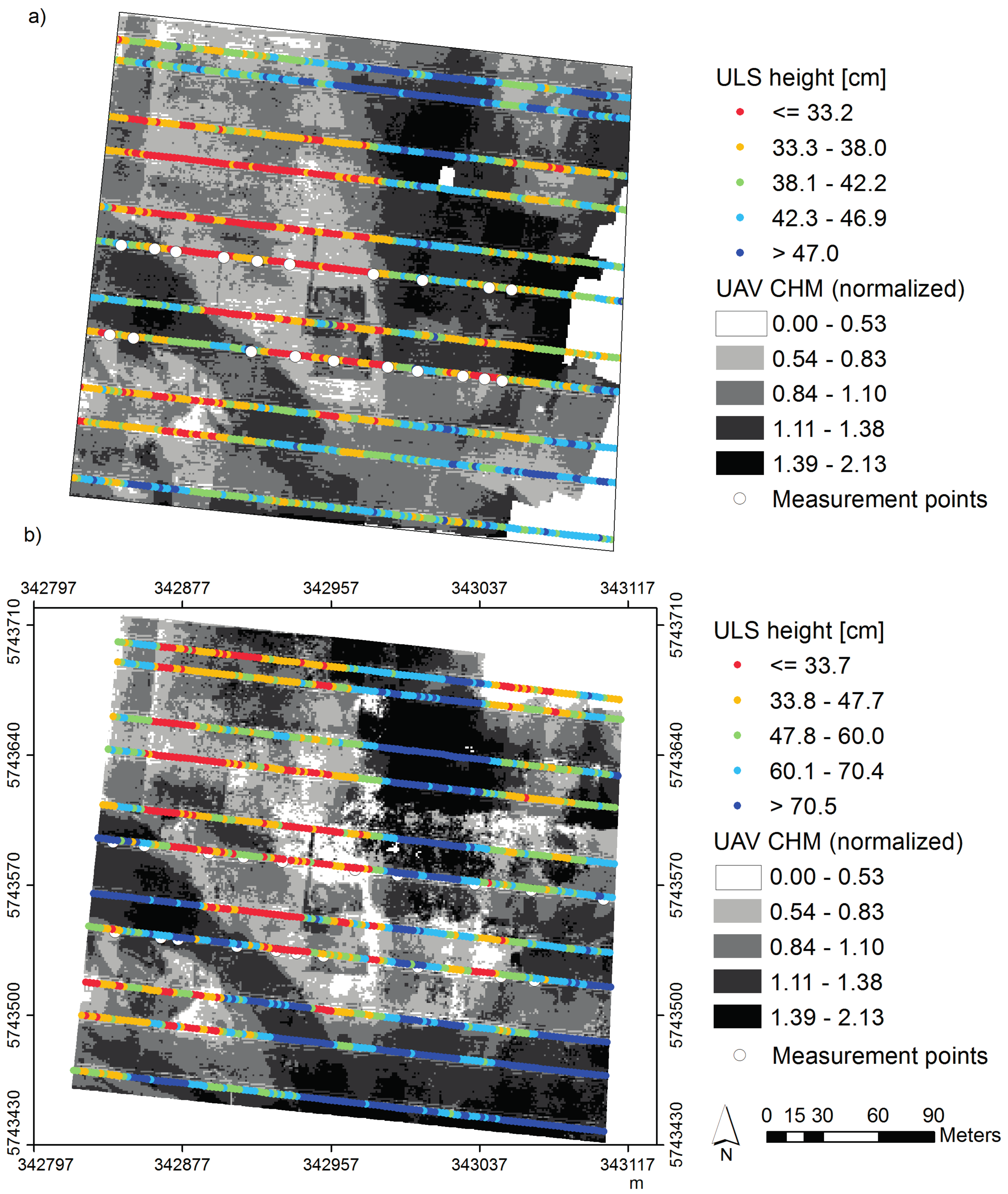
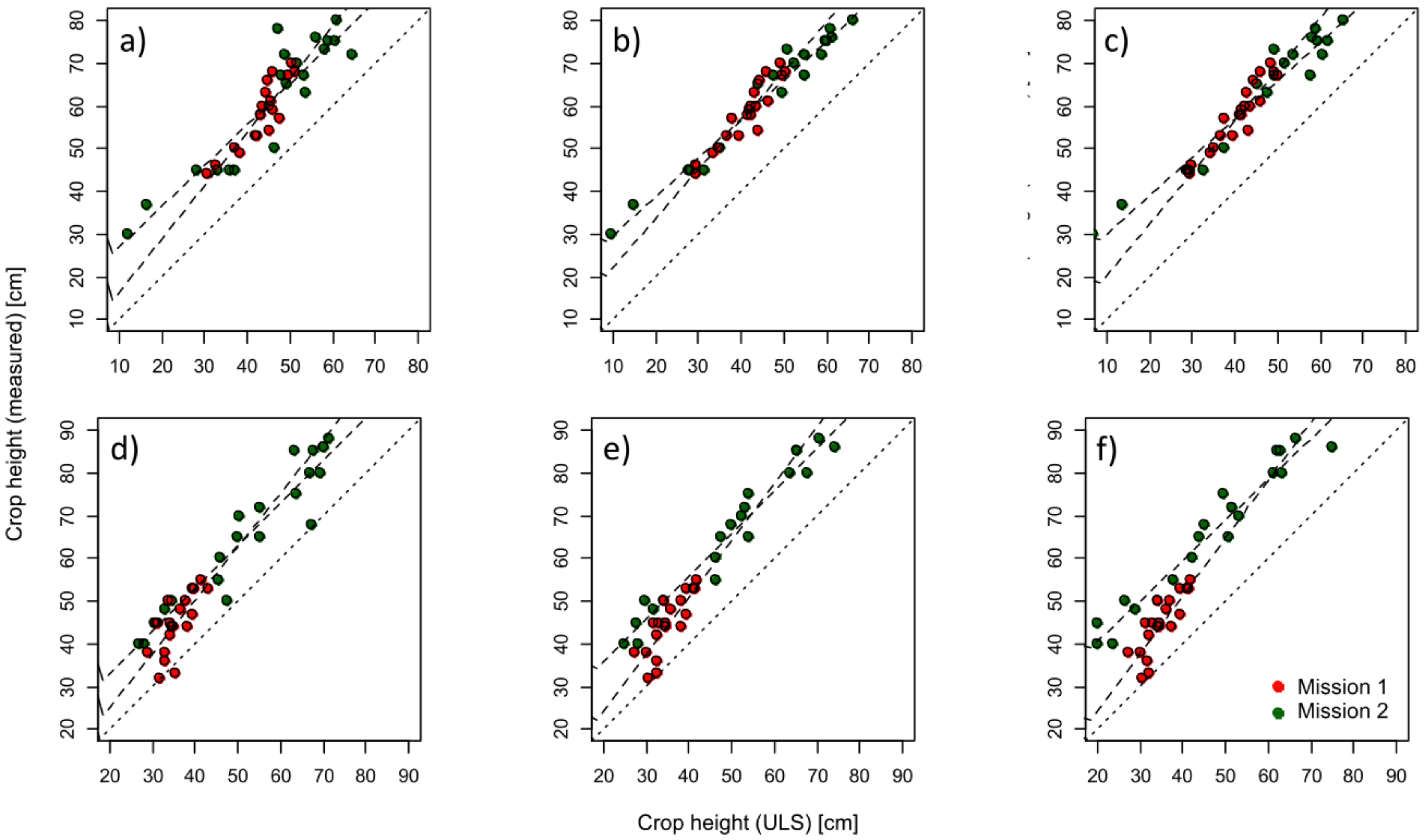
3.1. ULS and UAV Measurements and its Relation with Crop Height
3.2. Regression Kriging of the ULS Measurements
4. Discussion
5. Conclusions
Supplementary Material
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heege, H.J. Precision in Crop Farming; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Oerke, E.-C.; Gerhards, R.; Menz, G.; Sikora, R.A. Precision Crop Protection—The Challenge and Use of Heterogeneity; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Girma, K.; Martin, K.L.; Anderson, R.H.; Arnall, D.B.; Brixey, K.D.; Casillas, M.A.; Chung, B.; Dobey, B.C.; Kamenidou, S.K.; Kariuki, S.K.; et al. Mid-season prediction of wheat-grain yield potential using plant, soil, and sensor measurements. J. Plant Nutr. 2006, 29, 873–897. [Google Scholar] [CrossRef]
- Lati, R.N.; Filin, S.; Eizenberg, H. Estimating plant growth parameters using an energy minimization-based stereovision model. Comput. Electron. Agric. 2013, 98, 260–271. [Google Scholar] [CrossRef]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating biomass of barley using crop surface models (CSMs) derived from UAV-based RGB imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- Schirrmann, M.; Giebel, A.; Gleiniger, F.; Pflanz, M.; Lentschke, J.; Dammer, K.-H. Monitoring agronomic parameters of winter wheat crops with low-cost UAV imagery. Remote Sens. 2016, 8, 706. [Google Scholar] [CrossRef]
- Portz, G.; Amaral, L.R.; Molin, J.P.; Adamchuk, V.I. Field comparison of ultrasonic and canopy reflectance sensors used to estimate biomass and N-uptake in sugarcane. In Precision Agriculture’13; Springer: Dordrecht, The Netherlands, 2013; pp. 111–117. [Google Scholar]
- Floreano, D.; Wood, R.J. Science, technology and the future of small autonomous drones. Nature 2015, 521, 460–466. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
- Rosnell, T.; Honkavaara, E. Point Cloud Generation from Aerial Image Data Acquired by a Quadrocopter Type Micro Unmanned Aerial Vehicle and a Digital Still Camera. Sensors 2012, 12, 453–480. [Google Scholar] [CrossRef] [PubMed]
- Grenzdörffer, G.J. Crop height determination with UAS point clouds. ISPRS—International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2014, XL-1, 135–140. [Google Scholar]
- Bendig, J.; Bolten, A.; Bareth, G. UAV-based imaging for multi-temporal, very high resolution crop surface models to monitor crop growth variability Monitoring des Pflanzenwachstums mit Hilfe multitemporaler und hoch auflösender Oberflächenmodelle von Getreidebeständen auf Basis von Bildern aus UAV-Befliegungen. Photogramm. Fernerkund. Geoinf. 2013, 2013, 551–562. [Google Scholar]
- Geipel, J.; Link, J.; Claupein, W. Combined spectral and spatial modeling of corn yield based on aerial images and crop surface models acquired with an unmanned aircraft system. Remote Sens. 2014, 6, 10335–10355. [Google Scholar] [CrossRef]
- Dammer, K.-H. Real-time variable-rate herbicide application for weed control in carrots. Weed Res. 2016, 56, 237–246. [Google Scholar] [CrossRef]
- Thoele, H.; Ehlert, D. Biomass related nitrogen fertilization with a crop sensor. Appl. Eng. Agric. 2010, 26, 769–775. [Google Scholar] [CrossRef]
- Schirrmann, M.; Joschko, M.; Gebbers, R.; Kramer, E.; Zörner, M.; Barkusky, D.; Timmer, J. Proximal soil sensing—A contribution for species habitat distribution modelling of earthworms in agricultural soils? PLoS ONE 2016, 11, e0158271. [Google Scholar] [CrossRef] [PubMed]
- Tackenberg, M.; Volkmar, C.; Dammer, K.-H. Sensor-based variable-rate fungicide application in winter wheat: Sensor-based variable-rate fungicide application in winter wheat. Pest Manag. Sci. 2016, 72, 1888–1896. [Google Scholar] [CrossRef] [PubMed]
- Shibayama, M.; Akiyama, T.; Munakata, K. A portable field ultrasonic sensor for crop canopy characterization. Remote Sens. Environ. 1985, 18, 269–279. [Google Scholar] [CrossRef]
- Scotford, I.M.; Miller, P.C.H. Combination of spectral reflectance and ultrasonic sensing to monitor the growth of winter wheat. Biosyst. Eng. 2004, 87, 27–38. [Google Scholar] [CrossRef]
- Andújar, D.; Weis, M.; Gerhards, R. An ultrasonic system for weed detection in cereal crops. Sensors 2012, 12, 17343–17357. [Google Scholar] [CrossRef] [PubMed]
- Reusch, S. Use of ultrasonic transducer for on-line biomass estimation in winter wheat. In Precision Agriculture ’09: Papers Presented at the 7th European Conference on Precision Agriculture; Wageningen Academic Publishers: Wageningen, the Netherlands, 2009; pp. 169–175. [Google Scholar]
- Maertens, K.; Reyns, P.; de Clippel, J.; de Baerdemaeker, J. First experiments on ultrasonic crop density measurement. J. Sound Vib. 2003, 266, 655–665. [Google Scholar] [CrossRef]
- Andrade-Sanchez, P.; Gore, M.A.; Heun, J.T.; Thorp, K.R.; Carmo-Silva, A.E.; French, A.N.; Salvucci, M.E.; White, J.W. Development and evaluation of a field-based high-throughput phenotyping platform. Funct. Plant Biol. 2014, 41, 68. [Google Scholar] [CrossRef]
- Bai, G.; Ge, Y.; Hussain, W.; Baenziger, P.S.; Graef, G. A multi-sensor system for high throughput field phenotyping in soybean and wheat breeding. Comput. Electron. Agric. 2016, 128, 181–192. [Google Scholar] [CrossRef]
- Ehlert, D.; Adamek, R.; Horn, H.-J. Laser rangefinder-based measuring of crop biomass under field conditions. Precis. Agric. 2009, 10, 395–408. [Google Scholar] [CrossRef]
- Erdle, K.; Mistele, B.; Schmidhalter, U. Comparison of active and passive spectral sensors in discriminating biomass parameters and nitrogen status in wheat cultivars. Field Crop. Res. 2011, 124, 74–84. [Google Scholar] [CrossRef]
- Bilewski, M.; Putynkowski, G. Application of ultrasonic distance sensors for measuring height as a tool in unmanned aerial vehicles with a stabilized position in the vertical plane. Zeszyty Naukowe Akademia Morska w Szczecinie 2016. [Google Scholar] [CrossRef]
- Rischbeck, P.; Elsayed, S.; Mistele, B.; Barmeier, G.; Heil, K.; Schmidhalter, U. Data fusion of spectral, thermal and canopy height parameters for improved yield prediction of drought stressed spring barley. Eur. J. Agron. 2016, 78, 44–59. [Google Scholar] [CrossRef]
- Tilly, N.; Aasen, H.; Bareth, G. Fusion of plant height and vegetation indices for the estimation of barley biomass. Remote Sens. 2015, 7, 11449–11480. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Rossiter, D.G. About regression-kriging: From equations to case studies. Comput. Geosci. 2007, 33, 1301–1315. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef]
- Odeh, I.O.; McBratney, A.B.; Chittleborough, D.J. Further results on prediction of soil properties from terrain attributes: Heterotopic cokriging and regression-kriging. Geoderma 1995, 67, 215–226. [Google Scholar] [CrossRef]
- Cao, S.; Lu, A.; Wang, J.; Huo, L. Modeling and mapping of cadmium in soils based on qualitative and quantitative auxiliary variables in a cadmium contaminated area. Sci. Total Environ. 2017, 580, 430–439. [Google Scholar] [CrossRef] [PubMed]
- Ge, Y.; Thomasson, J.A.; Sui, R.; Wooten, J. Regression-kriging for characterizing soils with remotesensing data. Front. Earth Sci. 2011. [Google Scholar] [CrossRef]
- Sun, W.; Whelan, B.M.; Minasny, B.; McBratney, A.B. Evaluation of a local regression kriging approach for mapping apparent electrical conductivity of soil (ECa) at high resolution. J. Plant Nutr. Soil Sci. 2012, 175, 212–220. [Google Scholar] [CrossRef]
- Moral, F.J.; Terrón, J.M.; da Silva, J.R.M. Delineation of management zones using mobile measurements of soil apparent electrical conductivity and multivariate geostatistical techniques. Soil Tillage Res. 2010, 106, 335–343. [Google Scholar] [CrossRef]
- Zhang, C.; Pei, H. Oil spills boundary tracking using universal kriging and model predictive control by UAV. In Proceedings of the 11th World Congress on Intelligent Control and Automation (WCICA 2014), Shenyang, China, 29 June–4 July 2014; pp. 633–638. [Google Scholar]
- Zheng, Y.; Yu, J.; Kang, S.B.; Lin, S.; Kambhamettu, C. Single-image vignetting correction using radial gradient symmetry. In Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2008), Anchorage, AK, USA, 24–26 June 2008; pp. 1–8. [Google Scholar]
- Lelong, C.C.D.; Burger, P.; Jubelin, G.; Roux, B.; Labbé, S.; Baret, F. Assessment of unmanned aerial vehicles imagery for quantitative monitoring of wheat crop in small plots. Sensors 2008, 8, 3557–3585. [Google Scholar] [CrossRef] [PubMed]
- Verhoeven, G. Taking computer vision aloft—Archaeological three-dimensional reconstructions from aerial photographs with photoscan. Archaeol. Prospect. 2011, 18, 67–73. [Google Scholar] [CrossRef]
- Hamuda, E.; Glavin, M.; Jones, E. A survey of image processing techniques for plant extraction and segmentation in the field. Comput. Electron. Agric. 2016, 125, 184–199. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; Peña, J.M.; de Castro, A.I.; López-Granados, F. Multi-temporal mapping of the vegetation fraction in early-season wheat fields using images from UAV. Comput. Electron. Agric. 2014, 103, 104–113. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists (Statistics in Practice), 2nd ed.; Wiley: Chichester, UK, 2007. [Google Scholar]
- Matheron, G. Traité de Géostatistique Appliquée, Tome I: Mémoires du Bureau de Recherches Géologiques et Minières, No. 14; Editions Technip: Paris, France, 1962; p. 333. [Google Scholar]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2015; Available online: http://www.R-project.org/ (accessed on 6 June 2017).
- Aziz, S.A.; Steward, B.L.; Birrell, S.J.; Shrestha, D.S.; Kaspar, T.C. Ultrasonic sensing for corn plant canopy characterization. In Proceedings of the ASAE/CSAE Annual International Meeting, Ottawa, ON, Canada, 1–4 August 2004; Volume 8. [Google Scholar]
- Grenzdörffer, G.; Zacharias, P. Bestandeshöhenermittlung landwirtschaftlicher Kulturen aus UAS-Punktwolken. DGPF Tagungsband 2014, 23, 1–8. [Google Scholar]
- Zhu, Q.; Lin, H.S. Comparing ordinary kriging and regression kriging for soil properties in contrasting landscapes. Pedosphere 2010, 20, 594–606. [Google Scholar] [CrossRef]

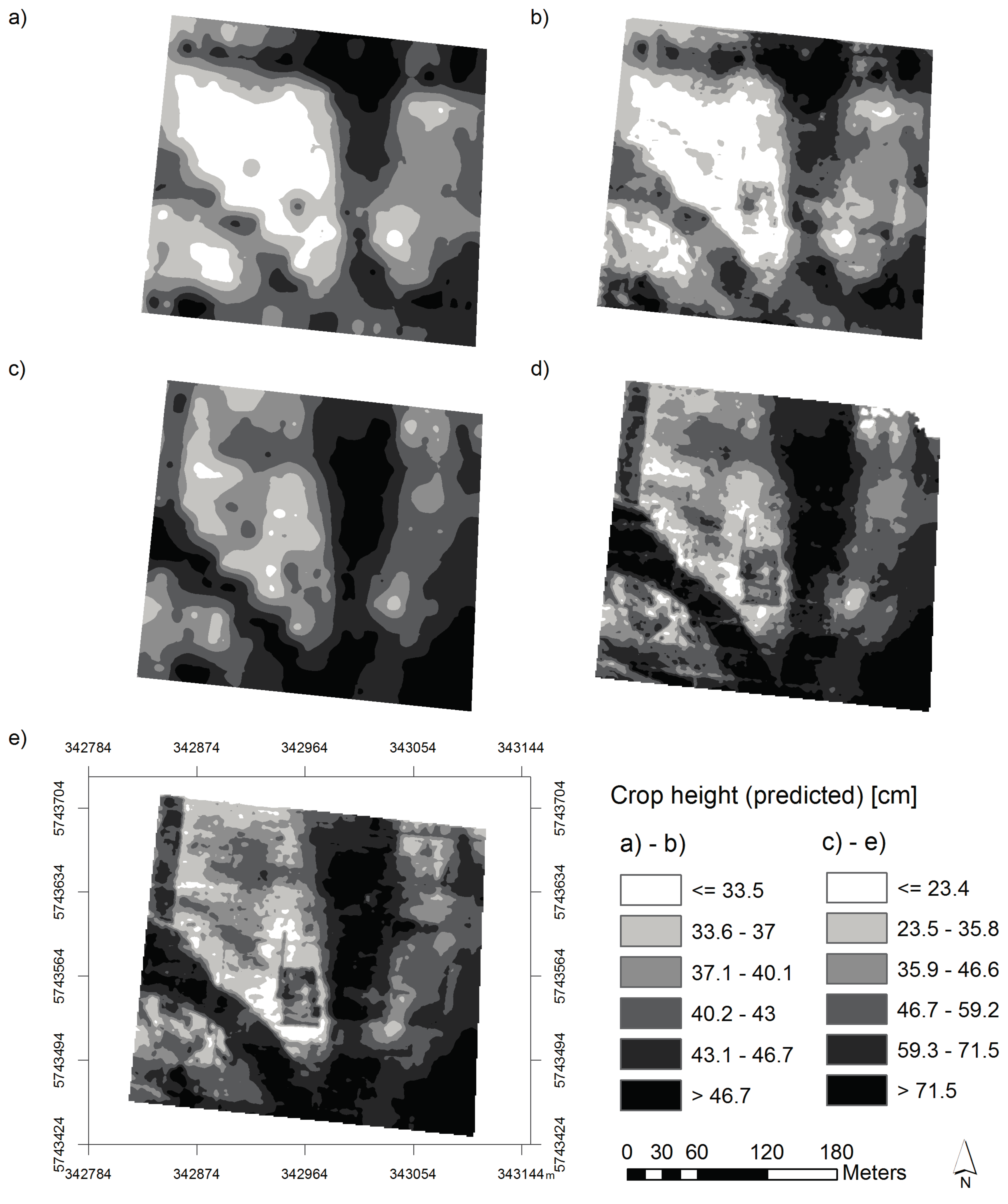
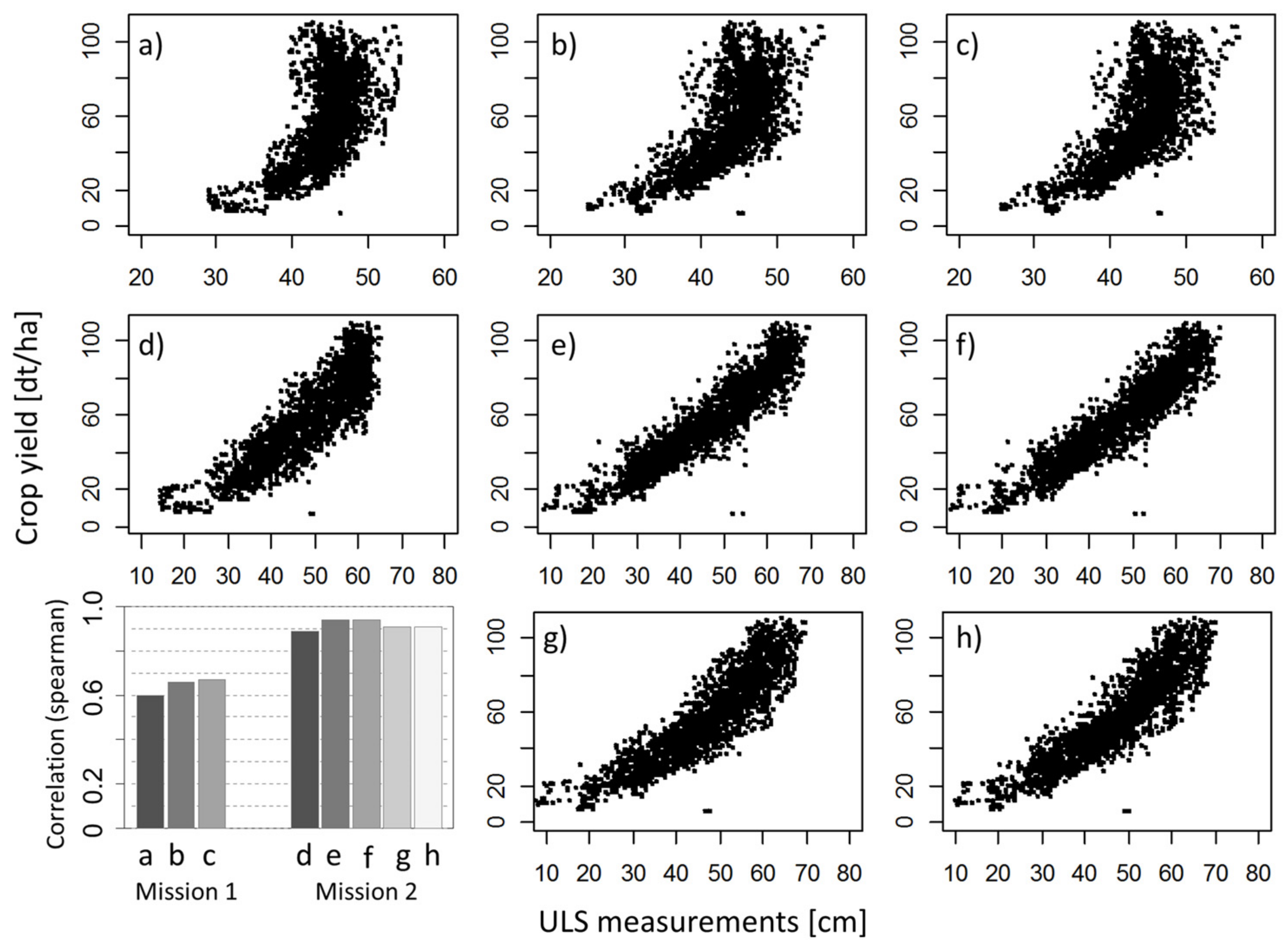
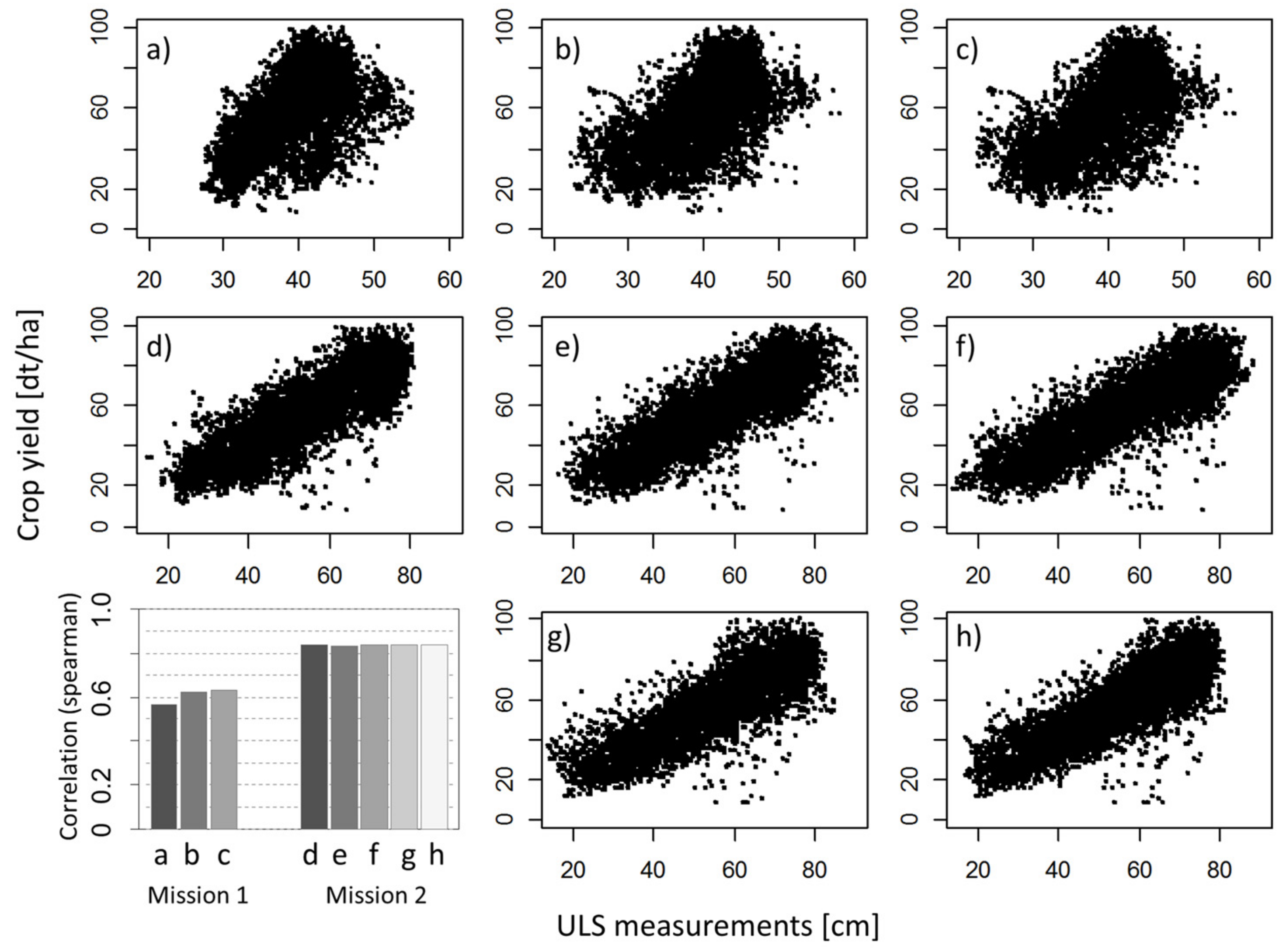
| Field | Mission | Variable | Crop Height (cm) RMSE | Crop Height r2 | FM (Kg·m−2) RMSE | FM r2 | Range | Nugget-to-Sill Ratio (NSR) |
|---|---|---|---|---|---|---|---|---|
| A | 1 | ULS | 2.50 | 0.90 | 0.46 | 0.76 | 53.61 | 18.55 |
| A | 1 | UAV CHM | 4.00 | 0.73 | 0.57 | 0.61 | 127.49 | 26.23 |
| A | 1 | UAV ortho | 5.09 | 0.57 | 0.50 | 0.66 | 110.89 | 18.30 |
| A | 2 | ULS | 4.55 | 0.92 | 0.57 | 0.81 | 108.84 | 10.98 |
| A | 2 | UAV CHM | 3.13 | 0.96 | 0.45 | 0.88 | 112.99 | 14.14 |
| A | 2 | UAV ortho | 9.08 | 0.67 | 0.45 | 0.88 | 106.60 | 10.60 |
| B | 1 | ULS | 3.52 | 0.71 | 0.39 | 0.82 | 152.89 | 6.13 |
| B | 1 | UAV CHM | 4.05 | 0.62 | 0.57 | 0.62 | 131.04 | 5.22 |
| B | 1 | UAV ortho | 3.16 | 0.77 | 0.46 | 0.76 | 72.88 | 11.88 |
| B | 2 | ULS | 3.27 | 0.96 | 0.34 | 0.90 | 100.50 | 4.44 |
| B | 2 | UAV CHM | 10.43 | 0.56 | 0.73 | 0.55 | 91.82 | 6.13 |
| B | 2 | UAV ortho | 5.51 | 0.88 | 0.32 | 0.92 | 74.56 | 8.01 |
| Field | Mission | Covariate | Crop Height (cm) RMSE | Crop Height r2 | FM (Kg·m−2) RMSE | FM r2 | Range | NSR |
|---|---|---|---|---|---|---|---|---|
| A | 1 | – | 3.45 | 0.78 | 0.63 | 0.55 | 57.01 | 18.80 |
| A | 1 | CHM | 2.60 | 0.87 | 0.51 | 0.70 | 116.38 | 36.22 |
| A | 1 | CHM+ortho | 2.57 | 0.88 | 0.49 | 0.73 | 118.53 | 38.49 |
| A | 2 | – | 6.12 | 0.83 | 0.72 | 0.70 | 107.53 | 12.02 |
| A | 2 | CHM | 2.62 | 0.97 | 0.44 | 0.89 | 103.49 | 53.72 |
| A | 2 | CHM+ortho | 3.51 | 0.95 | 0.47 | 0.87 | 23.51 | 12.29 |
| A | 2/1 | CHM | 4.46 | 0.91 | 0.62 | 0.77 | 139.99 | 15.03 |
| A | 2/1 | CHM+ortho | 4.37 | 0.92 | 0.60 | 0.79 | 124.82 | 14.53 |
| B | 1 | – | 4.62 | 0.50 | 0.55 | 0.65 | 145.21 | 15.88 |
| B | 1 | CHM | 3.76 | 0.67 | 0.42 | 0.80 | 170.85 | 9.00 |
| B | 1 | CHM+ortho | 3.64 | 0.69 | 0.40 | 0.81 | 158.64 | 14.88 |
| B | 2 | – | 4.93 | 0.90 | 0.45 | 0.83 | 85.32 | 0.00 |
| B | 2 | CHM | 3.32 | 0.96 | 0.29 | 0.93 | 101.03 | 14.87 |
| B | 2 | CHM+ortho | 3.54 | 0.95 | 0.33 | 0.91 | 99.02 | 19.21 |
| B | 2/1 | CHM | 3.42 | 0.95 | 0.36 | 0.89 | 130.45 | 9.11 |
| B | 2/1 | CHM+ortho | 4.80 | 0.91 | 0.44 | 0.84 | 125.49 | 10.12 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schirrmann, M.; Hamdorf, A.; Giebel, A.; Gleiniger, F.; Pflanz, M.; Dammer, K.-H. Regression Kriging for Improving Crop Height Models Fusing Ultra-Sonic Sensing with UAV Imagery. Remote Sens. 2017, 9, 665. https://doi.org/10.3390/rs9070665
Schirrmann M, Hamdorf A, Giebel A, Gleiniger F, Pflanz M, Dammer K-H. Regression Kriging for Improving Crop Height Models Fusing Ultra-Sonic Sensing with UAV Imagery. Remote Sensing. 2017; 9(7):665. https://doi.org/10.3390/rs9070665
Chicago/Turabian StyleSchirrmann, Michael, André Hamdorf, Antje Giebel, Franziska Gleiniger, Michael Pflanz, and Karl-Heinz Dammer. 2017. "Regression Kriging for Improving Crop Height Models Fusing Ultra-Sonic Sensing with UAV Imagery" Remote Sensing 9, no. 7: 665. https://doi.org/10.3390/rs9070665
APA StyleSchirrmann, M., Hamdorf, A., Giebel, A., Gleiniger, F., Pflanz, M., & Dammer, K.-H. (2017). Regression Kriging for Improving Crop Height Models Fusing Ultra-Sonic Sensing with UAV Imagery. Remote Sensing, 9(7), 665. https://doi.org/10.3390/rs9070665