On-Ground Retracking to Correct Distorted Waveform in Spaceborne Global Navigation Satellite System-Reflectometry
Abstract
:1. Introduction
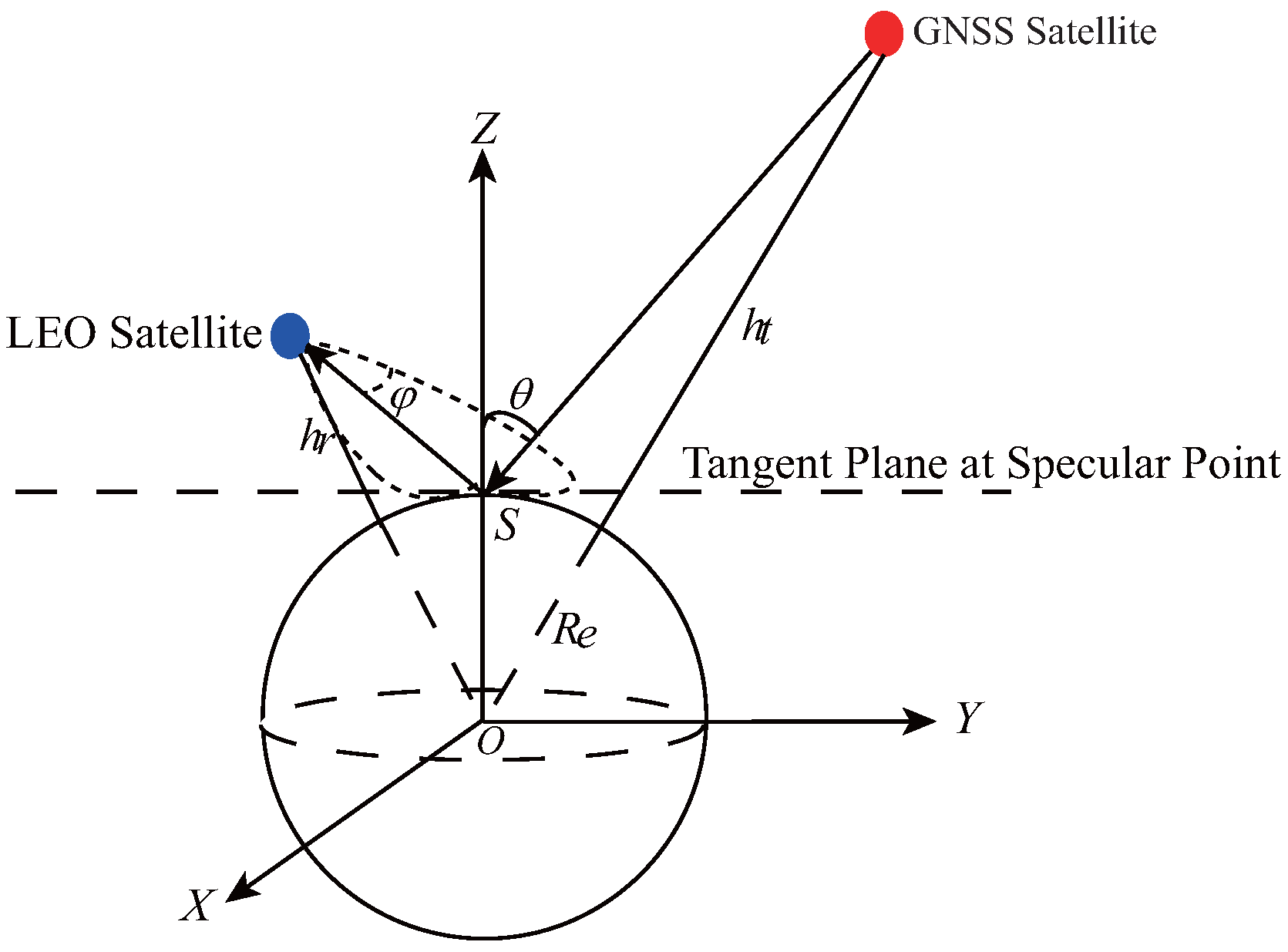
2. Simulation Scenario and Models
2.1. Scenario
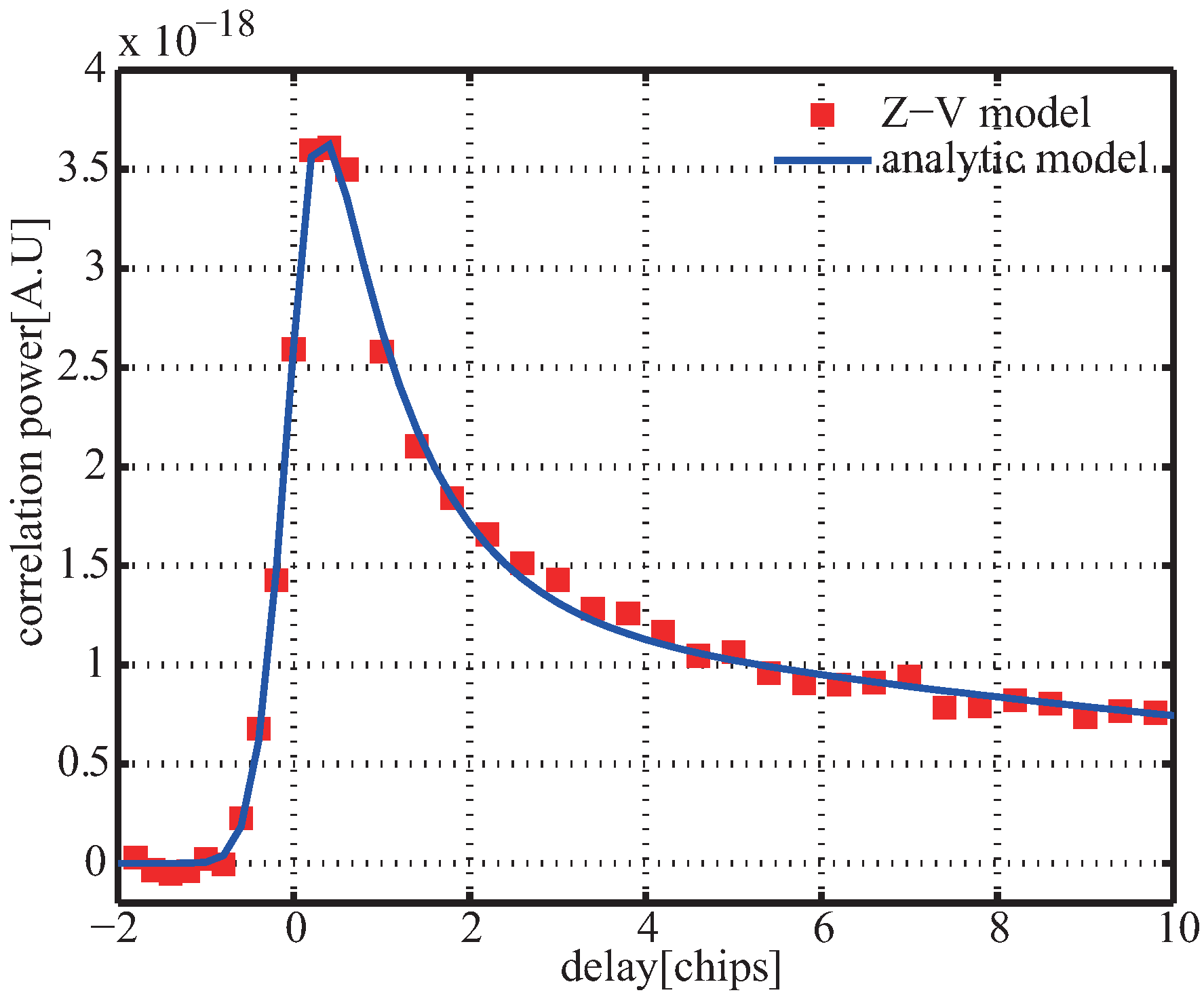
2.2. GNSS-R Scattering Models
2.3. Noise Models
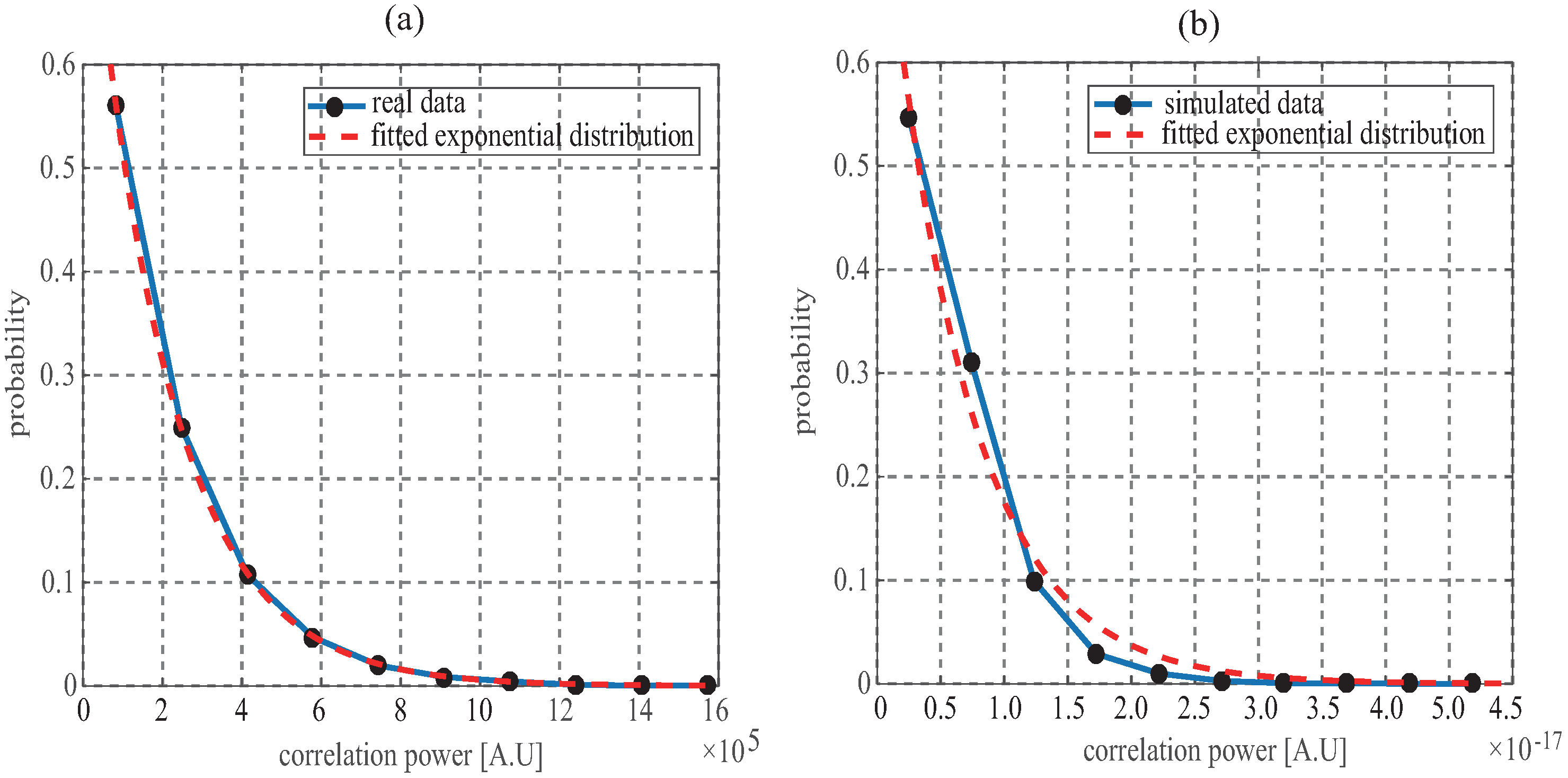
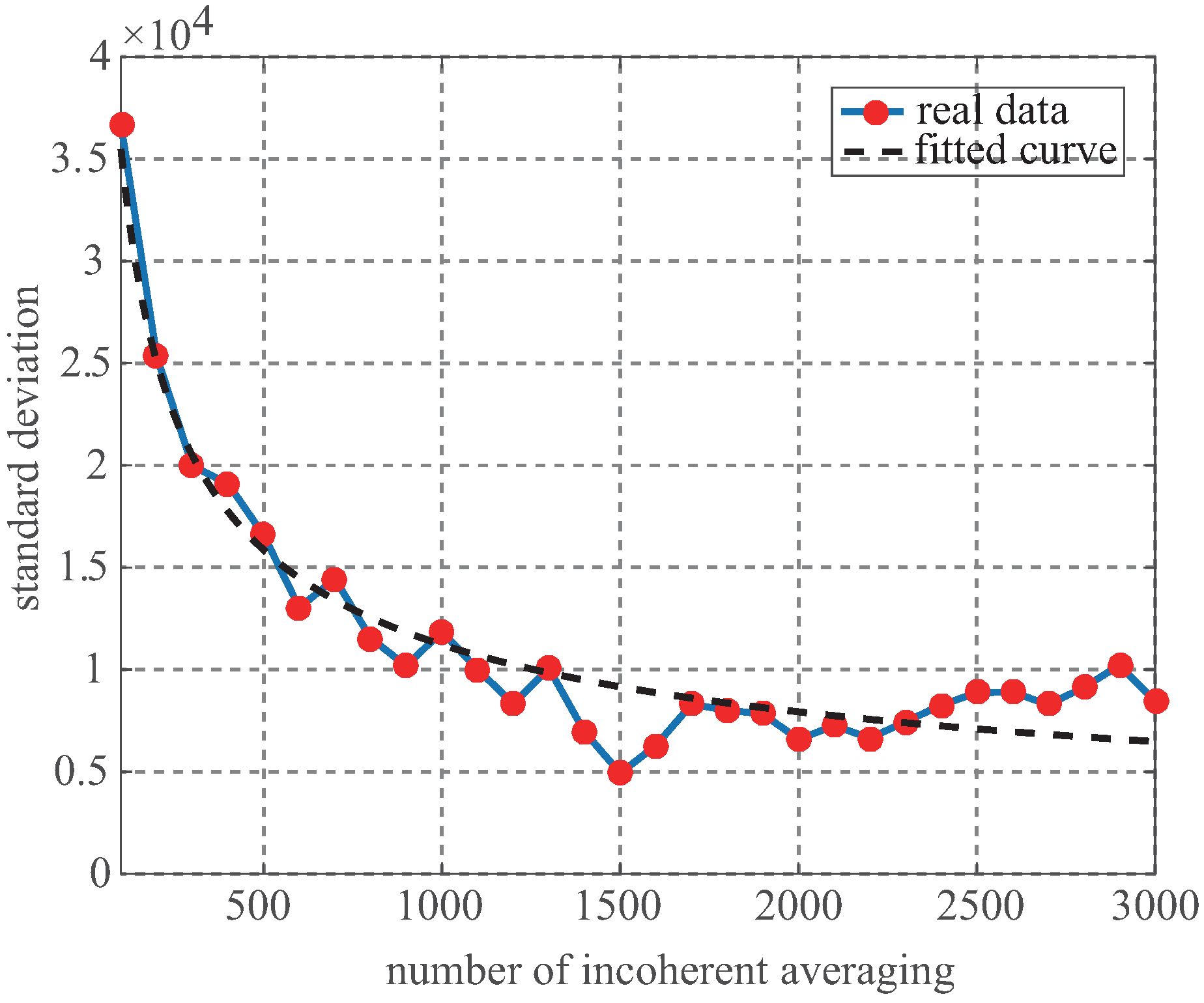
3. Speckle Noise vs. Incoherent Averaging
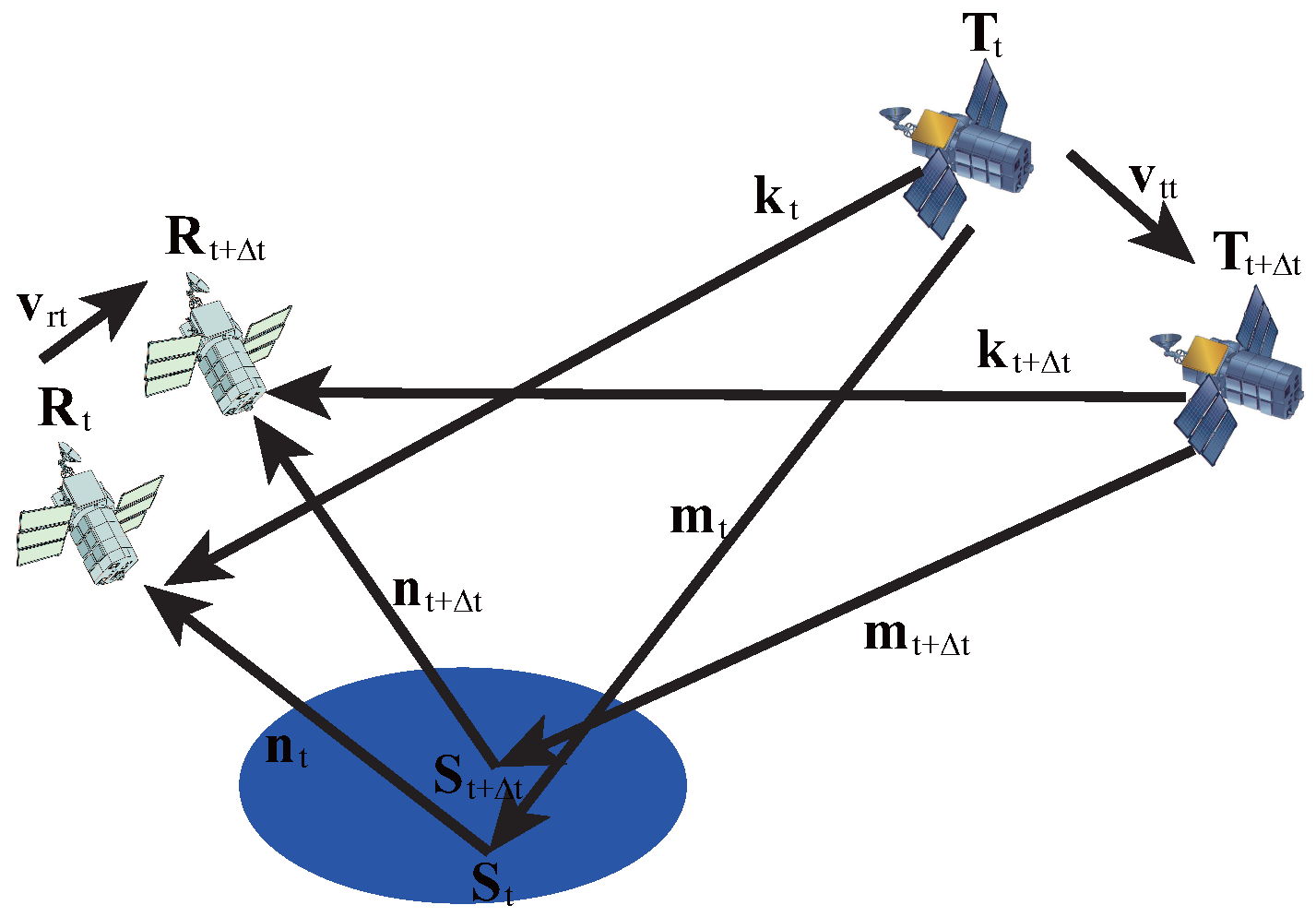
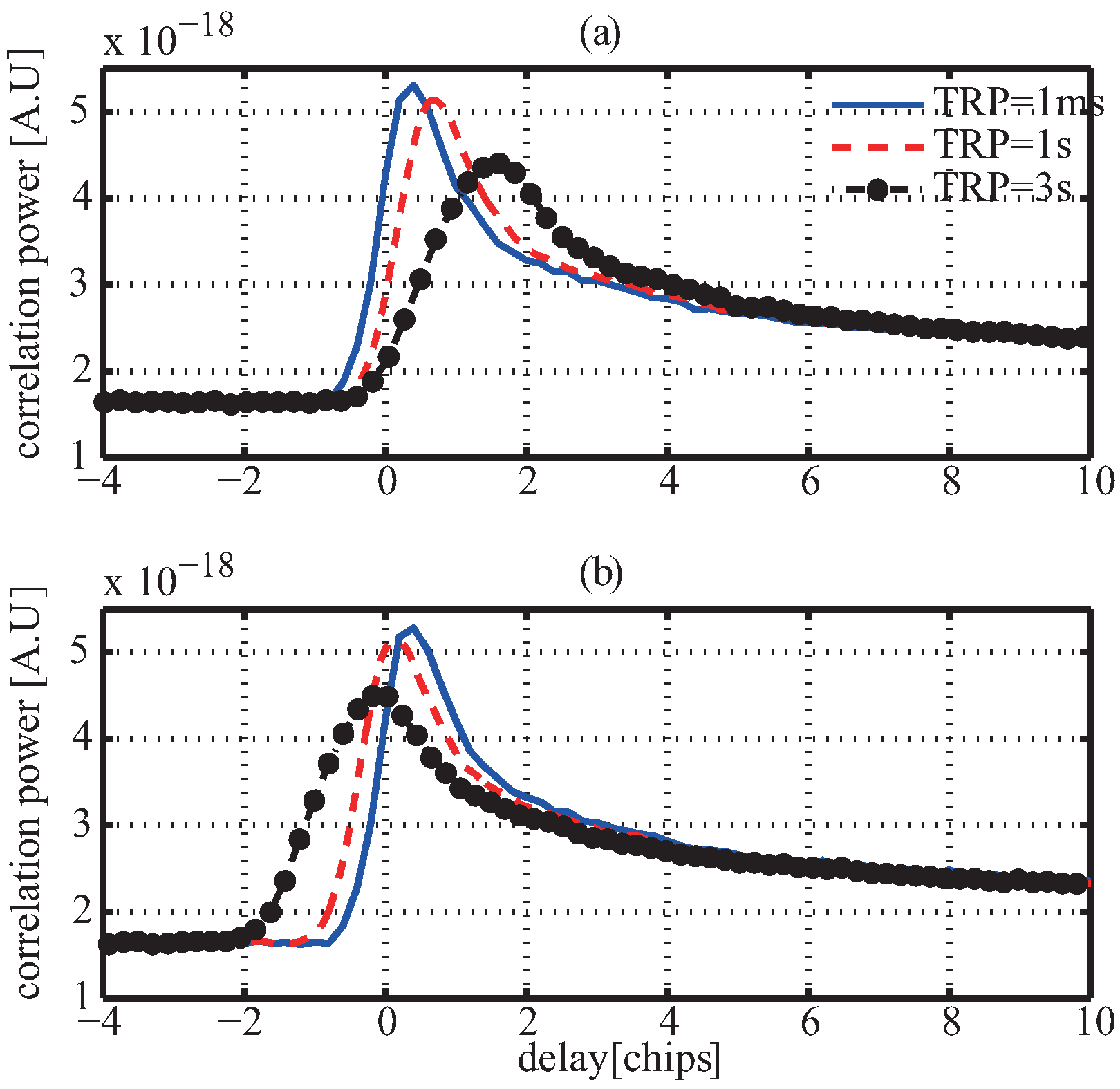
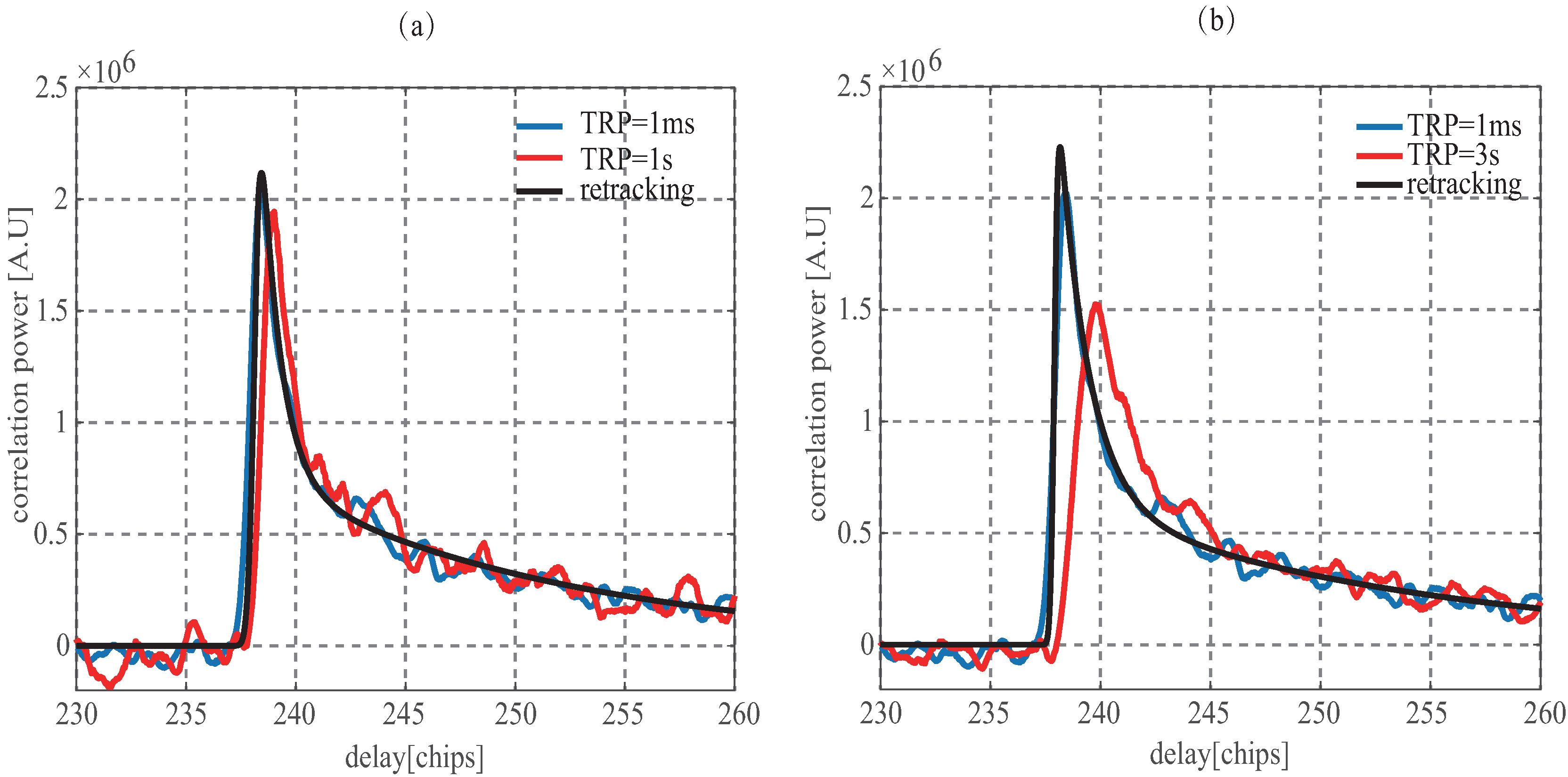
4. Influence of Dynamic on Waveform
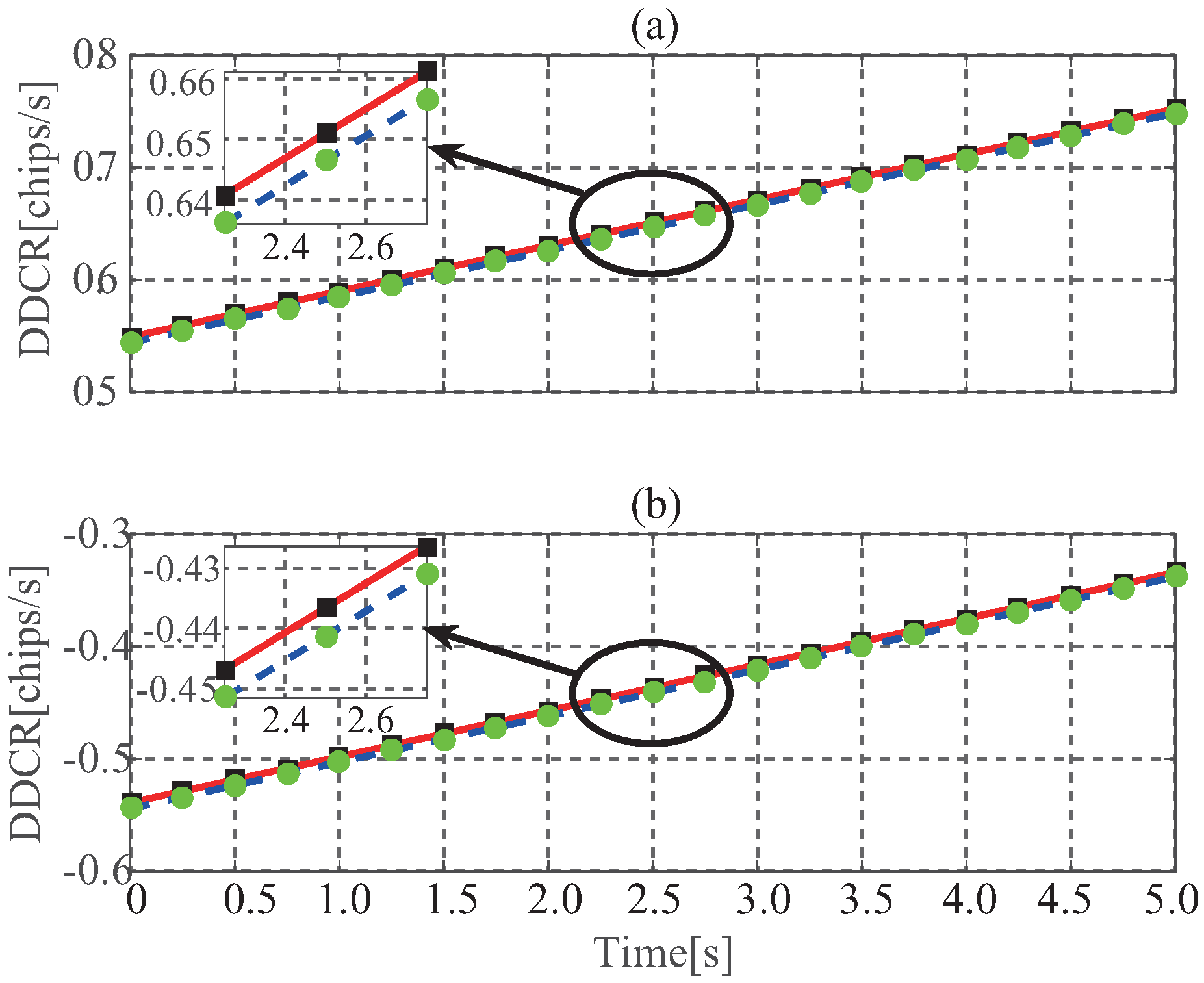
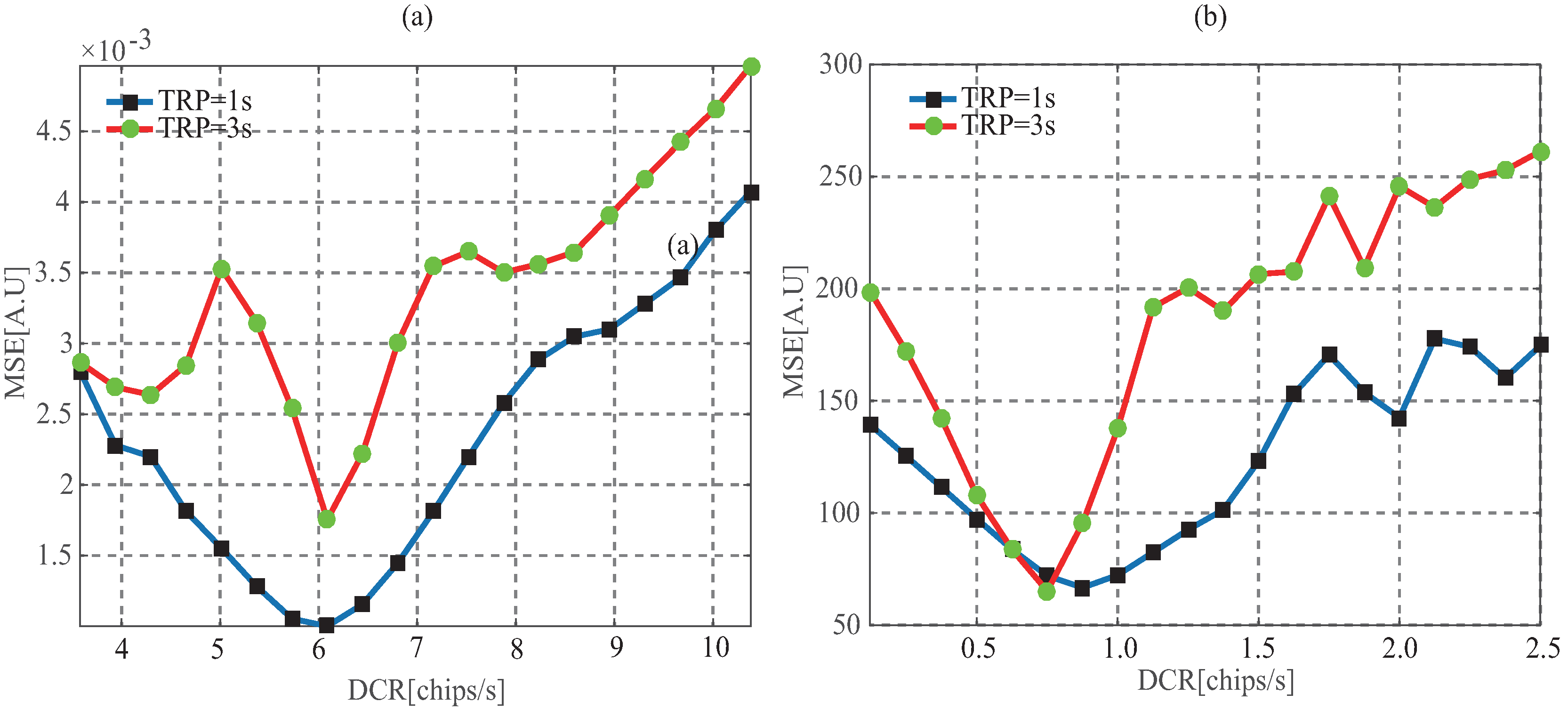
4.1. Delay Change Rate
5. Influence on Feature Parameter
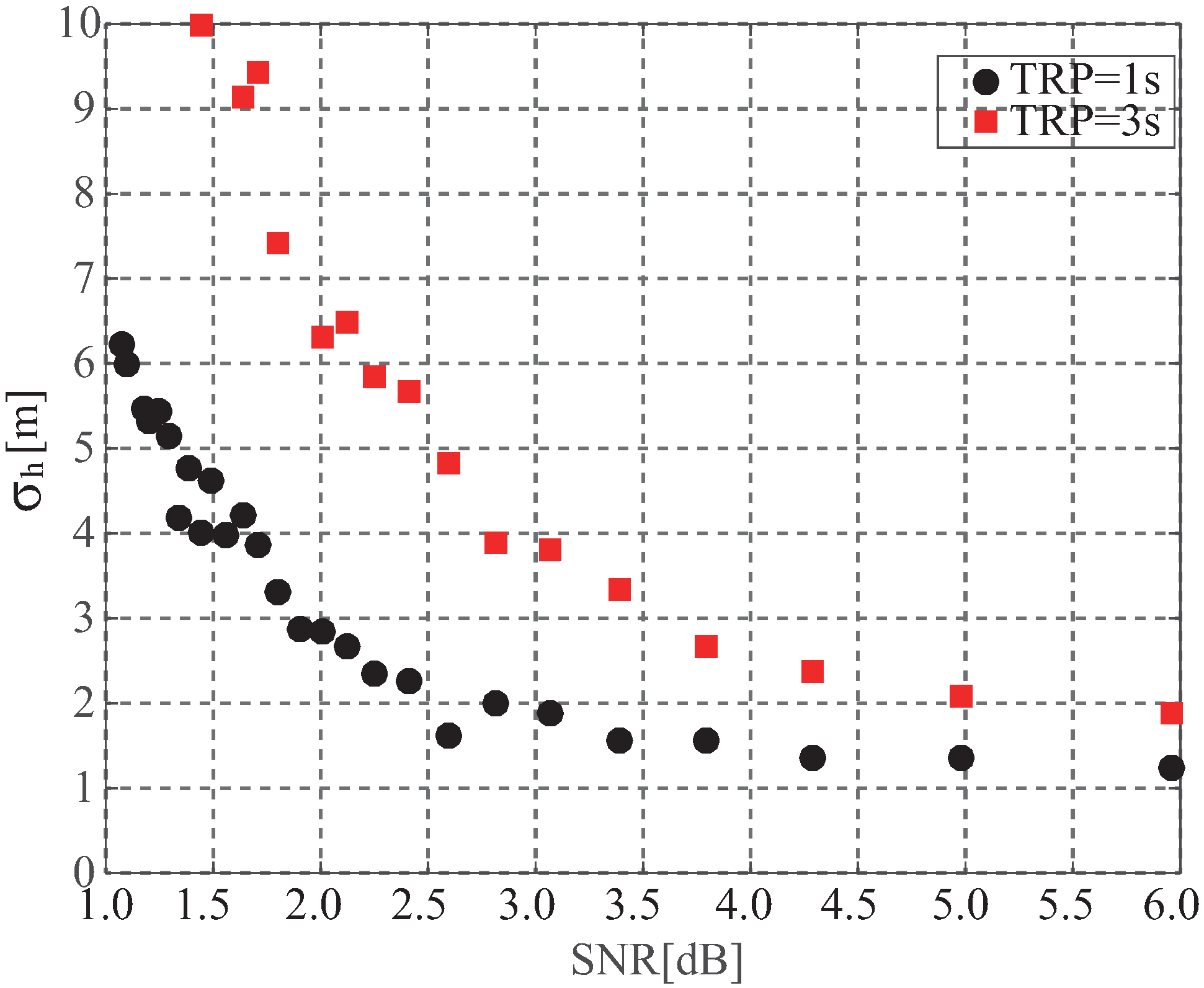
5.1. Sea Surface Height
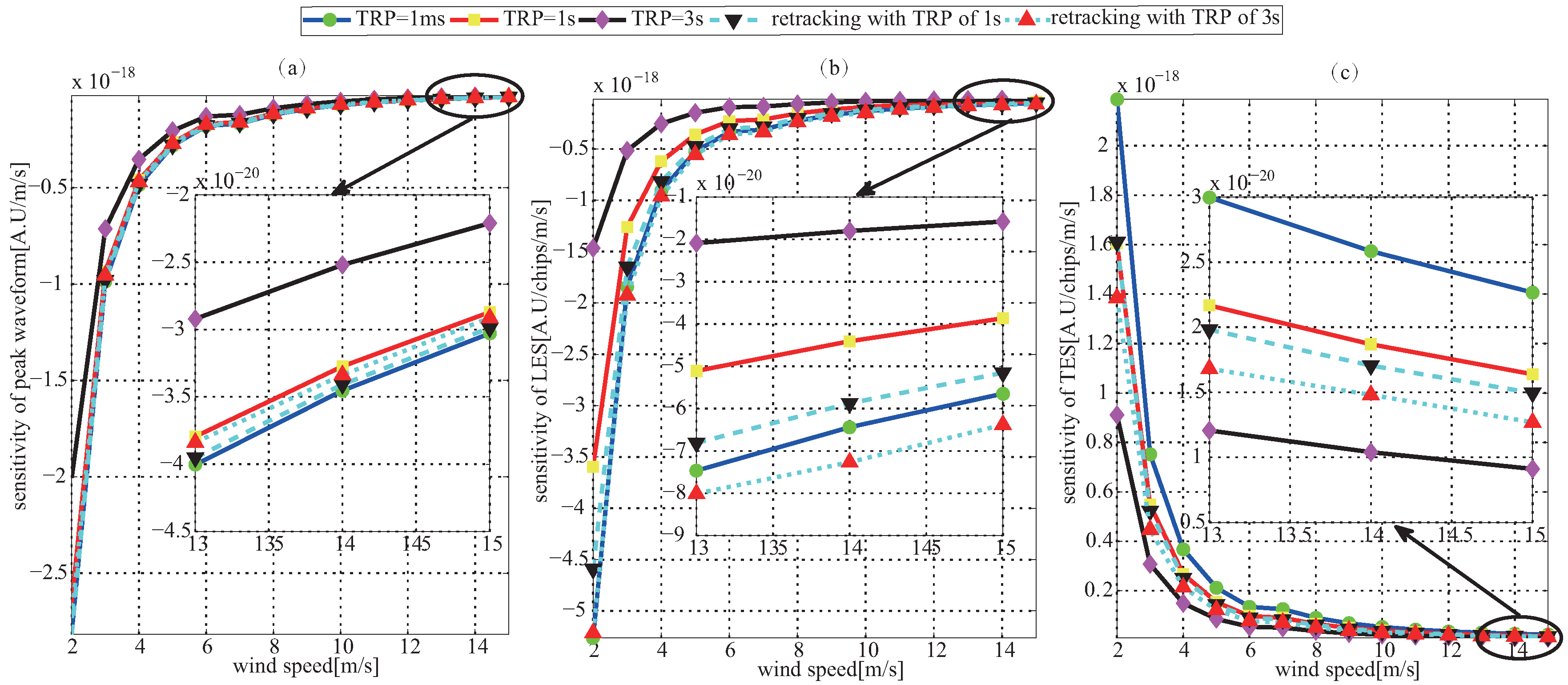
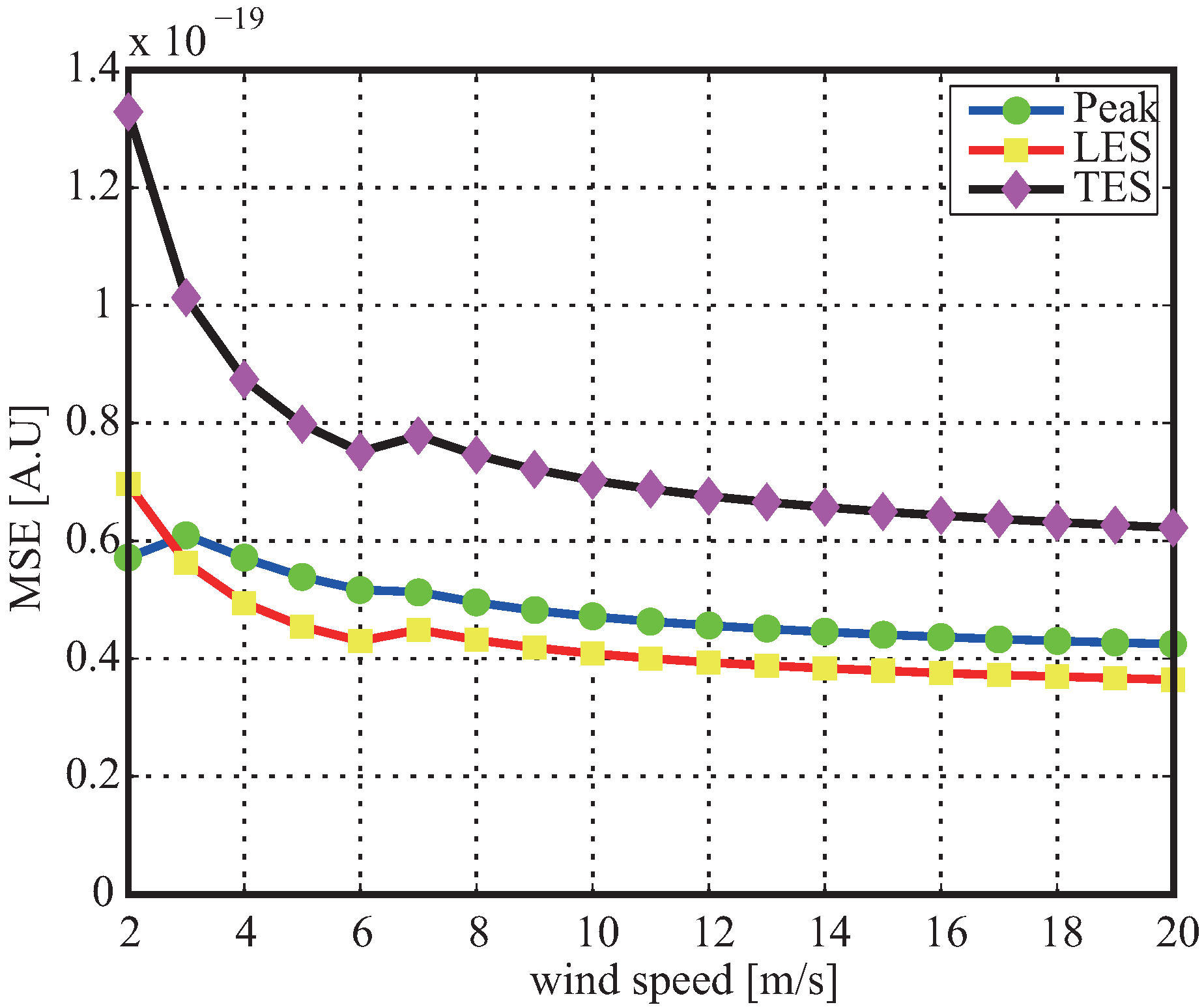
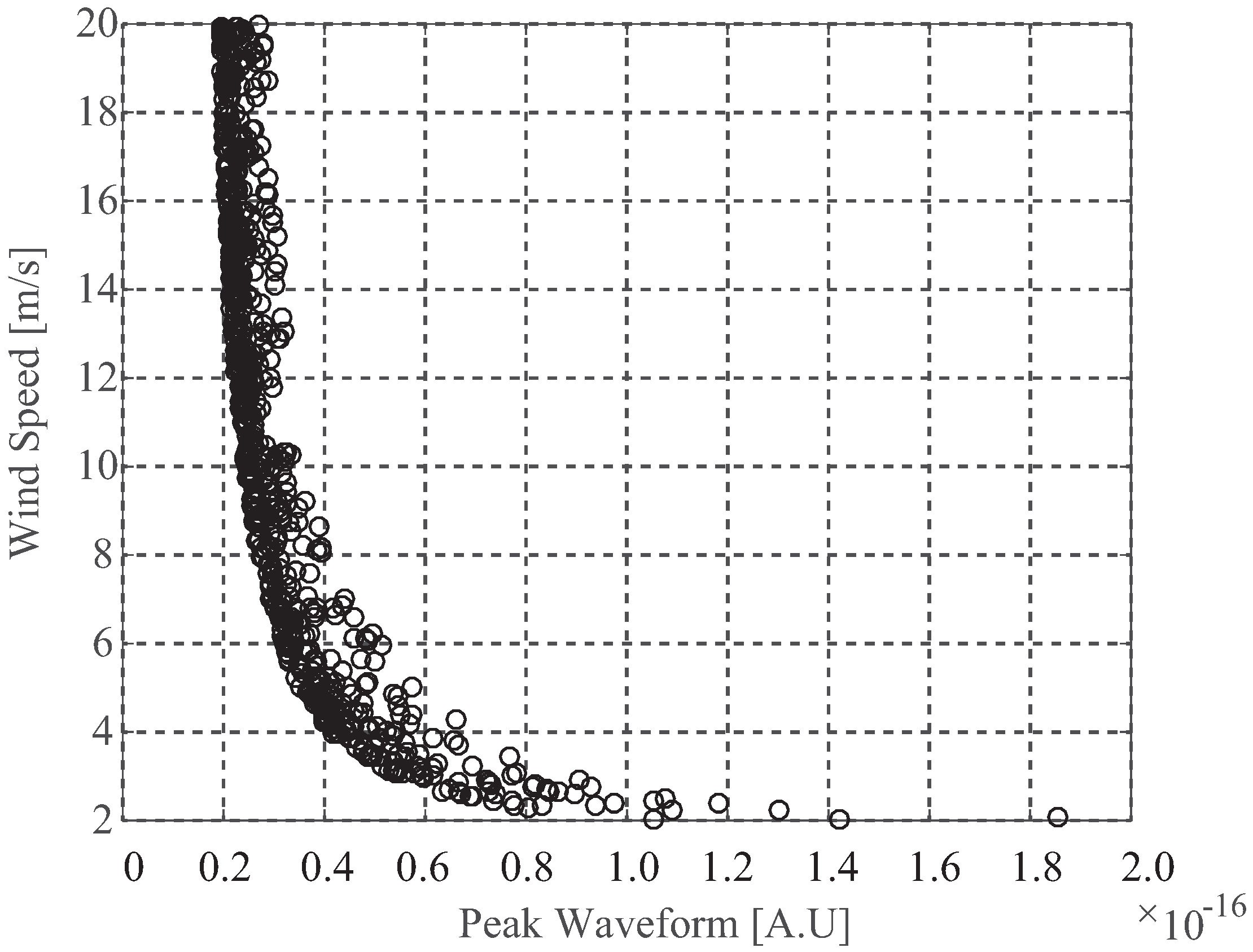
5.2. Wind Speed
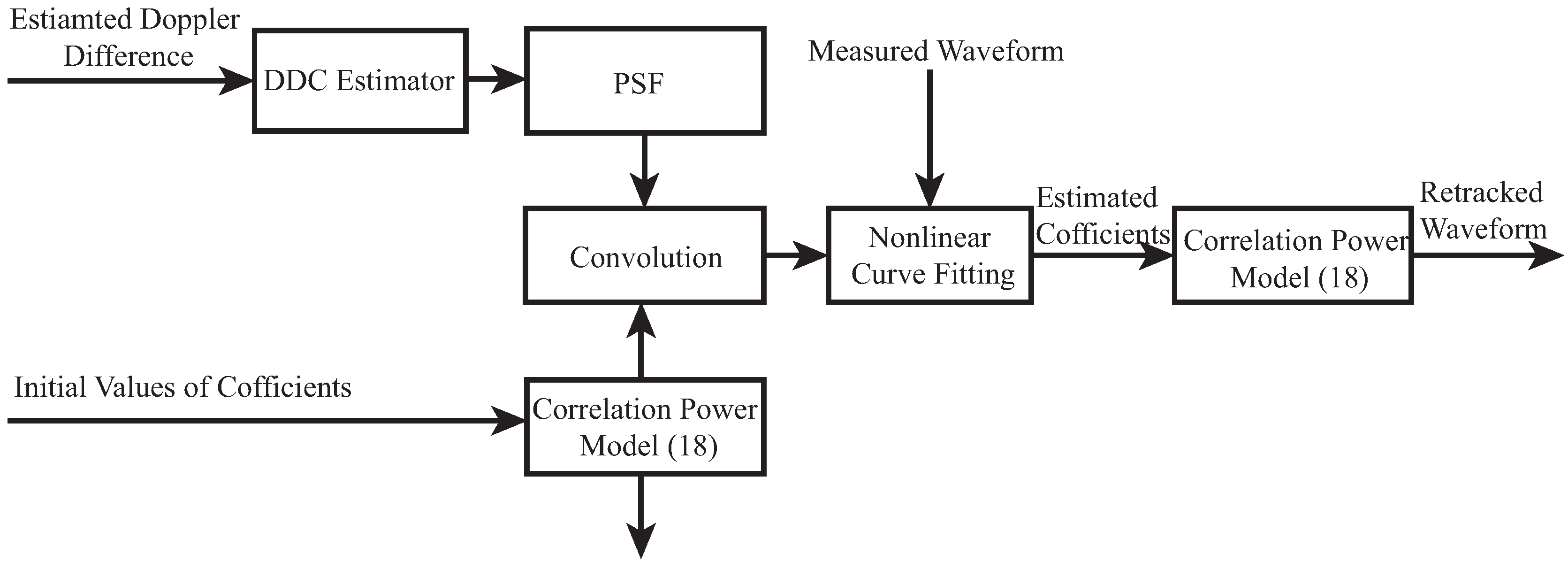
6. Methodology of Retracking
- using estimated Doppler difference between direct and reflected signals to produce the DDCR and PSF;
- developing model of the distorted waveform using convolution Equation (18) and the initial coefficients of the Model (20);
- fitting the distorted model above with the measured waveform using nonlinear least square to obtain the optimal coefficients of (20);
- reconstructing the pure waveform using the Model (20) and the estimated coefficients above.
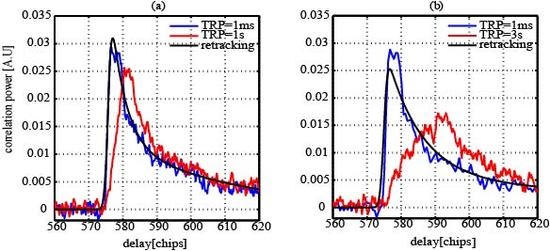
7. Results and Discussion
7.1. Validation Using UK-DMC Data
7.2. Validation Using UK-TDS-1 Data
7.3. Validation Using Simulation
7.4. Comparison with CLS and TSVD Result
7.5. Influence of DCR Accuracy
8. Retrieval Performance
- generating randomly 1000 sets of wind speed, incident angle, the moving direction of LEO and GNSS satellites as the input parameters of the models in Section 2;
- using scattering scenario and models in Section 2 to produce 1000 delay waveform corrupted by the noises and the dynamic of GNSS-R geometry;
- retracking above delay waveforms to obtain pure ones through proposed methods in Section 6 and estimating the retracked and non-retracked waveforms’ features defined by (11)∼(14);
- developing retrieval approaches and evaluating the root mean square error (RMSE) of sea surface height and wind speed measured using retracked and non-retracked waveforms.
8.1. Sea Surface Height
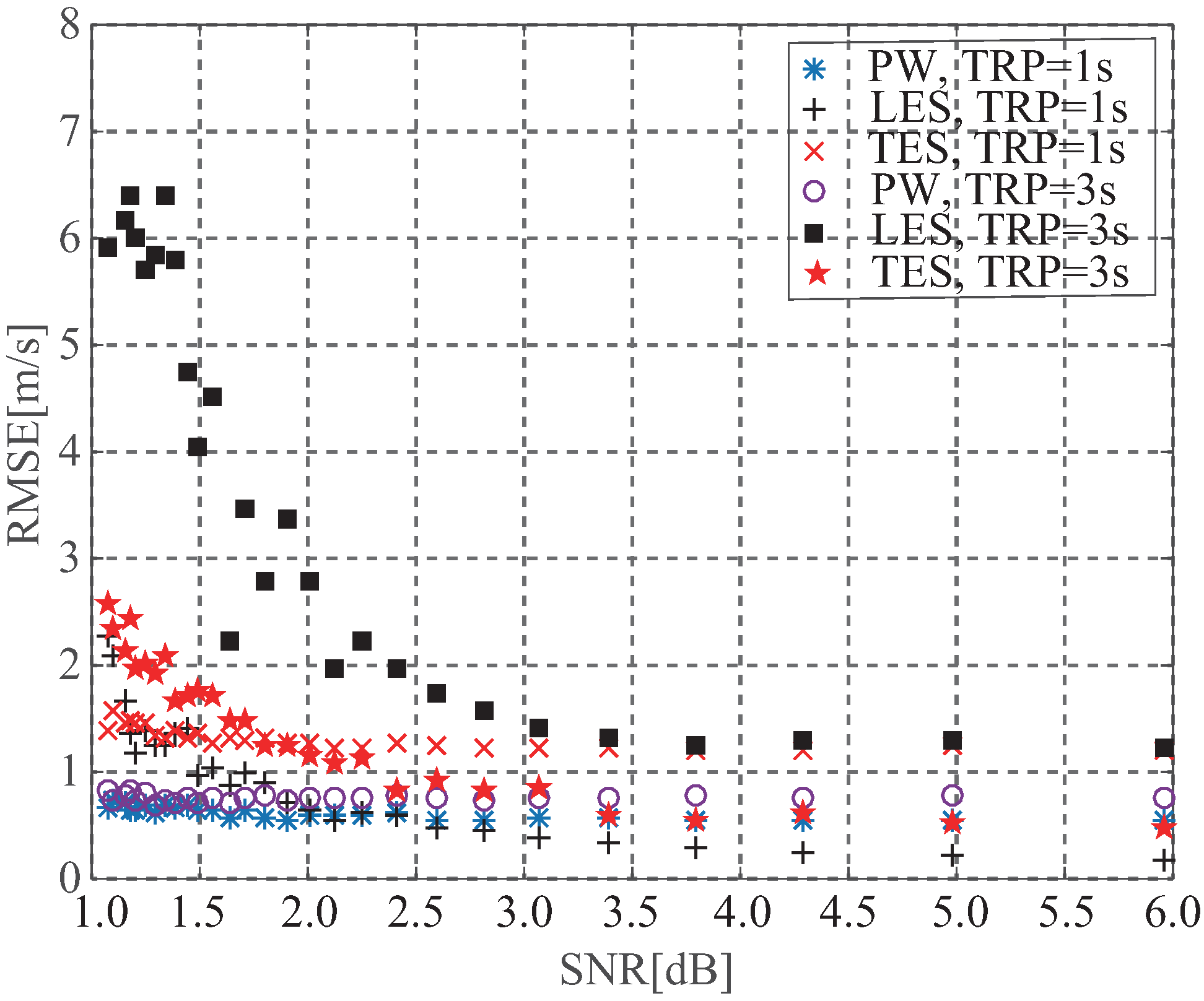
8.2. Wind Speed
- case 1: the single observable of the delay waveform, such as PW, is the input of neural network;
- case 2: the three observable are all considered as the input of the neural network.
8.3. Performance vs. SNR
9. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Derivation of Delay Difference Change Rate
References
- Martin-Neira, M. A passive reflectometry and interferometry system (PARIS): Applocation to ocean altimetry. Ecol. Soc. Am. J. 1993, 17, 331–335. [Google Scholar]
- Lowe, S.; LaBrecque, J.L.; Zuffada, C.; Romans, L.J.; Young, L.E.; Hajj, G.A. First spaceborne observation of an Earth-reflected GPS signal. Radio Sci. 2002, 37, 1–28. [Google Scholar] [CrossRef]
- Gleason, S.T.; Yiping, S.H.S.; Gommenginger, C.; Mackin, S.; Adjrad, M.; Unwin, M. Detection and processing of bistatically reflected GPS signlas from low Earth orbit for the purpose of ocean remote sensing. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1229–1241. [Google Scholar] [CrossRef]
- Unwin, M.; Duncan, S.; Jales, P.; Blunt, P.; Brenchley, M. Implementing GNSS reflectometry in space on the TechDemoSat-1 misson. In Proceedings of the 27th International Technical Meeting of The Satellite Division of the Institute of Navigation, Tampa, FL, USA, 8–12 September 2014. [Google Scholar]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Rosello, J. Spcaeboren GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef]
- Ruf, C.S.; Gleason, S.; Jelenak, Z.; Katzberg, S.; Ridley, A.; Rose, R.; Scherrer, J.; Zavorotny, V. The CYGNSS nanosatellite constellation hurricane mission. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 214–216. [Google Scholar]
- Clarizia, M.P.; Ruf, C.S.; Jales, P.; Gommenginger, C. Spaceborne GNSS-R minimum variance wind speed estimator. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6829–6843. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S. Wind speed retrieval algorithm for the Cyclone Global Navigation Satellite System (CYGNSS) mission. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4419–4432. [Google Scholar] [CrossRef]
- Rodriguez, N.; Garrison, J.L. Generalized linear observables for ocean wind retrieval from calibrated GNSS-R delay-Doppler maps. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1142–1155. [Google Scholar] [CrossRef]
- Soisuvarn, S.; Jelenak, Z.; Said, F.; Chang, P.S.; Egido, A. The GNSS reflectometry response to the ocean surface winds and waves. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4678–4699. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.; Cipollini, P.; Zuffada, C. First spaceborne observation of sea surface height using GPS-reflectometry. Geophys. Res. Lett. 2016, 43, 767–774. [Google Scholar]
- Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A. Demonstrating soil moisture remote sensing with observation from the UK TechDemoSat-1 satelllite mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Pablos, M.; Foti, G.; Gommenginger, C.P.; Liu, P.W.; Judge, J. Sensitivity of GNSS-R spaceborne observations to soil miosture and vegetation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4730–4742. [Google Scholar] [CrossRef]
- Hu, C.; Benson, C.; Rizos, C.; Li, Q. Single-pass sub-meter space-based GNSS-R ice altimetry: Results from TDS-1. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.; Moloney, C. Neural networks based sea ice detection and concentration retrieval from GNSS-R delay-Doppler maps. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Schiavulli, D.; Frappart, F.; Ramillaume, G.; Darrozes, J.; Nunziata, F.; Migliaccio, M. Observing sea/ice transition using radar images generated from TechDemoSat-1 delay Doppler maps. IEEE Geosci. Remote Sens. Lett. 2017, 13, 734–738. [Google Scholar] [CrossRef]
- Schiavulli, D.; Nunziata, F.; Pugliano, G.; Migliaccio, M. Reconstruction of the normalized radar cross section field from GNSS-R delay-Doppler map. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1573–1583. [Google Scholar] [CrossRef]
- Valencia, E.; Camps, A.; Marchan-Hernandez, J.; Park, H.; Bosch-Lluis, X.; Rodriguez-Alvares, N. Ocean surface’s scattering coefficient retrieval by delay-Doppler map inversion. IEEE Geosci. Remote Sens. Lett. 2011, 8, 750–754. [Google Scholar] [CrossRef]
- Tye, J.; Jales, P.; Unwin, M.; Underwood, G. The first application of stare processing to retrieve mean square slope using the SGE-ReSI GNSS-R experimenntal on TDS-1. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4669–4677. [Google Scholar] [CrossRef]
- Gleason, S. Remote Sensing of Ocean, Ice and Land Surfaces Using Bistatically Scattered GNSS Signals from Low Earth Orbit. Ph.D. Thesis, University Surrey, Guildford, UK, 2006. [Google Scholar]
- Park, H.; Camps, A.; Valencia, E.; Rodriguez-Alvatez, N.; Bosch-Lluis, X.; Ramos-Perez, I.; Carreno-Luengo, H. Retracking considerations in soaceborne GNSS-R altimetry. GPS Solut. 2012, 16, 507–518. [Google Scholar]
- Park, H.; Pascual, D.; Camps, A.; Martin, F.; Alonso-Arroyo, A.; Carreno-Luengo, H. Analysis of spaceborne GNSS-R delay-Doppler tracking. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1481–1492. [Google Scholar] [CrossRef]
- Park, H.; Valencia, E.; Camps, A.; Rius, A.; Ribo, S.; Martin-Neira, M. Delay tracking in spaceborne GNSS-R ocean altimetry. IEEE Geosci. Remote Sens. Lett. 2013, 10, 57–61. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Chapron, B.; Katsaros, K. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. 1997, 102, 15781–15795. [Google Scholar] [CrossRef]
- Migliaccio, M.; Ferrara, G.; Gambardella, A.; Nunziata, F.; Sorrentino, A. A physically consistent speckle model for Marine SLC SAR images. IEEE J. Ocean. Eng. 2007, 32, 839–847. [Google Scholar] [CrossRef]
- Goodman, J. Some fundamental properties of speckle. J. Opt. Soc. Am. 1976, 66, 1145–1150. [Google Scholar] [CrossRef]
- Gleason, S.; Gommenginger, C.; Cromwell, D. Fading statistics and sensing accuracy of ocean scattered GNSS and altimetry signals. Adv. Space Res. 2010, 46, 208–220. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive, Volume II: Radar Remote Sensing and Surface Scattering and Emissition Theory; Artech House: Norwood, MA, USA, 1982. [Google Scholar]
- Carreno-Luengo, H.; Csmps, A.; Ramos-Perez, I.; Rius, A. Experimental evaluation of GNSS-Reflectometry altimetric precison using P(Y) and C/A signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1493–1500. [Google Scholar] [CrossRef]
- Mashburn, J.; Axelrad, P.; Lowe, S.T.; Larson, K.M. An assessment of the precision and accuracy of altimetry retrievals for a monterey bay GNSS-R experiment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4660–4668. [Google Scholar] [CrossRef]
- Kostelecký, J.; Klokočník, J.; Wangner, C.A. Geometry and accuracy of reflecting points in bistatic satellite altimetry. J. Geod. 2005, 79, 421–430. [Google Scholar] [CrossRef]
- Gleason, S. Spaceborne-based GNSS scatterometry: Ocean wind sensing using an empirically calibrated model. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4853–4863. [Google Scholar] [CrossRef]
- Haupt, S.E.; Pasini, A.; Marzban, C. Artificial Intelligent Methods in the Environmental Sciences; Springer: Berlin, Germany, 2009. [Google Scholar]


| Parameter | Units | Value |
|---|---|---|
| GNSS Satellite Height | km | 20,200 |
| LEO Satellite Height | km | 659 |
| GNSS Satellite speed | km | 3.07 |
| LEO Satellite speed | km | 7.60 |
| Earth Radius | km | 6371 |
| Maximum Gain | dB | 12 |
| 3 dB Beam Width | deg | 25 |
| incident angle | deg | [0:50] |
| Moving direction of GNSS Satellite | deg | [0:360] |
| Moving direction of LEO Satellite | deg | [0:360] |
| Coherent integration time | ms | 1 |
| Incoherent Integration time | s | 16 |
| Tracking Refresh Period | ms | [1, 1000, 3000] |
| Wind Speed W | m/s | [1:20] |
| Methods | 1 s | 3 s | |||
|---|---|---|---|---|---|
| UK-DMC | UK-TDS-1 | UK-DMC | UK-TDS-1 | ||
| proposed | 0.026 | 70.10 | 0.044 | 61.80 | |
| CLS | 0.041 | 85.82 | 0.078 | 89.94 | |
| 0.103 | 111.90 | 0.115 | 202.57 | ||
| TSVD | 0.044 | 88.75 | 0.130 | 95.43 | |
| 0.116 | 86.79 | 0.329 | 202.74 | ||
| Parameter | 1 ms [m] | 1 s [m] | 3 s [m] | ||
|---|---|---|---|---|---|
| re. | non-re. | re. | non-re. | ||
| std | 4.66 | 6.19 | 40.98 | 11.49 | 125.45 |
| Observable | 1 ms [m/s] | 1 s [m/s] | 3 s [m/s] | ||
|---|---|---|---|---|---|
| re. | non-re. | re. | non-re. | ||
| PW | 2.24 | 2.25 | 2.55 | 2.43 | 3.37 |
| LES | 1.48 | 1.92 | 2.88 | 2.42 | 4.42 |
| TES | 1.59 | 1.84 | 2.33 | 2.51 | 4.95 |
| combined | 1.27 | 1.37 | 1.73 | 1.45 | 1.88 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Yang, D.; Li, W.; Yang, W. On-Ground Retracking to Correct Distorted Waveform in Spaceborne Global Navigation Satellite System-Reflectometry. Remote Sens. 2017, 9, 643. https://doi.org/10.3390/rs9070643
Wang F, Yang D, Li W, Yang W. On-Ground Retracking to Correct Distorted Waveform in Spaceborne Global Navigation Satellite System-Reflectometry. Remote Sensing. 2017; 9(7):643. https://doi.org/10.3390/rs9070643
Chicago/Turabian StyleWang, Feng, Dongkai Yang, Weiqiang Li, and Wei Yang. 2017. "On-Ground Retracking to Correct Distorted Waveform in Spaceborne Global Navigation Satellite System-Reflectometry" Remote Sensing 9, no. 7: 643. https://doi.org/10.3390/rs9070643
APA StyleWang, F., Yang, D., Li, W., & Yang, W. (2017). On-Ground Retracking to Correct Distorted Waveform in Spaceborne Global Navigation Satellite System-Reflectometry. Remote Sensing, 9(7), 643. https://doi.org/10.3390/rs9070643