Convolutional Neural Networks Based Hyperspectral Image Classification Method with Adaptive Kernels
Abstract
:1. Introduction
2. Related Work
2.1. Hand-Crafted Feature Based Methods
2.2. Deep Learning Feature Based Methods
3. MCFSFDP Based CNNs
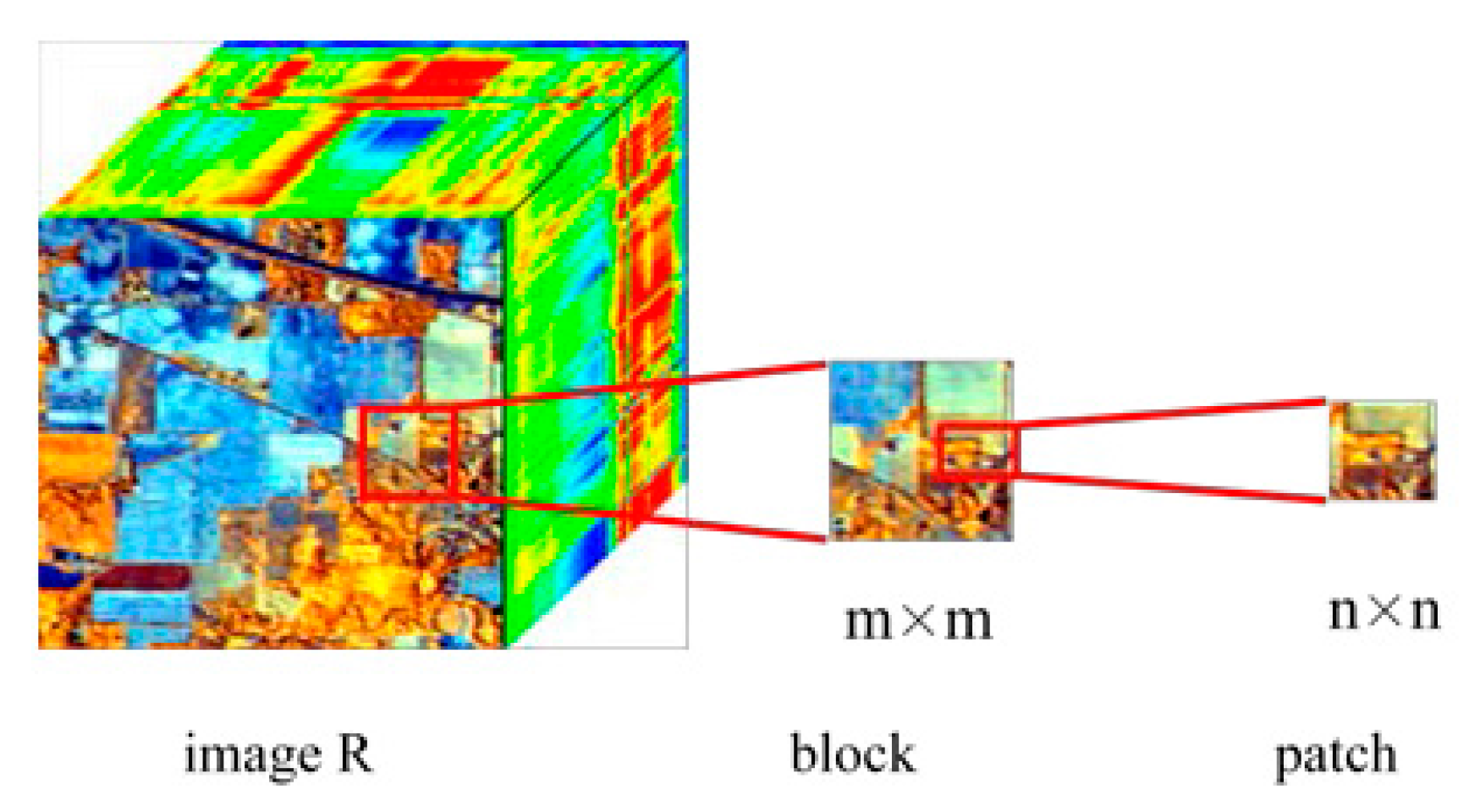
3.1. Data Pre-Processing
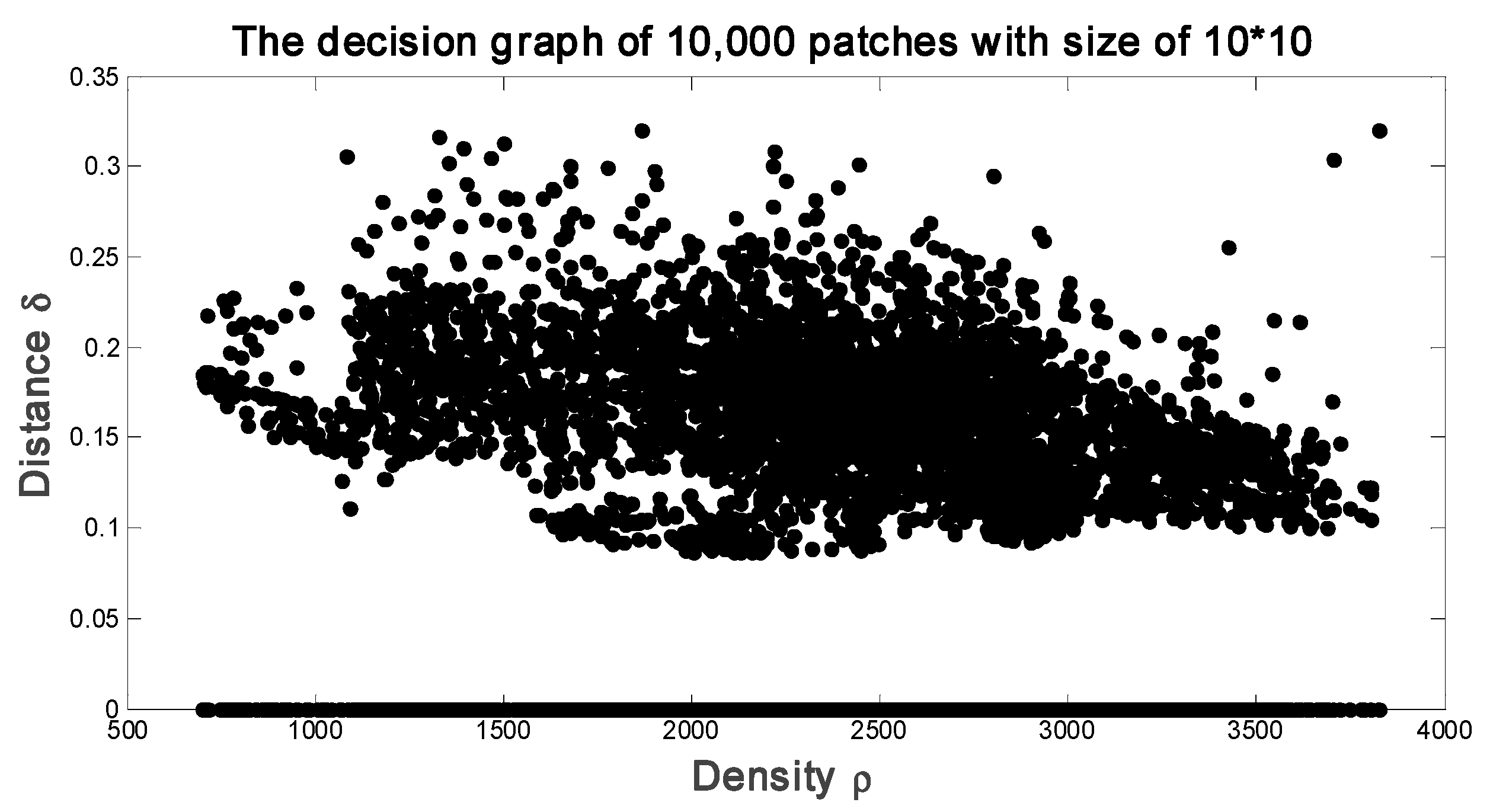
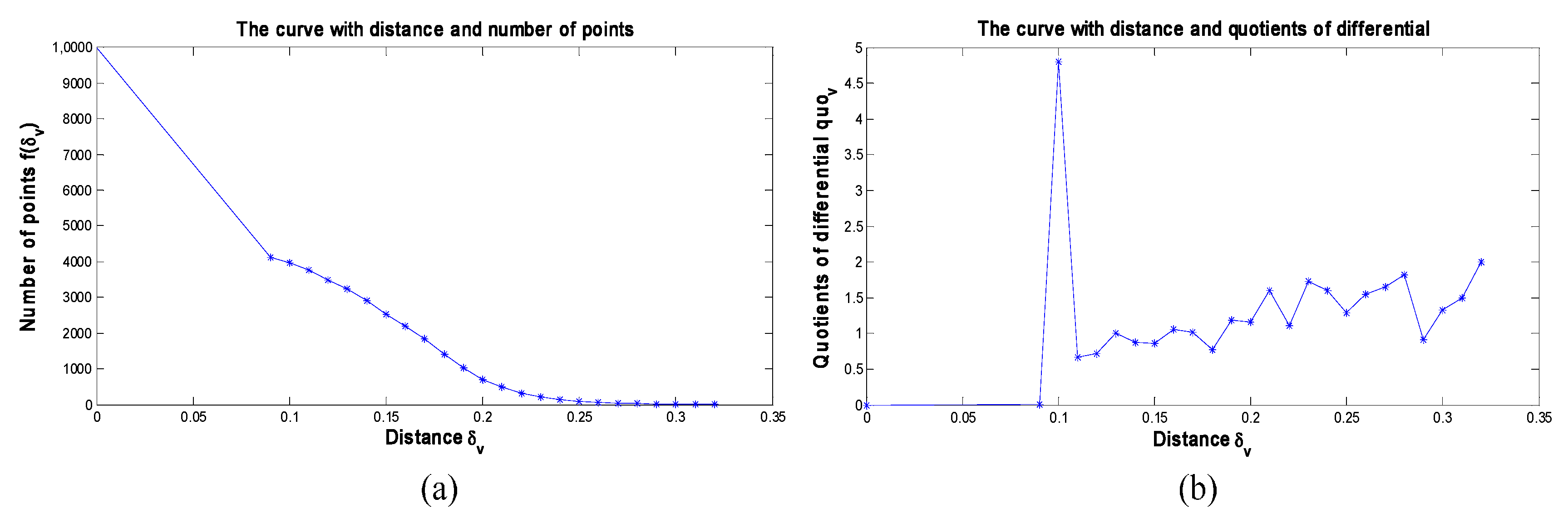
3.2. MCFSFDP Based CNNs Kernels Learning
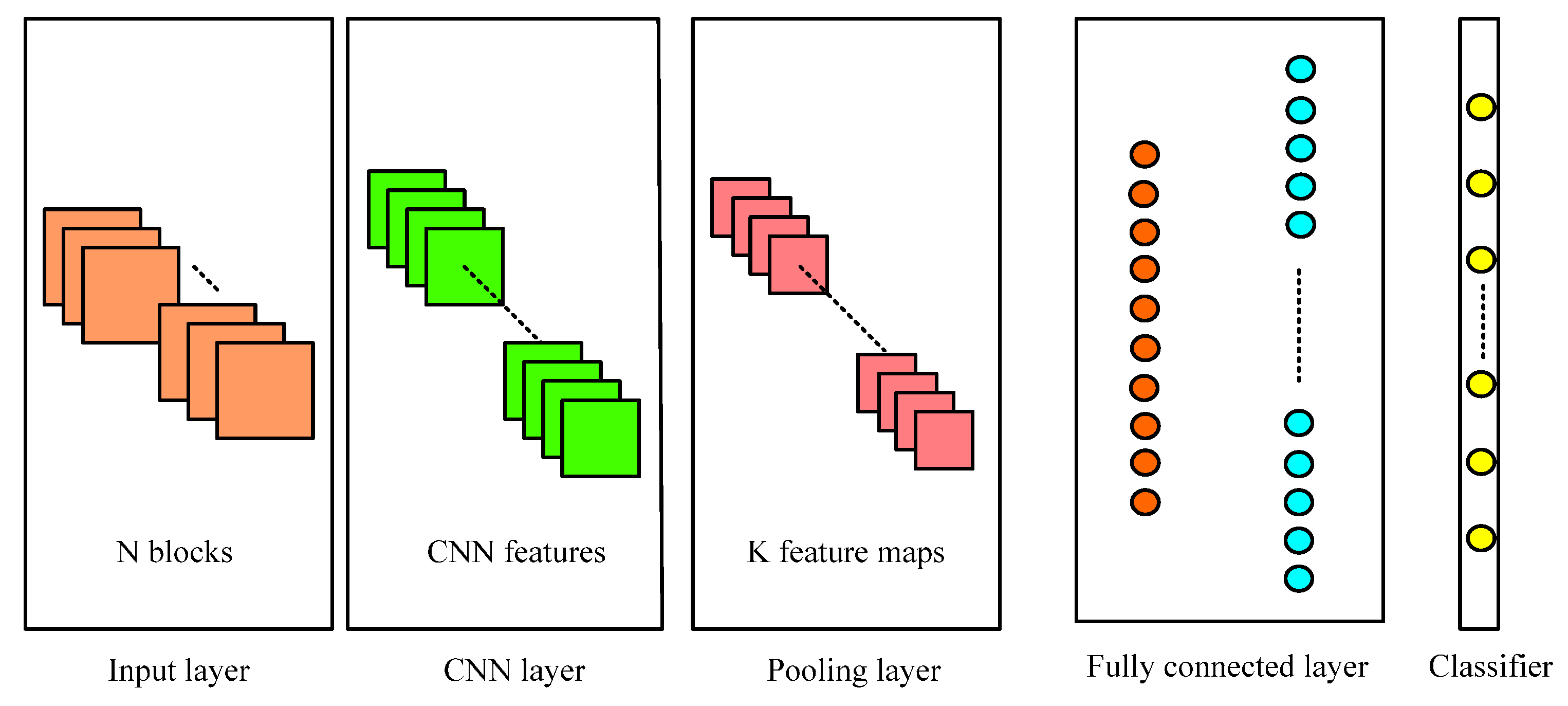
3.3. Convolutional Neural Networks
4. Experiments and Analysis
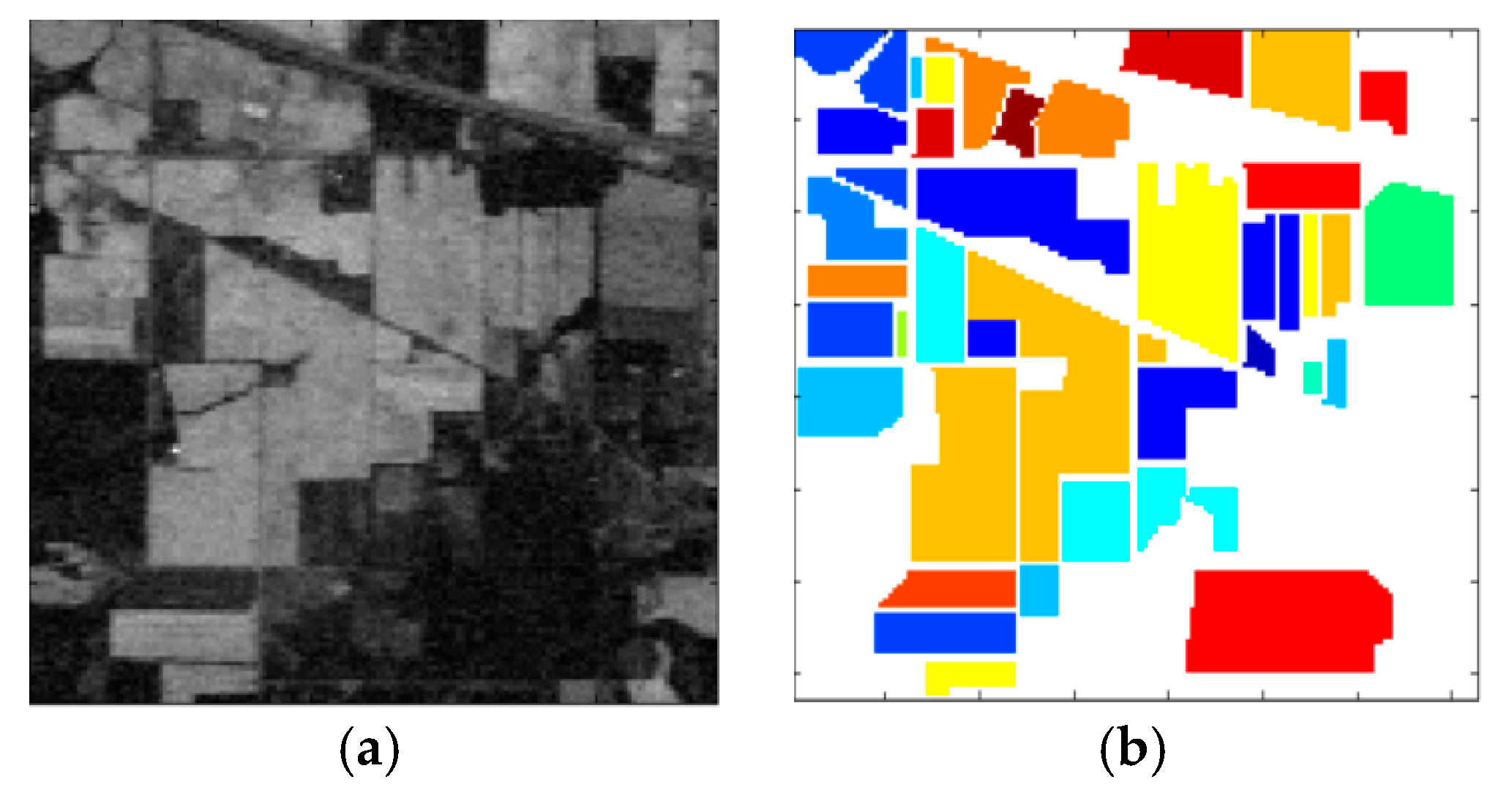
4.1. Datasets
4.2. Experimental Parameter Settings
4.3. Experimental Results
4.3.1. Effectiveness of the Kernels Learned by MCFSFDP
4.3.2. Effectiveness of the Kernels Number Determined by MCFSFDP
4.3.3. Performance Evaluation of MCFSFDP Net
5. Discussion
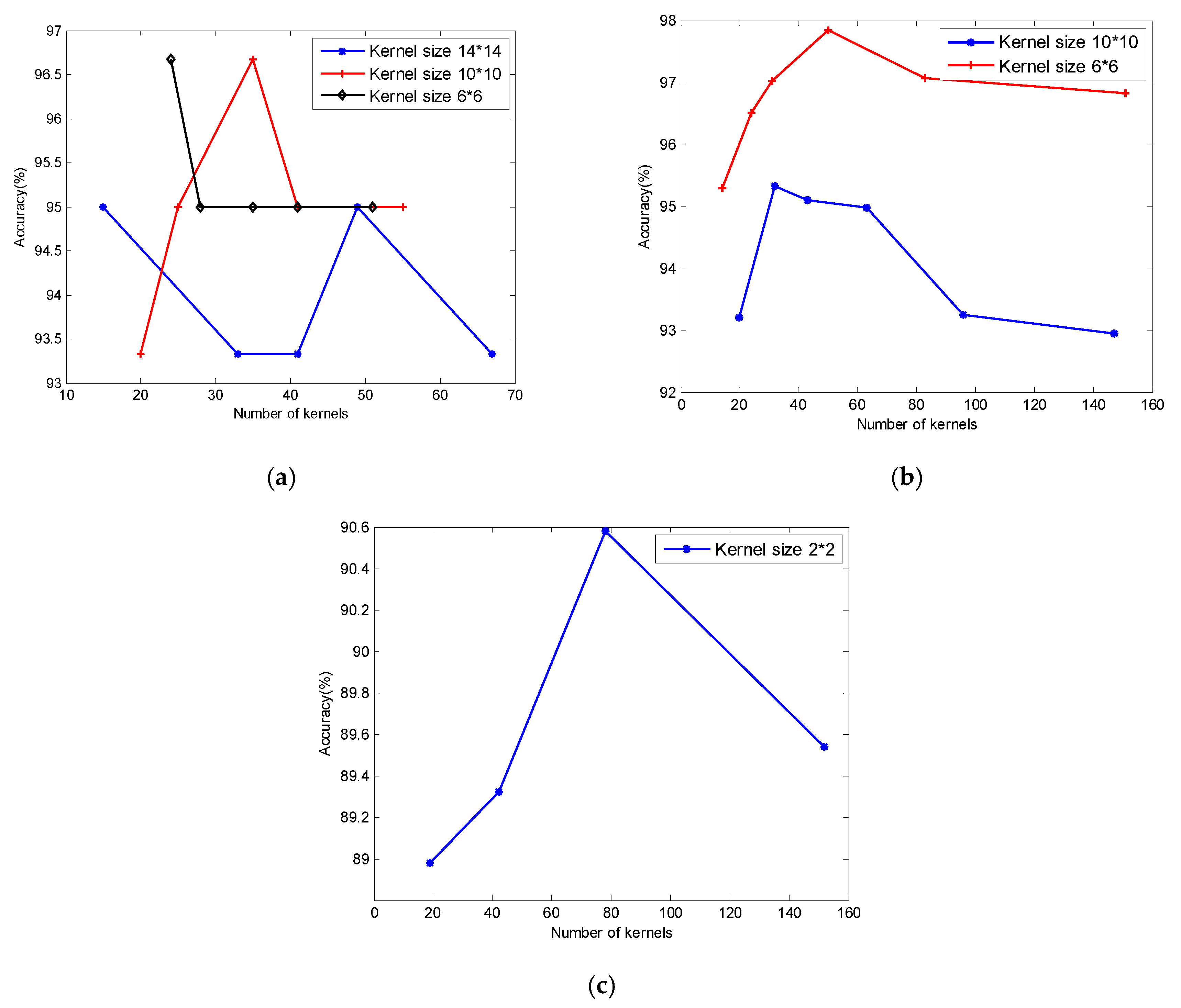
5.1. Effect ofthe Number of Kernels
5.2. Effect of the Kernel Size
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zortea, M.; Martino, M.D.; Serpico, S. A SVM ensemble approach for spectral-contextual classification of optical high spatial resolution imagery. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 1489–1492. [Google Scholar]
- Huang, X.; Zhang, L. An Adaptive Mean-Shift Analysis Approach for Object Extraction and Classification From Urban Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4173–4185. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral-Spatial Hyperspectral Image Segmentation Using Subspace Multinomial Logistic Regression and Markov Random Fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 809–823. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, Y.; Tian, C. Latent subclass learning-based unsupervised ensemble feature extraction method for hyperspectral image classification. Remote Sens. Lett. 2015, 6, 257–266. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, W.; Tian, C.; Li, F.; Zhang, Y. Exploring Structured Sparsity by a Reweighted Laplace Prior for Hyperspectral Compressive Sensing. IEEE Trans. Image Process. 2016, 25, 4974–4988. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, W.; Zhang, Y.; Shen, C.; van den Hengel, A.; Shi, Q. Dictionary learning for promoting structured sparsity in hyperspectral compressive sensing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7223–7235. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep Learning for Remote Sensing Data: A Technical Tutorial on the State of the Art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral-Spatial Feature Extraction for Hyperspectral Image Classification: A Dimension Reduction and Deep Learning Approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, J.; Yuan, Y. Salient Band Selection for Hyperspectral Image Classification via Manifold Ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Yuan, Y.; Yan, P. Visual Saliency by Selective Contrast. IEEE Trans. Circuits Syst. Video Technol. 2013, 23, 1150–1155. [Google Scholar] [CrossRef]
- Längkvist, M.; Kiselev, A.; Alirezaie, M.; Loutfi, A. Classification and Segmentation of Satellite Orthoimagery Using Convolutional Neural Networks. Remote Sens. 2016, 8, 329. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed]
- Timmerman, M.E. Principal Component Analysis (2nd ed.) by I.T. Jolliffe. J. Am. Stat. Assoc. 2003, 98, 1082–1083. [Google Scholar] [CrossRef]
- Rosipal, R.; Krämer, N. Overview and recent advances in partial least squares. In Subspace, Latent Structure and Feature Selection, Proceedings of the Statistical and Optimization Perspectives Workshop (SLSFS 2005), Bohinj, Slovenia, 23–25 February 2005; Springer: Berlin/Heidelber, Germany, 2006; pp. 34–51. [Google Scholar]
- Camps-Valls, G.; Bruzzone, L. Kernel Methods for Remote Sensing Data Analysis; John Wiley & Sons: River Street Hoboken, NJ, USA, 2009. [Google Scholar]
- Myint, S.W. Wavelets for Urban Spatial Feature Discrimination: Comparisons with Fractal, Spatial Autocorrelation, and Spatial Co-occurrence Approaches. Photogramm. Eng. Remote Sens. 2004, 70, 803–812. [Google Scholar] [CrossRef]
- Zhu, C.; Yang, X. Study of remote sensing image texture analysis and classification using wavelet. Int. J. Remote Sens. 1998, 19, 3197–3203. [Google Scholar] [CrossRef]
- Dong, Y.; Forester, B.C.; Milne, A.K. Segmentation of radar imagery using the Gaussian Markov random field model. Int. J. Remote Sens. 1999, 20, 1617–1639. [Google Scholar] [CrossRef]
- Dong, Y.; Forster, B.C.; Milne, A.K. Comparison of radar image segmentation by Gaussian-and Gamma-Markov random field models. Int. J. Remote Sens. 2003, 24, 711–722. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, X.; Huang, B.; Li, P. A pixel shape index coupled with spectral information for classification of high spatial resolution remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2950–2961. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Benediktsson, J.A.; Waske, B.; Bruzzone, L. Morphological Attribute Profiles for the Analysis of Very High Resolution Images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3747–3762. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 35, 1397. [Google Scholar]
- Kang, X.; Li, S.; Benediktsson, J.A. Spectral-Spatial Hyperspectral Image Classification With Edge-Preserving Filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2666–2677. [Google Scholar]
- Kang, X.; Li, S.; Benediktsson, J.A. Feature Extraction of Hyperspectral Images With Image Fusion and Recursive Filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3742–3752. [Google Scholar]
- Sivic, J.; Zisserman, A. Video Google: A Text Retrieval Approach to Object Matching in Videos. In Proceedings of the Ninth IEEE International Conference on Computer Vision (ICCV), Nice, France, 13–16 October 2003; pp. 1470–1477. [Google Scholar]
- Lazebnik, S.; Schmid, C.; Ponce, J. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; pp. 2169–2178. [Google Scholar]
- Xia, G.S.; Delon, J.; Gousseau, Y. Accurate Junction Detection and Characterization in Natural Images. Int. J. Comput. Vis. 2014, 106, 31–56. [Google Scholar]
- Xia, G.S.; Delon, J.; Gousseau, Y. Shape-based Invariant Texture Indexing. Int. J. Comput. Vis. 2010, 88, 382–403. [Google Scholar]
- Liu, W.; Liu, H.; Tao, D.; Wang, Y.; Lu, K. Manifold regularized kernel logistic regression for web image annotation. Neurocomputing 2016, 172, 3–8. [Google Scholar]
- Wang, Q.; Yuan, Y.; Yan, P.; Li, X. Saliency Detection by Multiple-Instance Learning. IEEE Trans. Cybern. 2013, 43, 660–672. [Google Scholar] [PubMed]
- Chen, Y.; Zhao, X.; Jia, X. Spectral-Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar]
- Yang, X.; Liu, W.; Tao, D.; Cheng, J. Canonical Correlation Analysis Networks for Two-view Image Recognition. Inf. Sci. 2017, 385–386, 338–352. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems 25, Proceedings of the Neural Information Processing Systems, Stateline, NV, USA, 3–8 December 2012; Neural Information Processing Systems Foundation, Inc.: La Jolla, CA, USA, 2012; pp. 1097–2013. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv, 2014; arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8–10 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Li, Y.; Zhang, H.; Shen, Q. Spectral-Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Hu, F.; Xia, G.S.; Hu, J.; Zhang, L. Transferring Deep Convolutional Neural Networks for the Scene Classification of High-Resolution Remote Sensing Imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Chan, T.H.; Jia, K.; Gao, S.; Lu, J.; Zeng, Z.; Ma, Y. PCANet: A Simple Deep Learning Baseline for Image Classification? IEEE Trans. Image Process. 2015, 24, 5017–5032. [Google Scholar] [CrossRef] [PubMed]


| Class | Samples | ||
|---|---|---|---|
| Training | Validation | Testing | |
| Mountain | 70 | 10 | 20 |
| Sky | 70 | 10 | 20 |
| Road | 70 | 10 | 20 |
| Class | Samples | ||||
|---|---|---|---|---|---|
| Number | Classes | Total | Training | Validation | Testing |
| 1 | Alfalfa | 46 | 23 | 4 | 19 |
| 2 | Corn-notill | 1288 | 636 | 132 | 520 |
| 3 | Corn-mintill | 63 | 29 | 7 | 27 |
| 4 | Corn | 35 | 17 | 3 | 15 |
| 5 | Grass-pasture | 180 | 90 | 14 | 76 |
| 6 | Grass-trees | 730 | 342 | 84 | 304 |
| 7 | Grass-pasture-mowed | 28 | 16 | 1 | 11 |
| 8 | Hay-windrowed | 94 | 45 | 8 | 41 |
| 9 | Oats | 20 | 10 | 2 | 8 |
| 10 | Soybean-notill | 807 | 406 | 71 | 330 |
| 11 | Soybean-mintill | 2067 | 1019 | 215 | 833 |
| 12 | Soybean-clean | 227 | 124 | 22 | 81 |
| 13 | Wheat | 204 | 107 | 28 | 69 |
| 14 | Woods | 560 | 307 | 44 | 209 |
| 15 | Buildings-Grass-Trees-Drives | 73 | 38 | 9 | 26 |
| 16 | Stone-Steel-Towers | 54 | 29 | 3 | 22 |
| Total | 6476 | 3238 | 647 | 2591 | |
| Class | Samples | ||||
|---|---|---|---|---|---|
| Number | Classes | Total | Training | Validation | Testing |
| 1 | Asphalt | 5446 | 2718 | 580 | 2148 |
| 2 | Meadows | 12,695 | 6307 | 1320 | 5068 |
| 3 | Gravel | 1314 | 674 | 126 | 514 |
| 4 | Trees | 2709 | 1329 | 241 | 1139 |
| 5 | Painted metal sheets | 1345 | 688 | 153 | 504 |
| 6 | Bare Soil | 5029 | 2517 | 453 | 2059 |
| 7 | Bitumen | 1330 | 686 | 120 | 524 |
| 8 | Self-Blocking Bricks | 3630 | 1810 | 362 | 1458 |
| 9 | Shadows | 902 | 471 | 85 | 346 |
| Total | 34,400 | 17,200 | 3440 | 13,760 | |
| Methods | CFSFDP Net | MCFSFDP Net |
|---|---|---|
| Accuracy (%) | 81.67 ± 0.5904 | 95.00 ± 0.5887 |
| Dataset | Dataset 1 | Dataset 2 | Dataset 3 |
|---|---|---|---|
| Block Size | 25 × 25 | 19 × 19 | 11 × 11 |
| Kernel Size | 10 × 10 | 6 × 6 | 2 × 2 |
| Pooling Size | 4 × 4 | 7 × 7 | 2 × 2 |
| Methods | MCFSFDP-M Net-20 | MCFSFDP-M Net-25 | MCFSFDP-M Net-41 | MCFSFDP-M Net-55 | MCFSFDP Net-35 |
|---|---|---|---|---|---|
| Accuracy (%) | 93.33 ± 0.5887 | 95.00 ± 0.5904 | 95.00 ± 0.5904 | 95.00 ± 0.5904 | 96.67 ± 0.5887 |
| Distance threshold | 0.19 | 0.18 | 0.16 | 0.15 | 0.17 |
| Number of kernels | 20 | 25 | 41 | 55 | 35 |
| Methods | MCFSFDP-M Net-14 | MCFSFDP-M Net-24 | MCFSFDP-M Net-31 | MCFSFDP-M Net-83 | MCFSFDP-M Net-151 | MCFSFDP Net-50 |
|---|---|---|---|---|---|---|
| Accuracy (%) | 95.29 ± 0.0870 | 96.51 ± 0.4146 | 97.03 ± 0.1940 | 97.07 ± 0.3434 | 96.82 ± 0.1457 | 97.84 ± 0.2249 |
| Distance threshold | 0.27 | 0.26 | 0.25 | 0.23 | 0.22 | 0.24 |
| Number of kernels | 14 | 24 | 31 | 83 | 151 | 50 |
| Methods | MCFSFDP-M Net-19 | MCFSFDP-M Net-42 | MCFSFDP-M Net-152 | MCFSFDP Net-78 |
|---|---|---|---|---|
| Accuracy (%) | 88.98 ± 0.2651 | 89.32 ± 0.1908 | 89.54 ± 0.1002 | 90.58 ± 0.1477 |
| Distance threshold | 0.08 | 0.07 | 0.05 | 0.06 |
| Number of kernels | 19 | 42 | 152 | 78 |
| Methods | K-Means Net-50 | PCA Net-50 | Random Net-50 | MCFSFDP Net-35 |
|---|---|---|---|---|
| Accuracy (%) | 93.33 ± 0.5887 | 90.00 ± 1.8175 | 95.00 ± 1.8175 | 96.67 ± 0.5887 |
| Methods | K-Means Net-50 | PCA Net-50 | Random Net-50 | MCFSFDP Net-50 |
|---|---|---|---|---|
| Accuracy (%) | 95.02 ± 0.3343 | 97.30 ± 1.1916 | 97.12 ± 0.6195 | 97.84 ± 0.2249 |
| Methods | K-Means Net-50 | PCA Net-50 | Random Net-50 | MCFSFDP Net-78 |
|---|---|---|---|---|
| Accuracy (%) | 89.77 ± 0.3399 | 90.14 ± 0.2652 | 90.47 ± 0.5113 | 90.58 ± 0.1477 |
| Dataset | Dataset 1 | Dataset 2 | |||
|---|---|---|---|---|---|
| Pooling Size | 4 × 4 | 4 × 4 | 4 × 4 | 5 × 5 | 7 × 7 |
| Kernel Size | 14 × 14 | 10 × 10 | 6 × 6 | 10 × 10 | 6 × 6 |
| Number of Kernels | 15 | 35 | 24 | 32 | 50 |
| Distance Value | 0.22 | 0.17 | 0.17 | 0.28 | 0.24 |
| Accuracy (%) | 95 | 96.67 | 96.67 | 95.33 | 97.84 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, C.; Li, Y.; Xia, Y.; Wei, W.; Zhang, L.; Zhang, Y. Convolutional Neural Networks Based Hyperspectral Image Classification Method with Adaptive Kernels. Remote Sens. 2017, 9, 618. https://doi.org/10.3390/rs9060618
Ding C, Li Y, Xia Y, Wei W, Zhang L, Zhang Y. Convolutional Neural Networks Based Hyperspectral Image Classification Method with Adaptive Kernels. Remote Sensing. 2017; 9(6):618. https://doi.org/10.3390/rs9060618
Chicago/Turabian StyleDing, Chen, Ying Li, Yong Xia, Wei Wei, Lei Zhang, and Yanning Zhang. 2017. "Convolutional Neural Networks Based Hyperspectral Image Classification Method with Adaptive Kernels" Remote Sensing 9, no. 6: 618. https://doi.org/10.3390/rs9060618
APA StyleDing, C., Li, Y., Xia, Y., Wei, W., Zhang, L., & Zhang, Y. (2017). Convolutional Neural Networks Based Hyperspectral Image Classification Method with Adaptive Kernels. Remote Sensing, 9(6), 618. https://doi.org/10.3390/rs9060618








