Comparing Passive Microwave with Visible-To-Near-Infrared Phenometrics in Croplands of Northern Eurasia
Abstract
:1. Introduction
2. Data and Methodology
2.1. Remote Sensing Data
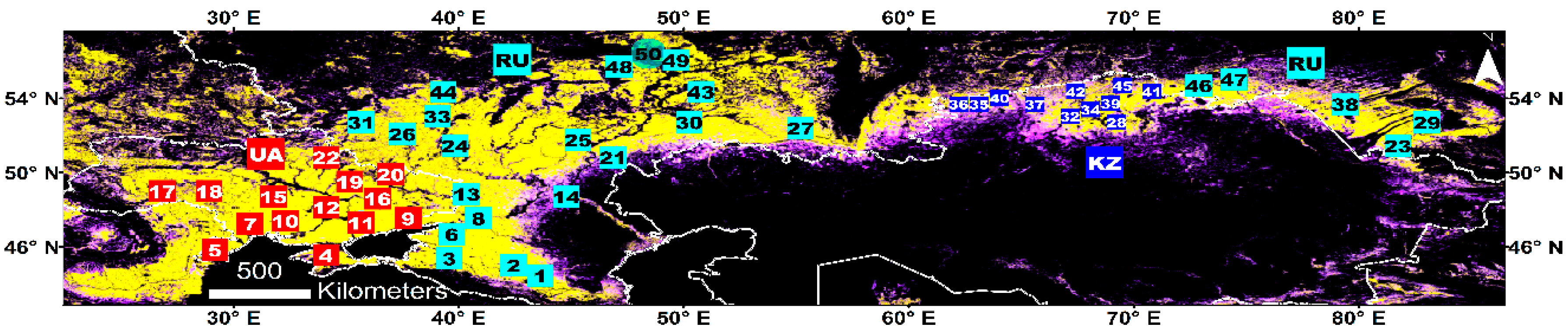
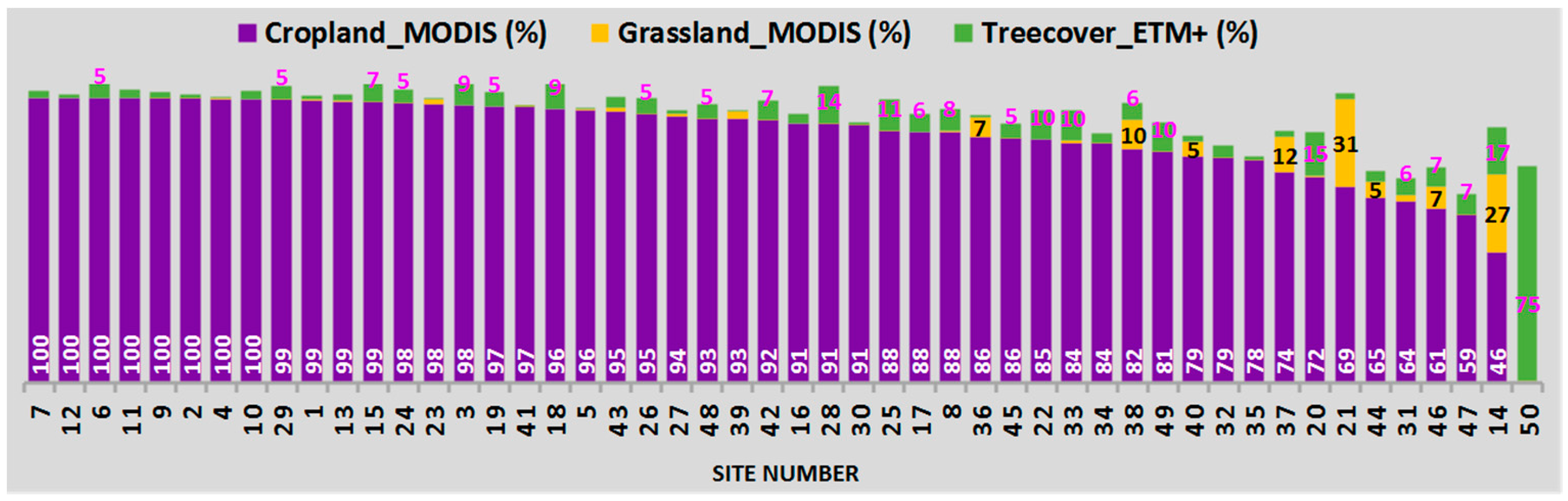
2.2. Study Region
2.3. Characterizing Land Surface Phenology in VODs and NDVI
3. Results
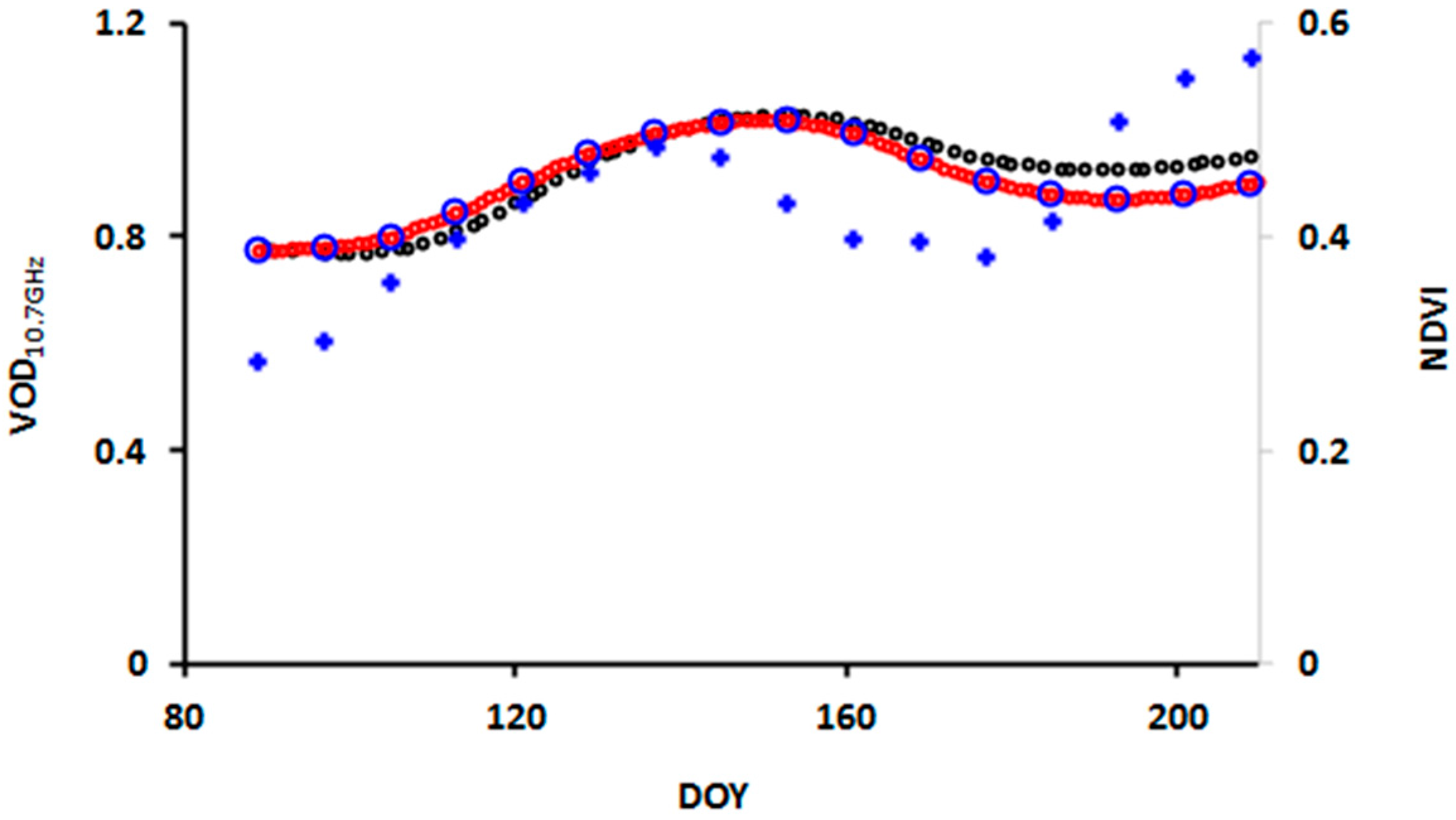
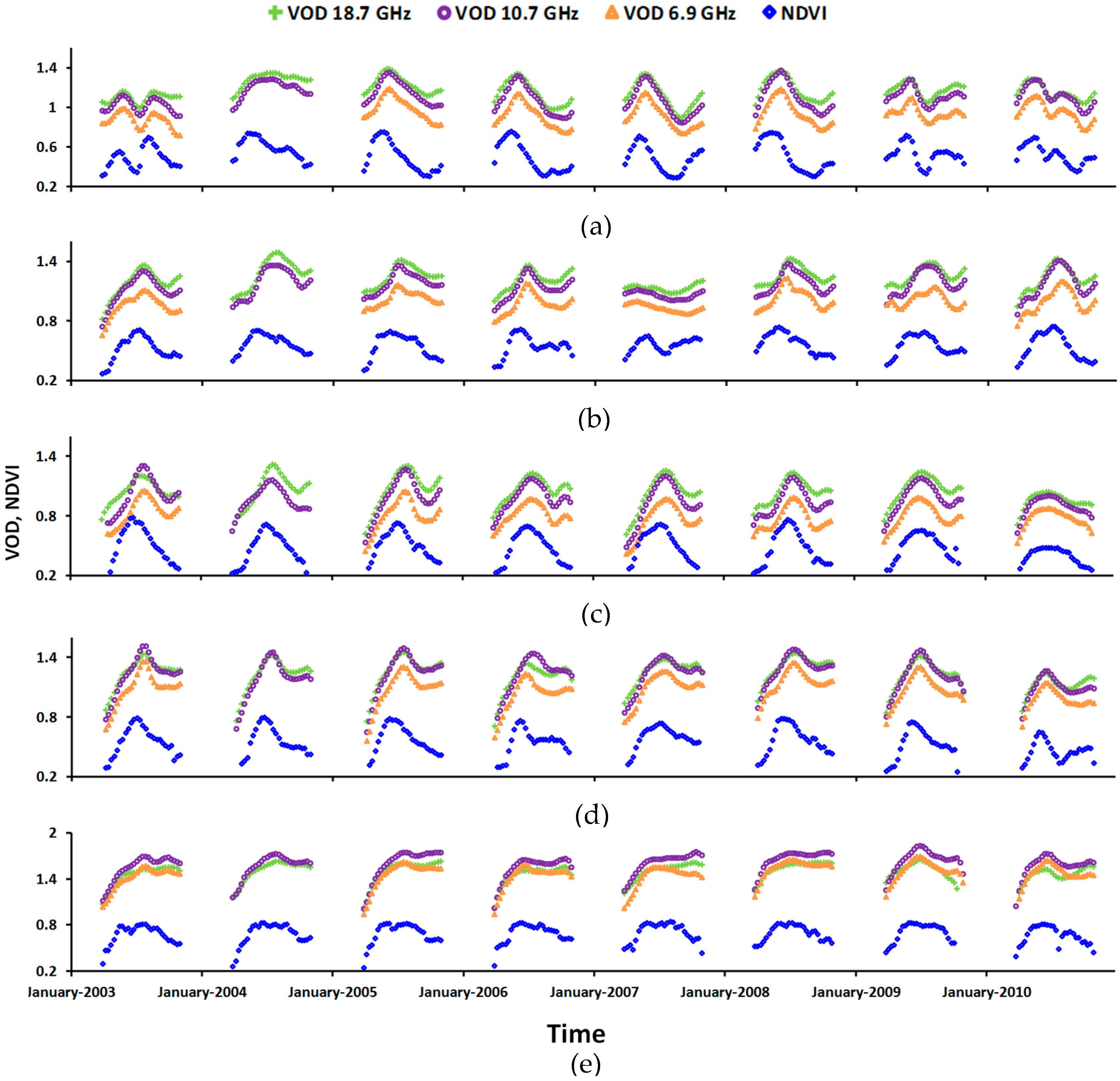
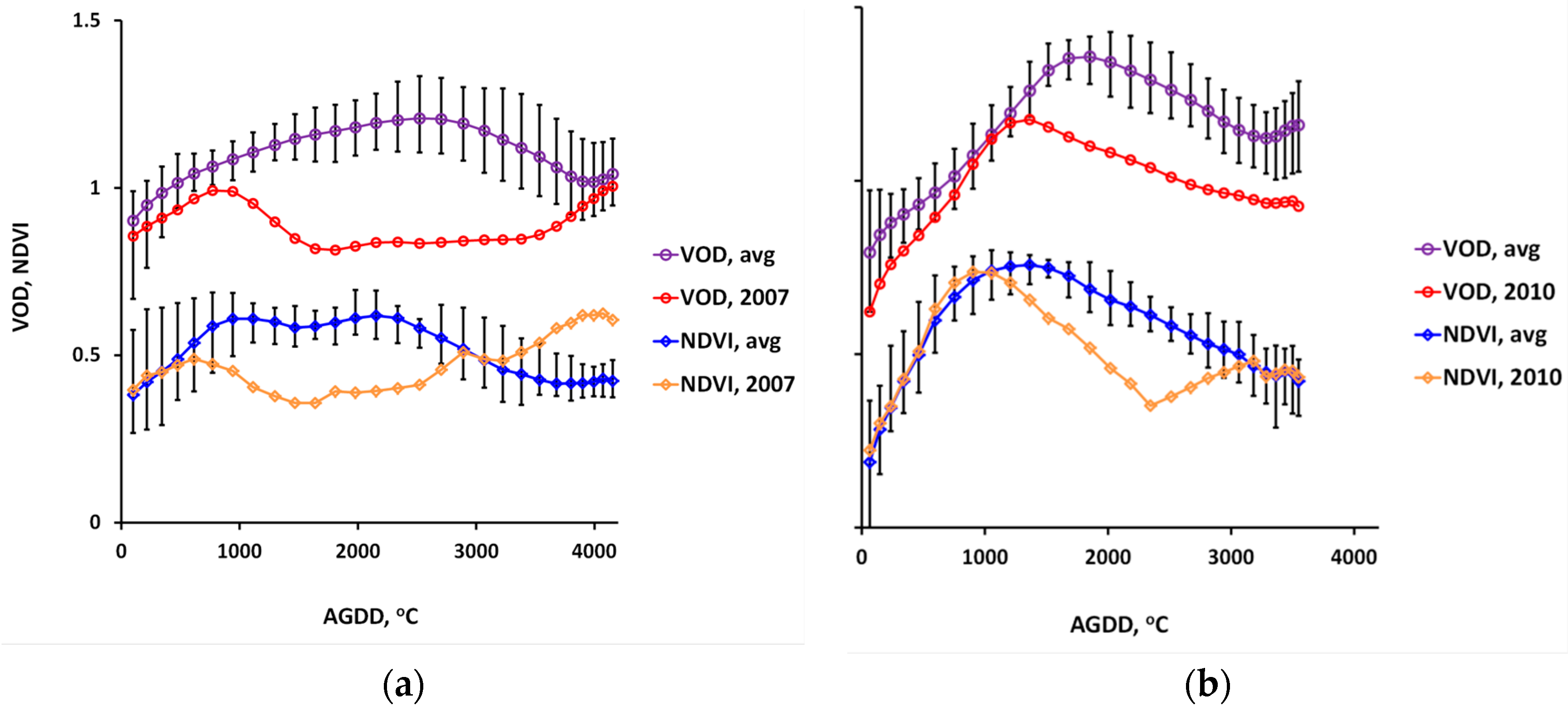
3.1. Time Series Land Surface Phenologies of NDVI and VODs
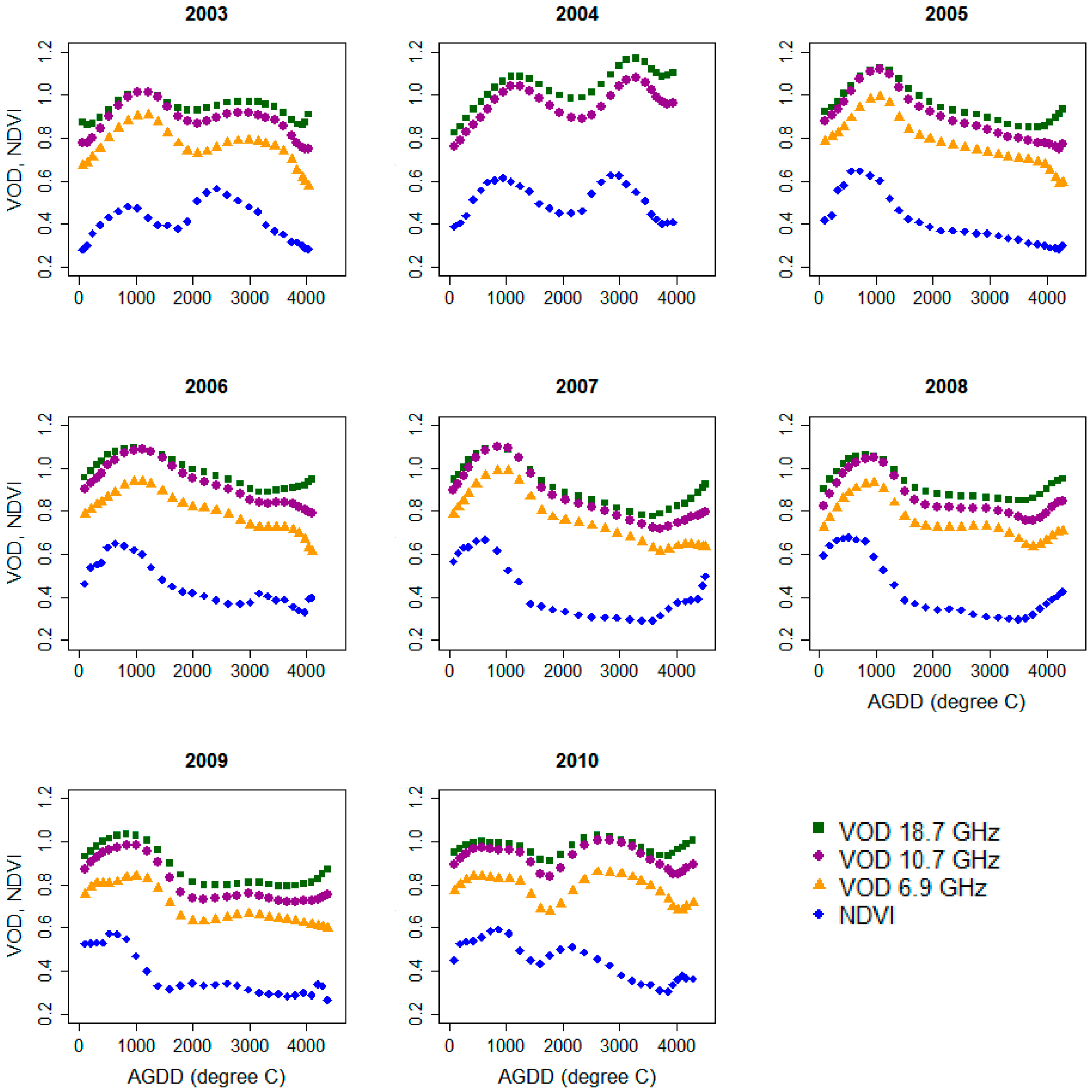
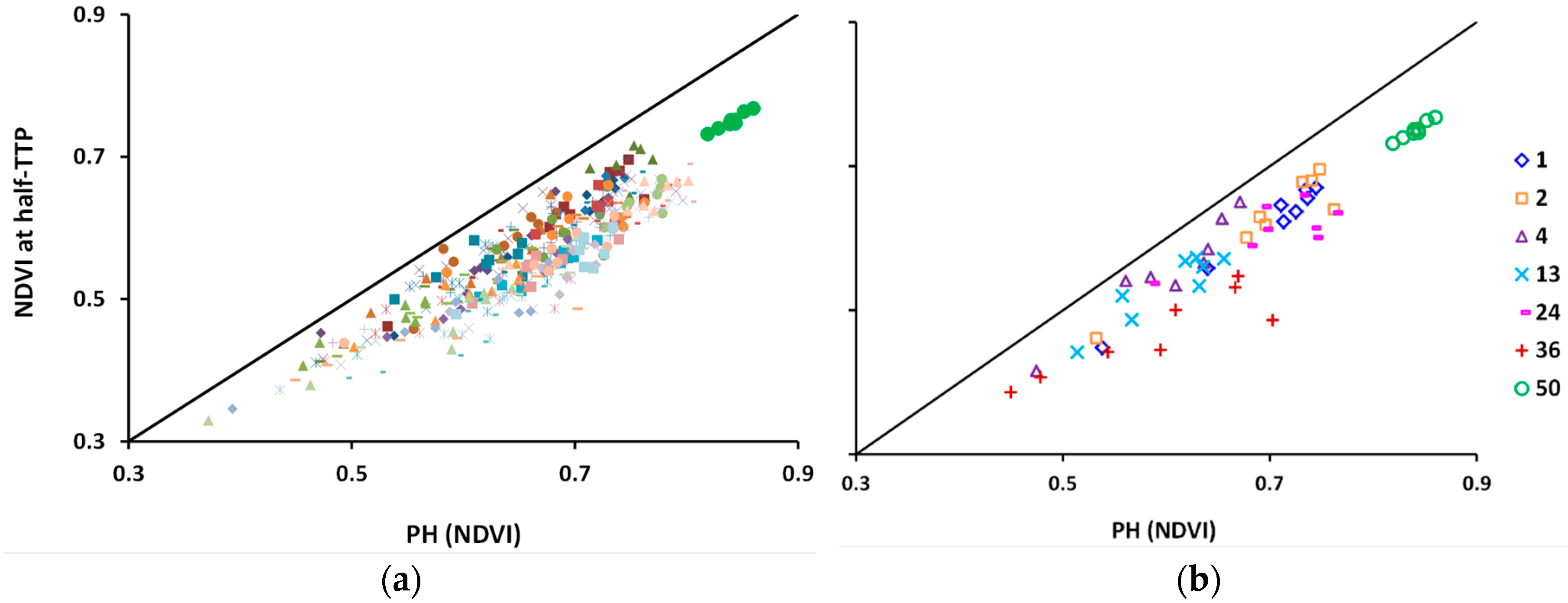
3.2. Thermal Time to Peak and Peak Height NDVI and VOD Phenometrics
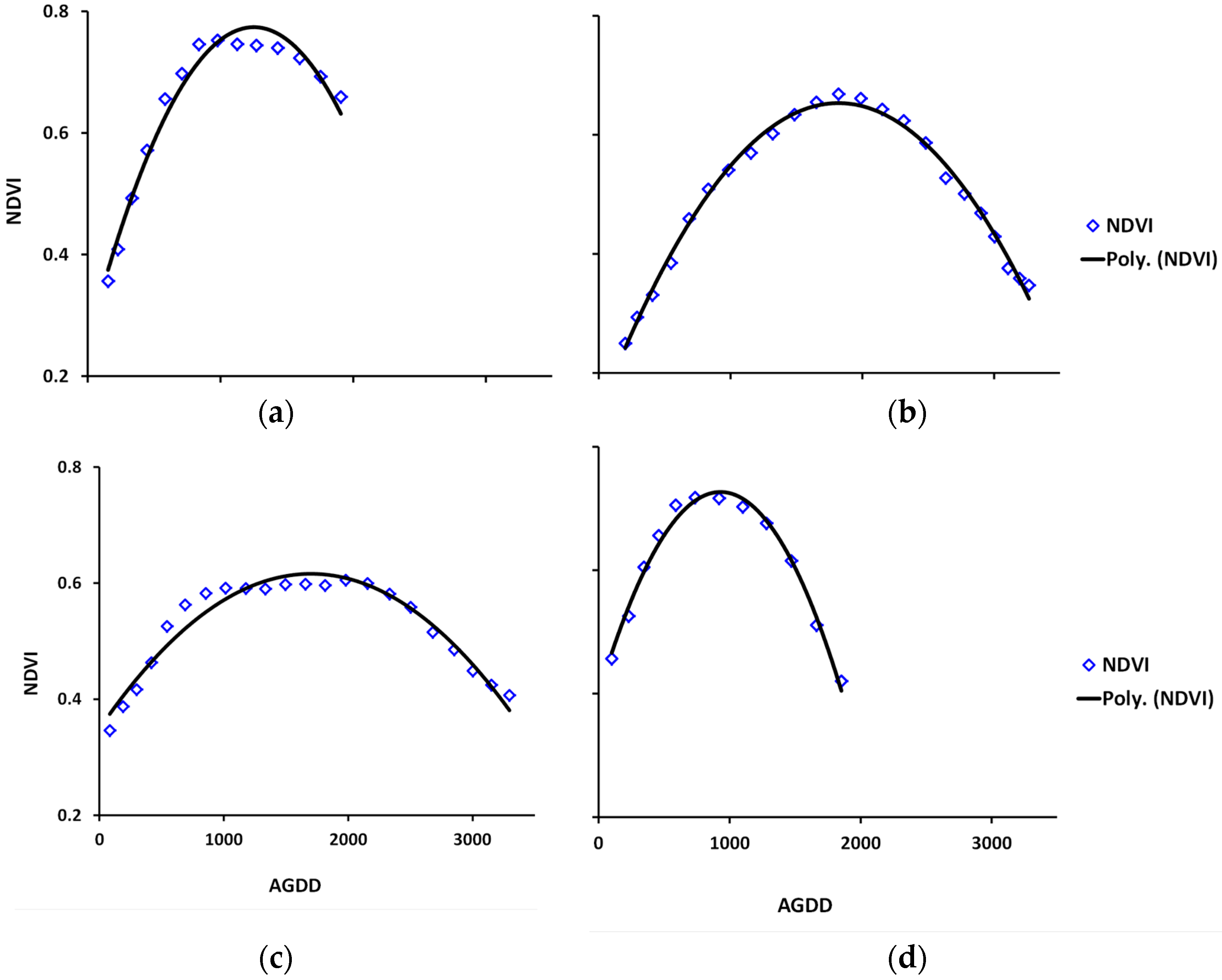
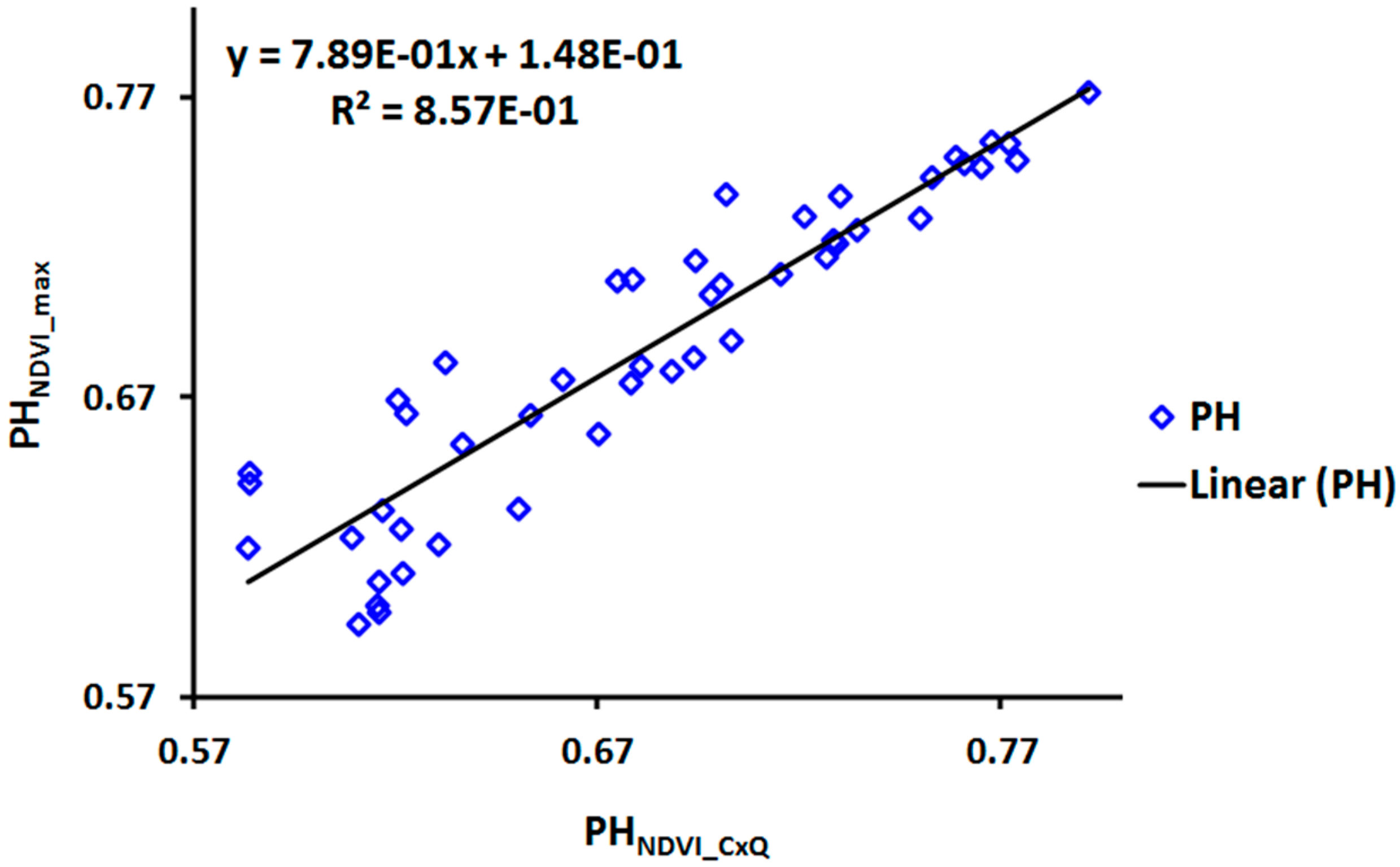
3.2.1. The CxQ Model Derived NDVI Phenometrics
3.2.2. The Maximum Value Approach for VOD Phenometrics
4. Discussion
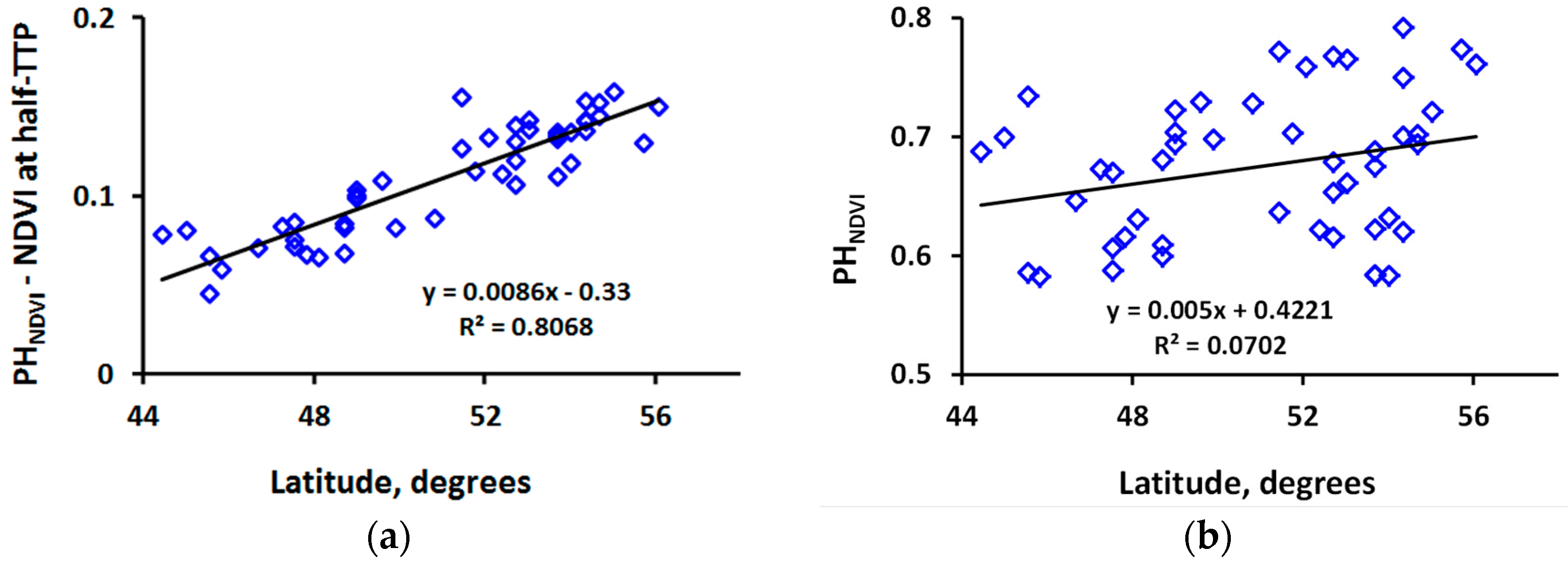
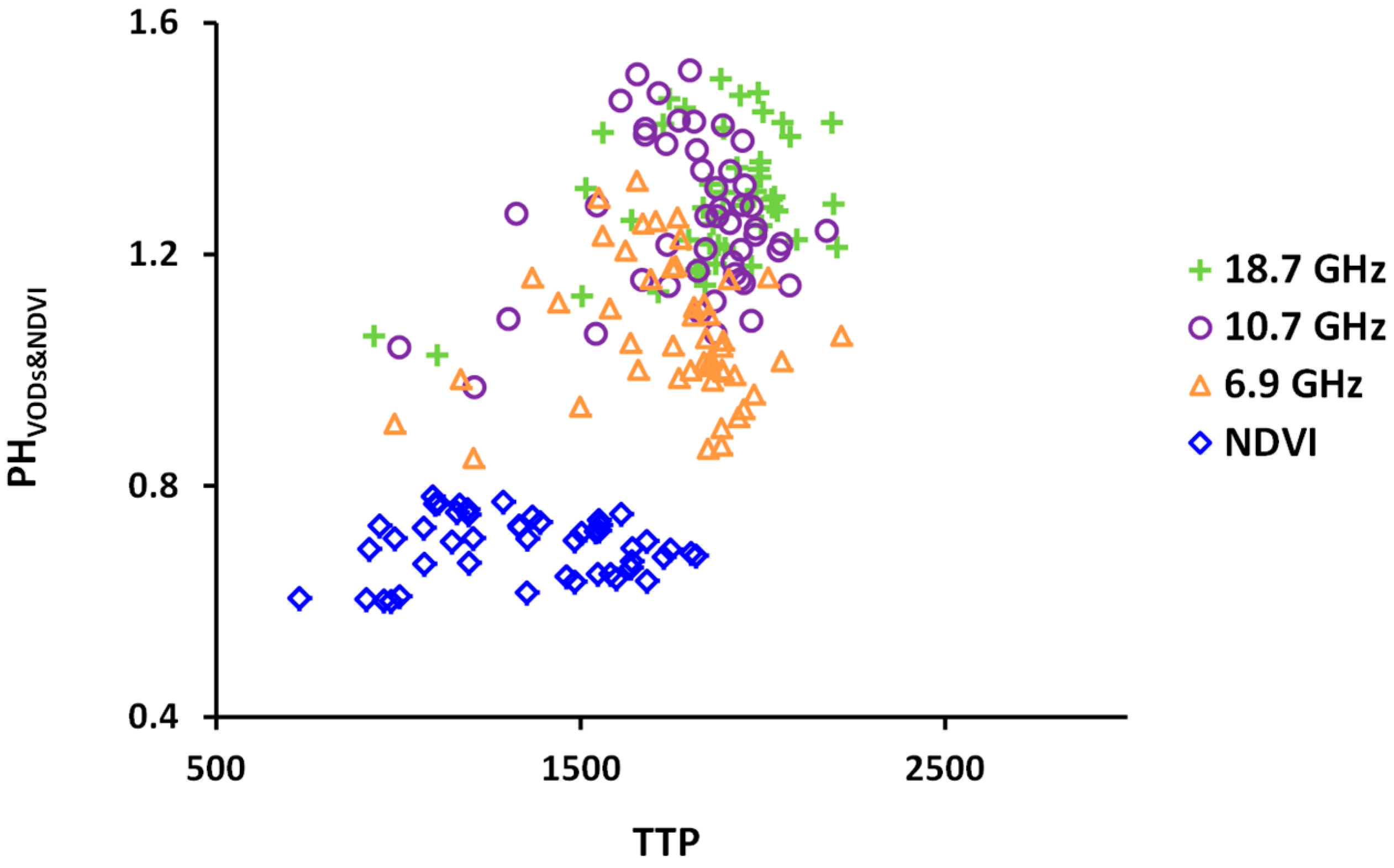
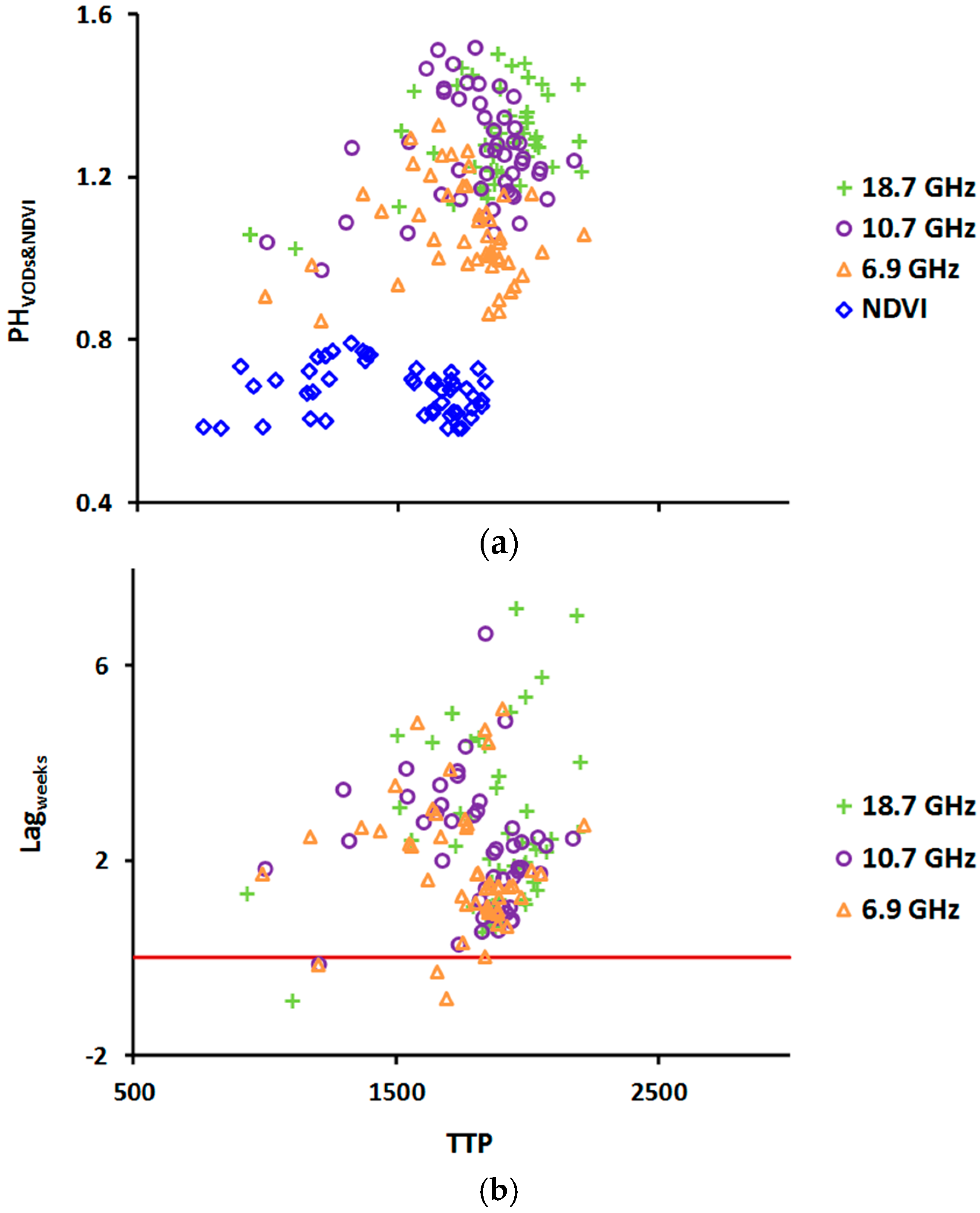
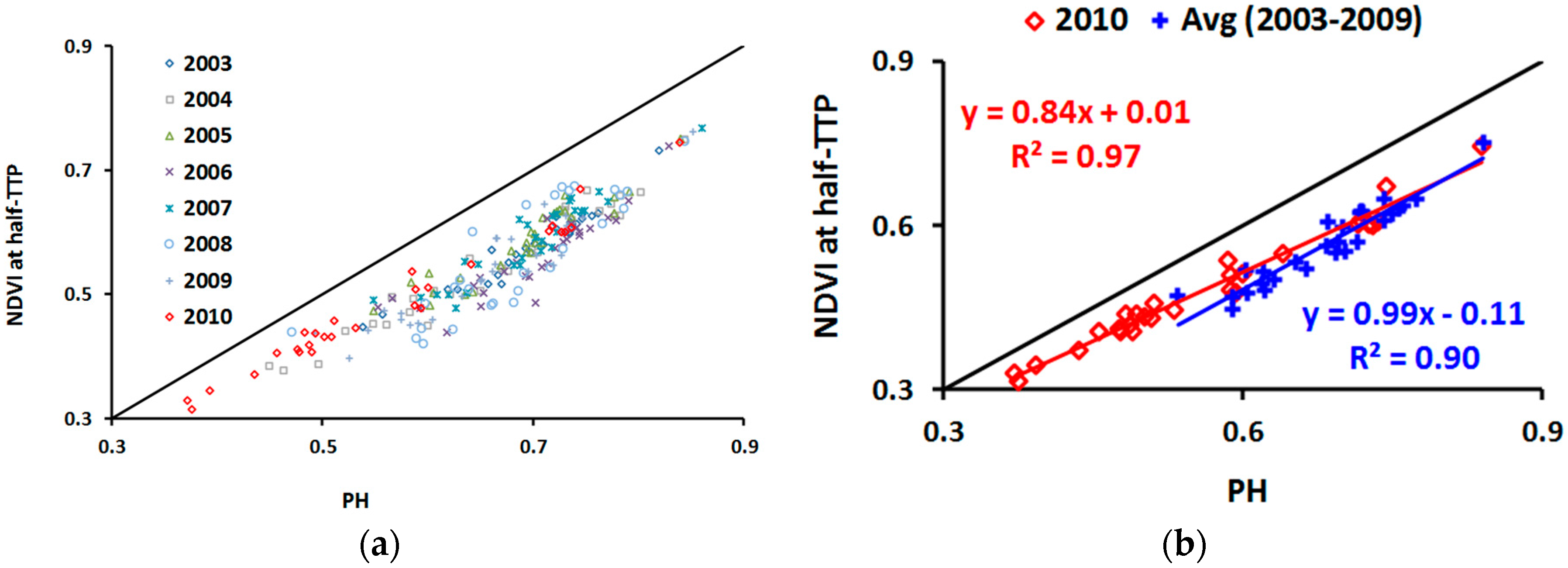
4.1. VOD and NDVI Peak Heights: Correlations and Biases
4.2. Heatwave Responses of VODs and NDVI
5. Conclusions and Recommendations
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Site No. | Name | Latitude | Longitude | Lag, 6.9 ** | Lag, 10.7 ** | Lag, 18.7 ** | Site No. | Name | Latitude | Longitude | Lag, 6.9 ** | Lag, 10.7 ** | Lag, 18.7 ** |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Cherkessk, RU | 44.4 | 43.5 | 2.7 | 2.4 | 4.4 | 26 | Kursk, RU | 52.1 | 37.5 | 5.1 | 3.8 | 7.0 |
| 2 | Stavropol, RU | 45.0 | 42.4 | 2.6 | 3.3 | 3.1 | 27 | Orenburg, RU | 52.4 | 55.2 | 1.4 | 1.2 | 1.1 |
| 3 | Krasnodar, RU | 45.6 | 39.6 | 4.8 | 6.7 | 7.2 | 28 | Kokshetau 1, KZ | 52.7 | 69.2 | 2.7 | 2.5 | 2.6 |
| 4 | Simferopol’, UA | 45.6 | 34.1 | 1.7 | 1.8 | 1.3 | 29 | Barnaul 2, RU | 52.7 | 83.0 | 1.0 | 1.7 | 1.9 |
| 5 | Tulcea, UA | 45.8 | 29.2 | 2.5 | 3.5 | 4.6 | 30 | Kuybyskev 2, RU | 52.7 | 50.2 | 1.1 | 2.3 | 4.0 |
| 6 | Rostov-on-Don 2, RU | 46.7 | 39.8 | 1.5 | 2.5 | 2.3 | 31 | Orel, RU | 52.7 | 35.7 | 2.7 | 2.9 | 3.5 |
| 7 | Odesa, UA | 47.3 | 30.7 | 3.1 | 3.7 | 4.4 | 32 | Kokshetau 2, KZ | 53.0 | 67.4 | 1.7 | 1.7 | 1.6 |
| 8 | Rostov-on-Do 1, RU | 47.5 | 40.9 | 4.7 | 3.5 | 4.5 | 33 | Lipetsk, RU | 53.0 | 39.1 | 1.6 | 2.0 | 2.3 |
| 9 | Donets’k, UA | 47.5 | 37.7 | 3.6 | 3.9 | 5.0 | 34 | Kokshetau 3, KZ | 53.7 | 68.2 | 0.9 | 0.8 | 1.2 |
| 10 | Mykolayiv, UA | 47.5 | 32.3 | 4.4 | 4.9 | 5.4 | 35 | Kostanay 1, KZ | 53.7 | 63.3 | 1.0 | 0.9 | 0.7 |
| 11 | Zaporiyhzhya 1, UA | 47.8 | 35.7 | −0.3 | 0.3 | 1.1 | 36 | Kostanay 2, KZ | 53.7 | 62.2 | 0.9 | 0.5 | 0.5 |
| 12 | Zaporiyhzhya 2, UA | 48.1 | 34.1 | 1.4 | 2.4 | 2.4 | 37 | Kurgan, KZ | 53.7 | 65.6 | 1.5 | 1.0 | 1.0 |
| 13 | Luhans’k, RU | 48.7 | 40.4 | 0.7 | 1.0 | 0.6 | 38 | Barnaul_1, RU | 53.7 | 79.4 | 1.5 | 1.6 | 1.9 |
| 14 | Volgograd, RU | 48.7 | 44.8 | −0.1 | −0.1 | −0.9 | 39 | Kokshetau 4, KZ | 54.0 | 69.0 | 1.1 | 1.8 | 1.9 |
| 15 | Kirovohrad, UA | 48.7 | 31.8 | 1.8 | 1.0 | 2.2 | 40 | Kostanay 3, KZ | 54.0 | 64.0 | 1.3 | 0.9 | 0.7 |
| 16 | Kharkiv 2, UA | 49.0 | 36.2 | 1.8 | 2.2 | 2.6 | 41 | Petropavlovsk 2, KZ | 54.4 | 70.8 | 1.5 | 2.3 | 2.4 |
| 17 | Khmel’nyts’kyz, UA | 49.0 | 26.8 | 3.9 | 4.3 | 4.4 | 42 | Petropavlovsk 3, KZ | 54.4 | 67.4 | 1.1 | 1.4 | 1.6 |
| 18 | Vinnytsya, UA | 49.0 | 28.9 | 2.3 | 3.1 | 5.8 | 43 | Kuybyskev 1, RU | 54.4 | 50.8 | 2.8 | 3.0 | 2.8 |
| 19 | Poltava, UA | 49.6 | 35.1 | 1.3 | 2.7 | 3.0 | 44 | Ryazan, RU | 54.4 | 39.3 | 2.5 | 2.8 | 3.0 |
| 20 | Kharkiv 1, UA | 49.9 | 37.0 | 0.0 | 0.8 | 1.1 | 45 | Petropavlovsk 1, KZ | 54.7 | 69.5 | 1.5 | 1.7 | 1.8 |
| 21 | Saratov 1, RU | 50.8 | 46.9 | 0.1 | −0.3 | −0.7 | 46 | Omsk 1, RU | 54.7 | 72.9 | 1.3 | 1.9 | 2.2 |
| 22 | Sumy, UA | 50.8 | 34.1 | −0.8 | 0.6 | 1.2 | 47 | Omsk 2, RU | 55.0 | 74.5 | 0.3 | 1.8 | 2.0 |
| 23 | Semipalatinsk, RU | 51.4 | 81.7 | 0.6 | 0.8 | 1.4 | 48 | Cheboksary, RU | 55.7 | 47.1 | 3.0 | 3.0 | 5.1 |
| 24 | Voronezh, RU | 51.4 | 39.8 | 2.9 | 3.2 | 3.7 | 49 | Kazan’, RU | 56.1 | 49.5 | 2.3 | 2.8 | 2.4 |
| 25 | Saratov 4, RU | 51.8 | 45.3 | 1.7 | 2.2 | 2.0 | 50 | Mari El * | 56.4 | 48.4 | −0.7 | 4.7 | 6.9 |
| Max * | 5.1 | 6.7 | 7.2 | ||||||||||
| Min * | −0.8 | −0.1 | −0.9 | ||||||||||
| Average * | 1.9 | 2.2 | 2.7 |
References
- Jones, M.O.; Kimball, J.S.; Jones, L.A.; McDonald, K.C. Satellite passive microwave detection of North America start of season. Remote Sens. Environ. 2012, 123, 324–333. [Google Scholar] [CrossRef]
- Henebry, G.M.; de Beurs, K.M. Remote sensing of land surface phenology: A prospectus. In Phenology: An Integrative Environmental Science; Schwartz, M.D., Ed.; Springer Netherlands: Dordrecht, The Netherlands, 2013; pp. 385–411. [Google Scholar]
- Schwartz, M.D.; Hanes, J.M. Intercomparing multiple measures of the onset of spring in eastern North America. Int. J. Climatol. 2010, 30, 1614–1626. [Google Scholar] [CrossRef]
- Wang, Q.; Tenhunen, J.; Dinh, N.Q.; Reichstein, M.; Otieno, D.; Granier, A.; Pilegarrd, K. Evaluation of seasonal variation of MODIS derived leaf area index at two european deciduous broadleaf forest sites. Remote Sens. Environ. 2005, 96, 475–484. [Google Scholar] [CrossRef]
- Frolking, S.; Milliman, T.; McDonald, K.; Kimball, J.; Zhao, M.; Fahnestock, M. Evaluation of the seawinds scatterometer for regional monitoring of vegetation phenology. J. Geophys. Res. Atmos. 2006, 111, D17302. [Google Scholar] [CrossRef]
- Jones, M.O.; Jones, L.A.; Kimball, J.S.; McDonald, K.C. Satellite passive microwave remote sensing for monitoring global land surface phenology. Remote Sens. Environ. 2011, 115, 1102–1114. [Google Scholar] [CrossRef]
- Min, Q.; Lin, B. Determination of spring onset and growing season leaf development using satellite measurements. Remote Sens. Environ. 2006, 104, 96–102. [Google Scholar] [CrossRef]
- Shi, J.; Jackson, T.; Tao, J.; Du, J.; Bindlish, R.; Lu, L.; Chen, K.S. Microwave vegetation indices for short vegetation covers from satellite passive microwave sensor AMSR-E. Remote Sens. Environ. 2008, 112, 4285–4300. [Google Scholar] [CrossRef]
- Frolking, S.; Fahnestock, M.; Milliman, T.; McDonald, K.; Kimball, J. Interannual variability in North American grassland biomass/productivity detected by seawinds scatterometer backscatter. Geophys. Res. Lett. 2005, 32, L2140. [Google Scholar] [CrossRef]
- Frolking, S.; Milliman, T.; Palace, M.; Wisser, D.; Lammers, R.; Fahnestock, M. Tropical forest backscatter anomaly evident in seawinds scatterometer morning overpass data during 2005 drought in Amazonia. Remote Sens. Environ. 2011, 115, 897–907. [Google Scholar] [CrossRef]
- Kimball, J.S.; McDonald, K.C.; Running, S.W.; Frolking, S.E. Satellite radar remote sensing of seasonal growing seasons for boreal and subalpine evergreen forests. Remote Sens. Environ. 2004, 90, 243–258. [Google Scholar] [CrossRef]
- Kimball, J.S.; McDonald, K.C.; Zhao, M. Spring thaw and its effect on terrestrial vegetation productivity in the western Arctic observed from satellite microwave and optical remote sensing. Earth Interact 2006, 10, 1–22. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Van Dijk, A.I.J.M.; McCabe, M.F.; Evans, J.P.; De Jeu, R.A.M. Global long-term passive microwave satellite-based retrievals of vegetation optical depth. Geophys. Res. Lett. 2011, 38, L18402. [Google Scholar] [CrossRef]
- Li, L.; Njoku, E.G.; Im, E.; Chang, P.S.; Germain, K.S. A preliminary survey of radio-frequency interference over the us in aqua AMSR-E data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 380–390. [Google Scholar] [CrossRef]
- Njoku, E.G.; Ashcroft, P.; Chan, T.K.; Li, L. Global survey and statistics of radio-frequency interference in AMSR-E land observations. IEEE Trans. Geosci. Remote Sens. 2005, 43, 938–947. [Google Scholar] [CrossRef]
- Owe, M.; De Jeu, R.; Walker, J. A methodology for surface soil moisture and vegetation optical depth retrieval using the microwave polarization difference index. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1643–1654. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Van Dijk, A.I.J.M.; McCabe, M.F.; Evans, J.P.; De Jeu, R.A.M. Global vegetation biomass change (1988–2008) and attribution to environmental and human drivers. Glob. Ecol. Biogeogr. 2013, 22, 692–705. [Google Scholar] [CrossRef]
- Jolly, W.M.; Nemani, R.; Running, S.W. A generalized, bioclimatic index to predict foliar phenology in response to climate. Glob. Chang. Biol. 2005, 11, 619–632. [Google Scholar] [CrossRef]
- Dole, R.; Hoerling, M.; Perlwitz, J.; Eischeid, J.; Pegion, P.; Zhang, T.; Quan, X.-W.; Xu, T.; Murray, D. Was there a basis for anticipating the 2010 Russian heat wave? Geophys. Res. Lett. 2011, 38, L06702. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T. Climate extremes and climate change: The Russian heat wave and other climate extremes of 2010. J. Geophys. Res. Atmos. 2012, 117, D17103. [Google Scholar] [CrossRef]
- Alemu, W.G.; Henebry, G.M. Land surface phenologies and seasonalities using cool earthlight in mid-latitude croplands. Environ. Res. Lett. 2013, 8, 045002. [Google Scholar] [CrossRef]
- Alemu, W.G.; Henebry, G.M. Characterizing cropland phenology in major grain production areas of Russia, Ukraine, and Kazakhstan by the synergistic use of passive microwave and visible to near infrared data. Remote Sens. 2016, 8, 1016. [Google Scholar] [CrossRef]
- De Beurs, K.M.; Henebry, G.M. Northern annular mode effects on the land surface phenologies of northern Eurasia. J. Clim. 2008, 21, 4257–4279. [Google Scholar] [CrossRef]
- De Beurs, K.M.; Henebry, G.M. Spatio-temporal statistical methods for modelling land surface phenology. In Phenological Research: Methods for Environmental and Climate Change Analysis, 2nd ed.; Hudson, I.L., Keatley, M.R., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 177–208. [Google Scholar]
- Brown, M.E.; de Beurs, K.M.; Marshall, M. Global phenological response to climate change in crop areas using satellite remote sensing of vegetation, humidity and temperature over 26 years. Remote Sens. Environ. 2012, 126, 174–183. [Google Scholar] [CrossRef]
- Jones, L.A.; Kimball, J.S. Daily Global Land Surface Parameters Derived From AMSR-E; National Snow and Ice Data Center: Boulder, CO, USA, 2011. [Google Scholar]
- DAAC-LP. MODIS Products Table. 2014. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table (accessed on 15 February 2017).
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.W.; Tsang, T.; Strugnell, N.C.; Zhang, X.Y.; Jin, Y.F.; Muller, J.P.; et al. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X.M. MODIS collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- USDA-FAS. Russia—Crop Production Maps. Available online: http://www.pecad.fas.usda.gov/rssiws/al/rs_cropprod.htm (accessed on 15 February 2017).
- USDA-FAS. Kazakhstan—Crop Production Maps. Available online: http://www.pecad.fas.usda.gov/rssiws/al/kz_cropprod.htm (accessed on 15 February 2017).
- USDA-FAS. Ukraine—Crop Production Maps. Available online: http://www.pecad.fas.usda.gov/rssiws/al/up_cropprod.htm (accessed on 15 February 2017).
- USGS. 30 Meter Global Land Cover; USGS: Sioux FAlls, SD, USA, 2016.
- Henebry, G.M.; de Beurs, K.M.; Wright, C.K.; Ranjeet, J.; Lioubimtseva, E. Dryland east Asia in hemispheric context. In Dryland East Asia: Land Dynamics Amid Social and Climate Change; Chen, J., Wan, S., Henebry, G., Qi, J., Gutman, G., Sun, G., Kappas, M., Eds.; Walter de Gruyter GmbH: Berlin, Germany, 2013; pp. 23–43. [Google Scholar]
- Kim, Y.; Kimball, J.S.; McDonald, K.C.; Glassy, J. Developing a global data record of daily landscape freeze/thaw status using satellite passive microwave remote sensing. IEEE Trans. Geosci. Remote Sens. 2011, 49, 949–960. [Google Scholar] [CrossRef]
- McMaster, G.S.; Wilhelm, W.W. Growing degree-days: One equation, two interpretations. Agric. For. Meteorol. 1997, 87, 291–300. [Google Scholar] [CrossRef]
- De Beurs, K.M.; Henebry, G.M. Land surface phenology, climatic variation, and institutional change: Analyzing agricultural land cover change in Kazakhstan. Remote Sens. Environ. 2004, 89, 497–509. [Google Scholar] [CrossRef]
- Sarma, A.; Kumar, T.V.L.; Koteswararao, K. Development of an agroclimatic model for the estimation of rice yield. J. Indian Geophys. Union 2008, 12, 89–96. [Google Scholar]
- Yang, W.; Yang, L.; Merchant, J.W. An assessment of AVHRR/NDVI-ecoclimatological relations in Nebraska, U.S.A. Int. J. Remote Sens. 1997, 18, 2161–2180. [Google Scholar] [CrossRef]
- Wang, J.; Price, K.P.; Rich, P.M. Spatial patterns of NDVI in response to precipitation and temperature in the central great plains. Int. J. Remote Sens. 2001, 22, 3827–3844. [Google Scholar] [CrossRef]
- Henebry, G.M. Phenologies of North American grasslands and grasses. In Phenology: An Integrative Environmental Science; Schwartz, M.D., Ed.; Springer: Rotterdam, The Nethrlands, 2013; pp. 197–210. [Google Scholar]
- McMaster, G.S. Phytomers, phyllochrons, phenology and temperate cereal development. J. Agric. Sci. 2005, 143, 137–150. [Google Scholar] [CrossRef]
- Jones, L.A.; Ferguson, C.R.; Kimball, J.S.; Zhang, K.; Chan, S.T.K.; McDonald, K.C.; Njoku, E.G.; Wood, E.F. Satellite microwave remote sensing of daily land surface air temperature minima and maxima from AMSR-E. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 111–123. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic Infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Owen, S.V.; Froman, R.D. Focus on qualitative methods uses and abuses of the analysis of covariance. Res. Nurs. Health 1998, 21, 557–562. [Google Scholar] [CrossRef]
- McNairn, H.; Duguay, C.; Boisvert, J.; Huffman, E.; Brisco, B. Defining the sensitivity of multi-frequency and multi-polarized radar backscatter to post-harvest crop residue. Can. J. Remote Sens. 2001, 27, 247–263. [Google Scholar] [CrossRef]
- McNairn, H.; Duguay, C.; Brisco, B.; Pultz, T.J. The effect of soil and crop residue characteristics on polarimetric radar response. Remote Sens. Environ. 2002, 80, 308–320. [Google Scholar] [CrossRef]
- Founda, D.; Giannakopoulos, C. The exceptionally hot summer of 2007 in Athens, Greece—A typical summer in the future climate? Glob. Planet. Chang. 2009, 67, 227–236. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pampaloni, P.; Pettinato, S. Ground-based microwave investigations of forest plots in italy. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3016–3025. [Google Scholar] [CrossRef]
- Guglielmetti, M.; Schwank, M.; Mätzler, C.; Oberdörster, C.; Vanderborght, J.; Flühler, H. Measured microwave radiative transfer properties of a deciduous forest canopy. Remote Sens. Environ. 2007, 109, 523–532. [Google Scholar] [CrossRef]
- Tian, F.; Brandt, M.; Liu, Y.Y.; Verger, A.; Tagesson, T.; Diouf, A.A.; Rasmussen, K.; Mbow, C.; Wang, Y.; Fensholt, R. Remote sensing of vegetation dynamics in drylands: Evaluating vegetation optical depth (VOD) using AVHRR NDVI and in situ green biomass data over west african Sahel. Remote Sens. Environ. 2016, 177, 265–276. [Google Scholar] [CrossRef]
- De Bono, A.; Peduzzi, P.; Kluser, S.; Giuliani, G. Impacts of Summer 2003 Heat Wave in Europe; UNEP/DEWA/GRID-Europe: Geneva, Switzerland, 2004. [Google Scholar]
- Grant, J.P.; Wigneron, J.P.; De Jeu, R.A.M.; Lawrence, H.; Mialon, A.; Richaume, P.; Al Bitar, A.; Drusch, M.; van Marle, M.J.E.; Kerr, Y. Comparison of SMOS and AMSR-E vegetation optical depth to four modis-based vegetation indices. Remote Sens. Environ. 2016, 172, 87–100. [Google Scholar] [CrossRef]
- Brown, M.E.; de Beurs, K.M. Evaluation of multi-sensor semi-arid crop season parameters based on ndvi and rainfall. Remote Sens. Environ. 2008, 112, 2261–2271. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.S.; Shi, J.; Jones, L.A.; Wu, S.; Sun, R.; Yang, H. Inter-calibration of satellite passive microwave land observations from AMSR-E and AMSR2 using overlapping FY3B-MWRI sensor measurements. Remote Sens. 2014, 6, 8594–8616. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.S.; Jones, L.A. Satellite microwave retrieval of total precipitable water vapor and surface air temperature over land from AMSR2. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2520–2531. [Google Scholar] [CrossRef]

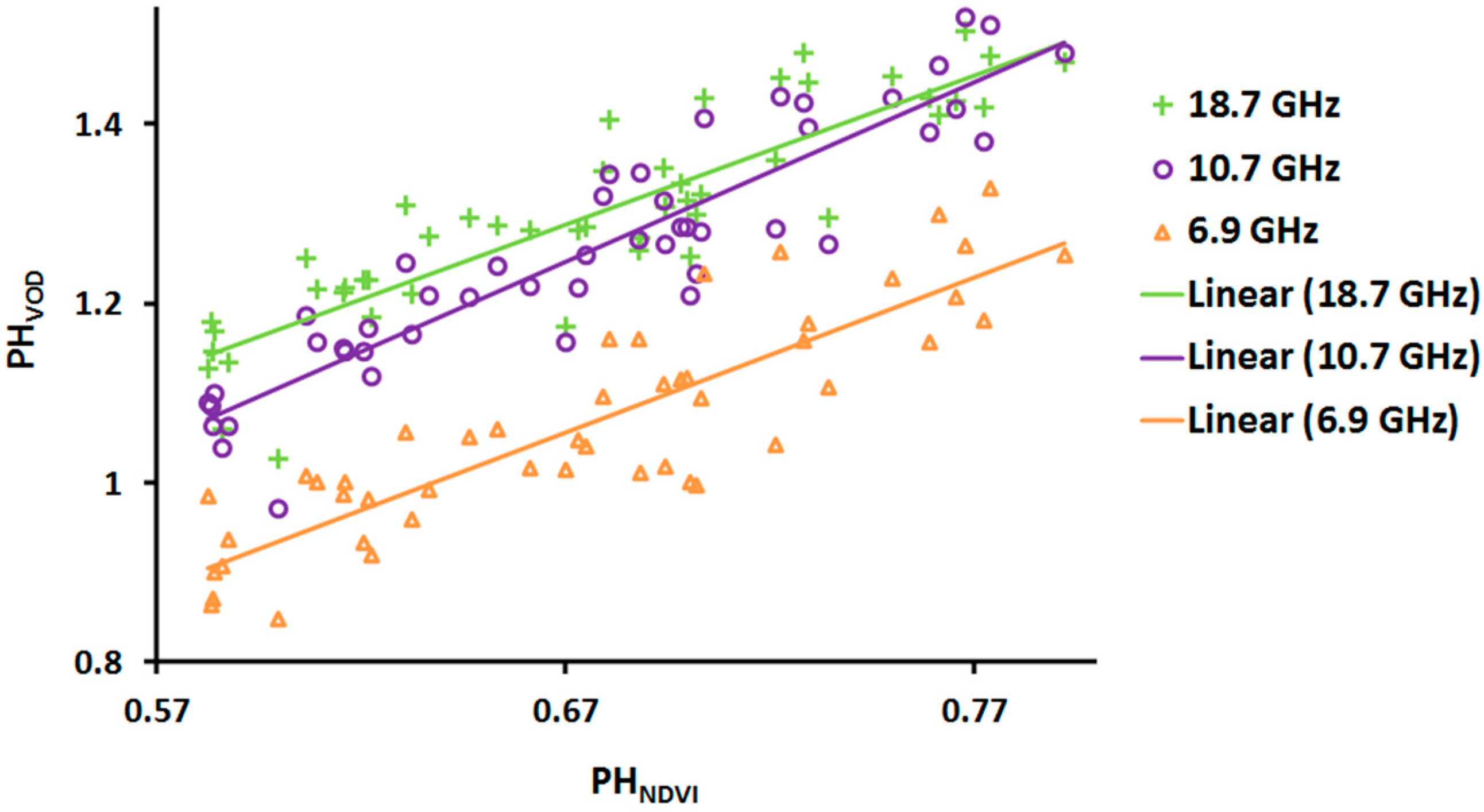
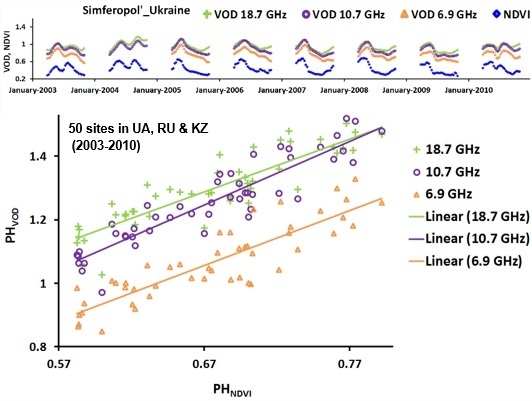
| Frequency (GHz) | n | Intercept | Slope | R2 | SEE * |
|---|---|---|---|---|---|
| 6.925 | 48 | −0.1065 | 1.7352 | 0.770 | 0.1401 |
| 10.65 | 48 | −0.0988 | 2.0079 | 0.844 | 0.1275 |
| 18.7 | 48 | 0.1728 | 1.6652 | 0.781 | 0.1298 |
| Pair of Microwave Frequencies (GHz) | p-Value for Slope Difference |
|---|---|
| 6.925 vs. 10.65 | 0.1582 |
| 6.925 vs. 18.7 | 0.6544 |
| 10.65 vs. 18.7 | 0.05497 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alemu, W.G.; Henebry, G.M. Comparing Passive Microwave with Visible-To-Near-Infrared Phenometrics in Croplands of Northern Eurasia. Remote Sens. 2017, 9, 613. https://doi.org/10.3390/rs9060613
Alemu WG, Henebry GM. Comparing Passive Microwave with Visible-To-Near-Infrared Phenometrics in Croplands of Northern Eurasia. Remote Sensing. 2017; 9(6):613. https://doi.org/10.3390/rs9060613
Chicago/Turabian StyleAlemu, Woubet G., and Geoffrey M. Henebry. 2017. "Comparing Passive Microwave with Visible-To-Near-Infrared Phenometrics in Croplands of Northern Eurasia" Remote Sensing 9, no. 6: 613. https://doi.org/10.3390/rs9060613
APA StyleAlemu, W. G., & Henebry, G. M. (2017). Comparing Passive Microwave with Visible-To-Near-Infrared Phenometrics in Croplands of Northern Eurasia. Remote Sensing, 9(6), 613. https://doi.org/10.3390/rs9060613