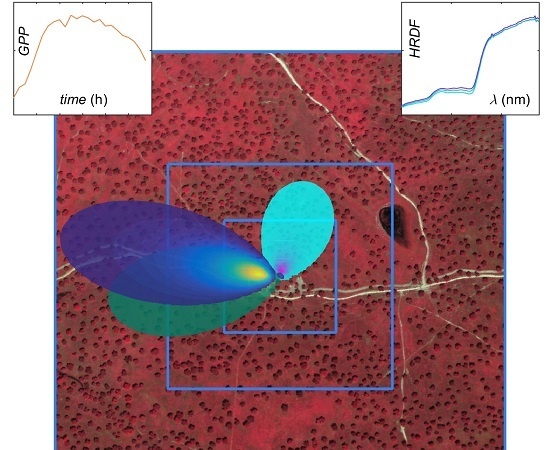
Spatio-Temporal Relationships between Optical Information and Carbon Fluxes in a Mediterranean Tree-Grass Ecosystem
Abstract
:1. Introduction
- (i)
- What is the impact of the spatial mismatch between EC and remote sensor footprints on the estimation of Half-hourly GPP (GPPhh)? Moreover, what is the role of spatial heterogeneity in is matter?
- (ii)
- What is the impact of the temporal mismatch between RS data and fluxes on the estimation of GPPhh?
2. Methods
2.1. Study Site
2.2. Airborne and Ground Hyperspectral Data
2.3. Eddy Covariance Data and Footprint Analysis
2.4. Eddy Covariance Footprint and Hyperspectral Data Integration
2.5. GPP Models: Definition, Inversion and Analysis
3. Results
3.1. Airborne Hyperspectral Imagery
3.2. Eddy Covariance and Optical Data
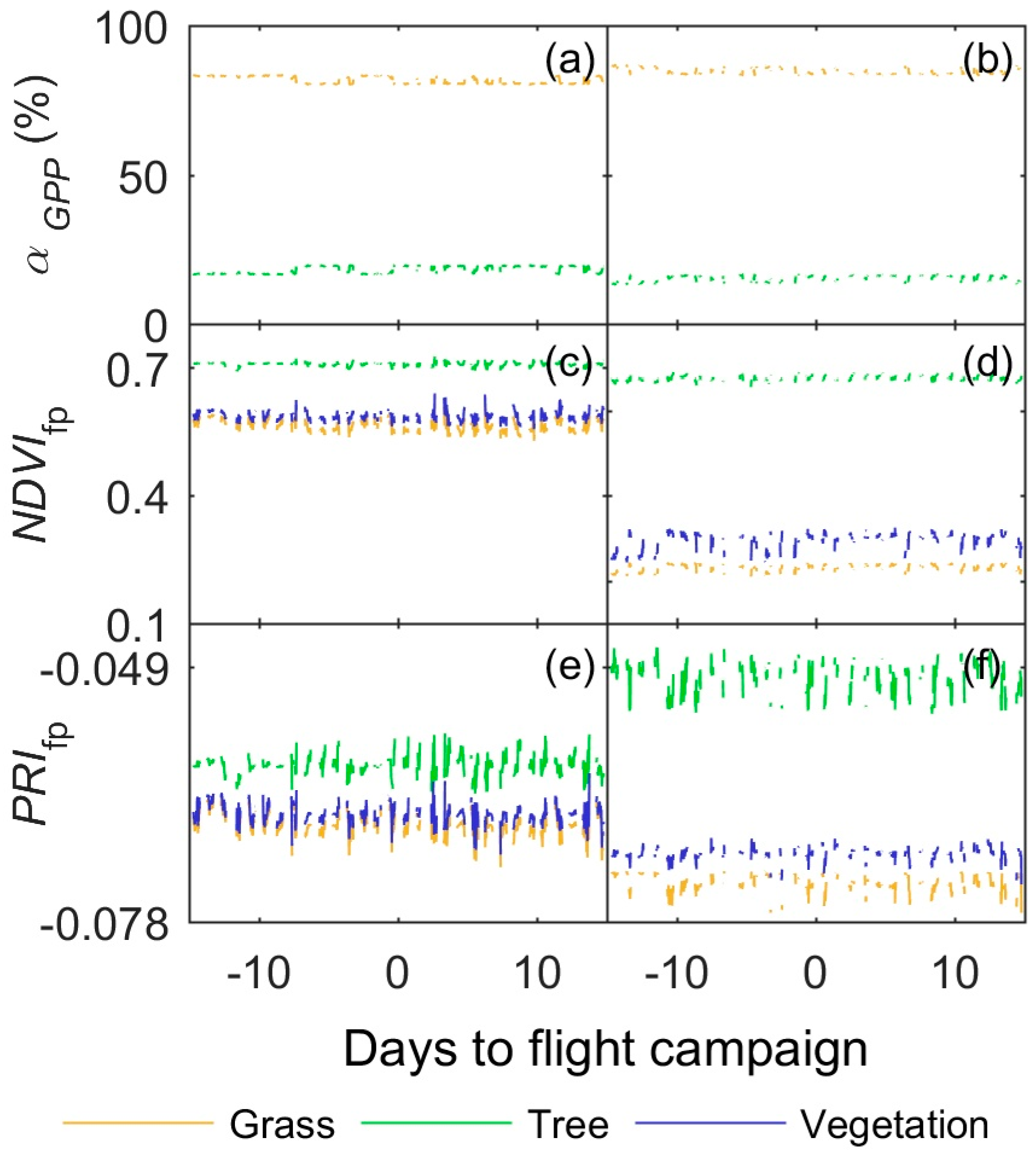
3.3. Footprint Climatology and Hyperspectral Data Integration
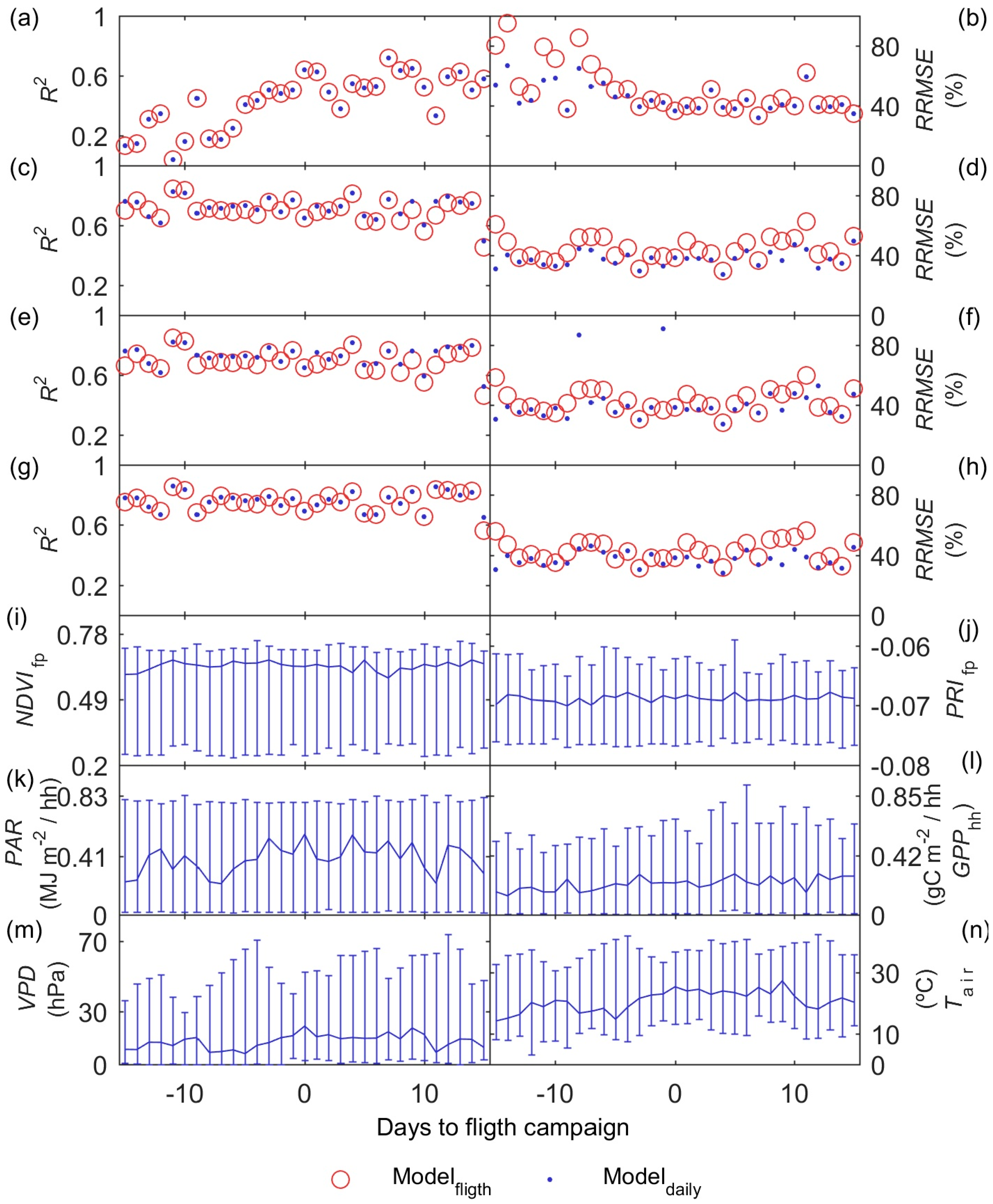
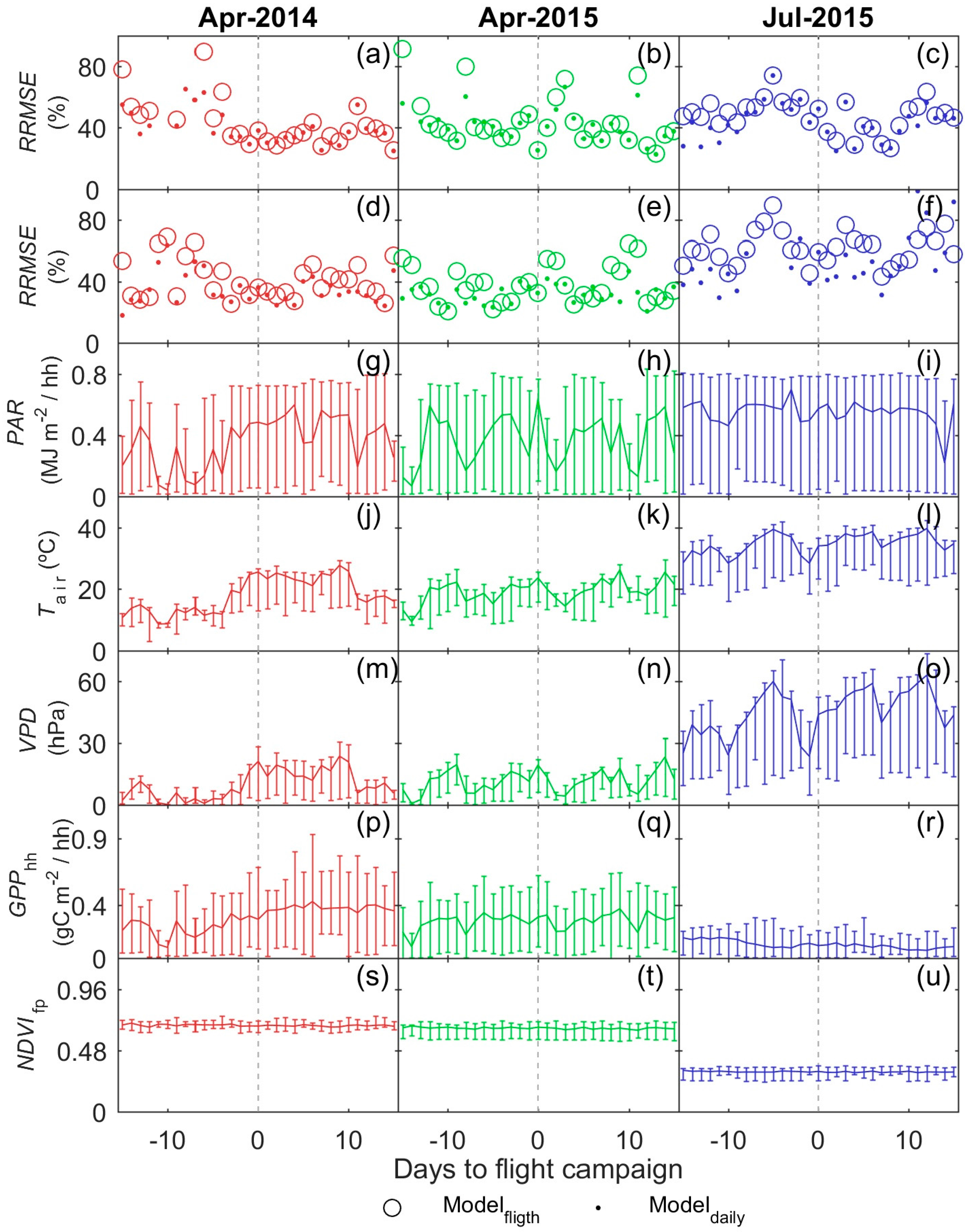
3.4. GPP Models Performance
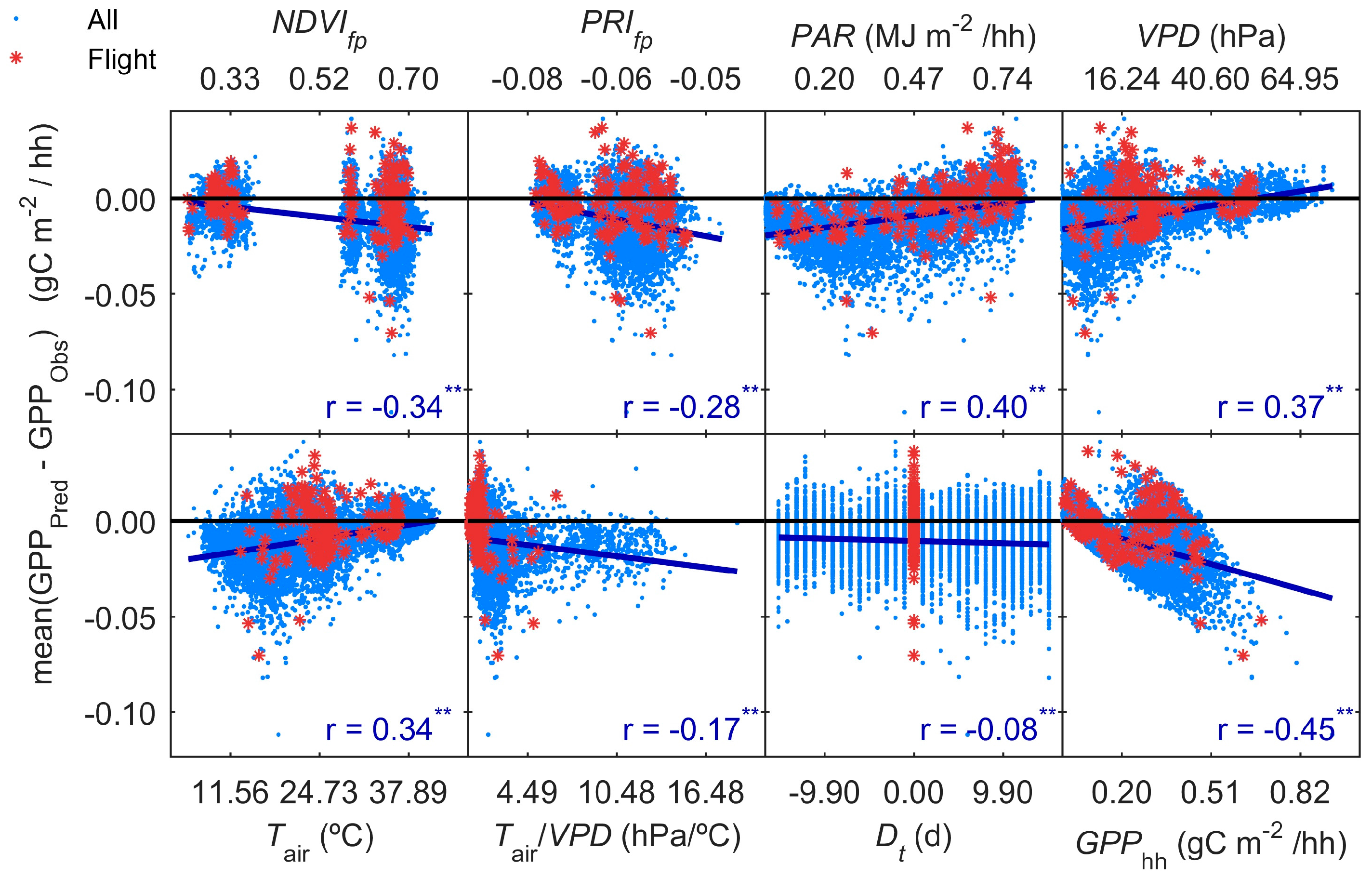
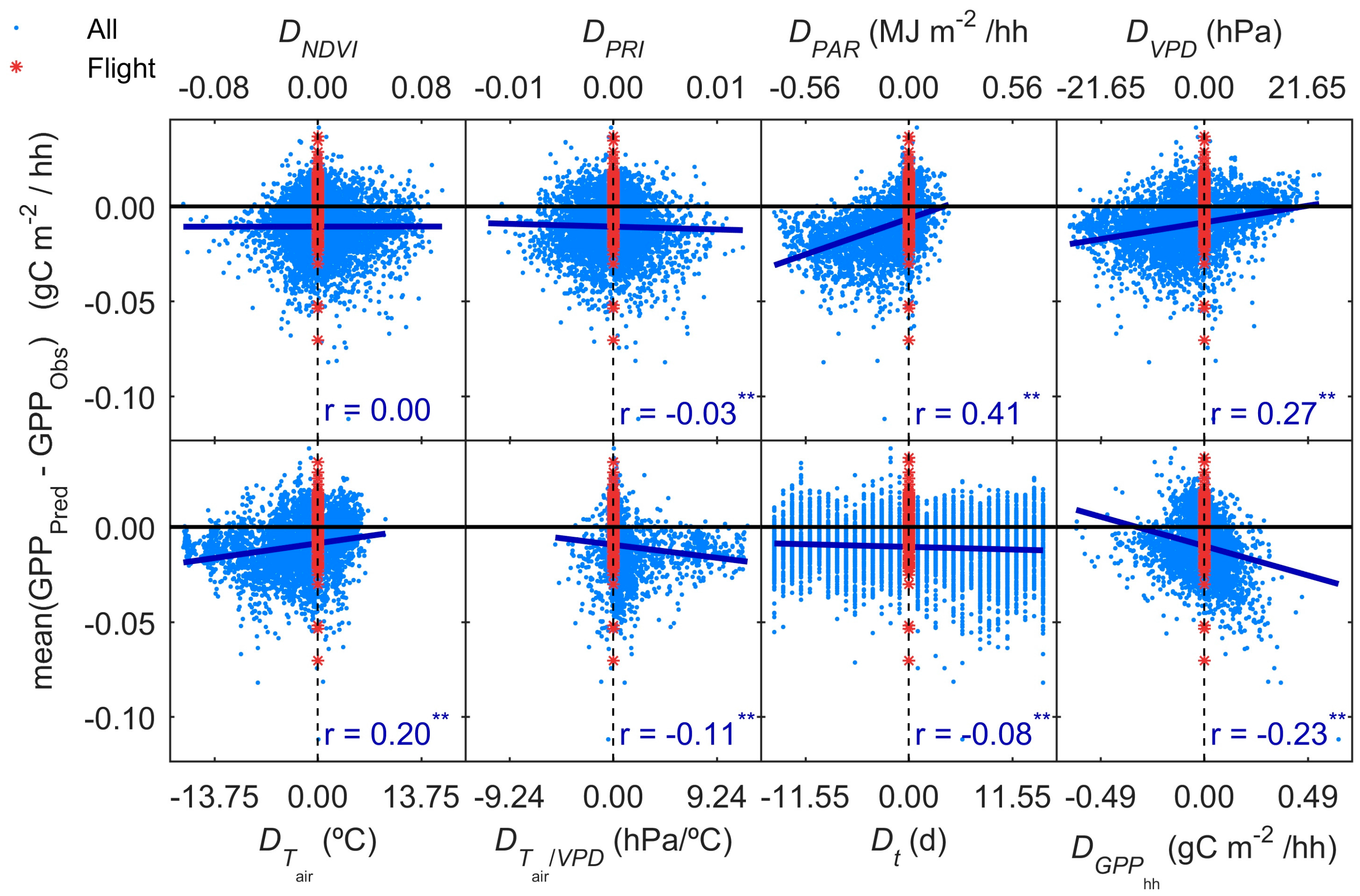
3.5. GPP Models Error Analysis
4. Discussion
- (i)
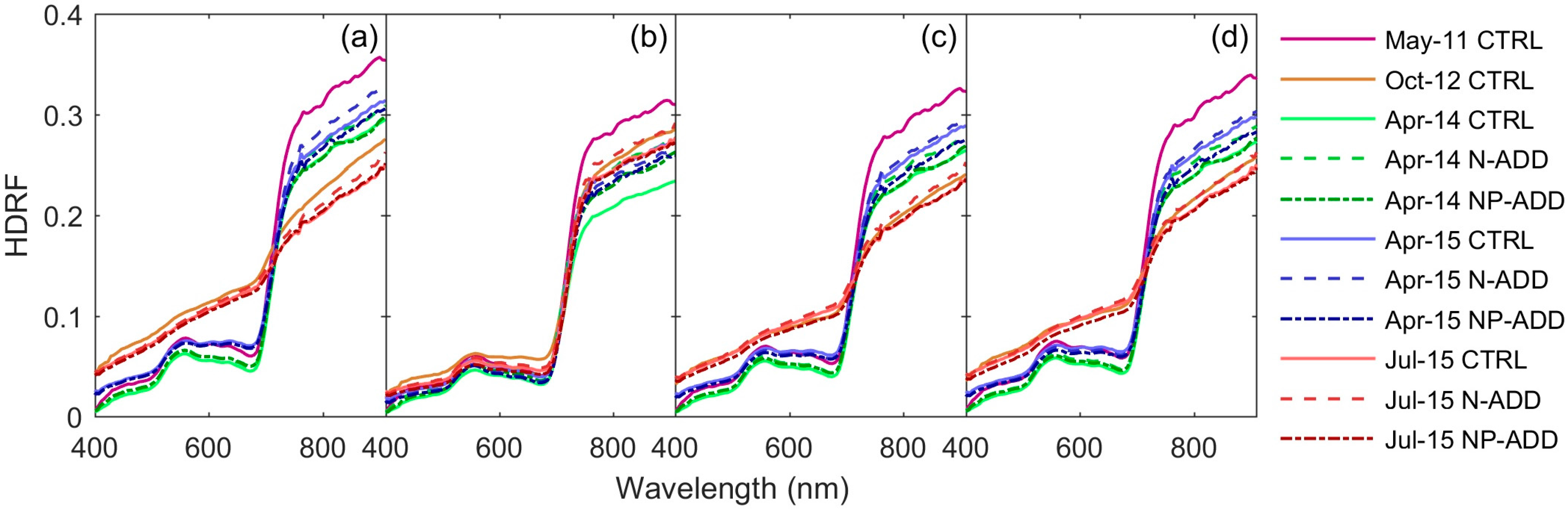
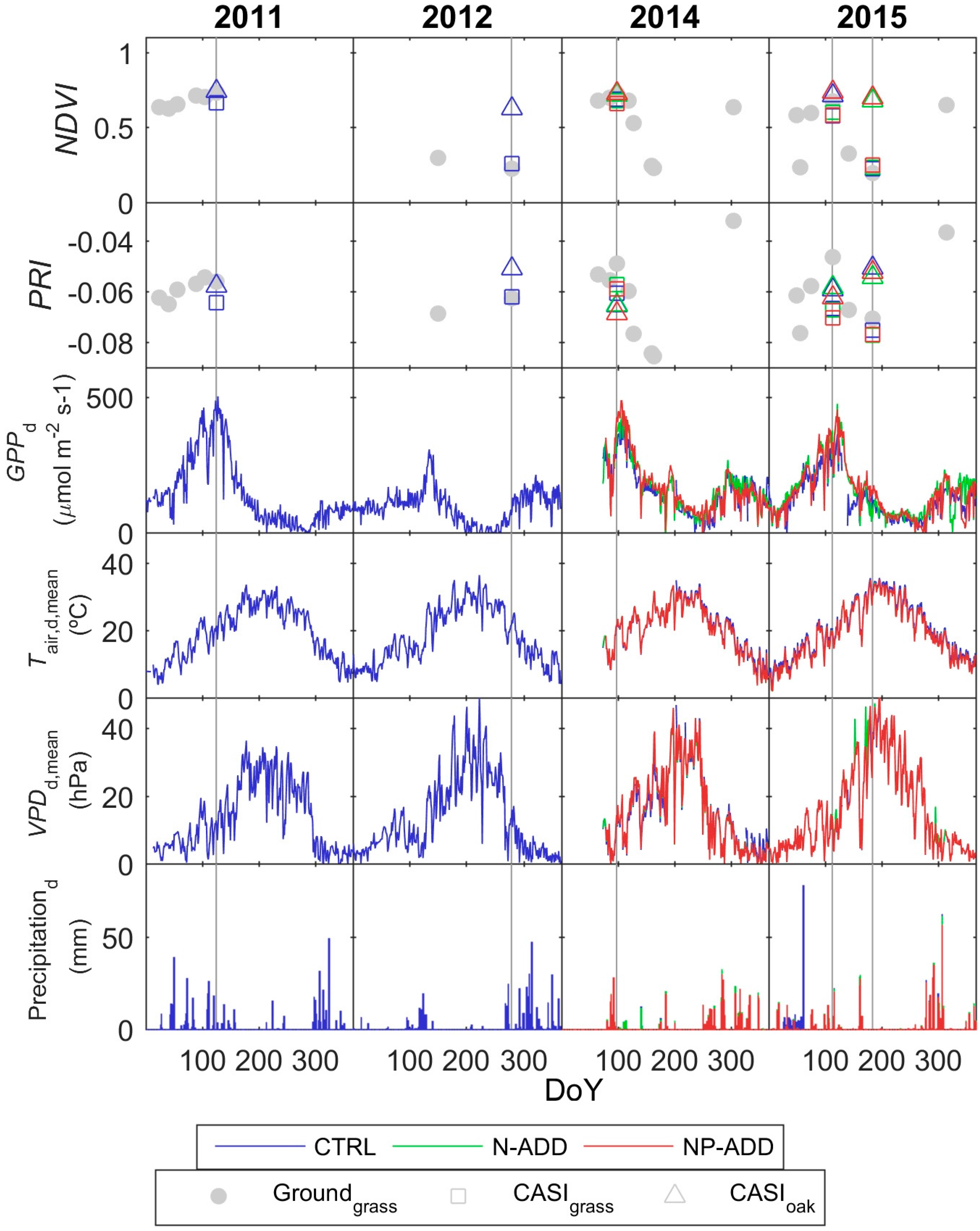
- Results show that, even in this ecosystem, relatively heterogeneous at the small scale but homogeneous at larger scale, the impact of the spatial mismatch between EC and RS footprints on the estimation of GPP is not very important. This means that when footprint climatology and RS pixels present similar characteristics, the spatial mismatch between EC footprint and optical footprint can become less relevant than other sources of variability or uncertainty. In our case, the impact of non-vegetated surfaces is low, and trees and grasses are quite homogeneously mixed at footprint and mid-low spatial resolution RS scales (Table 3, Figure 4). However, we hypothesize that the mix of trees and grasses hamper the accurate modeling of photosynthesis and GPPhh in this type of ecosystem with simple light use efficiency approaches or semi empirical models.
- (ii)
- Results also suggest that the impact of the temporal mismatch between RS data (i.e., flight overpass) and fluxes was low. Only slight increases of the errors were related to this mismatch. In general, “Daily” and “Flight” models showed similar performances as soon as they included PAR (MOD2–MOD4), and differences in RRMSE were sensitive to variations in meteorological variables. In our site, grasses show a strong phenological variability which might overrule trees contribution to RS and EC signals. Therefore, we hypothesize that larger accuracies or continuous acquisition of RS data would be needed to determine the actual impact of changes in vegetation properties between consecutive mid-temporal resolution remote observations.
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2014: SYNTHESIS Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Monteith, J.L.; Moss, C.J. Climate and the efficiency of crop production in britain [and discussion]. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1977, 281, 277–294. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Wulder, M.A.; Black, T.A.; Guy, R.D. The use of remote sensing in light use efficiency based models of gross primary production: A review of current status and future requirements. Sci. Total Environ. 2008, 404, 411–423. [Google Scholar] [CrossRef] [PubMed]
- Meroni, M.; Rossini, M.; Guanter, L.; Alonso, L.; Rascher, U.; Colombo, R.; Moreno, J. Remote sensing of solar-induced chlorophyll fluorescence: Review of methods and applications. Remote Sens. Environ. 2009, 113, 2037–2051. [Google Scholar] [CrossRef]
- Baldocchi, D. Measuring fluxes of trace gases and energy between ecosystems and the atmosphere—The state and future of the eddy covariance method. Glob. Chang. Biol. 2014, 20, 3600–3609. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Black, T.A.; Coops, N.C.; Hilker, T.; Trofymow, J.A.; Morgenstern, K. Assessing tower flux footprint climatology and scaling between remotely sensed and eddy covariance measurements. Bound. Layer Meteorol. 2009, 130, 137–167. [Google Scholar] [CrossRef]
- Pfeifer, M.; Disney, M.; Quaife, T.; Marchant, R. Terrestrial ecosystems from space: A review of earth observation products for macroecology applications. Glob. Ecol. Biogeogr. 2012, 21, 603–624. [Google Scholar] [CrossRef]
- Gamon, J.A.; Coburn, C.; Flanagan, L.B.; Huemmrich, K.F.; Kiddle, C.; Sanchez-Azofeifa, G.A.; Thayer, D.R.; Vescovo, L.; Gianelle, D.; Sims, D.A.; et al. SpecNet revisited: Bridging flux and remote sensing communities. Can. J. Remote Sens. 2010, 36, S376–S390. [Google Scholar] [CrossRef]
- Gamon, J.A.; Rahman, A.F.; Dungan, J.L.; Schildhauer, M.; Huemmrich, K.F. Spectral network (SpecNet)—What is it and why do we need it? Remote Sens. Environ. 2006, 103, 227–235. [Google Scholar] [CrossRef]
- Chen, B.; Coops, N.C.; Fu, D.; Margolis, H.A.; Amiro, B.D.; Black, T.A.; Arain, M.A.; Barr, A.G.; Bourque, C.P.A.; Flanagan, L.B.; et al. Characterizing spatial representativeness of flux tower eddy-covariance measurements across the canadian carbon program network using remote sensing and footprint analysis. Remote Sens. Environ. 2012, 124, 742–755. [Google Scholar] [CrossRef]
- Detto, M.; Montaldo, N.; Albertson, J.D.; Mancini, M.; Katul, G. Soil moisture and vegetation controls on evapotranspiration in a heterogeneous mediterranean ecosystem on sardinia, Italy. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Gelybó, G.; Barcza, Z.; Kern, A.; Kljun, N. Effect of spatial heterogeneity on the validation of remote sensing based GPP estimations. Agric. For. Meteorol. 2013, 174–175, 43–53. [Google Scholar]
- Verma, M.; Friedl, M.A.; Richardson, A.D.; Kiely, G.; Cescatti, A.; Law, B.E.; Wohlfahrt, G.; Gielen, B.; Roupsard, O.; Moors, E.J.; et al. Remote sensing of annual terrestrial gross primary productivity from MODIS: An assessment using the fluxnet la thuile data set. Biogeosciences 2014, 11, 2185–2200. [Google Scholar] [CrossRef]
- Hill, M.; Hanan, N.; Hoffmann, W.; Scholes, R.; Prince, S.; Ferwerda, J.; Lucas, R.; Baker, I.; Arneth, A.; Higgins, S. Remote sensing and modeling of savannas: The state of the dis-union. In 34th International Symposium on Remote Sensing of Environment—The GEOSS Era: Towards Operational Environmental Monitoring; ISPRS: Sydney, Australia, 2011; p. 6. [Google Scholar]
- Scholes, R.J.; Archer, S.R. Tree-grass interactions in savannas. Annu. Rev. Ecol. Syst. 1997, 28, 517–544. [Google Scholar] [CrossRef]
- Michael, J.H.; Miguel, O.R.; Crystal, B.S. Biogeography and dynamics of global tropical and subtropical savannas. In Ecosystem Function in Savannas; CRC Press: Boca Raton, FL, USA, 2010; pp. 3–37. [Google Scholar]
- Holdo, R.M.; Brocato, E.R. Tree-grass competition varies across select savanna tree species: A potential role for rooting depth. Plant Ecol. 2015, 216, 577–588. [Google Scholar] [CrossRef]
- Ludwig, F.; de Kroon, H.; Berendse, F.; Prins, H.H.T. The influence of savanna trees on nutrient, water and light availability and the understorey vegetation. Plant Ecol. 2004, 170, 93–105. [Google Scholar] [CrossRef]
- Sankaran, M.; Ratnam, J.; Hanan, N.P. Tree-grass coexistence in savannas revisited—insights from an examination of assumptions and mechanisms invoked in existing models. Ecol. Lett. 2004, 7, 480–490. [Google Scholar] [CrossRef]
- MEA. Millennium Ecosystem Assessment—Ecosystems and Human Well-Being: Desertification Synthesis; World Resources Institute: Washington, DC, USA, 2005. [Google Scholar]
- Baudena, M.; Dekker, S.C.; van Bodegom, P.M.; Cuesta, B.; Higgins, S.I.; Lehsten, V.; Reick, C.H.; Rietkerk, M.; Scheiter, S.; Yin, Z.; et al. Forests, savannas, and grasslands: Bridging the knowledge gap between ecology and dynamic global vegetation models. Biogeosciences 2015, 12, 1833–1848. [Google Scholar] [CrossRef]
- Hanan, N.P.; Tredennick, A.T.; Prihodko, L.; Bucini, G.; Dohn, J. Analysis of stable states in global savannas: Is the cart pulling the horse? Glob. Ecol. Biogeogr. 2014, 23, 259–263. [Google Scholar] [CrossRef] [PubMed]
- Moore, C.E.; Beringer, J.; Evans, B.; Hutley, L.B.; Tapper, N.J. Tree-grass phenology information improves light use efficiency modelling of gross primary productivity for an australian tropical savanna. Biogeosci. Discuss. 2016, 2016, 1–38. [Google Scholar] [CrossRef]
- Ma, X.; Huete, A.; Yu, Q.; Coupe, N.R.; Davies, K.; Broich, M.; Ratana, P.; Beringer, J.; Hutley, L.B.; Cleverly, J.; et al. Spatial patterns and temporal dynamics in savanna vegetation phenology across the north australian tropical transect. Remote Sens. Environ. 2013, 139, 97–115. [Google Scholar] [CrossRef]
- Colgan, M.; Baldeck, C.; Féret, J.-B.; Asner, G. Mapping savanna tree species at ecosystem scales using support vector machine classification and BRDF correction on airborne hyperspectral and LiDAR data. Remote Sens. 2012, 4, 3462. [Google Scholar] [CrossRef]
- Porcar-Castell, A.; Mac Arthur, A.; Rossini, M.; Eklundh, L.; Pacheco-Labrador, J.; Anderson, K.; Balzarolo, M.; Martín, M.P.; Jin, H.; Tomelleri, E.; et al. Eurospec: At the interface between remote-sensing and ecosystem CO2 flux measurements in europe. Biogeosciences 2015, 12, 6103–6124. [Google Scholar] [CrossRef]
- Chasmer, L.; Barr, A.; Hopkinson, C.; McCaughey, H.; Treitz, P.; Black, A.; Shashkov, A. Scaling and assessment of GPP from MODIS using a combination of airborne LiDAR and eddy covariance measurements over jack pine forests. Remote Sens. Environ. 2009, 113, 82–93. [Google Scholar] [CrossRef]
- Cheng, Y.; Gamon, J.A.; Fuentes, D.A.; Mao, Z.; Sims, D.A.; Qiu, H.-l.; Claudio, H.; Huete, A.; Rahman, A.F. A multi-scale analysis of dynamic optical signals in a southern california chaparral ecosystem: A comparison of field, AVIRIS and MODIS data. Remote Sens. Environ. 2006, 103, 369–378. [Google Scholar] [CrossRef]
- Christian, B.; Joshi, N.; Saini, M.; Mehta, N.; Goroshi, S.; Nidamanuri, R.R.; Thenkabail, P.; Desai, A.R.; Krishnayya, N.S.R. Seasonal variations in phenology and productivity of a tropical dry deciduous forest from MODIS and Hyperion. Agric. For. Meteorol. 2015, 214–215, 91–105. [Google Scholar] [CrossRef]
- Shim, C.; Hong, J.; Hong, J.; Kim, Y.; Kang, M.; Malla Thakuri, B.; Kim, Y.; Chun, J. Evaluation of MODIS GPP over a complex ecosystem in East Asia: A case study at gwangneung flux tower in Korea. Adv. Space Res. 2014, 54, 2296–2308. [Google Scholar] [CrossRef]
- Perez-Priego, O.; El-Madany, T.S.; Migliavacca, M.; Kowalski, A.S.; Jung, M.; Carrara, A.; Kolle, O.; Martín, M.P.; Pacheco-Labrador, J.; Moreno, G.; et al. Evaluation of eddy covariance latent heat fluxes with independent lysimeter and sapflow estimates in a Mediterranean savannah ecosystem. Agric. For. Meteorol. 2017, 236, 87–99. [Google Scholar] [CrossRef]
- Casals, P.; Gimeno, C.; Carrara, A.; Lopez-Sangil, L.; Sanz, M.J. Soil CO2 efflux and extractable organic carbon fractions under simulated precipitation events in a Mediterranean dehesa. Soil Biol. Biochem. 2009, 41, 1915–1922. [Google Scholar] [CrossRef]
- Pacheco-Labrador, J.; Martín, M.P.; Riaño, D.; Hilker, T.; Carrara, A. New approaches in multi-angular proximal sensing of vegetation: Accounting for spatial heterogeneity and diffuse radiation in directional reflectance distribution models. Remote Sens. Environ. 2016, 187, 447–457. [Google Scholar] [CrossRef]
- Manip—Manipulation Nitrogen and Phosphorous. Available online: https://www.bgc-jena.mpg.de/bgi/index.php/Research/Manip (accessed on 9 June 2017).
- El-Madany, T.; Reichstein, M.; Perez-Priego, O.; Carrara, A.; Moreno, G.; Martin Isabel, M.P.; Pacheco-Labrador, J.; Wohlfahrt, G.; Weber, U.; Kolle, O.; et al. Drivers of spatio-temporal variability of carbon dioxide and energy fluxes in a savanna ecosystem. 2017; In Preparation. [Google Scholar]
- Migliavacca, M.; El-Madany, T.; Perez-Priego, O.; Carrara, A.; Hammer, T.; Henkel, K.; Kolle, O.; Luo, Y.; Moreno, G.; Morris, K.; et al. Effects of A Large Scale Nitrogen and Phosphorous Fertilization on the Ecosystem Functioning of A Mediterranean Tree-Grass Ecosystem; Abstracts, G.R., Ed.; European Geosciences Union General Assembly: Vienna, Austria, 2017. [Google Scholar]
- Biospec—Linking Spectral Information at Different Spatial Scales with Biophysical Parameters of Mediterranean Vegetation in the Context of Global Change. Available online: http://www.lineas.cchs.csic.es/biospec (accessed on 9 June 2017).
- Fluχpec—Monitoring Changes in Water and Carbon Fluxes from Remote and Proximal Sensing in Mediterranean “Dehesa” Ecosystem. Available online: http://www.lineas.cchs.csic.es/fluxpec (accessed on 9 June 2017).
- Ceos-Spain. Available online: http://ceosspain.lpi.uv.es/home/project (accessed on 9 June 2017).
- Deheshyre—Monitoring Mass and Energy Fluxes in a Manipulated Mediterranean Tree-Grass Dehesa (Mediterranean Savanna) Ecosystem through the Integration of Ground and Satellite Data with Airborne Hyperspectral Imagery. Available online: https://www.bgc-jena.mpg.de/bgi/index.php/Research/Deheshyre (accessed on 9 June 2017).
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Mendiguren, G.; Pilar Martín, M.; Nieto, H.; Pacheco-Labrador, J.; Jurdao, S. Seasonal variation in grass water content estimated from proximal sensing and MODIS time series in a Mediterranean Fluxnet site. Biogeosciences 2015, 12, 5523–5535. [Google Scholar] [CrossRef]
- Mauder, M.; Foken, T. Processing and Quality Control of Eddy Covariance Measurements. Proceedings of European Geosciences Union General Assembly 2005, Vienna, Austria, 24–29 April 2005. [Google Scholar]
- Vickers, D.; Mahrt, L. Quality control and flux sampling problems for tower and aircraft data. J. Atmos. Ocean. Technol. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Papale, D.; Reichstein, M.; Aubinet, M.; Canfora, E.; Bernhofer, C.; Kutsch, W.; Longdoz, B.; Rambal, S.; Valentini, R.; Vesala, T.; et al. Towards a standardized processing of net ecosystem exchange measured with eddy covariance technique: Algorithms and uncertainty estimation. Biogeosciences 2006, 3, 571–583. [Google Scholar] [CrossRef]
- ReddyProc: Data Processing and Plotting Utilities of (Half-)Hourly Eddy-Covariance Measurements. Available online: https://www.bgc-jena.mpg.de/bgi/index.php/Services/REddyProcWebRPackage (accessed on 9 June 2017).
- Wutzler, T.; Moffat, A.; Migliavacca, M.; Knauer, J.; Menzer, O.; Sickel, K.; Reichstein, M. Reddyproc: Enabling researchers to process eddy-covariance data. Proceedings of European Geosciences Union General Assembly 2016, Vienna, Austria, 23–28 April 2017. [Google Scholar]
- Greco, S.; Baldocchi, D.D. Seasonal variations of CO2 and water vapour exchange rates over a temperate deciduous forest. Glob. Chang. Biol. 1996, 2, 183–197. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Richardson, A.D.; Hollinger, D.Y. Statistical modeling of ecosystem respiration using eddy covariance data: Maximum likelihood parameter estimation, and monte carlo simulation of model and parameter uncertainty, applied to three simple models. Agric. For. Meteorol. 2005, 131, 191–208. [Google Scholar] [CrossRef]
- Lasslop, G.; Reichstein, M.; Kattge, J.; Papale, D. Influences of observation errors in eddy flux data on inverse model parameter estimation. Biogeosciences 2008, 5, 1311–1324. [Google Scholar] [CrossRef]
- Migliavacca, M.; Reichstein, M.; Richardson, A.D.; Mahecha, M.D.; Cremonese, E.; Delpierre, N.; Galvagno, M.; Law, B.E.; Wohlfahrt, G.; Andrew Black, T.; et al. Influence of physiological phenology on the seasonal pattern of ecosystem respiration in deciduous forests. Glob. Chang. Biol. 2015, 21, 363–376. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, C.-I.; Katul, G.; Chi, T.-W. An approximate analytical model for footprint estimation of scalar fluxes in thermally stratified atmospheric flows. Adv. Water Resour. 2000, 23, 765–772. [Google Scholar] [CrossRef]
- El-Madany, T.; Migliavacca, M.; Pérez-Priego, O.; Reichstein, M.; Kollen, O.; Moreno, G.; Pacheco-Labrador, J.; Martín Isabel, M.P. Can Eddy Covariance Flux Magnitudes and Uncertainties Be Explained by Surface Heterogeneity?—A combined Multi-tower—Hyperspectral Remote Sensing Approach in A Mediterranean Savanna Ecosystem. In Proceedings of the 2015 American Geophysical Union (AGU) Fall Meeting, San Francisco, CA, USA, 14–18 December 2015. [Google Scholar]
- Rossini, M.; Cogliati, S.; Meroni, M.; Migliavacca, M.; Galvagno, M.; Busetto, L.; Cremonese, E.; Julitta, T.; Siniscalco, C.; Morra di Cella, U.; et al. Remote sensing-based estimation of gross primary production in a subalpine grassland. Biogeosciences 2012, 9, 2565–2584. [Google Scholar] [CrossRef]
- Rossini, M.; Migliavacca, M.; Galvagno, M.; Meroni, M.; Cogliati, S.; Cremonese, E.; Fava, F.; Gitelson, A.; Julitta, T.; Morra di Cella, U.; et al. Remote estimation of grassland gross primary production during extreme meteorological seasons. Int. J. Appl. Earth Obs. Geoinf. 2014, 29, 1–10. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. In Third Earth Resources Technology Satellite-1 Symposium; Freden, S.C., Mercanti, E.P., Becker, M.A., Eds.; NASA: Greenbelt, MD, USA, 1974; pp. 301–317. [Google Scholar]
- Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Hernández-Clemente, R.; Navarro-Cerrillo, R.M.; Suárez, L.; Morales, F.; Zarco-Tejada, P.J. Assessing structural effects on PRI for stress detection in conifer forests. Remote Sens. Environ. 2011, 115, 2360–2375. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Williams, L.E.; Suárez, L.; Berni, J.A.J.; Goldhamer, D.; Fereres, E. A pri-based water stress index combining structural and chlorophyll effects: Assessment using diurnal narrow-band airborne imagery and the CWSI thermal index. Remote Sens. Environ. 2013, 138, 38–50. [Google Scholar] [CrossRef]
- Rahimzadeh-Bajgiran, P.; Munehiro, M.; Omasa, K. Relationships between the photochemical reflectance index (PRI) and chlorophyll fluorescence parameters and plant pigment indices at different leaf growth stages. Photosynth. Res. 2012, 113, 261–271. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Running, S.W.; Zhao, M. User’s Guide Daily GPP and Annual NPP (MOD17A2/A3) Products NASA Earth Observing System MODIS Land Algorithm; MODIS Land Team: Washington, DC, USA, 2015; p. 28.
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Zhao, M.; Running, S.W.; Wofsy, S.C.; Urbanski, S.; Dunn, A.L.; Munger, J.W. Scaling gross primary production (GPP) over boreal and deciduous forest landscapes in support of MODIS GPP product validation. Remote Sens. Environ. 2003, 88, 256–270. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Gajardo Valenzuela, J. Estimation of Gap Fraction and Clumping Index with Terrestrial and Airborne Laser Scanner Data; Universidad de Alcalá: Alcalá de Henares, Spain, 2014. [Google Scholar]
- Vilar, L.; Pacheco-Labrador, J.; Pérez-Cabello, F.; Martín, M.P. Estimating Biophysical Vegetation Parameters in A Dehesa Ecosystem Using Non-Parametric Statistical Analysis: A Multi-Scale Approach. In Proceedings of the 2016 World Congress Silvo-Pastoral Systems, Évora, Portugal, 27–30 September 2016. [Google Scholar]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. Prospect + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113 (Suppl. S1), S56–S66. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Drolet, G.G.; Huemmrich, K.F.; Hall, F.G.; Middleton, E.M.; Black, T.A.; Barr, A.G.; Margolis, H.A. A MODIS-derived photochemical reflectance index to detect inter-annual variations in the photosynthetic light-use efficiency of a boreal deciduous forest. Remote Sens. Environ. 2005, 98, 212–224. [Google Scholar] [CrossRef]
- Middleton, E.M.; Huemmrich, K.F.; Landis, D.R.; Black, T.A.; Barr, A.G.; McCaughey, J.H. Photosynthetic efficiency of northern forest ecosystems using a MODIS-derived photochemical reflectance index (PRI). Remote Sens. Environ. 2016, 187, 345–366. [Google Scholar] [CrossRef]
- Goerner, A.; Reichstein, M.; Tomelleri, E.; Hanan, N.; Rambal, S.; Papale, D.; Dragoni, D.; Schmullius, C. Remote sensing of ecosystem light use efficiency with MODIS-based PRI. Biogeosciences 2011, 8, 189–202. [Google Scholar] [CrossRef]
- Guarini, R.; Nichol, C.; Clement, R.; Loizzo, R.; Grace, J.; Borghetti, M. The utility of MODIS-sPRI for investigating the photosynthetic light-use efficiency in a Mediterranean deciduous forest. Int. J. Remote Sens. 2014, 35, 6157–6172. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Catalina, A.; González, M.R.; Martín, P. Relationships between net photosynthesis and steady-state chlorophyll fluorescence retrieved from airborne hyperspectral imagery. Remote Sens. Environ. 2013, 136, 247–258. [Google Scholar] [CrossRef]
- Suárez, L.; Zarco-Tejada, P.J.; Berni, J.A.J.; González-Dugo, V.; Fereres, E. Modelling PRI for water stress detection using radiative transfer models. Remote Sens. Environ. 2009, 113, 730–744. [Google Scholar] [CrossRef]
- Hall, F.G.; Hilker, T.; Coops, N.C.; Lyapustin, A.; Huemmrich, K.F.; Middleton, E.; Margolis, H.; Drolet, G.; Black, T.A. Multi-angle remote sensing of forest light use efficiency by observing PRI variation with canopy shadow fraction. Remote Sens. Environ. 2008, 112, 3201–3211. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Hall, F.G.; Black, T.A.; Wulder, M.A.; Nesic, Z.; Krishnan, P. Separating physiologically and directionally induced changes in PRI using BRDF models. Remote Sens. Environ. 2008, 112, 2777–2788. [Google Scholar] [CrossRef]
- Hernández-Clemente, R.; Kolari, P.; Porcar-Castell, A.; Korhonen, L.; Mõttus, M. Tracking the seasonal dynamics of boreal forest photosynthesis using EO-1 Hyperion reflectance: Sensitivity to structural and illumination effects. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5105–5116. [Google Scholar] [CrossRef]
- Mõttus, M.; Takala, T.L.H.; Stenberg, P.; Knyazikhin, Y.; Yang, B.; Nilson, T. Diffuse sky radiation influences the relationship between canopy PRI and shadow fraction. ISPRS J. Photogramm. Remote Sens. 2015, 105, 54–60. [Google Scholar] [CrossRef]
- Gamon, J.A. Reviews and syntheses: Optical sampling of the flux tower footprint. Biogeosciences 2015, 12, 4509–4523. [Google Scholar] [CrossRef]
- Perez-Priego, O.; Guan, J.; Rossini, M.; Fava, F.; Wutzler, T.; Moreno, G.; Carvalhais, N.; Carrara, A.; Kolle, O.; Julitta, T.; et al. Sun-induced chlorophyll fluorescence and photochemical reflectance index improve remote-sensing gross primary production estimates under varying nutrient availability in a typical Mediterranean savanna ecosystem. Biogeosciences 2015, 12, 6351–6367. [Google Scholar] [CrossRef]
- Xin, Q.; Broich, M.; Suyker, A.E.; Yu, L.; Gong, P. Multi-scale evaluation of light use efficiency in MODIS gross primary productivity for croplands in the midwestern united states. Agric. For. Meteorol. 2015, 201, 111–119. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, H.; Liu, Z.; Che, M.; Chen, B. Evaluating parameter adjustment in the MODIS gross primary production algorithm based on eddy covariance tower measurements. Remote Sens. 2014, 6, 3321. [Google Scholar] [CrossRef]
- Running, S.W.; Thornton, P.E.; Nemani, R.; Glassy, J.M. Global terrestrial gross and net primary productivity from the earth observing system. In Methods in Ecosystem Science; Sala, O.E., Jackson, R.B., Mooney, H.A., Howarth, R.W., Eds.; Springer: New York, NY, USA, 2000; pp. 44–57. [Google Scholar]
- Wu, C.; Chen, J.M.; Desai, A.R.; Hollinger, D.Y.; Arain, M.A.; Margolis, H.A.; Gough, C.M.; Staebler, R.M. Remote sensing of canopy light use efficiency in temperate and boreal forests of north america using MODIS imagery. Remote Sens. Environ. 2012, 118, 60–72. [Google Scholar] [CrossRef]
- Flanagan, L.B.; Sharp, E.J.; Gamon, J.A. Application of the photosynthetic light-use efficiency model in a northern Great Plains grassland. Remote Sens. Environ. 2015, 168, 239–251. [Google Scholar] [CrossRef]
- Pacheco-Labrador, J.; González-Cascón, R.; Martín, M.P.; Riaño, D. Understanding the optical responses of leaf nitrogen in Nediterranean Holm oak (Quercus ilex) using field spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 105–118. [Google Scholar] [CrossRef]
- Hmimina, G.; Merlier, E.; Dufrêne, E.; Soudani, K. Deconvolution of pigment and physiologically related photochemical reflectance index variability at the canopy scale over an entire growing season. Plant Cell Environ. 2015, 38, 1578–1590. [Google Scholar] [CrossRef] [PubMed]
- Campbell, G.S. Extinction coefficients for radiation in plant canopies calculated using an ellipsoidal inclination angle distribution. Agric. For. Meteorol. 1986, 36, 317–321. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Leroy, M.; Deschamps, P.-Y. A bidirectional reflectance model of the earth’s surface for the correction of remote sensing data. J. Geophys. Res. Atmos. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-optical bidirectional reflectance modeling of the discrete crown vegetation canopy: Effect of crown shape and mutual shadowing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 276–292. [Google Scholar] [CrossRef]
- Le Roux, X.; Gauthier, H.; Bégué, A.; Sinoquet, H. Radiation absorption and use by humid savanna grassland: Assessment using remote sensing and modelling. Agric. For. Meteorol. 1997, 85, 117–132. [Google Scholar] [CrossRef]
- Lind, M.; Fensholt, R. The spatio-temporal relationship between rainfall and vegetation development in Burkina Faso. Geografisk Tidsskrift 1999, 2, 43–55. [Google Scholar]
- Bégué, A. Leaf area index, intercepted photosynthetically active radiation, and spectral vegetation indices: A sensitivity analysis for regular-clumped canopies. Remote Sens. Environ. 1993, 46, 45–59. [Google Scholar] [CrossRef]
- Myneni, R.B.; Williams, D.L. On the relationship between FAPAR and NDVI. Remote Sens. Environ. 1994, 49, 200–211. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Gao, X.; Huete, A.R.; Ni, W.; Miura, T. Optical–biophysical relationships of vegetation spectra without background contamination. Remote Sens. Environ. 2000, 74, 609–620. [Google Scholar] [CrossRef]
- Rossini, M.; Meroni, M.; Migliavacca, M.; Manca, G.; Cogliati, S.; Busetto, L.; Picchi, V.; Cescatti, A.; Seufert, G.; Colombo, R. High resolution field spectroscopy measurements for estimating gross ecosystem production in a rice field. Agric. For. Meteorol. 2010, 150, 1283–1296. [Google Scholar] [CrossRef]
| Date | GMT Time | Tower | Flight Azimuth (°) | Solar Azimuth (°) |
|---|---|---|---|---|
| 5 May 2011 | 10:31 | CTRL | 120 | 170.1 |
| 4 October 2012 | 11:23 | CTRL | 118 | 127.2 |
| 8 April 2014 | 12:31 | CTRL | 127 | 163.2 |
| 8 April 2014 | 12:38 | N-ADD | 74 | 182.6 |
| 8 April 2014 | 12:55 | NP-ADD | 75 | 186.1 |
| 23 April 2015 | 11:47 | CTRL | 75 | 182.6 |
| 23 April 2015 | 11:55 | N-ADD | 75 | 162.1 |
| 23 April 2015 | 11:29 | NP-ADD | 74 | 166.4 |
| 3 July 2015 | 11:25 | CTRL | 74 | 153.8 |
| 3 July 2015 | 11:35 | N-ADD | 84 | 138.1 |
| 3 July 2015 | 11:07 | NP-ADD | 66 | 143.3 |
| Model | Equation |
|---|---|
| MOD1 | |
| MOD2 | |
| MOD3 | |
| MOD4 |
| Date | Tower | Grass (%) | Trees (%) | Soil and Roads (%) | Water and Shadows (%) |
|---|---|---|---|---|---|
| 5 May 2011 | CTRL | 75.15 | 18.39 | 1.83 | 4.64 |
| 4 October 2012 | CTRL | 68.42 | 18.47 | 1.56 | 11.55 |
| 8 April 2014 | CTRL | 74.17 | 19.41 | 1.21 | 5.21 |
| 8 April 2014 | N-ADD | 74.81 | 17.40 | 1.36 | 6.43 |
| 8 April 2014 | NP-ADD | 71.28 | 21.55 | 1.08 | 6.09 |
| 23 April 2015 | CTRL | 77.13 | 17.18 | 1.04 | 4.65 |
| 23 April 2015 | N-ADD | 77.37 | 15.42 | 1.05 | 6.16 |
| 23 April 2015 | NP-ADD | 75.10 | 17.45 | 0.62 | 6.83 |
| 3 July 2015 | CTRL | 79.49 | 13.83 | 1.38 | 5.30 |
| 3 July 2015 | N-ADD | 79.08 | 15.41 | 1.53 | 3.98 |
| 3 July 2015 | NP-ADD | 75.03 | 17.46 | 0.97 | 6.54 |
| Model | a1 | a2 | a3 | a4 | a5 | a6 | a7 |
|---|---|---|---|---|---|---|---|
| MOD1 | 0.654 ∈ (0.592, 0.724) | −0.112 ∈ (−0.143, −0.082) | |||||
| MOD2 | 1.186 ∈ (1.071, 1.295) | −0.208 ∈ (−0.261, −0.156) | |||||
| MOD3 PRI | 4.022 ∈ (1.197, 5.761) | −0.553 ∈ (−0.827, −0.190) | 4.063 ∈ (−3.556, 5.823) | 0.540 ∈ (0.202, 1.047) | |||
| MOD3 PRI515 | −0.163 ∈ (−3.149, 2.089) | 2.415 ∈ (−0.237, 3.633) | 2.166 ∈ (−0.439, 3.995) | −0.042 ∈ (−0.143, 1.237) | |||
| MOD3 PRInorm | 0.990 ∈ (0.849, 1.102) | −0.071 ∈ (−0.183, 0.315) | 0.965 ∈ (−0.272, 1.162) | 1.066 ∈ (0.755, 1.329) | |||
| MOD3 CPRI | 1.014 ∈ (0.771, 1.480) | −0.226 ∈ (−0.379, −0.108) | 0.906 ∈ (−0.351, 1.534) | 0.826 ∈ (0.162, 1.426) | |||
| MOD4 | 1.644 ∈ (0.375, 2.832) | 72.230 ∈ (0.844, 134.347) | 2.186 ∈ (0.127, 23.907) | −7.809 ∈ (−15.000, 6.360) | 11.490 ∈ (1.137, 37.015) | 2.362 ∈ (2.119, 3.163) | −0.433 ∈ (−0.657, −0.309) |
| Statistics | MOD1 | MOD2 | MOD3 PRI | MOD3 PRI515 | MOD3 PRInorm | MOD3 CPRI | MOD4 |
|---|---|---|---|---|---|---|---|
| Models fit with Sfp,veg | |||||||
| R2 | 0.65 | 0.67 | 0.67 | 0.68 | 0.67 | 0.67 | 0.72 |
| RRMSE | 35.89 | 37.39 | 37.66 | 36.71 | 37.32 | 37.09 | 37.19 |
| AIC | 460.15 | 460.23 | 464.25 | 464.19 | 464.23 | 464.22 | 470.22 |
| Models fit with Sfp,all | |||||||
| R2 | 0.64 | 0.66 | 0.66 | 0.67 | 0.67 | 0.67 | 0.71 |
| RRMSE | 36.11 | 37.71 | 39.64 | 36.85 | 37.54 | 37.13 | 37.32 |
| AIC | 460.16 | 460.25 | 464.35 | 464.20 | 464.24 | 464.22 | 470.23 |
| Models fit with SP250,all | |||||||
| R2 | 0.65 | 0.68 | 0.67 | 0.69 | 0.67 | 0.69 | 0.72 |
| RRMSE | 36.38 | 37.70 | 65.40 | 36.85 | 37.88 | 36.90 | 37.75 |
| AIC | 494.26 | 494.34 | 499.44 | 498.29 | 498.35 | 498.29 | 504.34 |
| Models fit with SP500,all | |||||||
| R2 | 0.65 | 0.70 | 0.70 | 0.69 | 0.69 | 0.69 | 0.72 |
| RRMSE | 36.31 | 36.60 | 36.71 | 36.50 | 36.62 | 36.75 | 36.50 |
| AIC | 494.26 | 494.28 | 498.28 | 498.27 | 498.28 | 498.29 | 504.27 |
| Models fit with SP1000,all | |||||||
| R2 | 0.64 | 0.69 | 0.69 | 0.69 | 0.69 | 0.70 | 0.72 |
| RRMSE | 36.97 | 36.67 | 37.00 | 39.34 | 36.55 | 38.85 | 36.70 |
| AIC | 494.30 | 494.28 | 498.30 | 498.42 | 498.27 | 498.40 | 504.28 |
| Model | Statistic | DNDVI | DPRI | DPAR | DTair/VPD | Dt | DGPP |
|---|---|---|---|---|---|---|---|
| MOD1 | rerr|D | 0.10 | −0.06 | 0.04 | 0.24 | 0.02 | −0.61 |
| p | 0.00 | 0.00 | 0.03 | 0.00 | 0.16 | 0.00 | |
| MOD2 | rerr|D | 0.06 | −0.03 | 0.55 | −0.02 | 0.02 | −0.49 |
| p | 0.00 | 0.04 | 0.00 | 0.31 | 0.17 | 0.00 | |
| MOD3-PRI | rerr|D | 0.07 | −0.01 | 0.56 | −0.02 | 0.02 | −0.47 |
| p | 0.00 | 0.67 | 0.00 | 0.21 | 0.28 | 0.00 | |
| MOD3-PRI515 | rerr|D | 0.05 | −0.03 | 0.56 | −0.02 | 0.02 | −0.51 |
| p | 0.00 | 0.09 | 0.00 | 0.24 | 0.21 | 0.00 | |
| MOD3-PRInorm | rerr|D | −0.02 | 0.06 | 0.55 | −0.02 | 0.02 | −0.50 |
| p | 0.16 | 0.00 | 0.00 | 0.34 | 0.16 | 0.00 | |
| MOD3-CPRI | rerr|D | −0.08 | −0.12 | 0.55 | −0.02 | 0.02 | −0.49 |
| p | 0.00 | 0.00 | 0.00 | 0.14 | 0.19 | 0.00 | |
| MOD4 | rerr|D | 0.11 | −0.09 | 0.49 | 0.04 | 0.02 | −0.47 |
| p | 0.00 | 0.00 | 0.00 | 0.01 | 0.21 | 0.00 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pacheco-Labrador, J.; El-Madany, T.S.; Martín, M.P.; Migliavacca, M.; Rossini, M.; Carrara, A.; Zarco-Tejada, P.J. Spatio-Temporal Relationships between Optical Information and Carbon Fluxes in a Mediterranean Tree-Grass Ecosystem. Remote Sens. 2017, 9, 608. https://doi.org/10.3390/rs9060608
Pacheco-Labrador J, El-Madany TS, Martín MP, Migliavacca M, Rossini M, Carrara A, Zarco-Tejada PJ. Spatio-Temporal Relationships between Optical Information and Carbon Fluxes in a Mediterranean Tree-Grass Ecosystem. Remote Sensing. 2017; 9(6):608. https://doi.org/10.3390/rs9060608
Chicago/Turabian StylePacheco-Labrador, Javier, Tarek S. El-Madany, M. Pilar Martín, Mirco Migliavacca, Micol Rossini, Arnaud Carrara, and Pablo J. Zarco-Tejada. 2017. "Spatio-Temporal Relationships between Optical Information and Carbon Fluxes in a Mediterranean Tree-Grass Ecosystem" Remote Sensing 9, no. 6: 608. https://doi.org/10.3390/rs9060608
APA StylePacheco-Labrador, J., El-Madany, T. S., Martín, M. P., Migliavacca, M., Rossini, M., Carrara, A., & Zarco-Tejada, P. J. (2017). Spatio-Temporal Relationships between Optical Information and Carbon Fluxes in a Mediterranean Tree-Grass Ecosystem. Remote Sensing, 9(6), 608. https://doi.org/10.3390/rs9060608