Assessment of Chlorophyll-a Remote Sensing Algorithms in a Productive Tropical Estuarine-Lagoon System
Abstract
:1. Introduction
2. Materials and Methods
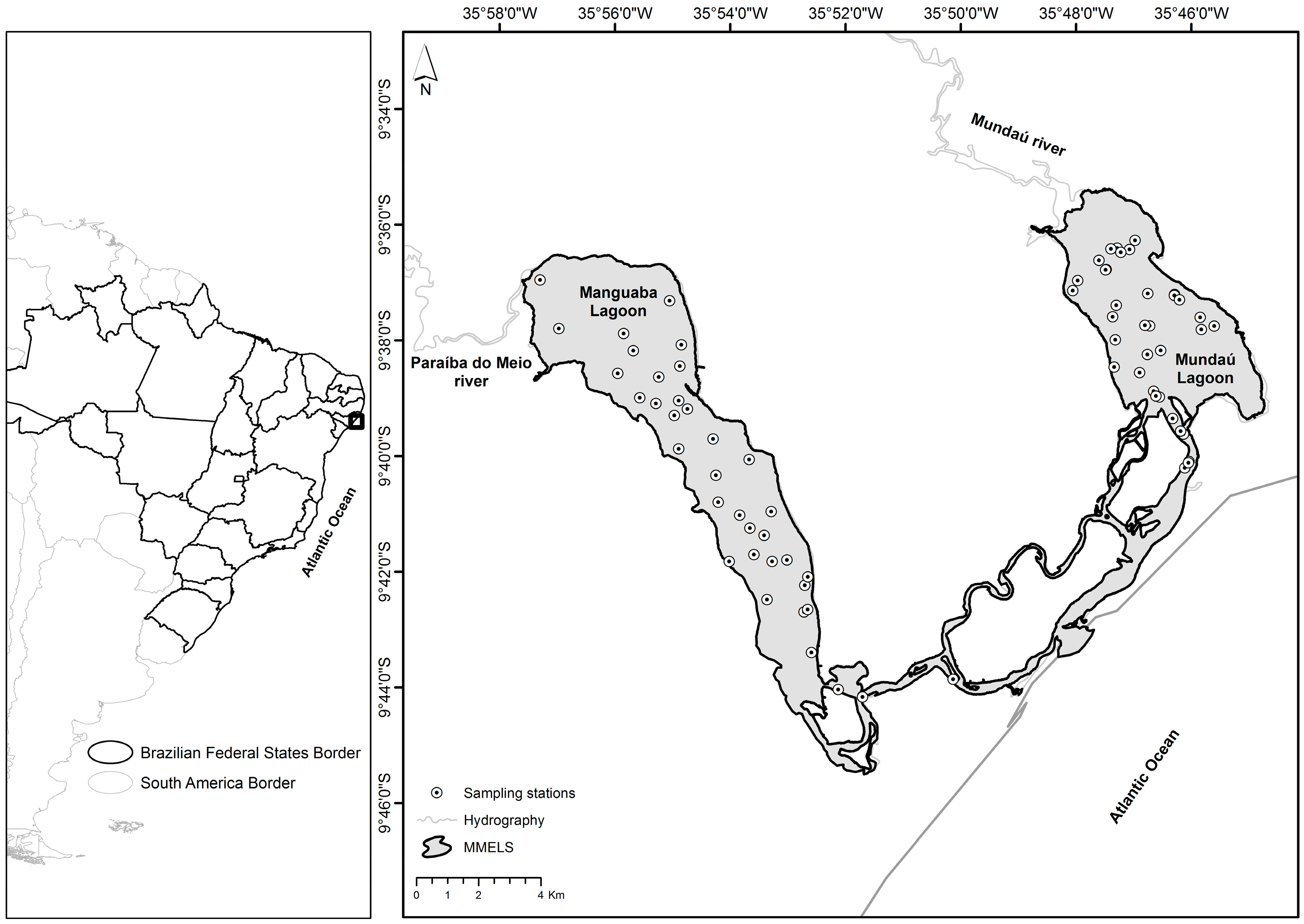
2.1. Study Area
2.2. Field Measurements
2.3. Water Sample Analysis
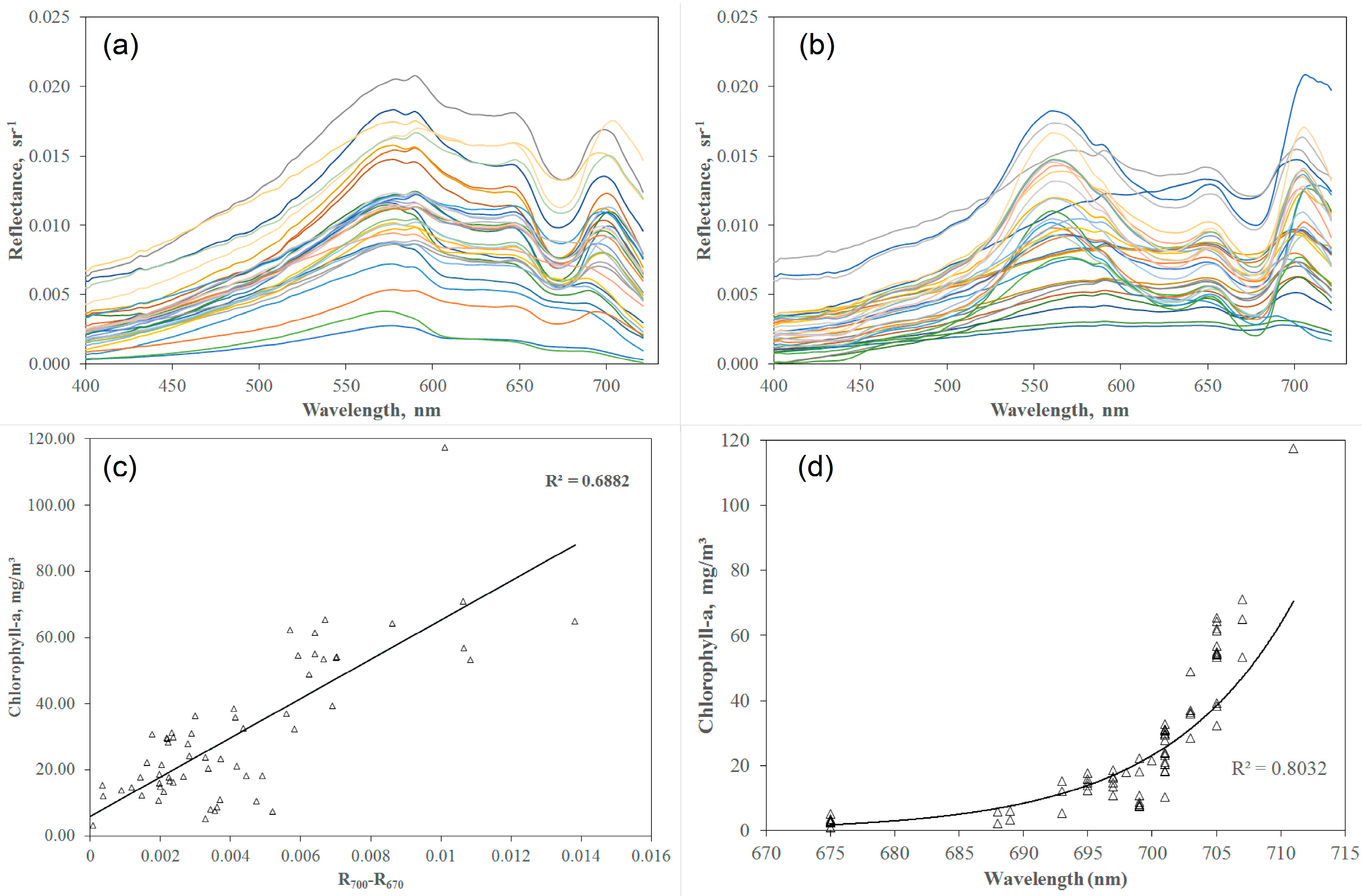
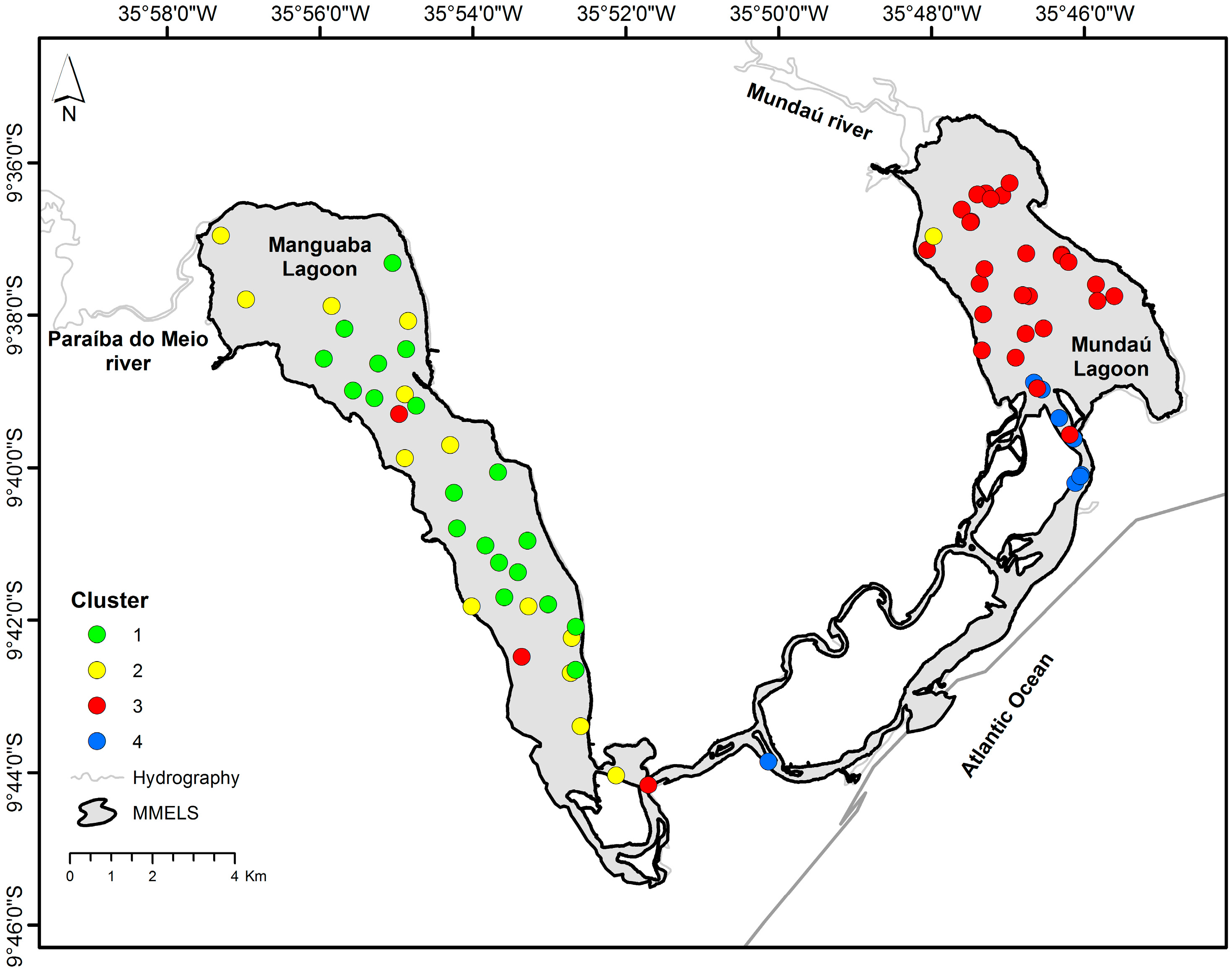
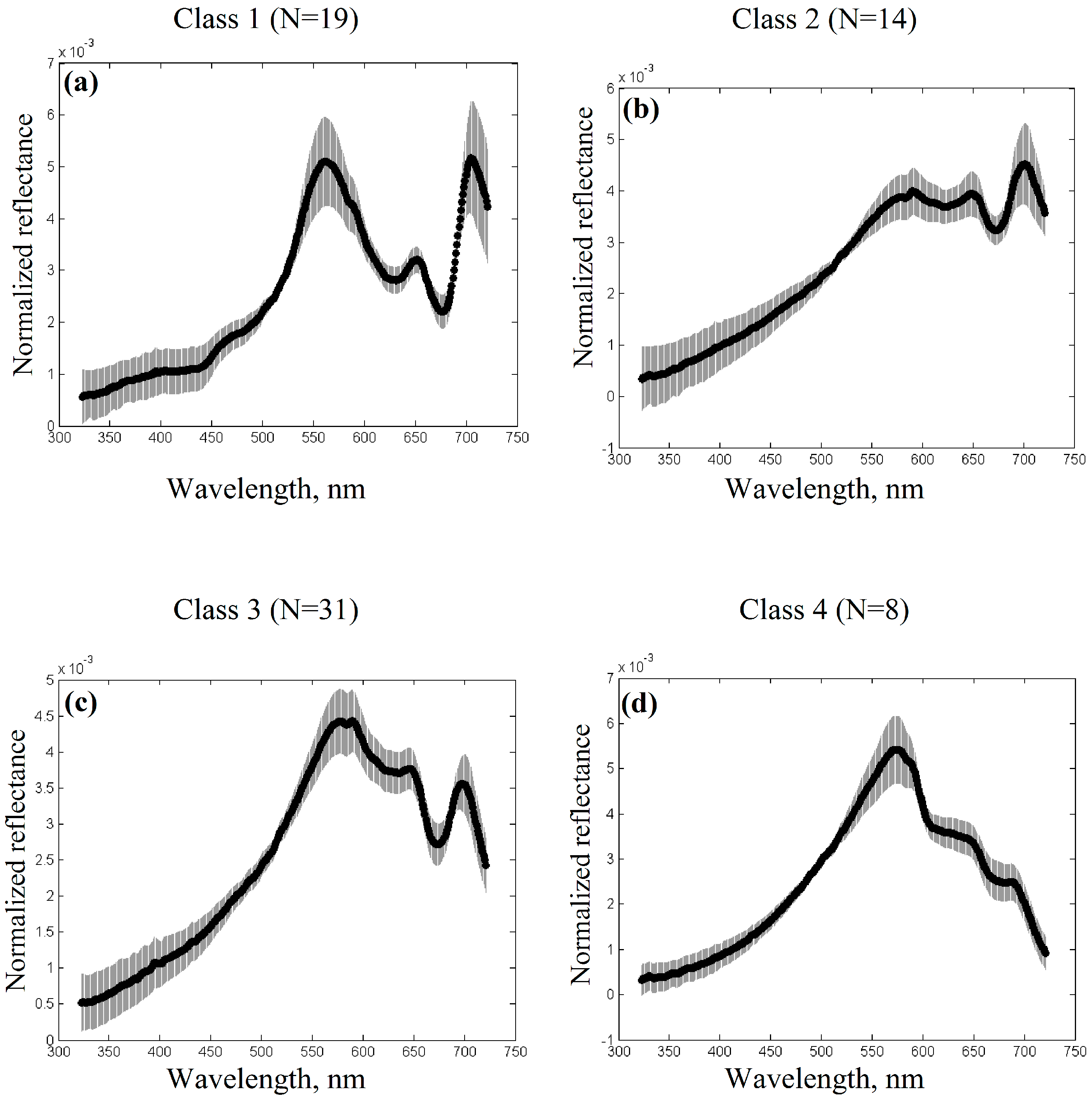
2.4. Reflectance Spectra Classification
2.5. Models to Estimate Chlorophyll-a from Rrs(λ)
2.5.1. The Blue-Green Ratio Model
2.5.2. The Two-Band NIR-Red Ratio Model
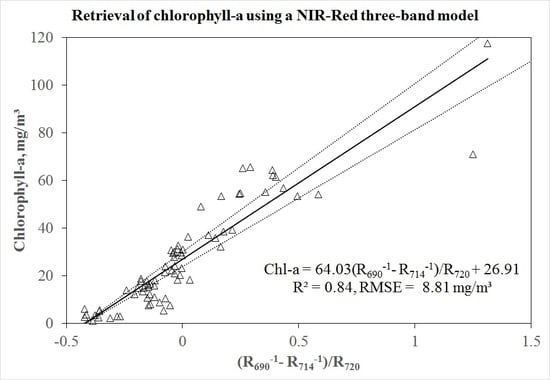
2.5.3. The Three-Band NIR-Red Model
2.5.4. The Four-Band NIR-Red Model
2.6. Algorithm, Model Evaluation and Validation
2.7. Retrieval of Chlorophyll-a Using Models Based on Simulated Satellite Bands
3. Results
3.1. Constituent Concentrations
3.2. Reflectance Spectra and Classification
3.3. Assessment of Chl-a Retrieval Models
3.4. Retrieval of Chlorophyll-a Using Models Based on Simulated Satellite Bands
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mitchell, S.B.; Jennerjahn, T.C.; Vizzini, S.; Zhang, W. Changes to processes in estuaries and coastal waters due to intense multiple pressures—An introduction and synthesis. Estuar. Coast. Shelf Sci. 2015, 156, 1–6. [Google Scholar] [CrossRef]
- Hardisty, J. Introduction to estuarine systems. In Estuaries: Monitoring and Modeling the Physical System; Blackwell Publishing: Hoboken, NJ, USA, 2007; pp. 3–22. [Google Scholar]
- Cadee, G.C. Book review: Nutrients and eutrophication in estuaries and coastal waters. Aquat. Ecol. 2004, 38, 616–617. [Google Scholar] [CrossRef]
- Boyer, J.N.; Kelble, C.R.; Ortner, P.B.; Rudnick, D.T. Phytoplankton bloom status: Chlorophyll a biomass as an indicator of water quality condition in the southern estuaries of florida, USA. Ecol. Indic. 2009, 9, S56–S67. [Google Scholar] [CrossRef]
- Scanes, P.; Coade, G.; Doherty, M.; Hill, R. Evaluation of the utility of water quality based indicators of estuarine lagoon condition in nsw, australia. Estuar. Coast. Shelf Sci. 2007, 74, 306–319. [Google Scholar] [CrossRef]
- Paerl, H.W.; Valdes-Weaver, L.M.; Joyner, A.R.; Winkelmann, V. Phytoplankton indicators of ecological change in the eutrophying pamlico sound system, north carolina. Ecol. Appl. 2007, 17, S88–S101. [Google Scholar] [CrossRef]
- Navalgund, R.R.; Jayaraman, V.; Roy, P.S. Remote sensing applications: An overview. Curr. Sci. 2007, 93, 1747–1766. [Google Scholar]
- Bukata, R.P. Retrospection and introspection on remote sensing of inland water quality: “Like déjà vu all over again”. J. Great Lakes Res. 2013, 39, 2–5. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef]
- Tyler, A.N.; Hunter, P.D.; Spyrakos, E.; Groom, S.; Constantinescu, A.M.; Kitchen, J. Developments in earth observation for the assessment and monitoring of inland, transitional, coastal and shelf-sea waters. Sci. Total Environ. 2016, 572, 1307–1321. [Google Scholar] [CrossRef] [PubMed]
- Cannizzaro, J.P.; Carder, K.L. Estimating chlorophyll a concentrations from remote-sensing reflectance in optically shallow waters. Remote Sens. Environ. 2006, 101, 13–24. [Google Scholar] [CrossRef]
- Palmer, S.C.J.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef]
- Mouw, C.B.; Greb, S.; Aurin, D.; DiGiacomo, P.M.; Lee, Z.; Twardowski, M.; Binding, C.; Hu, C.; Ma, R.; Moore, T.; et al. Aquatic color radiometry remote sensing of coastal and inland waters: Challenges and recommendations for future satellite missions. Remote Sens. Environ. 2015, 160, 15–30. [Google Scholar] [CrossRef]
- Xie, C.-H.; Chang, J.-Y.; Zhang, Y.-Z. A new method for estimating chlorophyll-a concentration in the pearl river estuary. Optik 2015, 126, 4510–4515. [Google Scholar] [CrossRef]
- Le, C.; Hu, C.; English, D.; Cannizzaro, J.; Chen, Z.; Kovach, C.; Anastasiou, C.J.; Zhao, J.; Carder, K.L. Inherent and apparent optical properties of the complex estuarine waters of tampa bay: What controls light? Estuar. Coast. Shelf Sci. 2013, 117, 54–69. [Google Scholar] [CrossRef]
- Tzortziou, M.; Subramaniam, A.; Herman, J.R.; Gallegos, C.L.; Neale, P.J.; Harding, L.W., Jr. Remote sensing reflectance and inherent optical properties in the mid chesapeake bay. Estuar. Coast. Shelf Sci. 2007, 72, 16–32. [Google Scholar] [CrossRef]
- Gons, H.J. Optical teledetection of chlorophyll a in turbid inland water. Environ. Sci. Technol. 1999, 33, 1127–1132. [Google Scholar] [CrossRef]
- Preisendorfer, R.W. Application of Radiative Transfer Theory to Light Measurements in the Sea, Monograph No. 10; L’Institut Géographique National: Champigneulles, France, 1961. [Google Scholar]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters: Its dependence on sun angle as influenced by the molecular scattering contribution. Appl. Opt. 1991, 30, 4427–4438. [Google Scholar] [CrossRef] [PubMed]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters. II. Bidirectional aspects. Appl. Opt. 1993, 32, 6864–6879. [Google Scholar] [CrossRef] [PubMed]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural waters (200–800 nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef] [PubMed]
- Morel, A. Optical properties of pure water and pure sea water. In Optical Aspects of Oceanography; Jerlov, N.G., Nielsen, E.S., Eds.; Academic Press: New York, NY, USA, 1974; pp. 1–24. [Google Scholar]
- Morel, A.; Prieur, L. Analysis of variations in ocean color1. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Gordon, H.R.; Morel, A.Y. In-water algorithms. In Remote Assessment of Ocean Color for Interpretation of Satellite Visible Imagery; Springer: Berlin, Germany, 1983; pp. 24–67. [Google Scholar]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll aalgorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for seawifs. J. Geophys. Res. Oceans 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- Harding, J.L.W.; Magnuson, A.; Mallonee, M.E. Seawifs retrievals of chlorophyll in chesapeake bay and the mid-atlantic bight. Estuar. Coast. Shelf Sci. 2005, 62, 75–94. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W.; Tang, J. Water property monitoring and assessment for china’s inland lake taihu from MODIS-aqua measurements. Remote Sens. Environ. 2011, 115, 841–854. [Google Scholar] [CrossRef]
- Le, C.; Hu, C.; English, D.; Cannizzaro, J.; Chen, Z.; Feng, L.; Boler, R.; Kovach, C. Towards a long-term chlorophyll-a data record in a turbid estuary using MODIS observations. Prog. Oceanogr. 2013, 109, 90–103. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A.; Rundquist, D.C. Towards a unified approach for remote estimation of chlorophyll-a in both terrestrial vegetation and turbid productive waters. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A.; Rundquist, D.C.; Leavitt, B.; Barrow, T.; Holz, J.C. Assessing the potential of seawifs and MODIS for estimating chlorophyll concentration in turbid productive waters using red and near-infrared bands. Remote Sens. Environ. 2005, 96, 176–187. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Dall’Olmo, G.; Moses, W.; Rundquist, D.C.; Barrow, T.; Fisher, T.R.; Gurlin, D.; Holz, J. A simple semi-analytical model for remote estimation of chlorophyll-a in turbid waters: Validation. Remote Sens. Environ. 2008, 112, 3582–3593. [Google Scholar] [CrossRef]
- Randolph, K.; Wilson, J.; Tedesco, L.; Li, L.; Pascual, D.L.; Soyeux, E. Hyperspectral remote sensing of cyanobacteria in turbid productive water using optically active pigments, chlorophyll a and phycocyanin. Remote Sens. Environ. 2008, 112, 4009–4019. [Google Scholar] [CrossRef]
- Chavula, G.; Brezonik, P.; Thenkabail, P.; Johnson, T.; Bauer, M. Estimating chlorophyll concentration in lake malawi from MODIS satellite imagery. Phys. Chem. Earth Parts A/B/C 2009, 34, 755–760. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Lu, H. A four-band semi-analytical model for estimating chlorophyll a in highly turbid lakes: The case of taihu lake, china. Remote Sens. Environ. 2009, 113, 1175–1182. [Google Scholar] [CrossRef]
- Gurlin, D.; Gitelson, A.A.; Moses, W.J. Remote estimation of chl-a concentration in turbid productive waters—Return to a simple two-band nir-red model? Remote Sens. Environ. 2011, 115, 3479–3490. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Zhang, H. Remote estimation of chlorophyll a in optically complex waters based on optical classification. Remote Sens. Environ. 2011, 115, 725–737. [Google Scholar] [CrossRef]
- Yacobi, Y.Z.; Moses, W.J.; Kaganovsky, S.; Sulimani, B.; Leavitt, B.C.; Gitelson, A.A. Nir-red reflectance-based algorithms for chlorophyll—A estimation in mesotrophic inland and coastal waters: Lake kinneret case study. Water Res. 2011, 45, 2428–2436. [Google Scholar] [CrossRef] [PubMed]
- Lyu, H.; Li, X.; Wang, Y.; Jin, Q.; Cao, K.; Wang, Q.; Li, Y. Evaluation of chlorophyll-a retrieval algorithms based on MERIS bands for optically varying eutrophic inland lakes. Sci. Total Environ. 2015, 530–531, 373–382. [Google Scholar] [CrossRef] [PubMed]
- Palmer, S.C.J.; Hunter, P.D.; Lankester, T.; Hubbard, S.; Spyrakos, E.; Tyler, A.N.; Présing, M.; Horváth, H.; Lamb, A.; Balzter, H.; et al. Validation of envisat MERIS algorithms for chlorophyll retrieval in a large, turbid and optically-complex shallow lake. Remote Sens. Environ. 2015, 157, 158–169. [Google Scholar] [CrossRef]
- Wang, L.; Pu, H.; Sun, D.-W. Estimation of chlorophyll-a concentration of different seasons in outdoor ponds using hyperspectral imaging. Talanta 2016, 147, 422–429. [Google Scholar] [CrossRef] [PubMed]
- Loisel, H.; Vantrepotte, V.; Ouillon, S.; Ngoc, D.D.; Herrmann, M.; Tran, V.; Mériaux, X.; Dessailly, D.; Jamet, C.; Duhaut, T.; et al. Assessment and analysis of the chlorophyll-a concentration variability over the vietnamese coastal waters from the MERIS ocean color sensor (2002–2012). Remote Sens. Environ. 2017, 190, 217–232. [Google Scholar] [CrossRef]
- Le, C.; Hu, C.; Cannizzaro, J.; English, D.; Muller-Karger, F.; Lee, Z. Evaluation of chlorophyll-a remote sensing algorithms for an optically complex estuary. Remote Sens. Environ. 2013, 129, 75–89. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Schalles, J.F.; Hladik, C.M. Remote chlorophyll-a retrieval in turbid, productive estuaries: Chesapeake bay case study. Remote Sens. Environ. 2007, 109, 464–472. [Google Scholar] [CrossRef]
- Hu, C.; Chen, Z.; Clayton, T.D.; Swarzenski, P.; Brock, J.C.; Muller-Karger, F.E. Assessment of estuarine water-quality indicators using MODIS medium-resolution bands: Initial results from tampa bay, FL. Remote Sens. Environ. 2004, 93, 423–441. [Google Scholar] [CrossRef]
- Chen, J.; Quan, W. An improved algorithm for retrieving chlorophyll-a from the yellow river estuary using MODIS imagery. Environ. Monit. Assess. 2012, 185, 2243–2255. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Hu, C.; Qiu, Z.; Cannizzaro, J.P.; Barnes, B.B. Influence of a red band-based water classification approach on chlorophyll algorithms for optically complex estuaries. Remote Sens. Environ. 2014, 155, 289–302. [Google Scholar] [CrossRef]
- Toming, K.; Kutser, T.; Laas, A.; Sepp, M.; Paavel, B.; Nõges, T. First experiences in mapping lake water quality parameters with Sentinel-2 msi imagery. Remote Sens. 2016, 8, 640. [Google Scholar] [CrossRef]
- Oliveira, A.M.; Kjerfve, B. Regular article: Environmental responses of a tropical coastal lagoon system to hydrological variability: Mundaú-manguaba, brazil. Estuar. Coast. Shelf Sci. 1993, 37, 575–591. [Google Scholar] [CrossRef]
- Mueller, J.; Davis, C.; Arnone, R.; Frouin, R.; Carder, K.; Lee, Z.P.; Steward, R.G.; Hooker, S.; Mobley, C.; McLean, S. Above-Water Radiance and Remote Sensing Reflectance Measurement and Analysis Protocols; Goddard Space Flight Space Center: Greenbelt, MD, USA, 2003; pp. 21–31. [Google Scholar]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef] [PubMed]
- Rice, E.W.; Baird, R.B.; Eaton, A.D.; Clesceri, L.S. Standard Methods for the Examination of Water and Wastewater; American Public Health Association: Washington, DC, USA, 2005. [Google Scholar]
- Lubac, B.; Loisel, H. Variability and classification of remote sensing reflectance spectra in the eastern english channel and southern north sea. Remote Sens. Environ. 2007, 110, 45–58. [Google Scholar] [CrossRef]
- Martinez, J.-M.; Espinoza-Villar, R.; Armijos, E.; Silva Moreira, L. The optical properties of river and floodplain waters in the amazon river basin: Implications for satellite-based measurements of suspended particulate matter. J. Geophys. Res. Earth Surf. 2015, 120, 1274–1287. [Google Scholar] [CrossRef]
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Gitelson, A. The peak near 700 nm on radiance spectra of algae and water-relationships of its magnitude and position with chlorophyll concentration. Int. J. Remote Sens. 1992, 13, 3367–3373. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Tyler, M.A. Satellite detection of bloom and pigment distributions in estuaries. Remote Sens. Environ. 1988, 24, 385–404. [Google Scholar] [CrossRef]
- Ruddick, K.G.; De Cauwer, V.; Park, Y.-J.; Moore, G. Seaborne measurements of near infrared water-leaving reflectance: The similarity spectrum for turbid waters. Limnol. Oceanogr. 2006, 51, 1167–1179. [Google Scholar] [CrossRef]
- Mélin, F.; Vantrepotte, V. How optically diverse is the coastal ocean? Remote Sens. Environ. 2015, 160, 235–251. [Google Scholar] [CrossRef]
- Silva, E.D.A.; Nogueira, E.M.S.; Dué, A.; Carnaúba, M.P.; Guedes, E.A.C. Microalgas perifiticas em caiçaras situadas nas lagoas: Mundaú e manguaba do sistema lagunar de maceió. In Congresso de Ecologia do Brasil; Sociedade de Ecologia do Brasil (SEB): Caxambu, Brazil, 2005; Available online: www.seb-ecologia.org.br/viiceb/resumos/31a.pdf (accessed on 21 October 2016).
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Cambridge, MA, USA, 1994; p. 592. [Google Scholar]
- Brezonik, P.L.; Olmanson, L.G.; Finlay, J.C.; Bauer, M.E. Factors affecting the measurement of cdom by remote sensing of optically complex inland waters. Remote Sens. Environ. 2015, 157, 199–215. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R.; Lee, Z.; Tucker, C.S. Quantifying cyanobacterial phycocyanin concentration in turbid productive waters: A quasi-analytical approach. Remote Sens. Environ. 2013, 133, 141–151. [Google Scholar] [CrossRef]
- Lyu, H.; Wang, Q.; Wu, C.; Zhu, L.; Yin, B.; Li, Y.; Huang, J. Retrieval of phycocyanin concentration from remote-sensing reflectance using a semi-analytic model in eutrophic lakes. Ecol. Inform. 2013, 18, 178–187. [Google Scholar] [CrossRef]
- Tao, B.; Mao, Z.; Pan, D.; Shen, Y.; Zhu, Q.; Chen, J. Influence of bio-optical parameter variability on the reflectance peak position in the red band of algal bloom waters. Ecol. Inform. 2013, 16, 17–24. [Google Scholar] [CrossRef]
- Binding, C.E.; Bowers, D.G.; Mitchelson-Jacob, E.G. Estimating suspended sediment concentrations from ocean colour measurements in moderately turbid waters; the impact of variable particle scattering properties. Remote Sens. Environ. 2005, 94, 373–383. [Google Scholar] [CrossRef]
- Augusto-Silva, P.B.; Ogashawara, I.; Barbosa, C.C.F.; De Carvalho, L.A.S.; Jorge, D.S.F.; Fornari, C.I.; Stech, J.L. Analysis of MERIS reflectance algorithms for estimating chlorophyll-α concentration in a brazilian reservoir. Remote Sens. 2014, 6, 11689–11707. [Google Scholar] [CrossRef]
| Features | Mundaú | Manguaba |
|---|---|---|
| Volume (106 m3) | 43 | 97.7 |
| Average depth (m) | 1.5 | 2.2 |
| Tidal range (m) | 0.2 | 0.03 |
| Tidal prism (106 m3) | 17.3 | 6.1 |
| Average freshwater discharge (m3/s) | 35 | 28 |
| Retention time (days) | 16 | 36 |
| Sensor | Satellite | Resolution | Central Wavelength (400–900 nm) | |||
|---|---|---|---|---|---|---|
| Spectral | Temporal | Radiometric | Spatial | |||
| (Bands) | (Days) | (Bit) | (m) | |||
| MODIS | Terra/Acqua | 36 | 1 | 12 | 250 | 645, 858 * |
| 500 | 469, 555 | |||||
| MERIS | Envisat | 15 | 3 | 16 | 300 | 412, 443, 490, 510, 560, 620, 665, 681, 709, 754 *, 761 *, 779 *, 865 *, 885 * |
| MSI | Sentinel-2 | 13 | <5 | 12 | 10 | 490, 560, 665, 842 * |
| 20 | 705, 740, 783, 865 * | |||||
| 60 | 443 | |||||
| OLCI | Sentinel-3 | 21 | <2 | 16 | 300 | 400, 412, 442, 490, 510, 560, 620, 665, 674, 681, 709, 754 *, 761 *, 764 *, 767 *, 779 *, 865 *, 885 * |
| Subset | Chlorophyll-a (mg/m3) | SST (mg/L) | ||||||
|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Stdev | Min | Max | Mean | SD | |
| Mundaú (N = 36) | 0.97 | 48.90 | 12.86 | 9.72 | 15.15 | 61.00 | 32.80 | 11.99 |
| Manguaba (N = 36) | 5.99 | 117.54 | 42.77 | 24.22 | 9.00 | 44.00 | 22.86 | 9.34 |
| MMELS (N = 72) | 0.97 | 117.54 | 27.81 | 23.72 | 9.00 | 61.00 | 27.83 | 11.79 |
| Water | Models | p | q | r² | RMSE | |
|---|---|---|---|---|---|---|
| Non-classified | Mundaú (N = 36) | R440/R550 | 3.55 | 11.54 | 0.00 | 9.86 |
| R713/R682 | 25.71 | −10.91 | 0.54 | 6.71 | ||
| (R690−1 − R706−1)·R721 | 81.96 | 15.13 | 0.60 | 6.23 | ||
| (R690−1 − R695−1)/(R709−1 − R702−1) | 10.83 | 7.54 | 0.74 | 5.02 | ||
| Manguaba (N = 36) | R440/R550 | −73.45 | 65.29 | 0.26 | 19.05 | |
| R714/R690 | 52.84 | −21.84 | 0.81 | 9.54 | ||
| (R690−1 − R714−1)·R721 | 57.87 | 31.15 | 0.82 | 9.51 | ||
| (R689−1 − R713−1)/(R721−1 − R720−1) | 0.76 | 31.45 | 0.71 | 11.73 | ||
| MMELS (N = 72) | R440/R550 (cal, N = 48) | −39.32 | 38.22 | 0.06 | 21.20 | |
| R440/R550 (val, N = 24) | 0.00 | 153.52 | ||||
| R440/R550 (global, N = 72) | −64.89 | 49.74 | 0.15 | 20.43 | ||
| R721/R660 (cal, N = 48) | 39.52 | −12.90 | 0.84 | 8.78 | ||
| R721/R660 (val, N = 24) | 0.66 | 12.25 | ||||
| R713/R690 (global, N = 72) | 56.21 | −29.30 | 0.83 | 9.06 | ||
| (R690−1 − R717−1)·R721 (cal, N = 48) | 56.70 | 27.53 | 0.86 | 8.32 | ||
| (R690−1 − R717−1)·R721 (val, N = 24) | 0.73 | 11.06 | ||||
| (R690−1 − R714−1)·R720 (global, N = 72) | 64.03 | 26.01 | 0.84 | 8.81 | ||
| (R660−1 − R6951)/(R721−1 − R720−1) (cal, N = 48) | 1.22 | 11.37 | 0.87 | 7.91 | ||
| (R660−1 − R695−1)/(R721−1 − R720−1) (val, N = 24) | 0.15 | 19.42 | ||||
| (R660−1 − R713−1)/(R721−1 − R720−1) (global, N = 72) | 0.81 | 21.11 | 0.72 | 11.78 | ||
| Classified | Class 1 (N = 19) | R440/R550 | −27.33 | 63.33 | 0.04 | 18.76 |
| R721/R690 | 43.36 | 0.88 | 0.66 | 11.26 | ||
| (R690−1 − R721−1)·R721 | 43.36 | 44.25 | 0.65 | 11.26 | ||
| (R660−1 − R713−1)/(R711−1 − R712−1) | 0.14 | 45.35 | 0.75 | 9.52 | ||
| Class 2 (N = 14) | R440/R550 | −30.64 | 40.49 | 0.19 | 8.45 | |
| R711/R690 | 122.20 | −94.94 | 0.80 | 4.16 | ||
| (R690−1 − R711−1)·R721 | 142.90 | 27.34 | 0.81 | 4.09 | ||
| (R663−1 − R703−1)/(R707−1 − R706−1) | 0.58 | 11.37 | 0.93 | 2.48 | ||
| Class 3 (N = 31) | R440/R550 | −18.04 | 21.82 | 0.06 | 7.15 | |
| R700/R660 | 60.49 | −49.12 | 0.45 | 5.49 | ||
| (R690−1 − R699−1)·R721 | 99.12 | 10.53 | 0.47 | 5.37 | ||
| (R660−1 − R713−1)/(R721−1 − R720−1) | 8.82 | 34.62 | 0.51 | 5.16 | ||
| Class 4 (N = 8) | R440/R550 | 6.32 | 1.33 | 0.07 | 1.66 | |
| R690/R687 | 41.83 | −38.11 | 0.14 | 1.6 | ||
| (R687−1 − R691−1)·R721 | 128.20 | 3.95 | 0.17 | 1.57 | ||
| (R690−1 − R701−1)/(R698−1 − R694−1) | 28.87 | 78.65 | 0.75 | 0.86 | ||
| Water | Models | p | q | r² | RMSE |
|---|---|---|---|---|---|
| Manguaba (N = 36) | MODIS − R645/R555 | 38.21 | −11.32 | 0.56 | 14.55 |
| MERIS − R709/R681 | 19.08 | 7.27 | 0.64 | 13.29 | |
| OLCI − R709/R681 | 19.97 | 6.51 | 0.65 | 13.07 | |
| MERIS − R709/R665 | 29.78 | −6.35 | 0.72 | 11.76 | |
| OLCI − R709/R665 | 28.43 | −4.53 | 0.71 | 11.87 | |
| MSI − R705/R665 | 34.39 | −12.52 | 0.72 | 11.73 | |
| MERIS − (R681−1 − R709−1)·R665 | 58.77 | 18.98 | 0.71 | 11.84 | |
| OLCI − (R681−1 − R709−1)·R674 | 73.60 | 18.97 | 0.70 | 12.11 | |
| MMELS (N = 72) | MODIS − R645/R555 | 34.63 | −17.27 | 0.31 | 18.42 |
| MERIS − R709/R681 | 23.98 | −6.73 | 0.70 | 12.12 | |
| OLCI − R709/R681 | 24.95 | −7.25 | 0.71 | 11.91 | |
| MERIS − R709/R665 | 34.12 | −17.29 | 0.77 | 10.66 | |
| OLCI − R709/R665 | 32.83 | −15.74 | 0.76 | 10.77 | |
| MSI − R705/R665 | 39.07 | −23.40 | 0.78 | 10.44 | |
| MERIS − (R681−1 − R709−1)·R665 | 39.74 | 20.92 | 0.60 | 14.00 | |
| OLCI − (R681−1 − R709−1)·R674 | 42.17 | 22.74 | 0.55 | 14.87 | |
| MERIS − (R665−1 − R709−1)/(R709−1 − R681−1) | 1.80 | 28.87 | 0.01 | 22.03 | |
| OLCI − (R674−1 − R709−1)/(R709−1 − R681−1) | 0.67 | 27.84 | 0.00 | 22.15 | |
| Class 2 (N = 14) | MODIS − R645/R555 | 18.12 | 10.48 | 0.02 | 9.30 |
| MERIS − R709/R681 | 44.75 | −28.22 | 0.65 | 5.58 | |
| OLCI − R709/R681 | 48.42 | −31.57 | 0.67 | 5.42 | |
| MSI − R705/R665 | 45.14 | −28.87 | 0.53 | 6.39 | |
| MERIS − (R681−1 − R709−1)·R665 | 71.65 | 14.33 | 0.70 | 5.15 | |
| OLCI − (R681−1 − R709−1)·R674 | 81.47 | 14.78 | 0.71 | 5.02 | |
| MERIS − (R665−1 − R709−1)/(R709−1 − R681−1) | −6.15 | 22.77 | 0.28 | 7.95 | |
| OLCI − (R674−1 − R709−1)/(R709−1 − R681−1) | −3.69 | 24.52 | 0.33 | 7.69 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lins, R.C.; Martinez, J.-M.; Motta Marques, D.D.; Cirilo, J.A.; Fragoso, C.R. Assessment of Chlorophyll-a Remote Sensing Algorithms in a Productive Tropical Estuarine-Lagoon System. Remote Sens. 2017, 9, 516. https://doi.org/10.3390/rs9060516
Lins RC, Martinez J-M, Motta Marques DD, Cirilo JA, Fragoso CR. Assessment of Chlorophyll-a Remote Sensing Algorithms in a Productive Tropical Estuarine-Lagoon System. Remote Sensing. 2017; 9(6):516. https://doi.org/10.3390/rs9060516
Chicago/Turabian StyleLins, Regina Camara, Jean-Michel Martinez, David Da Motta Marques, José Almir Cirilo, and Carlos Ruberto Fragoso. 2017. "Assessment of Chlorophyll-a Remote Sensing Algorithms in a Productive Tropical Estuarine-Lagoon System" Remote Sensing 9, no. 6: 516. https://doi.org/10.3390/rs9060516
APA StyleLins, R. C., Martinez, J.-M., Motta Marques, D. D., Cirilo, J. A., & Fragoso, C. R. (2017). Assessment of Chlorophyll-a Remote Sensing Algorithms in a Productive Tropical Estuarine-Lagoon System. Remote Sensing, 9(6), 516. https://doi.org/10.3390/rs9060516