Hypergraph Embedding for Spatial-Spectral Joint Feature Extraction in Hyperspectral Images
Abstract
:1. Introduction
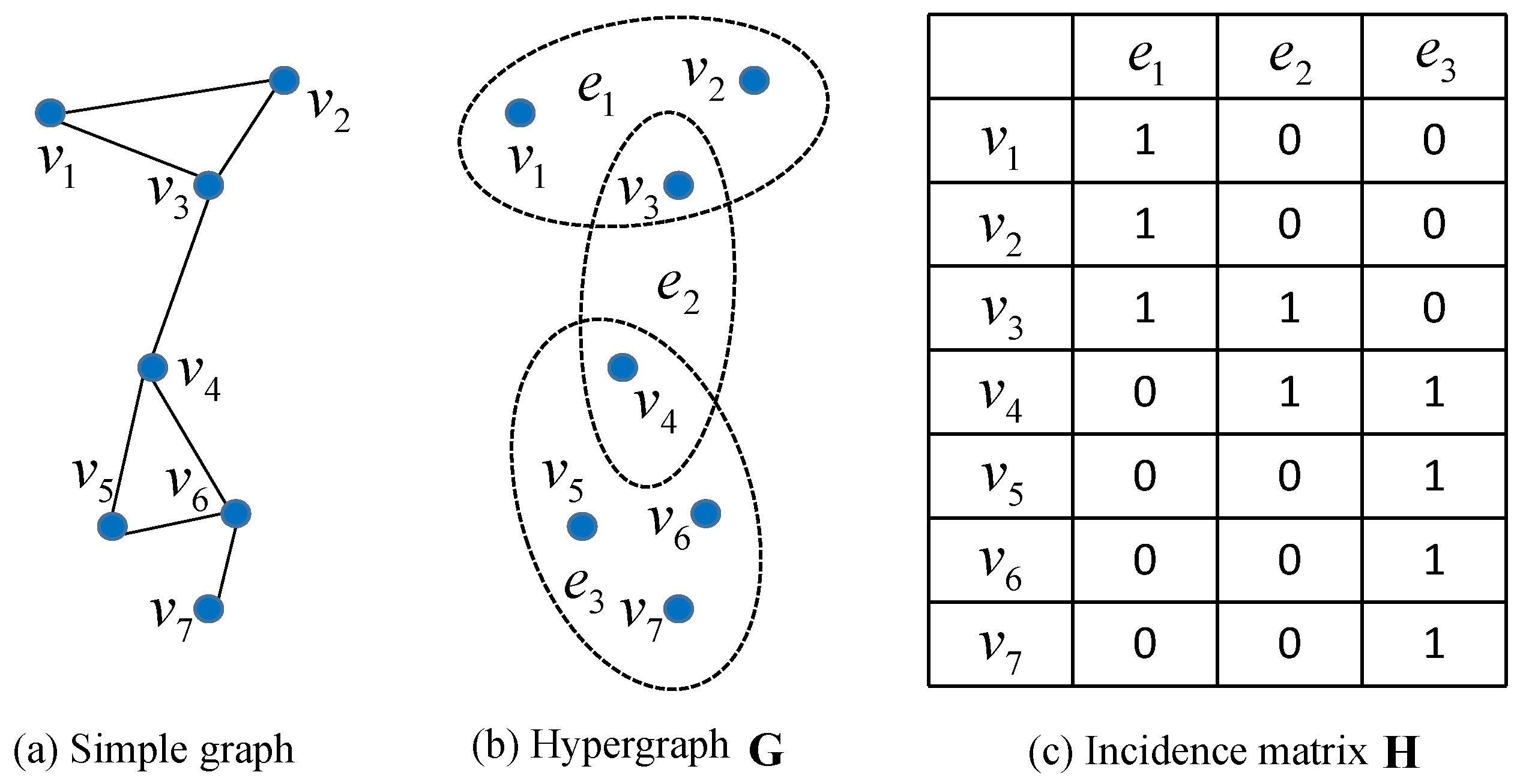
2. Hypergraph Model
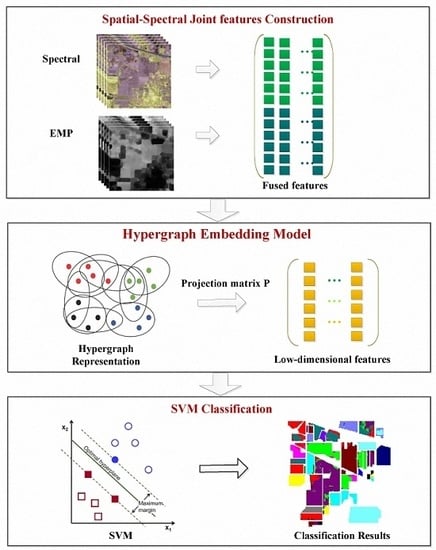
3. Hypergraph Embedding of Spatial-Spectral Joint Features
3.1. Spatial-Spectral Joint Feature Construction
3.2. Hypergraph Embedding
3.3. Optimization Algorithm
| Algorithm 1: The proposed method ( denoted as SSHG*) for HSI classification. |
|
4. Experiments and Discussion
4.1. Data Sets
- (1)
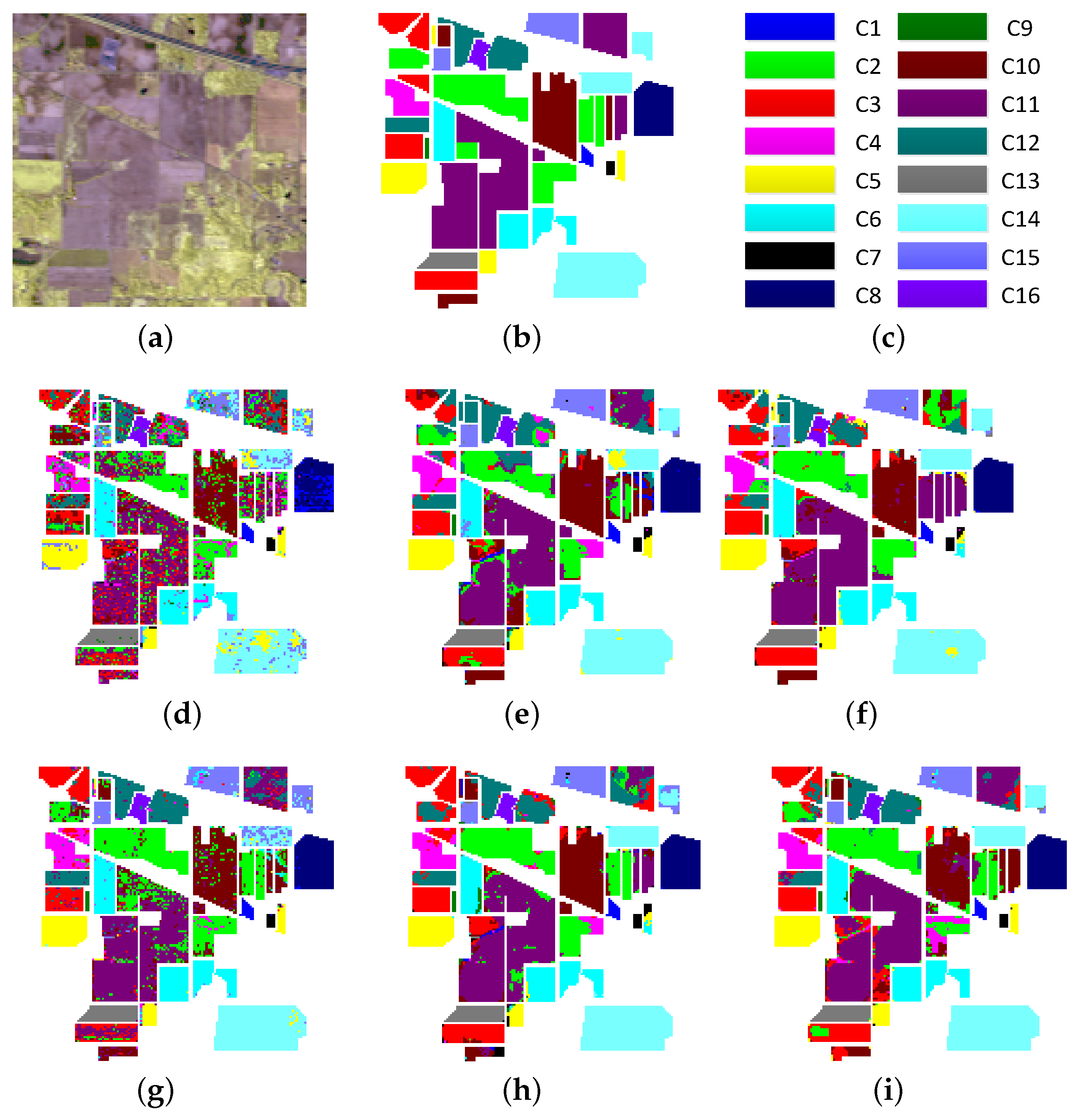
- Indian Pines data set—the first data set was acquired by the AVIRIS sensor over the Indian Pines test site in Northwestern Indiana, USA. The size of the image is 145 pixels × 145 pixels with a spatial resolution of 20 m per pixel. Twenty water absorption bands (104–108, 150–163, 220) were removed, and the 200-band image is used for experiments. Sixteen classes of interest are considered.
- (2)
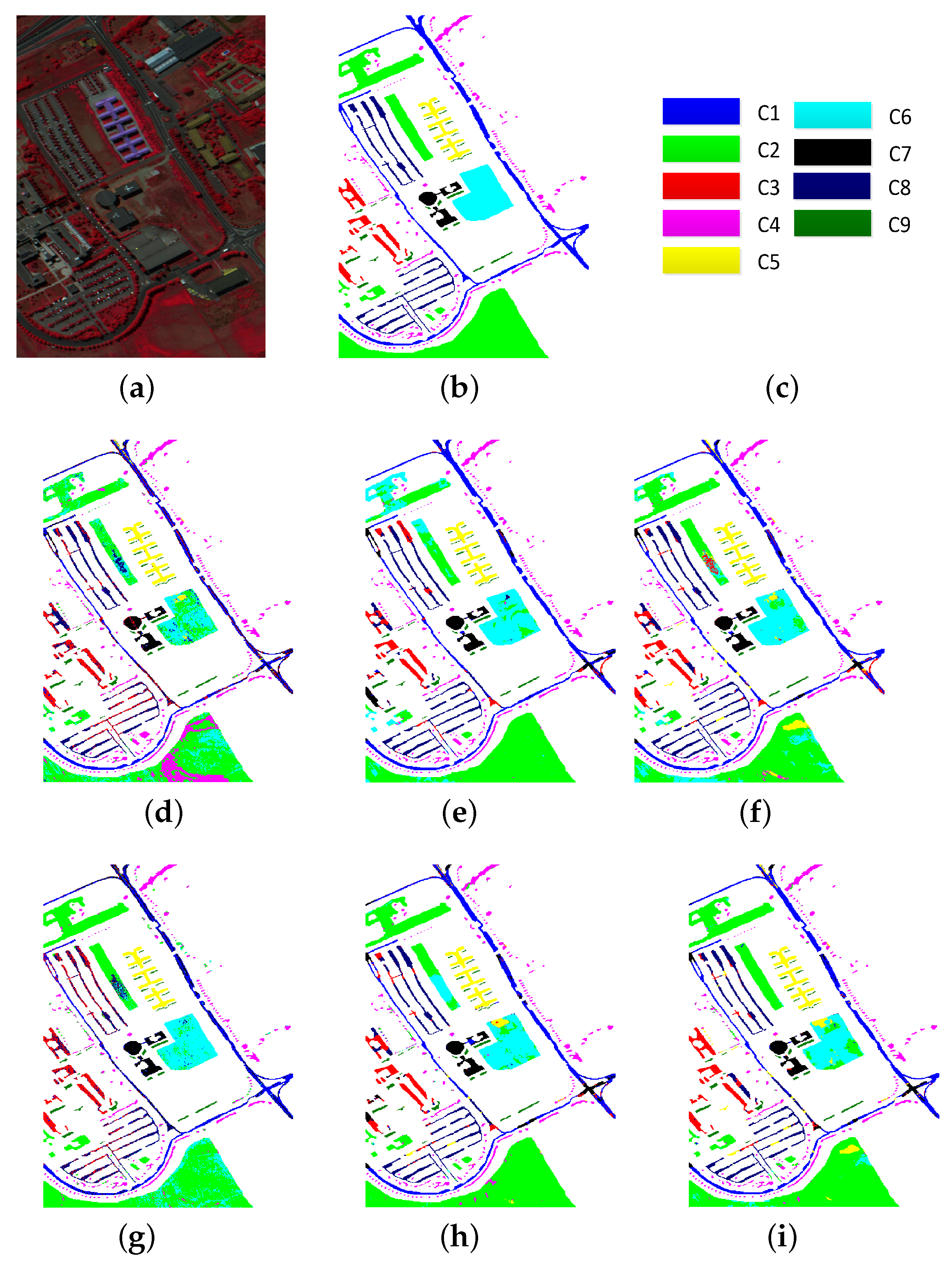
- Pavia University data set—the second data set was acquired by the ROSIS sensor during a flight campaign over Pavia, northern Italy. The size of the image is 610 pixels × 340 pixels with a spatial resolution of 1.3 m per pixel. Twelve channels were removed due to noise. The remaining 103 spectral bands are processed. Nine classes of interest are considered.
- (3)
- Botswana data set—the third data set was acquired by the NASA EO-1 satellite over the Okavango Delta, Botswana, in 2001. The size of the image is 1476 pixels × 256 pixels with a spatial resolution of 30 m per pixel. Uncalibrated and noisy bands that cover water absorption features were removed, and the remaining 145 bands are used for experiment. Fourteen classes of interest are considered.
4.2. Experimental Setting
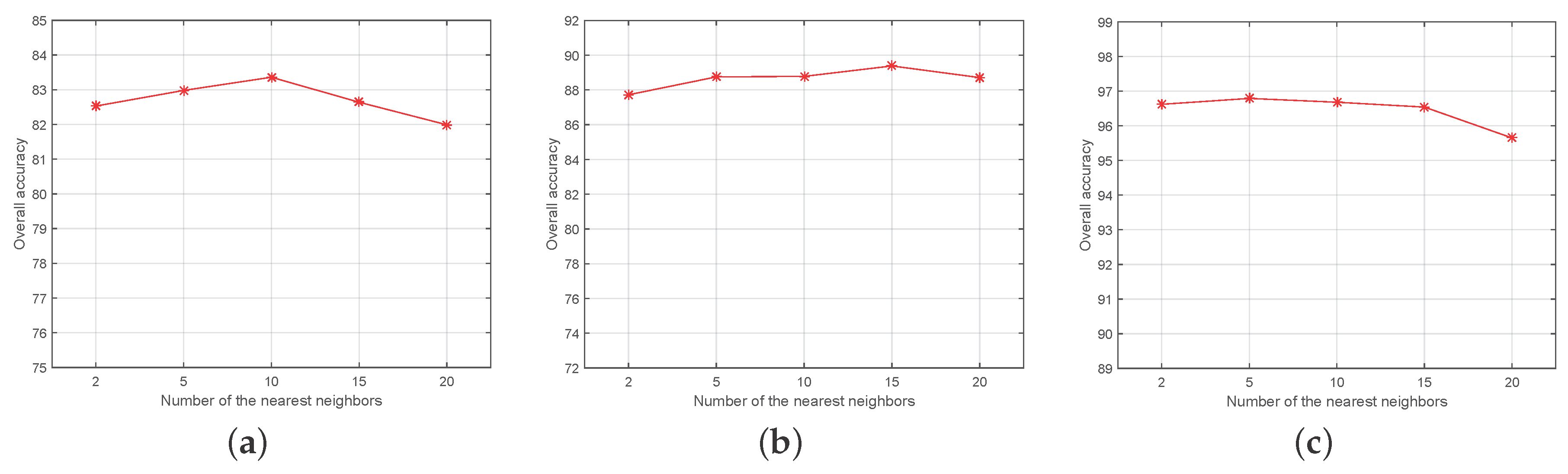
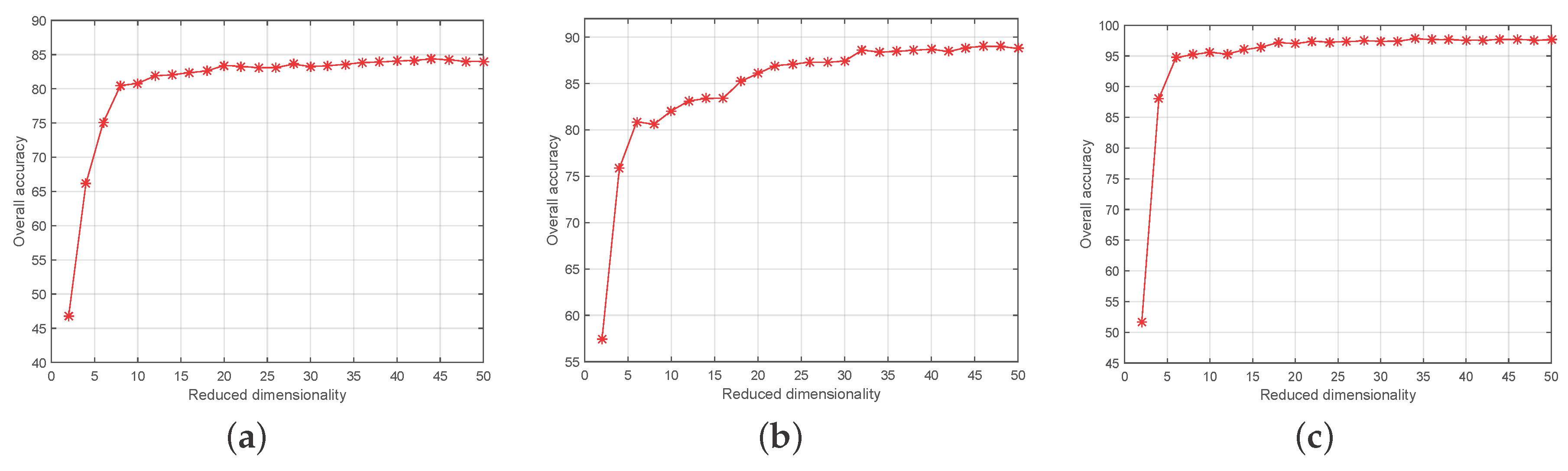
4.3. Experimental Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Clement, A. Advances in remote sensing of agriculture: context description, existing operational monitoring systems and major information needs. Remote Sens. 2013, 5, 949–981. [Google Scholar] [CrossRef]
- Shafri, H.Z.M.; Taherzadeh, E.; Mansor, S.; Ashurov, R. Hyperspectral remote sensing of urban areas: An overview of techniques and applications. Res. J. Appl. Sci. Eng. Technol. 2012, 4, 1557–1565. [Google Scholar]
- Abbate, G.; Fiumi, L.; De Lorenzo, C.; Vintila, R. Avaluation of remote sensing data for urban planning. Applicative examples by means of multispectral and hyperspectral data. In Proceedings of the GRSS/ISPRS Joint Workshop on Remote Sensing and Data Fusion over Urban Areas, Berlin, Germany, 22–23 May 2003; pp. 201–205. [Google Scholar]
- Wu, Z.; Wang, Q.; Plaza, A.; Li, J.; Sun, L. Parallel spatial-spectral hyperspectral image classification with sparse representation and markov random fields on GPUs. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2926–2938. [Google Scholar] [CrossRef]
- Yuan, Y.; Lin, J.; Wang, Q. Hyperspectral image classification via multitask joint sparse representation and stepwise MRF optimization. IEEE Trans. Cybern. 2016, 46, 2966–2977. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Lin, J.; Yuan, Y. Salient band selection for hyperspectral image classification via manifold ranking. IEEE IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
- Hang, R.; Liu, Q.; Sun, Y.; Yuan, X.; Pei, H.; Plaza, J.; Plaza, A. Robust matrix discriminative analysis for feature extraction from hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2002–2011. [Google Scholar] [CrossRef]
- Wu, Z.; Li, Y.; Plaza, A.; Li, J.; Xiao, F.; Wei, Z. Parallel and distributed dimensionality reduction of hyperspectral data on cloud computing architectures. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2270–2278. [Google Scholar] [CrossRef]
- Sun, Y.; Hang, R.; Liu, Q.; Zhu, F.; Pei, H. Graph-Regularized low rank representation for aerosol optical depth retrieval. Int. J. Remote Sens. 2016, 37, 5749–5762. [Google Scholar] [CrossRef]
- Fauvel, M.; Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J.; Tilton, J.C. Advances in spectral-spatial classification of hyperspectral images. Proc. IEEE 2013, 101, 652–675. [Google Scholar] [CrossRef]
- Yuan, Y.; Lin, J.; Wang, Q. Dual-Clustering-Based hyperspectral band selection by contextual analysis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1431–1445. [Google Scholar] [CrossRef]
- Kettig, R.L.; Landgrebe, D.A. Classification of multispectral image data by extraction and classification of homogeneous objects. IEEE Trans. Geosci. Electron. 1976, 14, 19–26. [Google Scholar] [CrossRef]
- Descombes, X.; Sigelle, M.; Preteu, F. GMRF parameter estimation in a non-stationary framework by a renormalization technique: application to remote sensing imaging. IEEE Trans. Image Process. 1999, 8, 490–503. [Google Scholar] [CrossRef] [PubMed]
- Jackson, Q.; Landgrebe, D.A. Adaptive bayesian contextual classification based on markov random fields. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2454–2463. [Google Scholar] [CrossRef]
- Pesaresi, M.; Benediktsson, J.A. A new approach for the morphological segmentation of high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 309–320. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and spatial classification of hyperspectral data using svms and morphological profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef]
- Guo, X.; Huang, X.; Zhang, L. Three-Dimensional wavelet texture feature extraction and classification for multi/hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2183–2187. [Google Scholar] [CrossRef]
- Li, L.; Marpu, P.R.; Plaza, A.; Bioucas-Dias, J.M. Generalized composite kernel framework for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4816–4829. [Google Scholar] [CrossRef]
- Hang, R.; Liu, Q.; Song, H.; Sun, Y. Matrix-based discriminant subspace ensemble for hyperspectral image spatial–spectral feature fusion. IEEE Trans. Geosci. Remote Sens. 2016, 54, 783–794. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Kang, X.; Benediktsson, J.A. Spectral-spatial hyperspectral image classification via multiscale adaptive sparse representation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7738–7749. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Du, Q. Modified fisher’s linear discriminant analysis for hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2007, 4, 503–507. [Google Scholar] [CrossRef]
- Fauvel, M.; Chanussot, J.; Benediktsson, J.; Atli, N. Kernel principal component analysis for the classification of hyperspectral remote sensing data over urban areas. EURASIP J. Adv. Signal Process. 2009, 2009, 1–14. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, J.E. Decision fusion in kernel-induced spaces for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3399–3411. [Google Scholar] [CrossRef]
- He, X.; Niyogi, P. Locality preserving projections. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 8–13 December 2003; pp. 186–197. [Google Scholar]
- Villa, A.; Benediktsson, J.A.; Chanussot, J.; Jutten, C. Hyperspectral image classification with independent component discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4865–4876. [Google Scholar] [CrossRef]
- Mura, M.D.; Villa, A.; Benediktsson, J.A.; Chanussot, J. Classification of hyperspectral images by using extended morphological attribute profiles and independent component analysis. IEEE Geosci. Remote Sens. Lett. 2011, 8, 542–546. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Xu, D.; Zhang, B.; Zhang, H.J. Graph embedding and extensions: A general framework for dimensionality reduction. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Luo, F.; Huang, H.; Liu, J.; Ma, Z. Fusion of graph embedding and sparse representation for feature extraction and classification of hyperspectral imagery. Photogramm. Eng. Remote Sens. 2017, 83, 37–46. [Google Scholar] [CrossRef]
- Chen, P.; Jiao, L.; Liu, F.; Zhao, J.; Zhao, Z. Dimensionality reduction for hyperspectral image classification based on multiview graphs ensemble. J. Appl. Remote Sens. 2016, 10, 030501. [Google Scholar] [CrossRef]
- Zhou, D.; Huang, J.; Schölkopf, B. Learning with hypergraphs: clustering, classification, and embedding. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007; pp. 1601–1608. [Google Scholar]
- Bu, J.; Tan, S.; Chen, C.; Wang, C.; Wu, H.; Zhang, L.; He, X. Music recommendation by unified hypergraph: combining social media information and music content. In Proceedings of the 18th ACM international conference on Multimedia, Firenze, Italy, 25–29 October 2010; pp. 391–400. [Google Scholar]
- Liu, Q.; Sun, Y.; Wang, C.; Liu, T.; Tao, D. Elastic net hypergraph learning for image clustering and semi-supervised classification. IEEE Trans. Image Process. 2017, 26, 452–463. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.; Tang, Y.Y. Learning with hypergraph for hyperspectral image feature extraction. IEEE Trans. Geosci. Remote Sens. Lett. 2015, 12, 1695–1699. [Google Scholar] [CrossRef]
- Kuo, B.C.; Landgrebe, D.A. Nonparametric weighted feature extraction for classification. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1096–1105. [Google Scholar] [CrossRef]
- Liao, W.; Pizurica, A.; Scheunders, P.; Philips, W.; Pi, Y. Semisupervised local discriminant analysis for feature extraction in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 184–198. [Google Scholar] [CrossRef]
- Pliakos, K.; Kotropoulos, C. Weight estimation in hypergraph learning. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, South Brisbane, Australia, 19–24 April 2015; pp. 1161–1165. [Google Scholar]
- Gao, Y.; Wang, W.; Zha, Z.J.; Shen, J.; Li, X.; Wu, X. Visual-textual joint relevance learning for tag-based social image search. IEEE Trans. Image Process. 2013, 22, 363–376. [Google Scholar] [CrossRef] [PubMed]

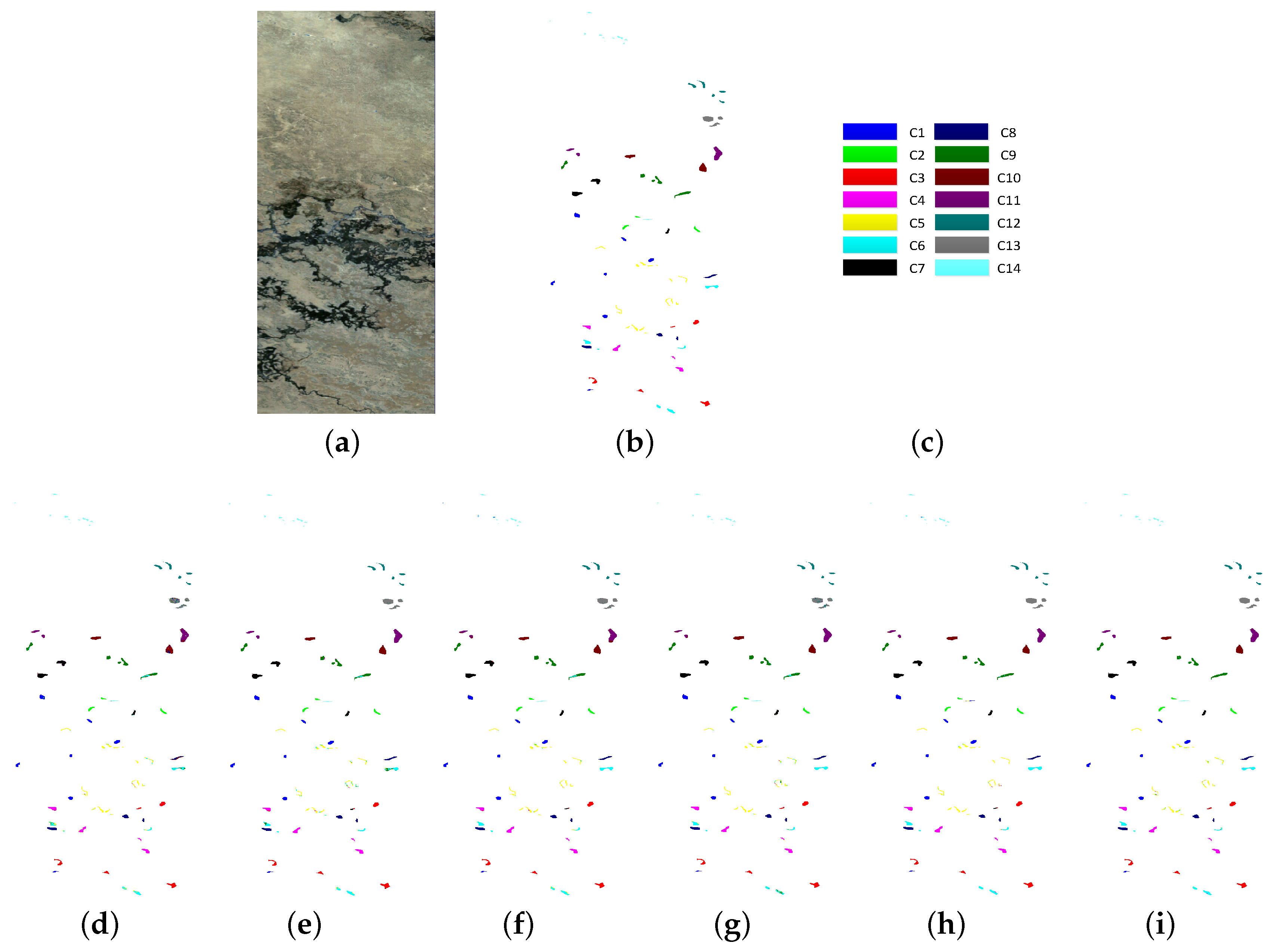
| Class | PCA (25) | EMP (27) | EMPSpe (227) | SH (22) | SSHG (44) | SSHG* (44) |
|---|---|---|---|---|---|---|
| 1 | 91.61 | 98.71 | 99.03 | 94.87 | 98.06 | 98.06 |
| 2 | 47.36 | 61.46 | 64.28 | 82.59 | 72.53 | 73.96 |
| 3 | 48.60 | 78.75 | 77.14 | 73.50 | 84.06 | 84.85 |
| 4 | 68.29 | 95.90 | 91.76 | 91.32 | 96.76 | 97.21 |
| 5 | 75.75 | 87.78 | 88.85 | 92.12 | 89.83 | 90.32 |
| 6 | 85.37 | 91.48 | 92.36 | 98.22 | 93.93 | 94.04 |
| 7 | 91.54 | 99.23 | 99.23 | 100 | 100 | 100 |
| 8 | 79.52 | 98.47 | 98.92 | 98.31 | 99.57 | 99.63 |
| 9 | 96.00 | 100 | 100 | 100 | 100 | 100 |
| 10 | 56.22 | 74.23 | 71.61 | 87.51 | 76.81 | 77.68 |
| 11 | 49.62 | 69.51 | 71.02 | 64.41 | 75.65 | 75.57 |
| 12 | 45.43 | 75.67 | 77.40 | 84.31 | 84.33 | 84.79 |
| 13 | 93.47 | 98.68 | 99.00 | 99.49 | 99.37 | 99.37 |
| 14 | 69.55 | 93.25 | 94.83 | 94.84 | 97.57 | 97.58 |
| 15 | 46.42 | 95.96 | 95.85 | 75.07 | 97.74 | 97.76 |
| 16 | 89.62 | 97.56 | 98.46 | 98.75 | 99.74 | 99.87 |
| OA | 58.90 | 79.14 | 79.88 | 82.33 | 84.36 | 84.75 |
| AA | 70.90 | 88.54 | 88.73 | 89.71 | 91.62 | 91.92 |
| kappa | 53.88 | 76.42 | 77.24 | 80.06 | 82.27 | 82.73 |
| Class | PCA (10) | EMP (27) | EMPSpe (130) | SH (30) | SSHG (46) | SSHG* (46) |
|---|---|---|---|---|---|---|
| 1 | 66.21 | 82.40 | 81.57 | 70.33 | 81.67 | 82.70 |
| 2 | 65.14 | 83.44 | 84.09 | 82.13 | 92.02 | 91.44 |
| 3 | 70.00 | 77.04 | 77.79 | 72.37 | 80.47 | 80.08 |
| 4 | 85.26 | 97.42 | 97.44 | 89.58 | 93.93 | 94.90 |
| 5 | 99.37 | 99.76 | 99.75 | 99.61 | 99.79 | 99.80 |
| 6 | 69.16 | 78.91 | 80.16 | 91.76 | 86.50 | 89.63 |
| 7 | 90.45 | 94.07 | 93.28 | 92.68 | 94.16 | 94.44 |
| 8 | 71.34 | 86.12 | 85.30 | 72.16 | 83.07 | 84.06 |
| 9 | 99.72 | 96.04 | 97.44 | 99.51 | 98.26 | 98.15 |
| OA | 70.59 | 84.77 | 85.05 | 81.88 | 89.01 | 89.43 |
| AA | 79.63 | 88.35 | 88.53 | 85.57 | 89.99 | 90.58 |
| kappa | 63.20 | 80.38 | 80.78 | 76.80 | 85.64 | 86.24 |
| Class | PCA (22) | EMP (27) | EMPSpe (172) | SH (25) | SSHG (34) | SSHG* (34) |
|---|---|---|---|---|---|---|
| 1 | 100 | 99.92 | 99.89 | 100 | 100 | 100 |
| 2 | 96.51 | 100 | 97.99 | 100 | 99.68 | 98.05 |
| 3 | 96.19 | 94.79 | 95.85 | 99.15 | 96.76 | 100 |
| 4 | 99.00 | 95.85 | 98.83 | 99.50 | 98.41 | 93.27 |
| 5 | 81.10 | 79.76 | 82.32 | 82.86 | 91.79 | 96.38 |
| 6 | 69.29 | 81.73 | 88.34 | 81.89 | 96.37 | 99.22 |
| 7 | 96.31 | 97.70 | 99.20 | 98.77 | 99.72 | 99.95 |
| 8 | 98.40 | 99.63 | 99.48 | 99.47 | 100 | 97.42 |
| 9 | 79.93 | 92.34 | 94.47 | 96.32 | 98.86 | 99.79 |
| 10 | 95.28 | 98.33 | 97.98 | 99.57 | 99.92 | 97.97 |
| 11 | 83.45 | 97.24 | 95.19 | 97.59 | 94.97 | 99.88 |
| 12 | 93.98 | 99.94 | 99.88 | 88.55 | 100 | 99.49 |
| 13 | 89.33 | 99.60 | 98.37 | 94.47 | 99.92 | 99.75 |
| 14 | 98.75 | 99.25 | 98.35 | 100 | 91.36 | 99.63 |
| OA | 89.83 | 94.69 | 95.65 | 95.10 | 97.79 | 98.38 |
| AA | 91.25 | 95.43 | 96.15 | 95.58 | 97.70 | 98.63 |
| kappa | 88.98 | 94.24 | 95.36 | 94.68 | 97.60 | 98.24 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Wang, S.; Liu, Q.; Hang, R.; Liu, G. Hypergraph Embedding for Spatial-Spectral Joint Feature Extraction in Hyperspectral Images. Remote Sens. 2017, 9, 506. https://doi.org/10.3390/rs9050506
Sun Y, Wang S, Liu Q, Hang R, Liu G. Hypergraph Embedding for Spatial-Spectral Joint Feature Extraction in Hyperspectral Images. Remote Sensing. 2017; 9(5):506. https://doi.org/10.3390/rs9050506
Chicago/Turabian StyleSun, Yubao, Sujuan Wang, Qingshan Liu, Renlong Hang, and Guangcan Liu. 2017. "Hypergraph Embedding for Spatial-Spectral Joint Feature Extraction in Hyperspectral Images" Remote Sensing 9, no. 5: 506. https://doi.org/10.3390/rs9050506
APA StyleSun, Y., Wang, S., Liu, Q., Hang, R., & Liu, G. (2017). Hypergraph Embedding for Spatial-Spectral Joint Feature Extraction in Hyperspectral Images. Remote Sensing, 9(5), 506. https://doi.org/10.3390/rs9050506