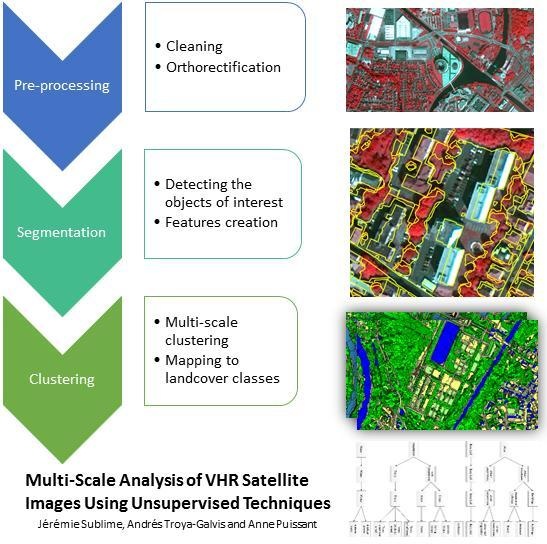
Multi-Scale Analysis of Very High Resolution Satellite Images Using Unsupervised Techniques
Abstract
:1. Introduction
- In [3], the authors propose an unsupervised algorithm that provides some low level semantic information on the clusters. This algorithm is the base that we used for the multi-scale method proposed in the learning step of this article. The improvements that we bring include that our proposed method covers the segmentation step, while the original algorithm does not. Furthermore, this algorithm was designed to produce a non-hierarchical hard partition, whereas our method can find the object at several scales of interest and produces multi-scale hierarchical clusters.
- In [4], the authors also tackle image data acquired from image segments. The method they used is based on the self-organizing map (SOM) algorithm, a known unsupervised neural network used for dimension reduction. While this methods considers dimension reduction aspects that our proposed algorithm does not handle, it is also limited to the learning step and can only provide hard partitions computed at a single scale of interest.
2. State of the Art on Unsupervised VHR Images Processing
2.1. Image Segmentation
- Subjective criteria, which basically rely on a visual examination of segmentation results. This task is long, tedious and does not provide an objective and quantitative evaluation.
- Supervised criteria [16,17], which consist of measuring the distance between one segmentation and a gold-standard segmentation. However, such a ground-truth generally has to be manually generated. Thus, it is very rare to dispose of complete reference datasets in remote sensing applications, making supervised metrics less reliable.
- Finally, unsupervised criteria [18], which consist of exploiting intrinsic segment and image properties. It is then necessary to accurately define and model the notion of quality without any external information. Many of these metrics rely on the number and size of segments [19], as well as statistics, such as band mean values or the standard deviation [17,20], or on local (per segment) quality estimation based on some homogeneity criterion in order to compute global quality metrics by aggregation of the local scores [21].
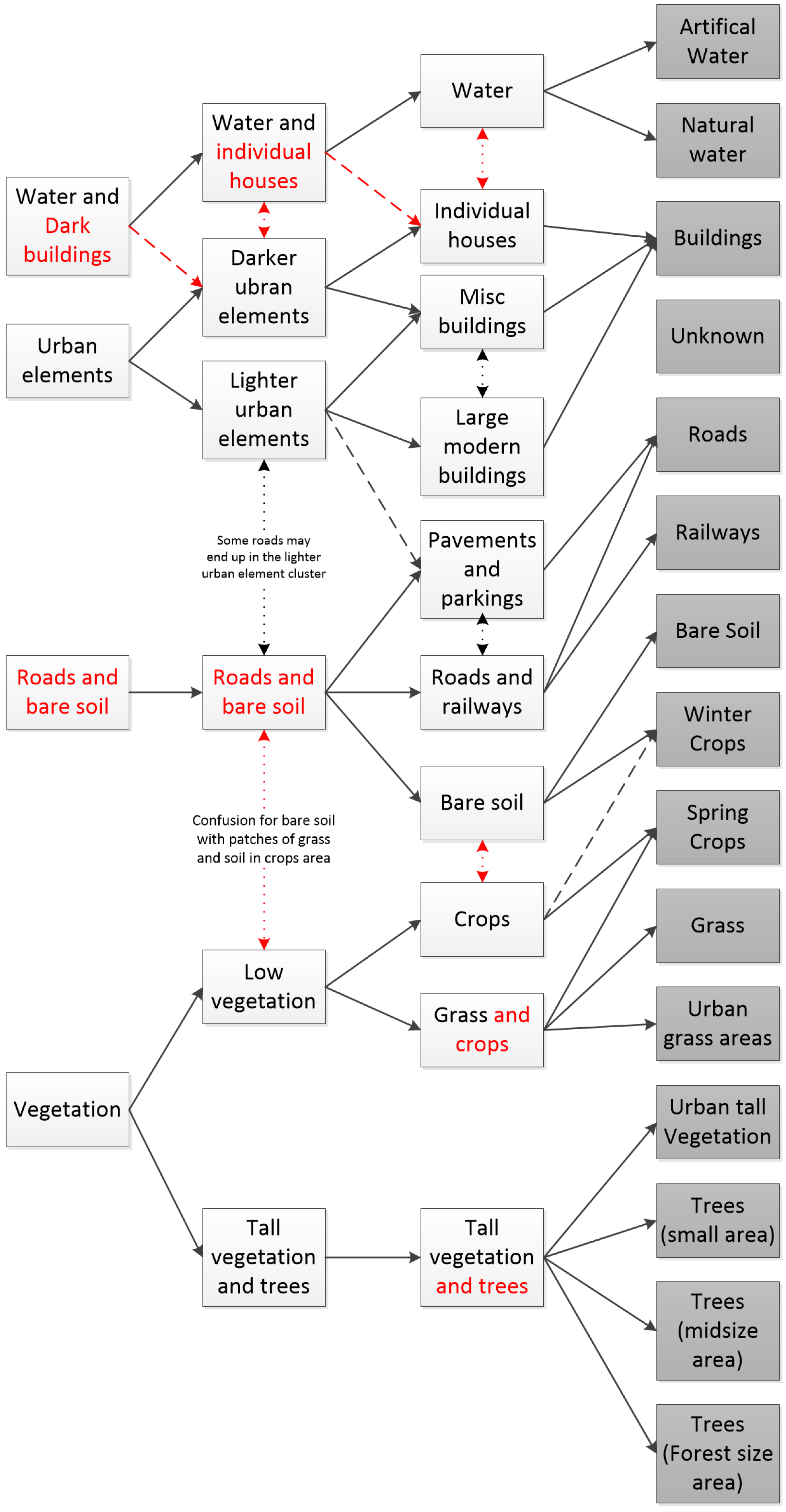
2.2. Unsupervised Analysis of the Segments
| Algorithm 1: Semantic-rich ICM algorithm. |
 |
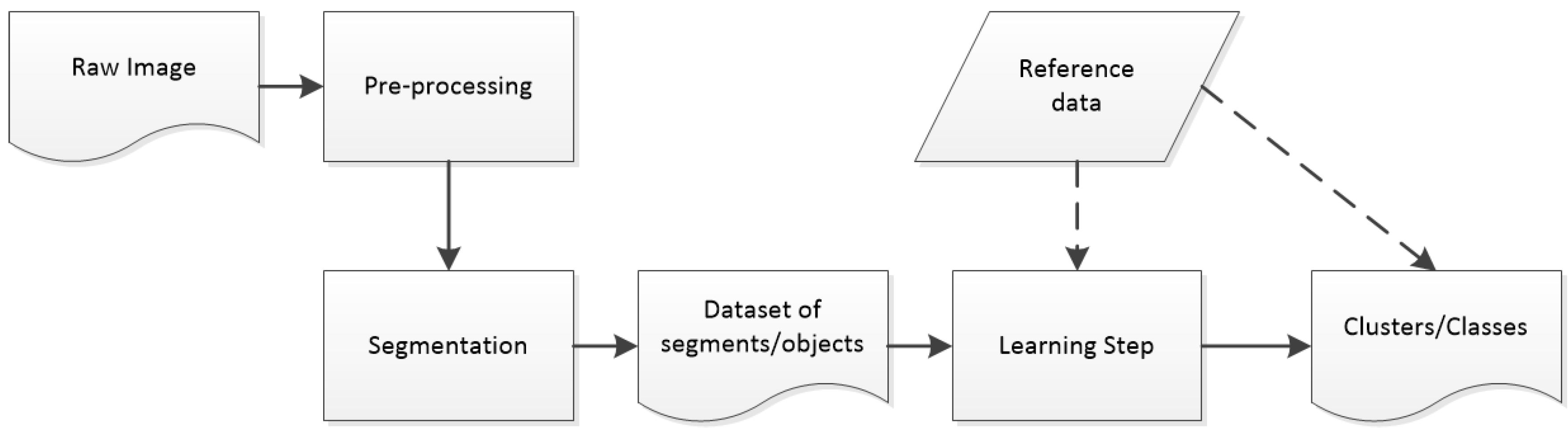
3. Material and Methods
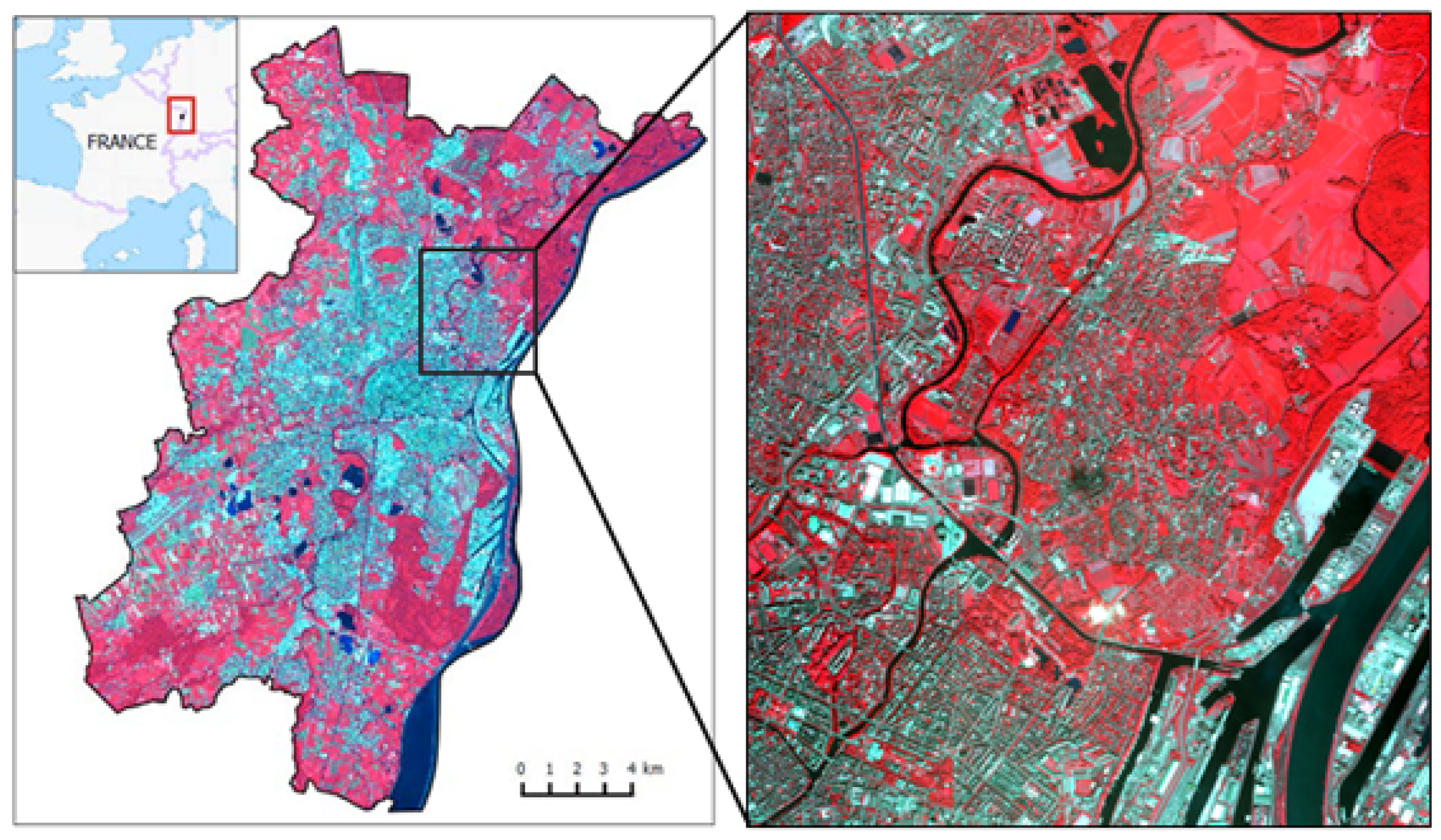
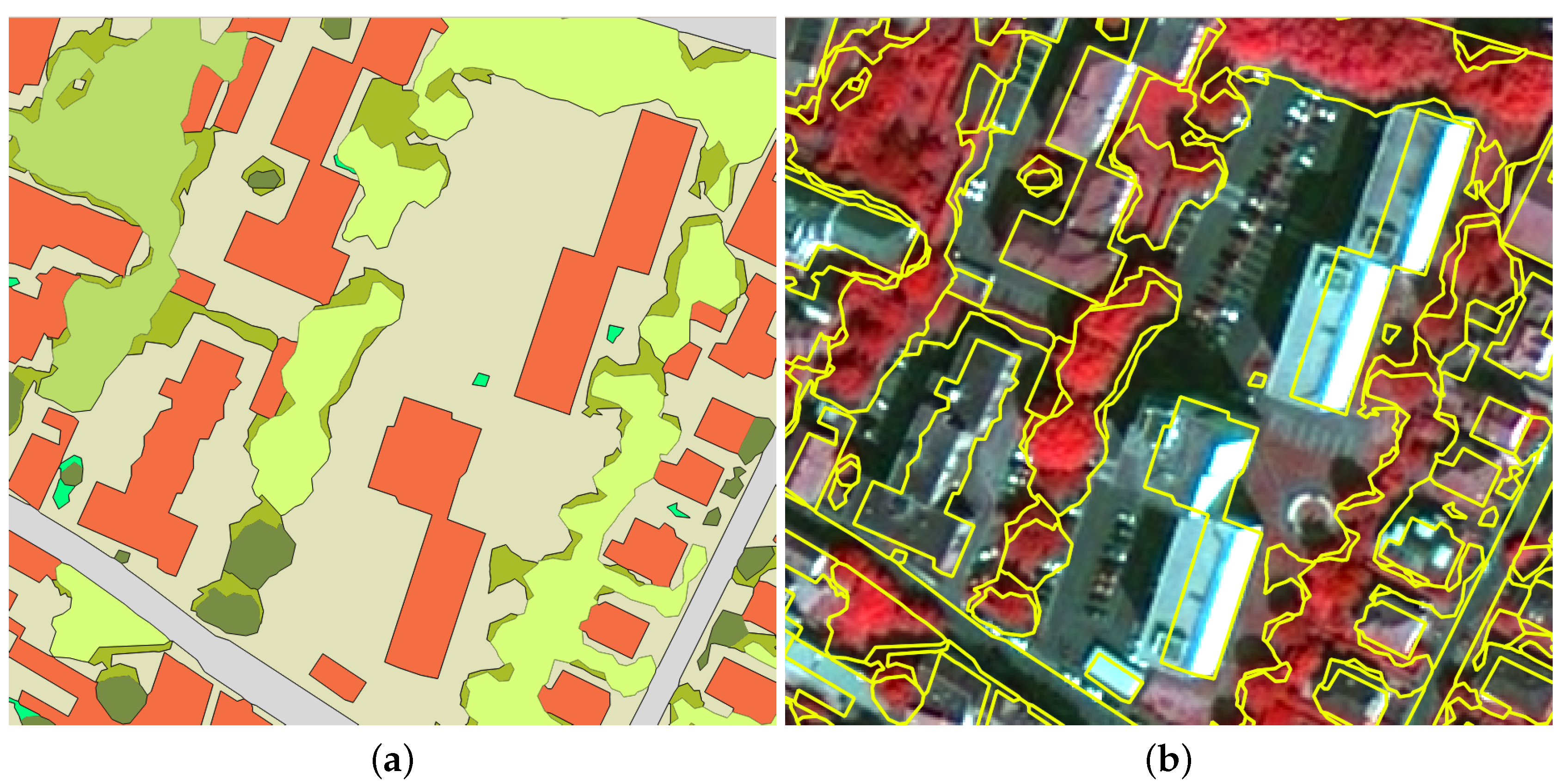
3.1. Presentation of the Strasbourg Dataset
3.2. Segmentation and Feature Computation
3.3. Adaptation of MRF-Based Methods to a Multi-Scale Context
| Algorithm 2: Parallel SR-ICM for hierarchical clusters. |
 |
4. Experimental Results
4.1. Numerical Results
- The Davies–Bouldin index [41]: It is a clustering index assessing that the clusters are compact and well separated. Its value is better when it is lower and tends to be biased towards a lower number of clusters.
- The silhouette index [42]: It is another clustering index assessing that each datum is closer to its clusters centroid than from the other clusters’. It takes its values between −1 and one and is better when closer to one.
- The Rand index [43]: It is an external index assessing the degree of similitude between two vectors. In the case of this experiment, we compared our solution vectors with our GIS hybrid reference data. It takes its values between zero and one, with one being a 100% match.
- An entropy measure assessing the entropy between each algorithm solutions and the GIS hybrid reference data using the confusion matrix as shown in Equation (10). It takes its values between zero and one, with zero being a 100% match and achievable only if the solution and the reference data have the same number of classes/clusters. This measure is therefore better when close to zero and is biased toward a greater number of clusters.
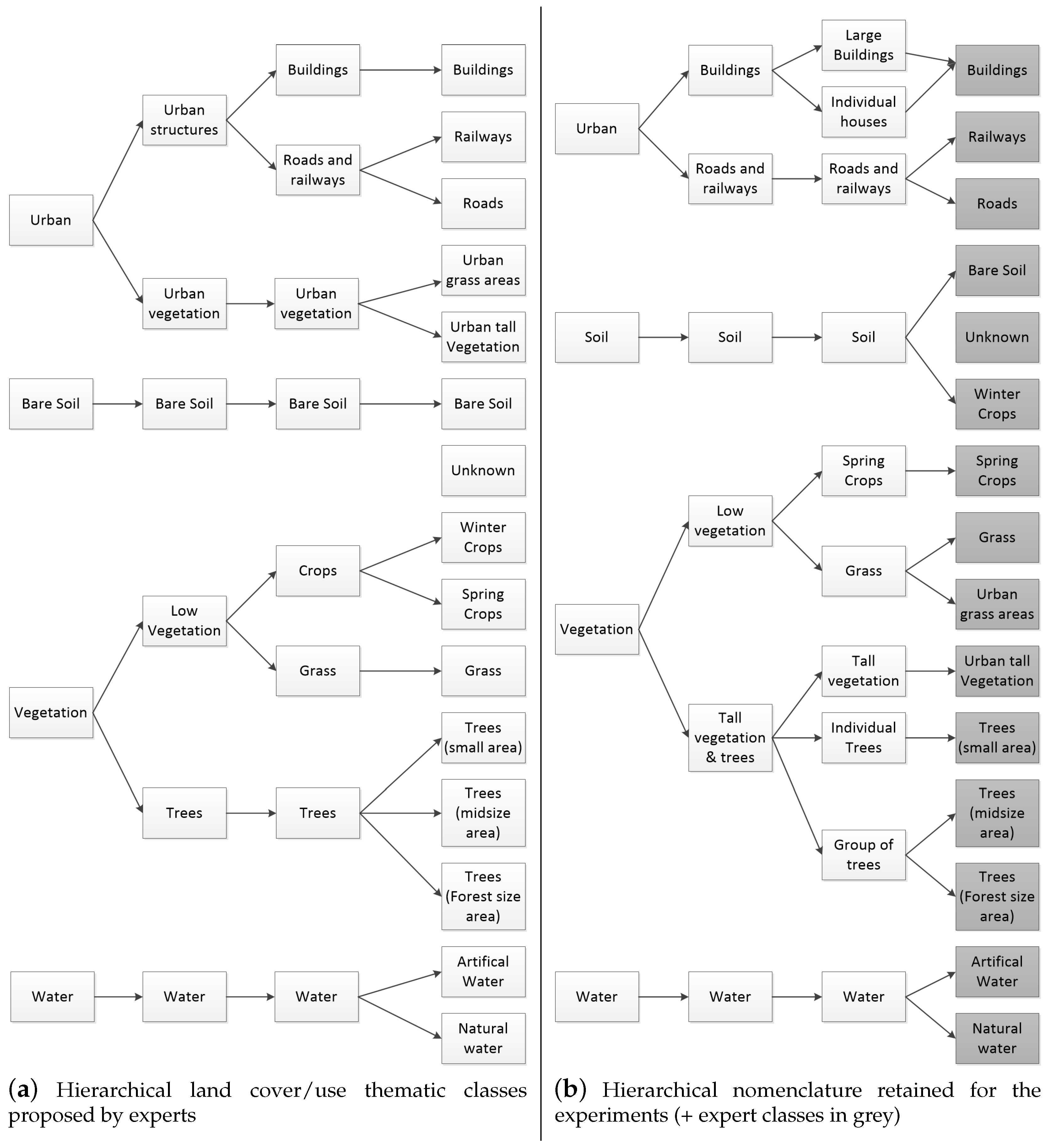
4.2. Visual Results
4.3. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ANR | “Agence Nationale de la Recherche” (French National Agency for Research) |
| EM | Expectation maximization |
| GIS | Geographic information systems |
| ICM | Iterated conditional modes |
| MRF | Markov random fields |
| MRIS | Multi-resolution image segmentation |
| OBIA | Object-based image analysis |
| VHR | Very high resolution |
References
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- d’Oleire-Oltmanns, S.; Eisank, C.; Dragut, L.; Blaschke, T. An Object-Based Workflow to Extract Landforms at Multiple Scales from Two Distinct Data Types. IEEE Geosci. Remote Sens. Lett. 2013, 10, 947–951. [Google Scholar] [CrossRef]
- Sublime, J.; Troya-Galvis, A.; Bennani, Y.; Gancarski, P.; Cornuéjols, A. Semantic Rich ICM Algorithm for VHR Satellite Image Segmentation. In Proceedings of the IAPR International Conference on Machine Vision Applications (MVA 2015), Tokyo, Japan, 18–22 May 2015. [Google Scholar]
- Grozavu, N.; Rogovschi, N.; Cabanes, G.; Troya-Galvis, A.; Gançarski, P. VHR satellite image segmentation based on topological unsupervised learning. In Proceedings of the 14th IAPR International Conference on Machine Vision Applications, Tokyo, Japan, 18–22 May 2015; pp. 543–546. [Google Scholar]
- Pal, N.R.; Pal, S.K. A review on image segmentation techniques. Pattern Recognit. 1993, 26, 1277–1294. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Cheng, H.; Jiang, X.; Sun, Y.; Wang, J. Color image segmentation: Advances and prospects. Pattern Recognit. 2001, 34, 2259–2281. [Google Scholar] [CrossRef]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Michel, J.; Youssefi, D.; Grizonnet, M. Stable mean-shift algorithm and its application to the segmentation of arbitrarily large remote sensing images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 952–964. [Google Scholar] [CrossRef]
- Fukunaga, K.; Hostetler, L. The estimation of the gradient of a density function, with applications in pattern recognition. IEEE Trans. Inf. Theory 1975, 21, 32–40. [Google Scholar] [CrossRef]
- Baatz, M.; Schäpe, A. Multiresolution Segmentation: An optimization approach for high quality multi-scale image segmentation. In Angewandte Geographische Informationsverarbeitung XII. Beiträge zum AGIT-Symposium Salzburg 2000; Strobl, J., Ed.; Herbert Wichmann Verlag: Karlsruhe, Germany, 2000; pp. 12–23. [Google Scholar]
- Wang, Z.; Jensen, J.R.; Im, J. An automatic region-based image segmentation algorithm for remote sensing applications. Environ. Model. Softw. 2010, 25, 1149–1165. [Google Scholar] [CrossRef]
- Derivaux, S.; Forestier, G.; Wemmert, C.; Lefèvre, S. Supervised image segmentation using watershed transform, fuzzy classification and evolutionary computation. Pattern Recognit. Lett. 2010, 31, 2364–2374. [Google Scholar] [CrossRef]
- Li, D.; Zhang, G.; Wu, Z.; Yi, L. An edge embedded marker-based watershed algorithm for high spatial resolution remote sensing image segmentation. IEEE Trans. Image Process. 2010, 19, 2781–2787. [Google Scholar] [PubMed]
- Peng, B.; Zhang, L.; Zhang, D. A survey of graph theoretical approaches to image segmentation. Pattern Recognit. 2013, 46, 1020–1038. [Google Scholar] [CrossRef]
- Paglieroni, D.W. Design considerations for image segmentation quality assessment measures. Pattern Recognit. 2004, 37, 1607–1617. [Google Scholar] [CrossRef]
- Corcoran, P.; Winstanley, A.; Mooney, P. Segmentation performance evaluation for object-based remotely sensed image analysis. Int. J. Remote Sens. 2010, 31, 617–645. [Google Scholar] [CrossRef]
- Srubar, S. Quality Measurement of Image Segmentation Evaluation Methods. In Proceedings of the 2012 Eighth International Conference on Signal Image Technology and Internet Based Systems (SITIS), Naples, Italy, 25–29 November 2012; pp. 254–258. [Google Scholar]
- Zhang, X.; Xiao, P.; Feng, X. An Unsupervised Evaluation Method for Remotely Sensed Imagery Segmentation. IEEE Geosci. Remote Lett. 2012, 9, 156–160. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multi-scale approach. ISPRS J. Photogramm. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Troya-Galvis, A.; Gançarski, P.; Passat, N.; Berti-Équille, L. Unsupervised quantification of under and over segmentation for object based remote sensing image analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1936–1945. [Google Scholar] [CrossRef]
- Liu, N.; Li, J.; Li, N. A Graph-segment-based Unsupervised Classification for Multispectral Remote Sensing Images. WSEAS Trans. Inf. Sci. Appl. 2008, 5, 929–938. [Google Scholar]
- Asmus, V.V.; Buchnev, A.A.; Pyatkin, V.P. Cluster analysis of earth remote sensing data. Optoelectron. Instrum. Data Process. 2010, 46, 149–155. [Google Scholar] [CrossRef]
- He, H.; Liang, T.; Hu, D.; Yu, X. Remote sensing clustering analysis based on object-based interval modeling. Comput. Geosci. 2016, 94, 131–139. [Google Scholar] [CrossRef]
- Li, H.; Zhang, S.; Ding, X.; Zhang, C.; Dale, P. Performance Evaluation of Cluster Validity Indices (CVIs) on Multi/Hyperspectral Remote Sensing Datasets. Remote Sens. 2016, 8, 295. [Google Scholar] [CrossRef]
- Chahdi, H.; Grozavu, N.; Mougenot, I.; Berti-Equille, L.; Bennani, Y. On the Use of Ontology as a priori Knowledge into Constrained Clustering. In Proceedings of the IEEE International Conference on Data Science and Advanced Analytics (DSAA), Montreal, QC, Canada, 17–19 October 2016. [Google Scholar]
- Chahdi, H.; Grozavu, N.; Mougenot, I.; Bennani, Y.; Berti-Equille, L. Towards Ontology Reasoning for Topological Cluster Labeling. ICONIP (3). In Lecture Notes in Computer Science; Hirose, A., Ozawa, S., Doya, K., Ikeda, K., Lee, M., Liu, D., Eds.; Springer: Cham, Switzerland, 2016; Volume 9949, pp. 156–164. [Google Scholar]
- Roth, S.; Black, M.J. Fields of experts. In Markov Random Fields for Vision and Image Processing; Blake, A., Kohli, P., Rother, C., Eds.; MIT Press: Cambridge, MA, USA, 2011; pp. 297–310. [Google Scholar]
- Ardila, J.; Tolpekin, V.; Bijker, W. Markov random field based super-resolution mapping for identification of urban trees in VHR images. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1402–1405. [Google Scholar]
- Sublime, J.; Cornuéjols, A.; Bennani, Y. A New Energy Model for the Hidden Markov Random Fields; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8835, pp. 60–67. [Google Scholar]
- Boykov, Y.; Veksler, O.; Zabih, R. Fast Approximate Energy Minimization via Graph Cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Leordeanu, M.; Hebert, M.; Sukthankar, R. An Integer Projected Fixed Point Method for Graph Matching and MAP Inference. In Proceedings of the Advances in Neural Information Processing Systems 22: 23rd Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; Bengio, Y., Schuurmans, D., Lafferty, J.D., Williams, C.K.I., Culotta, A., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2009; pp. 1114–1122. [Google Scholar]
- Liu, Z.Y.; Qiao, H.; Su, J.H. Neural Information Processing: 21st International Conference, ICONIP 2014, Kuching, Malaysia, November 3–6, 2014. Proceedings, Part II; Springer: Cham, Switzerland, 2014; pp. 404–412. [Google Scholar]
- Besag, J. On the statistical analysis of dirty pictures. J. R. Stat. Soc. Ser. B 1986, 48, 259–302. [Google Scholar] [CrossRef]
- Zhang, Y.; Brady, M.; Smith, S.M. Segmentation of Brain MR Images through a Hidden Markov Random Field Model and the Expectation Maximization Algorithm. IEEE Trans. Med. Imaging 2001, 20, 45–57. [Google Scholar] [CrossRef] [PubMed]
- Xu, K.; Yang, W.; Liu, G.; Sun, H. Unsupervised Satellite Image Classification Using Markov Field Topic Model. IEEE Geosci. Remote Sens. Lett. 2013, 10, 130–134. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar]
- Puissant, A.; Rougier, S.; Stumpf, A. Object-oriented mapping of urban trees using Random Forest classifiers. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 235–245. [Google Scholar] [CrossRef]
- Dragut, L.; Csillik, O.; Eisank, C.; Tiede, D. Automated parameterisation for multi-scale image segmentation on multiple layers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Neal, R.M.; Hinton, G.E. A view of the EM algorithm that justifies incremental, sparse, and other variants. In Learning in Graphical Models; Springer: Cham, The Netherlands, 1998; pp. 355–368. [Google Scholar]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [Google Scholar] [CrossRef] [PubMed]
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Rand, W. Objective criteria for the evaluation of clustering methods. J. Am. Stat. Assoc. 1971, 66, 846–850. [Google Scholar] [CrossRef]
- Yuan, Y.; Lin, J.; Wang, Q. Dual-Clustering-Based Hyperspectral Band Selection by Contextual Analysis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1431–1445. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, J.; Yuan, Y. Salient Band Selection for Hyperspectral Image Classification via Manifold Ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef] [PubMed]





| Attribute | Type | Comments |
|---|---|---|
| Brightness | Spectral | |
| Max. difference | Spectral | |
| Mean XS1 | Spectral | Blue |
| Mean XS2 | Spectral | Green |
| Mean XS3 | Spectral | Red |
| Mean XS4 | Spectral | near-infrared |
| Standard deviation XS1 | Spectral | Blue |
| Standard deviation XS2 | Spectral | Green |
| Standard deviation XS3 | Spectral | Red |
| Standard deviation XS4 | Spectral | Near-infrared |
| Ratio XS1 | Spectral | Blue |
| Ratio XS2 | Spectral | Green |
| Ratio XS3 | Spectral | Red |
| Ratio XS4 | Spectral | Near-infrared |
| Mean Diff. to neighbors XS1 | Spectral | Blue |
| Mean Difference to neighbors XS2 | Spectral | Green |
| Mean Difference to neighbors XS3 | Spectral | Red |
| Mean Difference to neighbors XS4 | Spectral | Near-infrared |
| Area | Shape | in pixels |
| Elliptic fit | Shape | |
| Density | Shape | |
| Rectangular Fit | Shape | |
| Shape index | Shape | |
| Asymmetry | Shape | |
| Gray level co-occurrence matrix contrast (all dir.) | Textural | |
| Gray level co-occurrence matrix entropy (all dir.) | Textural | |
| Gray level co-occurrence matrix correlation (all dir.) | Textural |
| Algorithm | Davies–Bouldin Index | Silhouette Index | Rand Index | Entropy |
|---|---|---|---|---|
| EM (4 clusters) | 2.09 | 0.23 | 0.69 | 0.64 |
| EM (6 clusters) | 2.10 | 0.19 | 0.72 | 0.62 |
| EM (10 clusters) | 2.59 | 0.11 | 0.70 | 0.61 |
| GMM-ICM (4 clusters) | 3.65 | 0.14 | 0.72 | 0.59 |
| GMM-ICM (6 clusters) | 2.52 | 0.16 | 0.73 | 0.58 |
| GMM-ICM (10 clusters) | 3.92 | 0.07 | 0.75 | 0.58 |
| SR-ICM (4 clusters) | 4.16 | 0.15 | 0.72 | 0.58 |
| SR-ICM (6 clusters) | 2.49 | 0.19 | 0.75 | 0.58 |
| SR-ICM (10 clusters) | 3.50 | 0.10 | 0.78 | 0.57 |
| ms-SR-ICM (4 clusters) | 4.27 | 0.14 | 0.72 | 0.57 |
| ms-SR-ICM (6 clusters) | 2.47 | 0.20 | 0.77 | 0.57 |
| ms-SR-ICM (10 clusters) | 3.33 | 0.10 | 0.80 | 0.55 |
| SOM (6 clusters) | 2.23 | 0.17 | 0.75 | 0.60 |
| SOM (10 clusters) | 4.04 | 0.05 | 0.75 | 0.63 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sublime, J.; Troya-Galvis, A.; Puissant, A. Multi-Scale Analysis of Very High Resolution Satellite Images Using Unsupervised Techniques. Remote Sens. 2017, 9, 495. https://doi.org/10.3390/rs9050495
Sublime J, Troya-Galvis A, Puissant A. Multi-Scale Analysis of Very High Resolution Satellite Images Using Unsupervised Techniques. Remote Sensing. 2017; 9(5):495. https://doi.org/10.3390/rs9050495
Chicago/Turabian StyleSublime, Jérémie, Andrés Troya-Galvis, and Anne Puissant. 2017. "Multi-Scale Analysis of Very High Resolution Satellite Images Using Unsupervised Techniques" Remote Sensing 9, no. 5: 495. https://doi.org/10.3390/rs9050495
APA StyleSublime, J., Troya-Galvis, A., & Puissant, A. (2017). Multi-Scale Analysis of Very High Resolution Satellite Images Using Unsupervised Techniques. Remote Sensing, 9(5), 495. https://doi.org/10.3390/rs9050495