Object-Based Detection of Linear Kinematic Features in Sea Ice
Abstract
:1. Introduction
2. Methods
2.1. Data
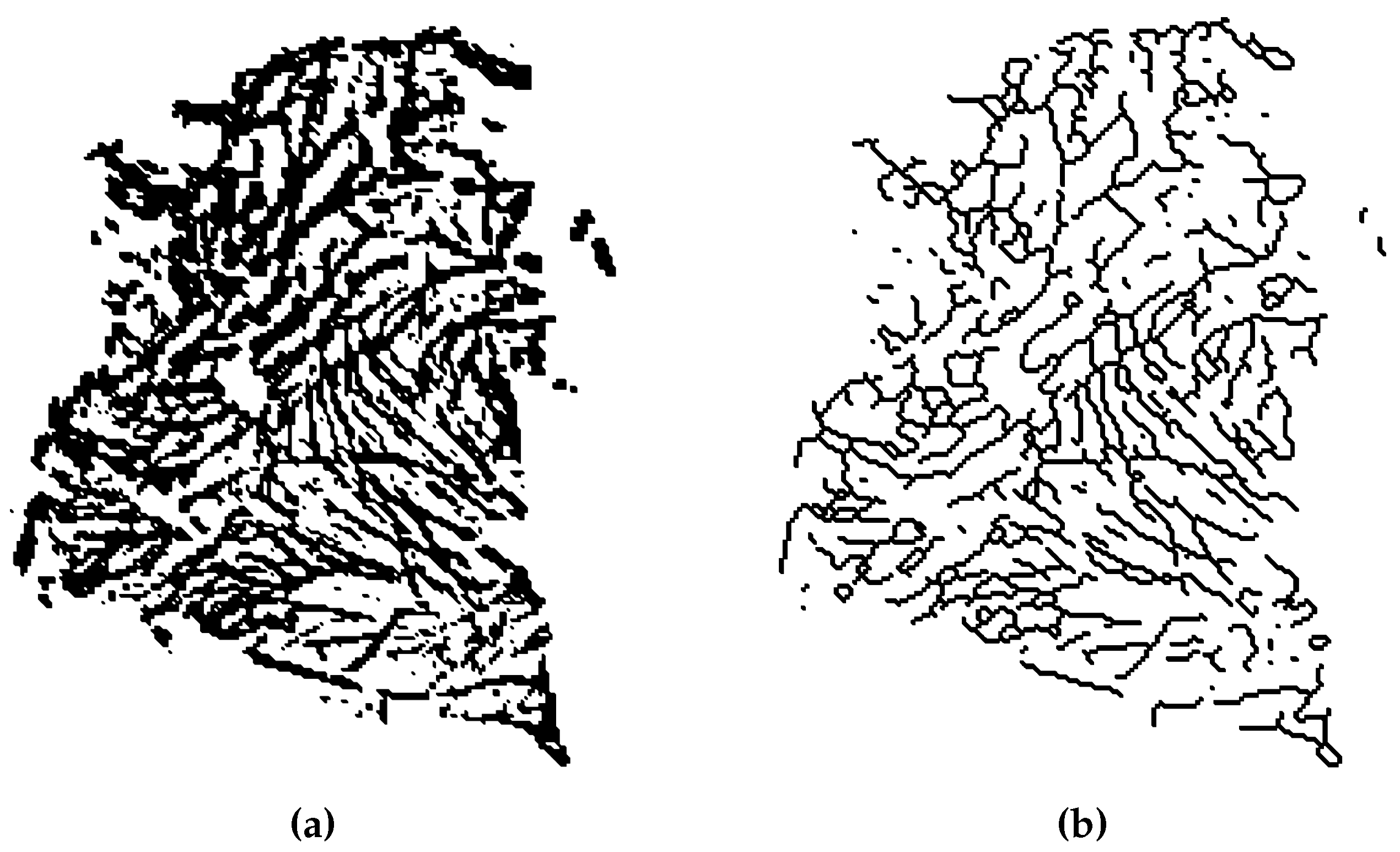
2.2. Image Enhancement, Segmentation and Edge Detection
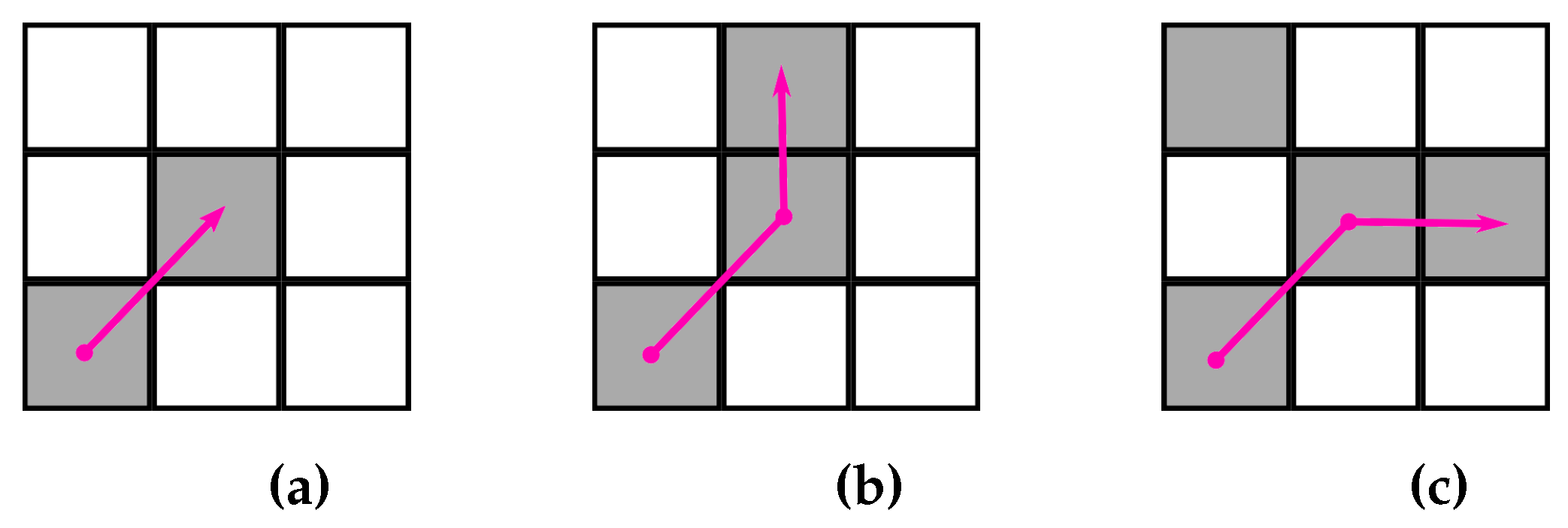
2.3. Object Detection
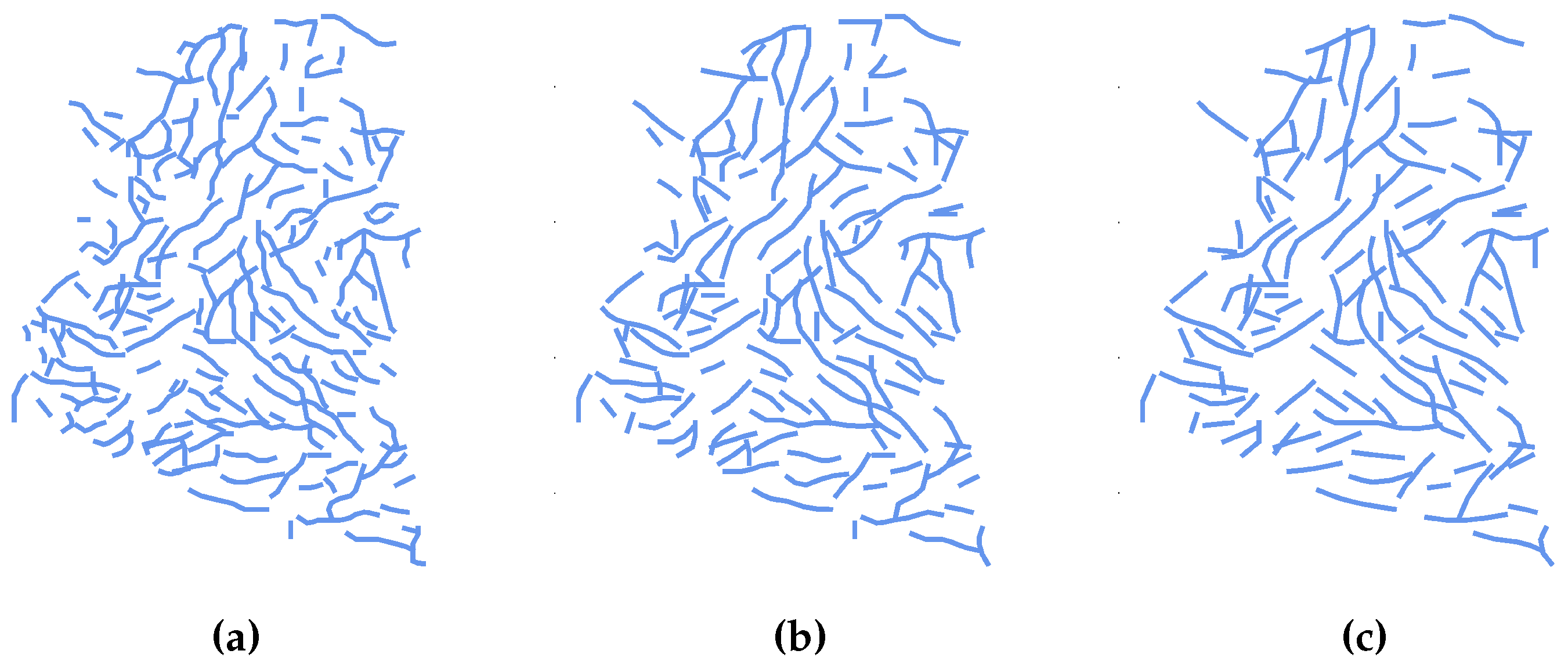
2.4. Semantic Postprocessing
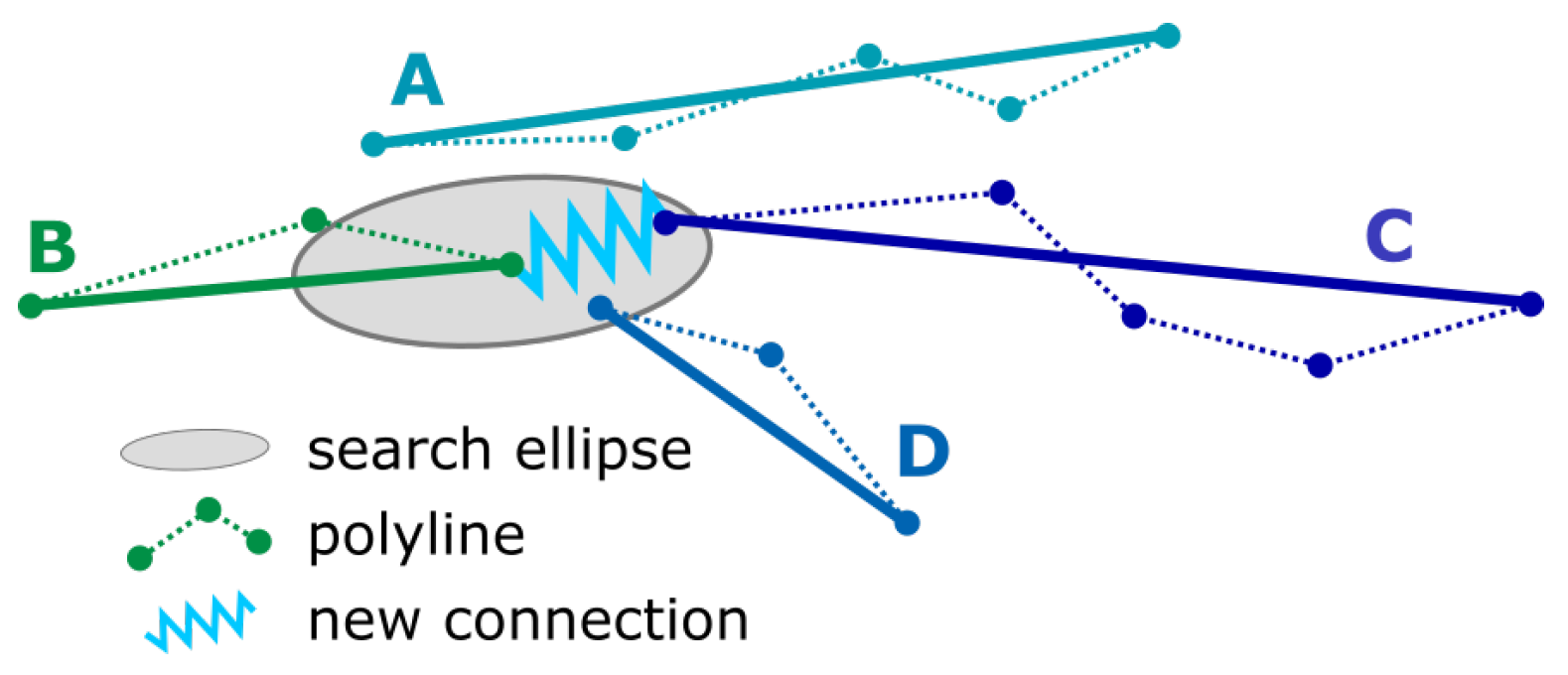
- Calculate the angle for each object i from a line connecting the polyline endpoints and normalize to orientation: . Hence, the entire polyline (rather than single polyline segments) is used to obtain the general object orientation.
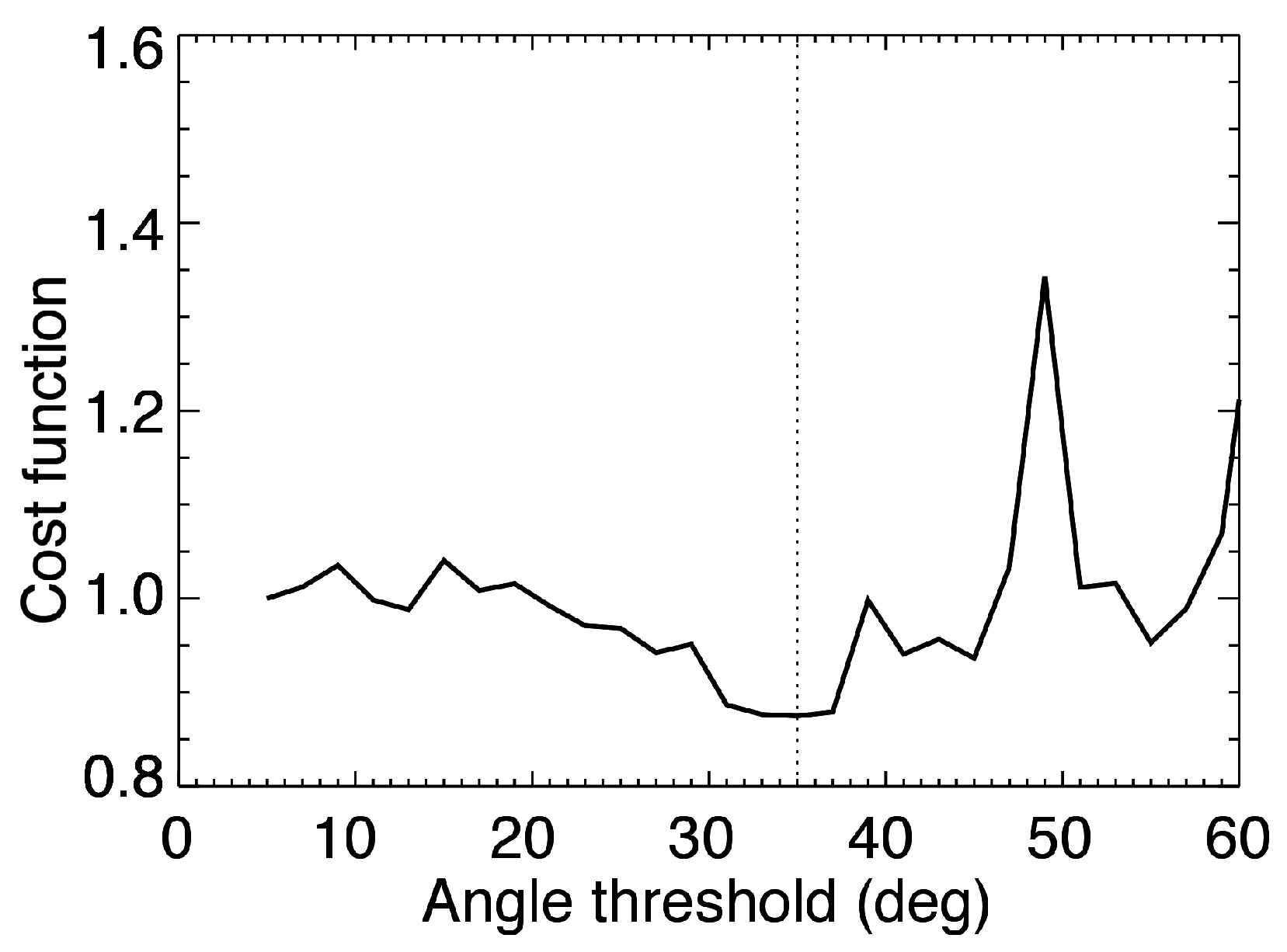
- For each object i, select the set L of objects j which have a similar orientation . The limit of 35° was chosen based on investigations of the data, a more detailed description is given in the Appendix A. The value introduced here allows to tolerate a small degree of curvature in the detected objects. In the example above, L would include lines A and C, if B was used as the reference object.
- Transform each object , to a local coordinate system with the -axis parallel to i and the origin at the start point of i, .In the practical implementation, the positions of matching candidates j with respect to the reference object i are not known. For each object i, a maximum of two objects and can be found which can be attached to the start- or the end segment of i.
- Now we apply anisotropic scaling to compress objects i and j along the – axis. In this way, we implement different search tolerances in and in direction to avoid connections between close parallel lines. The scaled coordinates are now:In the example shown in Figure 5, this would rule out line A and leave line C to be (correctly) connected to B.
- Calculate the endpoint distance . If is below a user-defined threshold, objects i and j are concatenated.
3. Results and Validation
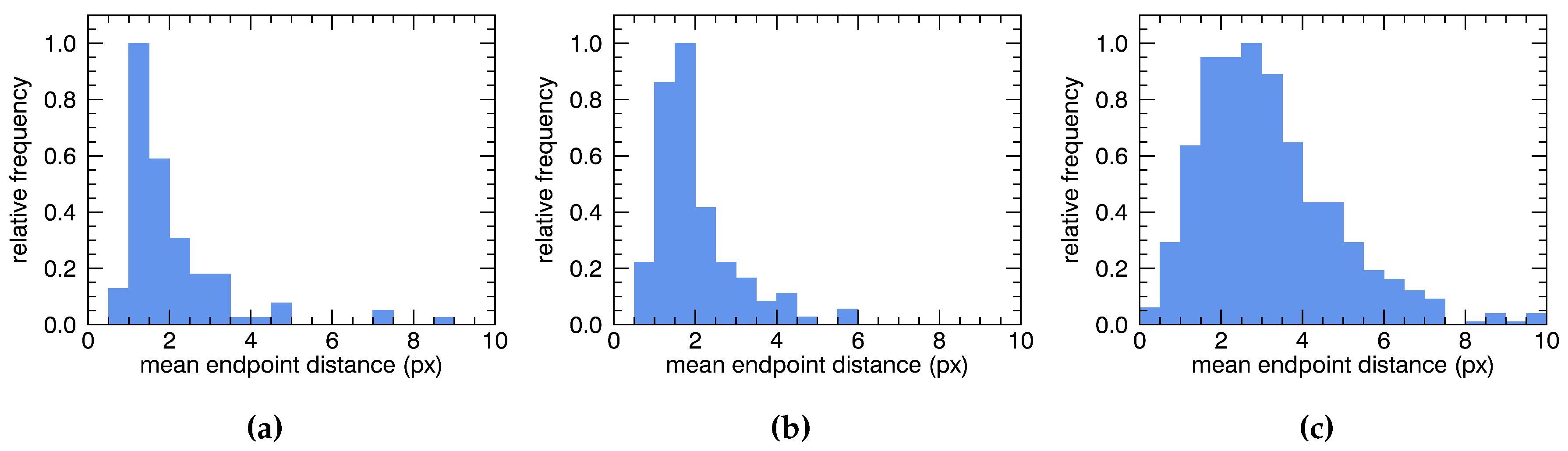
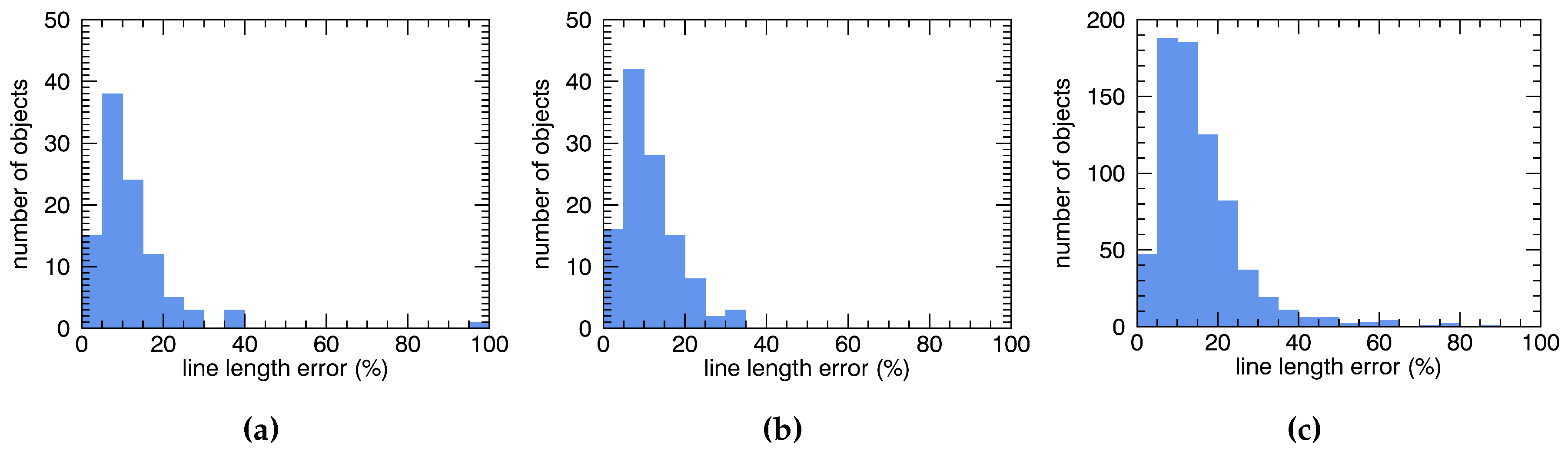
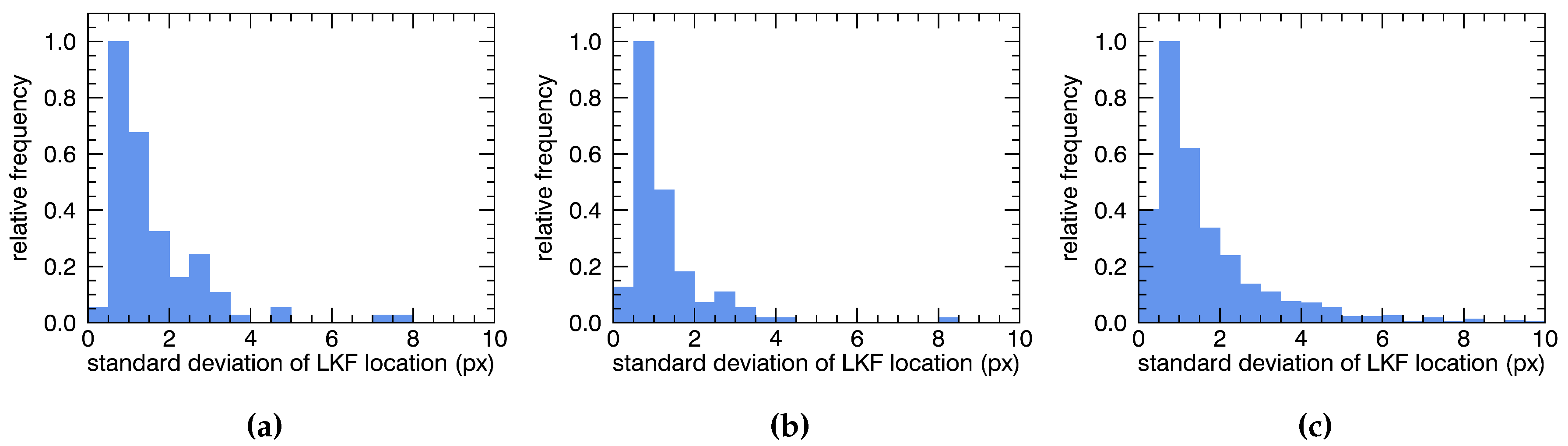
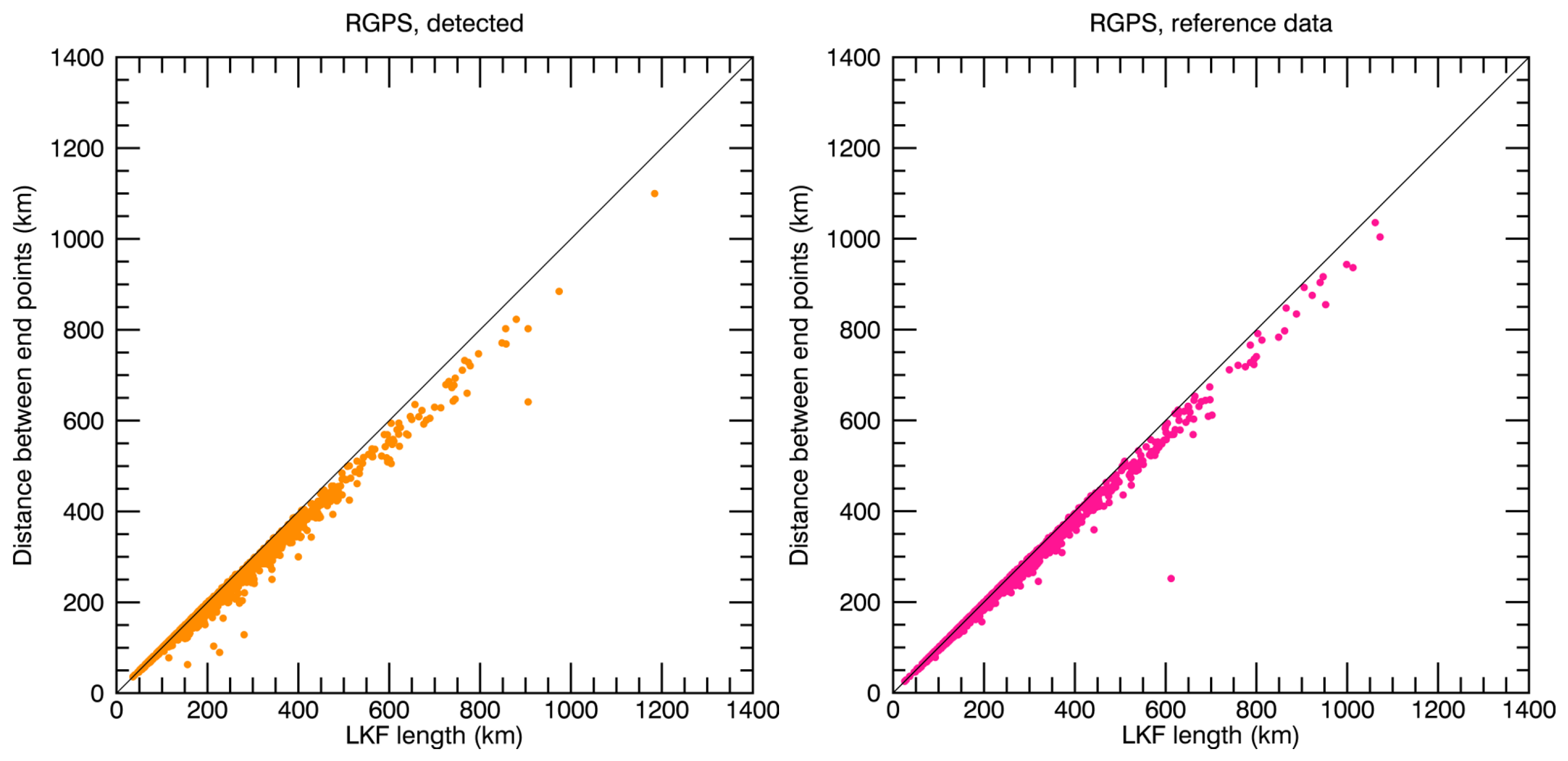
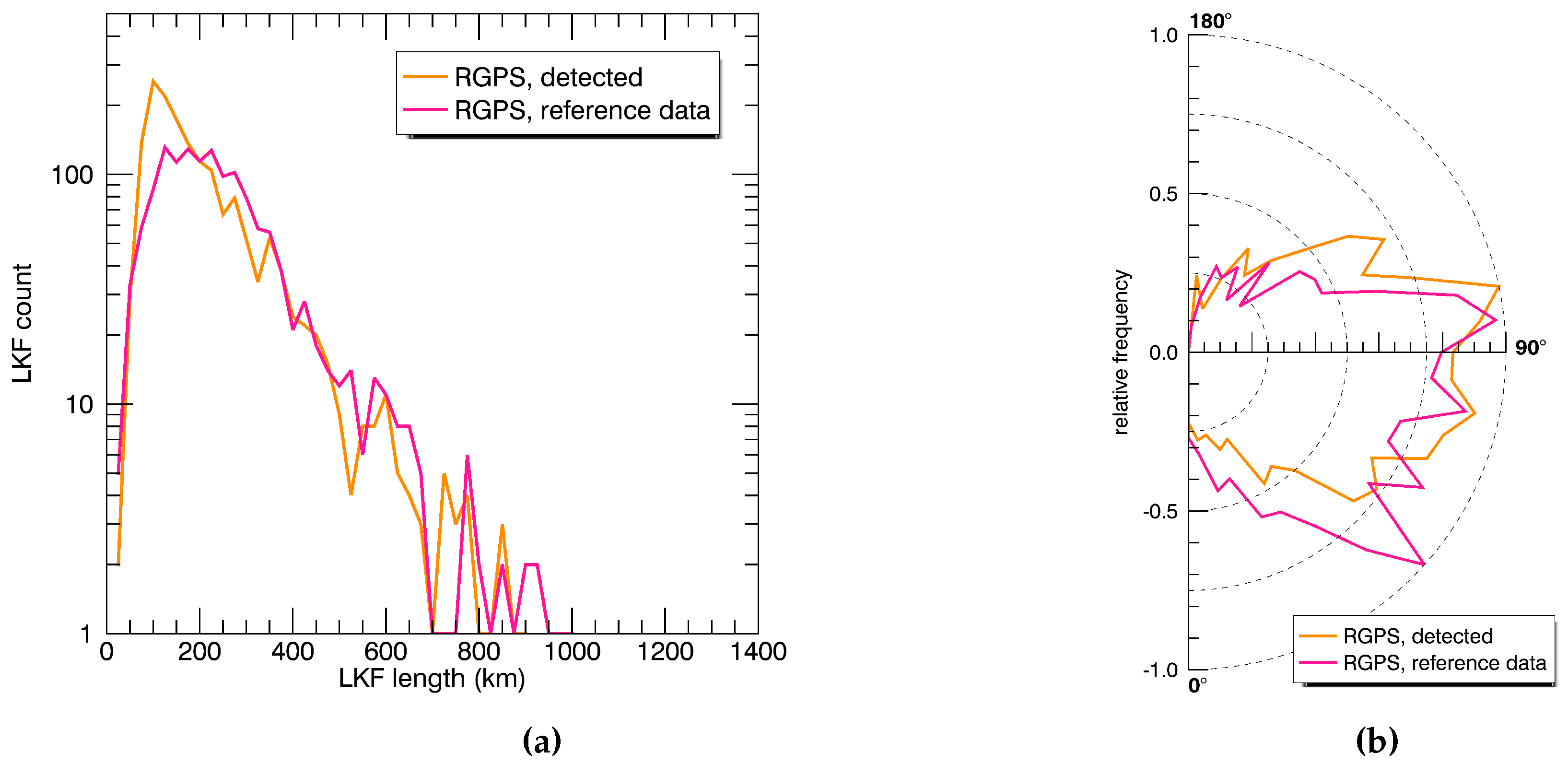
3.1. Validation with Reference Data
3.2. Plausibility Testing
4. Discussion
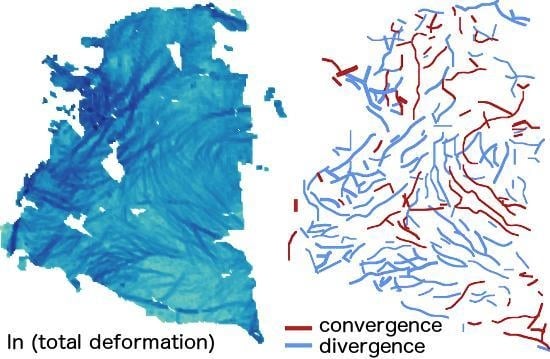
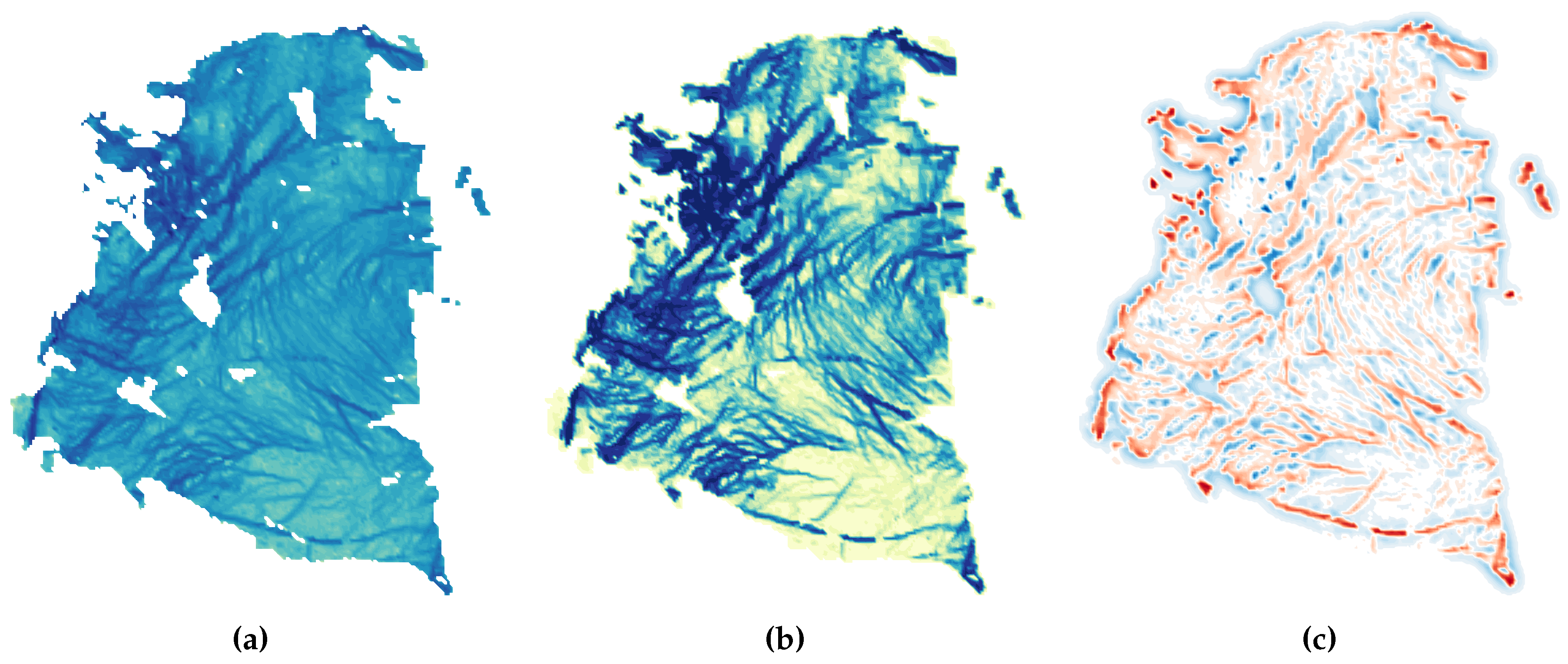
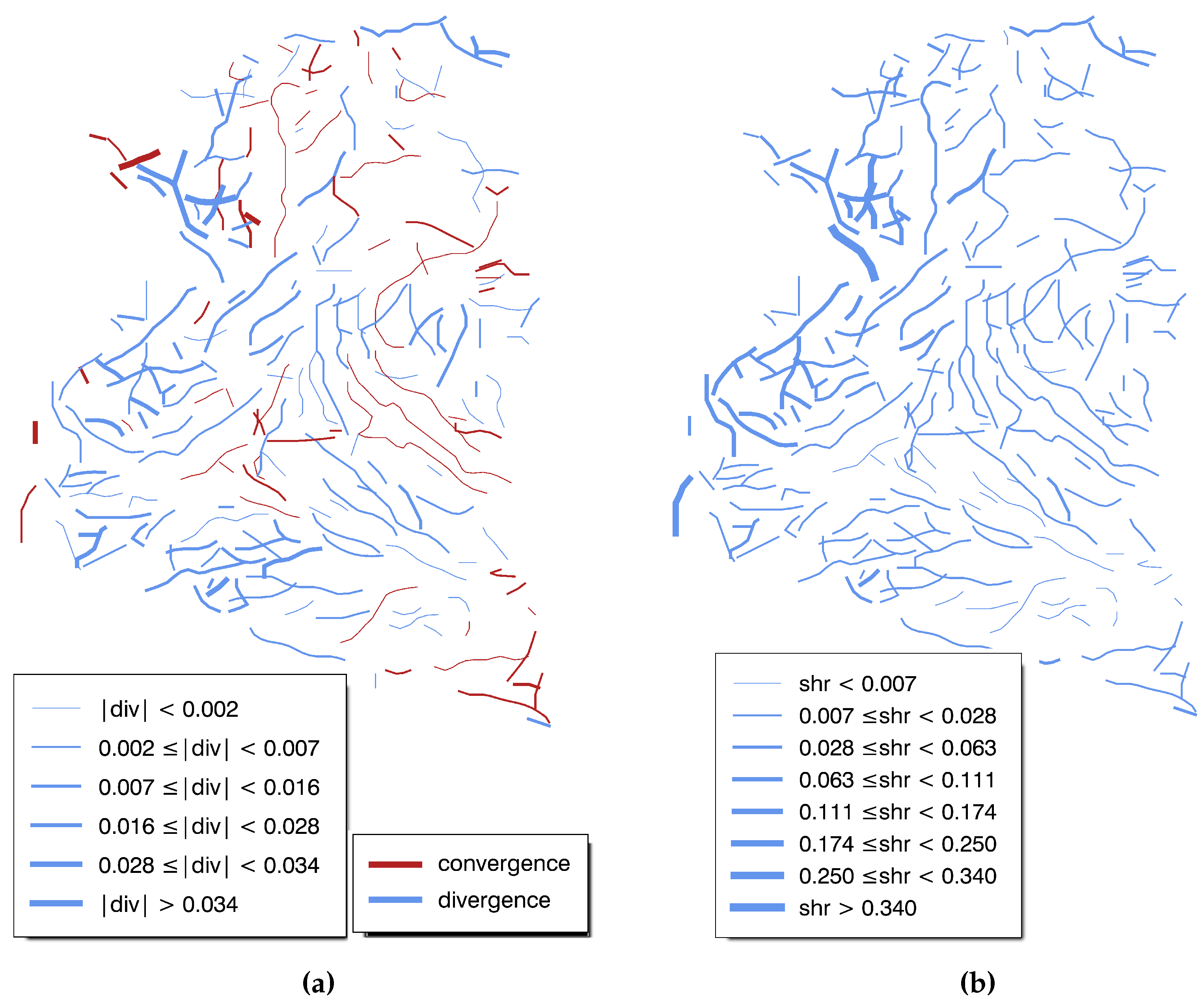
- analysis of individual features: as the geographical coordinates of each vertex of each detected object are known, LKFs can be analyzed on an individual basis. Values from the original deformation images or other parameters can be easily mapped back onto the observed features (Example: divergence and shear maps for the entire spatial domain, Figure 14).
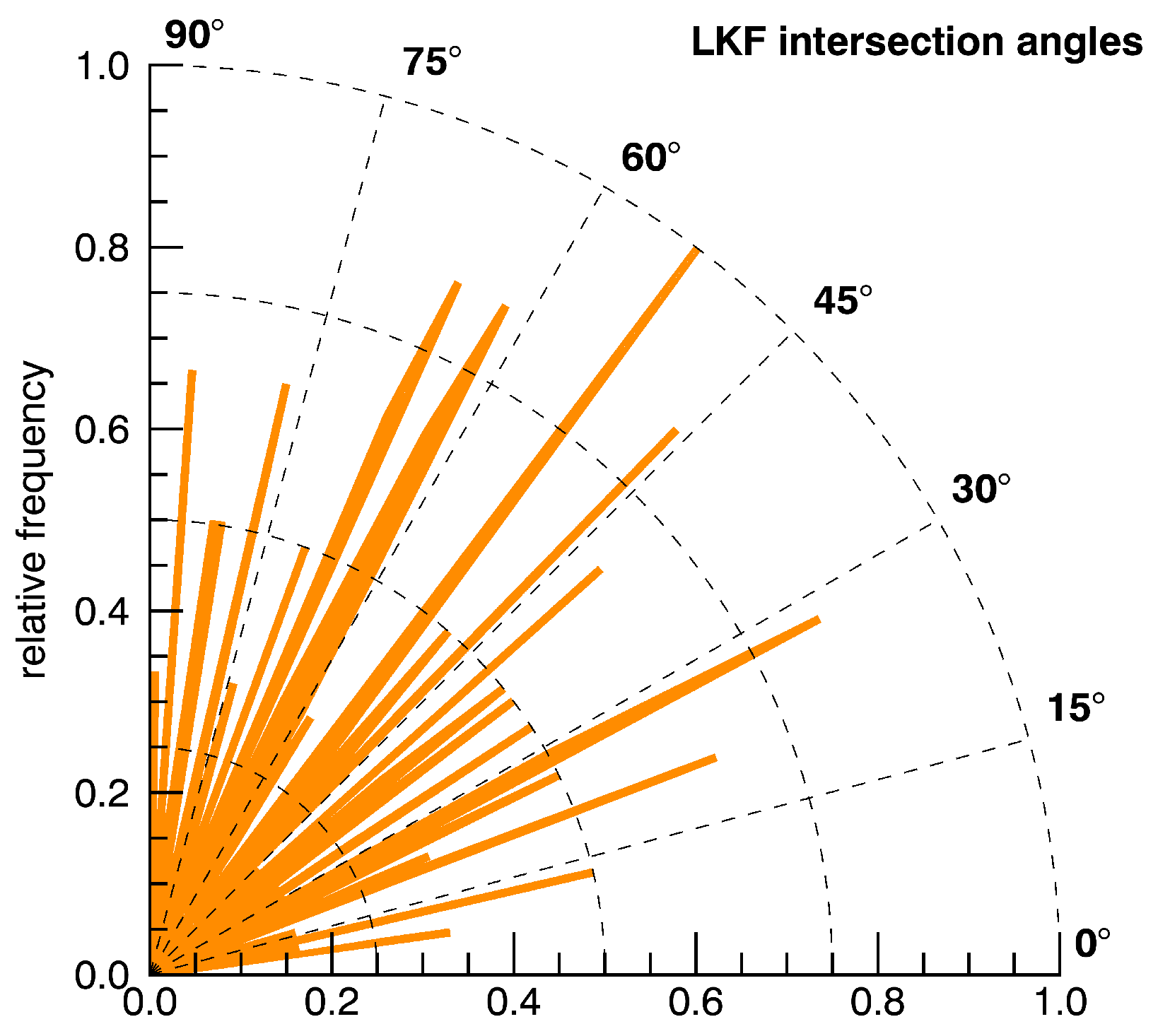
- LKF intersection angles: fracture mechanics of the ice cause “typical” fracture patterns, and the intersection angles depend on properties of the material, similar to stress faulting in rocks. Here, we also consider cases in which one LKF ends in the vicinity of another LKF instead of intersecting it by applying a simple distance criterion. Each pair of LKFs (consiting of several segments with slightly varying orientations) is approximated by a pair of lines fixed to the respective start- and endpoints, and the intersection angle between those lines is calculated. The result for the entire scene from Figure 6a is shown in Figure 15. The relationship between fracture angles and strain magnitude is rather complex and depends on the type of strain (e.g., shear or divergence) and on material properties [1]. With given strain rates (such as in Figure 14) and LKF intersection angles derived from the detected objects, the data basis is available to analyze the material/fracturing properties of the sea ice in more detail. However, this type of analysis would exceed the scope of this study.
5. Conclusions
Author Contributions
Conflicts of Interest
Appendix A
References
- Erlingsson, B. Two-dimensional deformation patterns in sea ice. J. Glaciol. 1988, 34, 301–308. [Google Scholar] [CrossRef]
- Schulson, E.M. Compressive shear faults within arctic sea ice: Fracture on scales large and small. J. Geophys. Res. 2004, 109, C07016. [Google Scholar] [CrossRef]
- Rampal, P.; Bouillon, S.; Ólason, E.; Morlighem, M. neXtSIM: A new Lagrangian sea ice model. Cryosphere 2016, 10, 1055–1073. [Google Scholar] [CrossRef]
- Marsan, D.; Stern, H.; Lindsay, R.; Weiss, J. Scale Dependence and Localization of the Deformation of Arctic Sea Ice. Phys. Rev. Lett. 2004, 93, 178501. [Google Scholar] [CrossRef] [PubMed]
- Hutchings, J.; Heil, P.; Steer, A.; Hibler, W. Subsynoptic scale spatial variability of sea ice deformation in the western Weddell Sea during early summer. J. Geophys. Res. 2012, 117, C01002. [Google Scholar] [CrossRef]
- Onana, V.D.P.; Kurtz, N.T.; Farrell, S.L.; Koenig, L.S.; Studinger, M.; Harbeck, J.P. A Sea-Ice Lead Detection Algorithm for Use With High-Resolution Airborne Visible Imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 38–56. [Google Scholar] [CrossRef]
- Willmes, S.; Heinemann, G. Pan-Arctic lead detection from MODIS thermal infrared imagery. Ann. Glaciol. 2015, 56, 29–37. [Google Scholar] [CrossRef]
- Lindsay, R.W.; Rothrock, D.A. Arctic sea ice leads from advanced very high resolution radiometer images. J. Geophys. Res. 1995, 100, 4533–4544. [Google Scholar] [CrossRef]
- Bröhan, D.; Kaleschke, L. A Nine-Year Climatology of Arctic Sea Ice Lead Orientation and Frequency from AMSR-E. Remote Sens. 2014, 6, 1451–1475. [Google Scholar] [CrossRef]
- Miles, M.; Barry, R. A 5-year satellite climatology of winter sea ice leads in the western Arctic. J. Geophys. Res. 1998, 103, 21723–21734. [Google Scholar] [CrossRef]
- Vesecky, J.F.; Smith, M.P.; Samadani, R. Extraction of Lead and Ridge Characteristics from SAR Images of Sea Ice. IEEE Trans. Geosci. Remote Sens. 1990, 28, 740–744. [Google Scholar] [CrossRef]
- Vesecky, J.F.; Smith, M.P.; Samadani, R. Remote Sensing of Pressure Ridge and Lead Characteristics Using Sar Images of Sea Ice. In Proceedings of the 10th Annual International Geoscience and Remote Sensing Symposium, College Park, MD, USA, 20–24 May 1990; pp. 1871–1874. [Google Scholar]
- Dierking, W.; Dall, J. Sea Ice Deformation State From Synthetic Aperture Radar Imagery—Part I: Comparison of C- and L-Band and Different Polarization. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3610–3622. [Google Scholar] [CrossRef]
- Kwok, R.; Curlander, J.; McConnell, R.; Pang, S. An Ice Motion Tracking System at the Alaska SAR Facility. IEEE J. Ocean. Eng. 1990, 15, 44–54. [Google Scholar] [CrossRef]
- Lindsay, R.; Zhang, J.; Rothrock, D. Sea Ice Deformation Rates From Satellite Measurements and in a Model. Atmos. Ocean 2003, 41, 35–47. [Google Scholar] [CrossRef]
- Kwok, R. Declassified high-resolution visible imagery for Arctic sea ice investigations: An overview. Remote Sens. Environ. 2014, 142, 44–56. [Google Scholar] [CrossRef]
- Thorndike, A.; Colony, R. Sea ice motion in response to geostrophic winds. J. Geophys. Res. 1982, 87, 5845–5852. [Google Scholar] [CrossRef]
- Bouillon, S.; Rampal, P. On producing sea ice deformation data sets from SAR-derived sea ice motion. Cryosphere 2015, 9, 663–673. [Google Scholar] [CrossRef]
- Weiss, J. Drift, Deformation and Fracture of Sea Ice. A Perspective Across Scales; Springer Netherlands: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Girard, L.; Weiss, J.; Molines, J.M.; Barnier, B.; Bouillon, S. Evaluation of high-resolution sea ice models on the basis of statistical and scaling properties of Arctic sea ice drift and deformation. J. Geophys. Res. 2009, 114, 281–325. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Machine Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- Marr, D.; Hildreth, E. Theory of Edge Detection. Proc. R. Soc. Lond. B 1980, 207, 187–217. [Google Scholar] [CrossRef] [PubMed]
- Lindeberg, T. Principles for Automatic Scale Selection. In Handbook on Computer Vision and Applications; Academic Press: Boston, MA, USA, 1999; Volume 2, pp. 239–274. [Google Scholar]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Szeliski, R. Computer Vision—Algorithms and Applications; Texts in Computer Science; Springer: London, UK, 2011. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Steger, C. An Unbiased Detector of Curvilinear Structures. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 113–125. [Google Scholar] [CrossRef]
- Zhou, J.; Bischof, W.; Caelli, T. Road tracking in aerial images based on human-computer interaction and Bayesian filtering. ISPRS J. Photogramm. Remote Sens. 2006, 61, 108–124. [Google Scholar] [CrossRef]
- Poullis, C.; You, S. Delineation and geometric modeling of road networks. ISPRS J. Photogramm. Remote Sens. 2010, 65, 165–181. [Google Scholar] [CrossRef]
- Maire, M.; Arbeláez, P.; Fowlkes, C.; Malik, J. Using contours to detect and localize junctions in natural images. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Martin, S. Polynyas. In Encyclopedia of Ocean Sciences; John, H., Steele, E., Eds.; Academic Press: Oxford, UK, 2001; pp. 2241–2247. [Google Scholar]
- Martin, D.; Fowlkes, C.; Malik, J. Learning to detect natural image boundaries using local brightness, color, and texture cues. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 530–549. [Google Scholar] [CrossRef] [PubMed]
- Miao, X.; Xie, H.; Ackley, S.F.; Zheng, S. Object-based Arctic sea ice ridge detection from high-spatial-resolution imagery. IEEE Geosci. Remote Sens. Lett. 2016, 13, 787–791. [Google Scholar] [CrossRef]
- Kwok, R.; Hunke, E.C.; Maslowski, W.; Menemenlis, D.; Zhang, J. Variability of sea ice simulations assessed with RGPS kinematics. J. Geophys. Res. 2008, 113, C11012. [Google Scholar] [CrossRef]
- Kwok, R. Sea ice convergence along the Arctic coasts of Greenland and the Canadian Arctic Archipelago: Variability and extremes (1992–2014). Geophys. Res. Lett. 2015, 42, 7598–7605. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Linow, S.; Dierking, W. Object-Based Detection of Linear Kinematic Features in Sea Ice. Remote Sens. 2017, 9, 493. https://doi.org/10.3390/rs9050493
Linow S, Dierking W. Object-Based Detection of Linear Kinematic Features in Sea Ice. Remote Sensing. 2017; 9(5):493. https://doi.org/10.3390/rs9050493
Chicago/Turabian StyleLinow, Stefanie, and Wolfgang Dierking. 2017. "Object-Based Detection of Linear Kinematic Features in Sea Ice" Remote Sensing 9, no. 5: 493. https://doi.org/10.3390/rs9050493
APA StyleLinow, S., & Dierking, W. (2017). Object-Based Detection of Linear Kinematic Features in Sea Ice. Remote Sensing, 9(5), 493. https://doi.org/10.3390/rs9050493