Glacier Changes in the Susitna Basin, Alaska, USA, (1951–2015) using GIS and Remote Sensing Methods
Abstract
:1. Introduction
2. Study Site
3. Data and Methods
3.1. Area Changes
3.2. Elevation and Mass Changes
3.3. Equilibrium Line Altitudes and Accumulation Area Ratios
4. Uncertainty Estimation
4.1. Area Changes
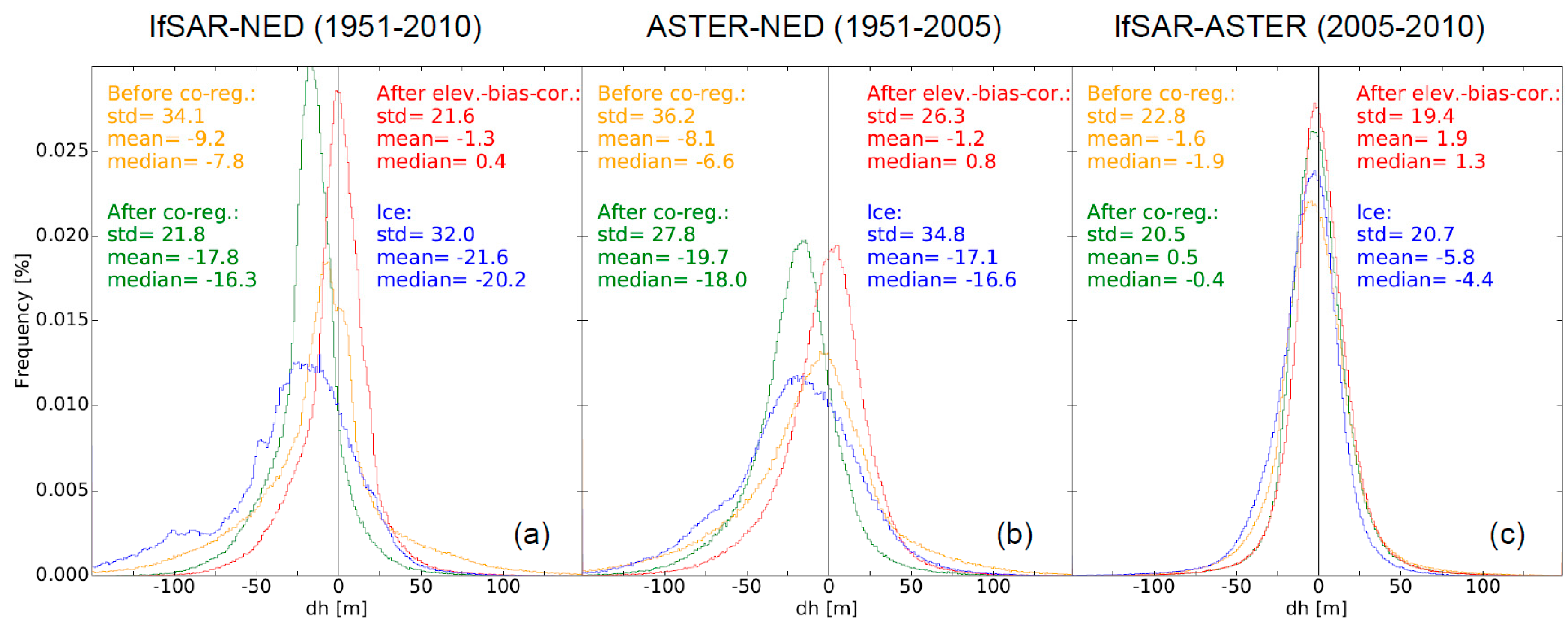
4.2. DEM-Differencing
4.3. Equilibrium Line Altitudes
5. Results
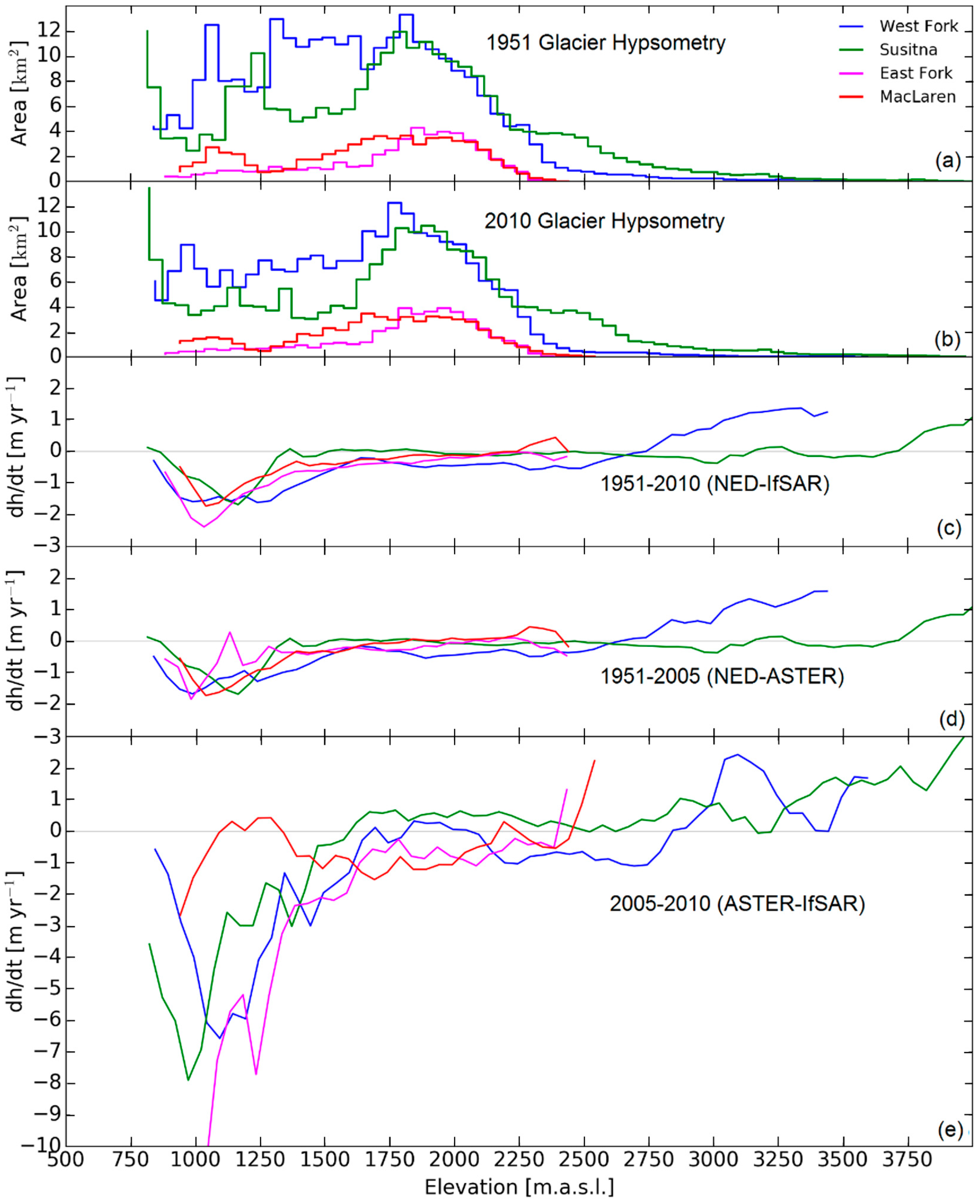
5.1. Area Changes
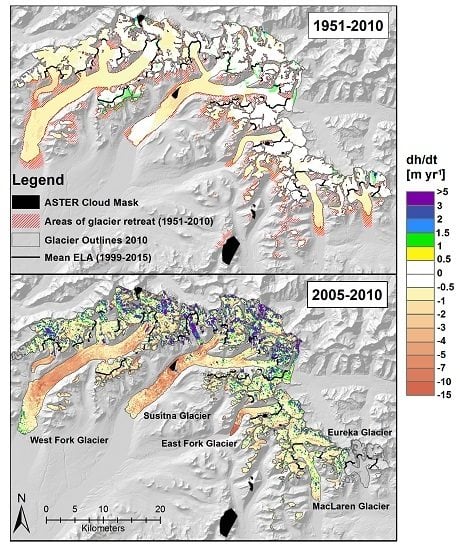
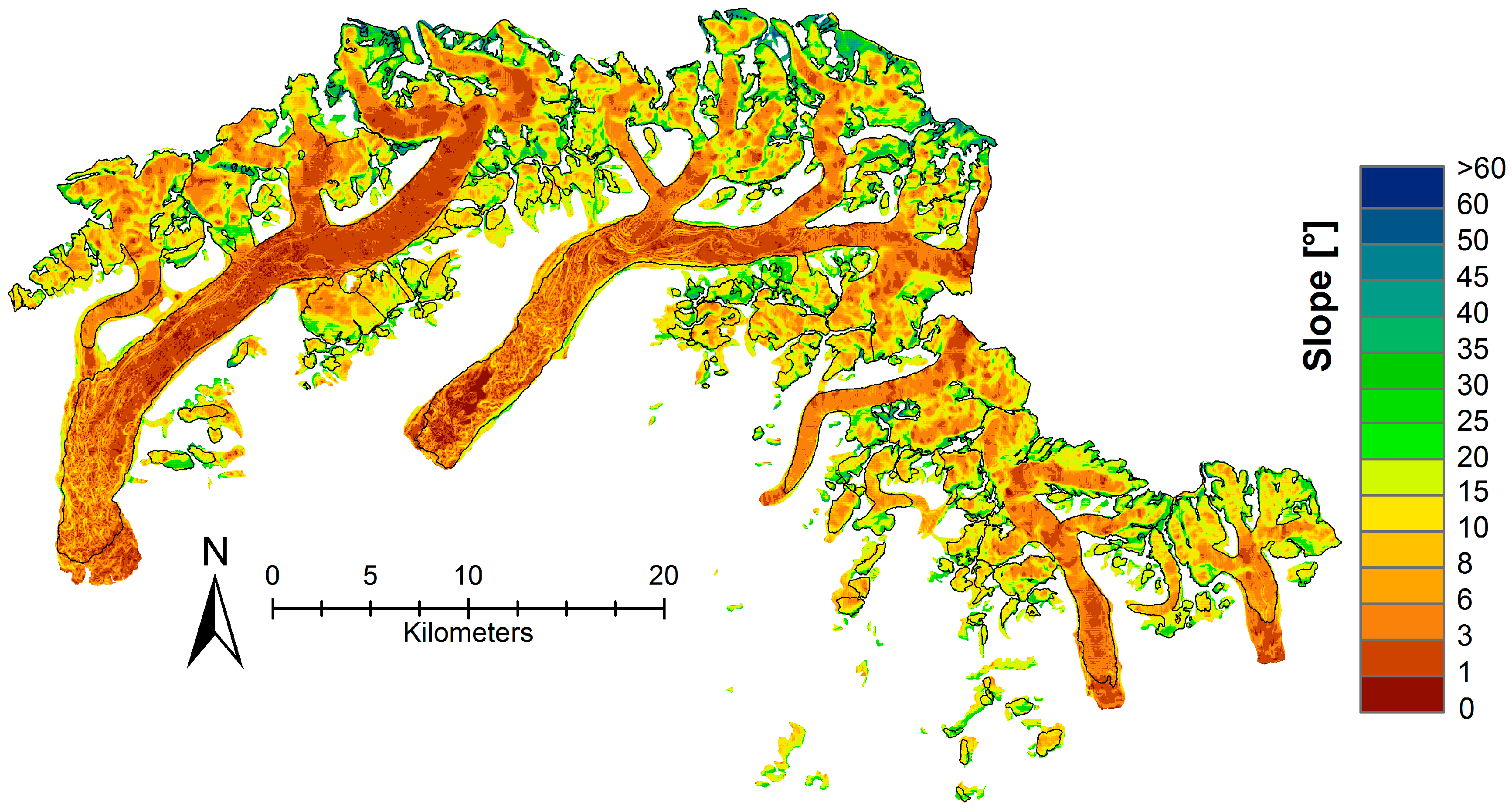
5.2. Spatial Patterns in Elevation Change
5.3. Glacier-wide Elevation and Mass Changes
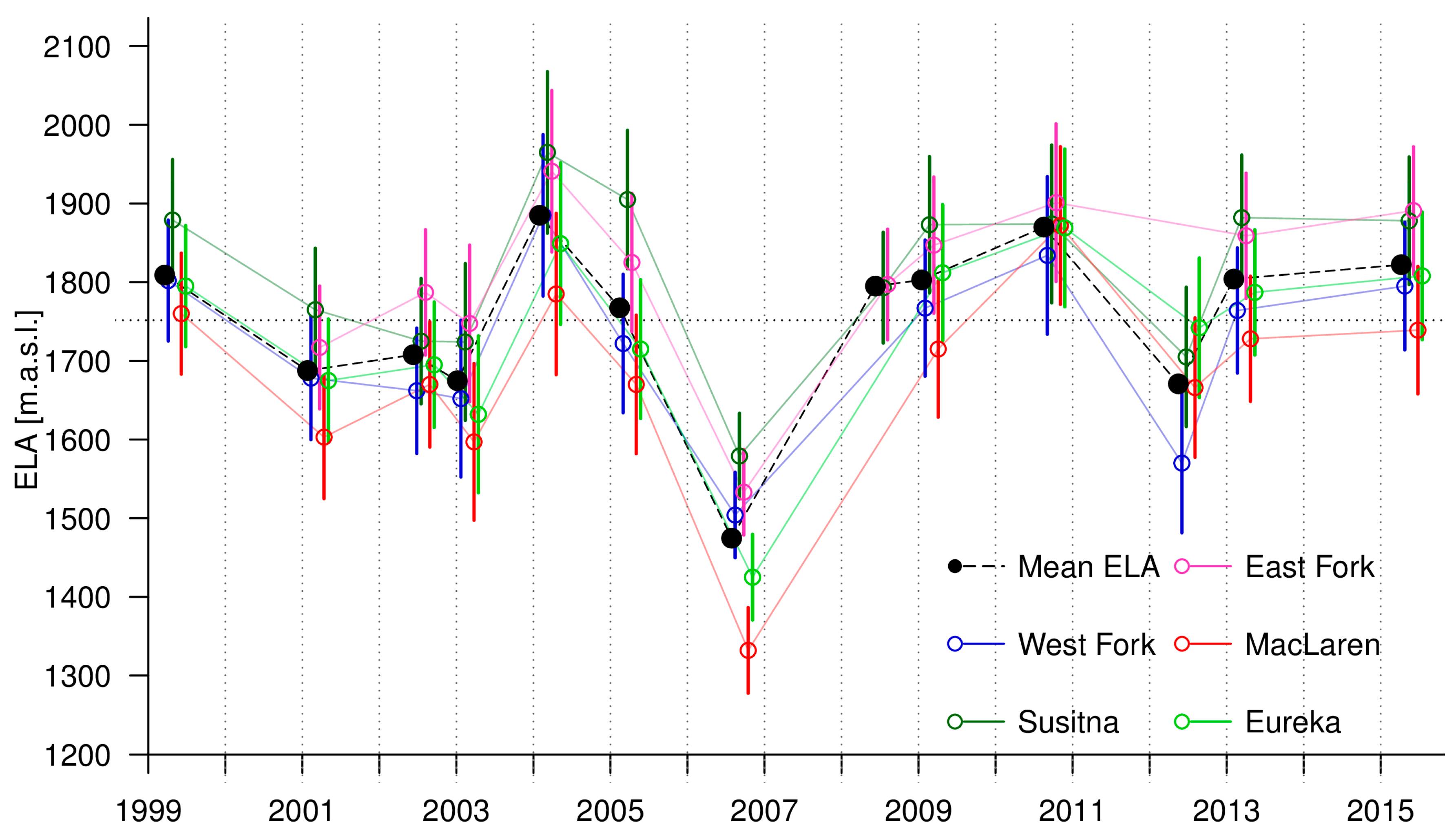
5.4. Changes in ELA
6. Discussion
6.1. Comparison with Other Studies
6.2. ELA and AAR
6.3. Surge Effects
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Sensor | Date Acquired | Product ID |
|---|---|---|
| Landsat 7 ETM+ | 16 August 1999 | LE70680161999228AGS00 |
| Landsat 7 ETM+ | 05 August 2001 | LE70680162001217AGS00 |
| Landsat 7 ETM+ | 02 September 2002 | LE70670162002245EDC01 |
| Landsat 7 ETM+ | 19 July 2003 | LE70670162003200EDC01 |
| Landsat 5 TM | 10 August 2003 | LT50690152003222PAC02 |
| Landsat 7 ETM+ | 06 August 2004 | LE70670162004219EDC01 |
| Landsat 7 ETM+ | 09 August 2005 | LE70670162005221EDC00 |
| Landsat 5 TM | 12 September 2006 | LT50680162006255PAC01 |
| Landsat 7 ETM+ | 02 September 2008 | LE70670162008246EDC00 |
| Landsat 5 TM | 03 August 2009 | LT50680162009215GLC00 |
| Landsat 5 TM | 16 September 2010 | LT50670162010259GLC00 |
| Landsat 7 ETM+ | 28 August 2012 | LE70670162012241EDC00 |
| Landsat 8 OLI | 07 August 2013 | LC80670162013219LGN00 |
| Landsat 8 OLI | 20 August 2015 | LC80680162015232LGN00 |
References
- Arendt, A.A.; Echelmeyer, K.A.; Harrison, W.D.; Lingle, C.S.; Valentine, V.B. Rapid wastage of Alaska glaciers and their contribution to rising sea level. Science 2002, 297, 382–386. [Google Scholar] [CrossRef] [PubMed]
- Berthier, E.; Schiefer, E.; Clarke, G.K.C.; Menounos, B.; Rémy, F. Contribution of Alaskan glaciers to sea-level rise derived from satellite imagery. Nat. Geosci. 2010, 3, 92–95. [Google Scholar] [CrossRef]
- Larsen, C.F.; Burgess, E.; Arendt, A.A.; O’Neel, S.; Johnson, A.J.; Kienholz, C. Surface melt dominates Alaska glacier mass balance. Geophys. Res. Lett. 2015, 42, 5902–5908. [Google Scholar] [CrossRef]
- Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A reconciled estimate of glacier contributions to sea level rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef] [PubMed]
- Das, I.; Hock, R.; Berthier, E.; Lingle, C.S. 21st-century increase in glacier mass loss in the Wrangell Mountains, Alaska, USA, from airborne laser altimetry and satellite stereo imagery. J. Glaciol. 2014, 60, 283–293. [Google Scholar] [CrossRef]
- Johnson, A.J.; Larsen, C.F.; Murphy, N.; Arendt, A.A.; Zirnheld, S.L. Mass balance in the Glacier Bay area of Alaska, USA, and British Columbia, Canada, 1995–2011, using airborne laser altimetry. J. Glaciol. 2013, 59, 632–648. [Google Scholar] [CrossRef]
- Shulski, M.; Wendler, G. The Climate of Alaska; University of Alaska Press: Fairbanks, AK, USA, 2007. [Google Scholar]
- Loso, M.; Arendt, A.A.; Larsen, C.; Rich, J.; Murphy, N. Alaskan National Park Glaciers-Status and Trends: Final Report; National Park Service: Fort Collins, CO, USA, 2014. [Google Scholar]
- Wolken, G.; Bliss, A.; Hock, R.; Whorton, E.; Braun, J.; Liljedahl, A.; Zhang, J.; Youcha, E.; Schulla, J.; Gusmeroli, A.; et al. Susitna-Watana Hydroelectric Project (FERC No. 14241) Glacier and Runoff Changes Study, Final Study Report; Alaska Energy Authority: Anchorage, AK, USA, 2015. [Google Scholar]
- Clarke, T.S.; Johnson, D.; Harrison, W.D. Glacier Mass Balances and Runoff in the Upper Susitna and Maclaren River Basins, 1981–1983. Available online: http://www.arlis.org/docs/vol1/Susitna/27/APA2781.pdf (accessed on 18 March 2017).
- Harrison, W.D.; Drage, B.T.; Bredthauer, S.; Johnson, D.; Schoch, C.; Follett, A.B. Reconnaissance of the glaciers of the Susitna River basin in connection with proposed hydroelectric development. Ann. Glaciol. 1983, 4. [Google Scholar] [CrossRef]
- Benn, D.I.; Lehmkuhl, F. Mass balance and equilibrium-line altitudes of glaciers in high-mountain environments. Quat. Int. 2000, 65–66, 15–29. [Google Scholar] [CrossRef]
- Clare, G.R.; Fitzharris, B.B.; Chinn, T.J.H.; Salinger, M.J. Interannual variation in end-of-summer snowlines of the Southern Alps of New Zealand, and relationships with Southern Hemisphere atmospheric circulation and sea surface temperature patterns. Int. J. Climatol. 2002, 22, 107–120. [Google Scholar] [CrossRef]
- Rabatel, A.; Letréguilly, A.; Dedieu, J.-P.; Eckert, N. Changes in glacier equilibrium-line altitude in the western Alps from 1984 to 2010: Evaluation by remote sensing and modeling of the morpho-topographic and climate controls. Cryosphere 2013, 7, 1455–1471. [Google Scholar] [CrossRef]
- Brabets, T. Precipitation Map of Alaska; USGS: Reston, VA, USA, 1997. Available online: https://agdc.usgs.gov/data/usgs/water/metadata/ak_precip.html (accessed on 18 March 2017).
- Post, A. Distribution of surging glaciers in western North America. J. Glaciol. 1969, 8, 229–240. [Google Scholar] [CrossRef]
- Meier, M.F.; Post, A. What are glacier surges? Can. J. Earth. Sci. 1969, 6, 807–817. [Google Scholar] [CrossRef]
- Clarke, T.S. Glacier dynamics in the Susitna River basin, Alaska, U.S.A. J. Glaciol. 1991, 37, 97–106. [Google Scholar] [CrossRef]
- Herreid, S.; Truffer, M. Automated detection of unstable glacier flow and a spectrum of speed-up behavior in the Alaska Range. J. Geophys. Res. Earth. Surf. 2016, 121, 64–81. [Google Scholar] [CrossRef]
- Kienholz, C.; Herreid, S.; Rich, J.L.; Arendt, A.A.; Hock, R.; Burgess, E.W. Derivation and analysis of a complete modern-date glacier inventory for Alaska and northwest Canada. J. Glaciol. 2015, 61, 403–420. [Google Scholar] [CrossRef]
- Pfeffer, W.T.; Arendt, A.A.; Bliss, A.; Bolch, T.; Cogley, J.G.; Gardner, A.S.; Hagen, J.-O.; Hock, R.; Kaser, G.; Kienholz, C.; et al. The Randolph Glacier inventory: A globally complete inventory of glaciers. J. Glaciol. 2014, 60, 537–552. [Google Scholar] [CrossRef]
- Manley, W.F. Geospatial inventory and analysis of glaciers: A case study for the Eastern Alaska range. In Satellite Image Atlas of Glaciers of the World: Alaska; Unites States Government Printing Office: Washington, DC, USA, 2008. [Google Scholar]
- Kienholz, C.; Hock, R.; Truffer, M.; Arendt, A.A.; Arko, S. Geodetic mass balance of surge-type Black Rapids Glacier, Alaska, 1980–2001–2010, including role of rockslide deposition and earthquake displacement. J. Geophys. Res. Earth Surf. 2016, 121, 2358–2380. [Google Scholar] [CrossRef]
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef]
- Huss, M. Density assumptions for converting geodetic glacier volume change to mass change. Cryosphere 2013, 7, 877–887. [Google Scholar] [CrossRef]
- Chinn, T.J.H. Glacier fluctuations in the Southern Alps of New Zealand determined from SNOWLINE elevations. Arct. Antarct. Alp Res. 1995, 27, 187–198. [Google Scholar] [CrossRef]
- Chinn, T.J.H.; Salinger, M.J. New Zealand Glacier Snowline Survey. Available online: https://sirgnz.files.wordpress.com/2014/09/snowline-survey-1999-chinn.pdf (accessed on 18 March 2017).
- Wu, Y.; He, J.; Guo, Z.; Chen, A. Limitations in identifying the equilibrium-line altitude from the optical remote-sensing derived snowline in the Tien Shan, China. J. Glaciol. 2014, 60, 1093–1100. [Google Scholar] [CrossRef]
- Ziemen, F.A.; Hock, R.; Aschwanden, A.; Khroulev, C.; Kienholz, C.; Melkonian, A.K.; Zhang, J. Modeling the evolution of the Juneau Icefield between 1971 and 2100 using the Parallel Ice Sheet Model (PISM). J. Glaciol. 2016, 62, 199–214. [Google Scholar] [CrossRef]
- Geographic Information Network of Alaska 2012. Alaska IfSAR Digital Elevation Model (DEM) Data: Alaska IfSAR DEM Data hosted by GINA. Available online: http://ifsar.gina.alaska.edu (accessed on 17 December 2016).
- Toutin, T. 3D Topographic mapping with ASTER Stereo Data in Rugged Topography. IEEE Trans Geosci Remote Sens 2002, 40, 2241–2247. [Google Scholar] [CrossRef]
- Mercer, B. Combining LIDAR and IfSAR: What can you expect? Procceedings of the Photogrammetric Week, Stuttgart, Germany, 5–9 September 2001. [Google Scholar]
- Wingham, D.; Shepherd, A.; Muir, A.; Marshall, G. Mass balance of the Antarctic ice sheet. Philos. Trans. R. Soc. Lond. A 2006, 364, 1627–1635. [Google Scholar] [CrossRef] [PubMed]
- Ridley, J.K.; Partington, K.C. A model of satellite radar altimeter return from ice sheets. Int. J. Remote Sens. 2007, 9, 601–624. [Google Scholar] [CrossRef]
- Zemp, M.; Thibert, E.; Huss, M.; Stumm, D.; Rolstad Denby, C.; Nuth, C.; Nussbaumer, S.U.; Moholdt, G.; Mercer, A.; Mayer, C.; et al. Reanalysing glacier mass balance measurement series. Cryosphere 2013, 7, 1227–1245. [Google Scholar] [CrossRef]
- Ruiz, L.; Berthier, E.; Viale, M.; Pitte, P.; Masiokas, M. Recent geodetic mass balance of Monte Tronador glaciers, North Patagonian Andes. Cryosphere Discuss. 2017, 11. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Widmann, M.; Dymnikov, V.P.; Wallace, J.M.; Bladé, I. The effective number of spatial degrees of freedom of a time-varying field. J. Climate 1999, 12, 1990–2009. [Google Scholar] [CrossRef]
- Schiefer, E.; Menounos, B.; Wheate, R. Recent volume loss of British Columbian glaciers, Canada. Geophys. Res. Lett. 2007, 34, 1–6. [Google Scholar] [CrossRef]
- DeBeer, C.M.; Sharp, M.J. Recent changes in glacier area and volume within the southern Canadian Cordillera. Ann. Glaciol. 2007, 46, 215–221. [Google Scholar] [CrossRef]
- Harrison, W.D.; Echelmayer, K.A.; Chacho, E.F.; Raymond, C.F.; Benedict, R.J. The 1987-88 surge of West Fork Glacier, Susitna Basin, Alaska, U.S.A. J. Glaciol. 1994, 40, 241–254. [Google Scholar] [CrossRef]
- Kirkbride, M.P. The temporal significance of transitions from melting to calving termini at glaciers in the central Southern Alps of New Zealand. Holocene 1993, 3, 232–240. [Google Scholar] [CrossRef]
- Sugiyama, S.; Minowa, M.; Sakakibara, D.; Skvarca, P.; Sawagaki, T.; Ohashi, Y.; Naito, N.; Chikita, K. Thermal structure of proglacial lakes in Patagonia. J. Geophys. Res. Earth Surf. 2016, 121, 2270–2286. [Google Scholar] [CrossRef]
- Larsen, C.F.; Motyka, R.J.; Arendt, A.A.; Echelmeyer, K.A.; Geissler, P.E. Glacier changes in southeast Alaska and northwest British Columbia and contribution to sea level rise. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Clarke, T.S.; Johnson, D.; Harrison, W.D. Some Aspects of Glacier Hydrology in the Upper Susitna and Maclaren River Basins, Alaska. Available online: http://www.arlis.org/docs/vol1/Susitna/41/APA4159.pdf (accessed on 18 March 2017).
- Arendt, A.A.; Luthcke, S.; Gardner, A.; O’Neel, S.R.; Hill, D.; Moholdt, G.; Abdalati, W. Analysis of a GRACE global mascon solution for Gulf of Alaska glaciers. J. Glaciol. 2013, 59, 913–924. [Google Scholar] [CrossRef]
- Dyurgerov, M.B.; Meier, M.F.; Bahr, D.B. A new index of glacier area change: A tool for glacier monitoring. J. Glaciol. 2009, 55, 710–716. [Google Scholar] [CrossRef]
- Shugar, D.H.; Rabus, B.T.; Clague, J.J. Elevation changes (1949–1995) of Black Rapids Glacier, Alaska, derived from a multi-baseline InSAR DEM and historical maps. J. Glaciol. 2010, 56, 625–634. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y.; Kääb, A. Region-wide glacier mass balances over the Pamir-Karakoram-Himalaya during 1999–2011. Cryosphere 2013, 7, 1263–1286. [Google Scholar] [CrossRef]
- Arendt, A.A.; Walsh, J.E.; Harrison, W.D. Changes of glaciers and climate in northwestern North America during the late twentieth century. J. Climate 2009, 22, 4117–4134. [Google Scholar] [CrossRef]
| Data | Spatial Resolution | Date | Product | Source |
|---|---|---|---|---|
| Landsat 5–8 | 30 m | 1999–2015 | ELA; AAR | NASA Landsat Program |
| ASTER DEM 1; | 30 m | 9 August 2005 | dh | NASA Land Processes Distributed Active Archive Center (LP DAAC) |
| National Elevation Dataset (NED) | 40 m | ~1951 | dh | USGS |
| IfSAR DEM | 30 m | 19/20 June 2010 | dh | Intermap Technologies |
| Topographic map quadrangles 2: | - | ~1951 | Outlines | USGS |
| Randolph Glacier Inventory v.5.0 | - | 2010 | Outlines | [20] |
| Area | Area change | Terminus | ||||
|---|---|---|---|---|---|---|
| Glacier | 1951 [km²] | 2010 [km²] | [km²] | [%] | 1951 [m a.s.l.] | 2010 [m a.s.l.] |
| West Fork | 268 | 233 | −35 ± 4 | −13 ± 1 | 839 | 844 |
| Susitna | 244 | 220 | −24 ± 3 | −10 ± 1 | 815 | 822 |
| East Fork | 46 | 44 | −2 ± 0 | −4 ± 0 | 884 | 884 |
| MacLaren | 59 | 56 | −3 ± 0 | −5 ± 0 | 940 | 942 |
| Eureka | 39 | 34 | −5 ± 1 | −13 ± 3 | 1115 | |
| Others | 138 | 81 | −58 ± 7 | −42 ± 5 | − | − |
| All | 796 | 668 | −128 ± 15 | −16 ± 2 | − | − |
| 1951–2005 | 2005–2010 | 1951–2010 | ||||
|---|---|---|---|---|---|---|
| Glacier | dh/dt [m yr−1] | dM/dt [Mt yr−1] | dh/dt [m yr−1] | dM/dt [Mt yr−1] | dh/dt [m yr−1] | dM/dt [Mt yr−1] |
| West Fork | −0.70 ± 0.12 | −0.15 ± 0.03 | −1.61 ± 0.43 | −0.32 ± 0.10 | −0.76 ± 0.13 | −0.16 ± 0.03 |
| Susitna | −0.22 ± 0.13 | −0.05 ± 0.03 | −0.91 ± 0.48 | −0.17 ± 0.12 | −0.30 ± 0.13 | −0.07 ± 0.03 |
| East Fork | −0.23 ± 0.28 | −0.01 ± 0.01 | −1.64 ± 1.02 | −0.06 ± 0.04 | −0.44 ± 0.18 | −0.02 ± 0.01 |
| MacLaren | −0.34 ± 0.24 | −0.02 ± 0.01 | −0.84 ± 0.90 | −0.04 ± 0.05 | −0.40 ± 0.17 | −0.02 ± 0.01 |
| Eureka | − | − | − | − | −0.34 ± 0.18 | −0.01 ± 0.0 |
| Others | −0.23 ± 0.16 | −0.03 ± 0.02 | −0.96 ± 0.59 | −0.06 ± 0.07 | −0.48 ± 0.14 | −0.04 ± 0.02 |
| All | −0.41 ± 0.07 | −0.24 ± 0.05 | −1.20 ± 0.25 | −0.75 ± 0.17 | −0.48 ± 0.09 | −0.34 ± 0.05 |
| Glacier | ELA [m a.s.l.] | Max ELA [m a.s.l.] | Min ELA [m a.s.l.] | EELA [m .a.s.l.] | N | AAR [%] |
|---|---|---|---|---|---|---|
| West Fork | 1714 ± 88 | 1885 ± 111 (2004) | 1504 ± 123 (2006) | 92 | 13 | 46 ± 9 |
| Susitna | 1805 ± 93 | 1965 ± 100 (2004) | 1579 ± 71 (2006) | 90 | 14 | 53 ± 8 |
| East Fork | 1799 ± 91 | 1941 ± 128 (2004) | 1533 ± 81 (2006) | 95 | 12 | 63 ± 8 |
| MacLaren | 1672 ± 62 | 1872 ± 89 (2010) | 1332 ± 25 (2006) | 62 | 13 | 60 ± 9 |
| Eureka | 1734 ± 82 | 1869 ± 71 (2010) | 1425 ± 78 (2006) | 76 | 12 | 57 ± 11 |
| All | 1745 ± 88 | 1885 ± 95 (2004) | 1425 ± 74 (2006) | 81 | − | 56 ± 11 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wastlhuber, R.; Hock, R.; Kienholz, C.; Braun, M. Glacier Changes in the Susitna Basin, Alaska, USA, (1951–2015) using GIS and Remote Sensing Methods. Remote Sens. 2017, 9, 478. https://doi.org/10.3390/rs9050478
Wastlhuber R, Hock R, Kienholz C, Braun M. Glacier Changes in the Susitna Basin, Alaska, USA, (1951–2015) using GIS and Remote Sensing Methods. Remote Sensing. 2017; 9(5):478. https://doi.org/10.3390/rs9050478
Chicago/Turabian StyleWastlhuber, Roland, Regine Hock, Christian Kienholz, and Matthias Braun. 2017. "Glacier Changes in the Susitna Basin, Alaska, USA, (1951–2015) using GIS and Remote Sensing Methods" Remote Sensing 9, no. 5: 478. https://doi.org/10.3390/rs9050478
APA StyleWastlhuber, R., Hock, R., Kienholz, C., & Braun, M. (2017). Glacier Changes in the Susitna Basin, Alaska, USA, (1951–2015) using GIS and Remote Sensing Methods. Remote Sensing, 9(5), 478. https://doi.org/10.3390/rs9050478