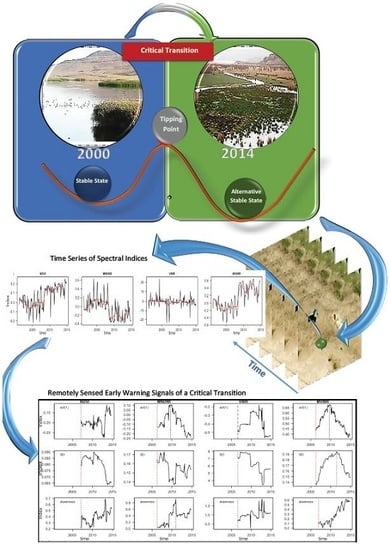
Remotely-Sensed Early Warning Signals of a Critical Transition in a Wetland Ecosystem
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Remote Sensing Data
2.2.1. MODIS Data
2.2.2. Spectral Indices
2.3. Leading Indicators for Critical Transition
2.3.1. Metric-Based Indicators
2.3.2. Model-Based Indicators
3. Results
3.1. Detecting Critical Transition
3.1.1. Metric-Based Indicators
3.1.2. Model-Based Indicators
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; Van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-warning signals for critical transitions. Nature 2009, 461, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Bestelmeyer, B.T.; Ellison, A.M.; Fraser, W.R.; Gorman, K.B.; Holbrook, S.J.; Laney, C.M.; Ohman, M.D.; Peters, D.P.; Pillsbury, F.C.; Rassweiler, A. Analysis of abrupt transitions in ecological systems. Ecosphere 2011, 2, art129. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [CrossRef] [PubMed]
- Brock, W.A.; Carpenter, S.R. Early warnings of regime shift when the ecosystem structure is unknown. PLoS ONE 2012, 7, e45586. [Google Scholar] [CrossRef] [PubMed]
- Dakos, V.; Carpenter, S.R.; Brock, W.A.; Ellison, A.M.; Guttal, V.; Ives, A.R.; Kefi, S.; Livina, V.; Seekell, D.A.; van Nes, E.H. Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS ONE 2012, 7, e41010. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, M.; Carpenter, S.R.; Lenton, T.M.; Bascompte, J.; Brock, W.; Dakos, V.; Van De Koppel, J.; Van De Leemput, I.A.; Levin, S.A.; Van Nes, E.H. Anticipating critical transitions. Science 2012, 338, 344–348. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, M. Critical Transitions in Nature and Society; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Carpenter, S.; Brock, W.; Cole, J.; Kitchell, J.; Pace, M. Leading indicators of trophic cascades. Ecol. Lett. 2008, 11, 128–138. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, M. Complex systems: Foreseeing tipping points. Nature 2010, 467, 411–412. [Google Scholar] [CrossRef] [PubMed]
- Carpenter, S.; Brock, W. Rising variance: A leading indicator of ecological transition. Ecol. Lett. 2006, 9, 311–318. [Google Scholar] [CrossRef] [PubMed]
- Dakos, V.; Scheffer, M.; van Nes, E.H.; Brovkin, V.; Petoukhov, V.; Held, H. Slowing down as an early warning signal for abrupt climate change. Proc. Natl. Acad. Sci. USA 2008, 105, 14308–14312. [Google Scholar] [CrossRef] [PubMed]
- Carpenter, S.R.; Cole, J.J.; Pace, M.L.; Batt, R.; Brock, W.; Cline, T.; Coloso, J.; Hodgson, J.R.; Kitchell, J.F.; Seekell, D.A. Early warnings of regime shifts: A whole-ecosystem experiment. Science 2011, 332, 1079–1082. [Google Scholar] [CrossRef] [PubMed]
- Vanderploeg, H.A.; Pothoven, S.A.; Fahnenstiel, G.L.; Cavaletto, J.F.; Liebig, J.R.; Stow, C.A.; Nalepa, T.F.; Madenjian, C.P.; Bunnell, D.B. Seasonal zooplankton dynamics in lake michigan: Disentangling impacts of resource limitation, ecosystem engineering, and predation during a critical ecosystem transition. J. Great Lakes Res. 2012, 38, 336–352. [Google Scholar] [CrossRef]
- Donangelo, R.; Fort, H.; Dakos, V.; Scheffer, M.; Van Nes, E.H. Early warnings for catastrophic shifts in ecosystems: Comparison between spatial and temporal indicators. Int. J. Bifurc. Chaos 2010, 20, 315–321. [Google Scholar] [CrossRef]
- Lade, S.J.; Gross, T. Early warning signals for critical transitions: A generalized modeling approach. PLoS Comput. Biol. 2012, 8, e1002360. [Google Scholar] [CrossRef] [PubMed]
- Zoffoli, M.L.; Kandus, P.; Madanes, N.; Calvo, D.H. Seasonal and interannual analysis of wetlands in south america using noaa-avhrr ndvi time series: The case of the parana delta region. Landsc. Ecol. 2008, 23, 833–848. [Google Scholar] [CrossRef]
- Ray, R.; Mandal, S.; Dhara, A. Characterization and mapping of inland wetland: A case study on selected bils on nadia district. Int. J. Sci. Res. Pub. 2012, 2, 12. [Google Scholar]
- Lotfi, A.; Moser, M. Water for Ecosystems; Ministry of Energy: Victoria, BC, Canada, 2005.
- Asem, A.; Mohebbi, F.; Ahmadi, R. Drought in urmia lake, the largest natural habitat of brine shrimp artemia. World Aquacult. 2012, 43, 36–38. [Google Scholar]
- Hoseinpour, M.; Fakheri Fard, A.; Naghili, R. Death of Urmia Lake, a Silent Disaster Investigating causes, results and solutions of Urmia Lake drying. In Proceedings of the 1st International Applied Geological Congress, Mashad, Iran, 26–28 April 2010; pp. 700–704. [Google Scholar]
- AghaKouchak, A.; Norouzi, H.; Madani, K.; Mirchi, A.; Azarderakhsh, M.; Nazemi, A.; Nasrollahi, N.; Farahmand, A.; Mehran, A.; Hasanzadeh, E. Aral sea syndrome desiccates lake urmia: Call for action. J. Great Lakes Res. 2015, 41, 307–311. [Google Scholar] [CrossRef]
- Birkett, C.; Reynolds, C.; Beckley, B.; Doorn, B. From research to operations: The usda global reservoir and lake monitor. In Coastal Altimetry; Springer: New York, NY, USA, 2011; pp. 19–50. [Google Scholar]
- Hassanzadeh, E.; Zarghami, M.; Hassanzadeh, Y. Determining the main factors in declining the urmia lake level by using system dynamics modeling. Water Resour. Manag. 2012, 26, 129–145. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Boston, MA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
- Sutela, T.; Vehanen, T. Effects of water-level regulation on the nearshore fish community in boreal lakes. In Ecological Effects of Water-Level Fluctuations in Lakes; Springer: Heidelberg, Germany, 2008; pp. 13–20. [Google Scholar]
- Brauns, M.; Garcia, X.-F.; Pusch, M.T. Potential effects of water-level fluctuations on littoral invertebrates in lowland lakes. In Ecological Effects of Water-Level Fluctuations in Lakes; Springer: Heidelberg, Germany, 2008; pp. 5–12. [Google Scholar]
- Muneepeerakul, C.P.; Miralles-Wilhelm, F.; Tamea, S.; Rinaldo, A.; Rodriguez-Iturbe, I. Coupled hydrologic and vegetation dynamics in wetland ecosystems. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Daly, E.; Porporato, A.; Rodriguez-Iturbe, I. Ecohydrological significance of the coupled dynamics of photosynthesis, transpiration, and soil water balance. J. Hydrometeorol. 2004, 5, 559–566. [Google Scholar] [CrossRef]
- Coops, H.; Hosper, S.H. Water-level management as a tool for the restoration of shallow lakes in the netherlands. Lake Reserv. Manag. 2002, 18, 293–298. [Google Scholar] [CrossRef]
- Ahmadi, R.; Mohebbi, F.; Hagigi, P.; Esmailly, L.; Salmanzadeh, R. Macro-invertebrates in the wetlands of the zarrineh estuary at the south of urmia lake (iran). Int. J. Environ. Res. 2011, 5, 1047–1052. [Google Scholar]
- Stephens, D.W. Changes in lake levels, salinity and the biological community of great salt lake (utah, USA), 1847–1987. In Saline Lakes; Springer: Berlin, Germany, 1990; pp. 139–146. [Google Scholar]
- Ministry of Agriculture-Jahad. National Map of Land Use; Ministry of Agriculture-Jahad: Tehran, Iran, 2001.
- Petus, C.; Lewis, M.; White, D. Monitoring temporal dynamics of great artesian basin wetland vegetation, australia, using modis ndvi. Ecol. Indicat. 2013, 34, 41–52. [Google Scholar] [CrossRef]
- Mao, D.; Wang, Z.; Luo, L.; Ren, C. Integrating avhrr and modis data to monitor ndvi changes and their relationships with climatic parameters in northeast china. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 528–536. [Google Scholar] [CrossRef]
- Funderburk, S.L. Habitat Requirements for Chesapeake Bay Living Resources; Chesapeake Research Consortium: Annapolis, MD, USA, 1991. [Google Scholar]
- Yuan, L.; Zhang, L. Identification of the spectral characteristics of submerged plant vallisneria spiralis. Acta Ecol. Sin. 2006, 26, 1005–1010. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Rugege, D. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: A review. Wetl. Ecol. Manag. 2010, 18, 281–296. [Google Scholar] [CrossRef]
- Rouse, J., Jr.; Haas, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the Great Plains with ERTS. In Goddard Space Flight Center 3d ERTS-1 Symp., Vol. 1, Sect. A; NASA: College Station, TX, USA, 1974; pp. 309–317. [Google Scholar]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Li, W.; Chen, Q.; Cai, D.; Li, R. Determination of an appropriate ecological hydrograph for a rare fish species using an improved fish habitat suitability model introducing landscape ecology index. Ecol. Model. 2015, 311, 31–38. [Google Scholar] [CrossRef]
- Mozumder, C.; Tripathi, N.; Tipdecho, T. Ecosystem evaluation (1989–2012) of ramsar wetland deepor beel using satellite-derived indices. Environ. Monit. Assess. 2014, 186, 7909–7927. [Google Scholar] [CrossRef] [PubMed]
- Rokni, K.; Ahmad, A.; Selamat, A.; Hazini, S. Water feature extraction and change detection using multitemporal landsat imagery. Remote Sens. 2014, 6, 4173–4189. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, C.; Ticehurst, C.; Merrin, L.; Thew, P. An evaluation of MODIS daily and 8-day composite products for floodplain and wetland inundation mapping. Wetlands 2013, 33, 823–835. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of dynamic thresholds for the normalized difference water index. Photogramm. Eng. Remote Sens. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Zhao, B.; Yan, Y.; Guo, H.; He, M.; Gu, Y.; Li, B. Monitoring rapid vegetation succession in estuarine wetland using time series modis-based indicators: An application in the yangtze river delta area. Ecol. Indic. 2009, 9, 346–356. [Google Scholar] [CrossRef]
- Li, W.; Du, Z.; Ling, F.; Zhou, D.; Wang, H.; Gui, Y.; Sun, B.; Zhang, X. A comparison of land surface water mapping using the normalized difference water index from tm, etm+ and ali. Remote Sens. 2013, 5, 5530–5549. [Google Scholar] [CrossRef]
- Dakos, V.; Carpenter, S.R.; van Nes, E.H.; Scheffer, M. Resilience indicators: Prospects and limitations for early warnings of regime shifts. Philos. Trans. R. Soc. B Biol. Sci. 2015, 370, 20130263. [Google Scholar] [CrossRef]
- Dakos, V.; van Nes, E.H.; Donangelo, R.; Fort, H.; Scheffer, M. Spatial correlation as leading indicator of catastrophic shifts. Theor. Ecol. 2010, 3, 163–174. [Google Scholar] [CrossRef]
- Kuehn, C. A mathematical framework for critical transitions: Bifurcations, fast–slow systems and stochastic dynamics. Phys. D Nonlinear Phenom. 2011, 240, 1020–1035. [Google Scholar] [CrossRef]
- Carpenter, S.R.; Kitchell, J.F.; Hodgson, J.R. Cascading trophic interactions and lake productivity. BioScience 1985, 35, 634–639. [Google Scholar] [CrossRef]
- Dai, L.; Vorselen, D.; Korolev, K.S.; Gore, J. Generic indicators for loss of resilience before a tipping point leading to population collapse. Science 2012, 336, 1175–1177. [Google Scholar] [CrossRef] [PubMed]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Naimi, B. RTS: Raster Time Series Analysis. Available online: https://cran.r-project.org/web/packages/rts/index.html (accessed on 4 January 2017).
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology and Chemistry; Perseus publishing: Boulder, CO, USA, 2001. [Google Scholar]
- Wissel, C. A universal law of the characteristic return time near thresholds. Oecologia 1984, 65, 101–107. [Google Scholar] [CrossRef] [PubMed]
- Held, H.; Kleinen, T. Detection of climate system bifurcations by degenerate fingerprinting. Geophys. Res. Lett. 2004, 31, L23207. [Google Scholar] [CrossRef]
- Lenton, T.; Livina, V.; Dakos, V.; Van Nes, E.; Scheffer, M. Early warning of climate tipping points from critical slowing down: Comparing methods to improve robustness. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 1185–1204. [Google Scholar] [CrossRef] [PubMed]
- Kendall, M. Rank Correlation Methods; Oxford University Press: Oxford, UK, 1962. [Google Scholar]
- Bandi, F.M.; Nguyen, T.H. On the functional estimation of jump–diffusion models. J. Econom. 2003, 116, 293–328. [Google Scholar] [CrossRef]
- Carpenter, S.; Brock, W. Early warnings of unknown nonlinear shifts: A nonparametric approach. Ecology 2011, 92, 2196–2201. [Google Scholar] [CrossRef] [PubMed]
- Johannes, M. The statistical and economic role of jumps in continuous-time interest rate models. J. Financ. 2004, 59, 227–260. [Google Scholar] [CrossRef]
- Pace, M.L.; Carpenter, S.R.; Johnson, R.A.; Kurtzweil, J.T. Zooplankton provide early warnings of a regime shift in a whole lake manipulation. Limnol. Oceanogr. 2013, 58, 525–532. [Google Scholar] [CrossRef]
- Seekell, D.A.; Carpenter, S.R.; Cline, T.J.; Pace, M.L. Conditional heteroskedasticity forecasts regime shift in a whole-ecosystem experiment. Ecosystems 2012, 15, 741–747. [Google Scholar] [CrossRef]
- Eslami-Andergoli, L.; Dale, P.; Knight, J.; McCallum, H. Approaching tipping points: A focussed review of indicators and relevance to managing intertidal ecosystems. Wetl. Ecol. Manag. 2015, 23, 791–802. [Google Scholar] [CrossRef]
- Boettiger, C.; Hastings, A. Tipping points: From patterns to predictions. Nature 2013, 493, 157–158. [Google Scholar] [PubMed]
- van Nes, E.H.; Hirota, M.; Holmgren, M.; Scheffer, M. Tipping points in tropical tree cover: Linking theory to data. Glob. Chang. Biol. 2014, 20, 1016–1021. [Google Scholar] [CrossRef] [PubMed]
- Hirota, M.; Holmgren, M.; Van Nes, E.H.; Scheffer, M. Global resilience of tropical forest and savanna to critical transitions. Science 2011, 334, 232–235. [Google Scholar] [CrossRef] [PubMed]
- Filella, I.; Penuelas, J. The red edge position and shape as indicators of plant chlorophyll content, biomass and hydric status. Int. J. Remote Sens. 1994, 15, 1459–1470. [Google Scholar] [CrossRef]
- Dakos, V.; Van Nes, E.H.; D’Odorico, P.; Scheffer, M. Robustness of variance and autocorrelation as indicators of critical slowing down. Ecology 2012, 93, 264–271. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.M.; Kolden, C.A.; Tinkham, W.T.; Talhelm, A.F.; Marshall, J.D.; Hudak, A.T.; Boschetti, L.; Falkowski, M.J.; Greenberg, J.A.; Anderson, J.W. Remote sensing the vulnerability of vegetation in natural terrestrial ecosystems. Remote Sens. Environ. 2014, 154, 322–337. [Google Scholar] [CrossRef]







| Spectral Indices | Indicators | ||
|---|---|---|---|
| Autocorrelation | Standard Deviation | Skewness | |
| NDVI | 0.296 *|−0.293 *** | −0.514 ***|−0.389 *** | 0.439 *|−0.409 *** |
| MNDWI | 0.397 ***|−0.268 *** | −0.782 ***|−0.499 *** | 0.127 ***|0.275 |
| VWR | 0.152|0.019 | −0.523 ***|0.698 *** | 0.145|−0.633 |
| MVWR | 0.850 ***|−0.225 *** | 0.406 ***|0.285 *** | 0.754 ***|−0.025 *** |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alibakhshi, S.; Groen, T.A.; Rautiainen, M.; Naimi, B. Remotely-Sensed Early Warning Signals of a Critical Transition in a Wetland Ecosystem. Remote Sens. 2017, 9, 352. https://doi.org/10.3390/rs9040352
Alibakhshi S, Groen TA, Rautiainen M, Naimi B. Remotely-Sensed Early Warning Signals of a Critical Transition in a Wetland Ecosystem. Remote Sensing. 2017; 9(4):352. https://doi.org/10.3390/rs9040352
Chicago/Turabian StyleAlibakhshi, Sara, Thomas A. Groen, Miina Rautiainen, and Babak Naimi. 2017. "Remotely-Sensed Early Warning Signals of a Critical Transition in a Wetland Ecosystem" Remote Sensing 9, no. 4: 352. https://doi.org/10.3390/rs9040352
APA StyleAlibakhshi, S., Groen, T. A., Rautiainen, M., & Naimi, B. (2017). Remotely-Sensed Early Warning Signals of a Critical Transition in a Wetland Ecosystem. Remote Sensing, 9(4), 352. https://doi.org/10.3390/rs9040352