1. Introduction
Supervised learning algorithms predominate over all other land cover mapping/monitoring techniques that use remote sensing (RS) data. However, the performance of supervised learning algorithms varies as a function of labeled training data properties, such as the sample size and the statistically unbiased and discriminative capabilities of the features extracted from the data [
1]. As monitoring requires multi-temporal images, radiometric differences, atmospheric and illumination conditions, seasonal variations, and variable acquisition geometries can affect supervised techniques, potentially causing a distribution shift in the training data [
2,
3]. Regardless of the cause, any distribution change or domain shift that occurs after learning a classifier can degrade performance.
In the pattern recognition (PR) and RS image classification communities, this challenge is commonly referred to as covariate shift [
4] or sample selection bias [
5]. Many solutions have been proposed to resolve this problem, including image-to-image normalization [
6], absolute and relative image normalization [
7,
8], histogram matching [
9], and a multivariate extension of the univariate matching [
10]. Recently, domain adaptation (DA) techniques, which attempt to mitigate performance the degradation caused by a distribution shift, has attracted increasing attention and is widely considered to provide an efficient solution [
11,
12,
13,
14,
15,
16].
According to the technical literature in PR and machine learning (ML), DA is a special case of transductive transfer learning (TTL). Its goal is to learn a function that predicts the label of a novel test sample in the target domain [
12,
15]. Depending on the availability of the source and the target domain data, the DA problem can result into supervised domain adaptation (SDA), semi-supervised domain adaptation (SSDA), unsupervised domain adaptation (UDA), multisource domain adaptation (MSDA) and heterogeneous domain adaption (HDA) [
14,
15,
16,
17,
18,
19].
Moreover, according to the “knowledge” transferred across domains or tasks, classical approaches to DA can be grouped into parameter adapting, instance transferring, feature representation, and relational knowledge transfer techniques.
Parameter adapting approaches aim to transfer and adapt a classification model and/or its parameters to the target domain; the model and/or parameters are learned from the source domain (SD) [
20]. The seminal work presented by Khosla et al. [
5] and Woodcock et al. [
7], which features parameter adjustment for a maximum-likelihood classifier in a multiple cascade classifier system by retraining, can be categorized into this group.
In instance transferring, the samples from the SD are reweighted [
21] or resampled [
22] for their use in the TD. In the RS community, active learning (AL) has also been applied to address DA problems. For example, AL for DA in the supervised classification RS images is proposed by Persello and Bruzzone [
23] via iteratively labeling and adding to the training set the minimum number of the most informative samples from the target domain, while removing the source-domain samples that do not fit with the distributions of the classes in the TD.
For the third group, feature representation-based adaptation searches for a set of shared and invariant features using feature extraction (FE), feature selection (FS) or manifold alignment to reduce the marginal, conditional and joint distributions between the domains [
16,
24,
25,
26]. Matasci et al. [
14] investigated the semi-supervised transfer component analysis (SSTCA) [
27] for both hyperspectral and multispectral high resolution image classification, whereas Samat et al. [
16] analyzed a geodesic Gaussian flow kernel based support vector machine (GFKSVM) in the context of hyperspectral image classification, which adopts several unsupervised linear and nonlinear subspace feature transfer techniques.
Finally, relational knowledge transfer techniques address the problem of how to leverage the knowledge acquired in SD to improve accuracy and learning speed in a related TD [
28].
Among these four groups, it is easy to recognize the importance of RS image classification of adaptation strategies based on feature representation. However, most previous studies have assumed that data from different domains are represented by the same types of features with the same dimensions. Thus, these techniques cannot handle the problem of data from source and target domains represented by heterogeneous features with different dimensions [
18,
29]. One example of this scenario is land cover updating using current RS data; each time, there are different features with finer spatial resolution and more spectral bands (e.g., Landsat 8 OLI with nine spectral bands at 15–30 m spatial resolution, and Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) with 224 spectral bands at 20 m spatial resolution), when the training data are only available at coarser spatial and spectral resolutions (e.g., MSS with four spectral bands and 60 m spatial resolution).
One of the simplest feature-based DA approaches is the feature augmentation proposed in [
17], whose extended versions, called heterogeneous feature augmentation (HFA) and semi-supervised HFA (SHFA), were recently proposed in [
18]. Versions that consider the intermediate domains as being manifold-based were proposed in [
30,
31]. However, none of these approaches have been considered in RS image classification.
Finding a joint feature representation between the source and target domains requires FS [
12,
19] or FE [
16] to select the most effective feature set. To accomplish this aim, canonical correlation analysis (CCA), which aims to maximize the correlation between two variable sets (in this case, the different domains) could be a very effective technique. Indeed, CCA and kernel CCA (KCCA) have already been applied with promising results in object recognition and text categorization [
29], action recognition and image-to-text classification [
32]. However, existing joint optimization frameworks such as [
32] are limited to scenarios in which the labeled data from both domains are available. This is not the case in many practical situations. To solve this problem, CTSVM was proposed in [
29], incorporating the DA ability into the classifier design for a cross-domain recognition scenario of labeled data that is available only in the SD. However, the CTSVM might fail to balance the possible mismatches between the heterogeneous domains.
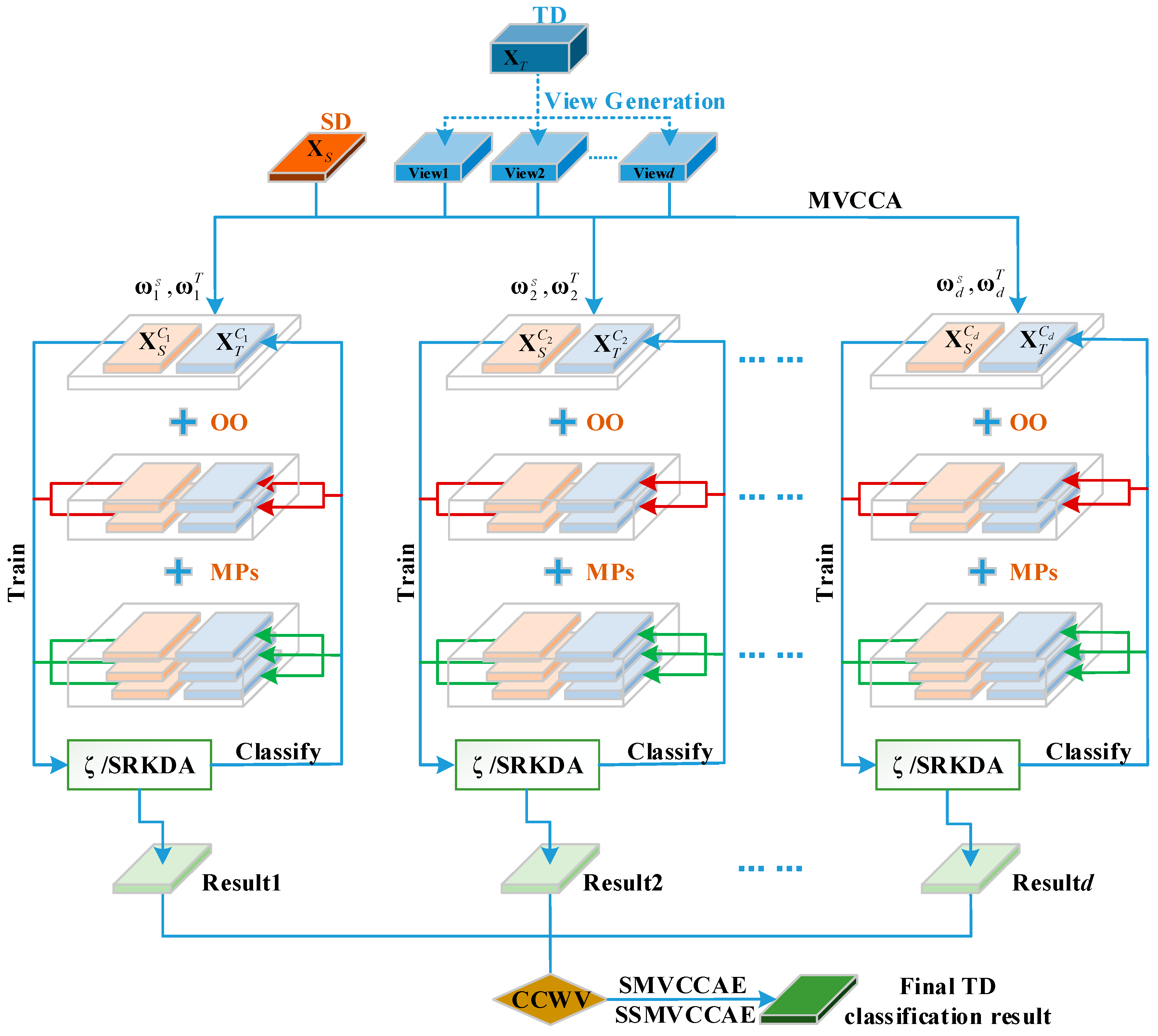
One solution might be to multi-view learning (MVL), a procedure that implies the splitting of high-dimensional data into multiple “views” [
33,
34]. If multiple views are available, then multiple classification results must be reconciled, and this step is efficiently performed using Ensemble Learning (EL) [
35,
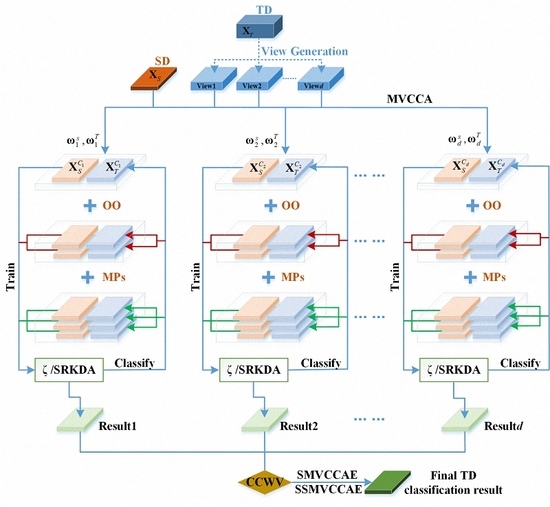
36]. Accordingly, this work introduces an EL technique based on supervised multi-view CCA, which is called supervised multi-view canonical correlation analysis ensemble (SMVCCAE), and we prove its effectiveness for DA (and specifically heterogeneous DA) problems.
Additionally, in real applications, it is typical to experience situations in which there are very limited or even no labeled samples available. In this case, a semi-supervised learning (SSL) technique (e.g., [
37]), which uses of unlabeled data to improve performance using a small amount of labeled data from the same domain, might be an appropriate solution. As a matter of fact, many SSDAs have been proposed. However, most existing studies, such as asymmetric kernel transforms (AKT) [
38], domain-dependent regularization (DDR) [
32], TCA, SSTCA [
14,
27], and co-regularization based SSDA [
39], were designed for homogeneous DA. Very recently, Li et al. [
18] proposed a semi-supervised heterogeneous DA by convex optimization of standard multiple kernel learning (MKL) with augmented features. Unfortunately, this optimization is quite challenging in real-world applications. This work instead proposes a semi-supervised version of the above-mentioned multi-view canonical correlation analysis ensemble (called SSMVCCAE), incorporating multiple speed-up spectral regression kernel discriminant analysis (SRKDA) [
40] into the original supervised algorithm.
2. Related Work
2.1. Notation for HDA
According to the technical literature, feature-based approaches to HDA can be grouped into the following three clusters, depending on the features used to connect the target and the SD:
- (1)
If data from the source and target domains share the same features [
41,
42,
43], then latent semantic analysis (LSA) [
44], probabilistic latent semantic analysis (pLSA) [
45], and risk minimization techniques [
46] may be used.
- (2)
If additional features are needed, “feature augmentation” approaches have been proposed, including the method in [
37], HFA and SHFA [
18], manifold alignment [
31], sampling geodesic flow (SGF) [
47], and geodesic flow kernel (GFK) [
16,
30]. All of these approaches introduce a common subspace for the source and target data so that heterogeneous features from both domains.
- (3)
If features are adapted across domains through learning transformations, feature transformation-based approaches are considered. This group of approaches includes the HSMap [
48], the sparse heterogeneous feature representation (SHFR) [
49], and the correlation transfer SVM (CTSVM) [
29]. The algorithms that we propose fit into this group.
Although all of the approaches reviewed above have achieved promising results, they also have some limitations of all the approaches reviewed above. For example, the co-occurrence features assumption used in [
41,
42,
43] may not hold in applications such as object recognition, which uses only visual features [
32]. For the feature augmentation based approaches discussed in [
18,
30,
31], the domain-specific copy process always requires large storage space, and the kernel version requires even more space and computational complexity because of the parameter tuning. Finally, for the feature transformation based approaches proposed in [
29,
32,
48], they do not optimize the objective function of a discriminative classifier directly, and the computational complexity is highly dependent on the total number of samples or features used for adaptation [
12,
19].
In this work, we assume that there is only one SD () and one TD (). We also define and as the feature spaces in the two domains, with the corresponding marginal distributions and for and , respectively. The parameters and represent the size of and , and are the sample sizes for and , and we have , . The labeled training samples from the SD are denoted by , and they refer to c classes. Furthermore, let us consider as “task” Y the task to assign to each element of a set a label selected in a label space by means of a predictive function , so that .
In general, if the feature sets belong to different domains, then either or , or both. Similarly, the condition implies that either (, ) or , or both. In this scenario, a “domain adaptation algorithm” is an algorithm that aims to improve the learning of the predictive function in the TD using the knowledge available in the SD and in the learning task , when either or . Moreover, in heterogeneous problems, the additional condition holds.
2.2. Canonical Correlation Analysis
Let us now assume that
for the feature sets (called “views” here) in the source and target domains. The CCA is the procedure for obtaining the transformation matrices
and
which maximize the correlation coefficient between the two sets [
50]:
where
,
,
,
, and “
” means the matrix transpose. In practice,
can be obtained by a generalized eigenvalue decomposition problem:
where
is a constraint factor. Once
is obtained,
can be obtained by
. By adding the regularization terms
and into
and
to avoid overfitting and singularity problems, Equation (2) becomes:
As a result, the source and target view data can be transformed into correlation subspaces by:
Note that one can derive more than one pair of transformation matrices and , where is the dimension of the resulting CCA subspace. Once the correlation subspaces and spanned by and are derived, test data in the target view can be directly labeled by any model that is trained using the source features .
2.3. Fusion Methods
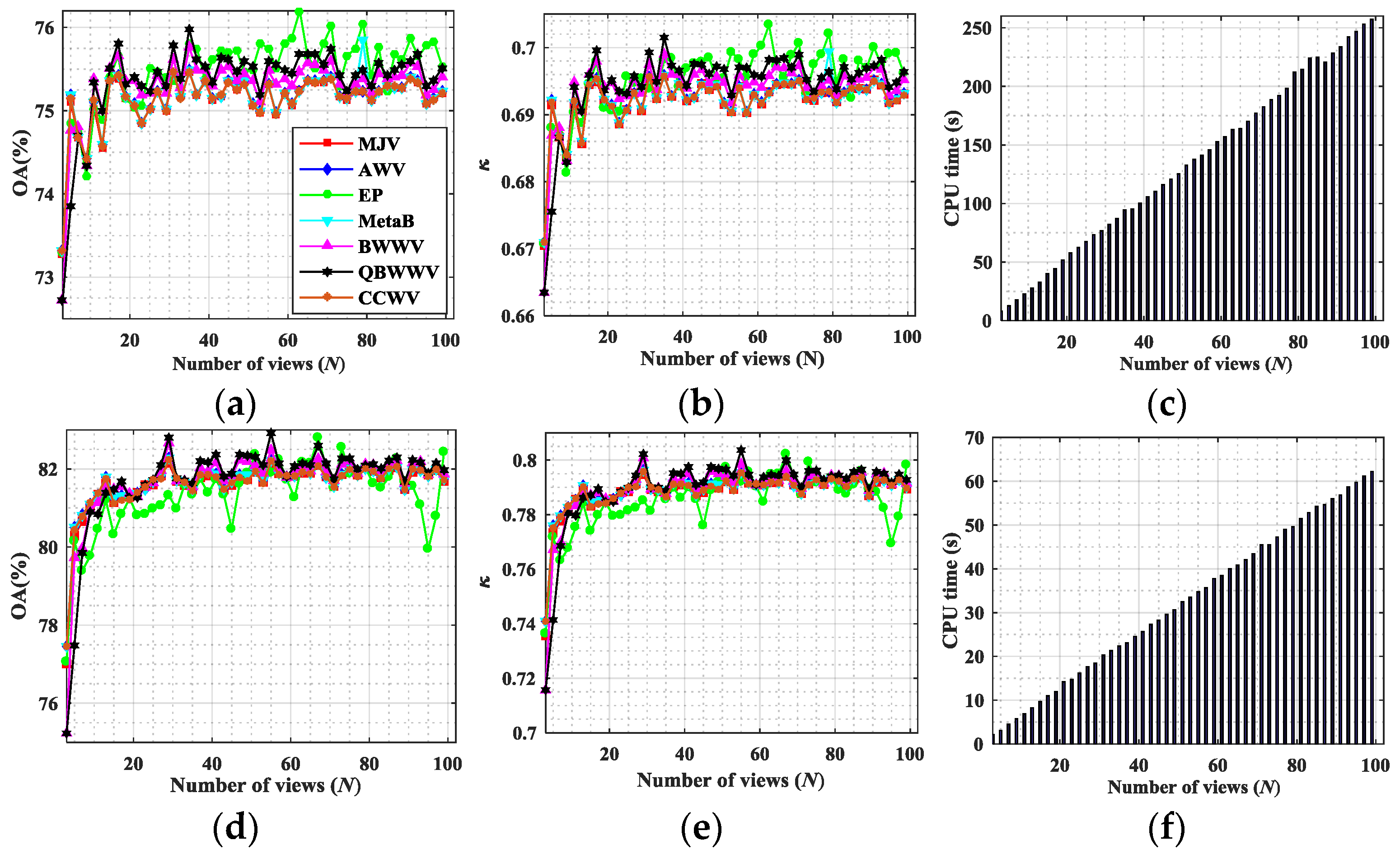
If multiple “views” are available, then for each view, a label can be associated with each pixel used, for instance, CCA. If multiple labels are present, then they must be fused to obtain a single value using a so-called decision-based fusion procedure. Decision-based fusion aims to provide the final classification label for a pixel by combining the labels obtained, in this case, by multiple view analysis. This usually is obtained using two classes of procedures: weighted voting methods and meta-learning methods [
51].
For weighted voting, the labels are combined using the weights assigned to each result. Many variants have been proposed in past decades. For the sake of comparison and because we must consider these options to evaluate the performance of the canonical correlation weighted voting (CCWV) scheme proposed in this paper, here, we consider only the following state-of-the-art techniques:
Accuracy weighted voting (AWV), in which the weight of each member is set proportionally to its accuracy performance on a validation set [
51]:
where
ai is a performance evaluation of the
i-th classifier on a validation set.
Best–worst weighted voting (BWWV), in which the best and the worst classifiers are given a weight of 1 or 0, respectively [
51], and for the ones the weights are compute according to:
where
ei is the error of the
i-th classifier on a validation set.
Quadratic best–worst weighted voting (QBWWV), that computes the intermediate weights between 0 and 1 via squaring the above-mentioned BWWV:
6. Conclusions
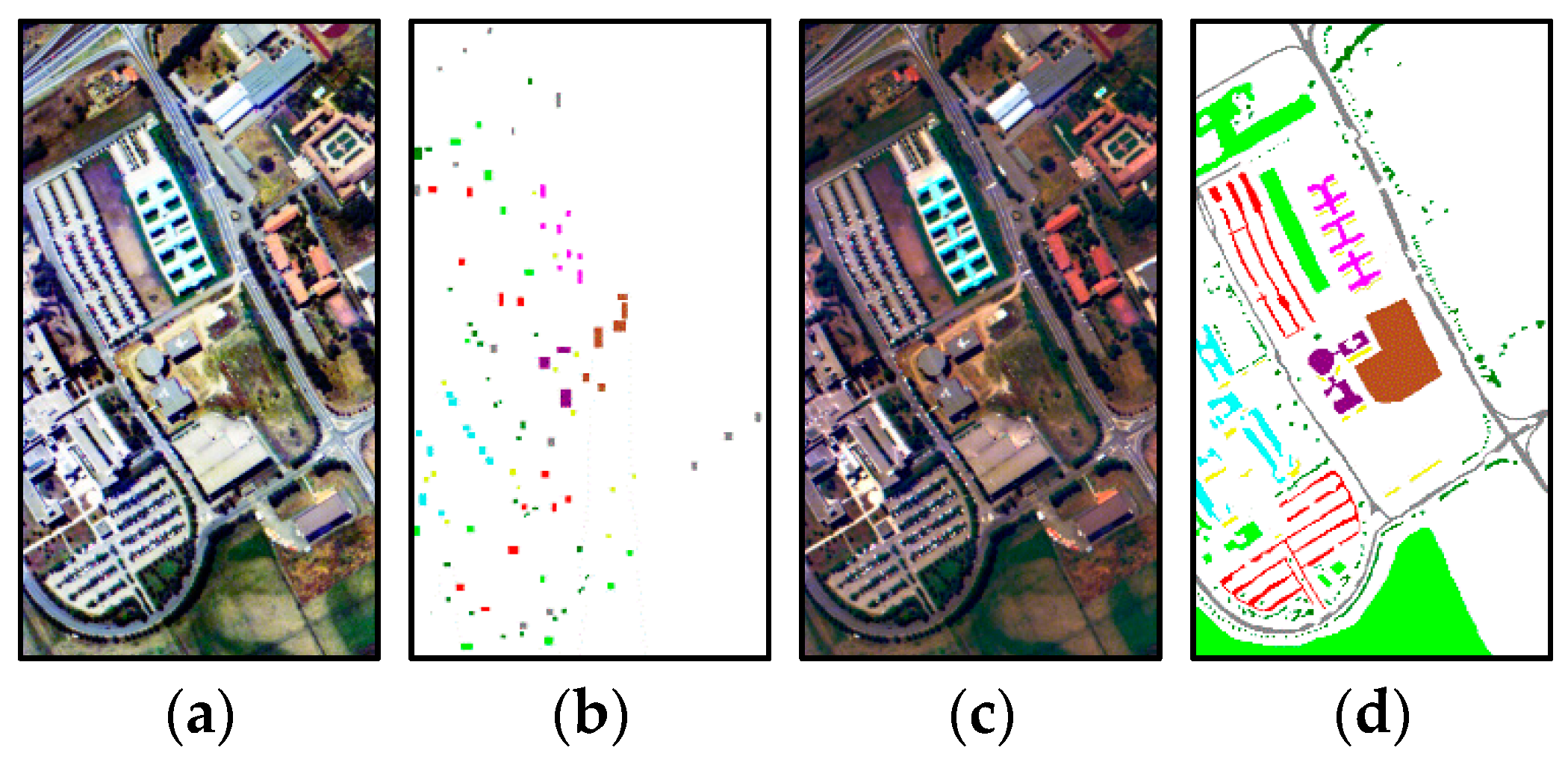
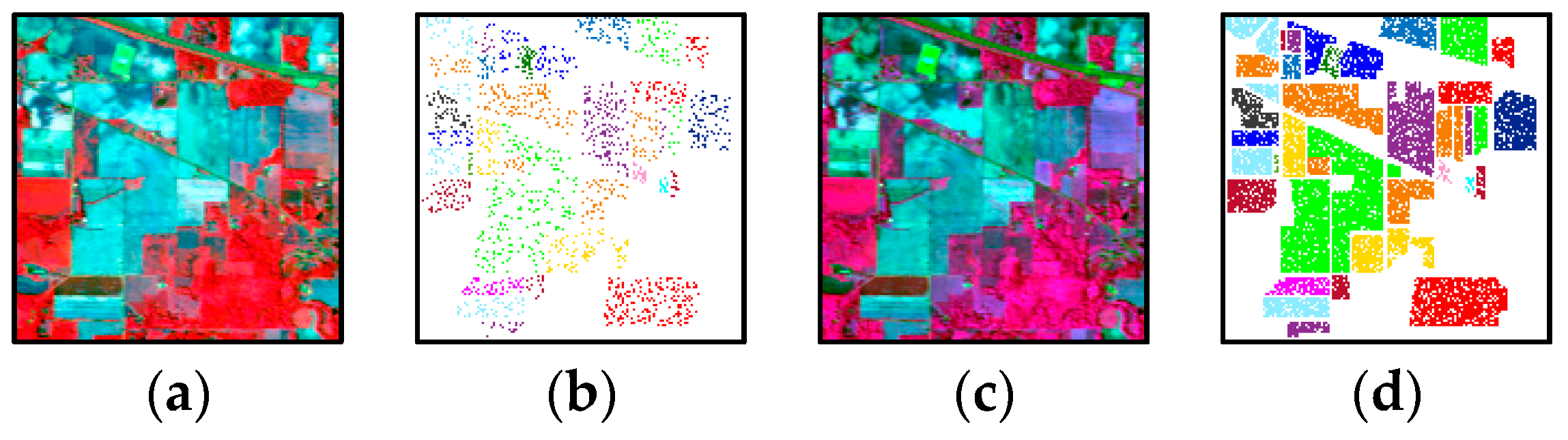
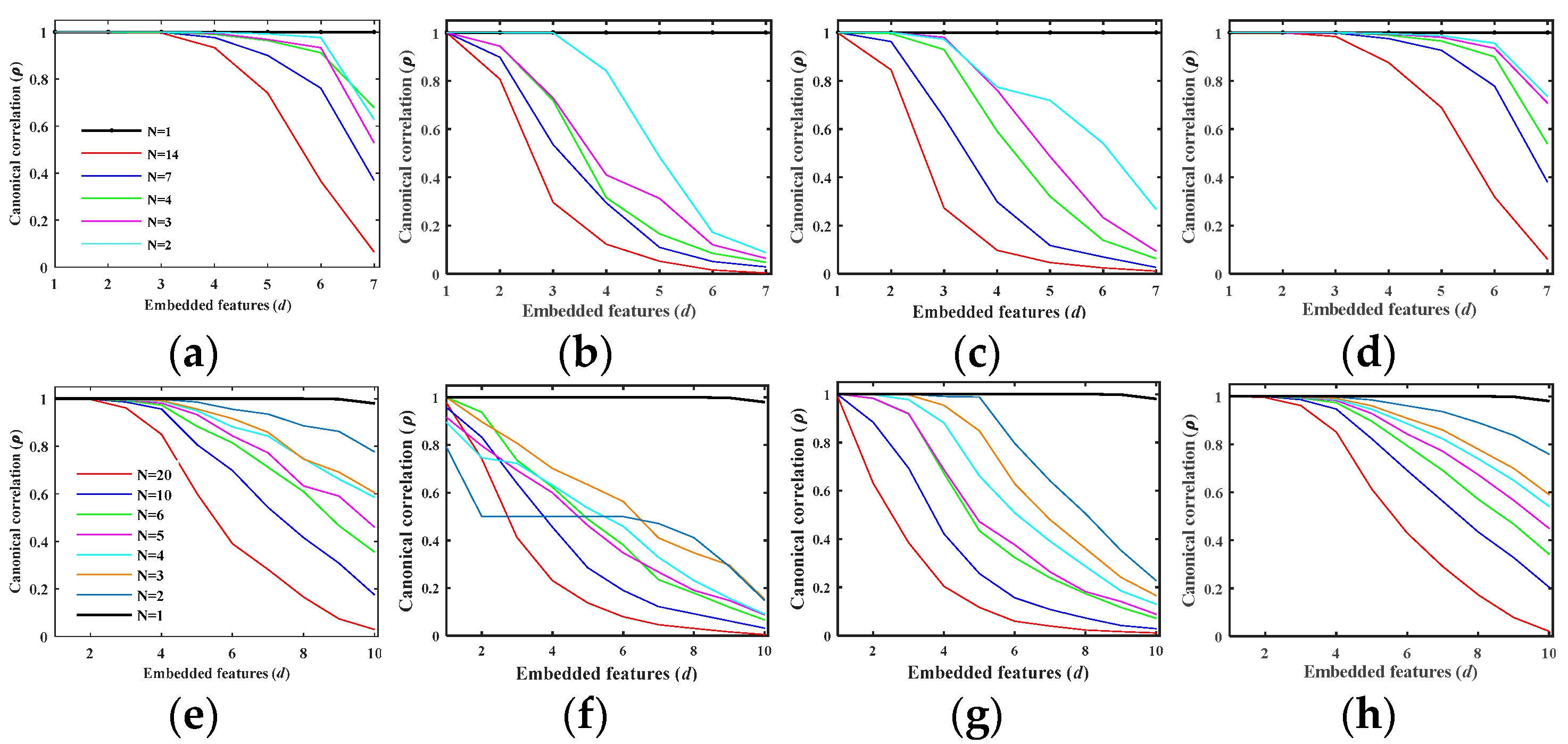
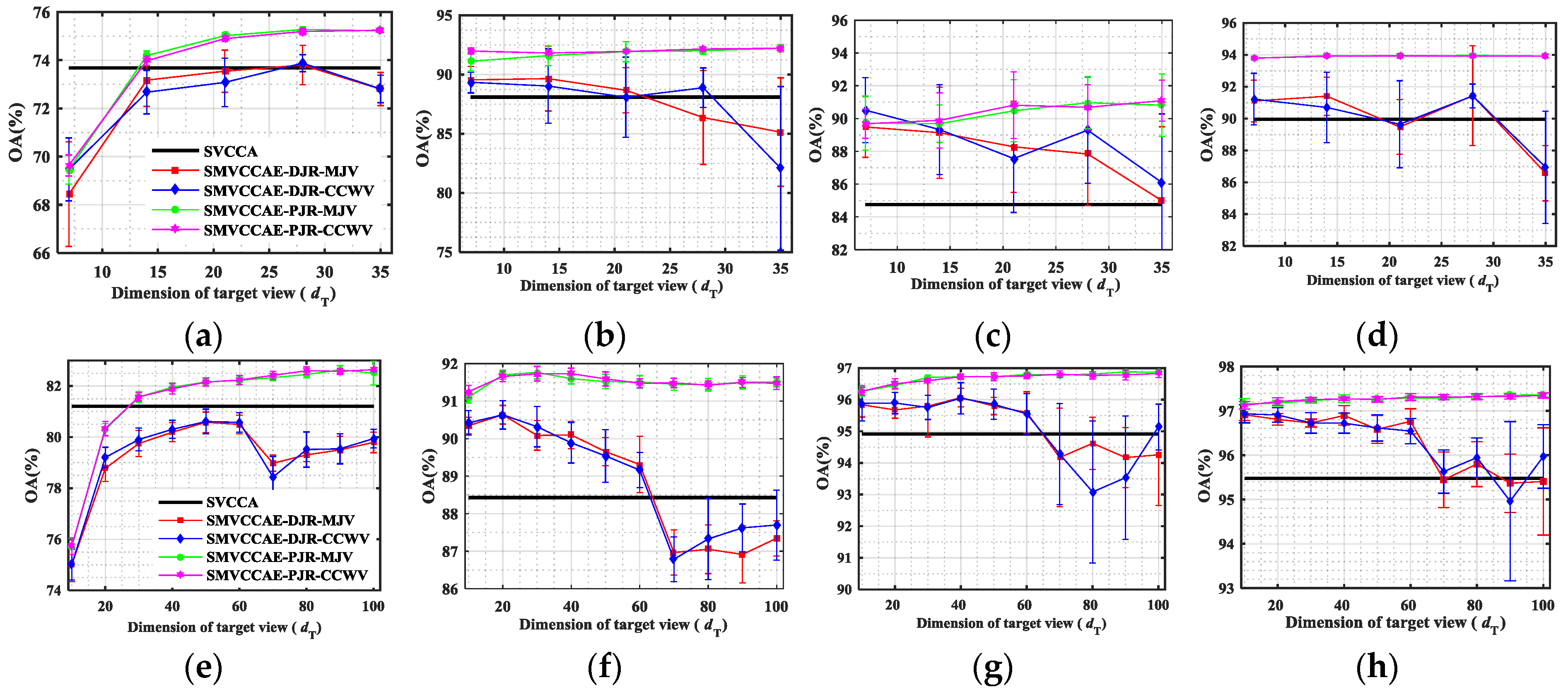
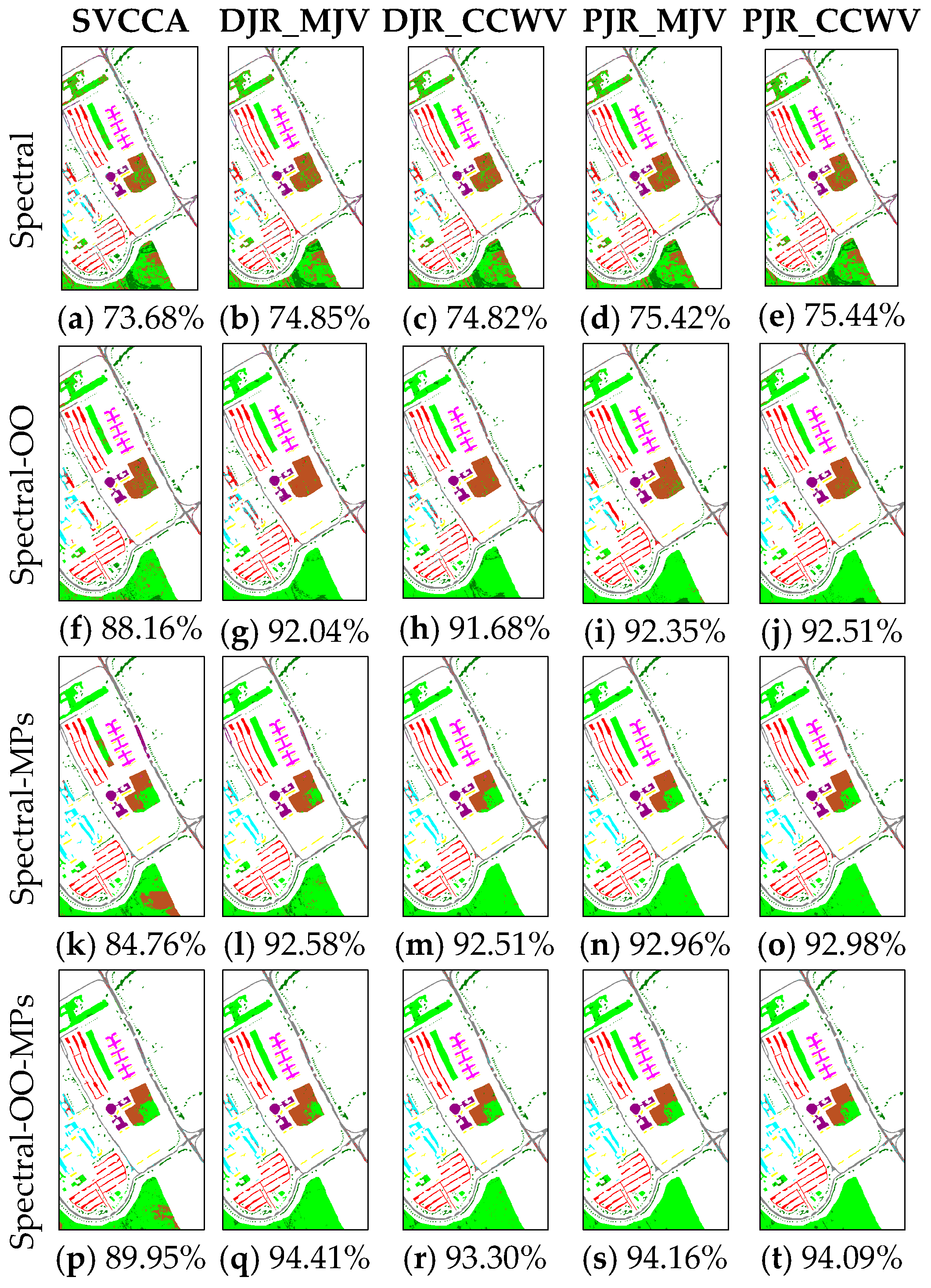
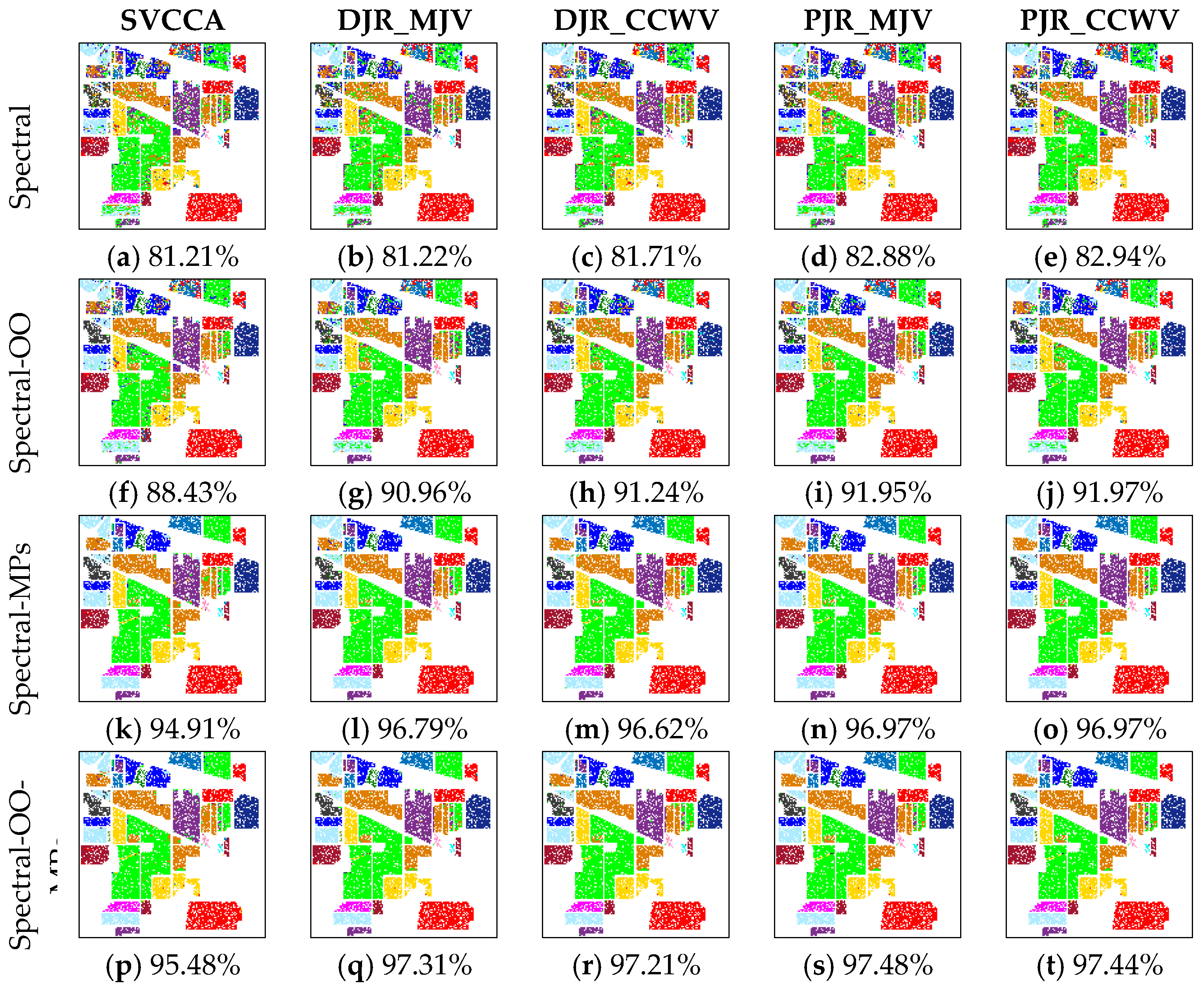
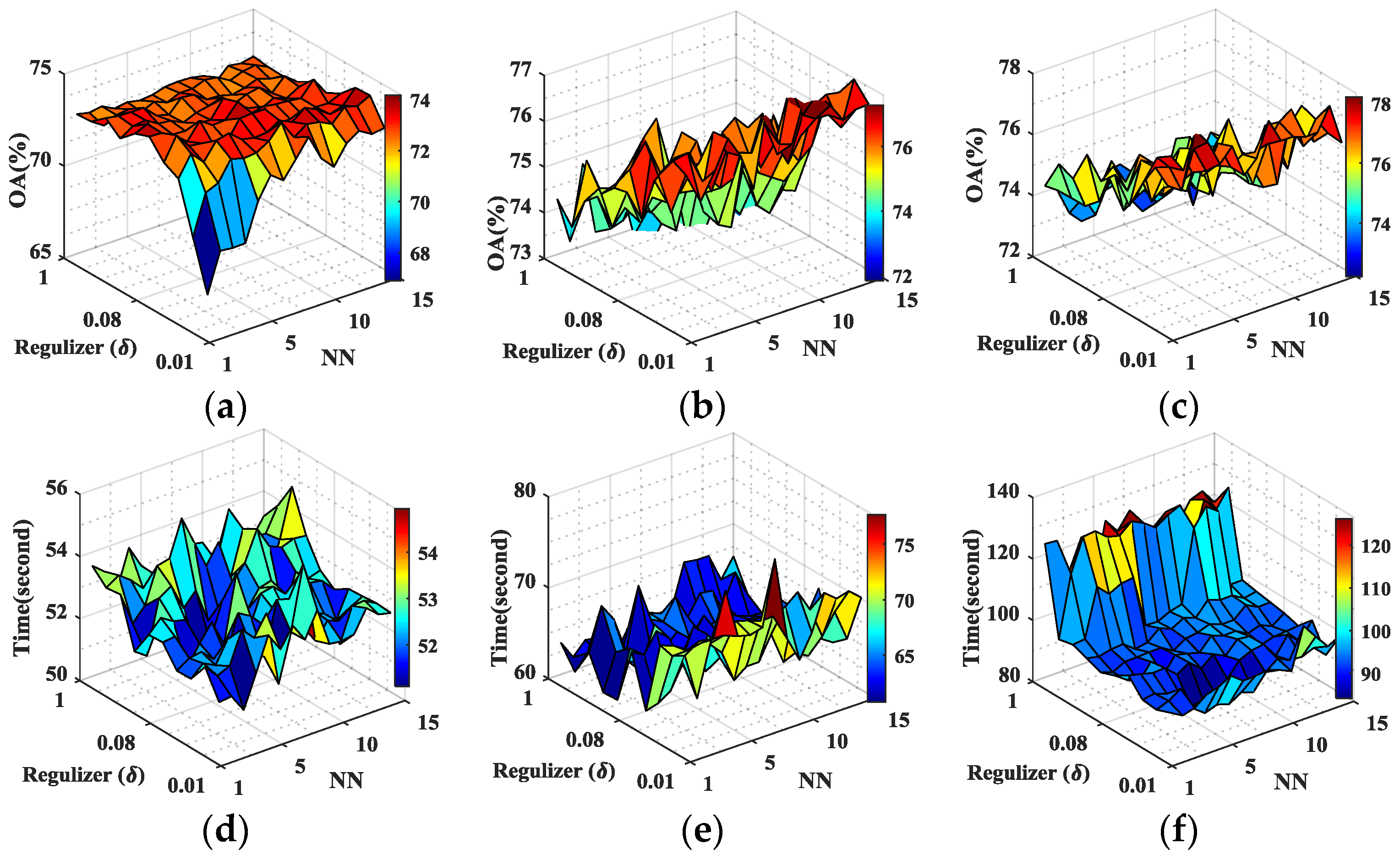
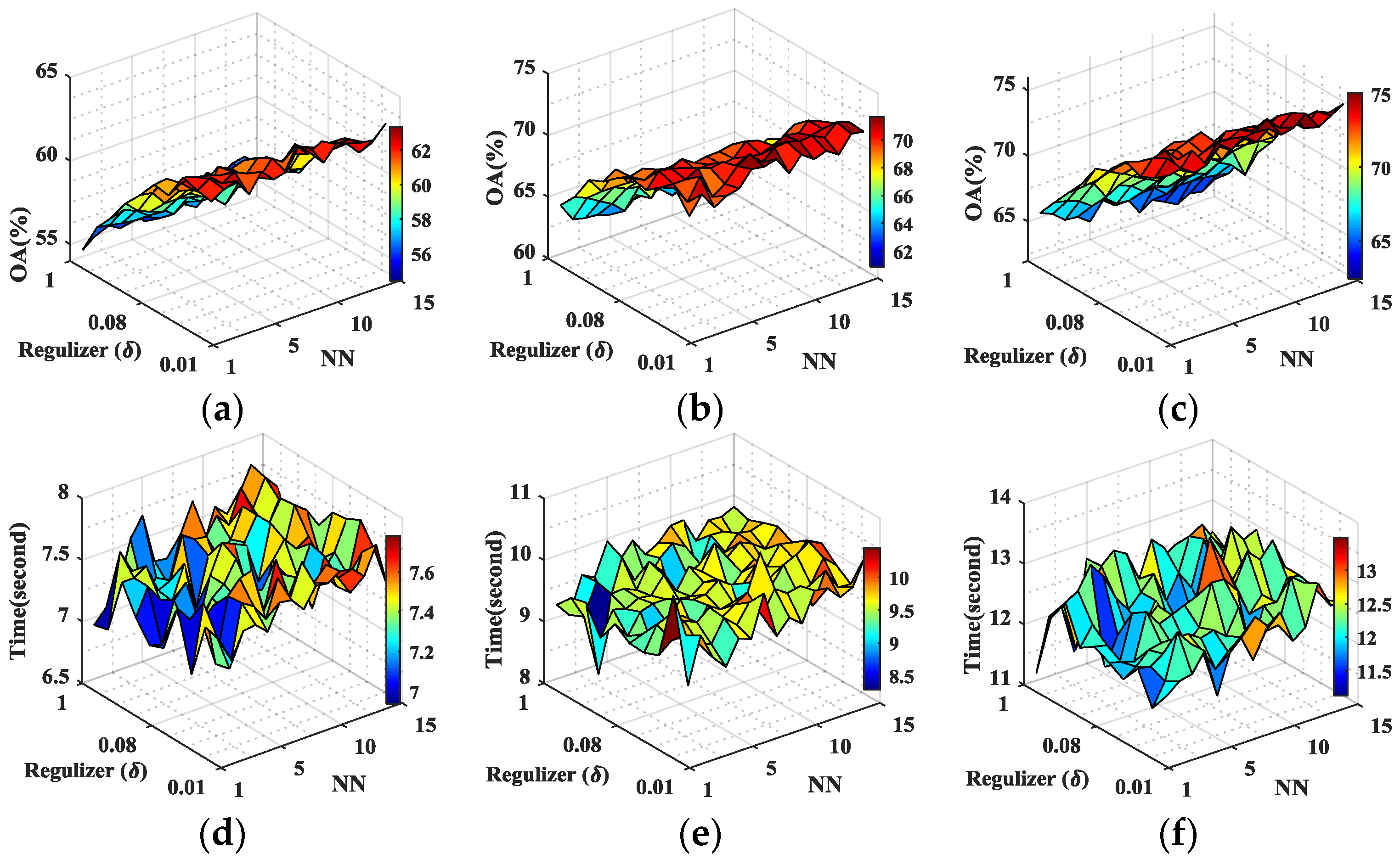
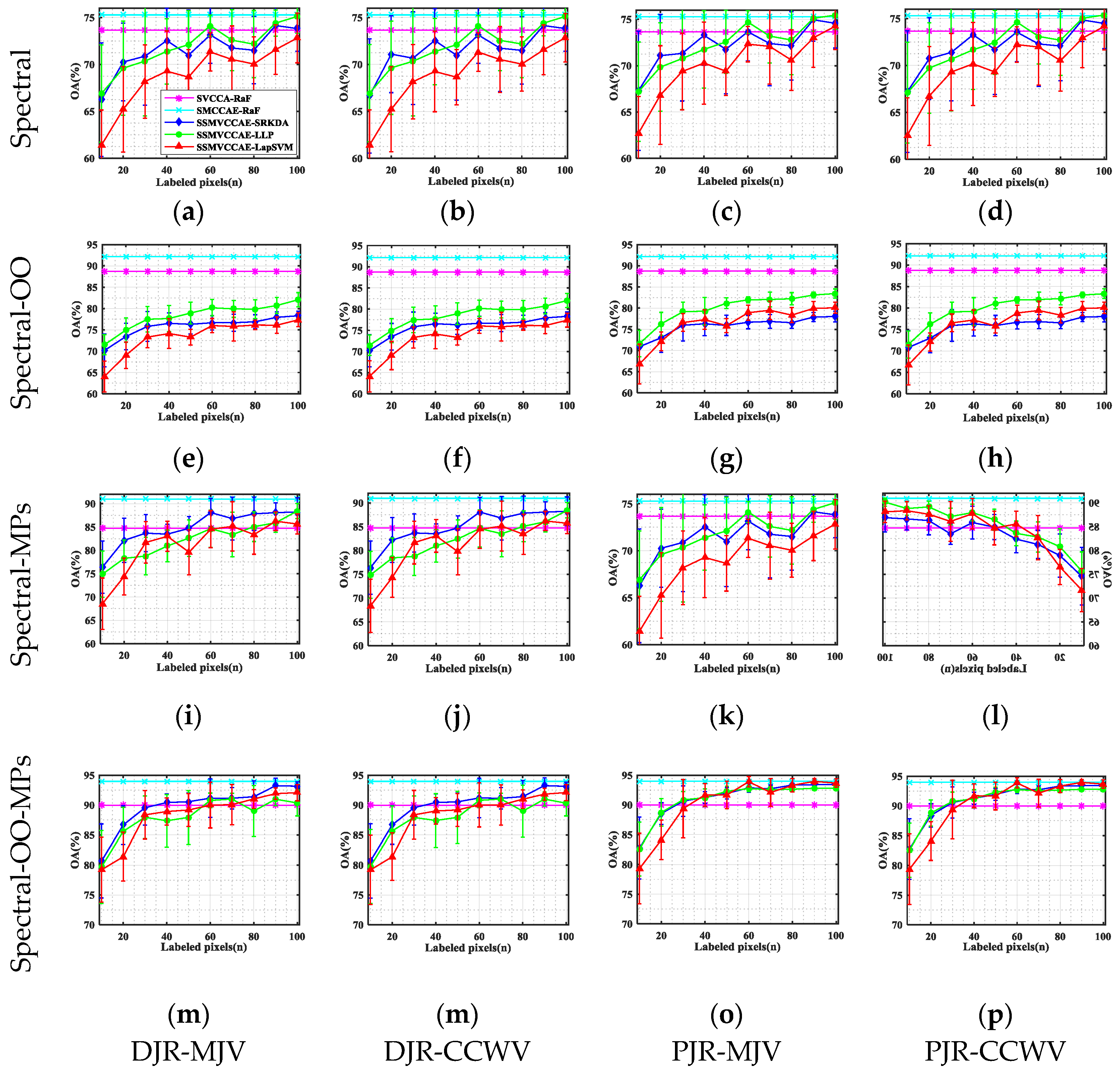
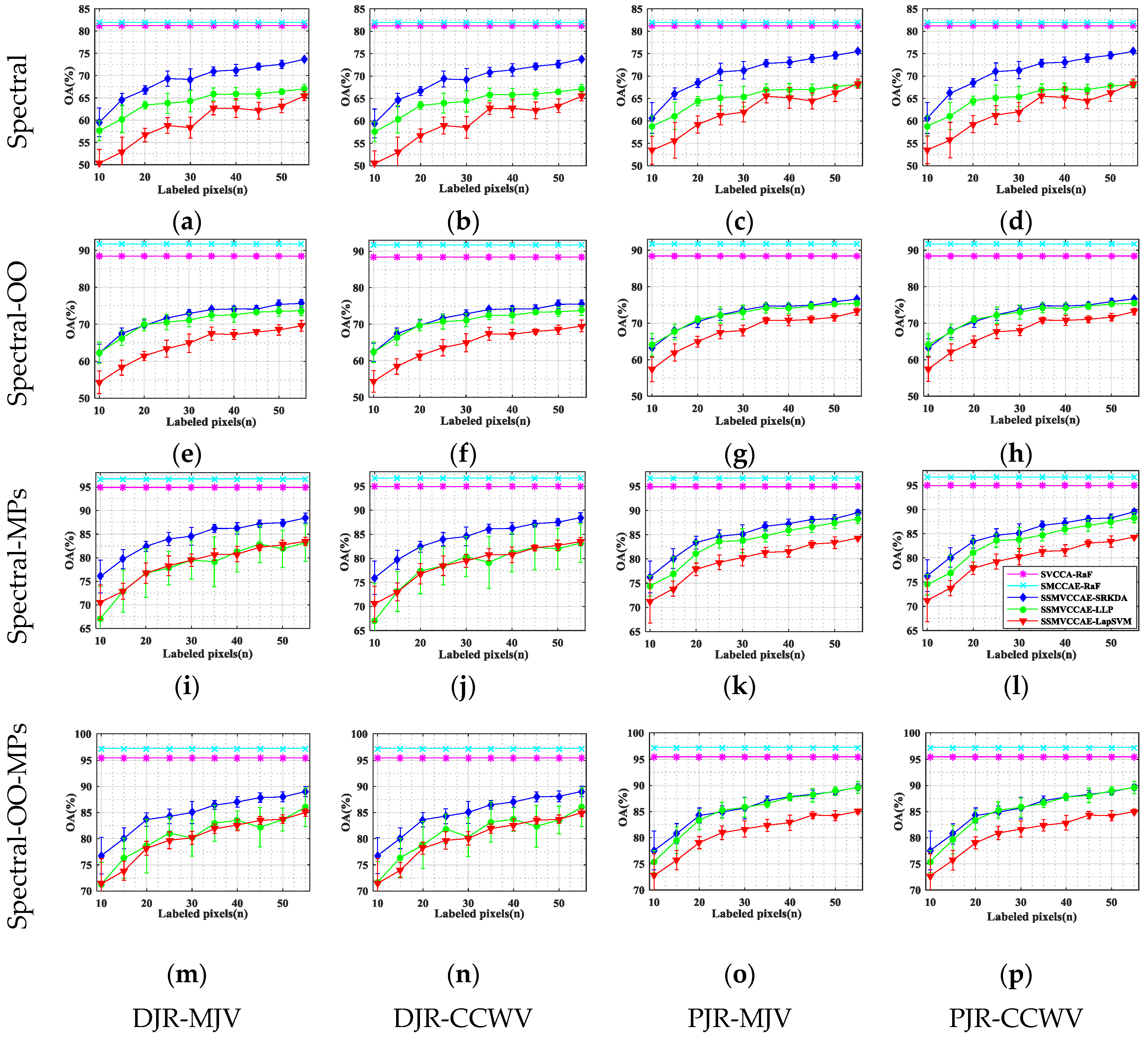
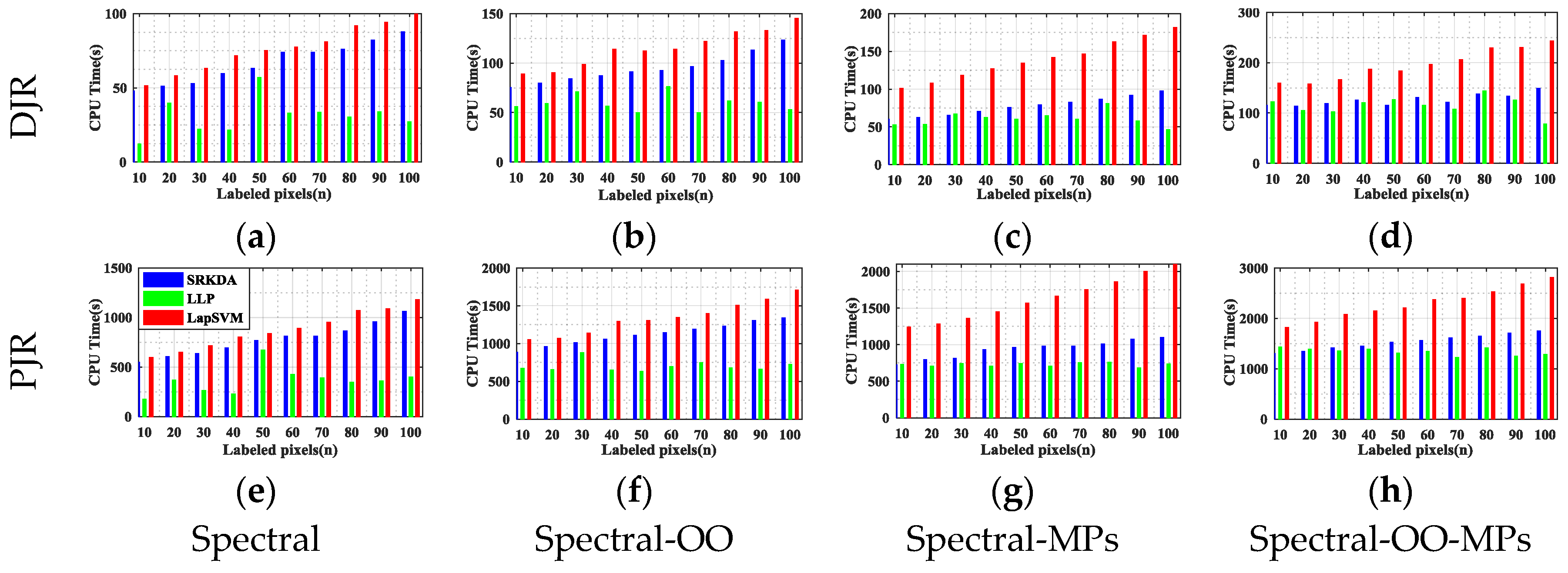
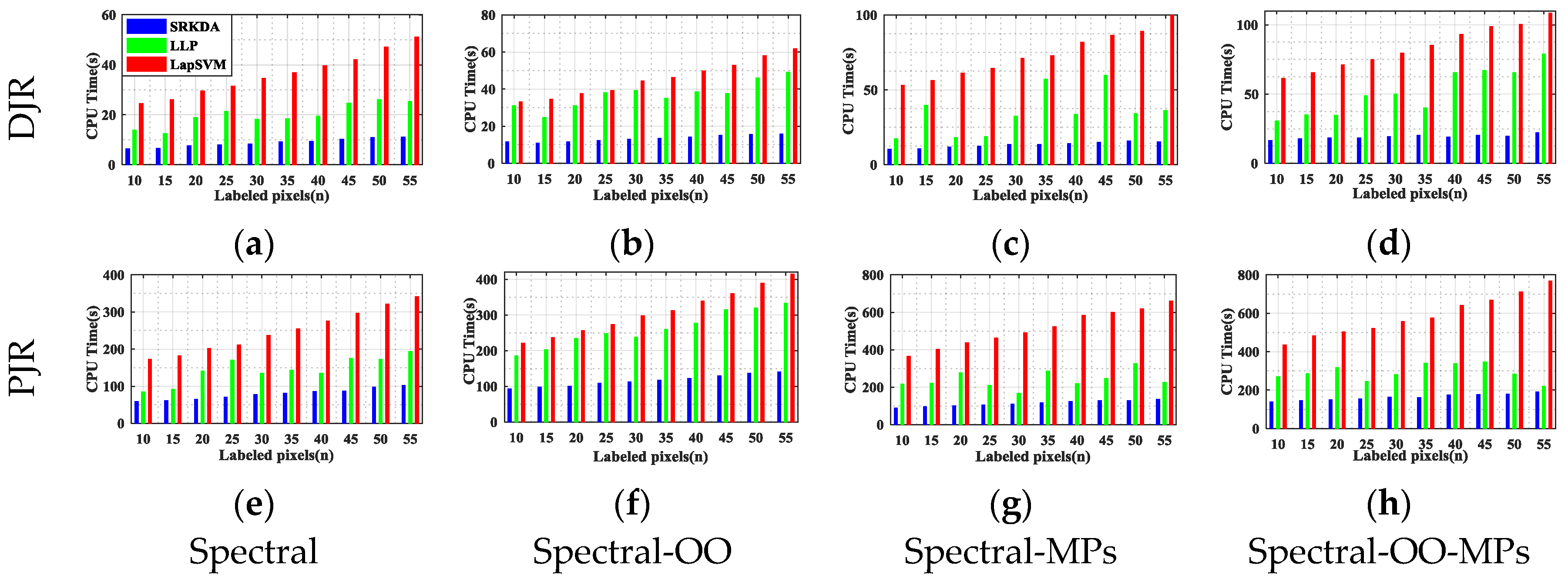
In this paper, we have presented the implementation details, analyzed the parameter sensitivity, and proposed a comprehensive validation of two versions of an ensemble classifier that is suitable for heterogeneous DA and based on multiple view CCA. The main idea is to overcome the limitations of SVCCA by incorporating multi view CCA into EL. Superior results have been proven using two high dimensional (hyperspectral) images, the ROSIS Pavia University and the AVIRIS Indian Pine datasets, as high dimensional target domains, with synthetic low dimensional (multispectral) images as associated SDs. The best classification results were always obtained by jointly considering the original spectral features stacked with object-oriented features assigned to segmentation results, and the morphological profiles, which were subdivided into multiple views using the PJR view generation technique.
To further mitigate the marginal and/or conditional distribution gap between the source and the target domains, when few or even no labeled samples are available from the target domain, we propose a semi-supervised version of the same approach via training multiple speed-up SRKDA.
For new research directions, we are considering more complex problems, such as single SD vs. multiple TDs, as well as multiple SDs vs. multiple TDs supervised and semi-supervised adaptation techniques.