1. Introduction
Wind turbines can modify the surface fluxes of momentum, sensible heat, water vapor, and carbon dioxide by enhancing turbulence, increasing surface roughness, and changing the stability of the atmospheric boundary layer (ABL) [
1,
2]. As reported in previous studies, the large establishment of wind farms (WFs) influence the local climate [
3,
4]. Based on field campaigns or model simulations, these studies found that large-scale WFs could alter local temperature, reduce precipitation and even mitigate extreme weather [
5,
6,
7]. However, due to lack of sufficient observations for validation and the simple parameterization of WFs, the simulated results have significant uncertainties [
4,
8]. In addition, field campaigns usually cover a short time span and include only a few measurements, limiting the representativeness of the results. Therefore, due to the limitations of climate models and field campaigns, an increasing number of studies are using remote-sensing data to investigate the effects of WFs on regional climate [
9,
10,
11,
12,
13]. Remote sensing data provides global spatial sampling information with high temporal and spatial resolution, and can thus be used to analyze the effects of large-scale WFs. Zhou et al. analyzed the effects of WFs on land surface temperature (LST) in Texas and found a nighttime warming effect of 0.31 °C–0.70 °C [
9,
10]. Slawsky et al. analyzed the impacts of three WFs in Northern Illinois and provided further observational evidence of a warming effect at night caused by WFs [
14].
Since wind farms can affect local climate [
9,
12,
15], changes in local climate, such as temperature and precipitation, may affect local vegetation growth and productivity over WFs [
16]. Since the beginning of the 21st century, China has built enormous wind turbines. In 2010, wind energy capacity in China reached 42.3 GW, exceeding the 40.3 GW capacity of the United States, and ranking first in the world. In 2015, newly-installed wind energy capacity in China amounted to 30.8 GW, accounting for 48.9% of newly-installed capacity worldwide [
17]. Within this newly installed wind energy capacity, wind energy development has been fastest in Hebei province and Inner Mongolia [
18,
19]. However, the effects of the rapid development of WFs on local climate and vegetation growth in China have not yet been thoroughly evaluated.
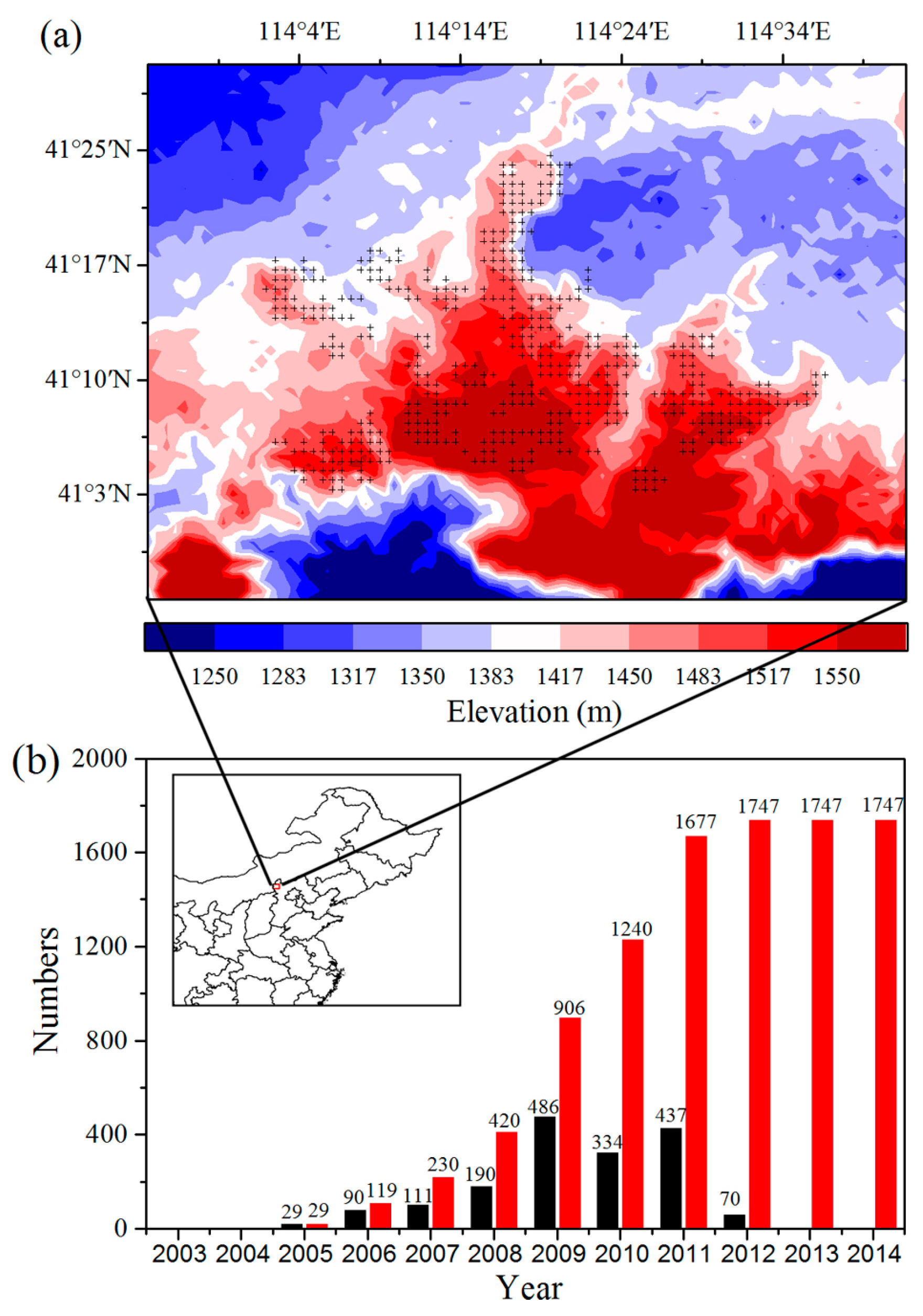
In this paper, we use the moderate-resolution imaging spectroradiometer (MODIS) vegetation index (leaf area index, LAI; normalized difference vegetation index, NDVI; and enhanced vegetation index, EVI) data, MODIS productivity data (gross primary production, GPP; net primary production, NPP), and other auxiliary data (temperature, soil moisture, evapotranspiration, albedo, and wind) to analyze the effects of WFs on summer (June–August, JJA) vegetation growth in the Bashang area of Northern China. The specific objectives of this paper are as follows: (1) to identify whether the WFs in Bashang can influence the summer vegetation growing status and productivity and (2) to further explore the possible processes for the effects of WFs on local vegetation growth.
3. Results
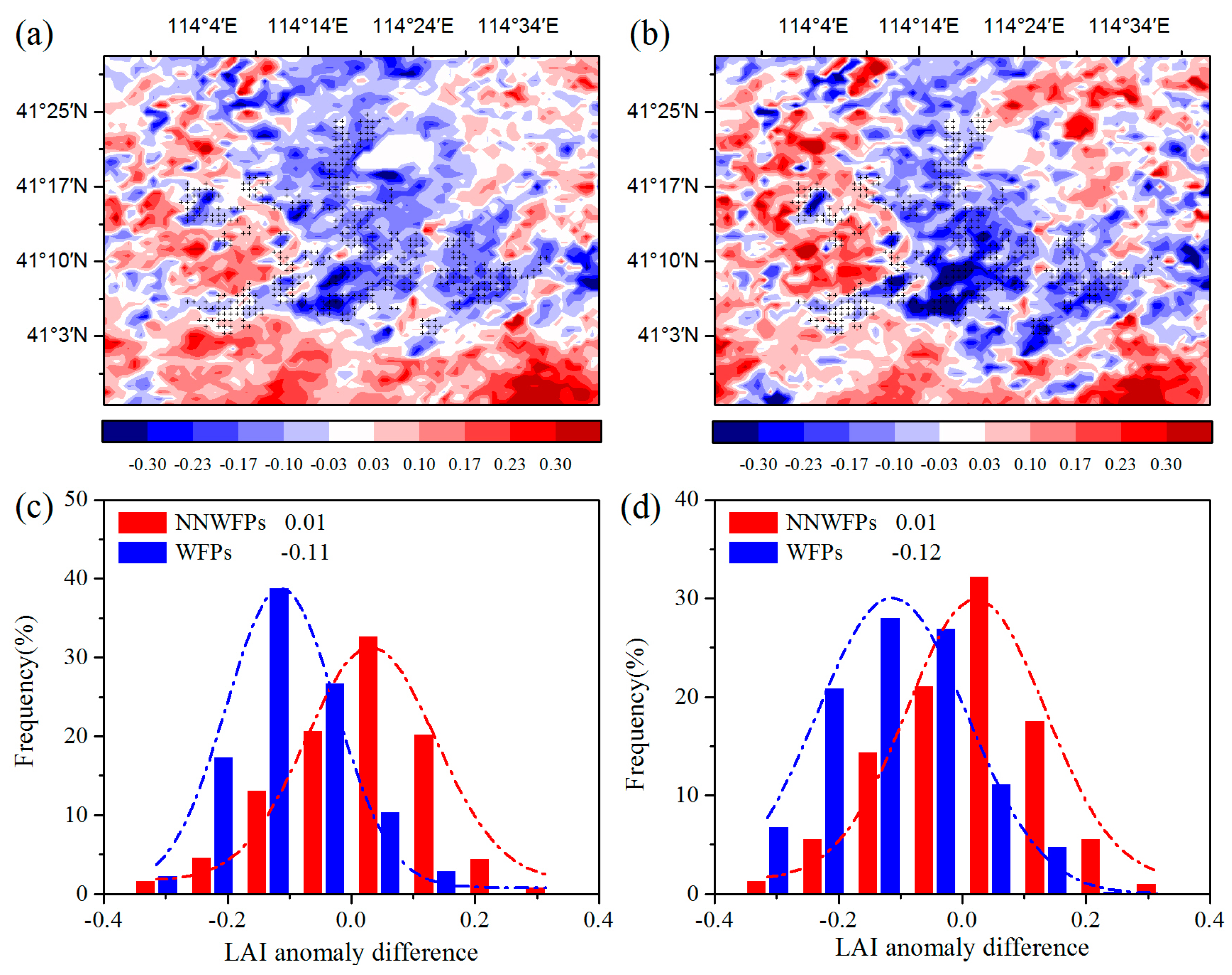
First, the spatial coupling of the layout of WFPs and LAI anomaly differences are calculated to analyze the effect of the WFs on vegetation growth.
Figure 3a–c show LAI anomaly differences at pixel scale in the summer between pre- and post-turbine construction periods (2012–2014 minus 2003–2005), and the probability distributions of LAI anomaly differences between WFPs and NNWFPs. The results show that negative LAI anomaly differences are spatially coupled with wind turbines, with 86.2% of WFPs corresponding to negative LAI anomaly differences. The average of LAI anomaly differences is −0.11 ± 0.10 and 0.01 ± 0.13 for WFPs and NNWFPs, a significant difference (
p < 0.01) according to the
t-test statistics. This result indicates that WFPs inhibit vegetation growth compared with NNWFPs. The spatial distributions of individual year average LAI anomaly differences are very similar to those of multi-year averages (
Figure 3b,d), with 84.1% of WFPs corresponding to the negative LAI anomaly differences. The average of LAI anomaly differences is −0.12 ± 0.13 and 0.01 ± 0.13 for WFPs and NNWFPs, respectively, which is also a significant difference (
p < 0.01). The anomaly differences for NDVI and EVI are also analyzed in this paper. The results for NDVI and EVI are found to be very similar to those for LAI, which indicates that the WFs inhibit vegetation growth in summer (
Figure S3). Note that, to the northeast of the WFs, there is a small area with zero anomalies in the vegetation index and net vegetation productivity. The reason for this observation is that the land cover type in this area is a lake, and the MODIS LAI and the vegetation productivity present no data for this area.
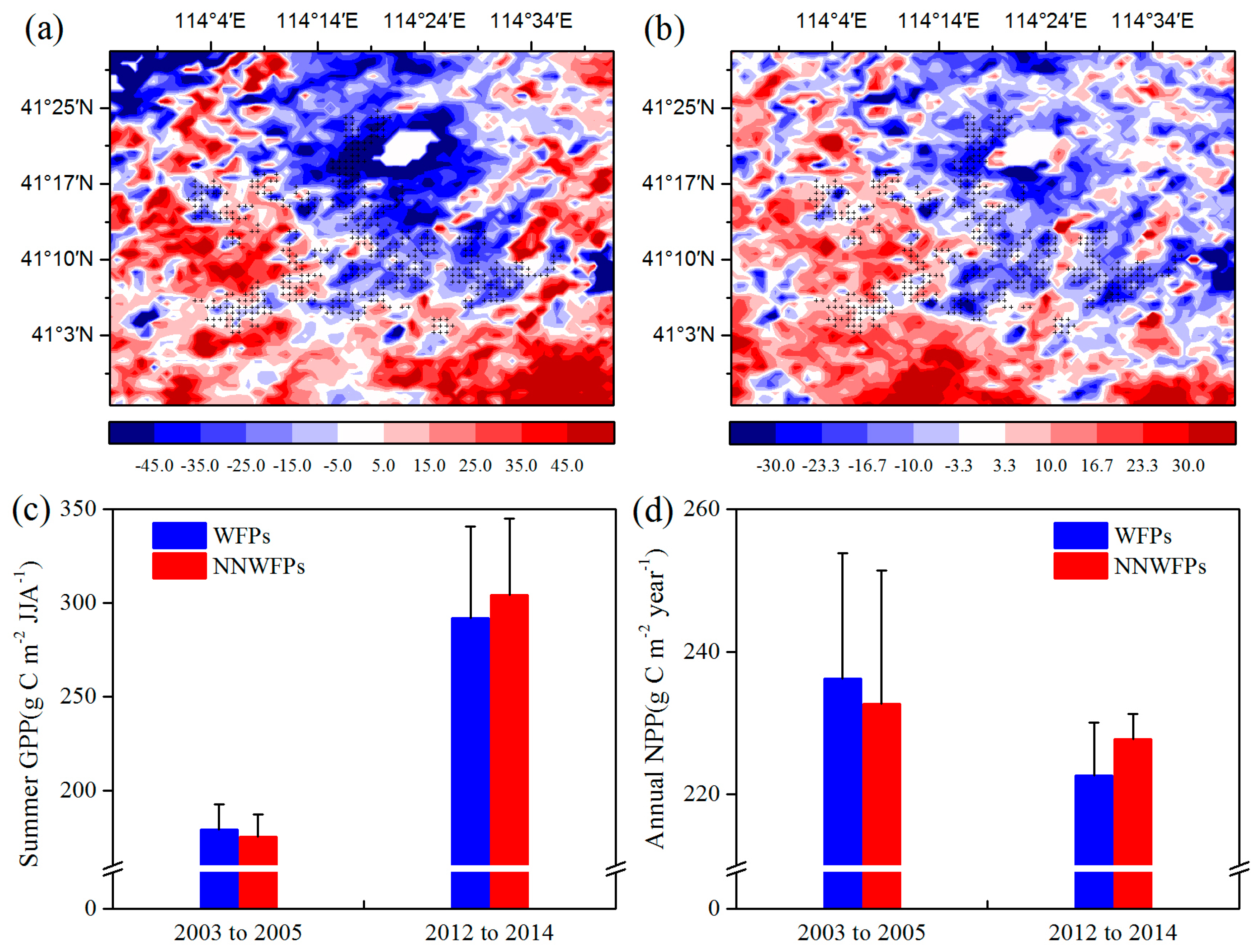
Then, the effects of WFs on vegetation productivity are analyzed.
Figure 4 shows the summer GPP and annual NPP differences at pixel scale between the pre- and post-turbine construction periods (2012–2014 minus 2003–2005) in the study area. The results show that 80.4% negative summer GPP anomaly differences are spatially coupled with the wind turbines (
Figure 4a). The average of GPP anomaly differences is −16.51 ± 21.10 (−0.42 ± 33.59) g C m
−2 JJA
−1 for WFPs (NNWFPs), which are significantly different (
p < 0.01) according to the
t-test statistics. The annual NPP anomaly differences over WFPs (−8.36 ± 13.08 g C m
−2 year
−1) are significantly smaller than that over NNWFPs (0.19 ± 19.02 g C m
−2 year
−1,
p < 0.01), with 71.9% of WFPs corresponding to negative NPP anomaly differences (
Figure 4b). We also calculated average summer GPP and annual NPP of WFPs and NNWFPs in 2003–2005 and 2012–2014 (
Figure 4c,d). From 2003 to 2005, the average summer GPP over WFPs is 179.03 g C m
−2 JJA
−1 and significantly larger than the GPP (175.26 g C m
−2 JJA
−1) over NNWFPs (
p < 0.01). From 2012 to 2014, the average summer GPP over WFPs (NNWFPs) increased to 291.78 (304.10 g C m
−2 JJA
−1). Vegetation productivity in WFPs has a smaller rate of increase in summer GPP, becoming significantly smaller than that in NNWFPs (
p < 0.01). From 2003 to 2005, the average annual NPP over WFPs (236.18 g C m
−2 year
−1) is significantly larger than that over NNWFPs (232.68 g C m
−2 year
−1,
p < 0.05). From 2012 to 2014, the average annual NPP over WFPs (NNWFPs) decreased to 222.67 (227.72 g C m
−2 year
−1). Vegetation productivity in the WFPs has a larger rate of decrease of NPP, becoming significantly smaller than that in NNWFPs (
p < 0.01). The results of summer GPP and annual NPP indicate that, compared with NNWFPs, WFPs inhibit vegetation productivity.
The spatial coupling of the layout of the WFPs and vegetation index and productivity anomaly differences, are quantified by comparing the SCI values of 5%, 10%, and 15% pixels of the smallest vegetation index as well as GPP, and NPP anomaly differences located in WFPs with the corresponding SCI threshold. Generally, the larger the SCI value, the stronger the spatial coupling. The SCI values for LAI, NDVI, EVI, GPP, and NPP in WFPs range from 9.5% to 35.5%, and 14 of the 15 are larger than the threshold (10.8%), indicating a strong spatial coupling between the layout of WFPs and vegetation anomaly differences. In other words, WFs can inhibit vegetation growth and productivity (
Table 1).
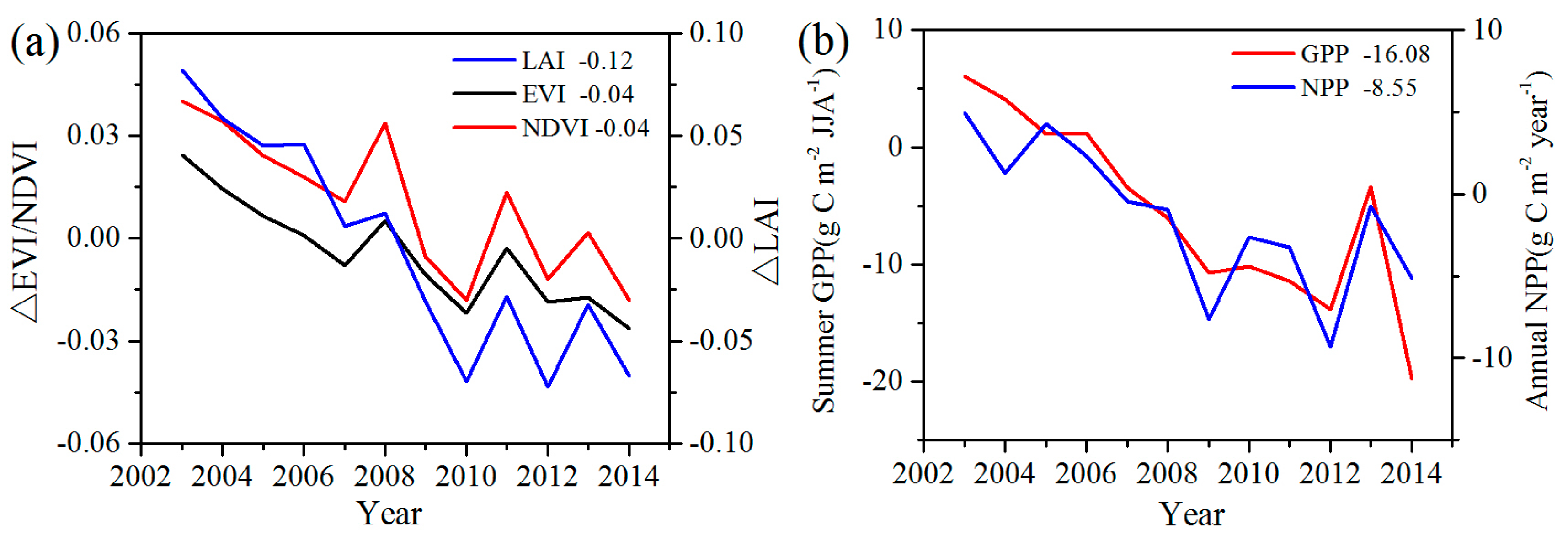
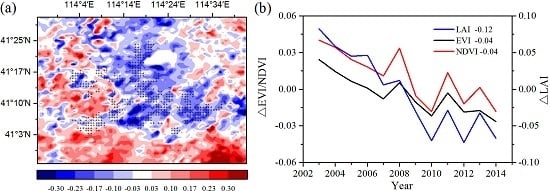
To analyze the quantitative effects of the WFs on vegetation growth and productivity for 2003–2014 in the study area, the area mean time series of differences in VI, GPP, and NPP between WFPs and NNWFPs (WFPs minus NNWFPs) are analyzed (
Figure 5). Although the time series is short, the LAI, EVI, and NDVI differences all present significant downward trends, which are as follows: −0.15/11 years (
p < 0.01), −0.04/11 years (
p < 0.01) and −0.05/11 years (
p < 0.01). The vegetation productivity also shows downward trends and the decreasing trends are −20.93 g C m
−2/11 years (
p < 0.01) for summer GPP and −10.19 g C m
−2/11 years (
p < 0.01) for annual NPP. Based on the vegetation index and productivity differences between post- and pre-turbines construction periods (2012–2014 minus 2003–2005), the effects of WFs on vegetation growth are quantified. From 2003 to 2014, the inhibiting effects of the WFs on vegetation growth are −0.12 (LAI), −0.04 (EVI), and −0.04 (NDVI), or 14.5%, 14.8%, and 8.9%, respectively, compared with the climatology values of 0.83 (LAI), 0.27 (EVI), and 0.45 (NDVI) for WFPs. The inhibiting effects of the WFs on vegetation productivity are −16.08 g C m
−2 JJA
−1 (GPP) and −8.55 g C m
−2 year
−1 (NPP), representing a change of 8.9% and 4.0% of the climatology value 180.81 g C m
−2 JJA
−1 and 214.86 g C m
−2 year
−1 over the WFPs. Note that the VI differences and vegetation productivity differences both remain relatively stable after 2012. The main reason for this trend may be that the wind turbine construction was essentially complete after 2012 and, as a result, the differences in VI, GPP and NPP between WFPs and NNWFPs gradually become stabilized. However, during the first few years, the number of wind turbines in WFPs gradually increased and, therefore, the differences between WFPs and NNWFPs gradually become larger (
Figure 1a).
4. Discussion
In this paper, MODIS vegetation index and productivity data are used to analyze the effects of WFs on vegetation growth in the Bashang area in Northern China. The results show that the WFs have a significant inhibiting effect on vegetation growth and productivity both spatially and temporally. The potential processes, such as land-use change, differences in vegetation type, changes in climate, and wind speed and direction, may contribute to the inhibiting effect of vegetation growth.
Construction of WFs and other human activities change the land cover type, thus affecting the vegetation growth in the study area. In this research, Finer Resolution Observation and Monitoring of Global Land Cover (FROM-GLC) data for two periods in 2000 and 2010 are used to analyze land use changes in WFPs and NNWFPs in the study area. The spatial resolution of the data is 30 m [
30]. The results show that the proportion of non-vegetation pixels (water and urban areas) in WFPs changes from 0.72% to 1.25%, while from 2000 to 2010, that in the NNWFPs changes from 2.50% to 3.48% (
Figure S1). The proportions of the non-vegetation pixels and their changes in WFPs and NNWFPs are very small. Although the construction of wind turbines may indeed damage the vegetation canopy, the annual plants (grassland and crop) in the study area are able to recover quickly after being damaged in the next year (
Figure S4). With the increase of the effect of WFs on daytime LST, vegetation growth cannot be restored to the level before the construction, or even continue to decrease, indicating that WFs do affect vegetation growth by changing the vegetation growth environment (
Figure S4).
The difference in land cover types, such as different crop species and crop management, may also have potential influences on vegetation growth. For two main vegetation types in the WFPs and NNWFPs (crop and grass), the effects of the WFs are approximately the same (
Figure S5). It is reasonable to assume that WFs have a similar effect on different crop species. The effect of crop species differences and crop managements would be much smaller than the strong and persistent signal of wind farm impacts. According to field campaigns, the support column of a wind turbine accounts for 4 m
2, and 1747 wind turbines account for approximately 7000 m
2, which represent a very small proportion (less than 0.1%) of the WFPs. Therefore, for the study area, land cover changes and differences in vegetation type for WFPs and NNWFPs have no significant effect on the underlying vegetation growth.
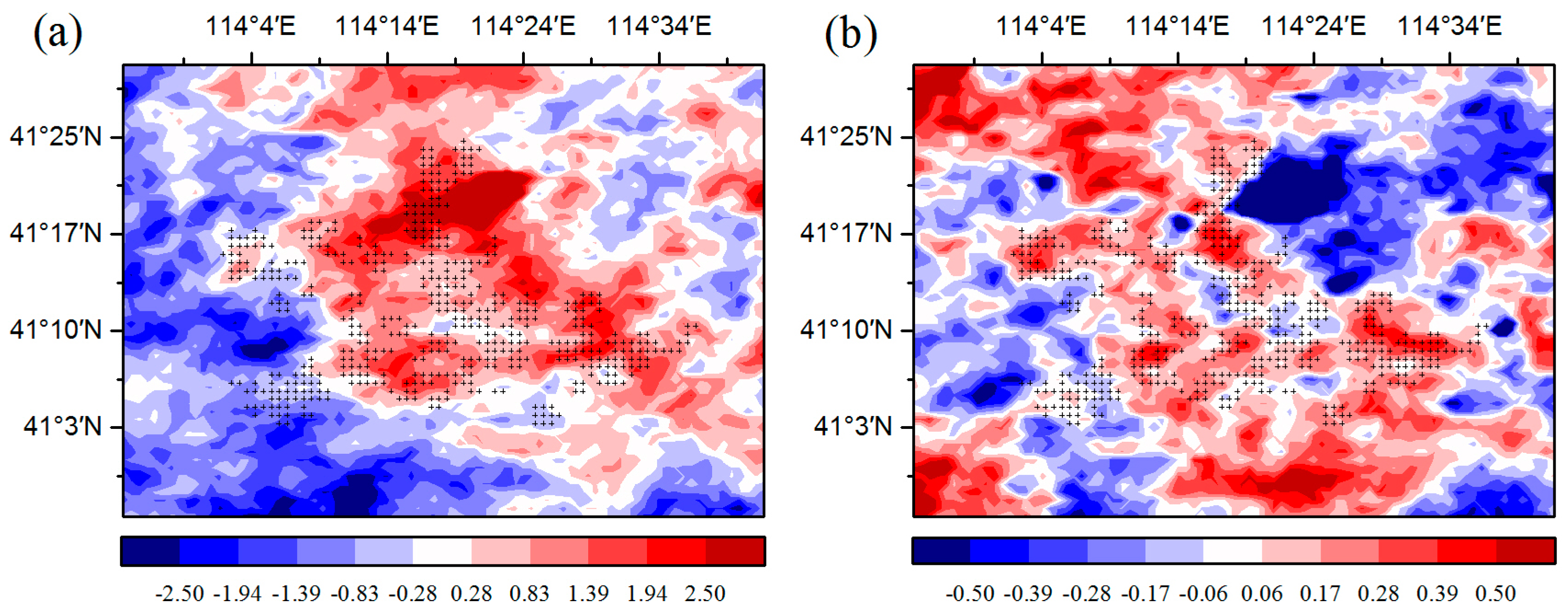
The changes in temperature may play an important role in the effect of WFs on vegetation growth. There is a warming effect of 0.15–0.18 °C coupled with WFs at night, which agrees with most existing studies (
Figure 6b) [
12,
13,
15]. The possible reason for this phenomenon is that the diurnal and seasonal variations in wind speed and the changes in near-surface atmospheric boundary layer (ABL) conditions due to wind turbines operations [
9]. Contrary to some existing studies, this research finds that there is also a warming effect of 0.45–0.65 °C coupled with WFs during the daytime (
Figure 6a). Zhou et al. [
9] speculated that the possible reason is the slow development of the daytime unstable and convective layer [
31]. Changes in ET may also play a role in daytime warming [
32]. The ET in the WFPs is lower than that in the NNWFPs, and reduced transpiration may contribute to a higher LST in WFPs (
Figure S6). In the study area, the LAI is negatively related to the daytime LST, and the correlations are all significant at a confidence level of 95% (
Figure S7). The main reason for this trend may be that the WFs can reduce soil moisture through increasing LST in the study area (
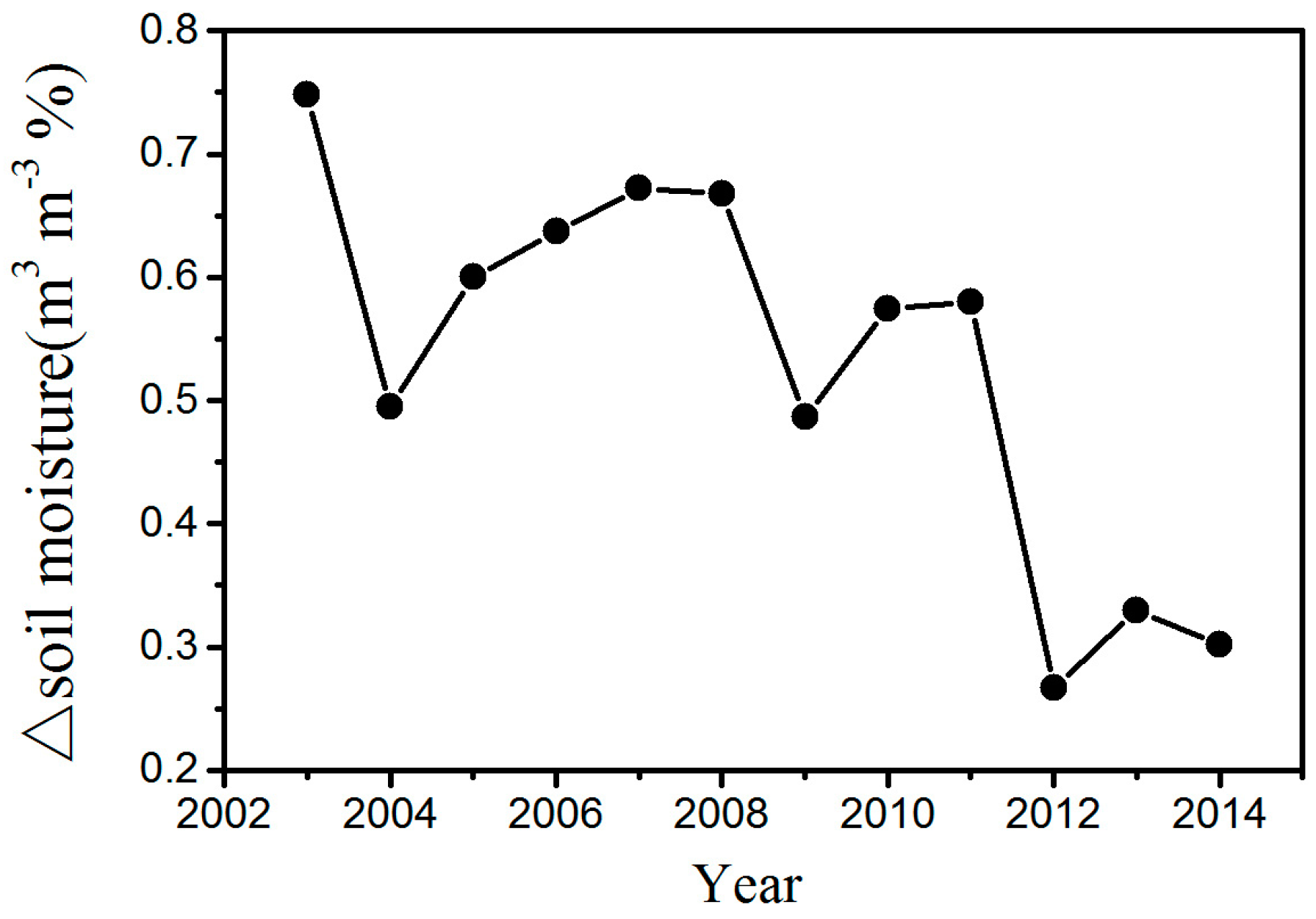
Figure 7). In this research, the study area is located in the semi-arid area of Northern China where soil moisture has a decisive effect on vegetation growth [
16]. An increase in the LST reduces soil moisture and enhances water stress on vegetation growth. As a result, growth conditions for vegetation growth are suppressed, leading to a lower vegetation index. Furthermore, we also observed decreasing vegetation productivity in the WFs, which may be caused by inhibited photosynthesis through increasing water stress and enhanced autotrophic respiration through increasing nighttime temperatures.
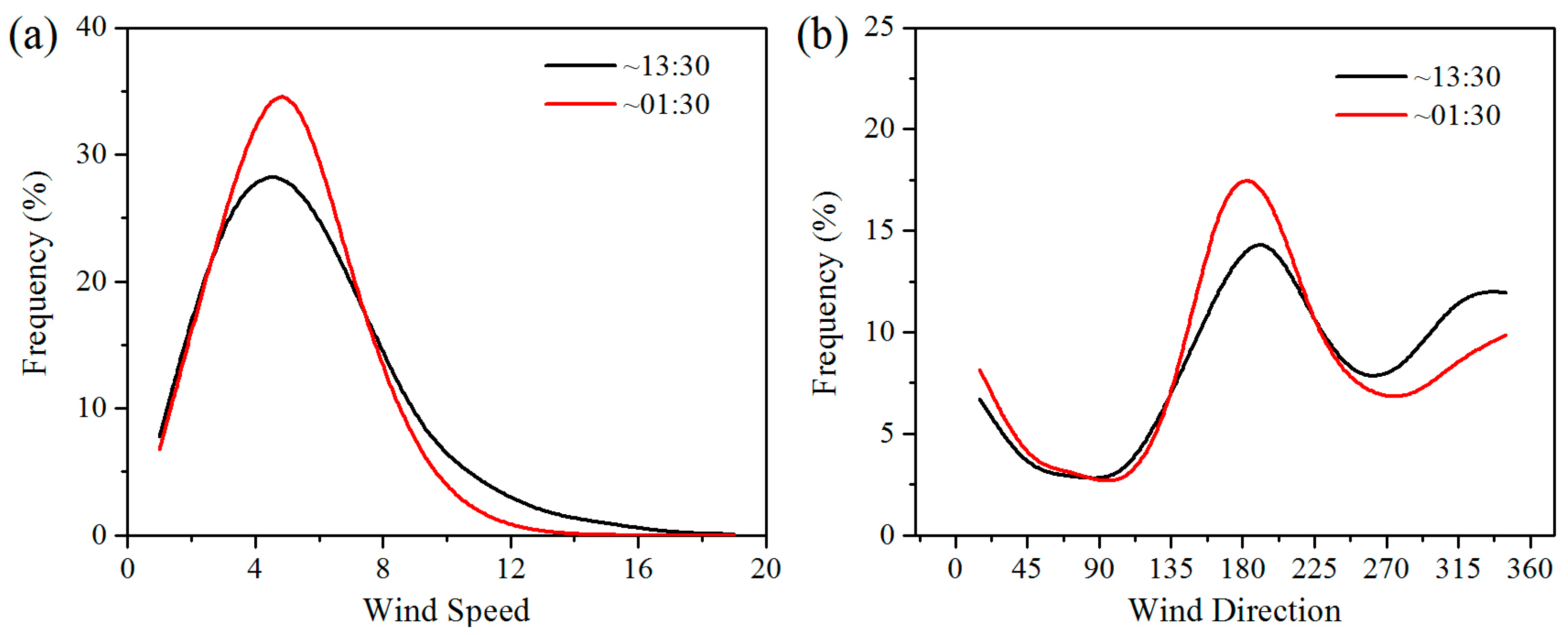
Wind speed is the main factor determining energy conversion in wind turbines. Wind turbines have a cut-in and a cut-out wind speed, which are approximately 3–4 m/s and 20 m/s, respectively [
10]. The wind speed in the study area is generally 4–8 m/s, meaning that the wind turbines can operate most of the time (
Figure 8). Wind direction in the study area can affect the effects of WFs on LST, and thereby affect vegetation growth and productivity. Generally, the winds blow mainly from the southeast and northwest at night and from the southwest during the daytime (
Figure 8). The positive LST anomaly differences all occur to the northwest and southeast of the WFs at night and to the northeast in the daytime (
Figure 6). This result indicates that a downwind warming effect is occurring in the study area. To assess the downwind effect on vegetation growth, the SCI values of 5%, 10%, and 15% pixels of the smallest vegetation index anomaly differences located in UWFPs, DWFPs, and NNWFPs are compared with the corresponding SCI thresholds (5.3%, 6.3%, and 14.9%). The higher the SCI value of the DWFPs, the stronger the downwind effect. The SCI of the DWFPs ranges from 6.1% to 10.8% and 14 of the 15 are higher than the corresponding SCI thresholds (6.3%), indicating the existence of a downwind effect on vegetation growth (
Table 1). In contrast, only 6 of the 15 SCI values for NNWFPs and none of the SCI values for UWFPs are higher than the corresponding SCI thresholds, indicating that the smallest vegetation index anomaly differences are unlikely to be found in the NNWFPs and UWFPs.
The main source of uncertainty in this paper comes from the errors in the MODIS vegetation index and productivity products [
20,
21,
24]. Although the MODIS products represent the highest-quality retrieval data from clear-sky conditions, it still contains errors and noise due to clouds, aerosols, and the imperfection of the retrieval algorithms. In addition, there may be discrepancies in determining the positions of the wind turbines. The matching of various kinds of data of different resolutions may also produce errors in the results. However, the spatial and temporal averaging used in this paper can effectively reduce errors and uncertainties. The remaining residuals may not produce a spatial coupling between the layout of WFs and the vegetation index anomaly differences, especially when many different kinds of vegetation indexes are used.
5. Conclusions
In this study, the effects of WFs on the underlying vegetation growth in the Bashang area of Northern China are analyzed. The results show that WFs inhibit local vegetation growth and productivity, decreasing LAI, EVI, and NDVI by approximately 14.5%, 14.8%, and 8.9% from 2003 to 2014. There is an inhibiting effect of 8.9% on summer GPP and 4.0% on annual NPP over WFs. Potential reasons for the inhibiting effects are as follows: (1) inhibited photosynthesis through increasing water stress and enhanced autotrophic respiration through increasing daytime and nighttime temperatures and (2) downwind inhibited growth status and photosynthesis induced by the downwind warming effect. Our analysis provides clear observational evidence of the inhibiting effect on vegetation growth caused by WFs in the Bashang area of Northern China.
As the analysis is from a short period over a local region with rapid growth of wind farms, it should be kept in mind that the estimated inhibiting effects cannot be generally applied to other WFs. Wind farms affect the vegetation growth by changing local climate and damaging vegetation structures through constructions. For a given wind farm, the inhibiting effect should be quantified by fully considering local background environmental factors (e.g., temperature and soil moisture) and the recovery of vegetation with different vegetation conditions. Our results raise intriguing questions whether these suppressing patterns are observed in other WFs as well, and about trade-offs between production of clean energy and potential suppression of ecosystem functions.