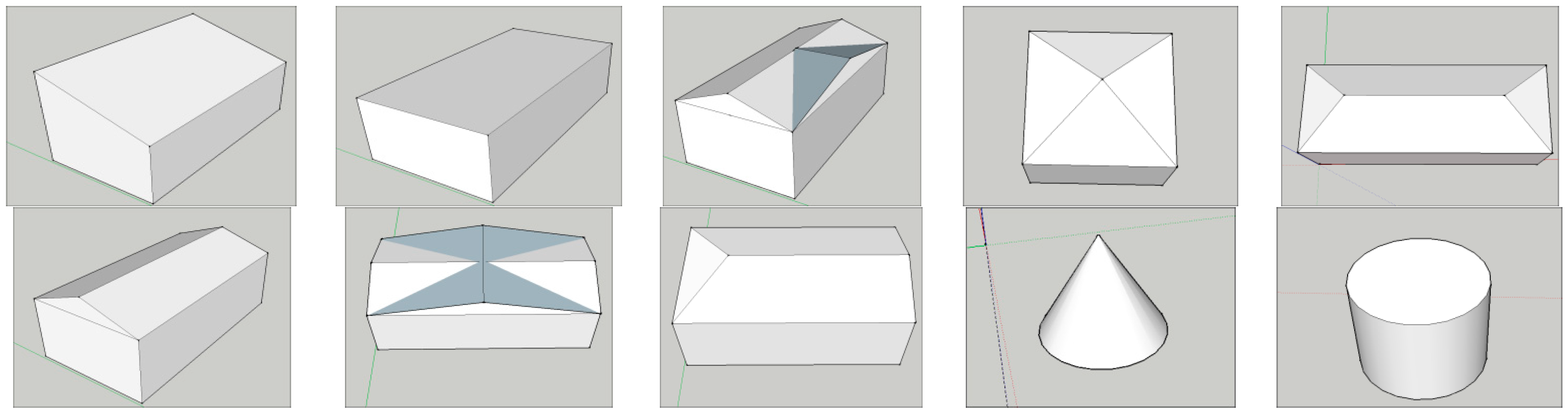
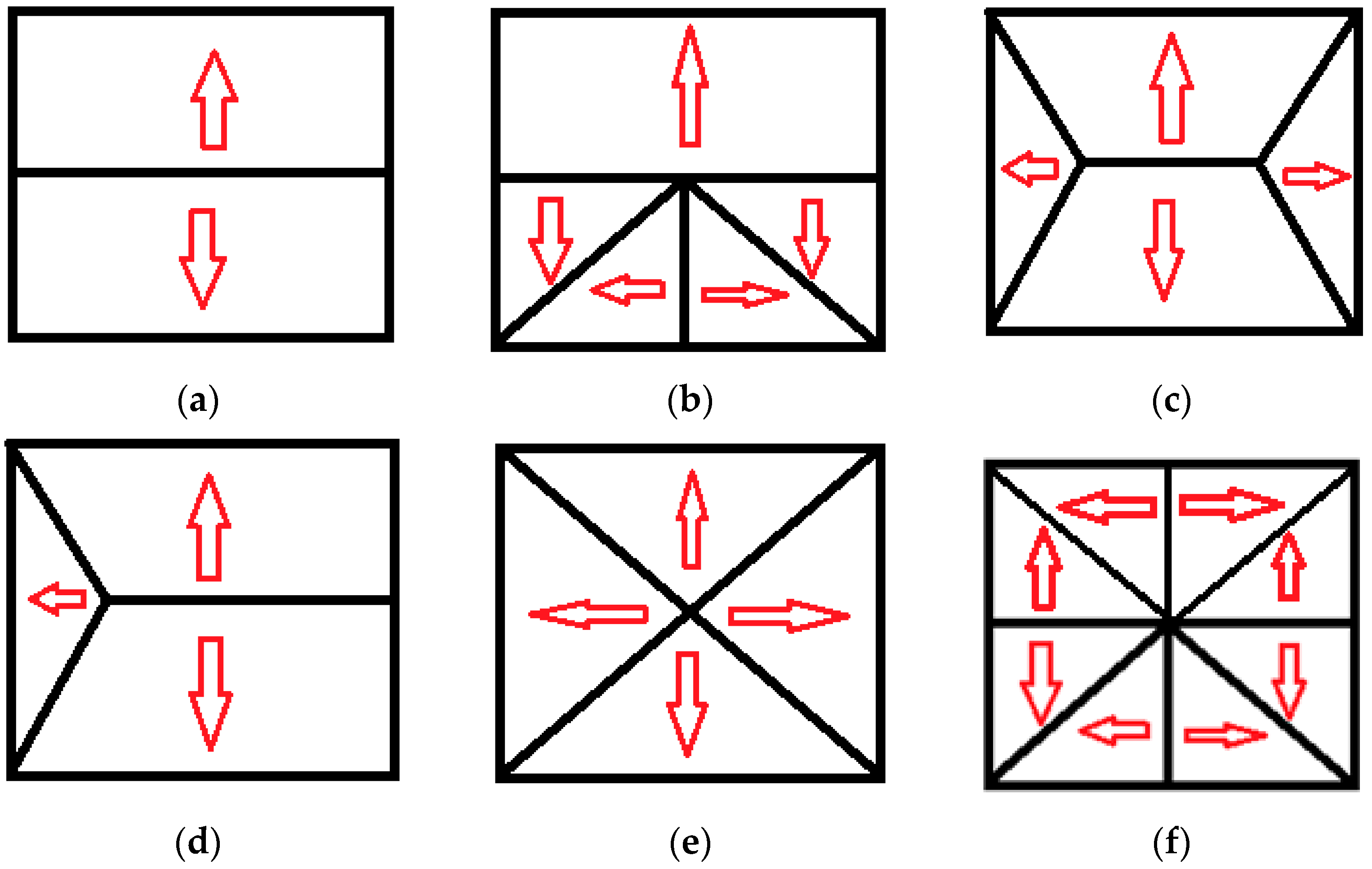
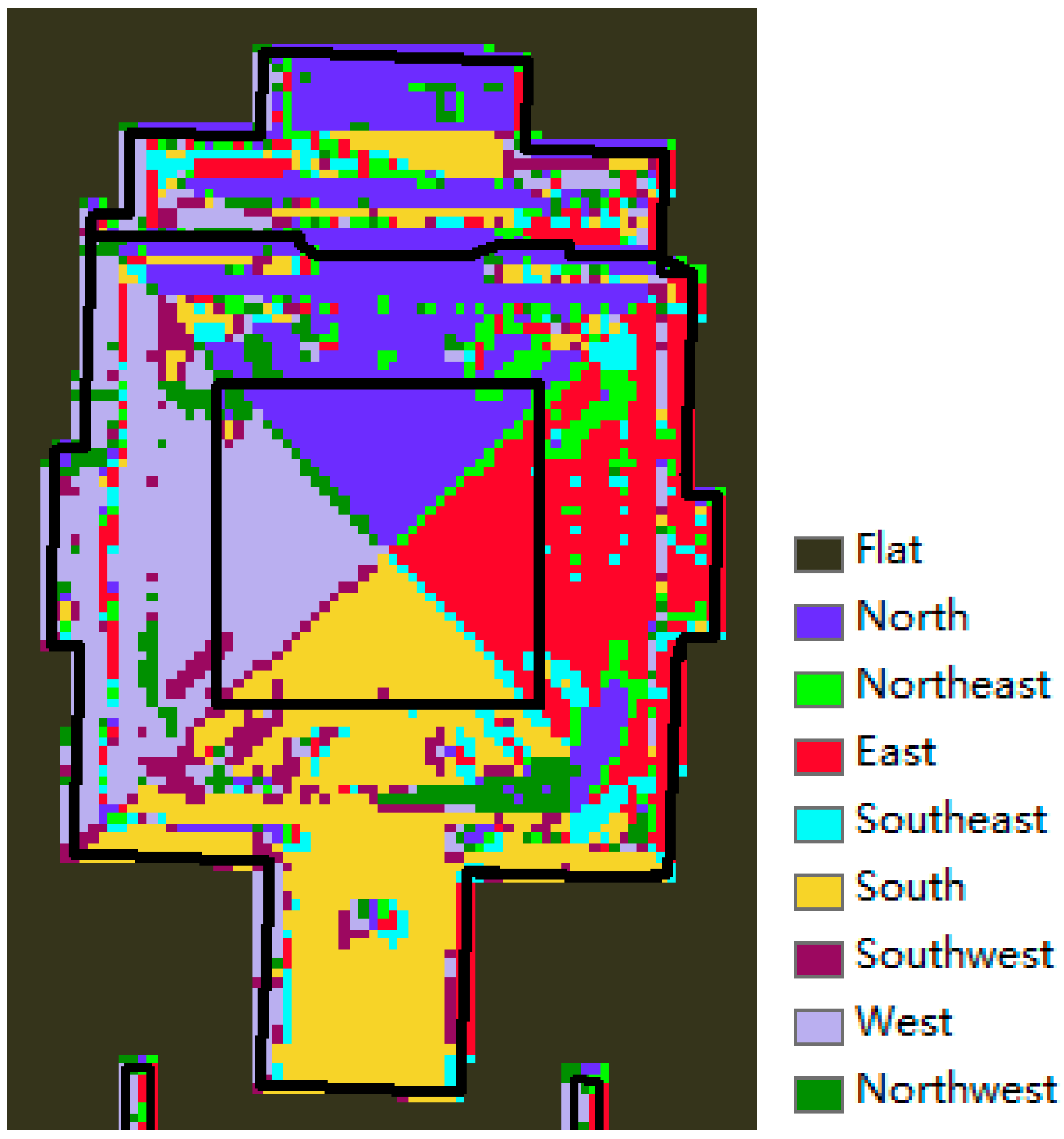
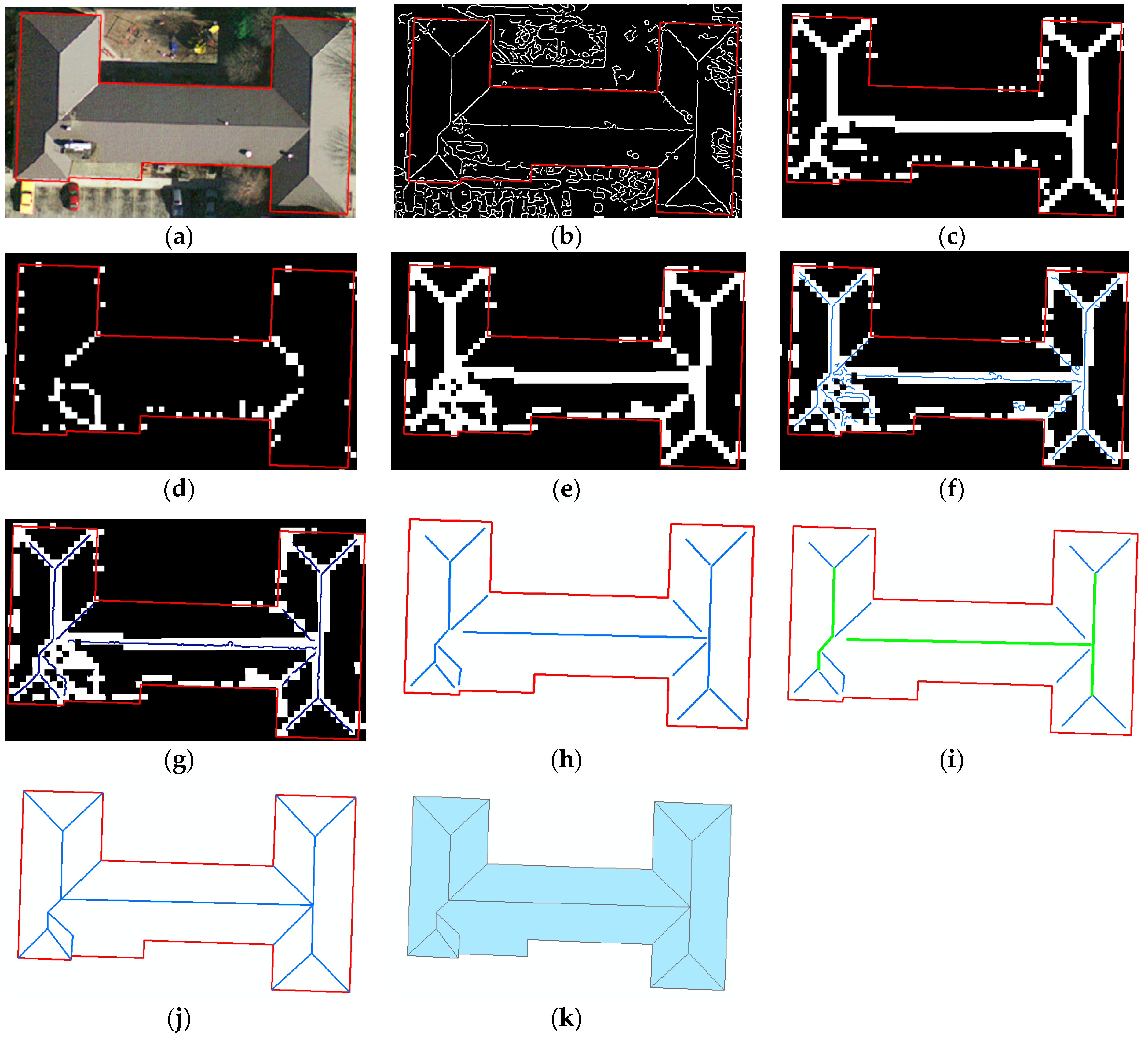
1. Introduction
3D building models with prototypical roofs are more valuable in applications of Geography Information Systems (GIS), urban planning and environmental modeling compared to the widely-existing 2D building footprints. They are extremely useful in solar radiation calculations, noise emission simulation [
1] and urban structure analysis since they contain more physical and morphological information for an individual building [
2]. According to Kolbe et al. [
3], the multi-scale 3D building model reconstruction can be categorized into five levels of detail: LoD0-1 presents a building model containing the 2.5D Digital Terrain Model (DTM) and building block models without roof structures; LoD2 presents building models including roof structures; LoD3–4 presents a building model including detailed architecture and interior models [
4]. Most of the cities in developed countries have LoD1 building data, which extrude 2D building footprints according to their height values. However, the box-shaped LoD1 model does not have the roof structures, but LoD2 has greater detail of roof planar shapes and also has the ability to represent commonly-seen tiled roofs, such as hipped roofs and gabled roofs. LoD4 and LoD3 currently can only be reconstructed manually or semi-automatically and often for small areas only [
1]. For a large area, LoD2 is sufficient since it can provide the basic physical parameters for each building.
The availability of laser scanning techniques, such as Light Detection and Ranging (LiDAR), makes the acquisition of height information of ground features more accurate and easier. In the past two decades, numerous methods for building modeling from LiDAR [
1,
5,
6,
7,
8], high resolution aerial imagery [
9,
10,
11,
12] and multiple data sources [
2,
13,
14,
15] have been developed. Henn [
1] used the supervise classification method to classify and reconstruct a 3D building with prototypical roofs (LoD2) from LiDAR point cloud data in Cologne, Germany. Haala et al. [
6] presented the 3D urban models based on the LiDAR Digital Surface Model (DSM). Alharthy and Bethel [
7] used a moving surface method to extract building roof information from airborne laser scanning altimetry data on Purdue University Campus, Indiana. Ghaffarian and Ghaffarian [
10] introduced simple color space transformation and a novel masking approach to detect buildings from high resolution Google Earth Imagery. Manno-Kovacs and Sziranyi [
11] proposed an aerial building detection method to delineate building outlines from multiple data sources, including aerial and high resolution optical satellite images. Sumer and Turker [
12] provided an adaptive fuzzy-genetic algorithm to detect buildings from 1-m resolution pan-sharpened IKONOS imagery. Haala and Brenner [
14] combined LiDAR DSM and 2D building footprints to build an urban surface model. Awrangjeb et al. [
15] presented an automatic building detection technique using LiDAR point clouds and multispectral imagery. LiDAR data and aerial imagery provide valuable geometry and spectral information of buildings, respectively. Research using multiple data sources can achieve higher building modeling quality than using LiDAR data or high resolution aerial imagery separately, because more information can be extracted.
The general procedure of building modeling includes two steps: the detection of building boundaries and the reconstruction of building models [
13,
15,
16,
17,
18,
19]. The building detection studies [
10,
11,
12,
15,
17,
18,
19] separated building roofs from other features by using a series of hypotheses, which are based on the spatial, spectral and texture characteristics of buildings. Rottensteiner et al. [
17] used the Dempster–Shafer method, which is based on a data fusion theory to detect buildings in densely built-up urban areas. Yang et al. [
18] implemented a marked point process method to extract building outlines from high resolution LiDAR point clouds. Dubois et al. [
19] detected building outlines and retrieved their geometry parameters in high resolution Interferometric Synthetic Aperture Radar (InSAR) phase images. Previous studies have developed the methods for detecting building boundaries well from various data sources, but the automatic reconstruction of accurate roof structures at the LoD2 level of detail remains challenging. Although using the high resolution LiDAR point clouds or InSAR data can improve the accuracy of 3D building reconstruction, it requires a large amount of data. In particular, the reconstruction of mixed and complicated roof structures within large-scale areas is computationally intensive and lacking in effective approaches.
Existing studies of the reconstruction of 3D city models from LiDAR-derived nDSM or high-density point cloud data with or without additional data sources included three major categories of strategies: data-driven (bottom-up) [
5,
7,
8,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32], model-driven (top-down) [
1,
2,
6,
9,
13,
14,
16,
33,
34,
35,
36,
37,
38,
39,
40] and hybrid approaches [
41,
42,
43,
44,
45,
46].
For the data-driven strategies, buildings are considered as the aggregation of roof planes represented by the blocks of point clouds or the digital surface model, which are segmented into different parts by utilizing such algorithms as region growing [
7,
20,
21], random sample consensus (RANSAC) [
22,
23], clustering [
24], ridge or edge based [
5,
25] or a combination of two or several of them [
26,
27,
28,
29,
30,
31,
32].Khoshelham et al. [
20] presented a split-and-merge algorithm, which split image regions whose associated height points do not fall in a single plane and merging coplanar neighboring regions. Rottensteiner and Briese [
21] proposed a method that grouped the decomposed building regions to create polyhedral building models from LiDAR DSM. The neighborhood relations of the planar segments considered for the grouping were derived from a Voronoi diagram of the segment labeled image. Ameri and Fritsch [
22] introduced a RANSAC-based method, which used boundary representation of building hypothesis obtained from high resolution imagery to reconstruct 3D building. Shan and Sampath [
24] used the density-based clustering algorithm to segment the coplanar roof segments based on LiDAR point clouds. Their method calculated the density at each data point and used a connectivity criterion to categorize all connected points that have similar density [
24]. Zhu et al. [
5] developed a building reconstruction pipeline based on sparse LiDAR point clouds (0.8 points/m
2), which was obtained from an open source database to segment the planes in complex flat roofs based on the position of step edges. Wang and Shan [
25] proposed an edge-based segmentation method to extract building roof planes from LiDAR point clouds based on an advanced similarity measure, which was generated by discrete computation geometry and machine learning. Dorninger and Pfeifer [
26] proposed a comprehensive approach to automatically determine 3D city models from LiDAR data by using a reliable 3D segmentation technique combining region growing and hierarchical clustering algorithms together. A similar approach was done by Jochem et al. [
28], which combined region growing and the clustering-based Approximate Nearest Neighbor library (ANN) algorithm together for larger area building reconstruction. Awrangjeb et al. [
29] and Awrangjeb et al. [
32] used the combination of the region growing and edge-based algorithms for automatic 3D roof extraction through the integration of LiDAR and multispectral orthoimagery. They proposed a similar methodology to extract building roofs in a subsequent study [
30], but based solely on raw LiDAR data.
The model-driven approach develops parametric building models, which are stored in a predefined library to reconstruct the given blocks of point clouds or DSM. At the end of the last century, some researchers have started to use this approach to reconstruct basic 3D buildings with rectangular boundaries in the 2D plane, for example, Haala and Brener [
6,
14,
33,
34] and Vosselman et al. [
35,
36]. Many researchers followed their works in recent years and developed advanced methodologiesto reconstruct more complicate roofs in relatively larger areas [
1,
2,
37,
38,
39,
40]. The automated generation of 3D city models can be achieved by using 2D building footprints and LiDAR data [
2,
6,
14,
33,
34,
36,
37,
38], since the 2D building footprints are widely available at a national level for European countries and other developed countries [
1]. Vosselman et al., 2001 [
36], proposed a 3D building reconstruction method using LiDAR data, 2D building footprints and the Hough transform segmentation algorithm. Lafarge et al. [
38] presented a method that reconstructs buildings from a Digital Surface Model (DSM) and 2D building footprints. The 3D blocks were placed on the 2Dsupports using a Gibbs model, which controls both the block assemblage and the fitting to data. A Bayesian decision found the optimal configuration of 3D blocks using a Markov Chain Monte Carlo (MCMC) sampler associated with original proposition kernels. A similar approach for point cloud data has been proposed by Huang et al. [
39].
The data-driven approach has the advantage of detecting basic elements, such as boundaries, ridges and step edges, but the reconstruction quality is limited by the algorithm used for roof planes’ segmentation. For example, the region growing algorithm is subject to seed selection, and it tends to fail to segment roof regions in areas where the roof segment is not smooth or its size is not large enough to contain enough LiDAR points [
7]. The RANSAC algorithm often leads to unneeded false plans, while Tarsha-Kurdi et al. [
23] state that the clustering algorithm needs to define the number of classes and the cluster center subjectively [
24]. The ridge- or edge-based algorithms are too sensitive to ridges or steep edge detection quality [
25]. Although many researchers [
26,
27,
28,
29,
30,
31,
32] attempted to combine multiple algorithms to improve the data-driven approach after they recognized the shortages of each algorithm, they still cannot avoid the common limitation for data-driven approaches that the modeling results are usually affected by the disturbing objects, such as chimneys, dormers and windows [
31]. In some cases, building roofs are occluded by large surrounding trees [
32]. Therefore, they can neither construct a complete roof plane, nor construct irregular planes, and it usually requires a manual mono-plotting procedure to remove incorrect boundaries [
27]. For instance, 15% of the buildings in the final results of [
26] were still lacking completeness. Although the approach in Awrangjeb et al. [
29] has a higher degree of automatic processing, the small planes and planes with low heights still could not be detected properly in the final result. Zhu [
5] identified and adjusted most of the step edges on the roof planes, but still, only 74.6% of the building patches were correctly detected, and errors were caused by noisy segments from vegetation and under-segmentation caused by the limitation of the sparse LiDAR point clouds used, which is 0.8 points per square meter (pts/m
2). The model-driven methods have several advantages. First, in roof primitives, the constraints of member facets are pre-defined and ensure regularized or completed reconstructions [
2]. Then, primitives are combined as if they were the organization of a bunch of facets [
37]. However, a common limitation of the model-driven approach is that there are limited types of models stored in the predefined library. Moreover, the predefined models made the assumptions of ideal roofs, such as that flat roofs always have equal height and convex roofs are symmetric, and significant structures of the roofs are often neglected. Therefore, its applicability for reconstructing accurate building models in a larger area is doubted.
Many researchers tried to utilize the hybrid approach [
41,
42,
43,
44,
45,
46], which integrates data-driven and model-driven approaches, as they think it might produce higher quality (more complete and detailed) building models. The principle is to use data-driven approaches to detect the features, such as ridges and edges, as prior knowledge for a subsequent model-driven approach. Arefi et al. [
41] reconstructed building roofs based on the directions of each extracted ridge line fitted using the RANSAC algorithm from detected local maxima pixels, which followed their previous work [
40]. The reconstruction result was found to be too sensitive to the location and accuracy of the extracted ridge lines. Wang et al. [
42] proposed an approach to reconstruct compound buildings with symmetric roofs using a semantic decomposition algorithm, which decomposes the compound roofs into different semantic primitives based on an attribute graph. However, their methods were limited to the buildings having rectangular footprints and symmetric roof structures. Moreover, the reconstruction did not include buildings with step edges and substructures on the roofs, which are commonly seen in urban commercial areas. Kwak and Habib [
43] introduced a Recursive Minimum Bounding Rectangle (RMBR) algorithm to reconstruct accurate right-angled-corner building models from LiDAR data. Although this approach can minimize the amount of processing in each step via transforming the irregular building shape into a rectangular one, it can only model the types of buildings that can be decomposed into rectangles without losing too many original shapes. In addition, no tiled roofs were reconstructed in this study. Tian et al., 2010 [
44], presented a method for the reconstruction of building models from video image sequences. The accuracy of reconstruction was limited by the video quality. As the author stated, the video camera cannot catch all of the building surfaces and frames at one time, which would lead to missing that information. Fan et al. [
45] presented a building reconstruction method using a hierarchical ridge-based decomposition algorithm to obtained ridge position, as well as the angle and size of roof planes for subsequent model-driven reconstruction, based on high-density (6–9 pts/m
2) LiDAR point cloud data. They achieved a 95.4% completeness for the reconstruction of seven buildings, but as they stated in the conclusion, the limitation of their method is that it has strict requirements for the density of LiDAR point clouds. Otherwise, it may fail. Xu et al. [
46] proposed another approach, which is based on high-density LiDAR point clouds. They applied a RANSAC and ridge detection combined segmentation algorithm to LiDAR point clouds covering two test sites, which have a 4-pts/m
2 and 15-pts/m
2 density, respectively. Their function improved the segmentation accuracy and the topology correctness.
According to the existing studies mentioned above, it can be concluded that the hybrid approach can produce higher reconstruction quality than using data-driven and model-driven approaches separately, as it is more flexible than the model-driven approach and can produce much more complete results than the data-driven approach. However, even more complete planes can be generated by the hybrid approaches’ accuracy of plane boundaries, which still can be limited by the precision of algorithms used in data-driven approaches, which detect the edges and ridges. Some studies [
42,
45,
46] rely on the high resolution LiDAR point cloud data to achieve a high 3D building reconstruction quality. Using the high-density LiDAR point clouds can produce high segmentation accuracy, but it requires very large storage memory in computers and large amounts of time to process when reconstructing buildings within large areas. Point cloud-based segmentation algorithms need to be performed in the computer’s main memory by creating a suitable spatial indexing method of the point dataset [
28]. This can lead to the consequence that the segmentation of large LiDAR point datasets is difficult to execute within a common GIS environment because the main memory of common computer hardware would likely be exceeded [
28]. The sparse LiDAR point clouds or downscaled moderate resolution LiDAR normalized DSM (nDSM), on the other hand, requires much smaller space for storage while maintaining acceptable precision compared to high resolution point clouds, which need less memory and time for processing to reconstruct 3D buildings in large areas. Moreover, many GIS raster-based algorithms can directly be applied to nDSM data, which is also convenient. However, the previous model-driven [
2,
34,
37,
39] and hybrid [
41] approaches, which utilized the LiDAR nDSM, only focused on rectangular or symmetric tiled roof reconstruction. The irregular or more complicated roofs, which mixed tiled, flat and shed structures, were not well presented. In addition, many small planes were not reconstructed properly, and the accuracies of ridge positions were not assessed. The major reason for those limitations in the existing studies is that there is an absence of robust methods to reconstruct 3D buildings based on medium spatial resolution nDSM.
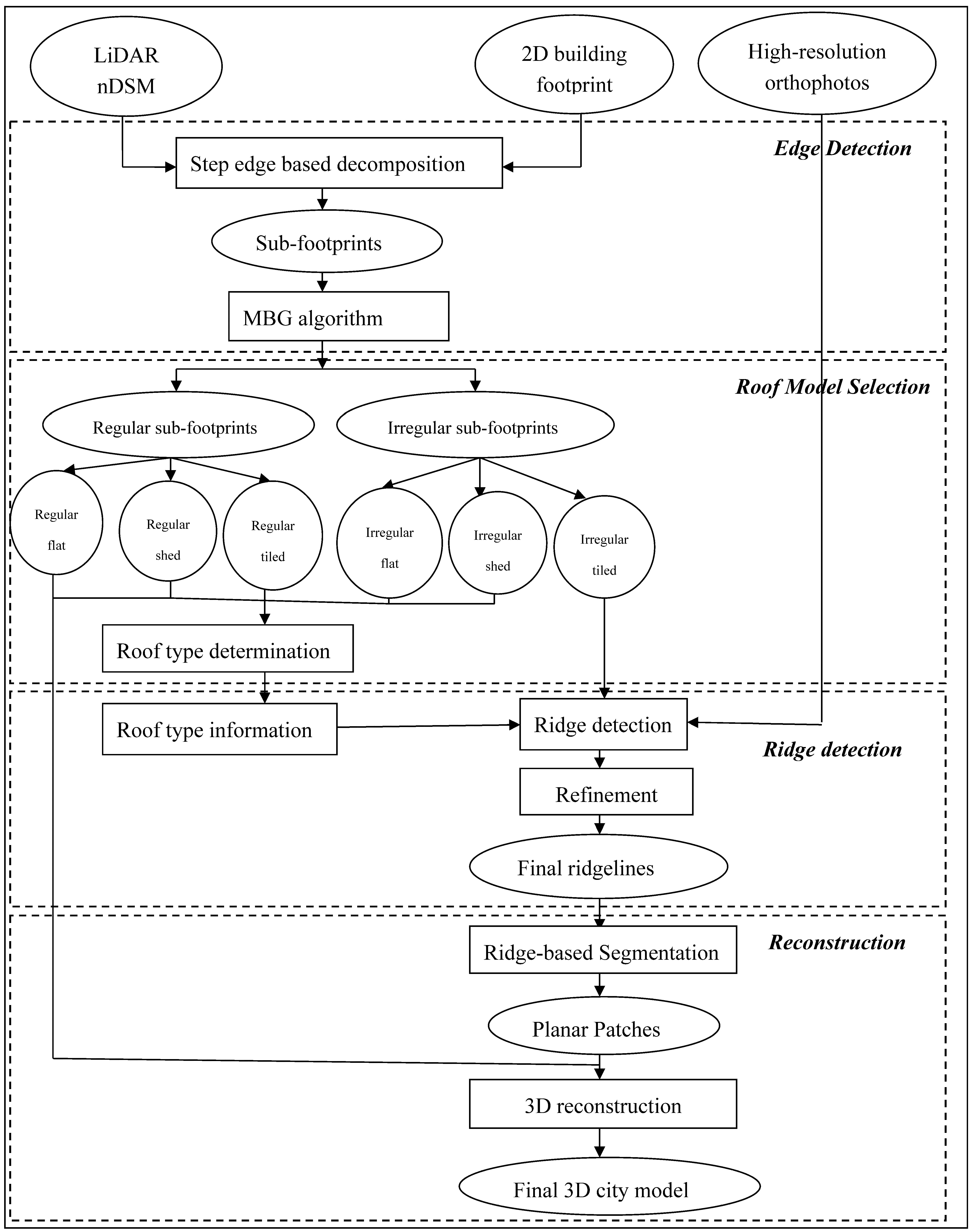
It can be concluded from the above studies that the limitation remains for current studies of 3D building reconstruction, even if the hybrid approaches were used. The greatest challenge is how to overcome the limitations of the efficiency of data processing and the robustness of the methodology to achieve higher accuracy when reconstructing complicated building roofs in large areas. In this paper, we propose a hybrid approach, combining the data- and model-driven approaches for generating LoD2-level building models by using downscaled LiDAR nDSM data. The main objective is to develop a GIS-based workflow for automatically reconstructing complicated building roof structures in large areas with high accuracy, but without requiring high-density point clouds and computationally-intensive algorithms. The proposed approach is expected to provide a product that is easy to operate in a GIS database environment, which allows additional attributes, such as materials, height, area, slope, aspect and time-dependent shadowing status, to be assigned in the attached attribute fields for further applications: urban morphology studies, urban building energy studies, environmental modeling studies and roof solar potential analysis.