Elevation Change and Improved Velocity Retrieval Using Orthorectified Optical Satellite Data from Different Orbits
Abstract
:1. Introduction
2. Image Processing Background
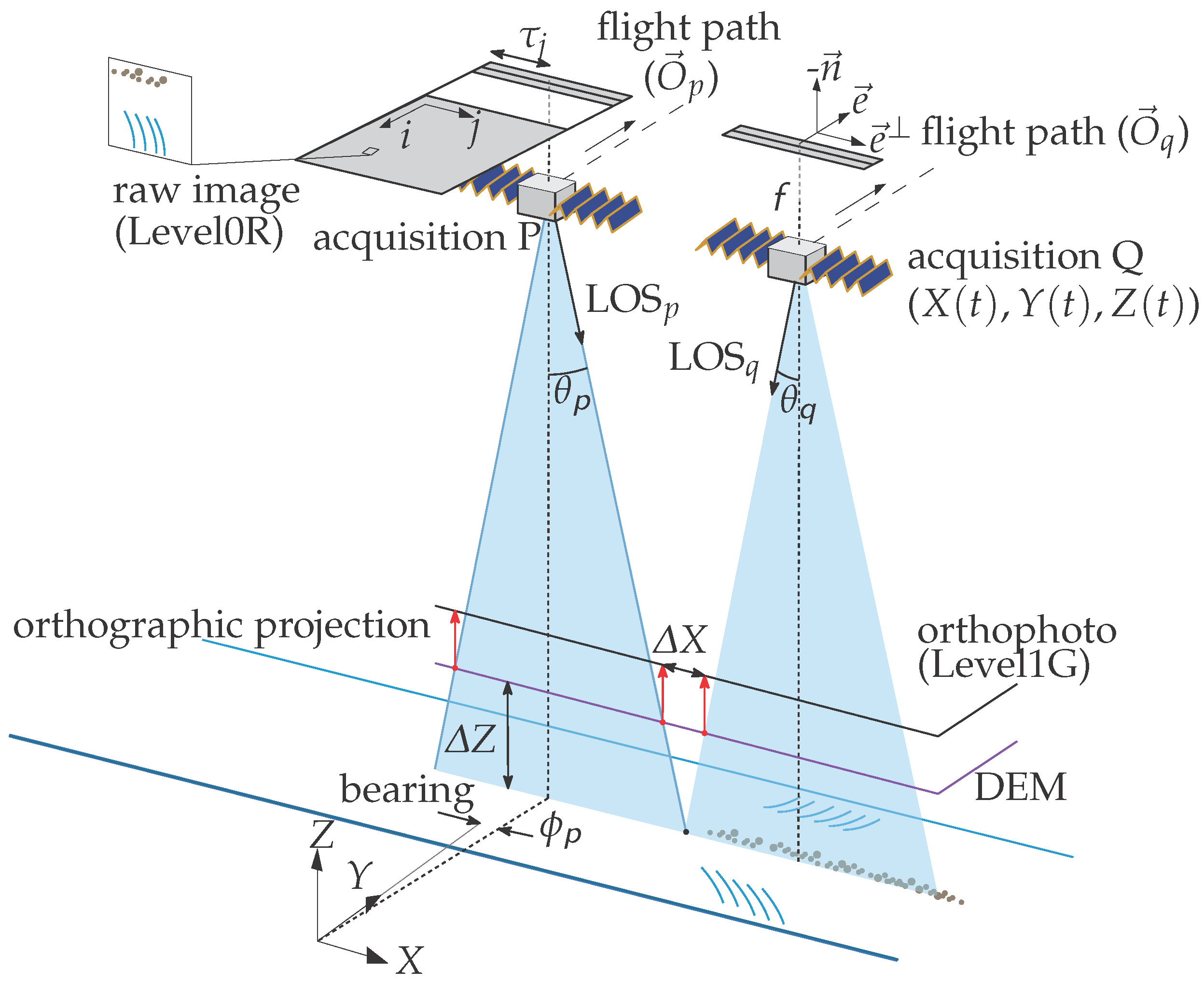
2.1. Sensor Geometry
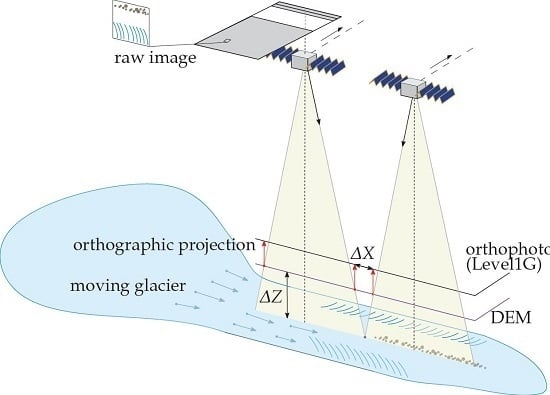
2.2. Orthorectification
2.3. Projective Geometry
2.4. Parameter Estimation
2.5. Image Matching
3. Implementation
3.1. Speed Regime
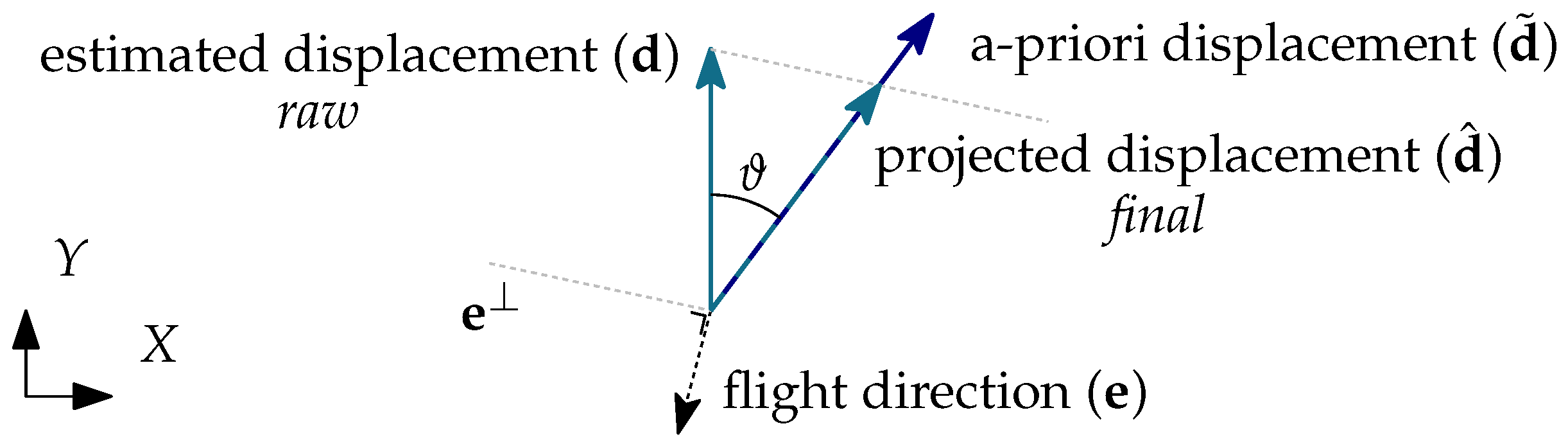
3.2. Velocity Projection
4. Data and Study Areas
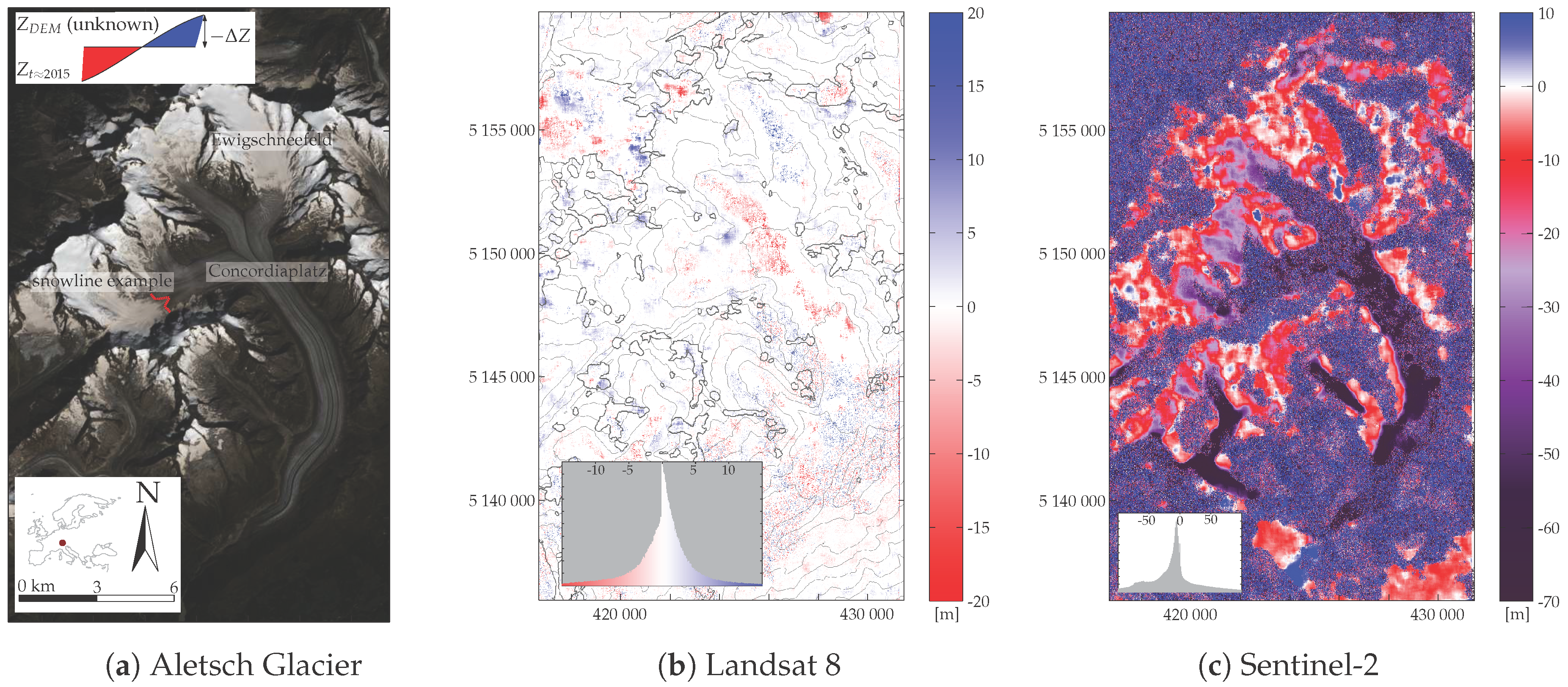
4.1. Aletsch, Switzerland
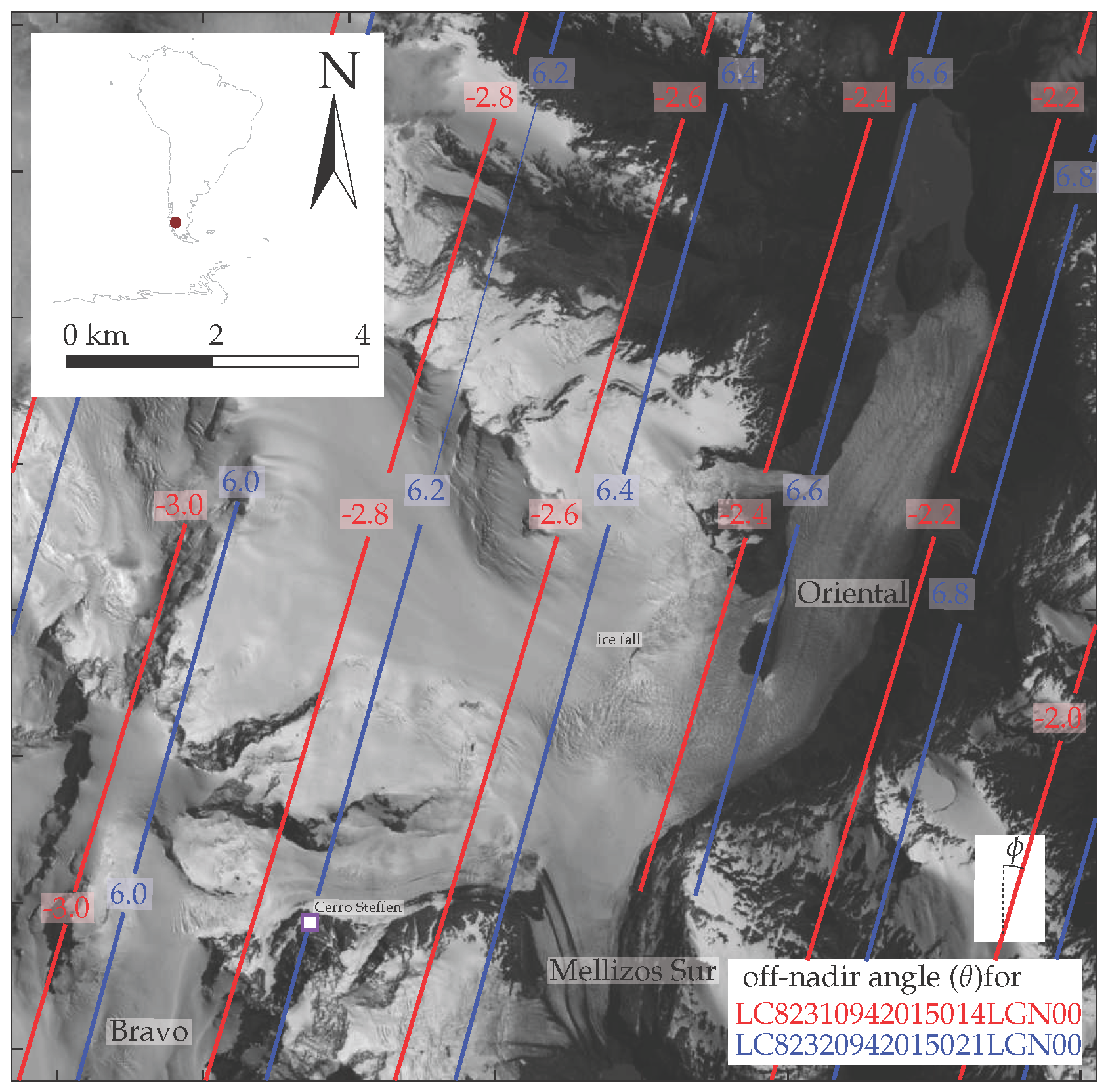
4.2. Oriental, Patagonia
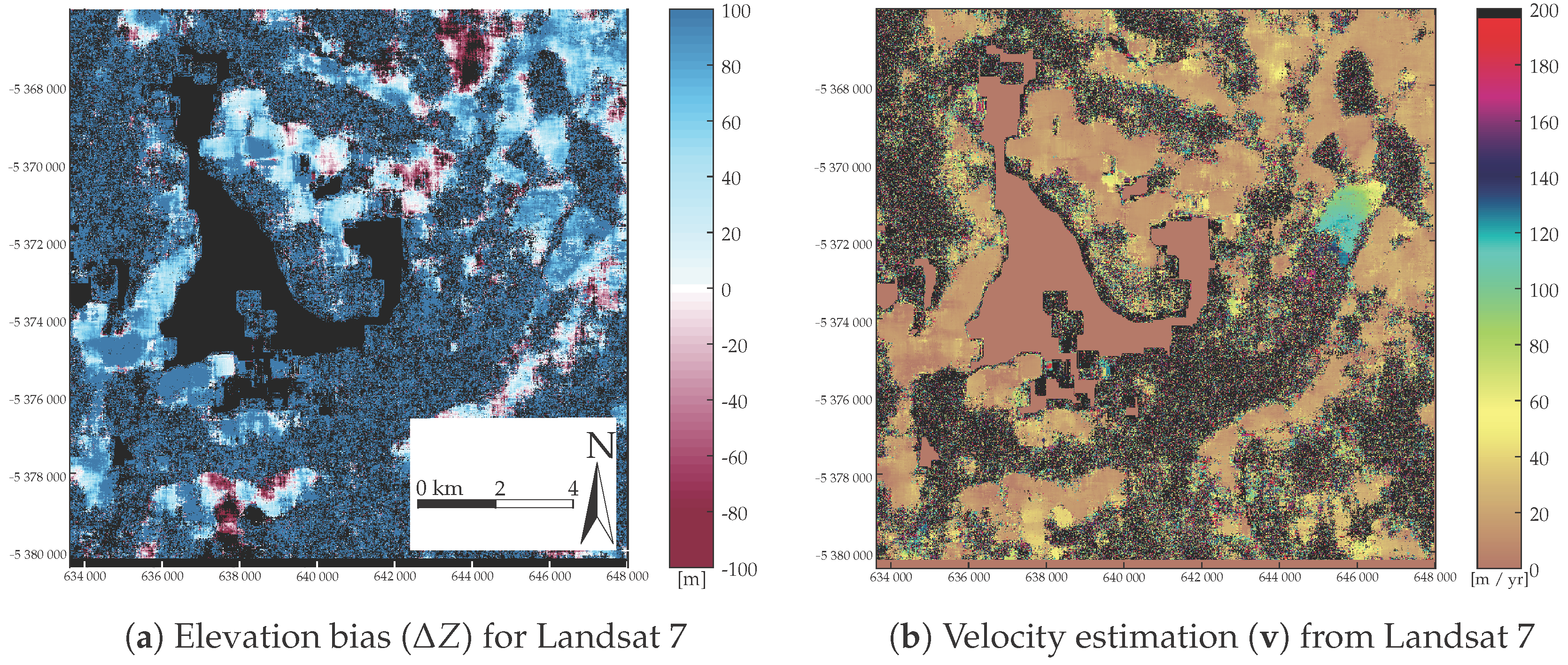
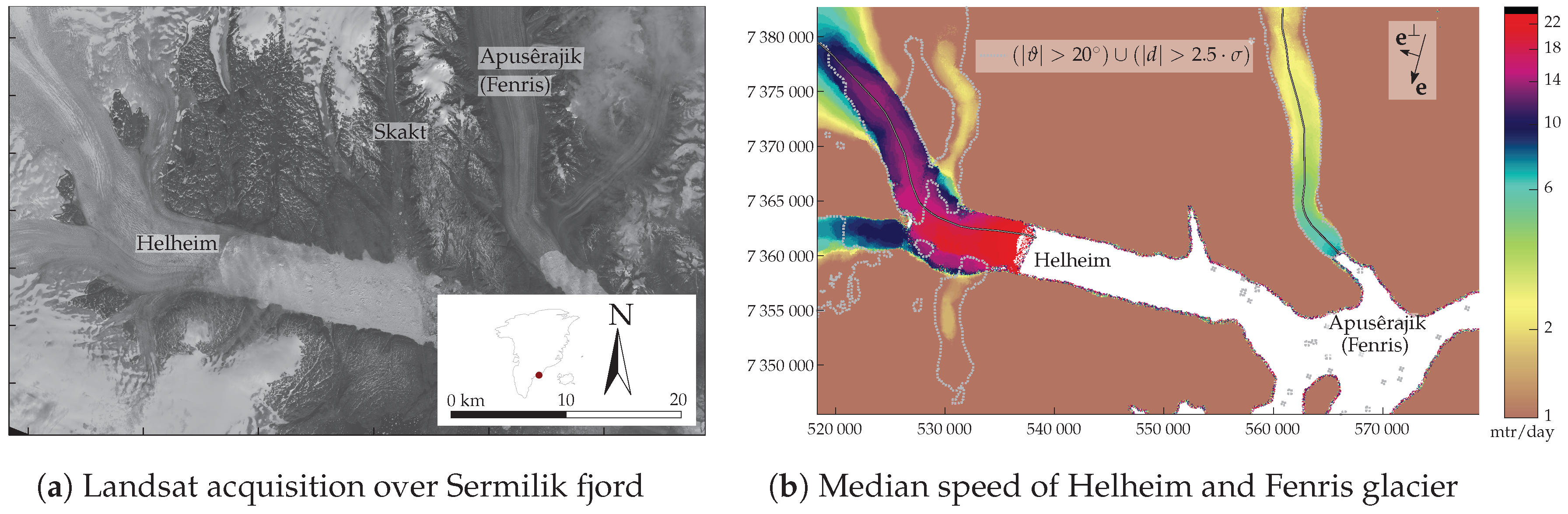
4.3. Helheim, Greenland
5. Results
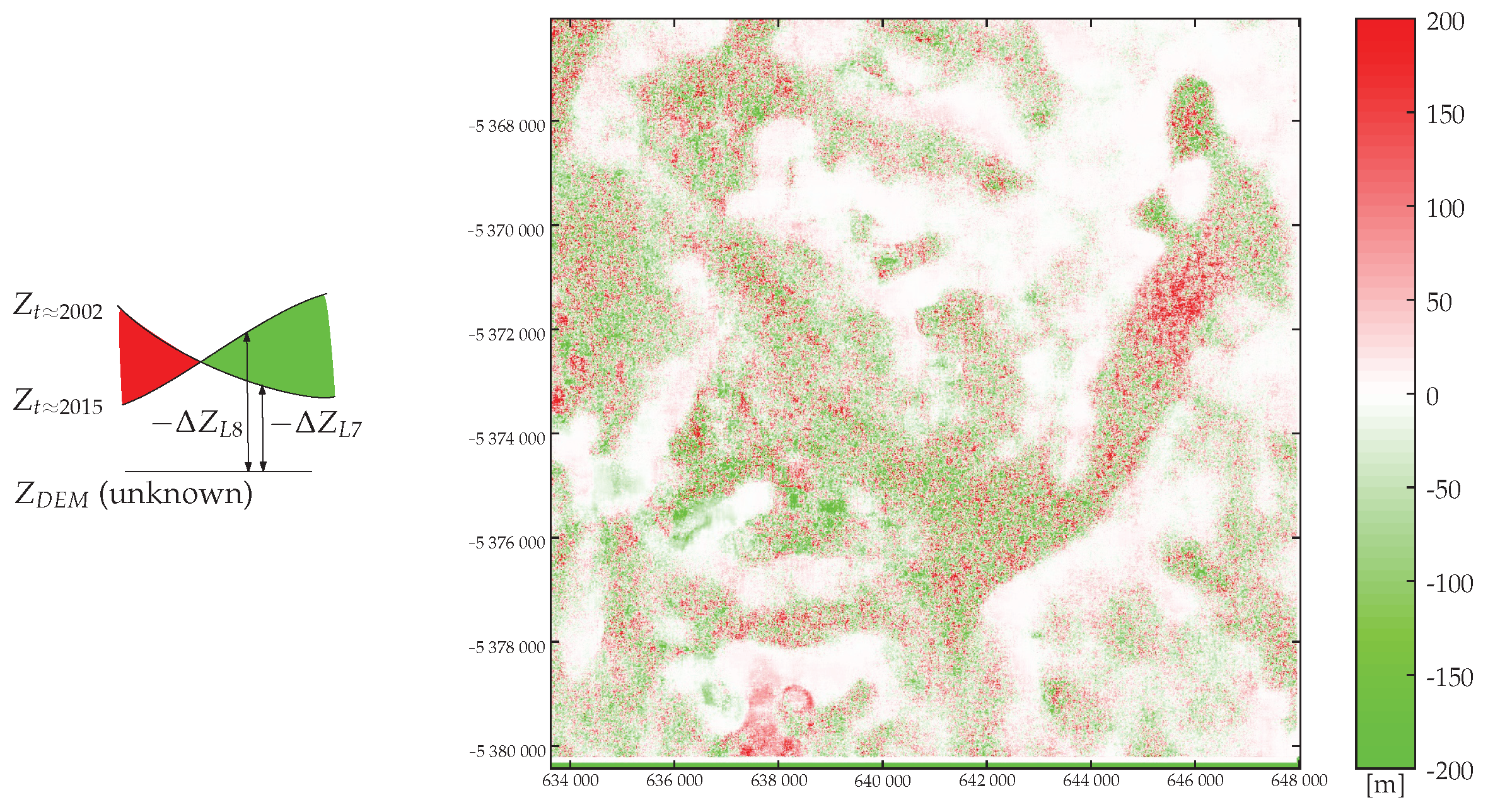
5.1. DEM Bias (Aletsch Glacier)
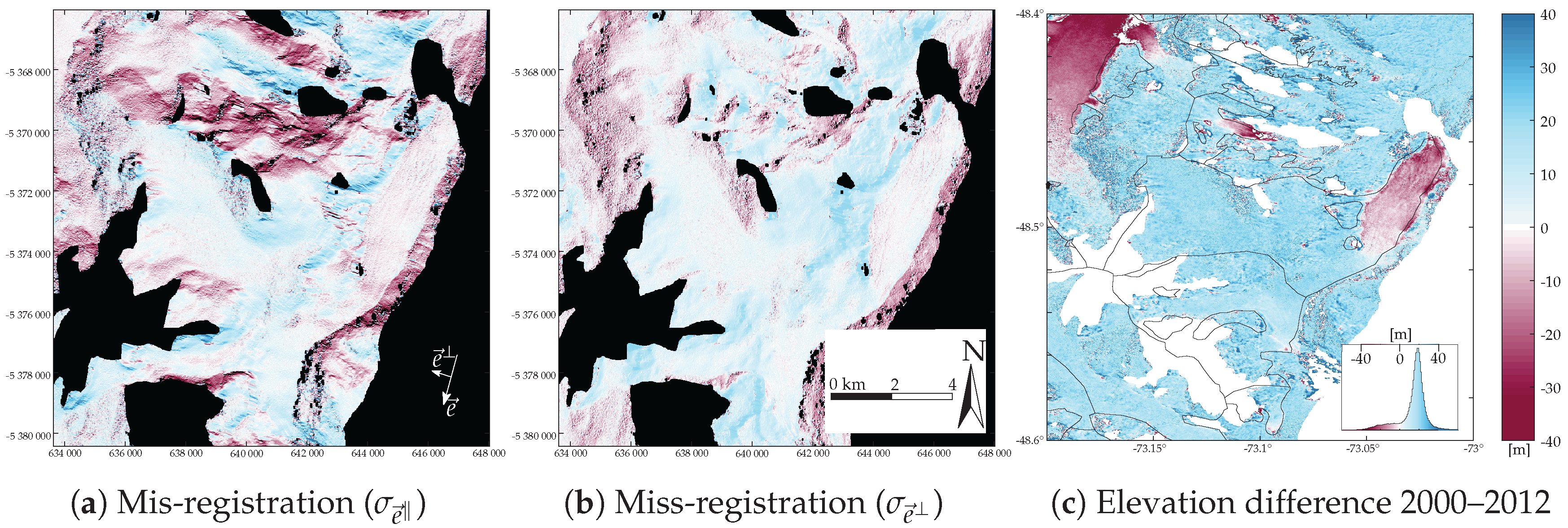
5.2. Elevation Change over Time (Oriental Glacier)
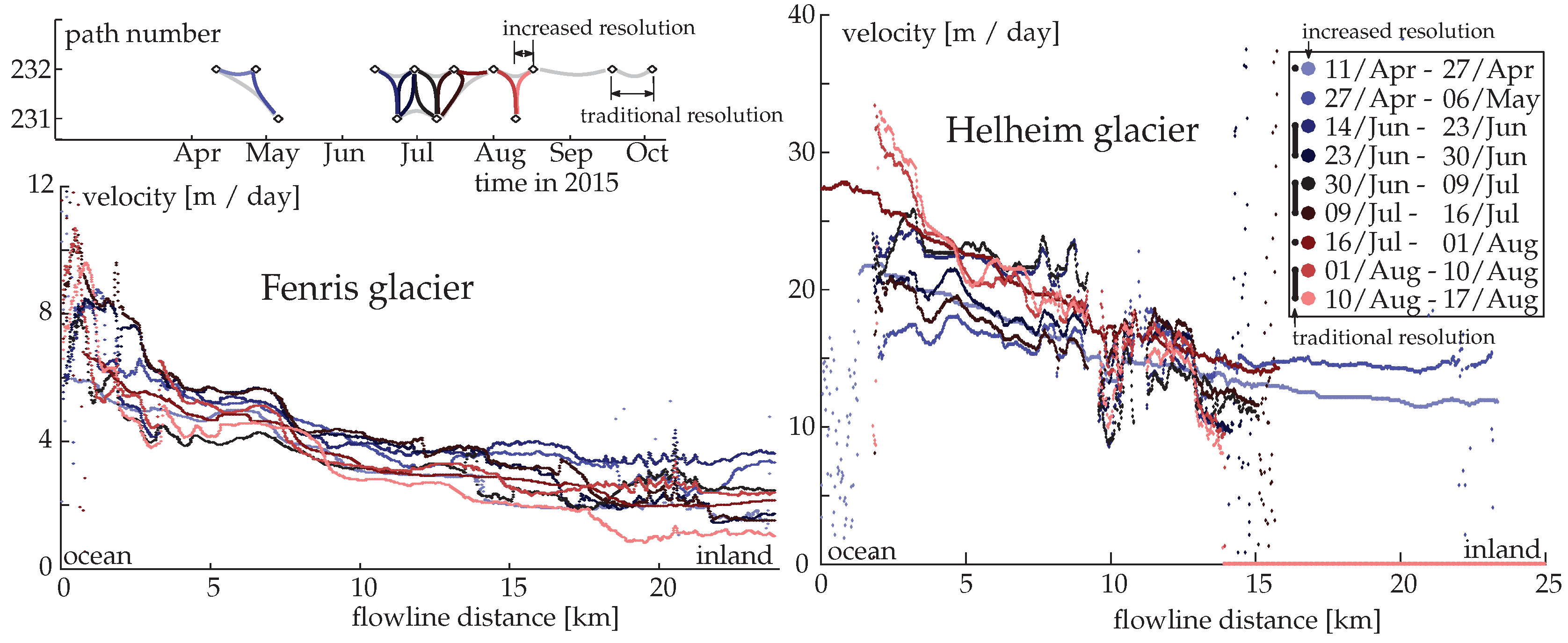
5.3. Increased Temporal Resolution (Helheim Glacier)
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ASTER | Advanced Spaceborne Thermal Emission and Reflection Radiometer |
| CBERS | China–Brazil Earth Resources Satellite |
| DEM | Digital Elevation Model |
| DLR | Deutsches zentrum für Luft- und Raumfahrt |
| DTED | Digital Terrain Elevation Data |
| ESA | European Space Agency |
| GDEM | Global Digital Elevation Model |
| ISS | International Space Station |
| LOS | line of sight |
| RADAR | RAdio Detection And Ranging |
| RMSE | Root Mean Square Error |
| SAR | Synthetic Aperture Radar |
| SNR | signal-to-noise ratio |
| SPOT | Satellite Pour l’Observation de la Terre |
| SRTM | Shuttle Radar Topography Mission |
| USGS | United States Geological Survey |
| ZY3 | Ziyuan-3, Resources-3 |
| Fourier transform | |
| Initial parameter | |
| Estimated parameter | |
| * | Complex conjugate |
| Matrix inverse | |
| Matrix transpose | |
| Expectation operator | |
| Rotation |
| i | Image coordinate in along-track direction |
| j | Image coordinate in cross-track direction |
| Image coordinate translation from center of scene to the corner of the sensor | |
| α | Normalized focal length |
| Flight direction of satellite | |
| Normal of satellite | |
| X | Metric coordinate in along-track direction |
| Y | Metric coordinate in cross-track direction |
| Z | Metric coordinate in zenit direction |
| Camera matrix | |
| Rotation matrix | |
| p | Point in an image |
| P | Point on the earth surface |
| f | Focal length |
| m | Size of photosensative cell |
| Vertical bias between real surface and elevation model | |
| Lateral displacement due to orthorectification error | |
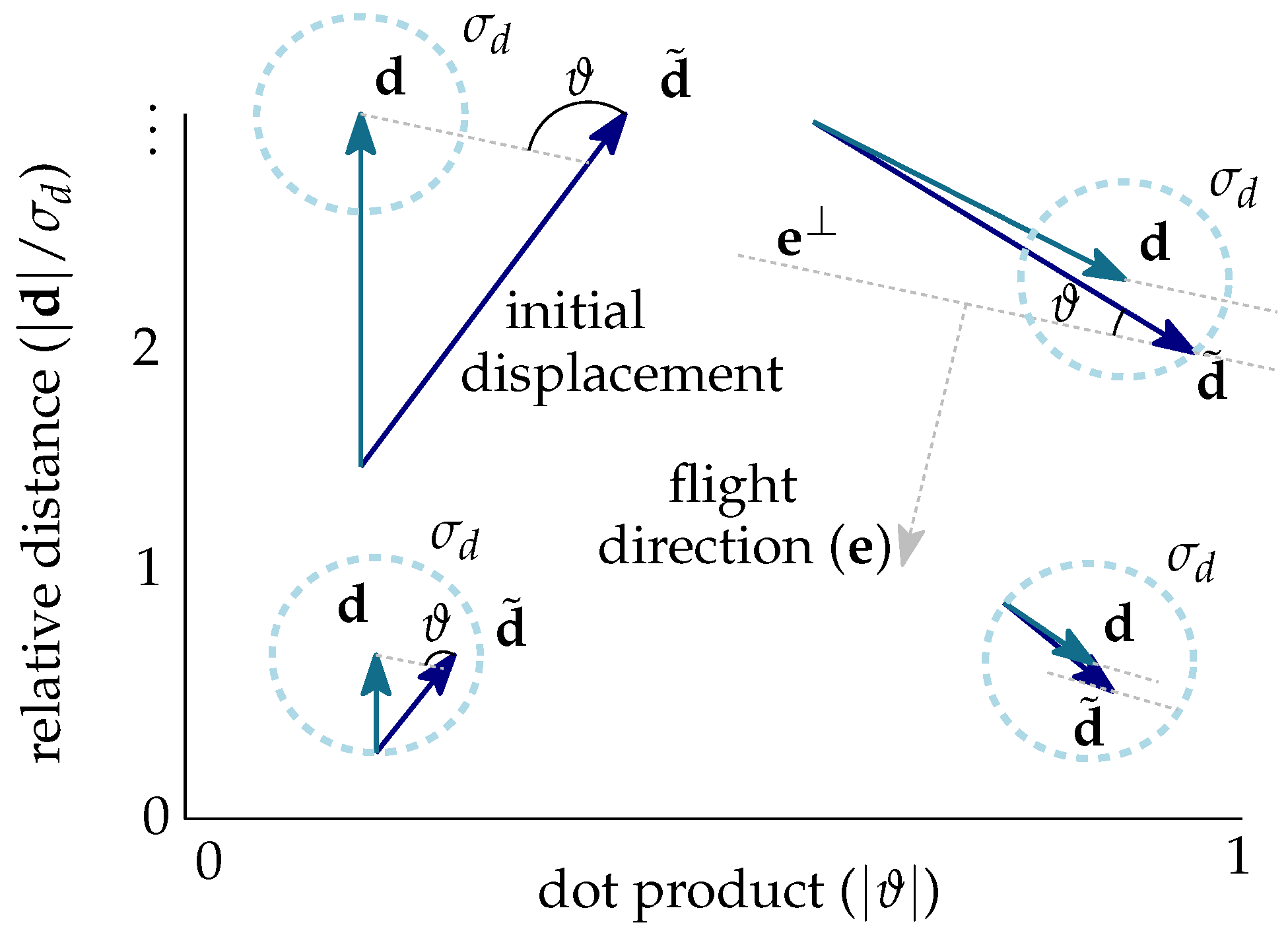
| θ | Zenit distance in cross-track direction |
| φ | Bearing of satellite flight path |
| Line of sight vector in cross-track direction | |
| Relative displacement of a feature between images | |
| Design matrix | |
| Measurement vector | |
| Vector with unknown parameter | |
| u | Velocity along the X-axis |
| v | Velocity along the Y-axis |
| Time separation between two acquisitions | |
| Configuration matrix | |
| ∇ | Terrain correction |
| Dispersion matrix | |
| σ | Dispersion |
| ϑ | Relative angle between initial displacement and epipolar line |
| Image (subset) | |
| Displacement matrix |
Appendix A

References
- Kääb, A.; Leprince, S. Motion detection using near-simultaneous satellite acquisitions. Remote Sens. Environ. 2014, 154, 164–179. [Google Scholar] [CrossRef]
- Van der Veen, C. Fundamentals of Glacier Dynamics; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Nick, F.; Van der Veen, C.; Vieli, A.; Benn, D. A physically based calving model applied to marine outlet glaciers and implications for the glacier dynamics. J. Glaciol. 2010, 56, 781–794. [Google Scholar] [CrossRef]
- Fahnestock, M.; Scambos, T.; Moon, T.; Gardner, A.; Haran, T.; Klinger, M. Rapid large-area mapping of ice flow using Landsat 8. Remote Sens. Environ. 2016, 185, 84–94. [Google Scholar] [CrossRef]
- Dehecq, A.; Gourmelen, N.; Trouve, E. Deriving large-scale glacier velocities from a complete satellite archive: Application to the Pamir–Karakoram–Himalaya. Remote Sens. Environ. 2015, 162, 55–66. [Google Scholar] [CrossRef]
- Rosenau, R.; Scheinert, M.; Dietrich, R. A processing system to monitor Greenland outlet glacier velocity variations at decadal and seasonal time scales utilizing the Landsat imagery. Remote Sens. Environ. 2015, 169, 1–19. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Wolfe, R. Automated registration and orthorectification package for Landsat and Landsat-like data processing. J. Appl. Remote Sens. 2009, 3, 033515. [Google Scholar]
- Bian, J.H.; Li, A.N.; Jin, H.A.; Lei, G.B.; Huang, C.Q.; Li, M.X. Auto-registration and orthorecification algorithm for the time series HJ-1A/B CCD images. J. Mt. Sci. 2013, 10, 754–767. [Google Scholar] [CrossRef]
- Devaraj, C.; Shah, C. Automated geometric correction of Landsat MSS L1G imagery. IEEE Geosci. Remote Sens. Lett. 2014, 11, 347–351. [Google Scholar] [CrossRef]
- Devaraj, C.; Shah, C. Automated geometric correction of multispectral images from High Resolution CCD Camera (HRCC) on-board CBERS-2 and CBERS-2B. ISPRS J. Photogramm. Remote Sens. 2014, 89, 13–24. [Google Scholar] [CrossRef]
- Altena, B.; Kääb, A.; Nuth, C. Robust glacier displacements using knowledge-based image matching. In Proceedings of the 2015 8th International Workshop on the Analysis of Multitemporal Remote Sensing Images (Multi-Temp), Annecy, France, 22–24 July 2015; pp. 1–4.
- Stumpf, A.; Malet, J.P.; Delacourt, C. Correlation of satellite image time-series for the detection and monitoring of slow-moving landslides. Remote Sens. Environ. 2017, 189, 40–55. [Google Scholar] [CrossRef]
- Jeong, S.; Howat, I.M.; Ahn, Y. Improved multiple matching method for observing glacier motion with repeat image feature tracking. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2431–2441. [Google Scholar] [CrossRef]
- Moons, T.; Van Gool, L.; Vergauwen, M. 3D Reconstruction from Multiple Images, Part 1: Principles; Foundations and Trends® in Computer Graphics and Vision; Now Publishers Inc.: Breda, The Netherlands, 2009. [Google Scholar]
- Tucker, C.; Grant, D.; Dykstra, J. NASAs global orthorectified Landsat data set. Photogramm. Eng. Remote Sens. 2004, 70, 313–322. [Google Scholar] [CrossRef]
- Storey, J.; Strande, D.; Hayes, R.; Meyerink, A.; Labahn, S.; Lacasse, J. Landsat 7 Image Assessment System (IAS) Geometric Algorithm Theoretical Basis Document; Technical Report; USGS: Reston, VA, USA, 2006.
- Chen, L.C.; Lee, L.H. Rigorous generation of digital orthophotos from SPOT images. Photogramm. Eng. Remote Sens. 1993, 59, 655–661. [Google Scholar]
- Sun, G.; Ranson, K.; Kharuk, V.; Kovacs, K. Validation of surface height from shuttle radar topography mission using shuttle laser altimeter. Remote Sens. Environ. 2003, 88, 401–411. [Google Scholar] [CrossRef]
- Kääb, A. Remote Sensing of Mountain Glaciers and Permafrost Creep; Geographisches Institut der Universität Zürich: Zürich, Switzerland, 2005. [Google Scholar]
- Kääb, A.; Winsvold, S.; Altena, B.; Nuth, C.; Nagler, T.; Wuite, J. Glacier Remote Sensing using Sentinel-2. Part I: Radiometric and Geometric Performance, Application to Ice Velocity, and Comparison to Landsat 8. Remote Sens. 2016, 8, 598. [Google Scholar] [CrossRef]
- Teunissen, P. Adjustment Theory. An Introduction, Series on Mathematical Geodesy and Positioning; VSSD: Delft, The Netherlands, 2003. [Google Scholar]
- Barron, J.; Fleet, D.; Beauchemin, S. Performance of optical flow techniques. Int. J. Comput. Vis. 1994, 12, 43–77. [Google Scholar] [CrossRef]
- Baker, S.; Scharstein, D.; Lewis, J.; Roth, S.; Black, M.; Szeliski, R. A database and evaluation methodology for optical flow. Int. J. Comput. Vis. 2011, 92, 1–31. [Google Scholar] [CrossRef]
- Vogel, C.; Bauder, A.; Schindler, K. Optical Flow for Glacier Motion Estimation. In Proceedings of the 22nd ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012.
- Altena, B.; Kääb, A. Weekly glacier flow estimation from dense satellite time series using adapted optical flow technology. Front. Earth Sci. 2017. in review. [Google Scholar]
- Tuytelaars, T.; Mikolajczyk, K. Local invariant feature detectors: A survey. Found. Trends Comput. Gr. Visi. 2008, 3, 177–280. [Google Scholar] [CrossRef]
- Tola, E.; Lepetit, V.; Fua, P. Daisy: An efficient dense descriptor applied to wide-baseline stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 815–830. [Google Scholar] [CrossRef] [PubMed]
- Kokkinos, I.; Bronstein, M.; Yuille, A. Dense Scale Invariant Descriptors for Images and Surfaces; INRIA: Paris, France, 2012. [Google Scholar]
- Muye, N.; Chunxia, Z.; Tingting, L. Derivation of ice-flow of Polar Record Glacier using an improved NCC algorithm. Chin. J. Polar Res. 2016, 28, 243–249. [Google Scholar]
- Bindschadler, R.; Scambos, T. Satellite-image-derived velocity field of an Antarctic ice stream. Science 1991, 252, 242. [Google Scholar] [CrossRef] [PubMed]
- Scambos, T.; Dutkiewicz, M.; Wilson, J.; Bindschadler, R. Application of image cross-correlation to the measurement of glacier velocity using satellite image data. Remote Sens. Environ. 1992, 42, 177–186. [Google Scholar] [CrossRef]
- Kääb, A.; Vollmer, M. Surface geometry, thickness changes and flow fields on creeping mountain permafrost: Automatic extraction by digital image analysis. Permafr. Periglac. Process. 2000, 11, 315–326. [Google Scholar] [CrossRef]
- Heid, T.; Kääb, A. Evaluation of existing image matching methods for deriving glacier surface displacements globally from optical satellite imagery. Remote Sens. Environ. 2012, 118, 339–355. [Google Scholar] [CrossRef]
- Ahn, Y.; Howat, I. Efficient automated glacier surface velocity measurement from repeat images using multi-image/multichip and null exclusion feature tracking. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2838–2846. [Google Scholar]
- Goshtasby, A. Image Registration: Principles, Tools and Methods; Advances in Computer Vision and Pattern Recognition; Springer: Berlin, Germany, 2012. [Google Scholar]
- Erten, E. Glacier velocity estimation by means of a polarimetric similarity measure. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3319–3327. [Google Scholar] [CrossRef]
- Rolstad, C.; Amlien, J.; Hagen, J.O.; Lundén, B. Visible and near-infrared digital images for determination of ice velocities and surface elevation during a surge on Osbornebreen, a tidewater glacier in Svalbard. Ann. Glaciol. 1997, 24, 255–261. [Google Scholar] [CrossRef]
- Hart, D. PIV error correction. Exp. Fluids 2000, 29, 13–22. [Google Scholar] [CrossRef]
- Bauder, A.; Funk, M.; Huss, M. Ice-volume changes of selected glaciers in the Swiss Alps since the end of the 19th century. Ann. Glaciol. 2007, 46, 145–149. [Google Scholar] [CrossRef]
- White, A.; Copland, L. Decadal-scale variations in glacier area changes across the Southern Patagonian Icefield since the 1970s. Arct. Antarct. Alp. Res. 2015, 47, 147–167. [Google Scholar] [CrossRef]
- Lopez, P.; Chevallier, P.; Favier, V.; Pouyaud, B.; Ordenes, F.; Oerlemans, J. A regional view of fluctuations in glacier length in southern South America. Glob. Planet. Chang. 2010, 71, 85–108. [Google Scholar] [CrossRef]
- Davies, B.; Glasser, N. Accelerating shrinkage of Patagonian glaciers from the Little Ice Age (AD 1870) to 2011. J. Glaciol. 2012, 58, 1063–1084. [Google Scholar] [CrossRef]
- Willis, M.; Melkonian, A.; Pritchard, M.; Rivera, A. Ice loss from the Southern Patagonian Ice Field, South America, between 2000 and 2012. Geophys. Res. Lett. 2012, 39, L17501. [Google Scholar] [CrossRef]
- Rignot, E.; Rivera, A.; Casassa, G. Contribution of the Patagonia Icefields of South America to sea level rise. Science 2003, 302, 434–437. [Google Scholar] [CrossRef] [PubMed]
- Howat, I.; Joughin, I.; Tulaczyk, S.; Gogineni, S. Rapid retreat and acceleration of Helheim Glacier, east Greenland. Geophys. Res. Lett. 2005. [Google Scholar] [CrossRef]
- Stearns, L.; Hamilton, G. Rapid volume loss from two East Greenland outlet glaciers quantified using repeat stereo satellite imagery. Geophys. Res. Lett. 2007. [Google Scholar] [CrossRef]
- Joughin, I.; Howat, I.; Alley, R.; Ekström, G.; Fahnestock, M.; Moon, T.; Nettles, M.; Truffer, M.; Tsai, V. Ice-front variation and tidewater behavior on Helheim and Kangerdlugssuaq Glaciers, Greenland. J. Geophys. Res. Earth Surf. 2008. [Google Scholar] [CrossRef]
- Mernild, S.; Malmros, J.; Yde, J.; Knudsen, N. Multi-decadal marine-and land-terminating glacier recession in the Ammassalik region, southeast Greenland. Cryosphere 2012, 6, 625–639. [Google Scholar] [CrossRef]
- Rignot, E.; Echelmeyer, K.; Krabill, W. Penetration depth of interferometric synthetic-aperture radar signals in snow and ice. Geophys. Res. Lett. 2001, 28, 3501–3504. [Google Scholar] [CrossRef]
- Berthier, E.; Arnaud, Y.; Vincent, C.; Remy, F. Biases of SRTM in high-mountain areas: Implications for the monitoring of glacier volume changes. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Strozzi, T.; Delaloye, R.; Kääb, A.; Ambrosi, C.; Perruchoud, E.; Wegmüller, U. Combined observations of rock mass movements using satellite SAR interferometry, differential GPS, airborne digital photogrammetry, and airborne photography interpretation. J. Geophys. Res. Earth Surf. 2010. [Google Scholar] [CrossRef]
- Paul, F. Calculation of glacier elevation changes with SRTM: Is there an elevation-dependent bias? J. Glaciol. 2008, 54, 945–946. [Google Scholar] [CrossRef]
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altena, B.; Kääb, A. Elevation Change and Improved Velocity Retrieval Using Orthorectified Optical Satellite Data from Different Orbits. Remote Sens. 2017, 9, 300. https://doi.org/10.3390/rs9030300
Altena B, Kääb A. Elevation Change and Improved Velocity Retrieval Using Orthorectified Optical Satellite Data from Different Orbits. Remote Sensing. 2017; 9(3):300. https://doi.org/10.3390/rs9030300
Chicago/Turabian StyleAltena, Bas, and Andreas Kääb. 2017. "Elevation Change and Improved Velocity Retrieval Using Orthorectified Optical Satellite Data from Different Orbits" Remote Sensing 9, no. 3: 300. https://doi.org/10.3390/rs9030300
APA StyleAltena, B., & Kääb, A. (2017). Elevation Change and Improved Velocity Retrieval Using Orthorectified Optical Satellite Data from Different Orbits. Remote Sensing, 9(3), 300. https://doi.org/10.3390/rs9030300