1. Introduction
Commercial Airborne Laser Scanning (ALS) systems emerged in the mid-1990s for bathymetric and topographic applications. With the aid of direct geo-referencing technique, laser scanning equipment installed in the aircraft collect a cloud of laser range measurements for calculating the 3D coordinates (xyz) of the survey area [
1]. In contrast to the 2D remote sensing imagery, an ALS point cloud is a swarm of points with XYZ coordinates [
2], and thus describes the 3D topographic profiles of natural surfaces. Moreover, ALS point clouds have other benefits such as no effects of relief displacement, penetration of vegetation, and insensitivity to lighting conditions [
1]. Therefore, ALS technique has been effectively used for ground point detection [
3,
4,
5,
6,
7], topographic mapping [
8], 3D city modelling [
9,
10,
11,
12,
13], object recognition [
14,
15,
16], solar energy estimation [
17], etc.
Over the last two decades, significant contributions to the consolidation and extension of ALS data processing methods have been witnessed [
1]. Among these processing methods, classifying the ALS data into categorical object instances is the first and most critical step for further data processing and model reconstruction [
18]. Based on the granularity of basic processing units, these existing classification strategies can be categorized into three groups, i.e., point-based classification [
18,
19,
20], segment-based classification [
21,
22,
23,
24], and multiple-entity-based classification [
25]. A brief description of these existing methods is provided as follows.
1.1. Strategies for ALS Data Classification
1.1.1. Point-Based Classification
This kind of classification has attracted the most majority of research works in contrast to the other two kinds of classification strategies. In the process of point-based classification, ALS features of individual points [
19] are firstly extracted. Then a classifier such as JointBoost [
18] is trained using a number of selected training samples. Finally, the input ALS point cloud is classified via the trained classifier and the extracted features.
Additionally, to compute the features of individual points, a respective neighborhood definition is required to describe the local 3D structure around each individual point. Generally, there are three kinds of neighborhoods, i.e., spherical neighborhood [
26], cylindrical neighborhood [
27], and
-closest neighborhood [
28]. Among the three neighborhoods, the scale parameter, either a fixed radius or a constant value
, is required. Due to the variation of local 3D structures and point densities, the constant scale parameter often fails to describe the local structural configurations. Thus, more and more studies such as [
18,
29,
30,
31,
32,
33,
34] focus on seeking an optimal neighborhood size for each individual point. Unfortunately, these neighborhood optimization methods require repetitive calculations of eigenvectors and eigenvalues for each point, therefore they are rather time-consuming [
35], which is the main disadvantage of this kind of classification.
1.1.2. Segment-Based Classification
Point cloud segmentation has been involved in ALS point cloud classification since its emergence. Generally, segment-based classification methods first perform segmentation on the point cloud after removing the ground points [
21]. Then, the non-ground points are segmented into a number of segments, and features are extracted for each segment. Finally, a fuzzy model classifier [
21,
36] or several classification rules [
22,
24] are utilized to classify the segments. However, most of these studies are for non-ground points, and none of them uses Random Forests (RF) for feature selection and classification.
In addition, segment-based classification relies heavily on its employed segmentation method. A variety of point cloud segmentation methods have been proposed, which can be roughly classified as model-fitting-based methods, region-growing-based (RG-based) methods, and clustering-feature-based methods [
37]. However, these existing methods segment input 3D point clouds into only one type of geometric structure. Actually, point clouds consist of a variety of geometric structures, such as planes, smooth surfaces and rough surfaces. In a complex 3D scene, there may exist regular and irregular man-made objects, and natural objects. Regular man-made objects such as buildings are composed of planar surfaces and smooth surfaces, while irregular man-made objects such as cars and natural objects like trees are composed of rough surfaces.
Therefore, segmenting point clouds into only one type of geometric structure is unreasonable. For example, existing planar segmentation methods segment all the points in an input point cloud into planes. If points are on building roofs, these methods are logical and perform well, however, if the points are on trees or cars, these methods which roughly segment these points into false planes are illogical. To obtain a superior classification result, we should consider a query point’s geometric structure, and then segment it into a planar surface, smooth surface, or rough surface.
Although the aforementioned limitations exist, segment-based methods still have two main benefits in contrast to point-based classification methods, i.e., (i) segments are helpful to compute geometric features which relieve the dependence on neighborhood optimization [
18,
34] methods, and (ii) segments give several new attributes which are helpful to employ semantic rules.
1.1.3. Multiple-Entity-Based Classification
Multiple-entity-based classification [
25] is considered as a combination of the segment-based and point-based classification. To solve the problem that a complex 3D scene is difficult to be characterized by only individual points or one kind of segments, this method utilizes three kinds of entities, i.e., points, planar segments, mean shift segments. In the process of classification, the input ALS point cloud is first divided into ground points and non-ground points. Next, planar segments are extracted from the non-ground points, and the scattered points are remained. Then, the planar segments are classified into several classes. The remained points are point-wise classified based on the contextual information offered by the classified planar segments. Finally, in complex areas where vegetation covers building roofs, mean shift segments are extracted to classify these areas.
However, the process of this method is a hierarchical classification procedure, which involves many steps. Besides, the mean shift segments and planar segments are derived from different segmentation methods, which adds additional classification steps. To simplify the classification process, a point cloud segmentation method that is able to extract more than one kind of segments is required.
These above three strategies have two common elements, including feature extraction and classifiers. Therefore, we present a brief description of both them as follows.
1.2. Feature Extraction
There are three main groups of features for ALS point cloud classification, i.e., reflectance-based features, descriptor-based features, and geometric features.
The reflectance-based features are often related to the intensity [
38] and echo [
18] recorded by scanner systems. Therefore, the distinctiveness of this kind of features relies heavily on the quality of the scanner’s signal.
The descriptor-based features often employ spin images [
39], shape distributions [
40], histograms [
41,
42,
43] to characterize a local 3D neighborhood. For all these descriptor-based features, a single object of the resulting feature vector is hardly interpretable [
20].
Common geometric features are height-based features [
19], eigenvalue-based features [
19,
36], projection-area-based features [
18,
39], surface-based features [
18], etc. Specifically, the eigenvalue-based features derived from the 3D structure tensor which is represented by the 3D covariance matrix derived from the 3D coordinates of all points within a local neighborhood, are discriminative in a variety of classification approaches. In contrast, the geometric features are deeply studied and widely used by state-of-the-art methods.
Most existing studies often compute as many features as possible to obtain a superior classification result. When a large number of features are extracted, some of them may be redundant. These redundant features not only increase the computational burden, but also waste the memory space. Therefore, recent studies introduce a feature selection procedure [
19,
20,
38,
44] as an additional step between feature extraction and classification steps.
1.3. Classifiers for ALS Data Classification
In the classification stage, many studies have tried locally independent classifiers, such as Support Vector Machine (SVM) [
45], Adaptive Boosting (AdaBoost) [
46], Expectation Maximum (EM) [
47], RF [
48,
49], JointBoost [
18], etc. The fundamental idea is to train a classifier by using given training samples which is used for prediction later [
20]. Specifically, due to the excellent performance, the RF classifier [
50] has received increasing attention [
51]. Some studies [
19,
20,
34,
38] have looked into the potential of the RF classifier to improve urban objects classification and select uncorrelated features for ALS point clouds.
However, the integration of RF and the segment-based classification is rarely studied, as well as the importance analysis of segment features. In addition, the robustness of the classification methods is rarely analyzed when noises exist in the extracted features.
In this paper, we focus on the segment-based classification due to its advantages over the point-based classification. To address the aforementioned problems, we design a segment-based classification framework. This framework has three improvements compared to the existing methods:
- (1)
A novel point cloud segmentation method is proposed. This method clusters the points with regular neighborhoods into planar and smooth surfaces, and the points with scattered neighborhoods into rough surfaces.
- (2)
RF is integrated with the segment-based classification to select features and perform classification. The integration of RF and the segment-based classification improves the robustness of ALS point cloud classification.
- (3)
Semantic rules are employed to optimize the classification result. The semantic rules are more convenient to be detected when we process segments.
The outline of this paper is shown as follows.
Section 2 presents the methodology of our proposed classification framework which contains a novel point cloud segmentation method, feature extraction based on segments, the integration of RF and segment-based classification, and post-processing based on semantic rules. The experiments and discussions are presented in
Section 3, followed by
Section 4 which summarizes the uncertainties, errors and accuracies of the proposed classification framework. The research conclusions are presented in
Section 5.
2. Methodology
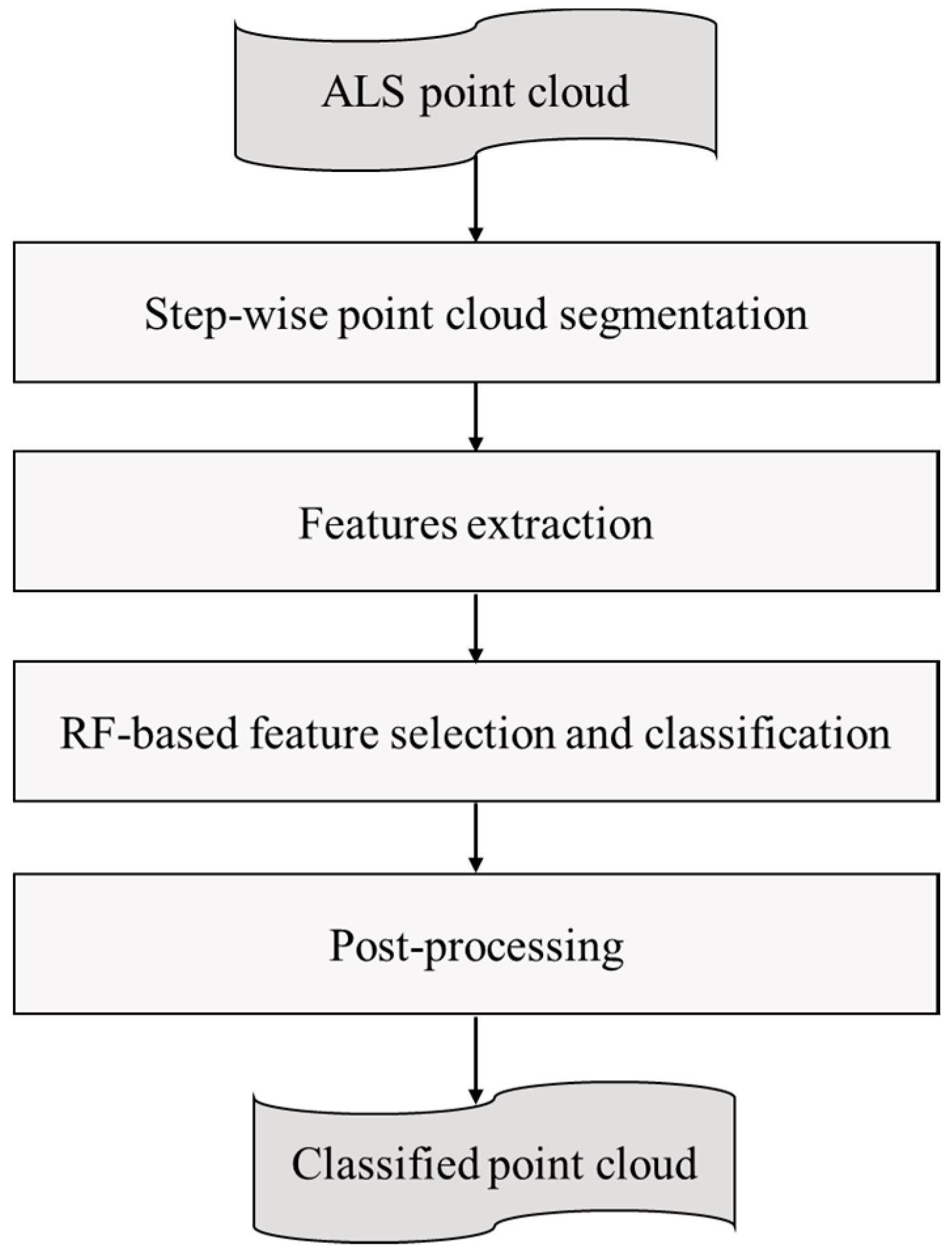
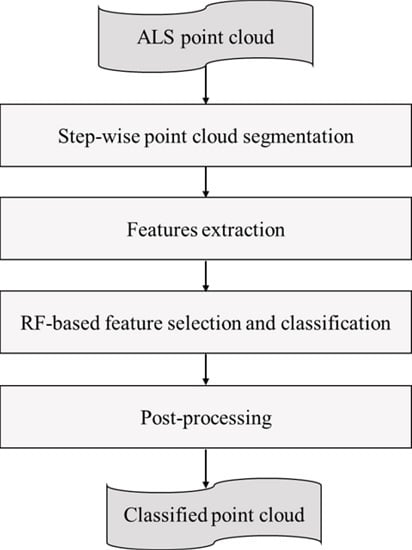
The proposed classification framework is composed of four stages as shown in
Figure 1. First of all, a step-wise point cloud segmentation method which is able to cluster points with different neighborhoods into different geometric structures is proposed (see
Section 2.1). Next, a segment rather than an individual point is considered as the basic processing unit for feature extraction (see
Section 2.2). Then, we employ RF to select uncorrelated features based on a backward elimination method [
52], and improve the robustness of ALS point clouds classification (see
Section 2.3). Finally, we utilize semantic rules to optimize the classification result in the post-processing stage (see
Section 2.4).
2.1. Step-Wise Point Cloud Segmentation
The proposed point cloud segmentation method is a RG-based one, and it clusters the points into planar surfaces, smooth surfaces, or rough surfaces.
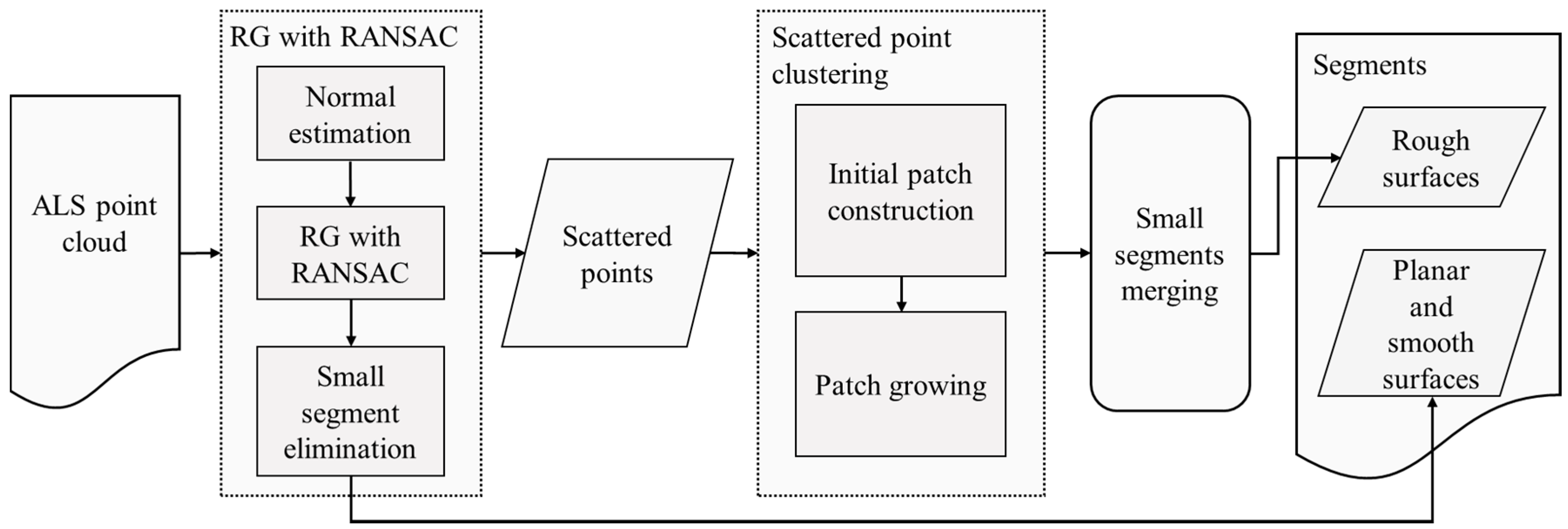
Our segmentation procedure consists of three steps: region growing (RG) with RANdom SAmple Consensus (RANSAC), scattered points clustering, and small segments merging (see
Figure 2). The first step extracts planar and smooth surfaces, and recognizes scattered points from the input point cloud. Then, the scattered points clustering step extracts rough surfaces from the scattered points. At last, an optional step is performed to merge small segments.
It is notable that rough surfaces are separated from the other types of segments by the aforementioned steps. However, planar surfaces and smooth surfaces are not distinguished when we extract them in RG with RANSAC step. For the application of semantic recognition, planar surfaces and smooth surfaces are easily to be distinguished by their curvatures. In this study, the feature extraction, and the RF-based feature selection and classification stages perform without distinguishing these three types of segments.
2.1.1. RG with RANSAC
The plane-based RANSAC algorithm is widely used in point cloud segmentation tasks [
53]. However, there is rare study employing RANSAC to improve RG-based segmentation methods.
To extract planar surfaces, two difficulties should be overcome for a RG-based method, i.e., non-optimal segmentations around edges where two surfaces meet [
54], and the detection of small or narrow planes [
55]. The integration of RANSAC and RG is able to solve both problems. In addition, we utilize a smooth RG procedure, which is able to extract smooth surfaces simultaneously.
There are three substeps in the RG with RANSAC step, i.e., normal estimation, RG with redefined constraints, and small segment elimination.
- (1)
Normal estimation
We employ RANSAC-Normal [
56] to the RG-based method. Our previous approach [
56] has validated that the RANSAC-Normal is efficient to extract a suitable plane from a complex neighborhood with intersecting surfaces. This procedure first determines the
neighbors of the
-th query point
, then fits a local plane based on the RANSAC algorithm, and finally, defines the normal of the fitted plane as the RANSAC-Normal.
In addition, during the normal estimation procedure, a number of scattered points are detected, and they are stored in a scattered point set
. The pseudo code which shows details of this procedure, is presented in Algorithm 1. The parameter
is utilized to determine how many neighbors of a query point will be detected in Row 4. The parameter
is the threshold of the plane-based RANSAC algorithm, which is utilized in Row 5.
| Algorithm 1. Normal estimation. |
| Input: Point cloud=. Parameters: , |
| 1: Regular point set , Scattered point set , Inlier Set , Proportion Set , Normal Set |
| 2: For to size () do |
| 3: Select -th point as the query point |
| 4: Find neighbors for |
| 5: Determine the inliers using plane-based RANSAC algorithm |
| 6: If then |
| 7: Compute proportion of to neighbors |
| 8: Normal estimation |
| 9: , |
| 10: Else then |
| 11: |
| 12: End If |
| 13: , |
| 14: End For |
| Output: , , , , |
Specifically, when plane-based RANSAC algorithm fits a local plane, it divides neighbors into inliers and outliers (Row 5). The points in are on the fitted plane. If the query point is in , we compute a proportion of the inliers to the neighbors (Row 7).
Five sets (, , , , ) are generated in Algorithm 1, and they are useful for the RG with redefined constraints.
- (2)
RG with redefined constraints
This procedure is similar to the RG method presented in [
57]. However, two constraints (local connectivity and surface smoothness [
57]) are redefined based on the plane-based RANSAC algorithm.
The pseudo code which shows details of the RG with redefined constraints procedure, is presented in Algorithm 2. The parameter
is utilized to restrict the dot product between normals in the Row 12 and its usage is presented in Formula (1).
| Algorithm 2. RG with redefined constraints. |
| Input: , , , . Parameters: |
| 1: Available point list |
| 2: While is not empty do |
| 3: Current segment (planar or smooth face) , Current seeds |
| 4: Find a point in with maximum |
| 5: , , |
| 6: For j=0 to size() do |
| 7: Set j-th point in as current seed |
| 8: Find Current inliers of (constraint 1) |
| 9: For k=0 to size() do |
| 10: Neighbor point index |
| 11: Compute |
| 12: if {} contains and then (constraint 2) |
| 13: , , {} |
| 14: End If |
| 15 End For |
| 16: End For |
| 17: |
| 18: End While |
| Output: Planar and smooth surfaces |
Specifically, the constraint 1 is utilized in Row 8, and the constraint 2 is utilized in Row 12 of Algorithm 2.
- (3)
Small segment elimination
If the point density of trees is dense, there may be some small segments (planar and smooth surfaces) in the tree areas. Therefore, we should remove these small segments from , and add the points in these small segments to . There is a parameter in this procedure, i.e., the minimum size threshold . is expressed via the number of points in a segment.
Specifically, The RG with RANSAC step divides the input 3D point cloud into two point sets. The first set is the regular point set
, and the second set is the scattered point set
. Points in
are clustered into planar and smooth surfaces, and points in
are clustered into rough surfaces in the subsequent step. In the RG with RANSAC step, there are two procedures for dividing regular points and scattered points, which are shown as follows:
For a query point in Algorithm 1, we first find neighbors of it, and then plane-based RANSAC is performed to determine inliers which is on the local fitted plane. If is not in , it will be recognized as a scattered point.
When the Algorithm 2 is performed, regular points are recognized and clustered into a number of segments containing planar and smooth surfaces. There may be misjudgment if a planar or smooth surface is small enough. Therefore, the small segment should be removed and points in it will be recognized as scattered points.
The result of the RG with RANSAC step is presented in
Figure 3a. Points rendered in black are scattered points and other points are regular points.
2.1.2. Scattered Points Clustering
In this step, the scattered points in
are first clustered into a number of initial patches, and then rough surfaces are extracted by growing these initial patches. The two substeps are detailed as follows:
- (1)
Initial patch construction
This substep is an iterative procedure. An initial patch is iteratively extracted from the scattered point set
until all the points in
have been traversed. There are two parameters in this procedure, i.e., the maximum size threshold
and the maximum distance threshold
. The number of points in an initial patch has to be smaller than
. Moreover, an initial patch has to satisfy the follow constraint:
where
is a point in an initial patch, and
is the centroid point of the initial patch. The details of this procedure is shown in Algorithm 3. To stabilize this procedure, the curvature of each point in
is estimated. These points in
are sorted according to their curvatures from minimum to maximum, and then are traversed in order.
| Algorithm 3. Initial patch construction. |
| Input: Scattered point set . Parameters: , |
| 1: Initial patch set , Dirty indicator , Covariance matrix set |
| 2: Estimate curvatures of the points in |
| 3: Sort from minimum to maximum, and obtain the sorted ID of each scattered point |
| 4: For to size () do |
| 5: Select i-th point as the query point |
| 6: Find nearest neighbors for based on a kd-tree |
| 7: Extract a subset of the nearest neighbors based on the threshold |
| 8: For to size do |
| 9: If |
| 10: Go to Row 4 |
| 11: End If |
| 12: End For |
| 13: |
| 14: Update for all the points in |
| 15: End For |
| 16: Merge non-dirty points to their nearest patch |
| 17: Compute covariance matrix for each in |
| 18: Sort initial patches based on their determinants with descending order |
| 19: Normalize covariance matrices |
| Output: , |
As shown in Algorithm 3, the parameter
is utilized in Row 2 and 6 to determine how many neighbors of a query point will be detected for
kd_tree search. The parameter
is utilized in Row 7 to restrict the distance between a neighbor and the query point. Only neighbors with the distance smaller than
are extracted to construct an initial patch. After all the initial patches are extracted, their covariance matrices are computed (Row 17). Let
for
, be the points in an initial patch, the covariance matrix
is defined as:
where
is the mean vector of all the points in the patch.
After all the covariance matrices are determined, these initial patches in
are sorted by the determinants of their covariance matrices. Finally, each covariance matrix is normalized by its determinant. The result of the initial patch construction is shown in
Figure 3b.
- (2)
Patch growing
The patch growing is similar to the RG with redefined constraints procedure. Therefore, we do not present the pseudo code in the following. In this procedure, the growing unit is an initial patch rather than an individual point. Each initial patch is considered as a seed and grew in the order obtained in the initial patch construction procedure (Row 18 of Algorithm 3). Two constraints for patch growing are defined as follows:
Constraint 1: local connectivity
Only adjacent patches of the seed patch can be added into the current segment.
Constraint 2: geometrical similarity
The geometrical difference
of two patches in a segment has to be smaller than a threshold
.
is defined by using log Euclidean Riemannian metric [
58] which measures how close two covariance matrices are. Given two covariance matrices
and
,
is computed as follows:
where
is the matrix logarithm operator and
is the Frobenius norm.
After these two steps have been performed, points are clustered into three kinds of segments, i.e., planar, smooth, and rough surfaces. If small segments with a size smaller than the minimum size threshold
still exist, we merge them with their nearest neighbor segments. This step, which is an optimizing procedure, will iterate until all the segments are traversed. The result of the step-wise point cloud segmentation method is shown in
Figure 3c.
2.2. Employed Features and Their Calculation
The difference of our method from the others is that we extract features of segments rather than individual points. Herein, we focus on four groups of geometric features, namely projection-area-based ones [
18], eigenvalue-based ones [
19], elevation-based ones [
18], and other ones.
2.2.1. Projection-Area-Based Features
Projection-area-based features are first proposed in [
39], and then are applied to 3D point cloud classification [
18]. In this paper, we borrow the idea from literature [
18] which is shown in
Figure 4. However, the difference of our method is that the basic processing unit is a segment rather than an individual point. A segment has no fixed size compared to the neighborhood of an individual point. Therefore, a larger segment has larger projection area than a smaller segment. This problem affects the distinctiveness of this kind of features. We define two ratios to overcome this problem. The first one is the tangent plane projection ratio
, and the second one is the horizontal projection ratio
.
2.2.2. Eigenvalue-Based Features
Herein, the covariance matrix is first determined by a segment, and then a set of positive eigenvalues
[
19] and normalized eigenvalues
with
are computed. We employ ten eigenvalue-based features: highest eigenvalue
, medium eigenvalue
, lowest eigenvalue
, linearity
, planarity
, scattering
, anisotropy
, omnivariance
, eigenentropy
(see
Figure 5b) and change of curvature
. The latter seven features are computed as:
2.2.3. Elevation-Based Features
In this part, we define four elevation-based features, the latter three borrow the idea from the height-based features for individual points presented in [
18].
Relative elevation
We first determine the adjacent segments for a query segment
in the
XY-plane. Neighbors of all the points in
are searched in XY-plane by a
kd_tree with a given distance threshold. The segments
for
which contain the searched neighbors are the adjacent segments of
. Next, a point
which is closest to
is determined in
. Then, a point
which is closest to
is determined in
, and
and
construct a neighboring point pair which represents the relationship between
and
. Finally, the relative elevation
is defined as:
where
is the z-coordinate of
, and
is the z-coordinate of
.
is shown in
Figure 5c.
Elevation variance
This feature
is the variance of elevation values of all points in each segment.
is computed as:
where
is the total number of points in the segment,
is the average elevation of all points in the segment,
is the elevation of the
-th point in the segment.
Elevation difference
This feature is the difference between the highest elevation and the lowest elevation of a segment. In other words, the elevation difference is computed as .
Normalized elevation
This feature is the elevation difference between the centroid point and the lowest point of a segment. The normalized elevation
is defined as:
where
is the elevation of the centroid point, and the
is elevation of the lowest point.
2.2.4. Other features
Overall, the extracted four groups of features are list in
Table 1.
2.3. Random Forests Based Feature Selection and Classification
2.3.1. Random Forests
The RF classifier [
50] is an ensemble of a set of decision trees. These trees in RF are created by drawing a subset of training data through a bagging approach. The bagging randomly selects about two thirds of the samples from a training data to train these trees. This means that the same sample can be selected several times, while others may not be selected at all [
51]. Then, the remaining samples are used in an internal cross-validation technique for estimating performs of RF. In addition, the Weighted Random Forest [
59] method is utilized for solving the imbalanced sample problem in RF.
Two parameters, i.e., the number of trees and the number of features, are required for using a RF classifier. Then, each tree in RF is independently produced without any pruning. The number of features is used for training each tree. Each node in a tree is split by selecting features from the d-dimensional input feature space at random. The splitting function usually uses Shannon entropy or Gini index as a measure of impurity. In prediction, each tree votes for a class membership for each test sample, the class with maximum votes will be considered as the final class.
2.3.2. Feature Selection
The objective of feature selection is to identify a small set of discriminative features that can still achieve a good predictive performance [
19]. The RF provides a measure
of variable importance based on averaging the permutation importance measure of all the trees which is shown to be a reliable indicator [
60]. The permutation importance measure is based on Out-Of-Bag (OOB) errors, and is utilized to select features.
Herein, we use the variable importance measure in RF and the backward elimination method [
52] to select features. The backward elimination method removes the most relevant features by iteratively fitting RF. In our approach, only one feature with the lowest importance value is eliminated at each iteration, and then a new forest is built by the remained
features. At the end of each iteration, we compute the mean decrease permutation accuracies [
19]
for
and rank the remained features by them. To measure the importance of the remained features at each iteration, the overall mean decrease permutation accuracy
is computed by averaging all the remained features’ importance values.
is computed as follow:
where
corresponds to the iteration times, and
is the total number of iterations. The iterative procedure stops and all the RFs are fitted when
is equal to
.
After all the RFs are fitted, we computed the range between the maximum and the minimum overall mean decrease permutation accuracies (). Then, we select a critical point according to the variation tendency of . In this paper, the principle of the selection is that the variation of caused by the eliminated features should be lower than 20%, i.e., the critical point which divides the range by a ratio of at least 8:2 is selected. At last, we select the most important features according to the critical point and the backward elimination results.
2.3.3. Supervised Classification
After the feature selection, the training samples with selected feature set are utilized to train a RF classifier, and the classifier is used to predict the labels of unlabeled segments.
2.4. Post-Processing
There may be some misjudgments in the above initial classification results. Actually, both natural and artificial objects generally have been associated with specific semantic information. For example, cars occupy small areas and are parked on ground, most of building roofs are composed of planar faces and have relatively large area, and wires are elevated over ground. Moreover, semantic information is more convenient to be detected via segments than individual points. Therefore, semantic information is utilized to define several rules for optimizing the initial results. Note that the post-processing stage cannot correct all the misjudgments.
To define the semantic rules, two types of neighborhoods are determined. The first one
is determined in 3D space, and the second one
is determined in
XY-plane. In the post-processing stage, if we find a misjudged segment based on these rules, we first detect labels of its adjacent segments based on
, then we relabel it as the class which arises the most times. Herein, we only list the useful rules for our approach. The rules for each class are shown as follows.
- (1)
Rule for ground
In the neighborhood of a query ground segment , for is the -th adjacent segment. The elevation difference between each segment pair containing and is in a small interval .
In the neighborhood of a query ground segment , there is no adjacent segment whose maximum elevation much lower than the minimum elevation of .
Considering an extreme case, if we want to obtain a high precision DTM from a complex mountainous region, we can combine the initial ground segments with the segment-based PTD (progressive TIN densification) filtering method [
61] or a progressive graph cut method [
62]. First, the ground segments in the initial classification result are considered as latent ground segments. Next, a 2D grid is constructed with a bin size equal to the maximum building size. Then, a latent ground segment which contains the lowest point in each bin is recognized as a ground seed segment. Finally, points in the ground seed segments are utilized to construct a TIN as the initial ground surface, and ground points will be extracted by a PTD or a progressive graph cut method.
- (2)
Rule for building roofs
In the neighborhood of a query building roof segment , it has the same characteristics as ground. However, in the neighborhood , we can find an adjacent segment whose maximum elevation is much lower than the minimum elevation of , the elevation difference threshold of this elevation difference is denoted as .
- (3)
Rule for vehicles
A car segment should have a certain range of area: .
In the neighborhood of a query car segment , there is at least one adjacent segment labeled as ground.
- (4)
Rule for wires
In the neighborhood of a query wire segment , there is no adjacent segment with a label of ground or car.
The 3D shape of a wire segment can be linear or planar, however, cannot be volumetric.
- (5)
Rule for vegetation
Vegetation segments are often confused with vehicle segments. Besides, the misjudged segments in the initial classification result tend to arise in high vegetation rather than low vegetation. Therefore, the misjudged segments in high vegetation are able to be corrected by the rules for vehicles simultaneously.
Considering an extreme case, we assume that some vehicle segments are misjudged as low vegetation segments. First, a misjudged query segment should have a neighbor labeled as ground, then, if the height, width and length of the segment are in certain ranges
,
,
, the segment will be relabeled as vehicle. The thresholds of these ranges are cited from the approach in literature [
24]. Besides, the height, width and length of a segment are computed in a local coordinate framework composed of
,
and
. The
,
and
are eigenvectors of the covariance matrix
constructed by points in the segment as formula (3).
3. Experiments and Discussions
We developed a protype framework for the proposed segment-based point cloud classification method using C++ language and Point Cloud Library (PCL) [
63]. We also implemented segment-based point cloud classification using SVM and the RG segmentation [
57], in which the open source libSVM [
64] is used for the implementation of SVM and PCL is used for the implementation of RG segmentation.
The experiments are conducted on a workstation running Microsoft Windows 7 () with two 16-Core Intel Xeon E5-2650, 64GB Random Access Memory (RAM) and 3TB hard disk.
There are two parts in the experiments and discussions. The first part is experimental setting which includes study areas and evaluation metrics. The second part is results and discussions which are presented in
Section 3.2,
Section 3.3,
Section 3.4,
Section 3.5 and
Section 3.6.
In the second part, there are three improvements compared with existing classification methods, i.e., the step-wise point cloud segmentation, the integration of RF and the segment-based classification, and the employment of semantic rules in the post-processing stage. Therefore, we first discuss the impact of the three improvements and analyze the advantages of them in
Section 3.2,
Section 3.3 and
Section 3.4. Then, the classification results and accuracies of the protype framework are shown in
Section 3.5 and
Section 3.6. Note that the classification results should be presented after the discussion of the three improvements. Because the classification results are obtained by the parameters which are determined by the discussion in
Section 3.2,
Section 3.3 and
Section 3.4.
3.1. Experimental Setting
3.1.1. Study Areas
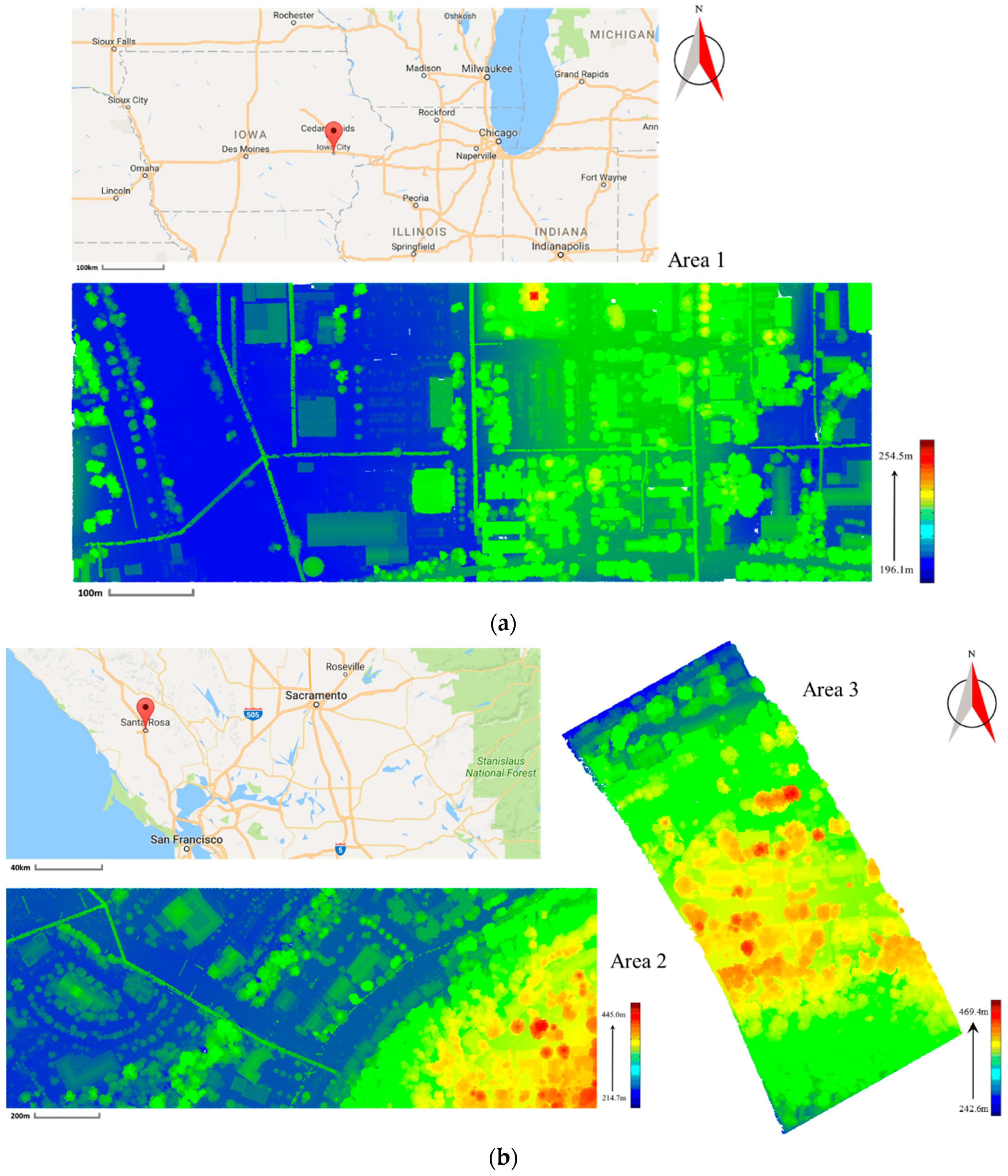
Three study areas are involved in our experiments. The first one is selected from a publicly available ALS dataset which is obtained by the University of Iowa in 2008 [
65]. The data are collected to survey the Iowa River Flood along the Iowa River and Clear Creek Watershed. The data collection is funded by NSF Small Grant for Exploratory Research (SGER) program. Area 1 is shown in
Figure 6a and it contains 1,512,092 points with an average point spacing of 0.6 m. In
Figure 6a, the point cloud of Area 1 is colored by elevation. In this area, the ground is flat and smooth. On the ground, there are some parking lots where many vehicles are parked. In addition, some vehicles are parked under tree crowns, or close to houses. Buildings in this area are composed of several planar faces with different geometric shapes and a number of building elements such as chimneys. Several wires are intersected, and cross the trees with high elevation. Most trees and building roofs are overlapped. After the step-wise point cloud segmentation performed, 5949 segments are extracted from Area 1. 250 segments are selected as training samples for the RF classifier. Details of the training samples in Area 1 are shown in
Table 2. Specifically, only one sample is selected for the class
ground. Ground in Area 1 is flat and smooth, and points on the ground are clustered into only one segment by the step-wise point cloud segmentation.
The second one is selected from a publicly available ALS dataset which is collected in Sonoma County [
66] between 28 September and 23 November 2013 by the Watershed Sciences, Inc. (WSI). The dataset is provided by the University of Maryland and the Sonoma Country Vegetation Mapping and Lidar Program under grant NNX13AP69G from NASA’s Carbon Monitoring System. Area 2 is shown in
Figure 6b and it contains 1509228 points with an average point spacing of 1.0 m. In
Figure 6b, the point cloud of Area 2 is colored by elevation. In this area, there is a mountain which is full of trees and ornamented by several houses. Buildings are overlapped with tree canopies significantly. Moreover, building elements such as skylights have complex 3D structure. Wires go across the trees have high elevations and are intersected with each other. A large number of vehicles are parked under tree crowns or near low vegetation. After the step-wise point cloud segmentation performed, 10697 segments are extracted from Area 2. 414 segments are selected as training samples for the RF classifier. Details of the training samples in Area 2 are shown in
Table 2. Specifically, the number of training samples for the class
ground is smaller than other classes. Although a mountain exists in Area 2, a majority of ground regions are flat and smooth. Therefore, points on ground in Area 2 are clustered into a smaller number of segments than other classes.
The third one is selected from the same dataset of Area 2. Area 3 is shown in
Figure 6b and it contains 685870 points with an average point spacing of 1.0 m. In
Figure 6b, the point cloud of Area 3 is colored by elevation. In this area, all the points are on a mountainous ground which is full of trees and ornamented by several houses. Area 3 is utilized to test the transplanting of the proposed classification framework to mountainous areas. There are only three types of objects, i.e., ground, buildings and vegetation. The ground of Area 3 is rugged with step edges. All the buildings are surrounded by vegetation. After the step-wise point cloud segmentation performed, 6658 segments are extracted from Area 3. 165 segments are selected as the training samples for the RF classifier. Details of the training samples in Area 3 are shown in
Table 2. Specifically, the number of training samples for the class
ground in Area 3 is larger than those in Area 1 and 2 because of the complex topographies.
In this paper, we classify Area 1 and 2 into five classes, i.e., ground, building, vegetation, vehicle and wire, and Area 3 into three classes, i.e., ground, building and vegetation. Area 1 and 2 are utilized to analyze the impact of the step-wise point cloud segmentation, the integration of RF and segment-based classification method, and the post-processing stage. Area 3 is employed to analyze to the classification result of a mountainous area with complex topographies.
To quantitatively analyze the classification accuracy, we obtain ground true for the three study areas by manual labelling. The details of the ground true for the three study areas are shown in
Table 3. Note that quantitative analysis is derived by individual points rather than segments, because the hypothesis that no error exists in segments is unreasonable. Therefore, we present the ground true using individual points rather than segments.
3.1.2. Evaluation Metrics
For evaluation, we employ the confusion matrix and consider five commonly used measures: overall accuracy
, Kappa coefficient
. , precision
, recall
, and
-score. They are computed according to the confusion matrix as follows:
where
is the main diagonal element in
-th row,
is computed from the sum of
-th column, excluding the main diagonal element,
is the sum along
-th row, excluding the main diagonal element,
is the number of classes, and
is the number of all the points in an input point cloud.
3.2. Impact of the Step-Wise Point Cloud Segmentation
Our proposed step-wise point cloud segmentation method can extract three kinds of segments, i.e., planar, smooth and rough surfaces. We compare our method with the RG method [
57], which has been published in PCL. The PCL supplies two kinds of processes based on the RG method. The first one is designed for plane extraction (RG-based plane segmentation) and the second one is designed for smooth surface extraction (RG-based smoothness segmentation). Six parameters in RG method published in PCL are used, i.e., the number
of neighbors for normal estimation, the number
of neighbors for growing, the smoothness threshold
, the curvature threshold
, the residual threshold
, and the minimum size threshold
.
3.2.1. Qualitative Comparison
To visually compare our segmentation method with the RG methods, we select a small part from Area 1 to present the segmentation results. The parameter setting of our segmentation method is shown in
Table 4 and the parameter setting of the RG method is shown in
Table 5.
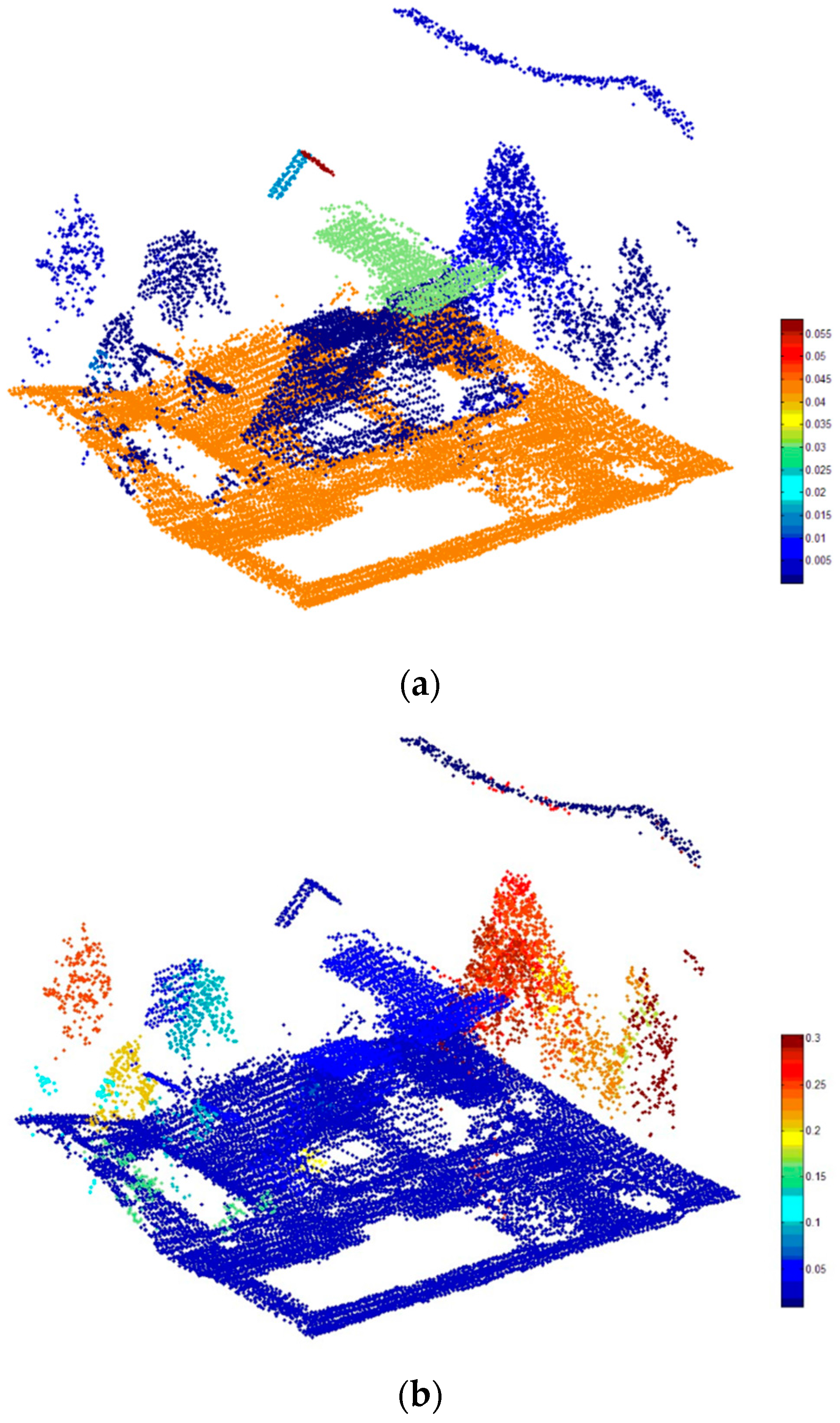
Figure 7 presents the comparison of these segmentation results. We can find that our segmentation method not only can detects three kinds of segments, but also can clusters the ground points into a small number of segments, especially a single segment. Besides, intersecting planes, building roofs covered by vegetation, and small or narrow planes can be extracted by our segmentation method (see
Figure 7a). The plane segmentation has the following shortcomings: (1) The segmentation result of the intersection between two planes is insufficient; (2) Small objects such as cars cannot be extracted; (3) Most majority of scattered points such as tree points cannot be segmented. The smoothness segmentation has the following shortcomings: (1) Intersected planes cannot be divided; (2) Small objects such as cars cannot be extracted, although it is implemented to extract smooth surfaces; (3) The building points and tree points could be clustered into the same region if they overlap with each other.
3.2.2. Quantitative Comparison
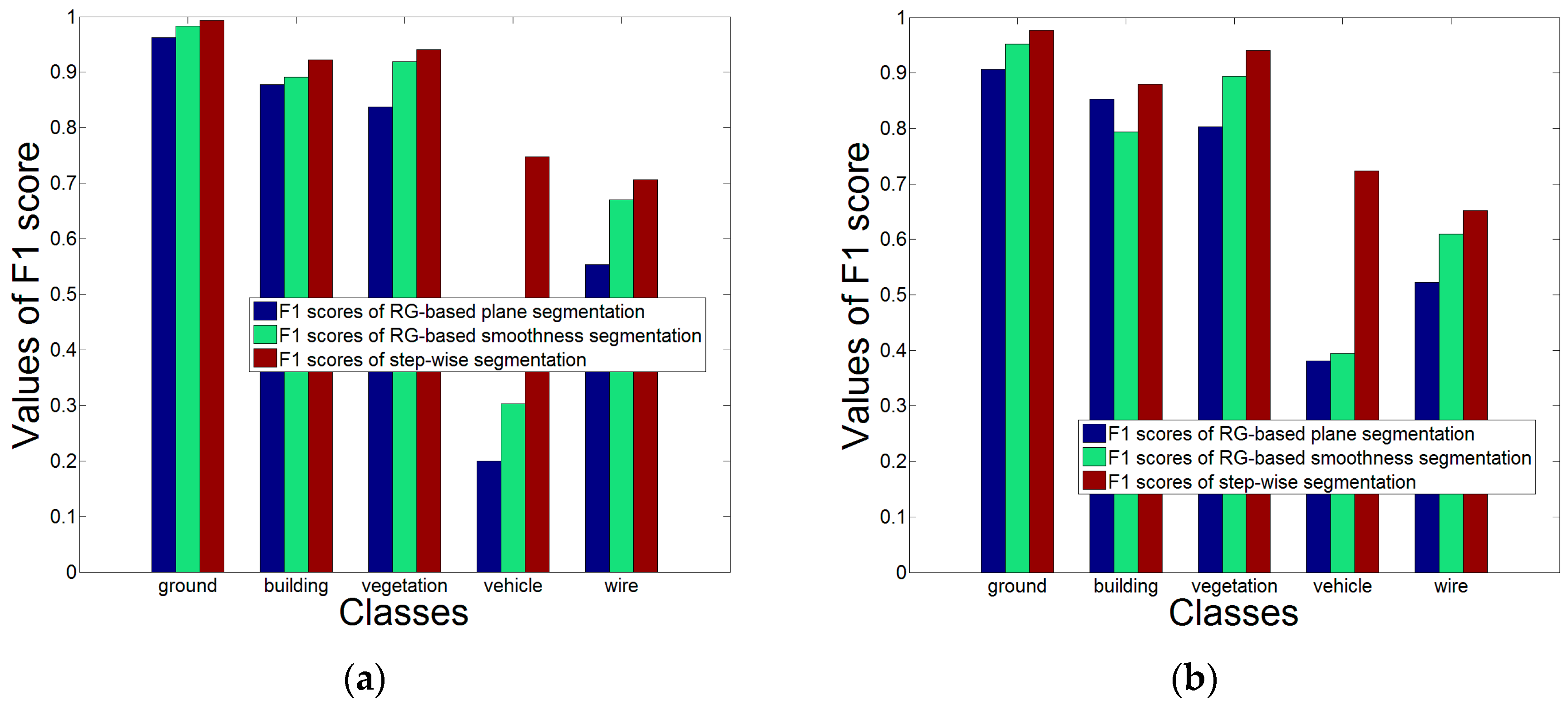
To quantitatively analyze the advantages of our segmentation method, the entire data of Area 1 and Area 2 are utilized. The time costs of our proposed segmentation method for processing Area 1 and 2 are 3.7 min and 4.4 min, respectively. We compare our method with the RG methods in terms of the classification measure
score. In order to facilitate an objective comparison, all results based on the RG methods are averaged over 20 runs. The parameter setting of the step-wise point cloud segmentation method is shown in
Table 6. The
-score comparison is shown in
Figure 8. The red bar describes the
-score of our segmentation method, while the green bar describes the
-score of the RG-based smoothness segmentation method, and the blue bar describes the
-score of the RG-based plane segmentation. All classes’
-score values of our segmentation method are larger than those of the RG methods for both Area 1 and 2. Specially, the
-score values of the class
vehicle derived by our method are significantly higher. The reason is that our segmentation method clusters all the points in a small-scale object into a few segments.
3.3. The Integration of RF and Segment-Based Classification
3.3.1. Parameter Tuning for Random Forests
The two parameters in the RF classifier, i.e.,
and
are utilized not only in the classification procedure, but also in the feature selection task. In the feature selection task,
is set to 4 according to the existing studies [
19,
38], which is a default setting and turned out to be a good choice of OOB rate [
19]. However, different studies have different settings of
. Therefore, we have to unfold a test before feature selection for finding an appropriate value of
. Besides, this test is also meaningful for supervised classification tasks in which the setting of
is still stochastic [
23].
To find an appropriate value of
for a stable classification, we test the classification procedure with
varying from 100 to 1000 and
from 1 to 9. For evaluating the classification results, we utilize overall accuracy and Kappa coefficient to analyze the overall performance.
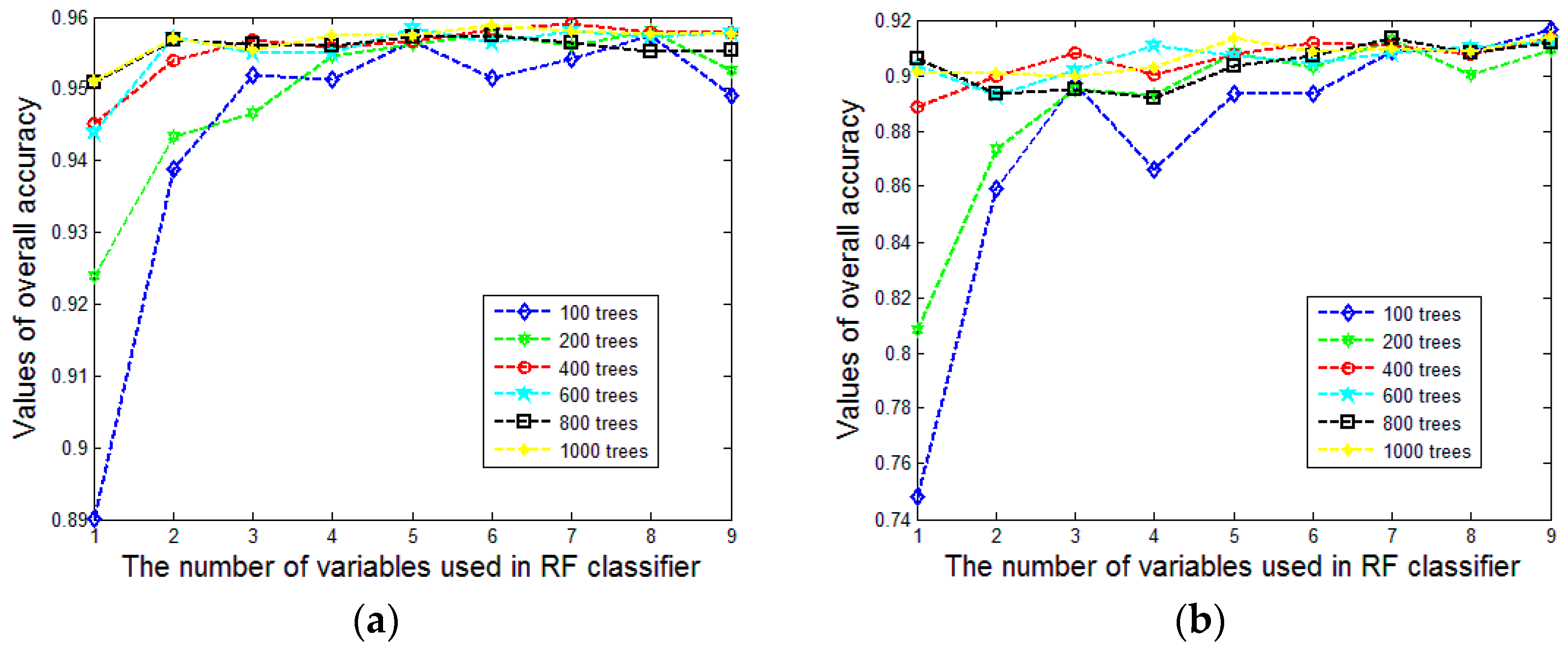
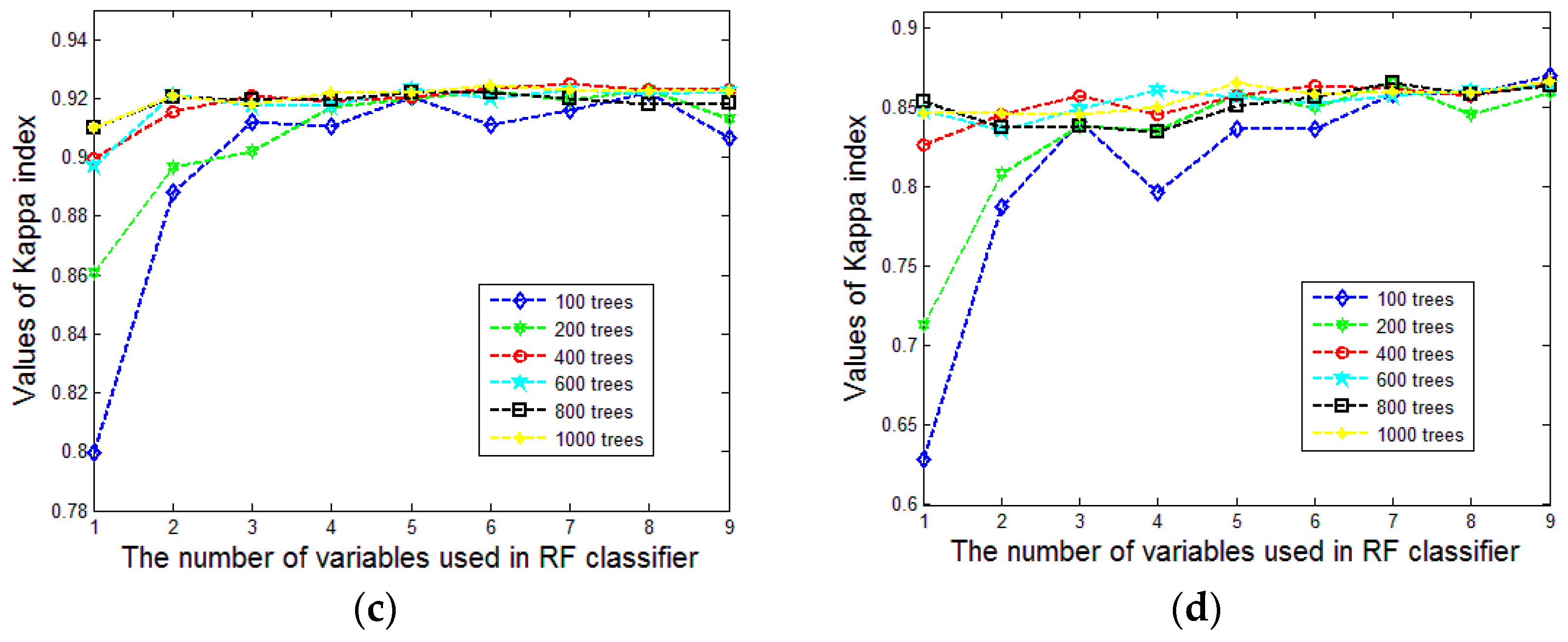
Figure 9a,b show the variation tendency of overall accuracy and
Figure 9c,d show the variation tendency of the Kappa coefficient. To make them more concise, we compute the mean and the standard deviation of the derived overall accuracy and kappa coefficient values under different settings of
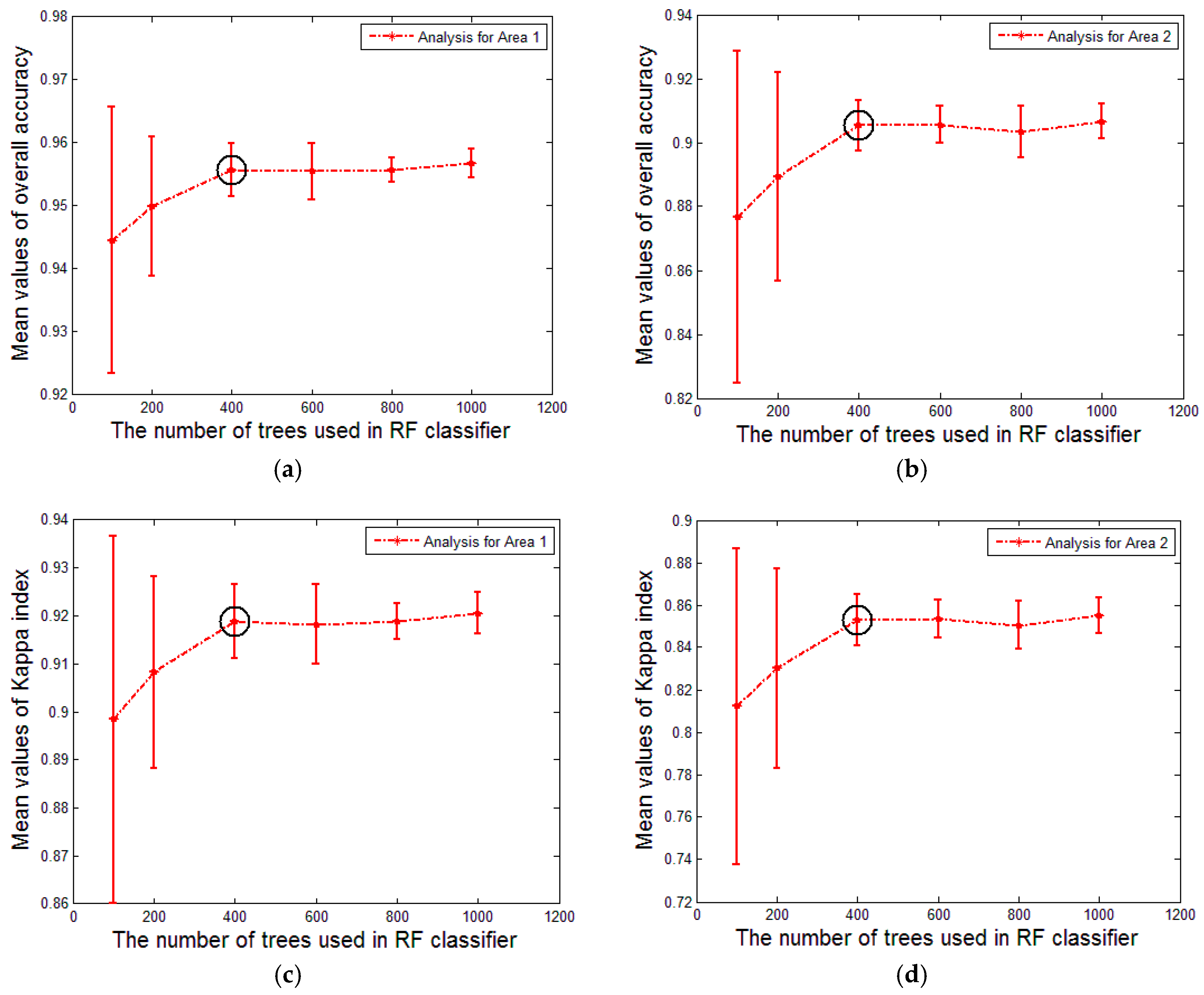
(see
Figure 10a–d). The stability of the classification result will increase with an increasing value of
. It is surprising that the overall accuracy and Kappa coefficient increase rapidly and the standard deviation decreases markedly with the augment of
until it reaches 400. This case occurs in both Area 1 and Area 2. It may be the reason that 500 is the default value of
in the R package for random forests [
51]. Therefore, setting
to 400 is reasonable in our approach, especially for decreasing the computational burden.
3.3.2. RF-Based Feature Selection
To select features, we utilize the backward elimination method and iteratively fit a RF with the aforementioned parameter setting. In each fitted RF, the importance of each feature is estimated.
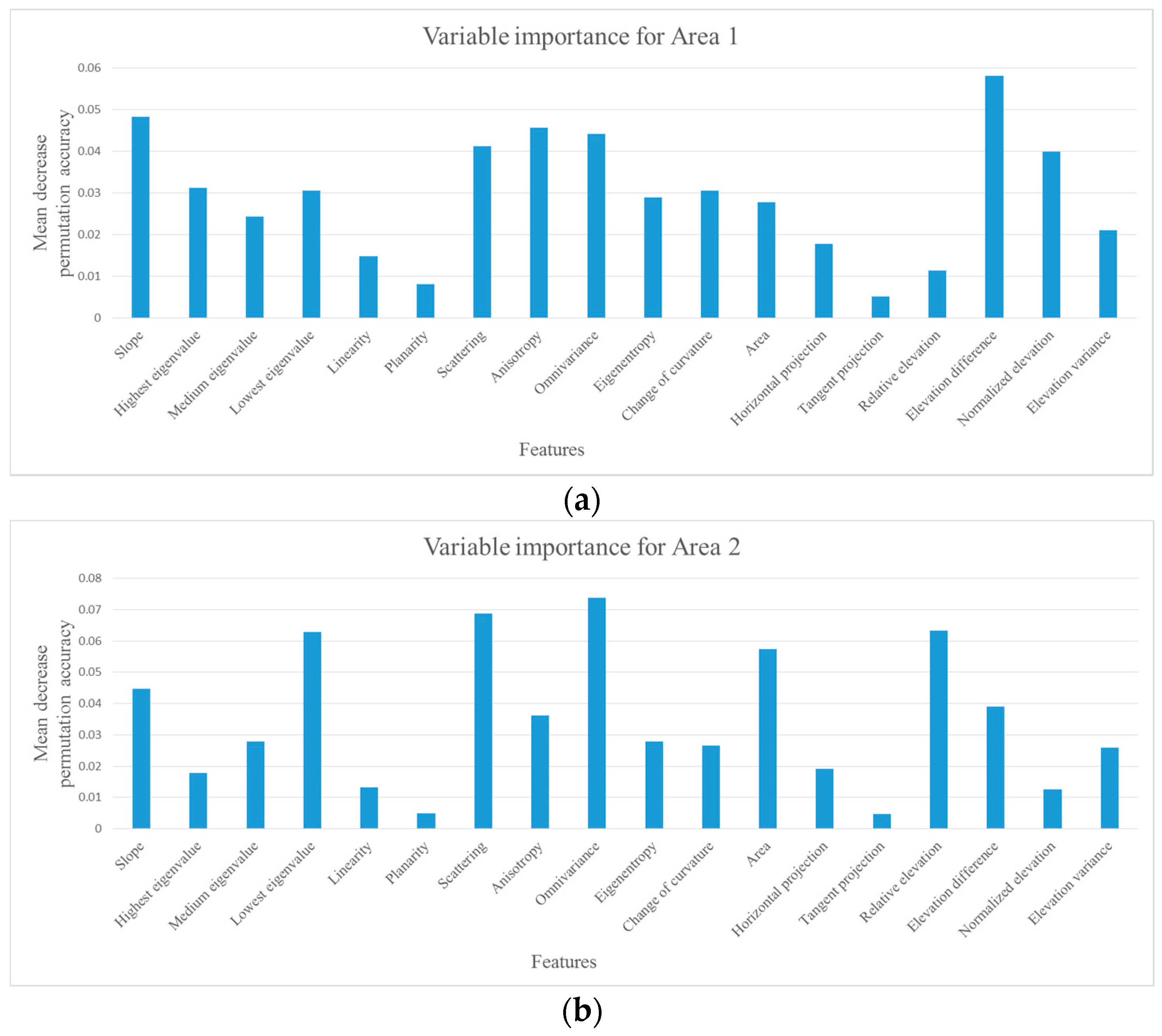
Figure 11 shows all the feature importance values of Area 1 and 2 which are estimated in the first time fitting.
The backward elimination method first fits a RF from the feature set , then the feature with the lowest importance value is eliminated from . The two steps are iterated until the number of features in is equal to 4. Subsequently, we select features based on the eliminating order.
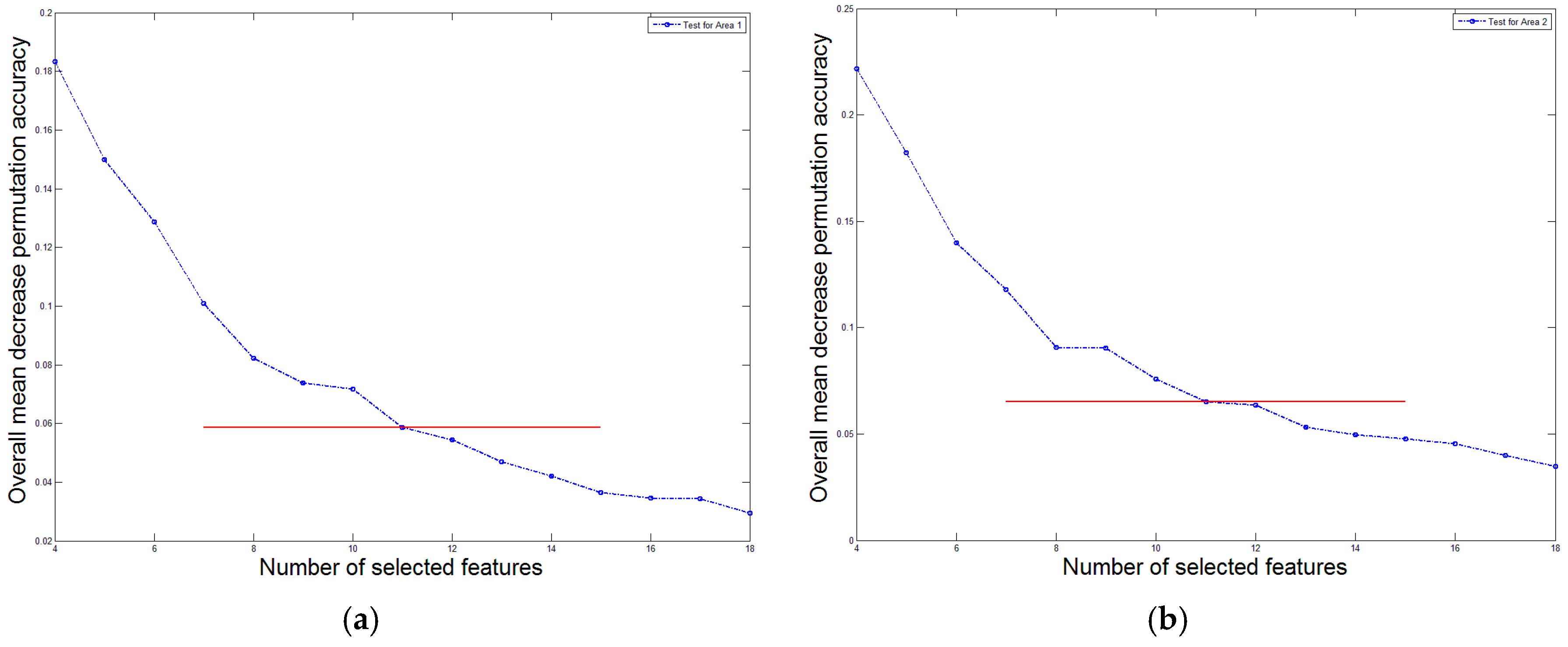
To determine the number of independent features, we present the variation tendency of the overall mean decrease permutation accuracy
in
Figure 12. For Area 1 (see
Figure 12a), the maximum overall mean decrease permutation accuracy
is 0.1834, and the minimum overall mean decrease permutation accuracy
is 0.03426. When only 11 features are remained, the overall mean decrease permutation accuracy
is 0.05864, which divides the range
with a ratio no less than 8:2. Besides, the tendency in
Figure 12a decreases rapidly until the remained feature number reaches 11. For Area 2 (see
Figure 12b), the maximum overall mean decrease permutation accuracy
is 0.2215, and the minimum overall mean decrease permutation accuracy
is 0.03991. When only 10 features are remained, the overall mean decrease permutation accuracy
is 0.07588, which divides the range
with a ratio no less than 8:2. However, the tendency of
Figure 12b decreases rapidly from 10 to 11 remained features, therefore, we select 11 features for Area 2 as a compromised solution. According to the aforementioned analysis, the number 11 of independent features is reasonable for both Area 1 and 2.
According to the aforementioned procedure, the selected features for Area 1 are slope , lowest eigenvalue , elevation difference , scattering , change of curvature , eigenentropy , omnivariance , anisotropy , highest eigenvalue , normalized elevation and area .
The selected features for Area 2 are scattering , area , elevation difference , lowest eigenvalue , omnivariance , relative elevation , slope , anisotropy , medium eigenvalue , eigenentropy and normalized elevation . The selected features are listed in elimination orders for Area 1 and 2 respectively.
3.3.3. Robustness of the Integration of RF and the Segment-Based Classification
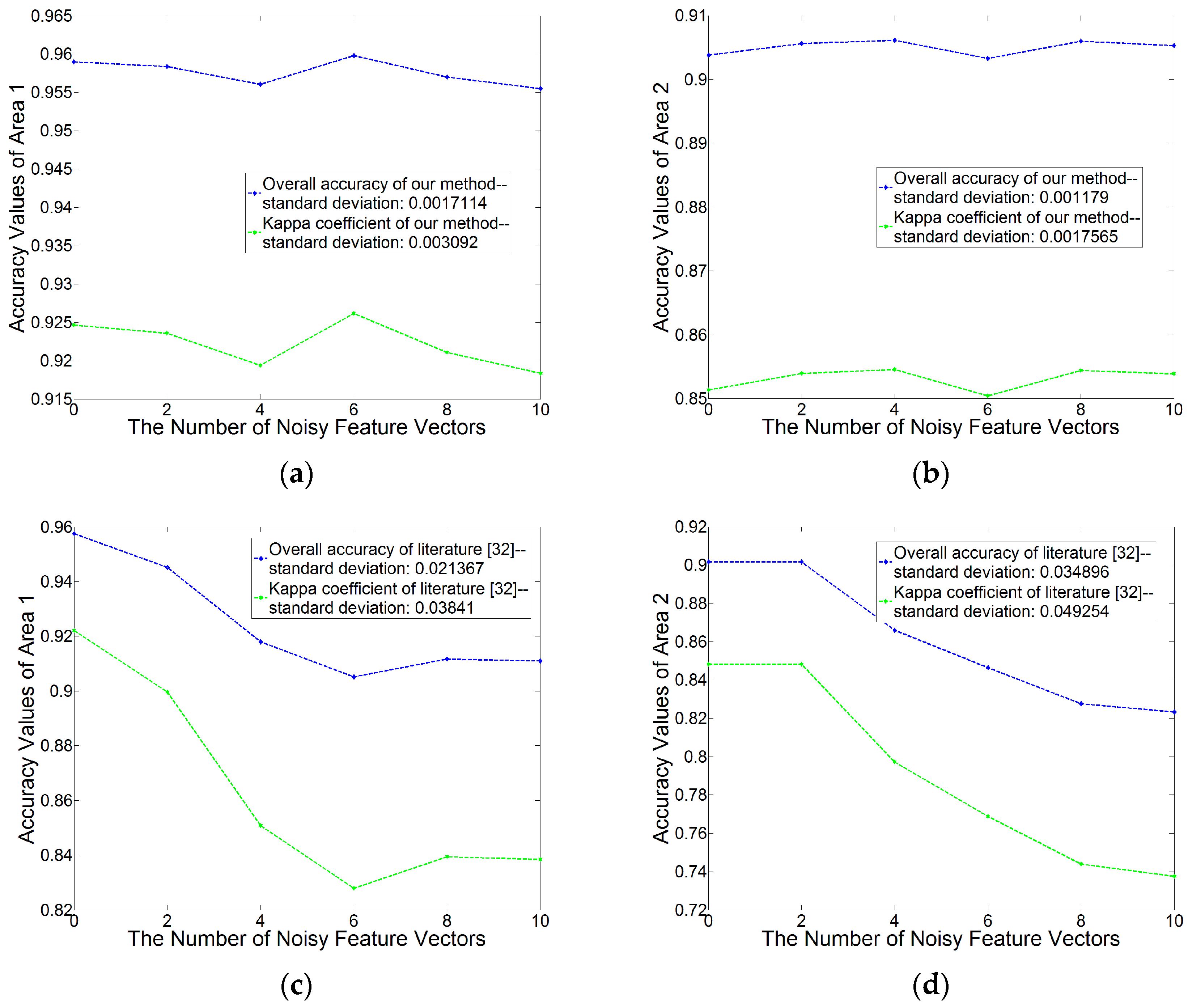
To test this robustness and the stability of the integration of RF and the segment-based classification, we add some noisy vectors to the computed feature set. It is worth noting that we do not record which feature vector is noisy, and therefore, we do not know which one is the noisy vector in the feature set when we train a RF and make prediction. Then, we analyze the overall accuracy and Kappa coefficient values of the classification results with different numbers of noisy vectors.
Besides, we implement the integration of SVM and the segment-based classification presented in [
36] and analyze its robustness. It is worth noting that both the two integration methods have no complemental step for dealing with noises. To impartially compare the robustness of the two integrations, the feature selection procedure in our method is not performed, due to the fact that feature selection is not employed to the integration in [
36].
As shown in
Figure 13, when there is no noisy feature vector, the two integration methods get the classification results with similar overall accuracy and kappa coefficient values. When the noisy vector number is increasing, the values of the integration presented in the literature [
36] decrease. Besides, our method obtains a mean standard deviation 0.0014 of overall accuracy values (0.0017 for Area 1 and 0.0012 for Area 2), and a mean standard deviation 0.0024 of kappa coefficient values (0.003 for Area 1 and 0.002 for Area 2), with the noisy feature vector number from 0 to 10.
In a close-up theoretical inspection, when RF classifier splits a subset of features in a node, it finds a feature with the maximum entropy or Gini decrease. In this case, the noisy features can be eliminated and the best feature corresponding to the maximum decrease is selected. Therefore, our method which integrates RF with the segment-based classification is more stable and robust.
3.4. Impact of the Post-Processing Stage Based on the Semantic Rules
After the supervised classification, an initial classification result is obtained, in which misjudged segments may exist. In the post-processing stage, we first define several semantic rules for each class, and then utilize them to optimize the initial classification result. Note that the utilized semantic rules may be different for different input data, and the post-processing stage cannot correct all the misjudgments, however is an optimizing procedure. The rules for ground and the rule 2 for vegetation are not employed when we optimize Area 1 while others are employed. The rule 3 for ground and the rule 2 for vegetation are not employed when we optimize Area 2 while others are employed. Some thresholds are utilized to constrain the optimization which are list in
Table 7. These threshold values are determined based on the natural form of an object and the point spacing of the input point cloud.
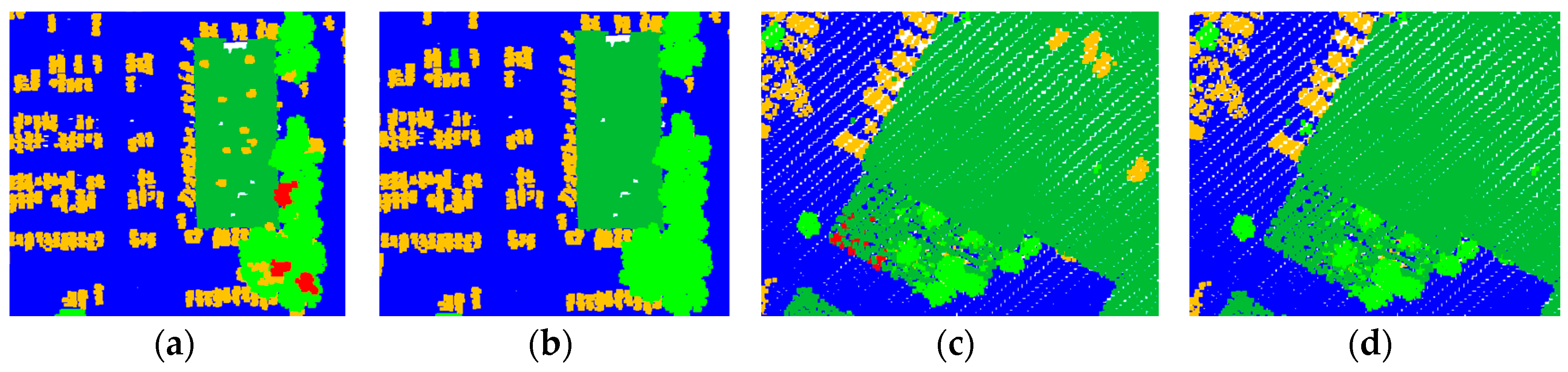
To qualitatively analyze the impact of the post-processing stage, we select two small areas in Area 1 and 2 respectively.
Figure 14 shows the initial and the final results of the small areas. In the initial classification results (see
Figure 14a,c), a number of segments are mislabeled as the class
vehicle or
wire. For example, building elements such as chimneys are often mislabeled as
vehicle, tree segments with small size are often mislabeled as the class
vehicle or
wire. In the post-processing stage, the second rule for vehicles can deal with the initial false results where other classes of objects are mislabeled as
vehicle, the rules for wires can deal with the initial false results where tree segments are mislabeled as
wire. In the final results presented in
Figure 14b,d, the initial false results are corrected based on these semantic rules.
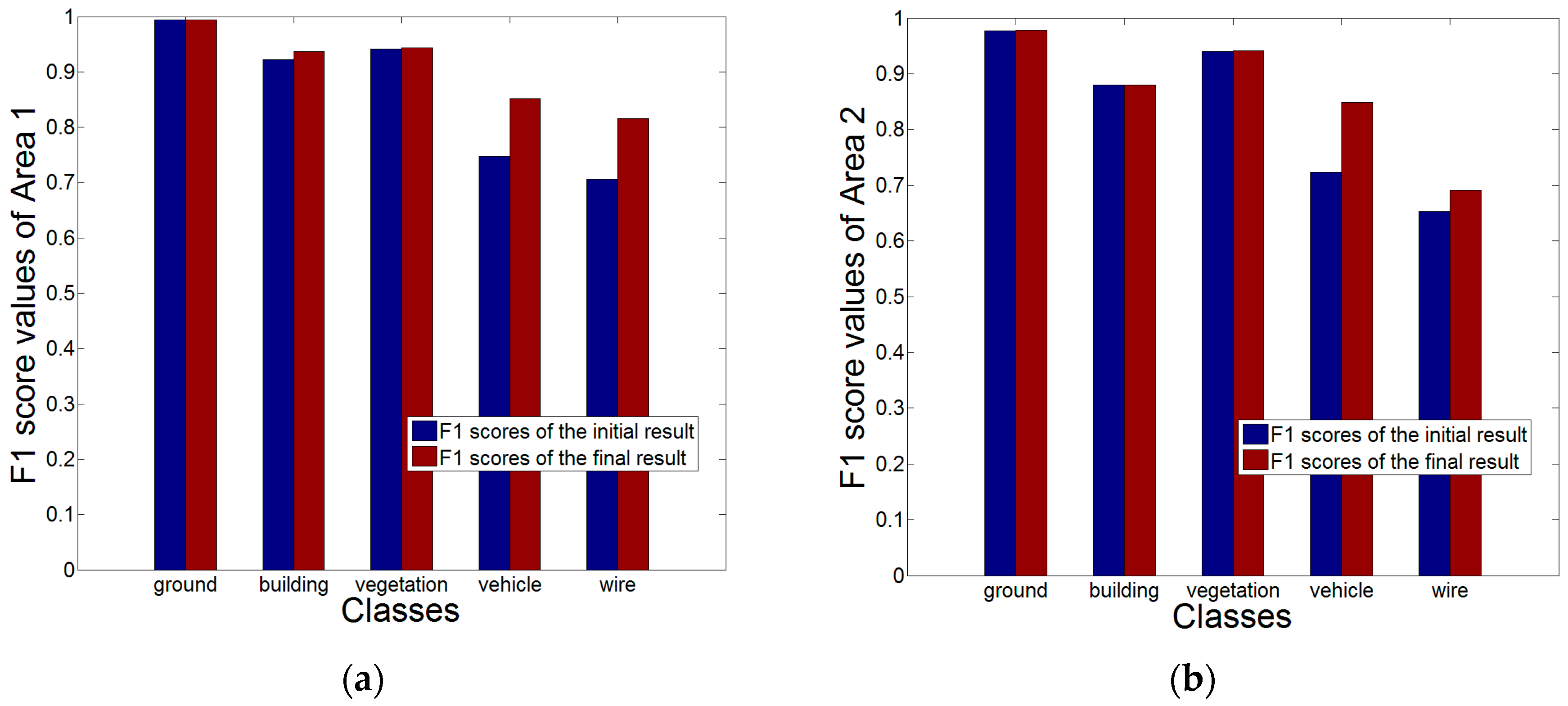
For quantitative analysis, we compare each class’s
-score for the initial results and the final results.
Figure 15a,b show the
-score comparison for Area 1 and Area 2. We can find that the
-score of the class
vehicle is improved obviously both in Area 1 and 2. Besides, the
-score values of other classes are also improved at different levels.
3.5. Classification Results and Accuracies
The final results of Area 1 and 2 are shown in
Figure 16. The time costs of our proposed classification framework for processing Area 1 and 2 are 21 min and 25 min, respectively. The feature extraction procedure is the most time consuming step which costs 9 min and 12 min for Area 1 and 2, respectively. To quantitatively analyze the accuracies of classification, we compute the confusion matrix and the aforementioned five measures in
Table 8 and
Table 9 based on the reference data generated by manual labelling. In addition, there may be missing points after the step-wise point cloud segmentation performed. These missing points will exist in the finial classification results and but are not labeled. In the quantitative evaluation, if some missing points belong to a class according to the ground true, they will be considered for evaluation. The revealed missing points are shown in the confusion matrices. Note that quantitative analysis is derived by individual points rather than segments, because the hypothesis that no error exists in segments is unreasonable.
As shown in
Table 8 and
Table 9, the proposed method achieves a mean overall accuracy of 0.95255 (0.9697 and 0.9374 for Area 1 and 2 respectively), and a mean kappa coefficient of 0.9231 (0.9442 and 0.9020 for Area 1 and 2 respectively). The accuracy values of classes
ground,
building and
vegetation are rather good. The accuracy values of
vehicle and
wire, are relatively lower than those of the other classes. The class
vehicle achieves a mean
-score of 0.8504 (0.8519 and 0.8488 for Area 1 and 2, respectively), and the class
wire achieves a mean
-score of 0.7531 (0.8155 and 0.6907 for Area 1 and 2, respectively).
The classification of small objects such as vehicles is the most challenging task. Generally, vegetation points make a 3D urban scene more complex and affect the classification of small objects. For example, wires often go across the trees with high elevation and vehicles are often parked near low vegetation or under tree canopies. Therefore, in the confusion matrices, vegetation points are often confused with another class points, and thus decrease the classification accuracy of other classes, especially for the classes of vehicle and wire. However, the accuracy of class vegetation achieves a mean -score of 0.9422 (0.9429 and 0.9415 for Area 1 and 2, respectively) which is superior.
3.6. Transplantation to Mountainous Areas
To test the transplanting of the proposed method, extracted features and obtained parameters to mountainous areas, we classify a different 3D scene represented by Area 3. Area 3 is a mountainous area with step edges and rock faces. First, Area 3 is segmented by the proposed step-wise point cloud segmentation method with the same parameters as Area 2, and segment features are extracted. Next, a small feature set is selected by the obtained parameters of RF, i.e.,
, and
. 9 features are selected by the backward elimination method presented in
Section 3.3.2, and they are lowest eigenvalue
, scattering
, omnivariance
, slope
, change of curvature
, planarity
, anisotropy
, eigenentropy
, tangent plane projection area
. Then, the ALS point cloud of Area 3 is classified by the select feature set. None of the semantic rules are utilized in the post-processing stage. 16 min are costed during the whole procedures among which the feature extraction procedure is the most time consuming step. The confusion matrix contained recall, precision, and
-score values is shown in
Table 10, and its corresponding segmentation and classification results are shown in
Figure 17.
As shown in
Table 10, the proposed classification framework and obtained parameters of RF achieve an overall accuracy of 0.9117, and a Kappa coefficient of 0.8379. The class
ground achieves a
-score of 0.9026 which is lower than Area 1 and 2, because the ground of Area 3 is mountainous and rugged with step edges. The class
building achieves a
-score of 0.8760, and the class
vegetation achieves a
-score of 0.9327.
4. Uncertainties, Errors and Accuracies
The above experiments suggest that our proposed method obtains good results. There are three improvements in our proposed classification framework, which improve the accuracies of the classification results. However, there are still some errors in the classification results. We will list them according to missing points and the five aforementioned classes.
In the confusion matrices, the missing points appear more likely in the classes building and vegetation. For the class vegetation, the laser beam may penetrate the tree surface and collects a point in an internal branch. The internal point may be an isolated point, however, belong to the class vegetation. For the class building, the missing points often appear on building facades duo to the fact that building facades are incomplete and points in them are sparse in large-scale ALS point clouds.
For the class
ground, uncertainties and errors are more likely to arise in the areas with mountainous and rugged topography. In
Table 8, the class
ground achieves a
-score of 0.9939 due to the fact that the ground in Area 1 is flat and smooth. In
Table 9, the
-score of ground (0.9783) is lower than that of Area 1, because there is a hill that causes the topographical complexity increasing. In Area 3, all the ground points are located at a mountainous region which are rugged and full of step edges and rock faces. The
-score of class
ground in Area 3 is 0.9026 which is much lower than those in Area 1 and 2. However, according to the recall and precision values of ground in Area 3, our proposed classification framework achieves the average accuracy of existing ALS point cloud filtering methods.
For the class building, the -score (0.9368) in Area 1 is superior to those in Area 2 and 3. A close-up visual inspection shows that there are more buildings with vegetation confused in Area 2 and 3. Especially in Area 3, all the buildings are surrounded by vegetation and most of them are overlapped by tall trees. Although the regions where buildings and vegetation are confused are segmented correctly by the step-wise point cloud segmentation method, these regions still decrease the classification accuracy of the class building.
For the class vegetation in confusion matrix, vegetation points are often confused with other classes points. A close-up visual inspection shows that man-made objects such as buildings, vehicles and wires are often near vegetation. For example, buildings tend to be surrounded by trees, wires often go across tall trees. Therefore, vegetation makes a 3D scene more complex and affects the classification accuracy of other classes. However, the class vegetation achieves a mean -score of 0.9390 (0.9429, 0.9415 and 0.9327 for Area 1, 2 and 3, respectively) which is superior due to the large cardinal number.
For the class
vehicle, the mean
-score is 0.8504 (0.8519 and 0.8488 for Area 1 and 2, respectively) which is lower than the classes
ground,
building, and
vegetation. Most misjudgments are caused by vegetation according to the confusion matrices, though the scene where vehicles are parked close to low vegetation is able to be correctly segmented. A close-up visual inspection shows that the mislabeled points always distribute randomly and irregularly. In an extreme case, it is inevitable that misjudgments exist in low vegetation which is in the same geometric form as a vehicle. However, the classification accuracy of the class
vehicle is superior to the existing studies according to the analysis presented in
Section 3.2.
For the class wire, the mean -score is 0.7531 (0.8155 and 0.6907 for Area 1 and 2, respectively). The wire is the class with the lowest accuracy in our experiments. The wires in our study areas are rather common low voltage electrical wires than some special parts of overhead electric power transmission corridors. The misjudgments arise in the areas where wires go across trees. In these areas, wires and trees have similar point densities and cannot be divided by the segmentation method. Therefore, there will be a number of mislabeled points in the classification results of these areas, which affect the accuracy of the class wire most.
5. Conclusions
In this paper, we classify ALS point clouds via a framework with four stages, i.e., (i) step-wise point cloud segmentation; (ii) feature extraction; (iii) RF-based feature selection and classification; (iv) post-processing. In the first stage, the step-wise point cloud segmentation extracts three kinds of segments, i.e., planar, smooth and rough surfaces. Planar and smooth surfaces are more easy to characterize piecewise planar objects, and rough surfaces are more easy to characterize objects with irregular shapes. In the second stage, we extract geometric features from the input ALS point cloud by considering segments as the basic computational units. In the third stage, we integrate RF with the segment-based classification method to classify ALS point clouds. Discriminative features are selected using the backward elimination method based on OOB errors, and an appropriate value (400) for the number of trees used in RF is determined. At last, we employ semantic information to define several rules for each class, and utilize them in the post-processing stage to optimize the classification results.
There are two contributions in the framework, i.e., step-wise point cloud segmentation, and the integration of RF and the segment-based classification method. In the step-wise point cloud segmentation, we utilize a RANSAC method to optimize the normal vector and neighborhood of each point, and next grow a region among the optimized neighborhood for each seed point. Then, scattered points are detected and initial patches are constructed. Finally, the log Euclidean Riemannian metric is utilized as a constraint to connect the initial patches to rough surfaces. Experiments validate that the step-wise segmentation is good at recognizing small-scale objects. To analyze the integration of RF and the segment-based classification, we first find a suitable parameter setting of RF, then select features based on these parameters, and finally analyze the robustness and show the benefits of the integration.
There is a limit existing in our method, i.e., objects with less geometric distinguishability cannot be recognized, such as flat roads which has similar geometric attributes with ground. In future work, we will take more features and complemental strategies into consideration to classify these kinds of objects.
Acknowledgments
This research was funded by: (1) the General Program sponsored by the National Natural Science Foundations of China (NSFC) under Grant 41371405; (2) the Foundation for Remote Sensing Young Talents by the National Remote Sensing Center of China; (3) the Basic Research Fund of the Chinese Academy of Surveying and Mapping under Grant 777161103; and (4) the General Program sponsored by the National Natural Science Foundations of China (NSFC) under Grant 41671440.
Author Contributions
All of the authors contributed extensively to the work presented in this paper. Huan Ni proposed the step-wise segmentation methods and the classification framework, implemented all the algorithms presented in this manuscript, and wrote this paper. Xiangguo Lin discussed the structure of this manuscript, revised this manuscript, named this method, supported this research, and supplied experimental facilities. Jixian Zhang revised this manuscript, supported this research, and guided the overall studies.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yan, W.Y.; Shaker, A.; El-Ashmawy, N. Urban land cover classification using airborne lidar data: A review. Remote Sens. Environ. 2015, 158, 295–310. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, X. Advances in fusion of optical imagery and lidar point cloud applied to photogrammetry and remote sensing. Int. J. Image Data Fusion 2017, 8, 1–31. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-earth extraction from airborne laser scanning point clouds. ISPRS-J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Meng, X.L.; Currit, N.; Zhao, K.G. Ground filtering algorithms for airborne lidar data: A review of critical issues. Remote Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef]
- Chen, C.F.; Li, Y.Y.; Yan, C.Q.; Dai, H.L.; Liu, G.L.; Guo, J.Y. An improved multi-resolution hierarchical classification method based on robust segmentation for filtering als point clouds. Int. J. Remote Sens. 2016, 37, 950–968. [Google Scholar] [CrossRef]
- Zhang, J.X.; Lin, X.G. Filtering airborne lidar data by embedding smoothness-constrained segmentation in progressive tin densification. ISPRS-J. Photogramm. Remote Sens. 2013, 81, 44–59. [Google Scholar] [CrossRef]
- Yang, B.; Huang, R.; Dong, Z.; Zang, Y.; Li, J. Two-step adaptive extraction method for ground points and breaklines from lidar point clouds. ISPRS-J. Photogramm. Remote Sens. 2016, 119, 373–389. [Google Scholar] [CrossRef]
- Lee, J.H.; Biging, G.S.; Radke, J.D.; Fisher, J.B. An improved topographic mapping technique from airborne lidar: Application in a forested hillside. Int. J. Remote Sens. 2013, 34, 7293–7311. [Google Scholar] [CrossRef]
- Sampath, A.; Shan, J. Building boundary tracing and regularization from airborne lidar point clouds. Photogramm. Eng. Remote Sens. 2007, 73, 805–812. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, L.Q.; Mathiopoulos, P.T.; Huang, X.F. A methodology for automated segmentation and reconstruction of urban 3-d buildings from als point clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4199–4217. [Google Scholar] [CrossRef]
- Jarzgbek-Rychard, M.; Borkowski, A. 3d building reconstruction from als data using unambiguous decomposition into elementary structures. ISPRS-J. Photogramm. Remote Sens. 2016, 118, 1–12. [Google Scholar] [CrossRef]
- Sampath, A.; Shan, J. Segmentation and reconstruction of polyhedral building roofs from aerial lidar point clouds. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1554–1567. [Google Scholar] [CrossRef]
- Yu, S.; Yu, B.; Song, W.; Wu, B.; Zhou, J.; Huang, Y.; Wu, J.; Zhao, F.; Mao, W. View-based greenery: A three-dimensional assessment of city buildings’ green visibility using floor green view index. Landsc. Urban Plan. 2016, 152, 13–26. [Google Scholar] [CrossRef]
- Polewski, P.; Yao, W.; Heurich, M.; Krzystek, P.; Stilla, U. Detection of fallen trees in als point clouds using a normalized cut approach trained by simulation. ISPRS-J. Photogramm. Remote Sens. 2015, 105, 252–271. [Google Scholar] [CrossRef]
- Rodriguez-Cuenca, B.; Garcia-Cortes, S.; Ordonez, C.; Alonso, M.C. Automatic detection and classification of pole-like objects in urban point cloud data using an anomaly detection algorithm. Remote Sens. 2015, 7, 12680–12703. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Wu, Q.; Huang, Y.; Chen, Z.; Wu, J. Individual tree crown delineation using localized contour tree method and airborne lidar data in coniferous forests. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 82–94. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Z.; Wu, B.; Chen, L.; Mao, W.; Zhao, F.; Wu, J.; Wu, J.; Yu, B. Estimating roof solar energy potential in the downtown area using a gpu-accelerated solar radiation model and airborne lidar data. Remote Sens. 2015, 7, 15877. [Google Scholar] [CrossRef]
- Guo, B.; Huang, X.F.; Zhang, F.; Sohn, G.H. Classification of airborne laser scanning data using jointboost. ISPRS-J. Photogramm. Remote Sens. 2015, 100, 71–83. [Google Scholar] [CrossRef]
- Chehata, N.; Guo, L.; Mallet, C. Airborne lidar feature selection for urban classification using random forests. Int. Arch. Photogramm. Remote Sens. 2009, 38, W8. [Google Scholar]
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS J. Photogramm. Remote Sens. 2015, 105, 286–304. [Google Scholar] [CrossRef]
- Tóvári, D. Segmentation Based Classification of Airborne Laser Scanner Data. Ph.D. Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2006. [Google Scholar]
- Darmawati, A. Utilization of Multiple Echo Information for Classification of Airborne Laser Scanning Data. Master’s Thesis, ITC Enschede, Enschede, The Netherlands, 2008. [Google Scholar]
- Yao, W.; Hinz, S.; Stilla, U. Object extraction based on 3d-segmentation of lidar data by combining mean shift with normalized cuts: Two examples from urban areas. In Proceedings of the 2009 Joint Urban Remote Sensing Event, Shanghai, China, 20–22 May 2009; pp. 1–6.
- Yang, B.S.; Dong, Z.; Zhao, G.; Dai, W.X. Hierarchical extraction of urban objects from mobile laser scanning data. ISPRS J. Photogramm. Remote Sens. 2015, 99, 45–57. [Google Scholar] [CrossRef]
- Xu, S.; Vosselman, G.; Elberink, S.O. Multiple-entity based classification of airborne laser scanning data in urban areas. ISPRS J. Photogramm. Remote Sens. 2014, 88, 1–15. [Google Scholar] [CrossRef]
- Lee, I.; Schenk, T. Perceptual organization of 3d surface points. Int. Arch. Photogramm. Remote Sens. 2002, 34, 193–198. [Google Scholar]
- Filin, S.; Pfeifer, N. Neighborhood systems for airborne laser data. Photogramm. Eng. Remote Sens. 2005, 71, 743–755. [Google Scholar] [CrossRef]
- Linsen, L.; Prautzsch, H. Local versus global triangulations. In Proceedings of the Eurographics’01, Manchester, UK, 5–7 September 2001.
- Mitra, N.J.; Nguyen, A. Estimating surface normals in noisy point cloud data. In Proceedings of the Nineteenth Annual Symposium on Computational Geometry, San Diego, CA, USA, 8–10 June 2003; pp. 322–328.
- Lalonde, J.-F.; Unnikrishnan, R.; Vandapel, N.; Hebert, M. Scale selection for classification of point-sampled 3D surfaces. In Proceedings of the Fifth International Conference on 3-D Digital Imaging and Modeling (3DIM’05), Ottawa, ON, Canada, 13–16 June 2005; pp. 285–292.
- Pauly, M.; Keiser, R.; Gross, M. Multi-scale feature extraction on point-sampled surfaces. Comput. Graph. Forum 2003, 22, 281–289. [Google Scholar] [CrossRef]
- Belton, D.; Lichti, D.D. Classification and segmentation of terrestrial laser scanner point clouds using local variance information. Int. Arch. Photogramm. Remote Sens. 2006, 36, 44–49. [Google Scholar]
- Demantke, J.; Mallet, C.; David, N.; Vallet, B. Dimensionality based scale selection in 3d lidar point clouds. Int. Arch. Photogramm. Remote Sens. 2011, 38, W12. [Google Scholar] [CrossRef]
- Weinmann, M.; Jutzi, B.; Mallet, C. Semantic 3d scene interpretation: A framework combining optimal neighborhood size selection with relevant features. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 181–188. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, L.; Chen, Y.M.; Wu, Y.; Li, M.C. Building point detection from vehicle-borne lidar data based on voxel group and horizontal hollow analysis. Remote Sens. 2016, 8, 419. [Google Scholar] [CrossRef]
- Zhang, J.X.; Lin, X.G.; Ning, X.G. Svm-based classification of segmented airborne lidar point clouds in urban areas. Remote Sens. 2013, 5, 3749–3775. [Google Scholar] [CrossRef]
- Vo, A.V.; Linh, T.H.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS-J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Guan, H.; Yu, J.; Li, J.; Luo, L. Random forests-based feature selection for land-use classification using lidar data and orthoimagery. Int. Arch. Photogramm. Remote Sens. 2012, 39, B7. [Google Scholar] [CrossRef]
- Johnson, A.E.; Hebert, M. Using spin images for efficient object recognition in cluttered 3d scenes. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 433–449. [Google Scholar] [CrossRef]
- Osada, R.; Funkhouser, T.; Chazelle, B.; Dobkin, D. Shape distributions. ACM Trans. Graph. 2002, 21, 807–832. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3d registration. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA’09), Kobe, Japan, 12–17 May 2009; pp. 3212–3217.
- Rusu, R.B.; Marton, Z.C.; Blodow, N.; Beetz, M. Persistent point feature histograms for 3d point clouds. In Proceedings of the 10th International Conference on Intelligent Autonomous Systems (IAS-10), Baden-Baden, Germany, 23–25 July 2008; pp. 119–128.
- Tombari, F.; Salti, S.; Di Stefano, L. Unique signatures of histograms for local surface description. In Proceedings of the European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; pp. 356–369.
- Guan, H.Y.; Li, J.; Chapman, M.; Deng, F.; Ji, Z.; Yang, X. Integration of orthoimagery and lidar data for object-based urban thematic mapping using random forests. Int. J. Remote Sens. 2013, 34, 5166–5186. [Google Scholar] [CrossRef]
- Lodha, S.K.; Kreps, E.J.; Helmbold, D.P.; Fitzpatrick, D.N. Aerial lidar data classification using support vector machines (svm). In Proceedings of the Third International Symposium on 3D Data Processing, Visualization, and Transmission, Chapel Hill, NC, USA, 14–16 June 2006; pp. 567–574.
- Lodha, S.K.; Fitzpatrick, D.M.; Helmbold, D.P. Aerial lidar data classification using adaboost. In Proceedings of the Sixth International Conference on 3-D Digital Imaging and Modeling, Montreal, QC, Canada, 21–23 August 2007; pp. 435–442.
- Lodha, S.K.; Fitzpatrick, D.M.; Helmbold, D.P. Aerial lidar data classification using expectation-maximization. Proc. SPIE 2007. [Google Scholar] [CrossRef]
- Kim, H.; Sohn, G. 3d classification of power-line scene from airborne laser scanning data using random forests. Int. Arch. Photogramm. Remote Sens 2010, 38, 126–132. [Google Scholar]
- Kim, H.; Sohn, G. Random forests based multiple classifier system for power-line scene classification. ISPRS Int. Arch. Photogramm., Remote Sens. Spat. Inf. Sci. 2011, 253–258. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Dragut, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Diaz-Uriarte, R.; de Andres, S.A. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Jiang, W.; Shan, J.; Zhang, J.; Li, L. Investigation on the weighted ransac approaches for building roof plane segmentation from lidar point clouds. Remote Sens. 2016, 8, 5. [Google Scholar] [CrossRef]
- Vosselman, G.; Klein, R. Visualisation and structuring of point clouds. In Airborne and Terrestrial Laser Scanning; Whittles Publishing: Dunbeath, UK, 2010; pp. 43–79. [Google Scholar]
- Lin, Y.; Wang, C.; Cheng, J.; Chen, B.; Jia, F.; Chen, Z.; Li, J. Line segment extraction for large scale unorganized point clouds. ISPRS J. Photogramm. Remote Sens. 2015, 102, 172–183. [Google Scholar] [CrossRef]
- Ni, H.; Lin, X.; Ning, X.; Zhang, J. Edge detection and feature line tracing in 3d-point clouds by analyzing geometric properties of neighborhoods. Remote Sens. 2016, 8, 710. [Google Scholar] [CrossRef]
- Rabbani, T.; van den Heuvel, F.; Vosselmann, G. Segmentation of point clouds using smoothness constraint. Int. Arch. Photogramm. Remote Sens. 2006, 36, 248–253. [Google Scholar]
- Arsigny, V.; Fillard, P.; Pennec, X.; Ayache, N. Log-euclidean metrics for fast and simple calculus on diffusion tensors. Magn. Reson. Med. 2006, 56, 411–421. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Liaw, A.; Breiman, L. Using Random Forest to learn Imbalanced Data; University of California, Berkeley: Berkeley, CA, USA, 2004; pp. 1–12. [Google Scholar]
- Strobl, C.; Boulesteix, A.L.; Augustin, T. Unbiased split selection for classification trees based on the gini index. Comput. Stat. Data Anal. 2007, 52, 483–501. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, J. Segmentation-based filtering of airborne lidar point clouds by progressive densification of terrain segments. Remote Sens. 2014, 6, 1294. [Google Scholar] [CrossRef]
- He, Y. Automated 3D Building Modelling from Airborne Lidar Data. Ph.D. Thesis, University of Melbourne, Melbourne, Victoria, Australia, 2015. [Google Scholar]
- PCL-The Point Cloud Library, 2012. Available online: http://pointclouds.org/ (accessed on 11 September 2014).
- Libsvm, 2014. Available online: http://www.csie.ntu.edu.tw/~cjlin/libsvm (accessed on 25 March 2015).
- 2008 Iowa River Flood Lidar, Iowa City, and the Clear Creek Watershed. Available online: http://opentopo.sdsc.edu/lidarDataset?opentopoID=OTLAS.012012.26915.1 (accessed on 21 January 2016).
- Umd-NASA Carbon Mapping/Sonoma County Vegetation Mapping and LiDAR Program. Available online: http://opentopo.sdsc.edu/datasetMetadata?otCollectionID=OT.092014.2871.1 (accessed on 21 January 2016).
Figure 1.
The proposed framework for airborne laser scanning (ALS) point cloud classification.
Figure 1.
The proposed framework for airborne laser scanning (ALS) point cloud classification.
Figure 2.
The flowchart of the step-wise point cloud segmentation.
Figure 2.
The flowchart of the step-wise point cloud segmentation.
Figure 3.
Results of internal steps in the step-wise point cloud segmentation: (a) Intermediate result after the process of the region growing (RG) with RANdom SAmple Consensus (RANSAC) step. The scattered points are rendered in black; (b) Intermediate result after the process of the initial patch construction; (c) The result of the step-wise point cloud segmentation.
Figure 3.
Results of internal steps in the step-wise point cloud segmentation: (a) Intermediate result after the process of the region growing (RG) with RANdom SAmple Consensus (RANSAC) step. The scattered points are rendered in black; (b) Intermediate result after the process of the initial patch construction; (c) The result of the step-wise point cloud segmentation.
Figure 4.
The calculation method of projection area [
18].
Figure 4.
The calculation method of projection area [
18].
Figure 5.
Segment-based features for 3D-point clouds classification, (a) horizontal projection area ratio ; (b) eigenentropy ; (c) relative elevation ; (d) slope .
Figure 5.
Segment-based features for 3D-point clouds classification, (a) horizontal projection area ratio ; (b) eigenentropy ; (c) relative elevation ; (d) slope .
Figure 6.
The testing data, (a) shows the point cloud of Area 1, (b) shows the point clouds for Area 2 and 3.
Figure 6.
The testing data, (a) shows the point cloud of Area 1, (b) shows the point clouds for Area 2 and 3.
Figure 7.
Comparison of our segmentation method with the RG methods presented in Point Cloud Library (PCL): (a) The result of our method; (b) The result of the RG-based plane segmentation; (c) The result of the RG-based smoothness segmentation.
Figure 7.
Comparison of our segmentation method with the RG methods presented in Point Cloud Library (PCL): (a) The result of our method; (b) The result of the RG-based plane segmentation; (c) The result of the RG-based smoothness segmentation.
Figure 8.
All classes’ -score values of different segmentation methods for Area 1 and Area 2: (a) -score values of Area 1; (b) -score values of Area 2.
Figure 8.
All classes’ -score values of different segmentation methods for Area 1 and Area 2: (a) -score values of Area 1; (b) -score values of Area 2.
Figure 9.
The variation tendencies of overall accuracy and Kappa coefficient under different settings of : (a,b) are for Area 1 and Area 2 respectively; (c,d) are for Area 1 and Area 2 respectively.
Figure 9.
The variation tendencies of overall accuracy and Kappa coefficient under different settings of : (a,b) are for Area 1 and Area 2 respectively; (c,d) are for Area 1 and Area 2 respectively.
Figure 10.
The variation tendencies of mean overall accuracy values and standard deviation values of overall accuracy and Kappa coefficient under different settings of ; (a,b) are for Area 1 and Area 2 respectively; (c,d) are for Area 1 and Area 2 respectively.
Figure 10.
The variation tendencies of mean overall accuracy values and standard deviation values of overall accuracy and Kappa coefficient under different settings of ; (a,b) are for Area 1 and Area 2 respectively; (c,d) are for Area 1 and Area 2 respectively.
Figure 11.
Feature importance values based on the mean decrease permutation accuracy estimated by the first time fitted RF: (a) is for Area 1; (b) is for Area 2.
Figure 11.
Feature importance values based on the mean decrease permutation accuracy estimated by the first time fitted RF: (a) is for Area 1; (b) is for Area 2.
Figure 12.
Feature selection via iterative elimination for Area 1 and 2 based on the overall mean decrease permutation accuracy: (a) is for Area 1; (b) is for Area 2.
Figure 12.
Feature selection via iterative elimination for Area 1 and 2 based on the overall mean decrease permutation accuracy: (a) is for Area 1; (b) is for Area 2.
Figure 13.
Comparison between the two integrations under different numbers of noisy feature vectors, (
a,
b) depict the accuracy values of our method for Area 1 and 2 respectively, (
c,
d) depict the accuracy values of the literature [
36] for Area 1 and 2 respectively.
Figure 13.
Comparison between the two integrations under different numbers of noisy feature vectors, (
a,
b) depict the accuracy values of our method for Area 1 and 2 respectively, (
c,
d) depict the accuracy values of the literature [
36] for Area 1 and 2 respectively.
Figure 14.
Analysis of the impact of the post-processing stage based on semantic rules: (a) The initial result of the first small area; (b) The final result of the first small area: (c) The initial result of the second small area; (d) The final result of the second small area.
Figure 14.
Analysis of the impact of the post-processing stage based on semantic rules: (a) The initial result of the first small area; (b) The final result of the first small area: (c) The initial result of the second small area; (d) The final result of the second small area.
Figure 15.
-score comparison between the initial and final results of Area 1 and 2: (a) The comparison of Area 1; (b) The comparison of Area 2.
Figure 15.
-score comparison between the initial and final results of Area 1 and 2: (a) The comparison of Area 1; (b) The comparison of Area 2.
Figure 16.
The results of the proposed classification framework for areas Area 1 and 2, (a) is the segmentation result of Area 1; (b) is the classification result of Area 1; (c) is the segmentation result of Area 2; (d) is the classification result of Area 2.
Figure 16.
The results of the proposed classification framework for areas Area 1 and 2, (a) is the segmentation result of Area 1; (b) is the classification result of Area 1; (c) is the segmentation result of Area 2; (d) is the classification result of Area 2.
Figure 17.
The results of the proposed classification framework for Area 3, (a) is the segmentation result of Area 3; (b) is the classification result of Area 3.
Figure 17.
The results of the proposed classification framework for Area 3, (a) is the segmentation result of Area 3; (b) is the classification result of Area 3.
Table 1.
The extracted features.
Table 1.
The extracted features.
| Features | Sign |
|---|
| Projection-area-based features | , |
| Eigenvalue-based features | , , , , , , , , , |
| Elevation-based features | , , , |
| Others | , |
Table 2.
Number of training samples (segments) per class for the three study areas.
Table 2.
Number of training samples (segments) per class for the three study areas.
| Data | Class |
|---|
| Ground | Building | Vegetation | Vehicle | Wire | |
|---|
| Area 1 | 1 | 47 | 107 | 65 | 30 | 250 |
| Area 2 | 4 | 66 | 228 | 94 | 22 | 414 |
| Area 3 | 19 | 65 | 81 | - | - | 165 |
Table 3.
Number of points per class in ground true of the three study areas.
Table 3.
Number of points per class in ground true of the three study areas.
| Data | Class |
|---|
| Ground | Building | Vegetation | Vehicle | Wire | |
|---|
| Area 1 | 949,431 | 218,835 | 309,889 | 24,138 | 9799 | 1,512,092 |
| Area 2 | 589,231 | 227,442 | 651,022 | 36,520 | 5013 | 1,509,228 |
| Area 3 | 202,755 | 64,337 | 418,778 | - | - | 685,870 |
Table 4.
The parameter setting of our method for a small part in Area 1.
Table 4.
The parameter setting of our method for a small part in Area 1.
| Parameters | | | | | | | |
|---|
| Our method | 50 | 0.1 | 0.1 | 30 | 15 | 1.0 | 1.5 |
Table 5.
The parameter setting of RG method for a small part in Area 1.
Table 5.
The parameter setting of RG method for a small part in Area 1.
| Parameters | | | | | | |
|---|
| RG-based plane segmentation | 50 | 50 | 0.1 | 0.1 | 0.3 | 0 |
| RG-based smoothness segmentation | 50 | 50 | 0.1 | 0.1 | 0.5 | 0 |
Table 6.
The parameter setting of our method for Area 1 and 2.
Table 6.
The parameter setting of our method for Area 1 and 2.
| Parameters | | | | | | | |
|---|
| Area 1 | 50 | 0.1 | 0.1 | 30 | 15 | 1.0 | 1.5 |
| Area 2 | 50 | 0.1 | 0.1 | 30 | 15 | 3.0 | 2.0 |
Table 7.
The threshold values for the post-processing stage used for Area 1 and 2.
Table 7.
The threshold values for the post-processing stage used for Area 1 and 2.
| | | | | |
|---|
| Area 1 | — | 10 | 500 | 2.5 |
| Area 2 | 2.0 | 10 | 300 | 3.0 |
Table 8.
The accuracy analysis of Area 1.
Table 8.
The accuracy analysis of Area 1.
| Overall Accuracy: 0.9697, Kappa Coefficient: 0.9442 |
|---|
| | Ground | Building | Vegetation | Vehicle | Wire | Missing Points | Recall |
|---|
| Ground | 942,652 | 129 | 5546 | 463 | 32 | 609 | 0.9929 |
| Building | 2161 | 199,672 | 13,493 | 435 | 782 | 2292 | 0.9124 |
| Vegetation | 933 | 6514 | 296,124 | 1575 | 1038 | 3705 | 0.9556 |
| Vehicle | 1604 | 569 | 2053 | 19,771 | 67 | 74 | 0.8191 |
| Wire | 0 | 547 | 995 | 35 | 8067 | 155 | 0.8232 |
| Precision | 0.9950 | 0.9626 | 0.9306 | 0.8874 | 0.8078 | | |
| -score | 0.9939 | 0.9368 | 0.9429 | 0.8519 | 0.8155 | | |
Table 9.
The accuracy analysis of Area 2.
Table 9.
The accuracy analysis of Area 2.
| Overall Accuracy: 0.9374, Kappa Coefficient: 0.9020 |
|---|
| | Ground | Building | Vegetation | Vehicle | Wire | Missing Points | Recall |
|---|
| Ground | 576,460 | 232 | 9337 | 201 | 225 | 2776 | 0.9783 |
| Building | 2837 | 187,101 | 28,992 | 282 | 306 | 7924 | 0.8226 |
| Vegetation | 8495 | 9737 | 616,655 | 4636 | 1042 | 10,457 | 0.9472 |
| Vehicle | 1467 | 629 | 3023 | 30,855 | 314 | 232 | 0.8449 |
| Wire | 0 | 37 | 846 | 206 | 3640 | 284 | 0.7261 |
| Precision | 0.9783 | 0.9462 | 0.9360 | 0.8528 | 0.6586 | | |
| -score | 0.9783 | 0.8801 | 0.9415 | 0.8488 | 0.6907 | | |
Table 10.
The accuracy analysis of Area 3.
Table 10.
The accuracy analysis of Area 3.
| Overall Accuracy: 0.9117, Kappa Coefficient: 0.8379 |
|---|
| | Ground | Building | Vegetation | Missing Points | Recall |
|---|
| Ground | 182,090 | 4144 | 16,159 | 362 | 0.8981 |
| Building | 495 | 60,045 | 3485 | 312 | 0.9333 |
| Vegetation | 18,120 | 8568 | 383,143 | 8947 | 0.9149 |
| Precision | 0.9072 | 0.8253 | 0.9512 | | |
| -score | 0.9026 | 0.8760 | 0.9327 | | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).