Next Article in Journal
Bohai Sea Ice Parameter Estimation Based on Thermodynamic Ice Model and Earth Observation Data
Previous Article in Journal
Radiometric Cross-Calibration of GF-4 in Multispectral Bands
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 9
Issue 3
10.3390/rs9030233
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Impacts of Land Cover and Seasonal Variation on Maximum Air Temperature Estimation Using MODIS Imagery

by
Yulin Cai
1,2,3,*,
Gang Chen
3,
Yali Wang
1 and
Li Yang
1
1
Geomatics College, Shandong University of Sciences and Technology, Qingdao 266590, Shandong, China
2
State Key Laboratory of Resources and Environmental Information System, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101,China
3
Laboratory for Remote Sensing and Environmental Change (LRSEC), Department of Geography and Earth Sciences, University of North Carolina at Charlotte, Charlotte, NC 28223, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2017, 9(3), 233; https://doi.org/10.3390/rs9030233
Submission received: 18 January 2017 / Accepted: 1 March 2017 / Published: 3 March 2017
Browse Figures
Versions Notes

Abstract

:
Daily maximum surface air temperature (Tamax) is a crucial factor for understanding complex land surface processes under rapid climate change. Remote detection of Tamax has widely relied on the empirical relationship between air temperature and land surface temperature (LST), a product derived from remote sensing. However, little is known about how such a relationship is affected by the high heterogeneity in landscapes and dynamics in seasonality. This study aims to advance our understanding of the roles of land cover and seasonal variation in the estimation of Tamax using the MODIS (Moderate Resolution Imaging Spectroradiometer) LST product. We developed statistical models to link Tamax and LST in the middle and lower reaches of the Yangtze River in China for five major land-cover types (i.e., forest, shrub, water, impervious surface, cropland, and grassland) and two seasons (i.e., growing season and non-growing season). Results show that the performance of modeling the Tamax-LST relationship was highly dependent on land cover and seasonal variation. Estimating Tamax over grasslands and water bodies achieved superior performance; while uncertainties were high over forested lands that contained extensive heterogeneity in species types, plant structure, and topography. We further found that all the land-cover specific models developed for the plant non-growing season outperformed the corresponding models developed for the growing season. Discrepancies in model performance mainly occurred in the vegetated areas (forest, cropland, and shrub), suggesting an important role of plant phenology in defining the statistical relationship between Tamax and LST. For impervious surfaces, the challenge of capturing the high spatial heterogeneity in urban settings using the low-resolution MODIS data made Tamax estimation a difficult task, which was especially true in the growing season.

Graphical Abstract

1. Introduction

Surface air temperature (Ta) not only serves as a direct indicator of climate change [1], but also plays a crucial role in a range of studies for understanding the complex land surface processes, such as drought monitoring [2,3], greenhouse effect [4], hydrological simulation [5], urban heat island analysis [6,7,8,9], epidemiological modeling [10], and snowpack investigation [11]. Spatially explicit Ta mapping has been traditionally relying spatial interpolation to scale up the point-based temperature measurements recorded by sample meteorological stations to the landscape level. However, the performance of such an approach is known to be highly dependent on the density of station network and the spatial heterogeneity of the geographic regions of interest [12].
Remote sensing provides a viable alternative that makes use of infrared sensors to measure land temperature through detecting thermal infrared radiation emitted from the geographic objects on land surfaces [13,14]. The detected thermal radiation describes the kinetic energy of the ground objects informing land surface temperature (LST). While the LST is not equivalent to the air temperature above the surface (i.e., Ta), previous studies have confirmed a promising relationship between LST and Ta using three main categories of modeling approaches, including statistical, TVX (temperature–vegetation index), and energy-balance modeling. Specifically, (i) statistical modeling aims to establish an empirical relationship between Ta and LST through statistical regression analysis [15,16,17,18,19,20]. To account for spatial heterogeneity in the land surface, ancillary data are included as supplementary explanatory variables, such as elevation, albedo, NDVI (normalized difference vegetation index), NDWI (normalized difference water index), and solar radiation [21,22,23,24,25,26,27,28,29,30]; (ii) The empirical TVX method relies on the negative linear relationship between LST and the abundance of live vegetation, as represented by a vegetation index, e.g., NDVI [31,32]. The basic assumption is that Ta approaches LST under full canopy cover. Hence, Ta can be estimated by extrapolation of the LST-NDVI relationship to an NDVI value corresponding to the full canopy cover. However, recent studies have discovered inconsistent, non-linear relationships between LST and NDVI under complex land-cover conditions, which could negatively affect the TVX modeling performance (e.g., [33,34]); (iii) Energy-balance modeling is a physically-based approach directly grounded in thermodynamics. It treats Ta as the function of a range of variables describing the behavior of energy dynamics in the Earth system, such as radiation balance, and soil, sensible, and latent heat fluxes [35]. While theoretically promising, it remains challenging to accurately estimate such a large number of model inputs solely through remote detection [16].
Among the three aforementioned categories of approaches, statistical modeling has been the most popular mainly due to its simplicity and relative robustness [36]. However, few studies have systematically evaluated how the statistical relationship between Ta and LST varies across major land cover types. This is a crucial issue, because the Ta-LST relationship was found to be inconsistent over various landscapes, even if supplementary explanatory variables are used [24,37]. Additionally, seasonal variation is likely to introduce extra uncertainties in Ta modeling. Especially at forested and agricultural sites, vegetation phenology plays a vital role affecting the actual land cover condition (e.g., leaf-on versus leaf-off). Previous efforts have discovered significantly varied modeling performance from the environments with low temperatures (or in winter seasons) versus those on hot summer days [38,39,40,41]. To date, the joint impacts of land cover and seasonal variation remain to be systematically evaluated.
The main objective of this study was to improve our understanding of the statistical relationship between Ta and LST through remote detection. Here, we emphasized peak daytime air temperature (Tamax). Although the daytime surface energy flux is more complex than that at night, accurately estimating daytime air temperature was proven to more effectively inform extreme heat events and the associated human health issues (e.g., mortality) than using nighttime or daily average temperature [25,27,34,39,42]. To achieve our goal, we ask two research questions in this study: (i) How do major land-cover types influence the statistical relationship between Ta and LST? (ii) How does seasonal variation affect such a relationship by changing land-cover conditions?

2. Data and Methods

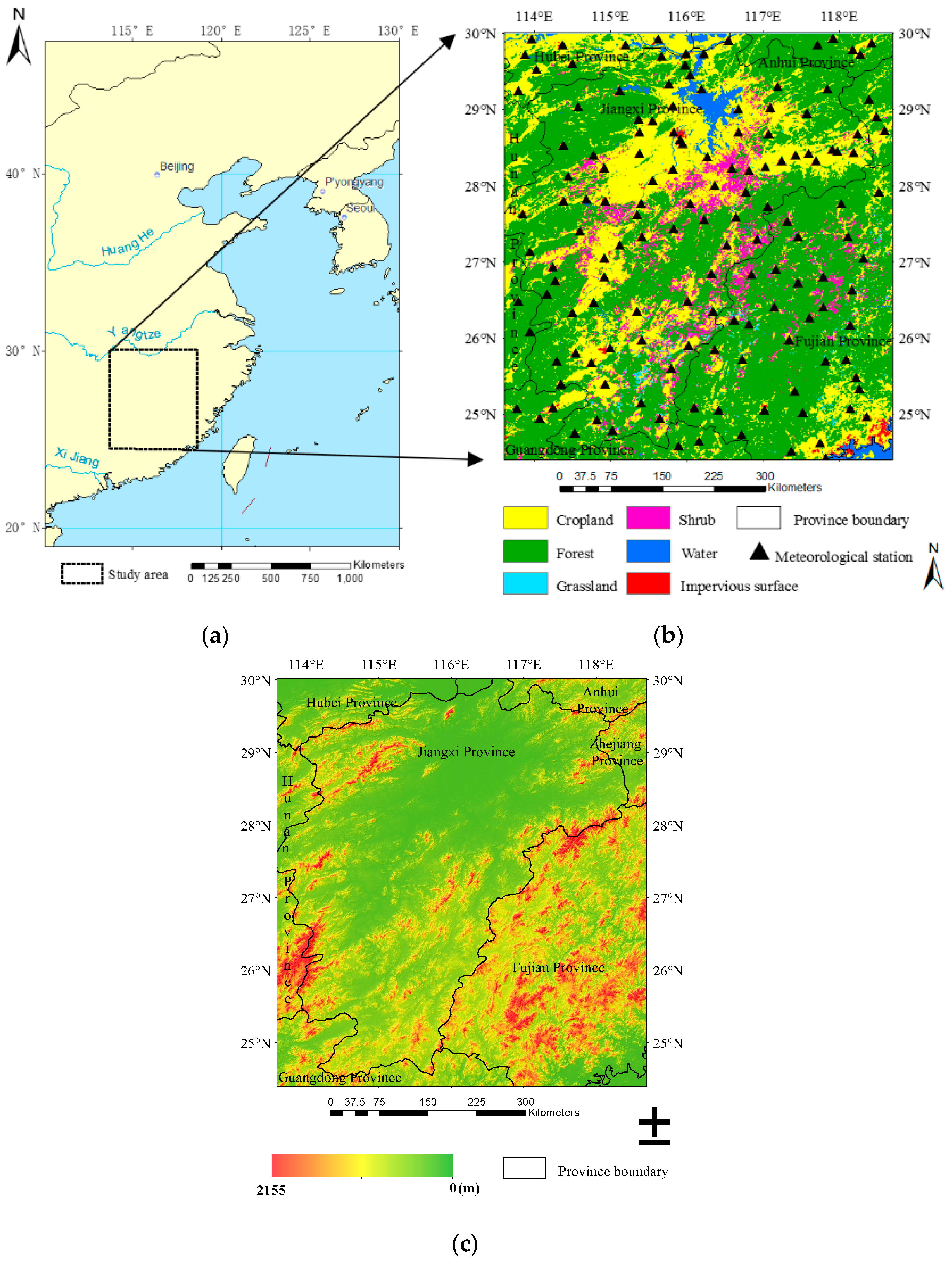
2.1. Study Area

Our study area is located in the middle and lower reaches of the Yangtze River (a.k.a., Changjiang River), the longest river in Asia and the third-longest in the world. The area is centered at the Poyang Lake Basin (Figure 1), which accounts for about 19% of the Yangtze River drainage area, with total coverage of 340,838 km2. Over the past decades, the region has experienced dramatic changes in landscape, resulting in variable land-cover types, significant environmental degradation, and substantial alteration in water and energy balance processes [43,44,45,46]. The need for improved conservation of natural resources has stimulated intensive management and research activities in the area, e.g., monitoring crucial climatic variables (e.g., surface air temperature) from the recently established meteorological network [45,47].

2.2. Air Temperature Meteorological Station Data

The meteorological time series of daily maximum air temperature observations from 1 December 2008 to 31 January 2010 were consistently collected by the China Meteorological Administration (CMA). We acquired data from 234 meteorological stations, which were evenly distributed throughout the study area (Figure 1). The locations of these stations can be identified on the MODIS (Moderate Resolution Imaging Spectroradiometer) LST images, then, LST data matching with daily maximum air temperature ground observations are extracted for study. Since MODIS LST products have a large amount of missing data due to cloud, heavy aerosols, only those observations matching with MODIS LST product data will be used for further study. Finally, our study used a total of 3916 observations, which were all taken at the height of 2 m above the ground level in accordance with the standards defined by the World Meteorological Organization (WMO).

2.3. MODIS Land Surface Temperature (LST) Data

The LST products from the MODIS system are one of the most widely used temperature products via remote detection. The system is comprised of sensors on two platforms of Terra (morning overpass at 10:30 am local) and Aqua (afternoon overpass at 1:30 pm local). Compared to Terra, Aqua has a closer overpass time when daily maximum air temperature occurs. However, previous efforts discovered superior performance of applying the LST data from MODIS/Terra to estimate air temperature [34,48]. Hence, this study employed one of the Terra’s daily land surface temperature and emissivity products, MOD11A1, in the succeeding analyses. MOD11A1 was produced at the spatial resolution of approximately 1 km (precisely 0.928 km), and gridded in the Sinusoidal projection. The MOD11A1 products were validated through field campaigns and radiance-based validation studies, with results indicating an accuracy of better than 1.0 K in most cases [49].
We downloaded the daily MOD11A1 products from the MODIS Land Processes Distributed Active Archive Center (LP DAAC) (http://lpdaac.usgs.gov/), with spatial and temporal coverage meeting the requirements of our research design. We further conducted data pre-processing by eliminating low-quality pixels (as indicated in the MOD11A1 Quality Control data layer) that corresponded to large errors induced by several factors, such as surface emissivity estimation error, atmospheric contamination, and viewing geometry on retrieval [49,50]. We retained the ‘good quality’ pixels in L1B bands 31 and 32, with an average emissivity error of less than 0.01, and an average LST error of no more than 1.0 K.

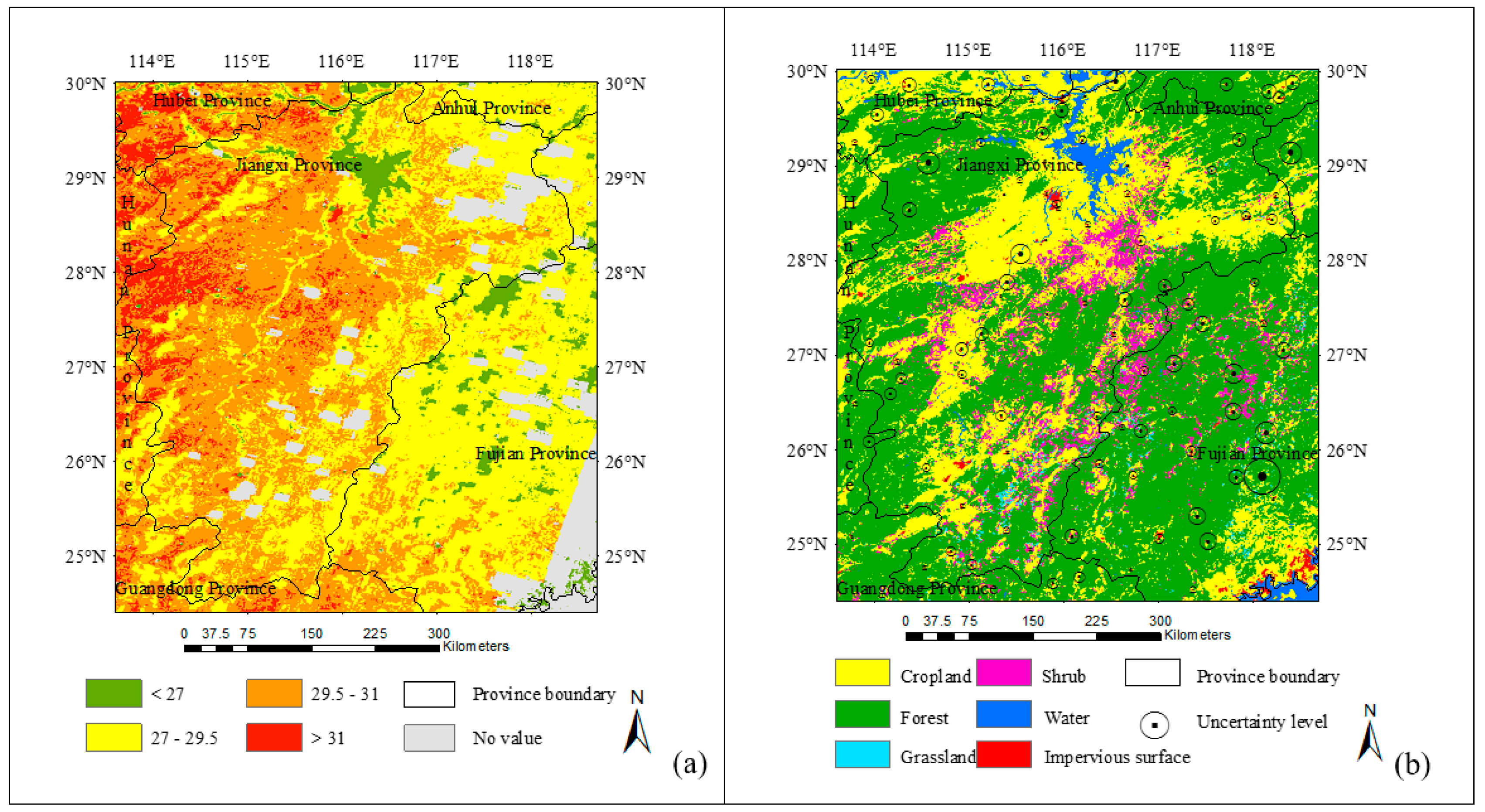
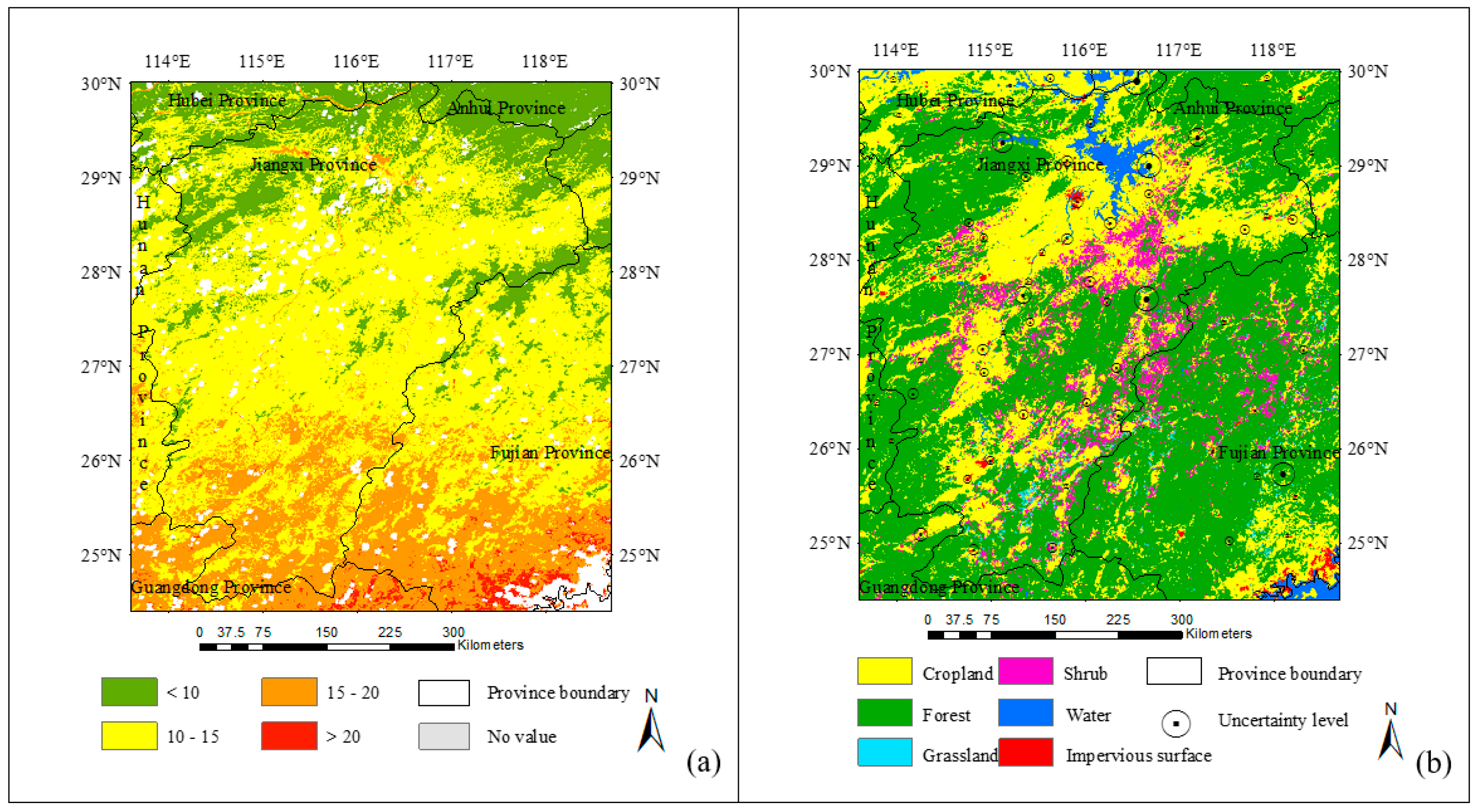
2.4. Land-Cover Map

To evaluate the potential impact of land cover on the Ta-LST relationship, we adopted a relatively new land-cover product FROM-GLC (Finer Resolution Observation and Monitoring of Global Land Cover), provided by the Center for Earth System Science (CESS) at Tsinghua University [51,52]. FROM-GLC was generated at the initial spatial resolution of 30 m using Landsat Thematic Mapper (TM) and Enhanced Thematic Mapper Plus (ETM+) data circa 2009 and 2010, which is consistent with the time period of our study. With the use of majority aggregation and proportion aggregation approaches, the products were delivered at multiple resolutions (e.g., 250 m, 500 m, 1 km, 5 km, and 10 km). To match the resolution of the selected MODIS LST product, the 1 km FROM-GLC map was chosen in this study, which was evaluated at an overall accuracy of 73.47% [52]. Because we only focused on major land-cover types, the land-cover classes in FROM-GLC were further combined to represent forest, shrub, water, impervious surface, cropland, and grassland. To evaluate the accuracy of the final land-cover map at our study site, we further selected 200 randomly distributed sample points through field surveys and image interpretation, with the result reaching an accuracy of 82%. The percentage and area extent of each land-cover type are demonstrated in Table 1.

2.5. Model Development and Validation

Statistical analysis of the relationship between air and land surface temperature has been primarily relying on regression modeling in previous studies (e.g., [16,36,37,40,41]). Here, we adopted such approach using ordinary least squares regression (OLS) to establish the linkage between Tamax and LST. To account for the impacts of land cover and seasonal variation, models were developed for six land-cover types (i.e., forest, shrub, water, impervious surface, cropland, and grassland) and two main seasons (plant growing and non-growing seasons). For comparison purposes, we also built OLS models without distinguishing between land-cover types, and between seasons. In total, 19 models were developed, calibrated by a randomly selected 80% of the observational data from ground stations.
Model validation was conducted with the remaining 20% of the observational data. The performance of the models was evaluated using three criteria: adjusted coefficient of determination (R2adjusted), mean absolute error (MAE), and root mean square error (RMSE).

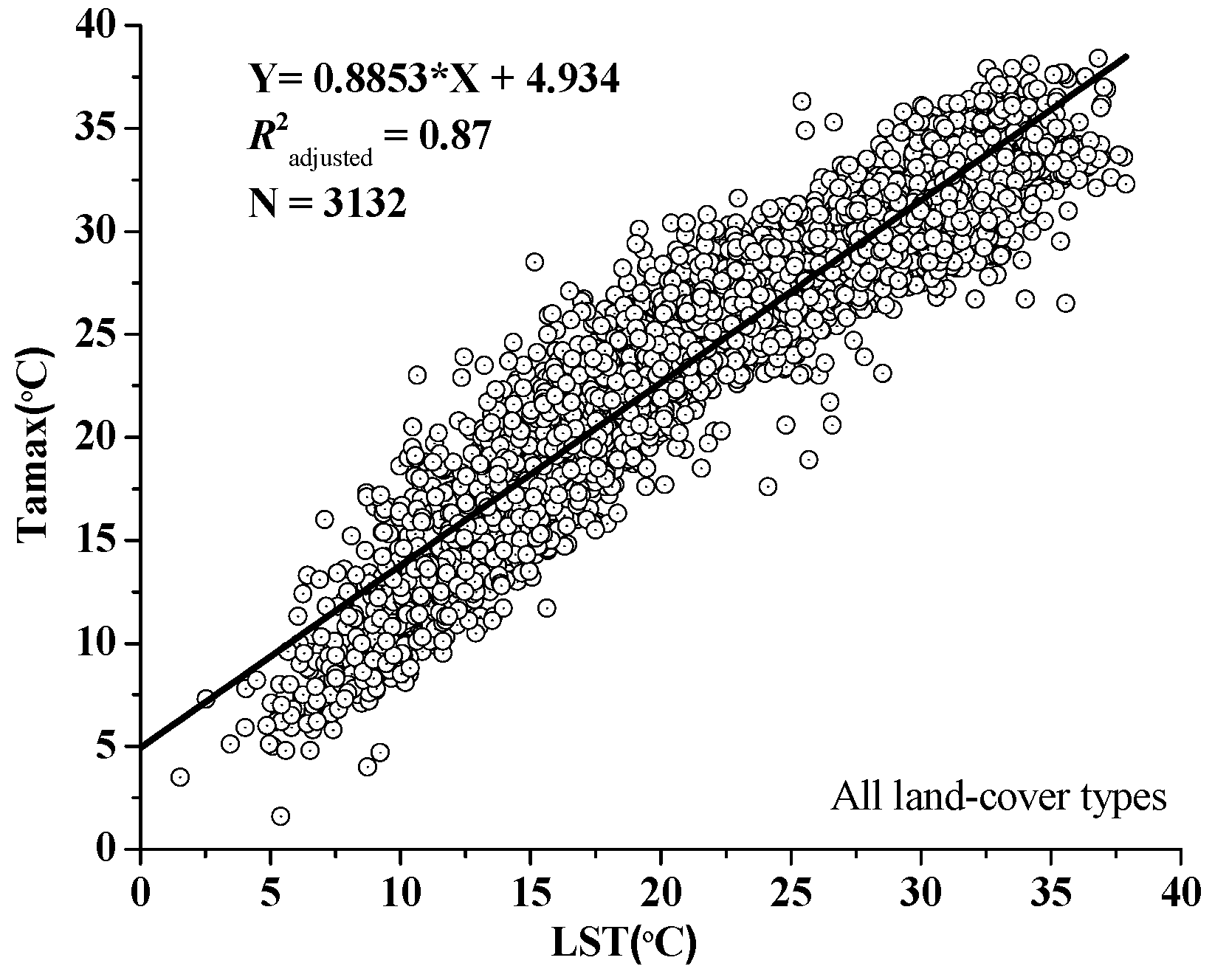
3. Results

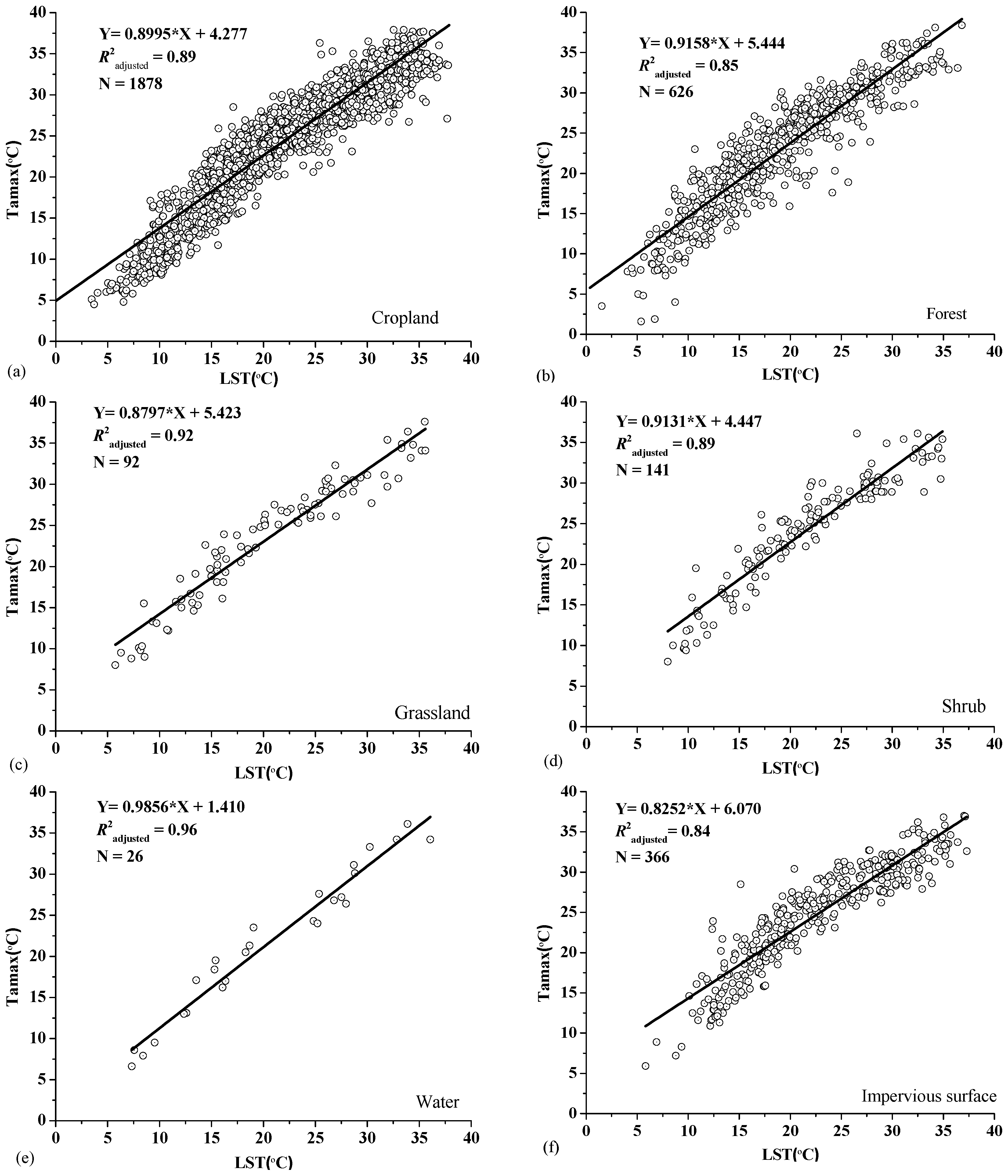
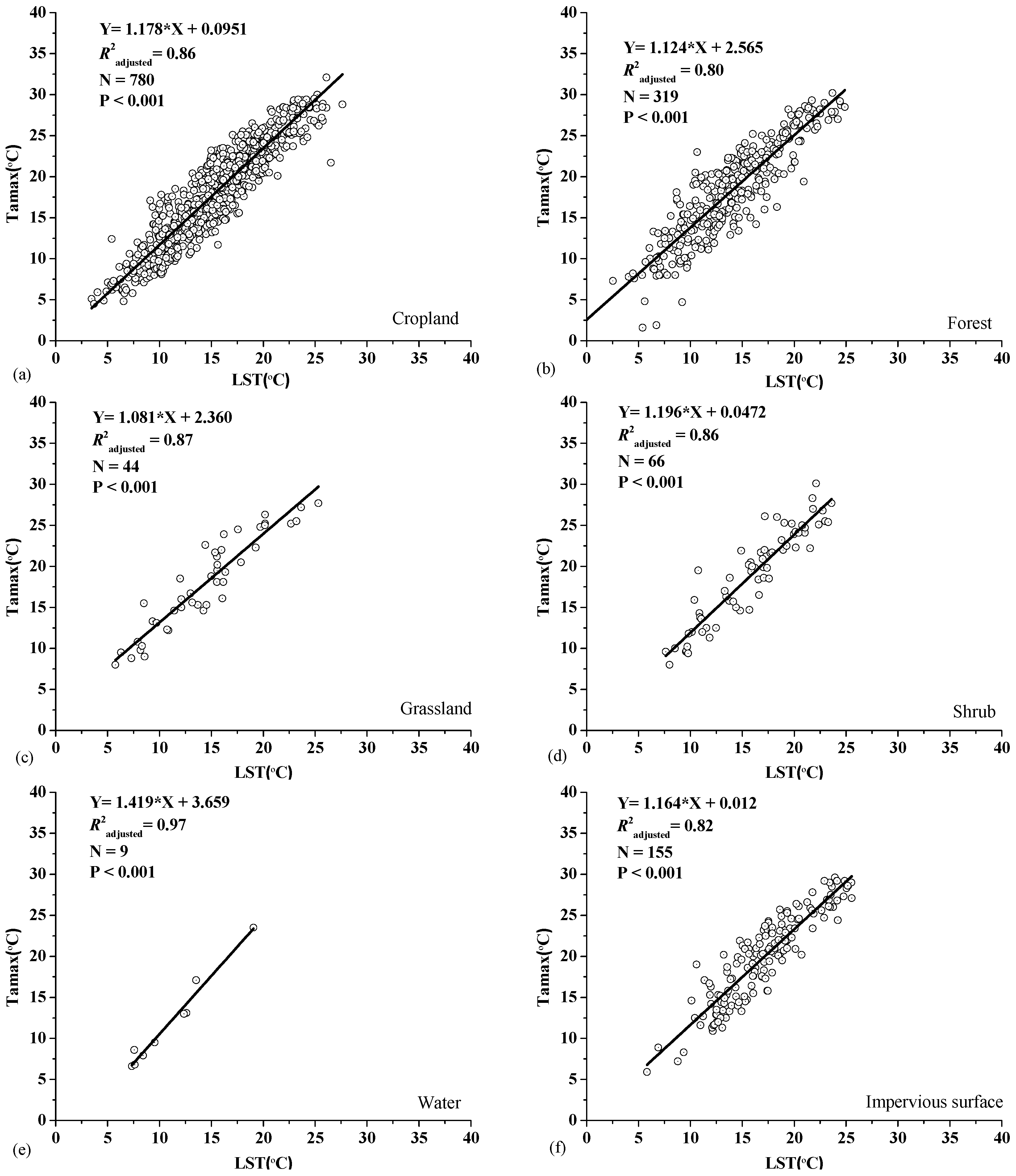
3.1. Estimation of Maximum Air Temperature for Major Land-Cover Types

The scatter plots in Figure 2 and Figure 3 illustrate the relationships between LST and the estimated Tamax across various land-cover types. Similar to previous studies [25,37,39,40], LST and Ta were found to have a relatively strong linear correlation. The general OLS model without considering land cover and seasonal variation reached an adjusted R2 value of 0.87 (Figure 2). Compared to the general model, the models developed for specific land-cover types demonstrated varying levels of performance. More specifically, cropland, grassland, shrub, and water had better performance with higher adjusted R2 values of 0.89, 0.92, 0.89, and 0.96 (Figure 3). Modeling forests and impervious surfaces showed inferior performance with lower adjusted R2 values of 0.85 and 0.84 (Figure 3). The corresponding model validation results presented similar trends of performance using RMSE and MAE (Table 2). Distinguishing between land-cover types introduced an average of 4.5% of variance in adjusted R2. Particularly for water and grassland, LST was found to explain 92% and 96% of the variation in Tamax, indicating noticeable improvement in model performance for certain land-cover types. In contrast, forests were found to weaken the strong relationship between LST and Tamax. Compared to the general model, the forest model reduced the adjusted R2 value by 2.0%, and considerably increased the model error by 15.2% in MAE and 19.6% in RMSE (Table 2), respectively.
Statistical significance tests showed that the effect of land cover on the Tamax-LST relationship was significant at the 0.01 level. The tests were performed by comparing the results predicted respectively using the general model and the land-cover specific models, using Paried-Samples T-TEST function in the SPSS software package (IBM, Armonk‎, NY, USA).

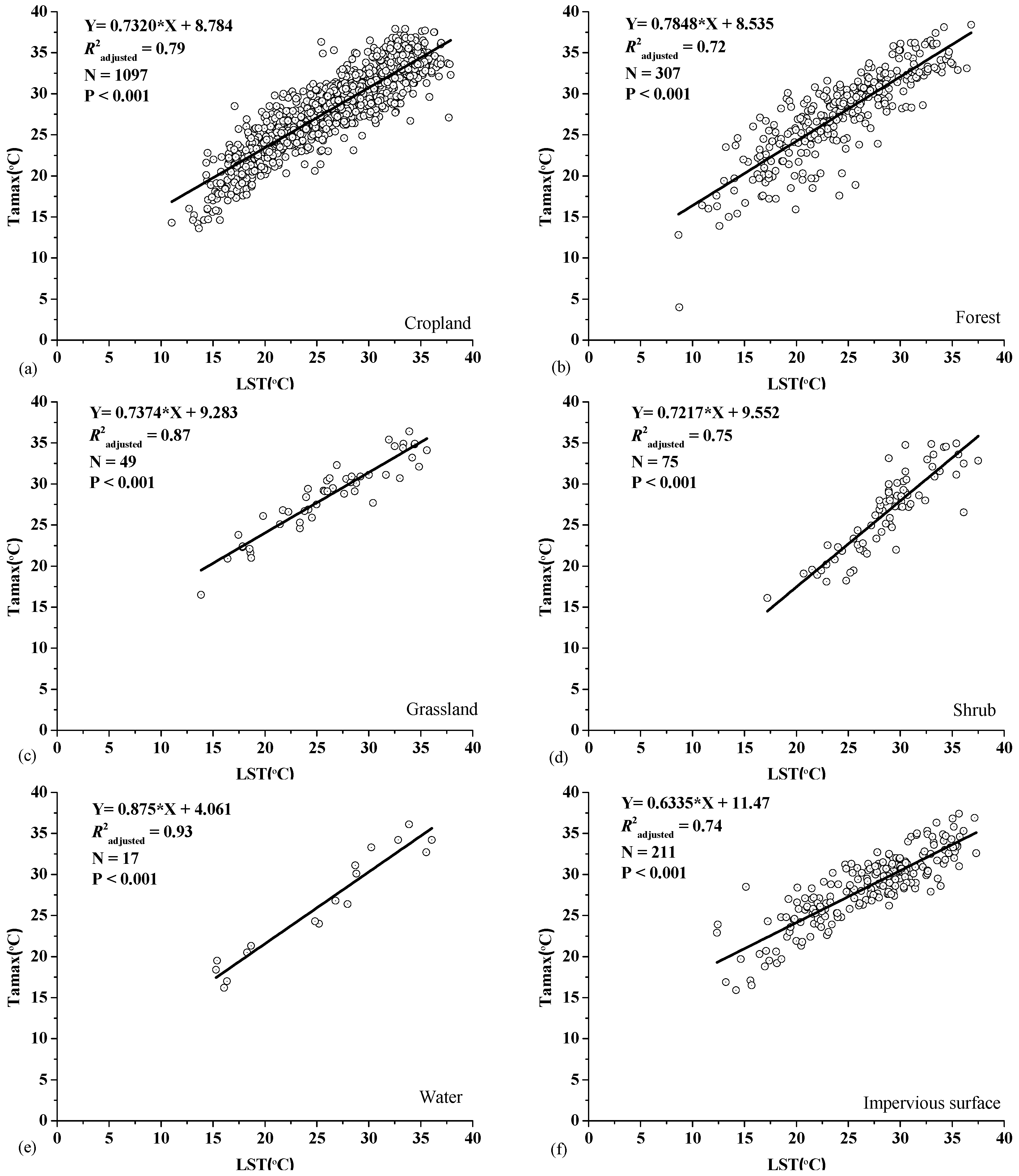
3.2. Estimation of Maximum Air Temperature for Growing and Non-Growing Seasons

The scatter plots in Figure 4 illustrate the relationships between LST and the estimated daily maximum surface air temperature (Tamax) in the plant growing season across the six major land-cover types; while Figure 5 shows a similar type of scatter plots illustrating the Tamax-LST relationship in the non-growing season. Specifically, in the growing season, LST was found to explain 79, 72, 87, 75, 93, and 74 percent R2 with Tamax across the six land-cover types of cropland, forest, grassland, shrub, water, and impervious surface, respectively. Compared to the growing season, most of non-growing season models revealed better performance with the corresponding adjusted R2 values found to be 86, 80, 87, 86, 97, and 82 percent. The difference in model performance mainly occurred over the landscape covered by vegetation, e.g., cropland (7% increase), forest (8% increase), and shrub (9% increase). We also discovered a better model fitting over impervious surfaces (8% increase). However, seasonal variation did not demonstrate itself as an essential factor influencing the Tamax-LST relationship over water and grasslands, where the changes in adjusted R2 were less than 5%.

4. Discussion

4.1. Impact of Land Cover on the Estimation of Maximum Air Temperature

The modeling results for the six land-cover types confirmed the hypothesis that land surface characteristics have an impact on the Tamax-LST relationship. Similar analyses were carried out by Xu (2012) [24], Benali et al. (2012) [25], and Janatian et al. (2016) [30]. The result in our study agrees with the findings of Xu (2012), although it seems contradictory to those of Benali et al. (2012) and Janatian et al. (2016). Benali et al. (2012) concluded that “model performance was independent of the meteorological stations’ land cover”. Janatian et al. (2016) indicated that a unique calibration equation can be adequately applied to a very large area (as large as half of Iran), despite an extreme heterogeneity of the land cover. We note that several auxiliary variables (e.g., elevation, zenith angle, reflectance, NDVI, etc.) were included in the Benali et al. (2012) and Janatian et al. (2016) models, which could have indirectly accounted for the effects by the land-cover variations. Another potential reason for contradiction is the differences in vegetation cover, and surface roughness, which may have influenced the surface–atmosphere energy exchanges. For example, Janatian et al. (2016) indicated that the land surface within the study area (eastern part of Iran) mainly consisted of bare or sparsely vegetated soils, which were different from our study area. In this study, such impact was found to vary across different types of terrestrial features. Particularly, estimating Tamax demonstrated superior performance over grasslands and water bodies (Figure 3). This may be explained by the fact that those landscapes are homogenous in surface cover, resulting in spatially homogenous energy exchange between land surfaces and the overlying atmosphere.
In contrast, modeling Tamax across forested areas showed noticeable inferior performance (Figure 3). This is possibly explained by the extensive heterogeneity in plant structure, live biomass, aerodynamic roughness, and leaf area index, which caused substantial variation of surface albedo in forests. Because our study area is located in the humid subtropical climatic region, highly mixed coniferous and broadleaved forest of rich species types (e.g., China fir (Cunninghamia lanceolata), slash pine (Pinus elliotii), and Chinese red pine (Pinus massoniana)) and structures dominate the region [53,54,55], which further complicated the Tamax-LST relationship. Topography is another crucial factor. Our study area features rugged landscapes (e.g., karst), with steep slopes, deep valleys, and mixed mountains and plains. For example, 60% of the area of Jiangxi Province, centered at the study area, are mountains and hills [56]. The elevation difference in some areas reaches over 2000 m [57]. As mountainous areas are difficult to access, they are mainly covered by natural or planted forests (e.g., fruit trees and fast-growing timber trees). Hence, the combined heterogeneity in topography and forest structure possibly have negatively contributed to Tamax modeling in forested areas.

4.2. Impact of Seasonal Variation on the Estimation of Maximum Air Temperature

Plant surfaces typically show distinct characteristics in growing versus non-growing seasons corresponding to their phenological development. This changed plant surface albedo, and in turn affected the LST-Tamax relationship as revealed by the study (Figure 4 and Figure 5). Their variation in adjusted R2 was found to be 8% and 6% for the growing and non-growing season, respectively. However, such variation was 4% without considering seasonal variation (Figure 3).
Our results further indicated that the errors of estimating Tamax likely increase during the growing season for the landscapes covered by crops, forests, and shrubs (Figure 4 and Figure 5). However, their models all achieved better performance in the non-growing season, with an average increase of 8% in adjusted R2. This was possibly owing to the subtropical climate of the study area, featuring a wide range of vegetation types. For example, local crops include cereal, wheat, cotton, peanut, tea, and tobacco. These areas demonstrated a sharp contrast in vegetation cover between growing and non-growing seasons. Forests in the study area consist of both natural and planted trees, such as those producing non-timber products of pineapple, oak, sugarcane, tea, and orange [58,59]. The 1 km resolution data was coarse, which did not allow us to capture such heterogeneity in vegetation type and structure. From the phenology perspective, those plants exhibited various forms of growth during the growing season. In one of our earlier evaluations, we tried to divide the long growing season into several sub-seasons; however, the performance of the developed models exhibited high variation with no clear patterns. Such variation led to a high level of heterogeneity in surface characteristics in the growing season, as compared to the landscapes with reduced vegetation cover in the non-growing season.
Besides the vegetation-covered landscapes, impervious surfaces also demonstrated noticeable model improvement using data from the non-growing season, with results showing an increase of 8% in adjusted R2 (Figure 4 and Figure 5). This may be explained from two aspects. First, impervious surfaces were primarily located in urban areas, interspersed with vegetation within the city bounds. At the spatial resolution of 1 km, a land patch classified as impervious surface possibly contained plants, where their spectral variation in the non-growing season was much lower than that in the growing season as described in the previous paragraph [60]. Second, the growing season in the study site is part of the year with a significant increase of precipitation. Researchers have argued that topography and land cover can lead to substantial variability of rainfall both spatially and temporally [61,62], which adds variation to land-atmosphere interactions across the urban areas.
Our analysis was based on a linear relationship between Tamax and LST, although several scatter plots of Figure 2, Figure 3, Figure 4 and Figure 5 indicate a ‘convex upward’ distribution. This suggests a potential nonlinear quadratic relationship between those two variables, inferring a potential effect of within-season variation on Tamax estimation. It can be further observed that the regression lines for the non-growing season (Figure 5) are steeper than those for the growing season (Figure 4). That is, Tamax rises more rapidly when LST increases in colder seasons than that in warmer seasons. However, our emphasis was the model comparison among various land-cover types, and the nonlinear quadratic relationship only showed slightly improved model performance. We decided to use linear models in this study.

4.3. Spatial Uncertainties in the Estimation of Maximum Air Temperature

Since land cover and seasonal variation were found to affect the estimation of Tamax, we have applied the previously developed models to produce two temperature maps considering major land-cover types for two dates in the growing season (on 24 May 2010; Figure 6a) and non-growing season (on 31 December 2010; Figure 7a), respectively. Figure 6a reveals a clear temperature gradient in spring, i.e., the closer to water bodies, the lower the maximum air temperature. For example, Fujian Province in the southeast faces East China Sea to the east, and South China Sea to the south, and its estimated Tamax was much lower than that in Hubei Province, located in the Central China region. Besides ocean, inland water (e.g., the Poyang Lake in Jiangxi Province) also showed an evident impact in cooling down the neighborhood regions in the upper middle of our study area. In contrast, the spatial pattern of winter temperature was mainly controlled by the latitudinal variation that has more than five degrees across out study area (Figure 7a).
To better understand the spatial uncertainty of our estimates, the same-day field observations were used as a comparison, where the radius of each circle corresponds to the level of error at individual meteorological stations (Figure 6b and Figure 7b). The MAE in Figure 6b and Figure 7b ranges from 2.46 to 3.00 and from 1.34 to 1.60 respectively. The land-cover map was used as a backdrop. The circles in the two figures demonstrated consistent findings, where the low-performance stations were mostly located in vegetated areas, especially those vegetated areas in the mountains. In addition to the aforementioned reason of high level of heterogeneity in species types and topography, a portion of errors may stem from the data acquisition stage. For example, as pointed out by Lee et al. (2011) [63], meteorological stations that represent the surrounding forests are in fact typically located in forest clearings, which makes the observations less representative with high variation. Another source of error is possibly from land cover classification. Benali et al. (2012) [25] argued that land cover data with different accuracies and from various classification schemes could result in high uncertainties in temperature estimation. To mitigate the impact of error propagation from a complex classification scheme, a relatively simple and straightforward classification system may be a better option [49]. In addition, we suggest that such a system needs to incorporate vegetation phenology in classification, so the results can better assist with our assessment of the Tamax-LST relationship in the plant growing season.

5. Conclusions

Results in this study revealed noticeable impacts of land cover and seasonal variation on the estimation of Tamax using MODIS-derived LST. Owing to the high level of heterogeneity in plant structure and topography, the Tamax-LST relationship was found to be negatively affected in forest landscapes with high uncertainties. Estimating Tamax over grasslands and water bodies achieved superior performance, which could be explained by the spatially homogenous energy exchange between land surfaces and the overlying atmosphere. We also found that all the land-cover specific models developed for the non-growing season outperformed the corresponding models developed for the growing season. Discrepancies in model performance mainly occurred in the vegetated areas (forest, cropland, and shrub), suggesting that plant phenology plays an important role defining the statistical relationship between Tamax and LST. Because different plant species exhibit varying growth patterns over time, understanding specific species types may significantly improve model performance in the growing season. Compared to the other land-cover types, impervious surfaces in urban areas contained high spatial heterogeneity that was difficult to capture by MODIS, which led to high uncertainties in Tamax estimation. In contrast to previous studies, this research provides a more in-depth analysis emphasizing on major land-cover types and seasons in the middle-low reaches of Yangtze River featuring high variation in topography and climatic conditions. Our research suggests the necessity of improving the current Tamax-LST relationship through modeling the seasonal, sub-pixel landscape heterogeneity that typically relies on medium to coarse spatial resolution Earth observation data, although we take advantage of the sensors’ short revisit intervals.

Acknowledgments

This research was partially supported by a research innovation fund from the Geomatics College of Shandong University of Science and Technology, the National Natural Science Foundation of China (#41471331, and #41601408), and the scholarship of Shandong Provincial Education Association for International Exchanges. Gang Chen gratefully acknowledges the financial support from North Carolina Space Grant, and the University of North Carolina at Charlotte.

Author Contributions

Yulin Cai, Gang Chen, and Yali Wang conceived and designed the research plan; Yulin Cai and Gang Chen analyzed data, reviewed literature, prepared the manuscript and figures; Li Yang performed some of the experiments.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Core Writing Team; Pachauri, R.K.; Meyer, L.A. Climate Change 2014. Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2014. [Google Scholar]
  2. Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2013, 3, 52–58. [Google Scholar] [CrossRef]
  3. Sheffield, J.; Wood, E.F.; Roderick, M.L. Little change in global drought over the past 60 years. Nature 2012, 491, 435–438. [Google Scholar] [CrossRef] [PubMed]
  4. Nes, E.H.V.; Scheffer, M.; Brovkin, V.; Lenton, T.M.; Ye, H.; Deyle, E.; Sugihara, G. Causal feedbacks in climate change. Nat. Clim. Chang. 2015, 5, 445–448. [Google Scholar]
  5. Mo, M.C.; Lettenmaier, D.P. Hydrologic Prediction over the Conterminous United States Using the National Multi-Model Ensemble. J. Hydrometeorol. 2014, 15, 1457–1472. [Google Scholar] [CrossRef]
  6. Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm. Remote Sens. 2009, 64, 335–344. [Google Scholar] [CrossRef]
  7. Rajasekar, U.; Weng, Q. Urban heat island monitoring and analysis using a non-parametric model: A case study of Indianapolis. ISPRS J. Photogramm. Remote Sens. 2009, 64, 86–96. [Google Scholar] [CrossRef]
  8. Pichierri, M.; Bonafoni, S.; Biondi, R. Satellite air temperature estimation for monitoring the canopy layer heat island of Milan. Remote Sens. Environ. 2012, 127, 130–138. [Google Scholar] [CrossRef]
  9. Keramitsoglou, I.; Kiranoudis, C.T.; Sismanidis, P.; Zakšek, K. An Online System for Nowcasting Satellite Derived Temperatures for Urban Areas. Remote Sens. 2016, 8, 306. [Google Scholar] [CrossRef]
  10. Goetz, S.J.; Prince, S.D.; Small, J. Advances in satellite remote sensing of environmental variables for epidemiological applications. Adv. Parasitol. 2000, 47, 289–307. [Google Scholar] [PubMed]
  11. Shamir, E.; Georgakakos, K.P. MODIS Land Surface Temperature as an index of surface air temperature for operational snowpack estimation. Remote Sens. Environ. 2014, 152, 83–98. [Google Scholar] [CrossRef]
  12. Stahl, K.; Moore, R.D.; Floyer, J.A.; Asplin, M.G.; McKendry, I.G. Comparison of Approaches for Spatial Interpolation of Daily Air Temperature in a Large Region with Complex Topography and Highly Variable Station Density. Agric. For. Meteorol. 2006, 139, 224–236. [Google Scholar] [CrossRef]
  13. Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
  14. Wan, Z.; Li, Z.-L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar]
  15. Vogt, J.; Viau, A.A.; Paquet, F. Mapping regional air temperature fields using satellite derived surface skin temperatures. Int. J. Climatol. 1997, 17, 1559–1579. [Google Scholar] [CrossRef]
  16. Mostovoy, G.V.; King, R.L.; Reddy, K.R.; Kakani, V.G.; Filippova, M.G. Statistical estimation of daily maximum and minimum air temperatures from MODIS LST data over the state of Mississippi. GISci. Remote Sens. 2006, 43, 78–110. [Google Scholar] [CrossRef]
  17. Bechtel, B.; Wiesner, S.; Zakšek, K. Estimation of Dense Time Series of Urban Air Temperatures from Multitemporal Geostationary Satellite Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4129–4137. [Google Scholar] [CrossRef]
  18. Fan, N.; Xie, G.; Li, W.; Zhang, Y.; Zhang, C.; Li, N. Mapping Air Temperature in the Lancang River Basin Using the Reconstructed MODIS LST Data. J. Resour. Ecol. 2014, 5, 253–262. [Google Scholar]
  19. Zeng, L.; Wardlow, B.D.; Tadesse, T.; Shan, J.; Hayes, M.J.; Li, D.; Xiang, D. Estimation of Daily Air Temperature Based on MODIS Land Surface Temperature Products over the Corn Belt in the US. Remote Sens. 2015, 7, 951–970. [Google Scholar] [CrossRef]
  20. Chen, Y.; Quan, J.; Zhan, W.; Guo, Z. Enhanced Statistical Estimation of Air Temperature Incorporating Nighttime Light Data. Remote Sens. 2016, 8, 656. [Google Scholar] [CrossRef]
  21. Jang, J.D.; Viau, A.A.; Anctil, F. Neural network estimation of air temperatures from AVHRR data. Int. J. Remote Sens. 2004, 25, 4541–4554. [Google Scholar] [CrossRef]
  22. Meyer, H.; Katurji, M.; Appelhans, T.; Müller, M.U.; Nauss, T.; Roudier, P.; Zawar-reza, P. Mapping daily air temperature for Antarctica based on MODIS LST. Remote Sens. 2016, 8, 732. [Google Scholar] [CrossRef]
  23. Zaksek, K.; Schroedter-Homscheidt, M. Parameterization of air temperature in high temporal and spatial resolution from a combination of the SEVIRI and MODIS instruments. ISPRS J. Photogramm. Remote Sens. 2009, 64, 414–421. [Google Scholar] [CrossRef]
  24. Xu, Y.; Qin, Z.; Shen, Y. Study on the estimation of near-surface air temperature from MODIS data by statistical methods. Int. J. Remote Sens. 2012, 33, 7629–7643. [Google Scholar] [CrossRef]
  25. Benali, A.; Carvalho, A.; Nunes, J. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
  26. Chen, F.; Liu, Y.; Liu, Q.; Qin, F. A statistical method based on remote sensing for the estimation of air temperature in China. Int. J. Climatol. 2014, 35, 2131–2143. [Google Scholar] [CrossRef]
  27. Ho, H.C.; Knudby, A.; Sirovyak, P.; Xu, Y.; Hodul, M.; Henderson, S.B. Mapping maximum urban air temperature on hot summer days. Remote Sens. Environ. 2014, 154, 38–45. [Google Scholar] [CrossRef]
  28. Xu, Y.; Knudby, A.; Ho, H.C. Estimating daily maximum air temperature from MODIS in British Columbia, Canada. Int. J. Remote Sens. 2014, 35, 8108–8121. [Google Scholar] [CrossRef]
  29. Noi, P.; Kappas, M.; Degener, J. Estimating Daily Maximum and Minimum Land Air Surface Temperature Using MODIS Land Surface Temperature Data and Ground Truth Data in Northern Vietnam. Remote Sens. 2016, 8, 1002. [Google Scholar] [CrossRef]
  30. Janatian, N.; Sadeghi, M.; Sanaeinejad, S.H.; Bakhshian, E.; Farid, A.; Hasheminia, S.M.; Ghazanfari, S. A statistical framework for estimating air temperature using MODIS land surface temperature data. Int. J. Climatol. 2016. [Google Scholar] [CrossRef]
  31. Goward, S.N.; Waring, R.H.; Dye, D.G.; Yang, J. Ecological remote sensing at OTTER: Satellite macroscale observations. Ecol. Appl. 1994, 4, 322–343. [Google Scholar] [CrossRef]
  32. Prihodko, L.; Goward, S.N.Z. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar] [CrossRef]
  33. Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
  34. Zhu, W.; Lű, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
  35. Sun, Y.J.; Wang, J.F.; Zhang, R.H.; Gillies, R.R.; Xue, Y.; Bo, Y.C. Air temperature retrieval from remote sensing data based on thermodynamics. Theor. Appl. Climatol. 2005, 80, 37–48. [Google Scholar] [CrossRef]
  36. Cresswell, M.P. Estimating surface air temperatures, from Meteosat land surface temperatures, using an empirical solar zenith angle. Int. J. Remote Sens. 1999, 20, 1125–1132. [Google Scholar] [CrossRef]
  37. Shen, S.; Leptoukh, G.G. Estimation of surface air temperature over central and eastern Eurasia from MODIS land surface temperature. Environ. Res. Lett. 2011, 6, 045206. [Google Scholar] [CrossRef]
  38. Mildrexler, D.J.; Zhao, M.; Running, S.W. A global comparison between station air temperatures and MODIS land surface temperatures reveals the cooling role of forests. J. Geophys. Res. Biogeosci. 2011, 116, 1–15. [Google Scholar] [CrossRef]
  39. Zhang, W.; Huang, Y.; Yu, Y.; Sun, W. Empirical models for estimating daily maximum, minimum and mean air temperatures with MODIS land surface temperatures. Int. J. Remote Sens. 2011, 32, 9415–9440. [Google Scholar] [CrossRef]
  40. Urban, M.; Eberle, J.; Hüttich, C.; Schmullius, C.; Herold, M. Comparison of Satellite-Derived Land Surface Temperature and Air Temperature from Meteorological Stations on the Pan-Arctic Scale. Remote Sens. 2013, 5, 2348–2367. [Google Scholar] [CrossRef]
  41. Kloog, I.; Nordio, F.; Coull, B.A.; Schwartz, J. Predicting spatiotemporal mean air temperature using MODIS satellite surface temperature measurements across the Northeastern USA. Remote Sens. Environ. 2014, 150, 132–139. [Google Scholar] [CrossRef]
  42. Pielke, R.A.; Davey, C.A.; Niyogi, D.; Fall, S.; Steinweg-Woods, J.; Hubbard, K.; Lin, X.; Cai, X.; Lim, Y.; Li, H.; et al. Unresolved issues with the assessment of multidecadal global land surface temperature trends. J. Geophys. Res. Almos. 2017, 112, 177–180. [Google Scholar] [CrossRef]
  43. Wei, W.; Chang, Y.; Dai, Z. Streamflow changes of the Changjiang (Yangtze) River in the recent 60 years: Impacts of the East Asian summer monsoon, ENSO, and human activities. Q. Int. 2014, 336, 98–107. [Google Scholar] [CrossRef]
  44. Gu, C.; Hu, L.; Zhang, X.; Wang, X.; Guo, J. Climate change and urbanization in the Changjiang River Delta. Habitat Int. 2011, 35, 544–552. [Google Scholar] [CrossRef]
  45. Guo, H.; Hu, Q.; Jiang, T. Annual and seasonal streamflow responses to climate and land-cover changes in the Poyang Lake basin, China. J. Hydrol. 2008, 355, 106–122. [Google Scholar] [CrossRef]
  46. Shankman, D.; Keim, B.D.; Song, J. Flood frequency in China’s Poyang Lake region: Trends and teleconnections. Int. J. Climatol. 2006, 26, 1255–1266. [Google Scholar] [CrossRef]
  47. Sun, S.; Chen, H.; Ju, W.; Yu, M.; Hua, W.; Yin, Y. On the attribution of the changing hydrological cycle in Poyang Lake Basin, China. J. Hydrol. 2014, 514, 214–225. [Google Scholar] [CrossRef]
  48. Fu, G.; Shen, Z.; Zhang, X.; Shi, P.; Zhang, Y.; Wu, J. Estimating air temperature of an alpine meadow on the Northern Tibetan Plateau using MODIS land surface temperature. Acta Ecol. Sin. 2011, 3, 8–13. [Google Scholar] [CrossRef]
  49. Wan, Z. New refinements and validation of the MODIS Land-Surface Temperature/Emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
  50. Coll, C.; Caselles, V.; Galve, J.M.; Valor, E.; Niclos, R.; Sanchez, J.M.; Rivas, R. Ground measurements for the validation of land surface temperatures derived from AATSR and MODIS data. Remote Sens. Environ. 2005, 97, 288–300. [Google Scholar] [CrossRef]
  51. Gong, P.; Wang, J.; Yu, L.; Zhao, Y.C.; Zhao, Y.Y.; Liang, L.; Niu, Z.G.; Huang, X.M.; Fu, H.H.; Liu, S.; et al. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
  52. Yu, L.; Liang, L.; Wang, J.; Zhao, Y.Y.; Cheng, Q.; Hu, L.Y.; Liu, S.; Yu, L.; Wang, X.Y.; Zhu, P.; et al. Meta-discoveries from a synthesis of satellite-based land cover mapping research. Int. J. Remote Sens. 2014, 35, 4573–4588. [Google Scholar] [CrossRef]
  53. Lu, P.; Xie, C. The current situation and quality improving strategy of forest resources in Jiangxi Province. J. Fujian Forest. Sci. Technol. 2008, 35, 259–262. [Google Scholar]
  54. Wei, W.; Wang, P.; Guo, H. Forest Carbon Sink of Jiangxi Province Based on Forest Resource Inventory Data. Meteorol. Dis. Reduct. Res. 2008, 31, 18–23. [Google Scholar]
  55. Wu, D.; Shao, Q.Q.; Li, J.; Liu, J.Y. Carbon fixation estimation for the main plantation forest species in the red soil hilly region of southern-central Jiangxi Province, China. Acta Ecol. Sin. 2012, 32, 142–150. [Google Scholar]
  56. Huang, Z.Q.; Lu, L.; Dai, N.H.; Jiao, G.Y. Vacancy analysis on the development of nature reserves in Jiangxi Province. Acta Ecol. Sin. 2014, 34, 3099–3106. [Google Scholar]
  57. Guo, Y.; Yan, Y.; Lei, P.; Yuan, R.; Wu, S. The forest stock volume composition characteristics along altitudinal gradient on the northwest slope of Huanggang Mountain in Wuyi mountain of Jiangxi province. South China Forest. Sci. 2015, 5, 10–17. [Google Scholar]
  58. Jiangxi Provincial Bureau of Statistics. Jiangxi Statistical Yearbook. 2015. Available online: http://www.jxstj.gov.cn/resource/nj/2015CD/indexch.htm (accessed on 8 July 2016). [Google Scholar]
  59. Fujian Provincial Bureau of Statistics. Fujian Statistical Yearbook. 2015. Available online: http://www.stats-fj.gov.cn/tongjinianjian/dz2015/index-cn.htm (accessed on 8 July 2016). [Google Scholar]
  60. Godwin, C.; Chen, G.; Singh, K.K. The impact of urban residential development patterns on forest carbon density: An integration of LiDAR, aerial photography and field mensuration. Landsc. Urban Plan. 2015, 136, 97–109. [Google Scholar] [CrossRef]
  61. Johnson, K.R.; Ingram, B.L. Spatial and temporal variability in the stable isotope systematics of modern precipitation in China: implications for paleoclimate reconstructions. Earth Planet. Sci. Lett. 2004, 220, 365–377. [Google Scholar] [CrossRef]
  62. Liu, Q.; Yang, Z.; Cui, B. Spatial and temporal variability of annual precipitation during 1961–2006 in Yellow River Basin, China. J. Hydrol. 2008, 361, 330–338. [Google Scholar] [CrossRef]
  63. Lee, X.; Goulden, M.L.; Hollinger, D.Y.; Barr, A.; Black, T.A.; Bohrer, G.; Bracho, R.; Drake, B.; Goldstein, A.; Gu, L.; et al. Observed increase in local cooling effect of deforestation at higher latitudes. Nature 2011, 497, 384–387. [Google Scholar] [CrossRef] [PubMed]
Remotesensing 09 00233 g001 550
Figure 1. Maps of the study area (a) Location map; (b) Land cover and the spatial distribution of meteorological stations map; (c) Topographic map.
Figure 1. Maps of the study area (a) Location map; (b) Land cover and the spatial distribution of meteorological stations map; (c) Topographic map.
Remotesensing 09 00233 g001
Remotesensing 09 00233 g002 550
Figure 2. Scatter plot of the daily maximum air temperature (Tamax) and surface temperature (LST) relationship without distinguishing between land covers.
Figure 2. Scatter plot of the daily maximum air temperature (Tamax) and surface temperature (LST) relationship without distinguishing between land covers.
Remotesensing 09 00233 g002
Remotesensing 09 00233 g003 550
Figure 3. Scatter plots of the daily maximum air temperature (Tamax)-surface temperature (LST) relationship over six major land-cover types: (a) Cropland; (b) Forest; (c) Grassland; (d) Shrub; (e) Water; (f) Impervious surface.
Figure 3. Scatter plots of the daily maximum air temperature (Tamax)-surface temperature (LST) relationship over six major land-cover types: (a) Cropland; (b) Forest; (c) Grassland; (d) Shrub; (e) Water; (f) Impervious surface.
Remotesensing 09 00233 g003
Remotesensing 09 00233 g004 550
Figure 4. Scatter plots of the daily maximum air temperature (Tamax)-surface temperature (LST) relationship over six land-cover types in the growing season: (a) Cropland; (b) Forest; (c) Grassland; (d) Shrub; (e) Water; (f) Impervious surface.
Figure 4. Scatter plots of the daily maximum air temperature (Tamax)-surface temperature (LST) relationship over six land-cover types in the growing season: (a) Cropland; (b) Forest; (c) Grassland; (d) Shrub; (e) Water; (f) Impervious surface.
Remotesensing 09 00233 g004
Remotesensing 09 00233 g005 550
Figure 5. Scatter plots of the daily maximum air temperature (Tamax)-surface temperature (LST) relationship over six land-cover types in the non-growing season: (a) Cropland; (b) Forest; (c) Grassland; (d) Shrub; (e) Water; (f) Impervious surface.
Figure 5. Scatter plots of the daily maximum air temperature (Tamax)-surface temperature (LST) relationship over six land-cover types in the non-growing season: (a) Cropland; (b) Forest; (c) Grassland; (d) Shrub; (e) Water; (f) Impervious surface.
Remotesensing 09 00233 g005
Remotesensing 09 00233 g006 550
Figure 6. Spatial patterns of the estimated Tamax (a) on 24 May 2010, and the corresponding uncertainties at the stations (b). The level of uncertainty is represented by the size of circle.
Figure 6. Spatial patterns of the estimated Tamax (a) on 24 May 2010, and the corresponding uncertainties at the stations (b). The level of uncertainty is represented by the size of circle.
Remotesensing 09 00233 g006
Remotesensing 09 00233 g007 550
Figure 7. Spatial patterns of the estimated Tamax (a) on 31 December 2010, and the corresponding uncertainties at the stations (b). The level of uncertainty is represented by the size of circle.
Figure 7. Spatial patterns of the estimated Tamax (a) on 31 December 2010, and the corresponding uncertainties at the stations (b). The level of uncertainty is represented by the size of circle.
Remotesensing 09 00233 g007
Table
Table 1. Areal coverage of individual major land cover types in the study area.
Table 1. Areal coverage of individual major land cover types in the study area.
Land-Cover TypeCroplandForestGrasslandShrubWaterImpervious Surface
Percentage (%)29.2760.811.215.782.290.63
Area (km2)92,158191,459381718,19172151985
Table
Table 2. Model performance for the combined and individual land-cover types.
Table 2. Model performance for the combined and individual land-cover types.
Land-Cover TypeR2adjustedMAE (°C)RMSE (°C)Change in MAE (%)Change in RMSE (%)
All combined0.872.042.55\\
Cropland0.891.972.423.45.1
Forest0.852.353.05−15.2−19.6
Grassland0.921.892.407.45.9
Shrub0.892.012.451.53.9
Water0.961.932.225.412.9
Impervious surface0.841.982.482.92.8

Share and Cite

MDPI and ACS Style

Cai, Y.; Chen, G.; Wang, Y.; Yang, L. Impacts of Land Cover and Seasonal Variation on Maximum Air Temperature Estimation Using MODIS Imagery. Remote Sens. 2017, 9, 233. https://doi.org/10.3390/rs9030233

AMA Style

Cai Y, Chen G, Wang Y, Yang L. Impacts of Land Cover and Seasonal Variation on Maximum Air Temperature Estimation Using MODIS Imagery. Remote Sensing. 2017; 9(3):233. https://doi.org/10.3390/rs9030233

Chicago/Turabian Style

Cai, Yulin, Gang Chen, Yali Wang, and Li Yang. 2017. "Impacts of Land Cover and Seasonal Variation on Maximum Air Temperature Estimation Using MODIS Imagery" Remote Sensing 9, no. 3: 233. https://doi.org/10.3390/rs9030233

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop