1. Introduction
Detailed knowledge about leaf and plant surface distributions in forests and urban environments is of importance for the understanding of a wide range of ecosystem functions. It defines the distribution of biomass [
1] and characterizes ecological habitats [
2]. By controlling, e.g., the magnitude of evapotranspiration, it leads to microclimatic modulations [
3]. In order to describe processes that are influenced by canopy densities, the Leaf Area Index (LAI), defined as one half of the total green leaf area per unit ground area [
4], is an important key parameter. The true LAI per ground unit includes the full three-dimensional distribution of leaves.
If it were possible to map LAI by remote sensing techniques on a regional scale, the mapping product will be an ideal input for physically-based environmental simulations to study, e.g., temperature, wind and solar irradiation regimes; carbon fluxes; and vegetation dynamics over landscapes [
5,
6]. One important implication of leaf and plant surface distributions is the attenuation of sunlight (e.g., [
7,
8,
9,
10,
11]). If LAI distributions are available in sufficient detail for a 3D radiative transfer modelling (RTM) scene, ray tracing based techniques will be usable in order to simulate direct and diffuse radiation for individual positions in the canopy. This could be proven by, e.g., Musselman et al. [
7], using tLiDAR as input for the simulation of solar direct beam transmittance. In a complex RTM even multiple scattering of light within the true LAI distributions can be studied [
12]. The leaf surfaces involved into light attenuation can be much smaller than the total true LAI per ground area and thus can be very different for parallel rays (direct radiation) and rays coming from the whole upper hemisphere of a position (diffuse radiation) [
13].
However, using traditional field methods, true LAI can only be measured by destructive harvesting [
14]. Thus, LAI is most often derived in an indirect way, by correlating canopy transmissivity measures such as angular canopy closure (ACC) or vertical canopy cover (VCC) with LAI. ACC describes the attenuation of diffuse radiation at a given sub-canopy position and can be estimated in the field by the use of, e.g., digital hemispherical photographs (DHP) [
15,
16,
17,
18]. The main advantage of DHPs is a relatively simple and fast field acquisition capability. ACC refers to the proportion of canopy gaps in an angular field of view. Thereby the image pixels representing open sky and those representing canopy are related. In contrast, vertical canopy cover (VCC) refers to the vertical projection of tree crowns onto a horizontal plane and can be estimated in the field by, e.g., vertical sighting tubes [
19,
20]. Although ACC and VCC show correlations with true LAI distributions, they cannot resolve the vertical layering and clumping within tree canopies, leading to a bias.
Besides their role as LAI proxy data, ACC and VCC are also direct measures of canopy transmissivity (controlling the attenuation of sunlight and precipitation). However, they show the disadvantage that the derived transmissivity estimates are only valid for the used instrument orientation and position. The analysis of the directionality of solar canopy transmittance is limited, using the described estimates [
7], which is not the case when 3D true LAI estimates are used in an RTM.
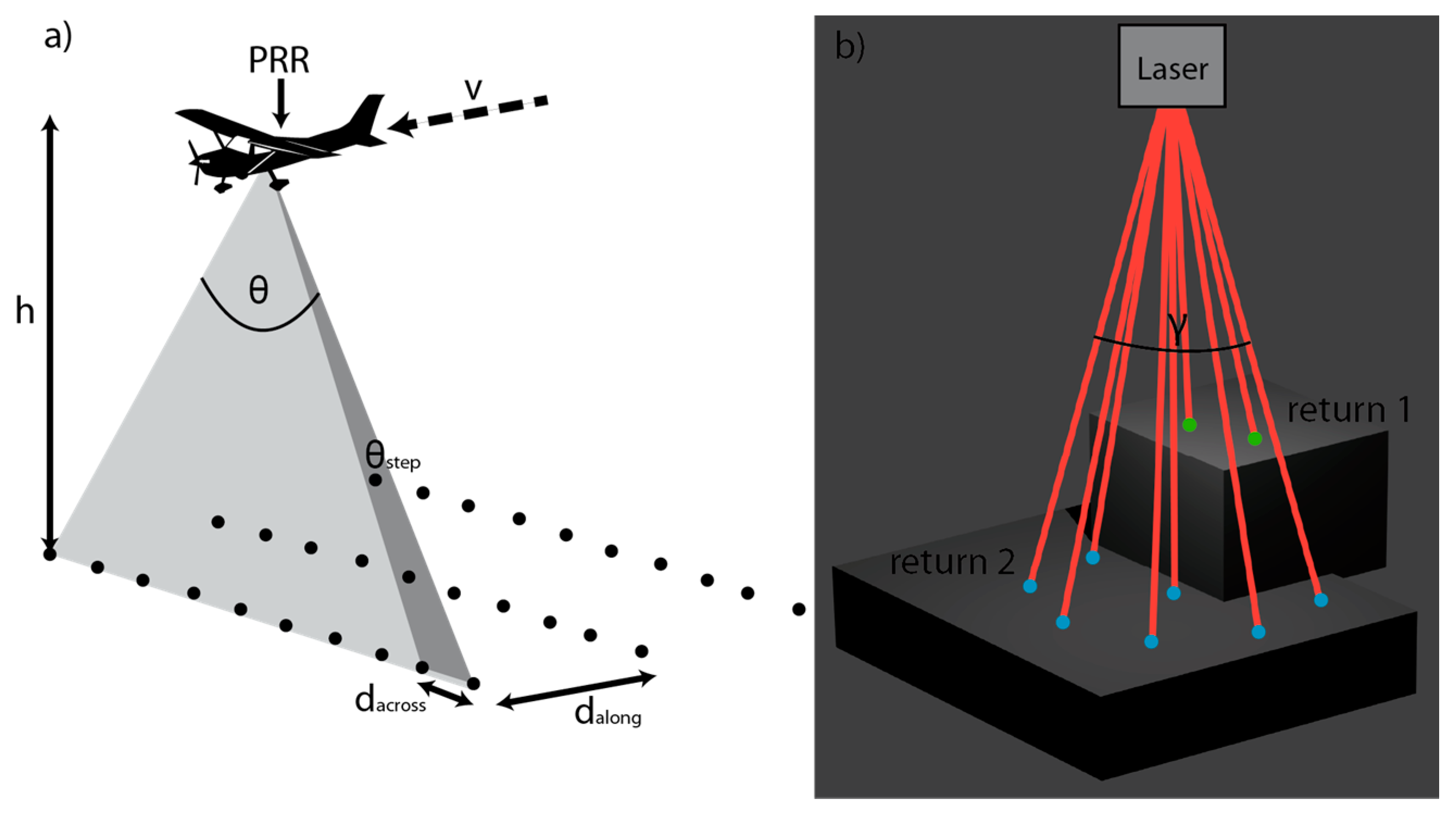
In recent studies, the advantages of Light Detection and Ranging (LiDAR) from both terrestrial and airborne platforms (tLiDAR and aLiDAR, respectively) could be demonstrated in order to estimate LAI and canopy transmissivity. Hancock et al. [
21] stressed, that state of the art tLiDAR instruments are able to capture the full structure of a forest canopy with a high level of detail. The effects of occlusions due to the object sensor relationship can be minimized by multiple scan positions. Hancock et al. [
22] and Durrieu et al. [
23] presented methods for correcting the attenuation of laser beams within canopies. Thereby the amount of energy that was intercepted before the position of interest is considered for the correction of the signals. The disadvantages of the tLiDAR technique are relatively complex field protocols (in comparison with traditional in-situ techniques), which reduces the flexibility in field data acquisitions. This becomes a crucial point when foliage dynamics of high temporal resolution have to be analysed.
Technical advances have also been made in the aLiDAR domain working on regional scale. Traditional discrete return aLiDAR based approaches, for LAI estimation, are mainly based on the inversion of laser penetration metrics (LPM) as proxy data (e.g., [
24,
25,
26,
27,
28]). LPMs are relating the number of laser shots sent into a spatial unit (e.g., a pixel) to the number of (intercepted) canopy hits within the same spatial unit [
13]. Although such LAI estimations show a certain bias due to the object sensor relationship, an improved description of true LAI became possible with the use of full waveform aLiDAR, where the whole energy distribution of a returned laser pulse is analysed [
29,
30]. This could be proven, even for tropical rainforest, in comparison to destructive samplings [
29].
As the capabilities of LiDAR have been proven, especially the high level of detail of tLiDAR point clouds allows the development of complex RTM scenes [
21].
This was shown by a number of studies, where tLiDAR data were used in order to simulate, e.g., ACC for given query positions [
7,
21], light attenuation for direct radiation [
7,
10] or single laser beam cross sections (mimicking full waveform LiDAR signals [
22]). For the simulation of various sensors, very accurate and complex RTMs can be used [
31,
32]. Showing the described capabilities, RTMs can improve the integration between traditional monitoring and modelling techniques [
7]. For the facilitated comparison with DHPs, such approaches are used in order to simulate synthetic hemispherical images (SHI) on the basis of LiDAR point cloud data [
9,
21,
33]. Thereby, the approaches range from complex ray tracing strategies to simple coordinate transformations into a spherical reference system. Hancock et al. [
22] use tLiDAR data in order to simulate the energy distribution which is returned within the laser beam cross-section of an aLiDAR instrument. RTMs offer the advantage of systematic analysis of object sensor relationships for various virtual sensor characteristics and settings, which improves the understanding of a sensor in a given forest domain.
While the advantages of RTM based approaches are obvious, there are some limitations, when LiDAR data are directly integrated into a modelling scene. Most critical are these limitations for tLiDAR data, where a very high geometrical detail is aimed: On the one hand, there is no reliable measure available on how each individual LiDAR point is contributing to the total leaf and plant surface area and to the attenuation of light. To overcome this, each point has to be converted into a spherical solid object, whereby the sphere radius is adapted to the LiDAR beam radius, the distance to the scanner and the return intensity of the point (e.g., [
9,
21]). Musselman et al. [
7] converted tLiDAR data into a voxel structure. Alexander et al. [
8] converted a hemispherical field of view into discrete pyramidal structures, in order to obtain an occluding surface area from the point cloud data. These approaches are strongly affected by the resolution of the mentioned voxels and pyramids. On the other hand, a direct use of LiDAR data has to deal with a certain amount of noise. Branches and leaves might be only partly hit by the laser beam cross section. In this case, a part of material located at the edge of the laser beam cross section leads to a point stored at the centre line of the laser beam, which induces an overestimation of object silhouettes and thus canopy closure [
34].
Raw point cloud data provide no ready to use object information. Thus, no discrimination of LAI and the total Plant Area Index (PAI) is possible. This inhibits the discrimination of, e.g., solid and porous canopy elements [
21] and the consideration of varying object reflectance. Single tree delineation could also improve the estimation of object surface sizes with respect to the branching architecture of a tree.
Most of the described limitations can be overcome with non-trivial reconstruction approaches, which already showed first success [
21]: the L-Architect approach by Cote et al. [
35,
36,
37,
38] is a hybrid method for the detailed architectural vector modelling of single trees. The resulting polygonal plot reconstructions are promising due to their robustness towards object occlusions and noise in the input data. The approach extracts and reconstructs the basic branching architecture from tLiDAR data as a pipe model, defining a reliable basis for further procedural modelling. Exploiting tree crown inherent topological, point density and lighting information, a set of plausible production rules for twig- and foliage modelling, comparable to a Lindenmayer system [
39], is derived. The result is a virtual polygonal tree model following the architectural characteristics of the scanned real tree. In contrast to the raw point cloud data, foliage and wood distributions are decoupled from the pure tLiDAR point measurement densities. Both materials are represented as polygonal meshes, optimized for ray tracing based routines and able to overcome the above-mentioned limitations of surface size definition. Wood elements are treated as cylindrical solids and a robust description of branch radii is given by the pipe model approach [
40,
41]. Leaves and needles are stored as polygonal objects of defined size. The models allow direct queries on modelled biomass and leaf area in the virtual domain and therefore could provide a plausible approximation of true LAI distributions. However, as stated by Hancock et al. [
21], the basic method is not yet practical for characterizing larger areas especially in dense stands with overlapping crowns.
1.1. Main Goals and Applicability
We propose a strategy for target-oriented and detailed forest plot reconstruction, able to fully describe both 3D leaf and plant surface areas in the form of polygonal meshes. Leaf and branch surfaces should be treated separately.
Most regional methods such as aLiDAR-approaches need to be calibrated by plausible plot data in order to be able to estimate LAI and canopy transmissivity. Supporting such calibration and validation scenarios for selected plots within a regional project is one major application of the presented approach.
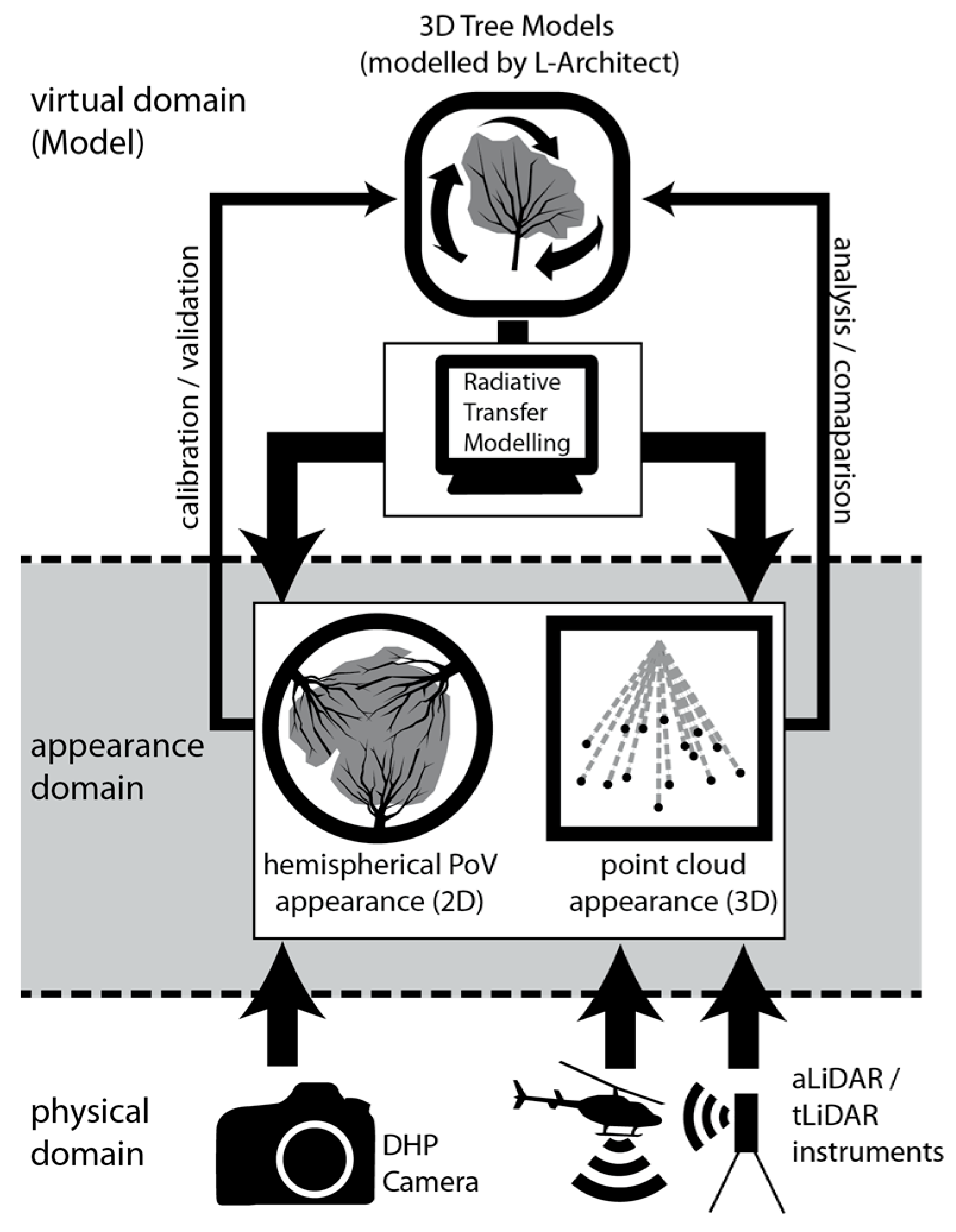
Thereby, the integration of various object appearances captured by different sensors is aimed. As shown in
Figure 1 we distinguish between three conceptional domains: (i) the physical domain, which can be measured by various instruments and sensors; (ii) the virtual domain, in which instruments and sensors can be simulated in combination with detailed 3D models coming from the suggested 3D plot reconstruction; and (iii) the appearance domain containing both the real sensor and simulated data for comparison and evaluation. An important goal is to exploit RTM (virtual domain) for the integration of data from different sensors (appearance domain), avoiding the direct comparison of different sensor metrics.
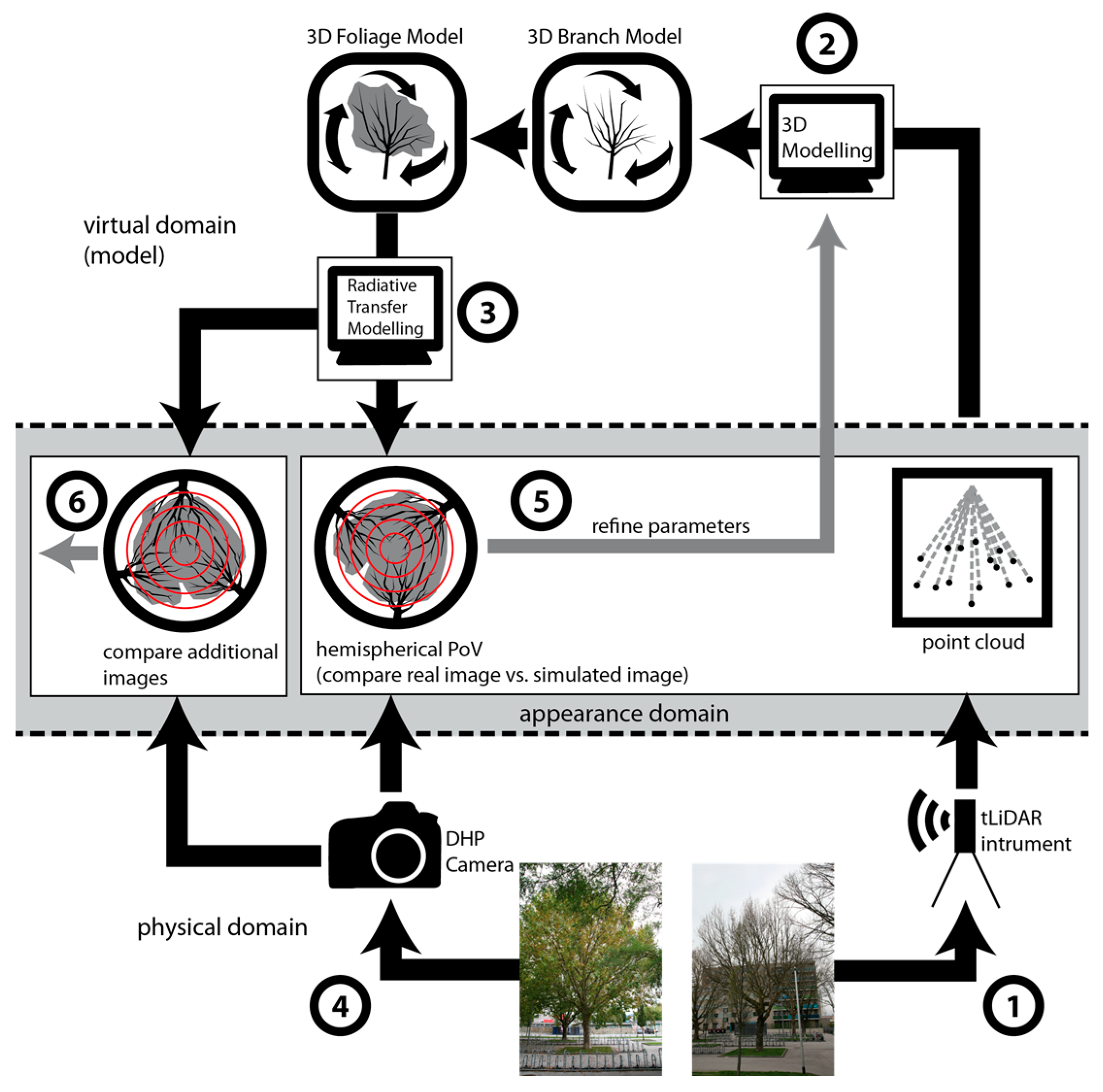
The detailed reconstruction of architectural canopy models as input for the virtual domain is the main focus of the presented paper. The strategy should be optimized in order to derive 3D mesh descriptions of tree crowns from tLiDAR and DHP data in order to be applicable in the virtual domain of a RTM scene.
Fulfilling the described needs, acquisition efforts should be kept as small as possible: if the branching geometries (based on tLiDAR data) are reconstructed and available in the virtual domain, the generation of various foliage densities should be controlled by DHPs only, allowing flexible photo acquisitions and rapid updates of the 3D canopy models without a need for additional tLiDAR campaigns. We aim at a user-friendly and highly automatic derivation of complex canopy and tree parameters for a whole set of trees and not for single trees only.
In order to reach the above-mentioned goals, we rely on three hypotheses which have to be validated:
Hypothesis 1. The reconstructed leaf-off 3D branching structures show no bias according to the object sensor relationship.
Hypothesis 2. As procedural foliage modelling is constrained by the 3D branching axes of the 3D model, calibration and validation by multiple DHPs leads not only to correct foliage distributions in the hemispherical views, but also in 3D (including effects of layering and clumping).
Hypothesis 3. Simulating aLiDAR data based on the modelled polygonal meshes allows systematic analysis of the object–sensor relationships.
1.2. Overview
In order to validate the given hypotheses and to show the capabilities of the suggested strategy, we build a controlled exemplary test set up, described in
Section 2. In
Section 3, we present the methods section. In
Section 3.1, the branch reconstruction and foliage modelling method, which is an adaptation of the L-Architect approach [
35] is described. In
Section 3.2, calibration and validation by DHPs is described in detail. In
Section 3.3, the data analysis techniques are described. Respective results of the proposed strategy are presented in
Section 4 and discussed in
Section 5.
Section 6 draws some conclusions.
5. Discussion
5.1. Plausibility of Derived 3D Models (Validation of Hypotheses 1–2)
In
Section 4.1 and
Section 4.2, it could be shown that the analysed 3D tree models (derived by the presented approach) led to plausible GFDs for multiple SHI-DHP comparisons (6%–7% GFD). This was especially the case for the leaf-off case, validating hypothesis 1 (
Section 1.1), which states, that the branching models show almost no bias.
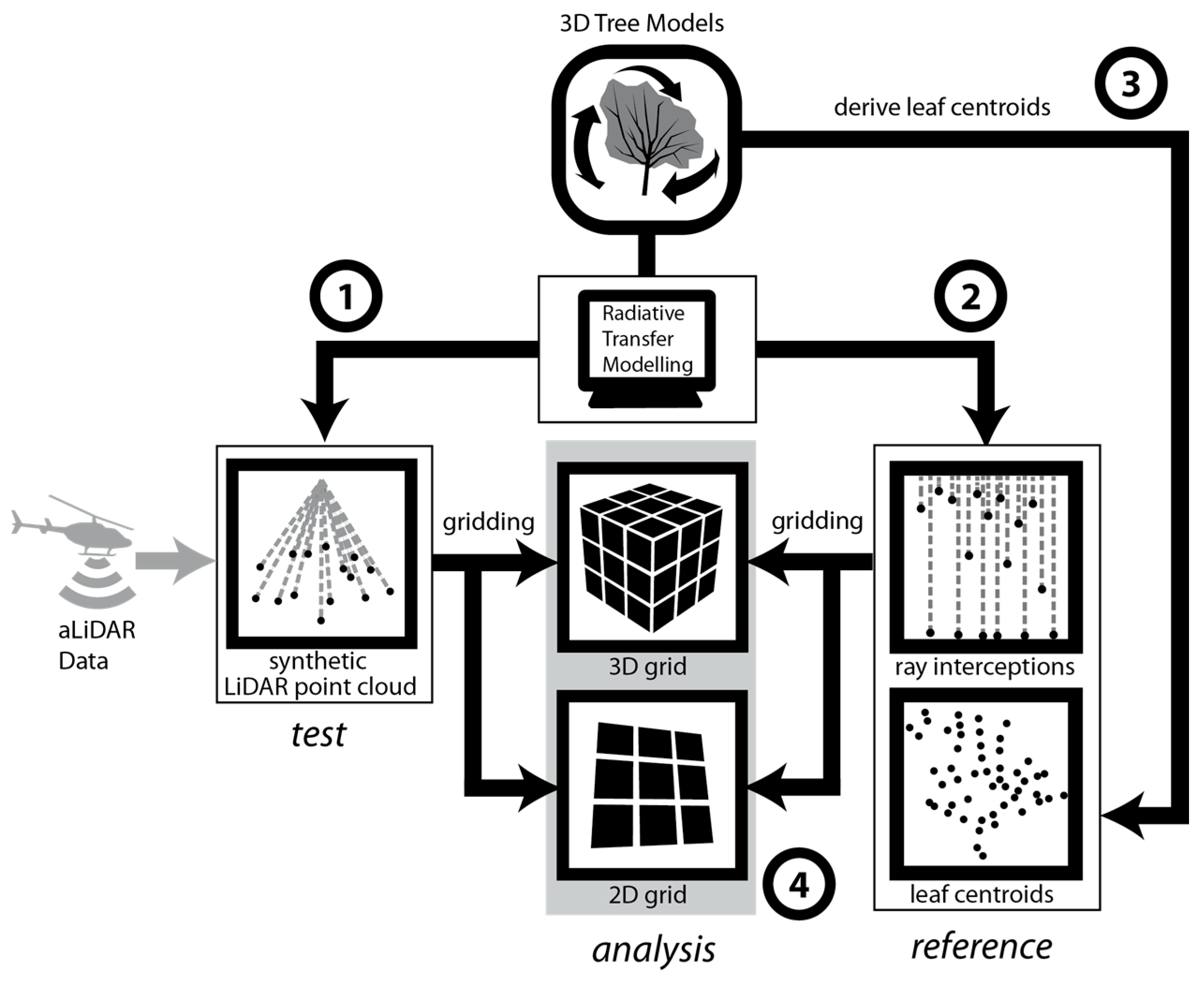
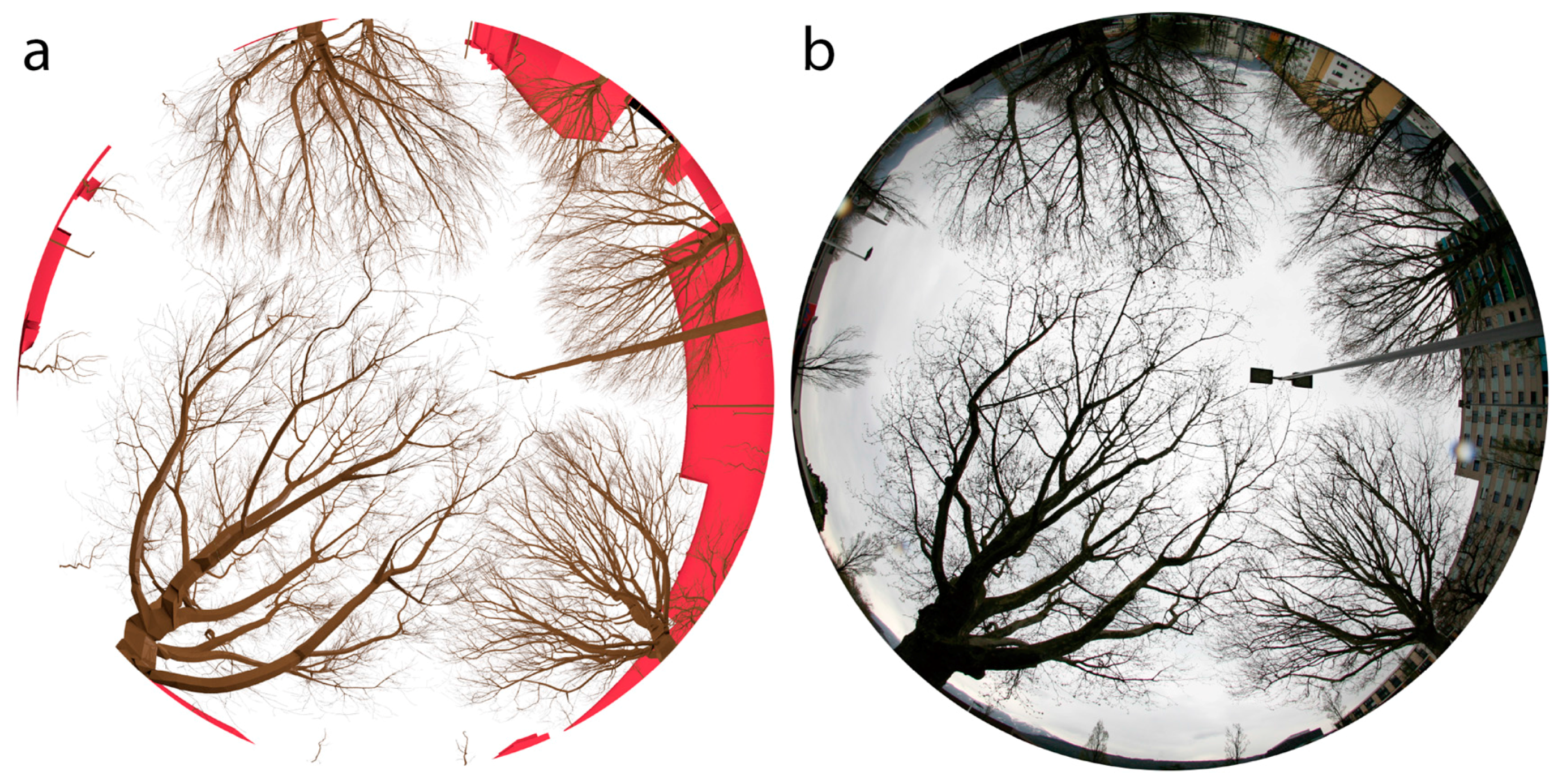
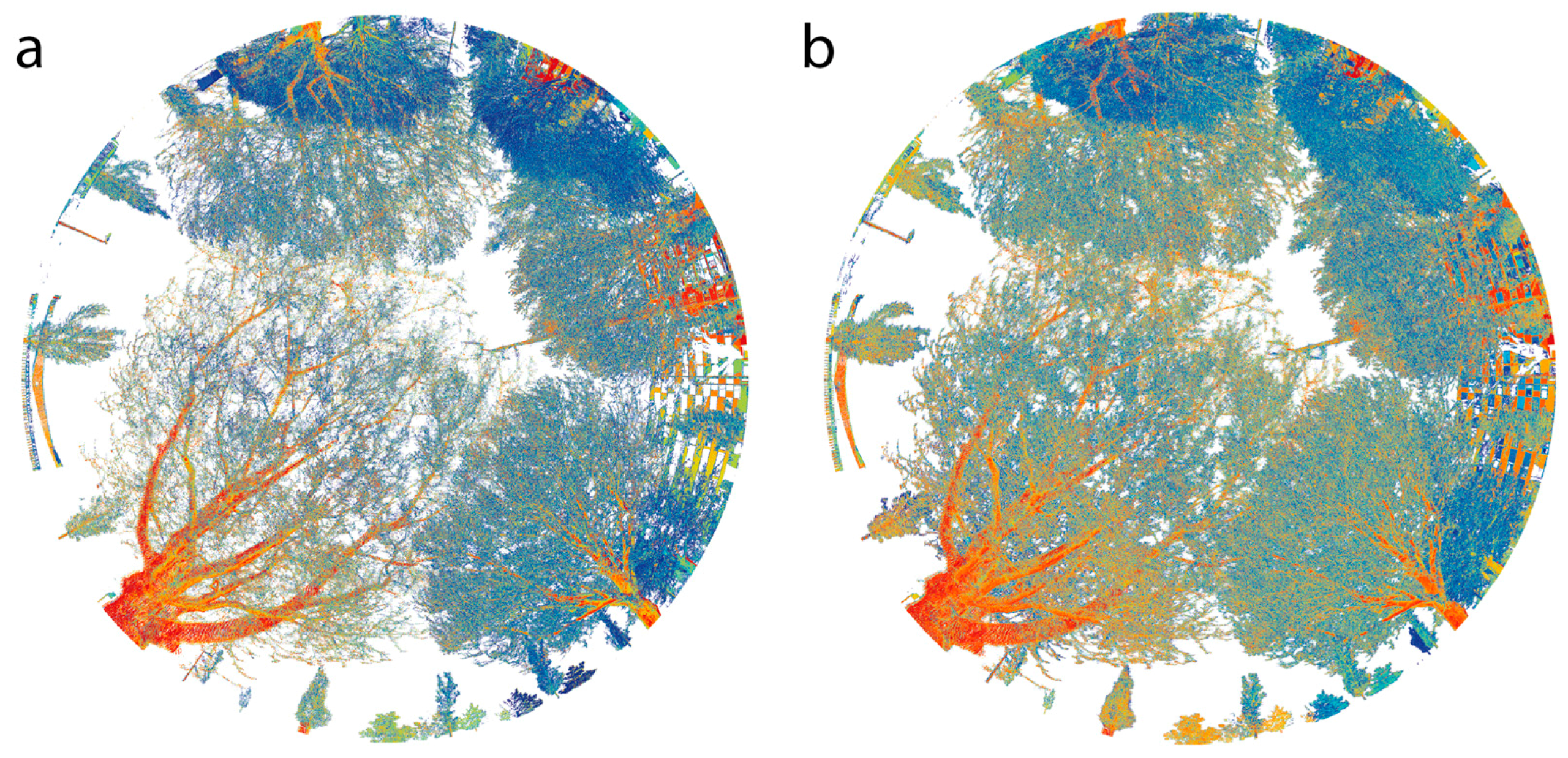
Section 4.1 shows that the calibration process led to a foliage distribution, which agrees with the DHPs of multiple fields of views. This supports hypothesis 2, stating that DHPs can be used in order to calibrate and validate the characteristics of the modelled 3D models. Looking at the quality of SHIs derived from the 3D models, a facilitated generation is possible, while leaf and branch surface sizes are well defined and stored in a mesh structure. The advantages of such data representation become clear, when these VHIs are compared to SHIs directly derived from tLiDAR data (see
Figure 6 and
Figure 8).
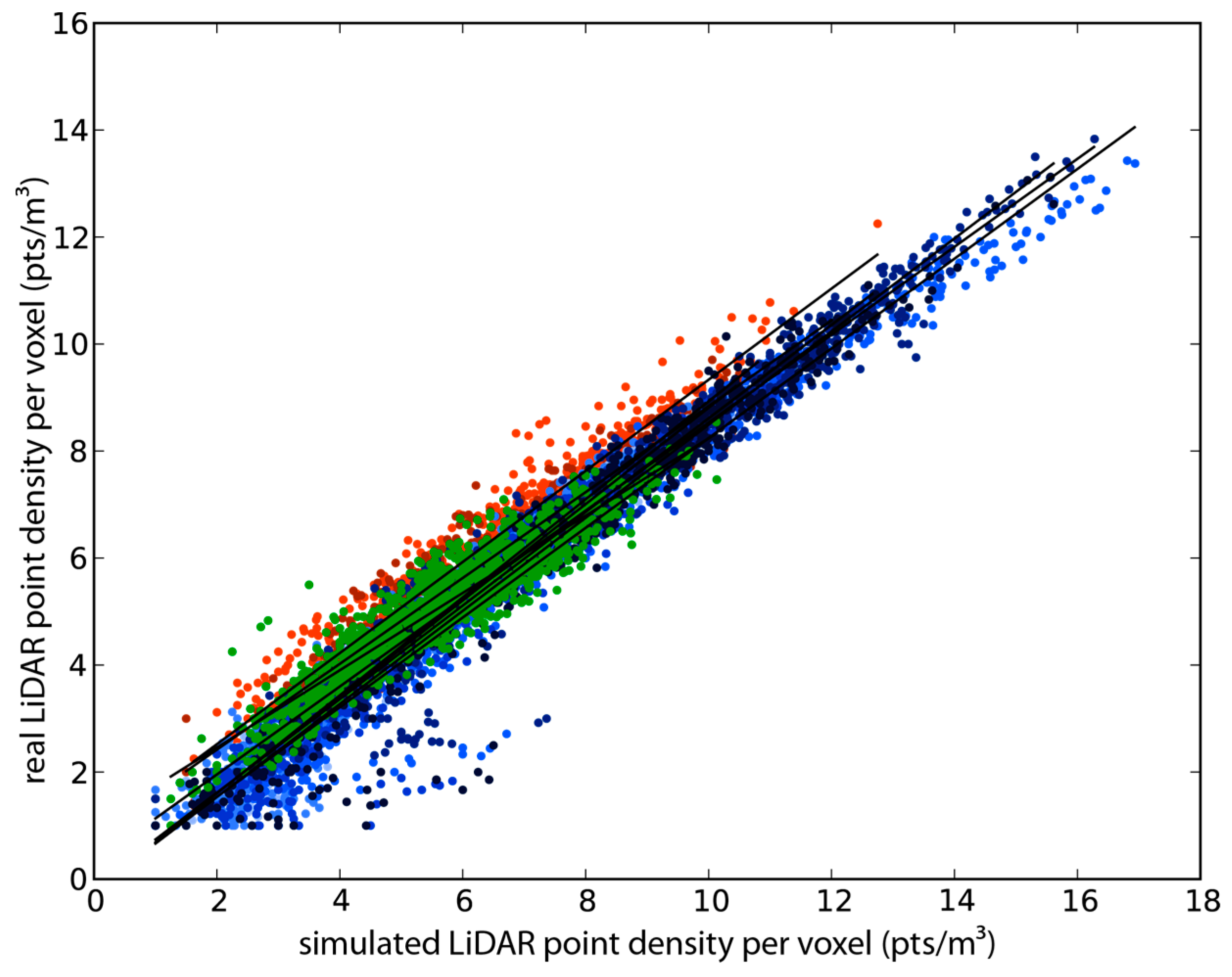
The comparisons of synthetic and real LiDAR data show that plausible aLiDAR point densities were simulated using the presented workflow (R2 of 0.81 for the correlation between synthetic and real LiDAR data). This can approve the plausibility of the described setup. Thus, the described set of unknown error sources must show only a negligible influence, which validates the given hypotheses 1 and 2. As the average correlation coefficient was 0.81, Hypothesis 3 could also be validated, stating that the derived 3D model setup is suitable for the systematic simulation of aLiDAR sensors. As the simulated aLiDAR point cloud shows strong similarities to the real data, we can assume a correct representation of the interactions of real foliage densities and the aLiDAR acquisition physics for our model.
The multi-view DHP validation strategy (
Figure 3, Step 6) for the modelled data narrows down the pool of error sources approximating the true proportion of errors. A combination of multiple views and sensors minimizes the proportion of uncaptured tree characteristics. Achieving good results for all validation datasets, allowed us to validate the plausibility of the derived virtual domain and thus of the given hypotheses.
It has to be stated, that the suggested strategy is not able to represent a real ground truth. A real ground truth can only be provided by destructive harvesting. Relying on object signatures only, the real canopy status and capturing geometries for both field and flight campaigns remain unknown. However, the strategy represents an additional technique for reference data collection, trying to combine the advantages of tLiDAR and DHP data with those of 3D polygonal mesh representations with attached object information. Thus, it can be used for the calibration and validation of regional scale data. Moreover, the validated 3D models can be used for systematic analysis in a standalone virtual domain (virtual experiment). As a “virtual ground truth” they will permit the comparison of simulated data with the input data of simulation (3D foliage arrangement). This might allow the systematic assessment of the potential of specific physically-based sensors (e.g., discrete return aLiDAR) in a complex RTM [
31,
32] for the estimation of foliage densities. Additionally, the influences of specific acquisition setups onto the predictive power of sensor metrics can be assessed, serving as a helpful tool for the planning of a flight campaign.
5.2. Prediction of Foliage Densities by Simulated aLiDAR Data
In order to show the potential of the 3D models for usage in a “virtual experiment”, we evaluated the capabilities of simulated aLiDAR data for the prediction of virtual foliage densities (virtual truth). It was demonstrated that systematic relationships between foliage densities and simulated data can be analysed in detail. The given results are exemplary for the given discrete return simulation approach. They show that it is possible to predict both rLAI and AC by LIR and AC_L derived from simulated aLiDAR.
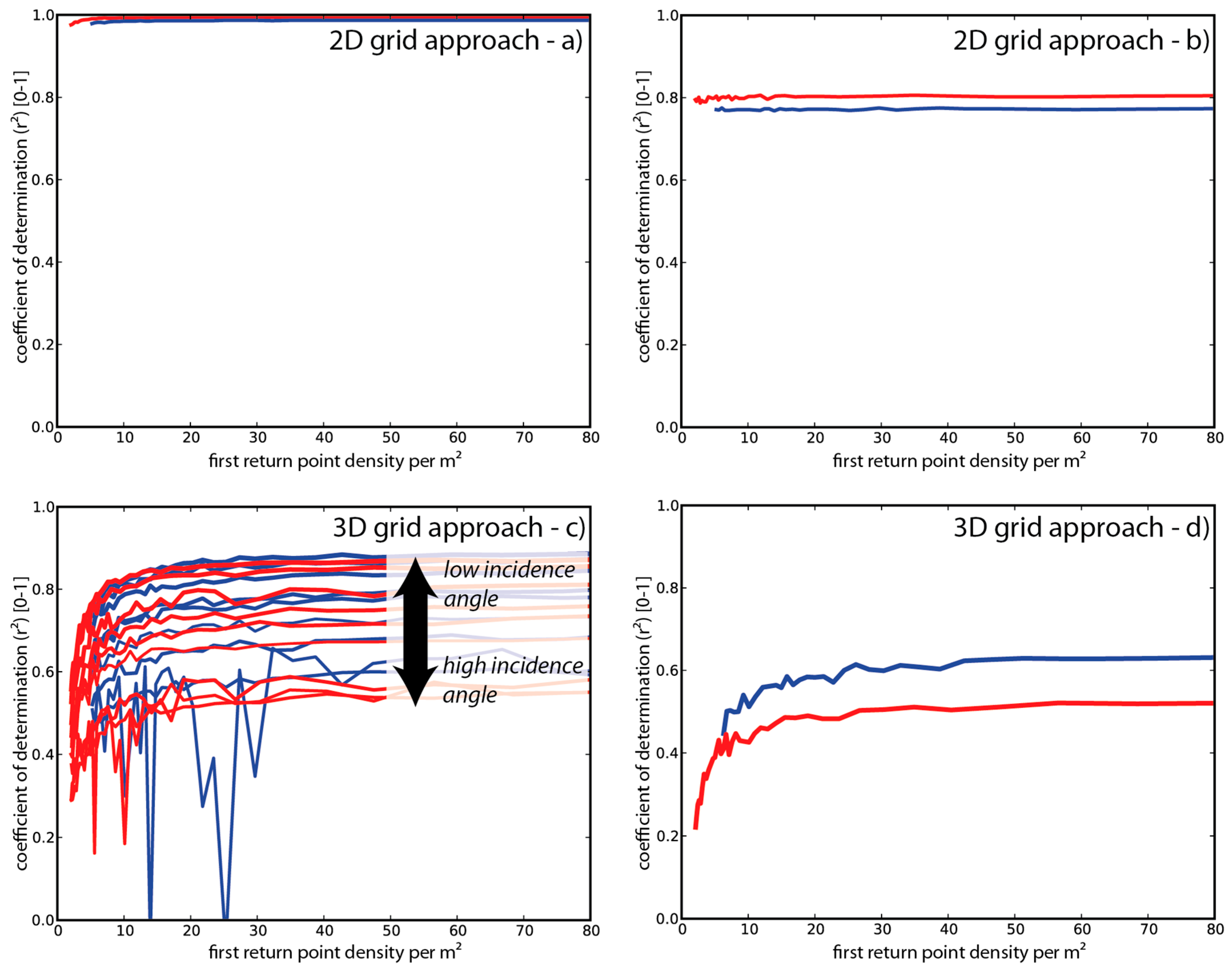
When the determinants of correlation are used for the evaluation of the relationships, the limiting factors are mainly the number of point samples per analysis unit (voxel or pixel) and the number of acquisition directions. The number of point samples is defined by the scanning parameters, leading to a given first return density per m2.
The number of acquisition directions is limited by the flight protocol of the simulated campaign, defining the number of overlapping parallel and cross-strips.
In general, AC is predictable with a higher reliability than rLAI, which is due to the acquisition geometry of the aLiDAR. Especially for close nadir laser shots, the sampling geometry is very similar to a vertical penetration of precipitation or light and its respective attenuation coefficient. With higher incidence angles of ray penetration, the sampling geometries become increasingly different, leading to a decrease in predictive power. Essentially, incoming parallel light with high incidence angles interacts with a completely different object silhouette than incoming laser light (with close nadir directions). One possibility to study the magnitude of this effect is to use a virtual experimental setup for detailed RTM. Such a virtual experimental setup has been used in the presented experiment.
rLAI predictions in general show lower predictive power than AC predictions, but improve when multiple strips are used. While the distribution of AC shows no multi-layering orthogonal to the penetration direction, rLAI shows strong vertical layering. This can be quantified using the given 3D model set up, which includes a plausible representation of vertical canopy layering.
Comparing the 3D model and the simulated point cloud data allowed us to quantify an improvement of
rLAI predictions with the use of multiple scan strips. This is not only due to a simple increase in point sampling but also due to an improved capture of the multi layered distributions of
rLAI with multiple strips: For a single strip, only one dominant penetration direction is considered, increasing the probability of under-sampling of the multi-layered tree crown. With triple strip overlap, the object is captured by a combination of smaller and larger incidence angles from three different trajectories. If rays, coming in from one direction, are not able to penetrate to a certain position of the tree crowns, another set of rays, coming from another direction, have the chance to penetrate to this position and sample the foliage density. This decreases the probability of under-sampling of the multi-layered leaf distribution. For a perfect sampling of this
rLAI distribution, an infinite number of viewing directions would be needed. In
Section 4.4 it can be shown that the maximum correlation coefficient describing the relationship between
rLAI and
LIR is limited to 0.8. However, as could be shown in previous work, realistic LAI estimates can be derived from waveform LiDAR [
29,
30]. In an enhanced virtual experiment, these capabilities could be proofed by using 3D models in combination with a waveform LiDAR simulator [
32] exceeding the scope of this paper.
5.3. Comparison of Data Structures for Analysis
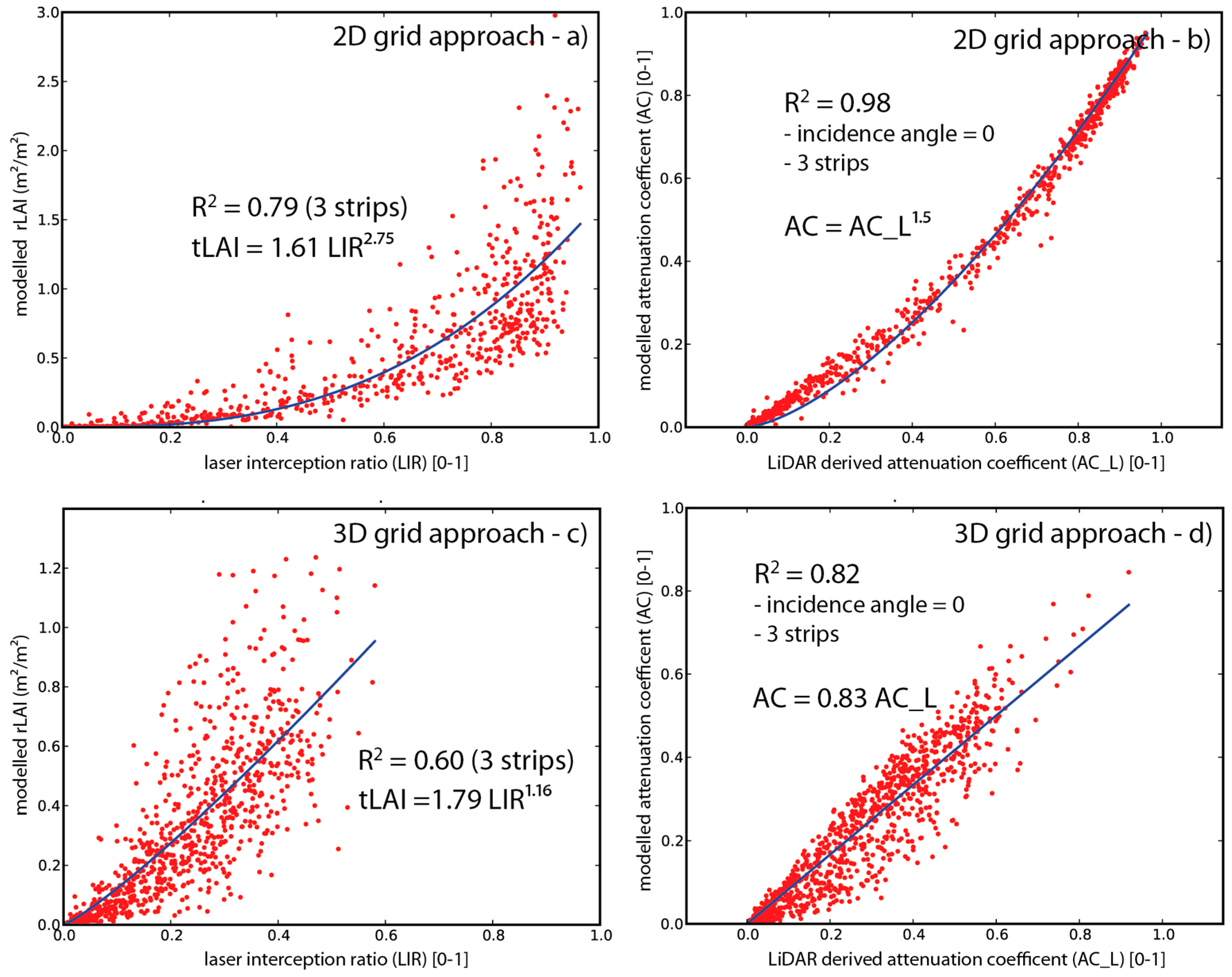
Comparing the analysed data structures (2D grid, 3D grid) by the determinants of correlation for the density predictions, the voxel data structure was the more problematic description. Compared to the pixel approach, this is mainly due to the smaller size of the voxel analysis unit compared to the pixel analysis unit of the same cell size. As a smaller analysis unit the voxel shows an average point count which is only 30% of the average pixel point count (
Section 4.3). This implies a smaller number of samples per analysis unit leading to more noisy observations compared to the pixel unit, where the reduction of noise by averaging is intensified due to an increased number of samples. Neglecting the sampling based effects, it has to be stated, that the derived relationships show linear behaviours for the 3D grid and are slightly biased for the 2D grid (
Figure 10). A bias is visible especially with
LIR and
AC_L values between 0.8 and 1.0. The effect is indicated by higher exponents of the fitting functions. This effect can be explained by the characteristics of the analysis units. The 2D grid represents a vertical column unifying parts of the interior crown, which are problematic in terms of under-sampling, with less critical top canopy parts. This unifying effect does not exist for the voxel analysis unit, which discretizes the vertical density distribution. The vertical discretization allows a correction of attenuation with depth into canopy (see Equation (9) according to Durrieu et al. [
23]), which is not possible for the vertically unified 2D grid unit.
5.4. Comparison of Scan Settings and Point Densities for Analysis
In general, it can be stated that the quality of canopy density prediction increases with increasing first return point densities. The number of point samples per analysis unit controls the quality of the predictions. Thus, the decision for a scan pattern is also related to the respective data structure to be used for analysis.
For the 2D data structure, where the vertical density distribution is unified within each pixel and where point sampling densities are sufficient, the predictive power is hardly affected by varying point densities and strip overlaps. This results in correlation coefficients remaining in the same range for all tested setups. As the pixel analysis unit shows a sufficient number of samples for the whole tested range of scan settings, the R2 reaches its maximum already at a first return density of 5 pts/m2. For AC, which shows no vertical clumping, this leads to almost perfect predictions. The R2 of rLAI prediction did never exceed 0.8. This suggests that the quality has reached a saturation level. Sampling density and additional flight strips have a negligible effect onto the quality of the predictions. Only a capturing technique, which is able to sample the inner crown in a homogeneous manner, would be able to further improve the R2.
Due to the smaller size of the voxel analysis unit, the increase of predictive power with increasing point density is more pronounced. A sufficient number of sampling points is reached at a first return density of 30 pts/m2. For rLAI in particular, this is not enough in order reach an R2 higher than 0.6, which can also be explained by the limitations of the object–sensor relationship.
The “virtual experiment” showed that the 2D grid approach was more reliable than the 3D grid approach, especially for LAI mapping. Nevertheless, it has to be noted that the 2D approach aims only at a 2D mapping of LAI ignoring the vertical LAI profile within canopy. In order to achieve this goal, point densities higher than 5 pts/m
2 are already suitable for 2D LAI description (not significantly improvable with increased point densities). Nevertheless, it has to be stated that with only 4 pts/m
2, LiDAR based height estimates show errors of up to 1 m, which can lead to errors of aboveground biomass estimates of 80–125 Mg·ha
−1 [
50]. The 3D grid approach aims at a three dimensional mapping of LAI, which is more ambitious and can only be achieved with moderate predictive power. This suggests the exploitation of more advanced sensing techniques, such as full-waveform LiDAR, which has already been proofed for vertical LAI mapping [
29,
30].
6. Conclusions
In order to evaluate aLiDAR based canopy metrics, we presented a strategy to upgrade traditional in-situ data such as leaf-off tLiDAR and leaf-on DHP-data into plausible 3D canopy models. Using a highly automated reconstruction and modelling workflow has the advantage of an almost unbiased virtual 3D representation of branch and leaf densities. In contrast to the primary in-situ data, systematic errors due to the object–sensor relationship are minimized (hypothesis 1). Calibration and validation is done based on synthesized (SHI) and real (DHP) canopy signatures of sensed data. As the foliage modelling is constrained by the 3D branching architecture of a tree, calibrating the foliage density for a reference DHP leads to plausible foliage densities also in 3D, which was validated by additional DHPs (hypothesis 2). The plausibility of 3D foliage densities could also be cross-checked by comparing a synthesized and a real aLiDAR point cloud.
It could be shown that the reconstructed models permit the evaluation of aLiDAR based rLAI and AC predictions under various scan settings and different data structures (hypothesis 3). Thereby, the importance of laser point sampling density as well as the diversity of scan angles and their quantitative effect onto error margins became clear. It could also be shown that the improved vertical discretization of foliage density in a voxel structure suffers from a lower sampling resolution defined by a critical number of laser points per analysis unit.
The reconstructed polygonal mesh geometries of the 3D models are predestinated for the development of a RTM scenes, usable for a wide range of simulations.
As the presented approach is based on highly automated workflows for model derivation, it can serve as reference data complementing future regional flight campaigns: tLiDAR data have only to be acquired once. (If the 3D branching framework is created, a practical foliage density monitoring can be done only using DHPs and automatically calibrating and validating the 3D canopy density modelling for the given time step or flight campaign date.)
In future, the strategy could also be used for an extended experimental setup including a broad sample of tree species. Doing so, single tree based allometric functions could be found based on the 3D models and compared to measures from discrete return or waveform aLiDAR and, e.g., optical satellite imagery. This could improve the understanding of canopy metrics and their ability to predict canopy density measures and could support the development of new canopy density metrics and correction functions.