LiDAR-Assisted Multi-Source Program (LAMP) for Measuring Above Ground Biomass and Forest Carbon
Abstract
:1. Introduction
Principles of REDD+ and Monitoring, Reporting and Verification (MRV)
2. Materials and Methods
2.1. LiDAR-Assisted Multisource Programme
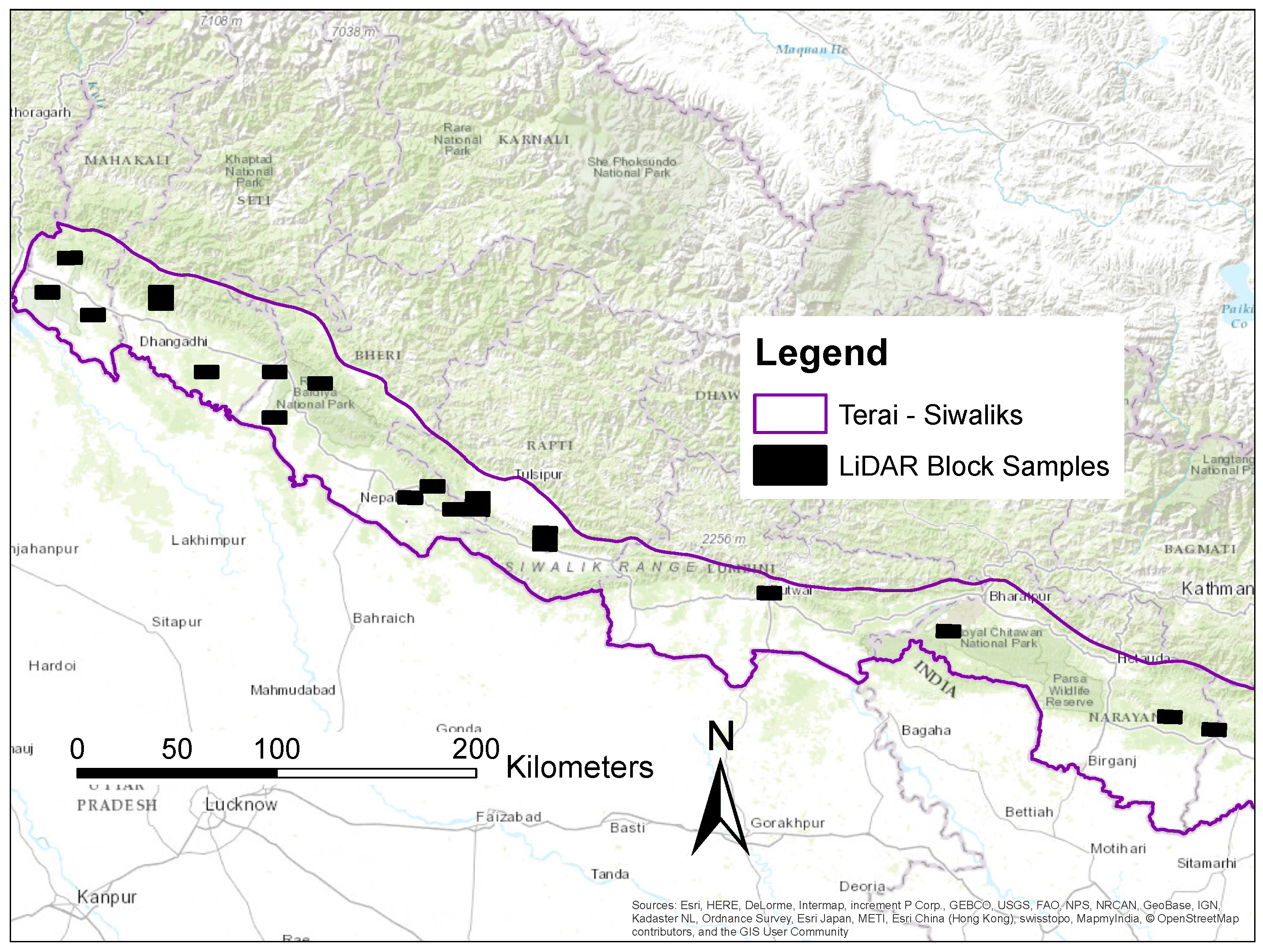
2.2. Study Site
2.3. Conducting the LiDAR Campaign
2.4. Field Campaigns
2.5. LAMP2 with Stratification for Reference Level Generation
2.5.1. Satellite Data Acquisition and Processing
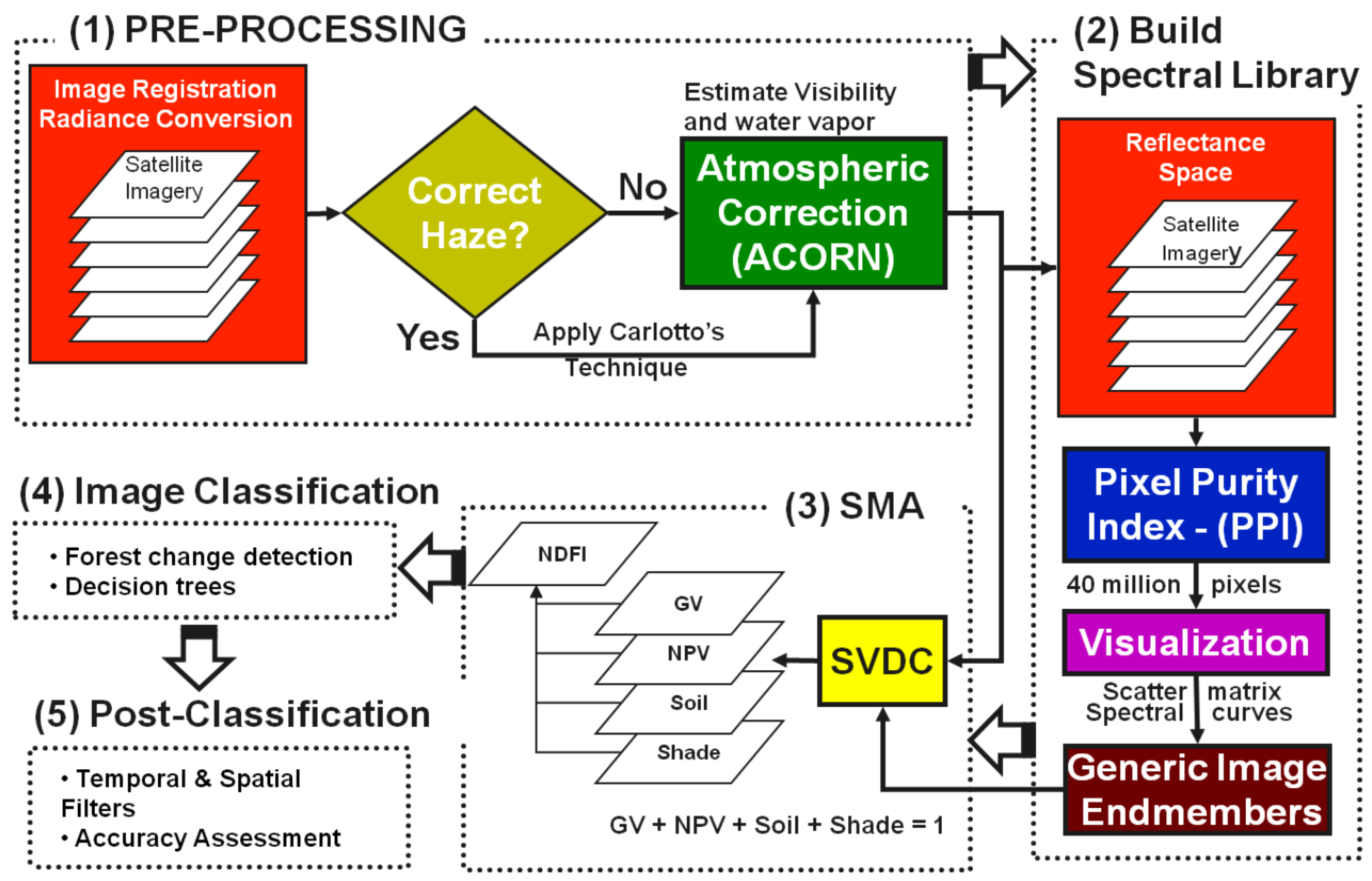
2.5.2. Image Processing
- Spectral Mixture Analysis (SMA): ImgTools was used to carry out spectral mixture analysis for each Landsat scene. The SMA module of ImgTools decomposes the spectral mixture, commonly found in the pixel reflectance values of remotely sensed data, into fractions with natural break points, known as endmembers. SMA module uses these endmembers to develop generic spectral libraries for green vegetation (GV), non-photosynthetic vegetation (NPV), bare soil and clouds [55,56].
- Water Mask: This module creates a water mask as a layer using fractional image.
- Cloud and Shade Mask: This module creates a cloud and shade mask layer that is used in deriving NDFI.
- Normalized Difference Factional Index (NDFI): In this module, the fractions developed from the SMA analysis: GV, NPV, Soil are processed to quantify the percentage of pixels lying outside the range of zero to 100% and to evaluate fraction value consistency for pixels over time (i.e., that pixels with intact forest values were similar over time). Only pixels with at least 98% of the values within zero to 100% and those that showed mean fraction value consistency over time were used by the software algorithm for computing Normalized Difference Fraction Index [55].where (or ) is the shade-normalized GV fraction given by .
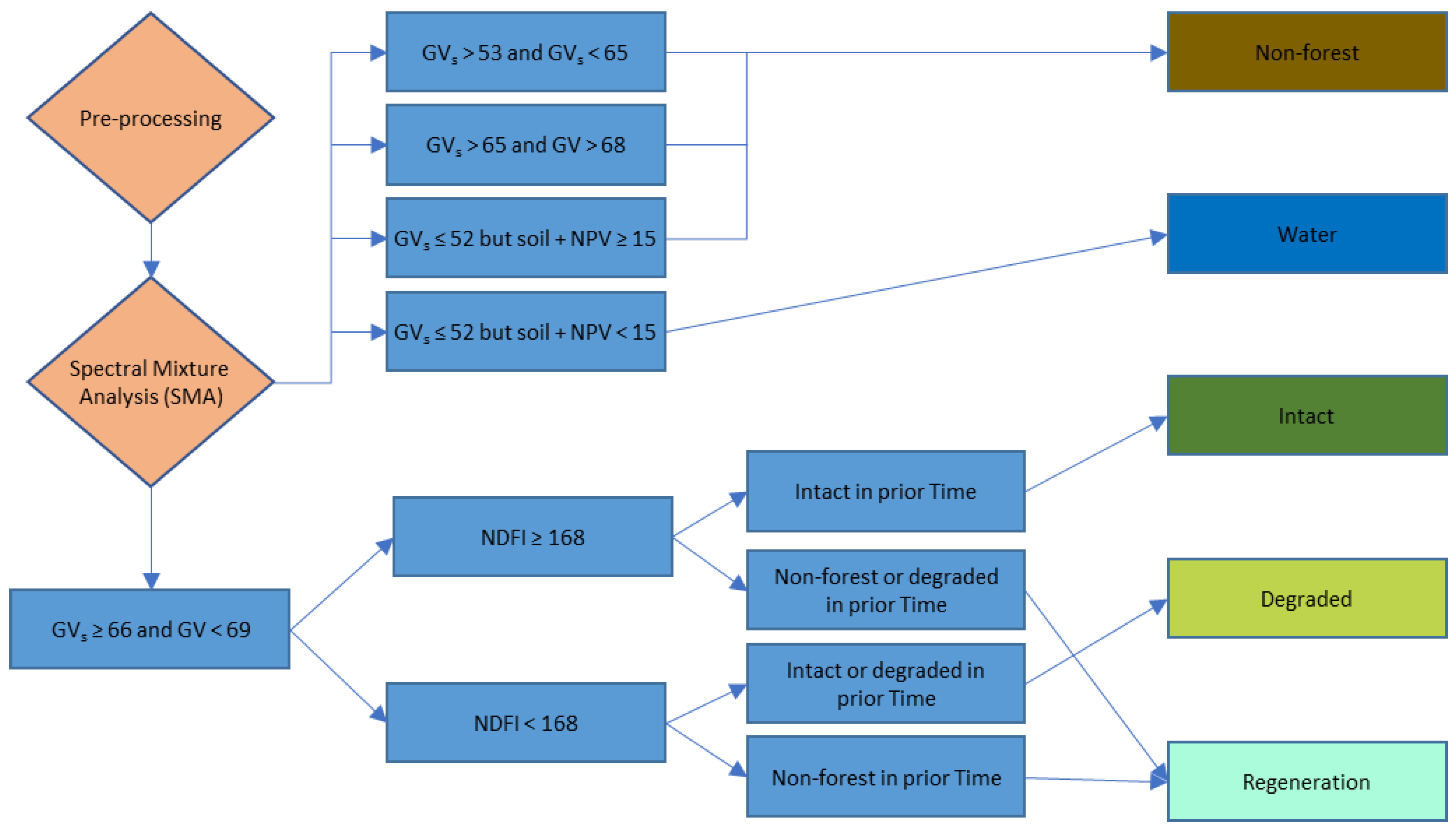
2.5.3. Image Classification
- Non-Forest—An area is classified as non-forest when it meets one of following criteria:
- and
- but
- Water: but
- Forest: and (Justification here is forest will have shade from tall trees but the grassland will have virtually no shade)
- Intact forest: and
- Degraded forest: and
- Regeneration
- Classified as intact forest in step 3 above and classified in previous time period as non-forest or degraded
- Classified as degraded forest in step 3 above and classified in previous time period as deforested
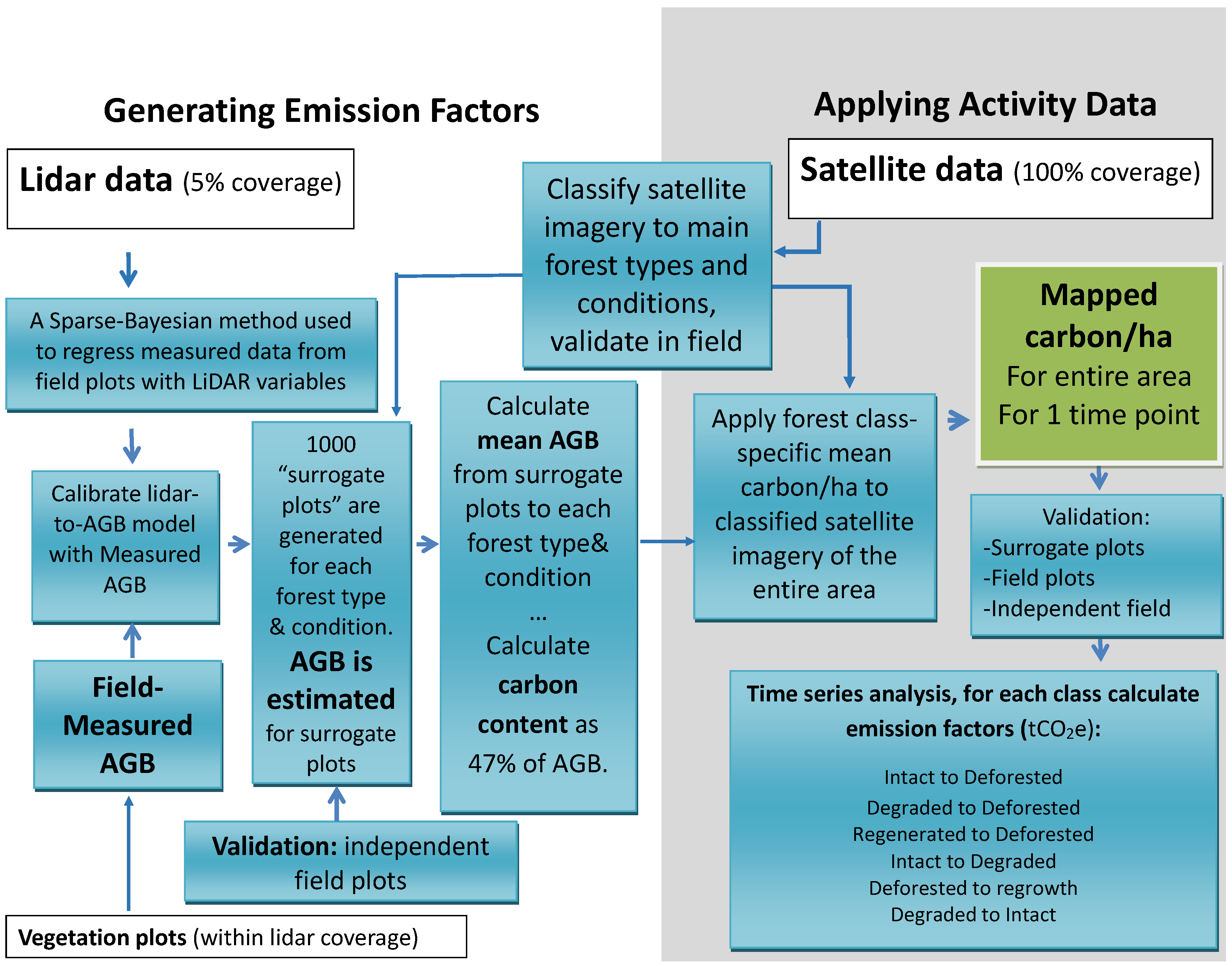
2.5.4. Generation of Emission Factors Using Tier-2 LiDAR-Assisted Multi-Source Programme (LAMP2)
- LAMP2 step 1: Stratifying of forest on the study area using satellite dataIn the first step of the LAMP2 approach, the forest extent over the entire study area was stratified based on the forest types into Sal, Sal mixed, other mixed and riverine [48]. These strata were further divided into two conditions, intact and degraded, resulting in a total of eight forest classes.
- LAMP2 step 2: Estimating forest parameters for LiDAR blocksIn the second step of the LAMP approach, a regression model was generated based on the relationship between LiDAR metrics (height and density distribution) and field based biomass data. It has been shown that Sparse Bayesian methods offer a flexible and robust tool for regressing LiDAR pulse histograms with forest parameters. While performing comparably to traditional regression methods, they are computationally more efficient and allow better flexibility than step-wise regression [7,58]. To correspond to the field plot size of 500 m, the modelling of forest parameters was carried out at 22.4 m × 22.4 m grid-cell level. By using this grid size we also reduce the impact of potential Lidar-DEM errors introduced by steep terrain that will have a more pronounced effect on smaller grid cells. The Lidar metrics selected by the model for estimating above-ground biomass are described in [40]. The model was validated against an independent sample of 46 plots.
- LAMP2 step 3: Deriving forest class-specific mean biomass valuesIn the third step of the LAMP2 approach, LiDAR model estimates are generated for a random sample of locations within the LiDAR blocks. These estimates are combined with the forest strata map to calculate mean biomass for each forest class. The procedure of this calculation is described in more detail in the paragraph below.
2.5.5. Calculation of Emissions from Below-Ground Biomass
2.5.6. Time-Series Analysis of Satellite Data to Generate Activity Data
2.5.7. Generating Reference Level (RL)
2.5.8. Calculating Net Emissions Level
2.6. LAMP3 with Estimation of Above-Ground Biomass at 1 ha-Scale
2.6.1. Variance-Preserving Landsat Image Mosaicking
2.6.2. Applying the LiDAR Model to Calculate AGB Estimates on Surrogate Plots
2.6.3. LAMP3 Model Construction
2.6.4. Variance-Preserving Histogram Matching
3. Results
3.1. Reference Emissions Level (RL) Estimation
3.2. Reference Level at District Level
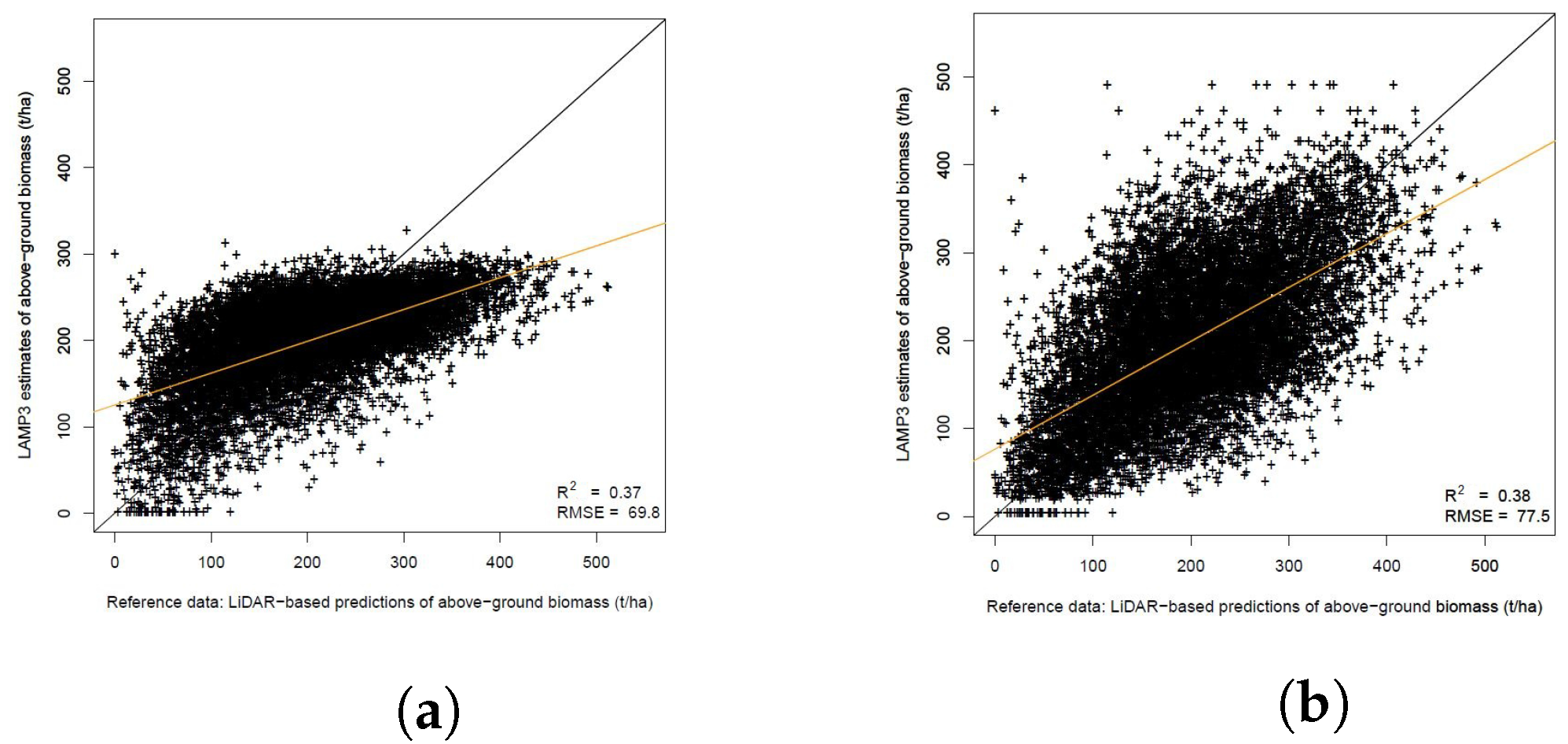
3.3. High-Resolution AGB Maps Calculated in TAL with LAMP3
Estimation of AGB Change with LAMP3
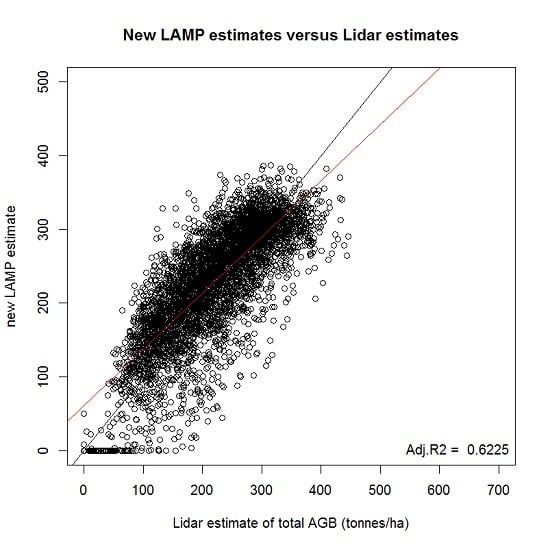
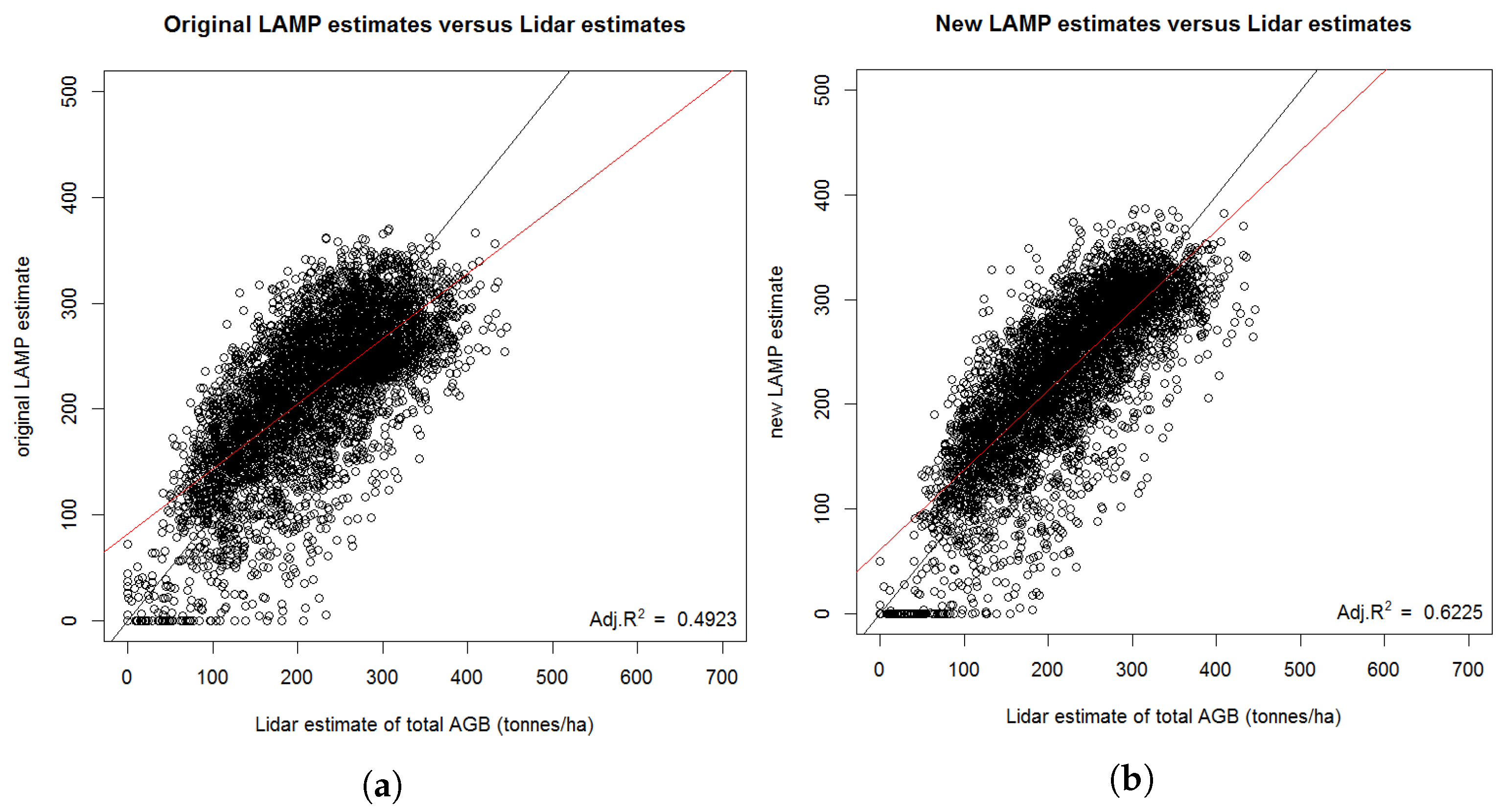
3.4. Uncertainty Assessment
3.4.1. Variance Estimation of Two-Level Regression Models
3.4.2. Validation of Activity Data through Additional Field Verification
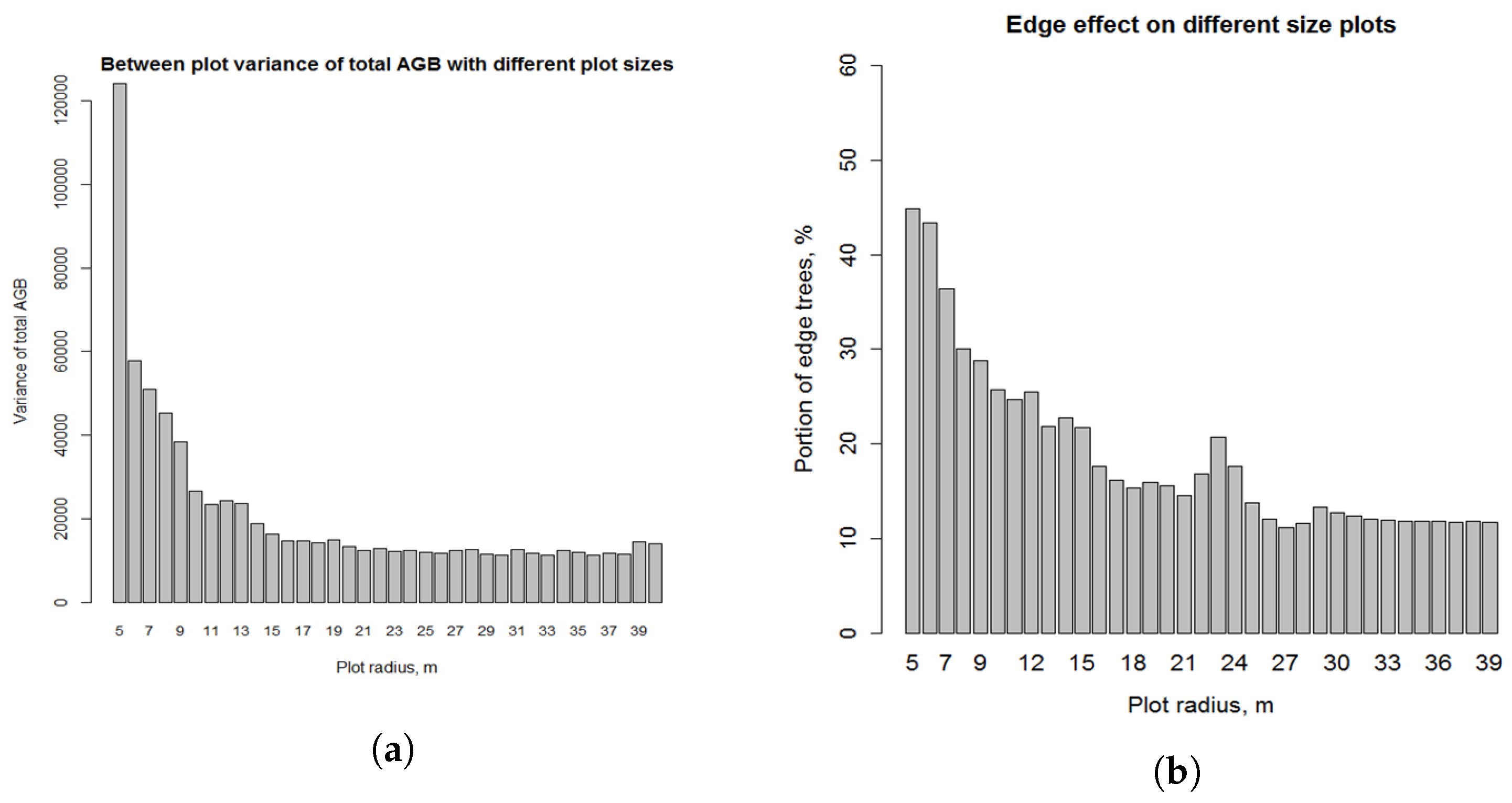
3.4.3. Impact of Field Plot Size
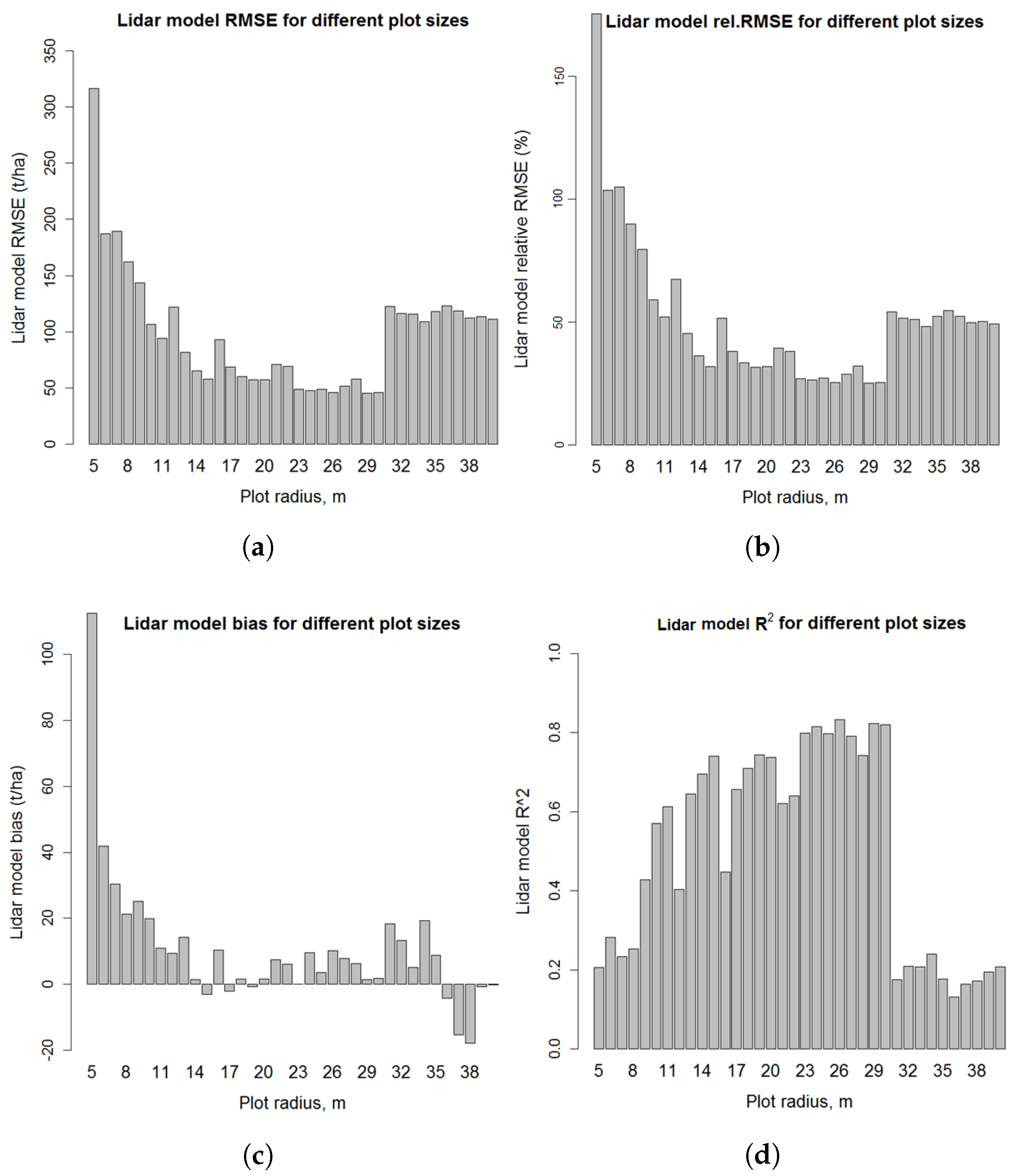
3.4.4. LiDAR Model Errors on Different Plot Sizes
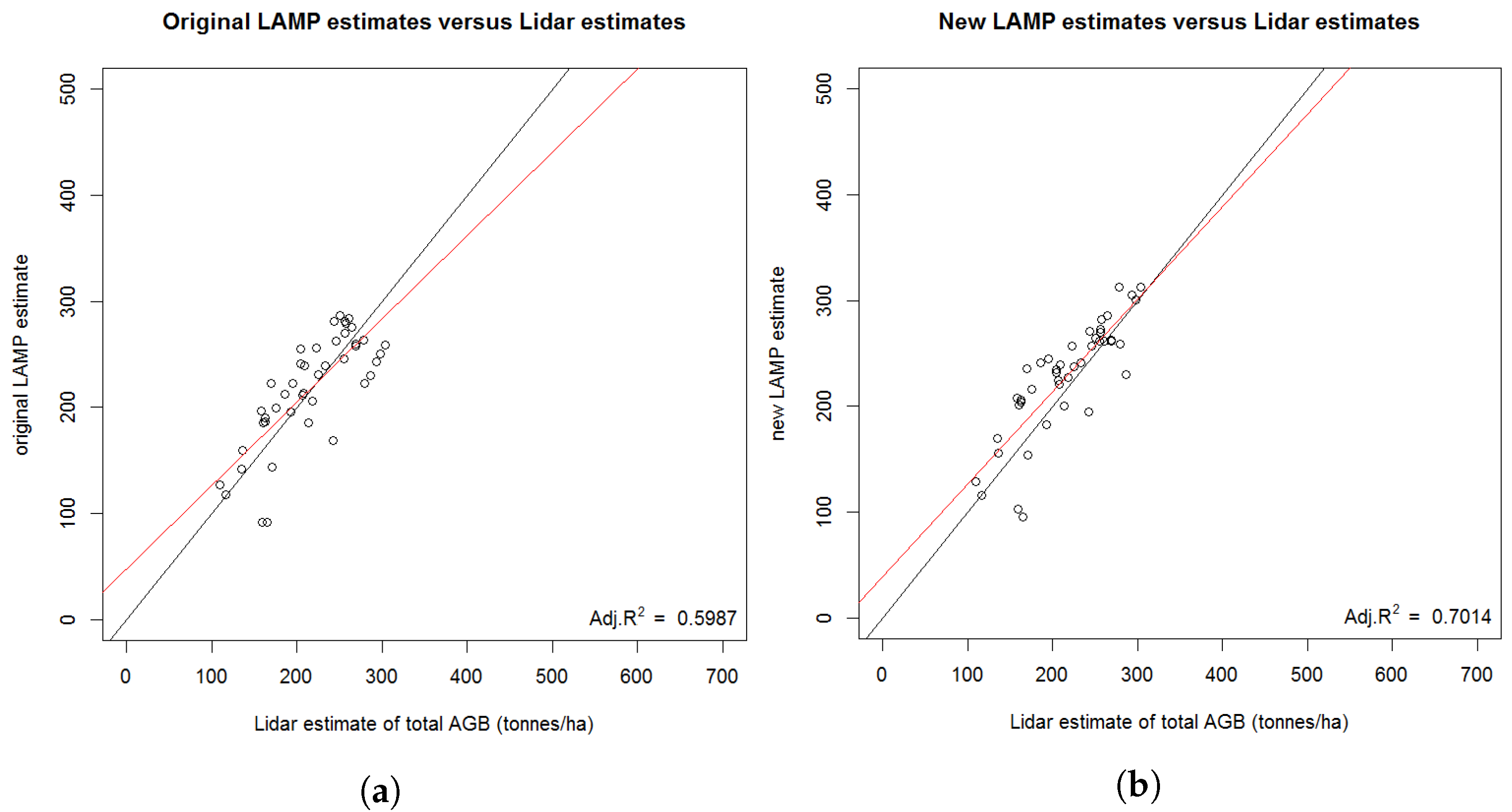
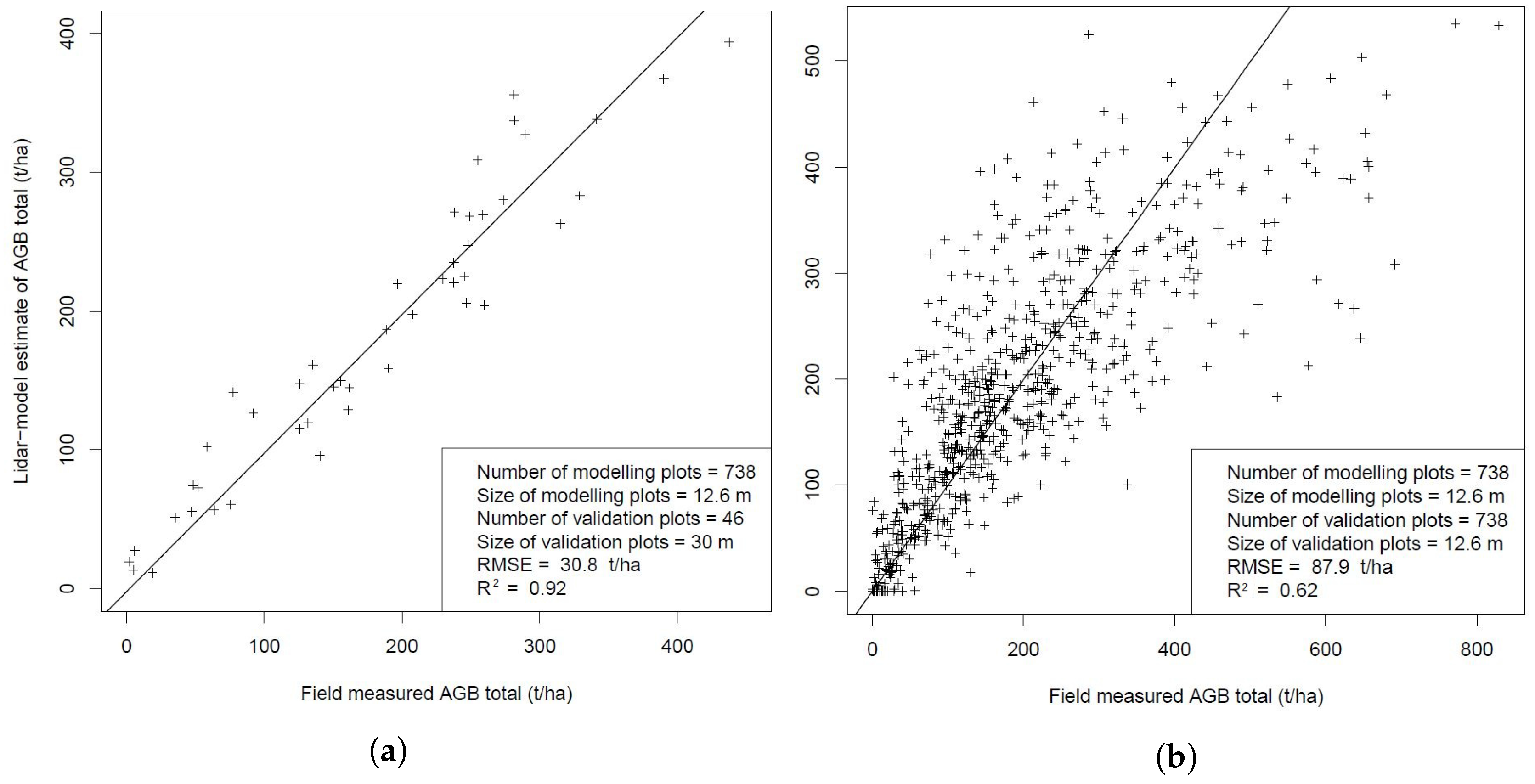
3.4.5. Validation of Results by a Separate Field Campaign
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AGB | Above-Ground Biomass |
| ALS | Airborne Laser Scanning |
| ARVI | Atmospherically Resistant Vegetation Index |
| COP | Conference of the Parties |
| dbh | mean Diameter at Breast Height |
| ERPIN | Emission Reduction Project Idea Note |
| ERPD | Emission Reductions Program Document |
| FCPF | Forest Carbon Partnership Facility |
| FRA | Forest Resource Assessment |
| FREL | Forest Reference Emission Level |
| FRL | Forest Reference Level |
| GHG | GreenHouse Gas |
| GPS | Global Positioning System |
| HAG | Height Above Ground |
| IPCC | Intergovernmental Panel on Climate Change |
| LAMP | LiDAR-Assisted Multi-source Program |
| L-BFGS | Limited memory Broyden-Fletcher-Goldfarb-Shanno |
| LiDAR | Light Detection And Ranging |
| MRV | Measuring, Reporting and Verification |
| NDVI | Normalized Difference Vegetation Index |
| NFI | National Forest Inventory |
| PCM | Persistent Change Monitoring |
| REDD+ | Reduce Emissions from Deforestation and forest Degradation |
| RL | Reference Level |
| RMSE | Root Mean Square Error |
| SMA | Spectral Matrix Analysis |
| TAL | Terai Arc Landscape |
| UNFCCC | United Nations Framework Convention on Climate Change |
| VPM | Variance-Preserving Mosaic |
Appendix A. LAMP2 Algorithm Diagram
Appendix B. Estimation of Population Variance and Standard Deviation in LAMP3 Methods
| OLSLAMP | OLSLAMP | LAMP3 | OLSLAMP | LAMP3 | OLSLAMP | LAMP3 | ||
|---|---|---|---|---|---|---|---|---|
| Data Size | Area, ha | Estimates, | Variance, | Variance, | SD, | SD, | Relative SD, | Relative SD |
| tons/ha | (tons/ha) | (tons/ha) | tons/ha | tons/ha | % | % | ||
| 2.5 ha | ||||||||
| 500 ha | 198.2 | 32972.2 | 33,985.4 | 181.6 | 184.4 | 91.6 | 93.0 | |
| 5 ha | ||||||||
| 1000 ha | 198.2 | 6211.1 | 6453.1 | 78.8 | 80.3 | 39.8 | 40.5 | |
| 25 ha | ||||||||
| 5000 ha | 198.2 | 260.9 | 280.4 | 16.2 | 16.7 | 8.2 | 8.5 | |
| 36.9 ha | ||||||||
| 9805 ha | 198.2 | 141.7 | 149.5 | 11.9 | 12.2 | 6.0 | 6.2 |
| Estimation | Estimates | Reference | RMSE | RMSE Rel. | Bias | Bias Rel. | |||
|---|---|---|---|---|---|---|---|---|---|
| Size ha | Method | Mean tons/ha | Std tons/ha | Mean tons/ha | Std tons/ha | tons/ha | % | tons/ha | % |
| 1 | OLSLAMP | 218.1 | 70.3 | 221.3 | 80.1 | 58.9 | 26.6 | ||
| 1 | LAMP3 | 229.9 | 77.6 | 221.3 | 80.1 | 52.0 | 23.5 | 8.6 | 3.9 |
| 10 | OLSLAMP | 217.8 | 60.8 | 218.1 | 65.6 | 43.4 | 19.9 | ||
| 10 | LAMP3 | 229.4 | 66.1 | 218.1 | 65.6 | 38.6 | 17.7 | 11.3 | 5.2 |
| 100 | OLSLAMP | 217.8 | 51.9 | 216.2 | 51.4 | 33.9 | 15.7 | 1.6 | 0.7 |
| 100 | LAMP3 | 228.2 | 53.5 | 216.2 | 51.4 | 31.6 | 14.6 | 12.0 | 5.5 |

References
- Tomppo, E.; Gschwantner, T.; Lawrence, M.; McRoberts, R.E. National Forest Inventories—Pathways for Common Reporting; Springer Science+Business Media B.V.: Berlin, Germany, 2010. [Google Scholar]
- McRoberts, R.E. Probability- and model-based approaches to inference for proportion forest using satellite imagery as ancillary data. Remote Sens. Environ. 2010, 114, 1017–1025. [Google Scholar] [CrossRef]
- Särndal, C.-E.; Swensson, B.; Wretman, J. Model Assisted Survey Sampling; Springer: Berlin, Germany, 1992. [Google Scholar]
- Gregoire, T.G.; Ståhl, G.; Næsset, E.; Gobakken, T.; Nelson, R.; Holm, S. Model-assisted estimation of biomass in a LiDAR sample survey in Hedmark County, Norway. Can. J. For. Res. 2011, 41, 83–95. [Google Scholar] [CrossRef]
- Varvia, P.; Lähivaara, T.; Maltamo, M.; Packalén, P.; Tokola, T.; Seppänen, A. Unvertainty Quantification in ALS-Based Species-Specific Growing Stock Volume Estimation. IEEE Trans. Geosci. Remote Sens. 2016. [Google Scholar] [CrossRef]
- Nyström, M.; Lindgren, N.; Wallerman, J.; Grafström, A.; Muszta, A.; Nyström, K.; Bohlin, J.; Willén, E.; Fransson, J.E.S.; Ehlers, S.; et al. Data Assimilation in Forest Inventory: First Empirical Results. Forests 2015, 6, 4540–4557. [Google Scholar] [CrossRef]
- Junttila, V.; Kauranne, T.; Leppänen, V. Estimation of Forest Stand Parameters from LiDAR Using Calibrated Plot Databases. For. Sci. 2010, 56, 257–270. [Google Scholar]
- Gregoire, T.G.; Næsset, E.; McRoberts, R.E.; Ståhl, G.; Andersen, H.-E.; Gobakken, T.; Ene, L.; Nelson, R. Statistical rigor in LiDAR-assisted estimation of aboveground forest biomass. Remote Sens. Environ. 2016, 173, 98–108. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Bollandsås, O.M.; Gregoire, T.G.; Nelson, R.; Ståhl, G. Comparison of precision of biomass estimates in regional field sample surveys and airborne LiDAR-assisted surveys in Hedmark County, Norway. Remote Sens. Environ. 2013, 130, 108–120. [Google Scholar] [CrossRef]
- Ene, L.T.; Næsset, E.; Gobakken, T.; Gregoire, T.G.; Ståhl, G.; Nelson, R. Assessing the accuracy of regional LiDAR-based biomass estimation using a simulation approach. Remote Sens. Environ. 2012, 123, 579–592. [Google Scholar] [CrossRef]
- Nelson, R.; Gobakken, T.; Næsset, E.; Gregoire, T.G.; Ståhl, G.; Holm, S.; Flewelling, J. Lidar sampling—Using an airborne profiler to estimate forest biomass in Hedmark County, Norway. Remote Sens. Environ. 2012, 123, 563–578. [Google Scholar] [CrossRef]
- Ståhl, G.; Holm, S.; Gregoire, T.G.; Gobakken, T.; Næsset, E.; Nelson, R. Model-based inference for biomass estimation in a LiDAR sample survey in Hedmark County, Norway. Can. J. For. Res. 2011, 41, 96–107. [Google Scholar] [CrossRef]
- Mitchard, E.T.A.; Saatchi, S.S.; Baccini, A.; Asner, G.P.; Goetz, S.J.; Harris, N.L.; Brown, S. Uncertainty in the spatial distribution of tropical forest biomass: A comparison of pan-tropical maps. Carbon Balance Manag. 2013, 8, 10. [Google Scholar] [CrossRef] [PubMed]
- Saatchi, S.S.; Houghton, R.A.; dos Santos Alvala, R.C.; Soares, J.V.; Yu, Y. Distribution of aboveground live biomass in the Amazon basin. Glob. Chang. Biol. 2007, 13, 816–837. [Google Scholar] [CrossRef]
- Le Toan, T.; Quegan, S.; Davidsoc, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Reimer, F.; Asner, G.P.; Joseph, S. Advancing reference emission levels in subnational and national REDD+ initiatives: A CLASlite approach. Carbon Balance Manag. 2015, 10, 5. [Google Scholar] [CrossRef] [PubMed]
- Bellot, F.F.; Bertram, M.; Navratil, P.; Siegert, F.; Dotzauer, H. The High-Resolution Global Map of 21st-Century Forest Cover Change from the University of Maryland (’Hansen Map’) Is Hugely Overestimating Deforestation in Indonesia. FORCLIME Forests and Climate Change Programme: Indonesia, 2014. Available online: http://forclime.org/documents/press_release/FORCLIME_Overestimation%20of%20Deforestation.pdf (accessed on 2 September 2016).
- Corona, P.; Fattorini, L.; Franceschi, S.; Scrinzi, G.; Torresan, C. Estimation of standing wood volume in forest compartments by exploiting airborne laser scanning information: Model-based, design-based, and hybrid perspectives. Can. J. For. Res. 2014, 44, 1303–1311. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial- and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Johnson, K.D.; Birdsey, R.; Finley, A.O.; Swantaran, A.; Dubayah, R.; Wayson, C.; Riemann, R. Integrating forest inventory and analysis data into a LIDAR-based carbon monitoring system. Carbon Balance Manag. 2014, 9, 3. [Google Scholar] [CrossRef] [PubMed]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; rka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Asner, G.P. Tropical forest carbon assessment: Integrating satellite and airborne mapping approaches. Environ. Res. Lett. 2009, 4, 034009. [Google Scholar] [CrossRef]
- Asner, G.P.; Knapp, D.E.; Martin, R.E.; Tupayachi, R.; Anderson, C.B.; Mascaro, J.; Sinca, F.; Chadwick, K.D.; Sousan, S.; Higgins, M.; et al. The High-Resolution Carbon Geography of Perú; A Collaborative Report of the Carnegie Airborne Observatory and the Ministry of Environment of Perú; Carnegie Airborne Observatory; the Ministry of Environment of Peru: Lima, Peru, 2014.
- Asner, G.P.; Mascaro, J.; Anderson, C.; Knapp, D.E.; Martin, R.E.; Kennedy-Bowdoin, T.; van Breugel, M.; Davies, S.; Hall, J.S.; Muller-Landau, H.C.; et al. High-fidelity national carbon mapping for resource management and REDD+. Carbon Balance Manag. 2013, 8, 7. [Google Scholar] [CrossRef] [PubMed]
- Avitabile, V.; Herold, M.; Heuvelink, G.B.M.; Lewis, S.L.; Phillips, O.L.; Asner, G.P.; Armston, J.; Asthon, P.; Banin, L.F.; Bayol, N.; et al. An integrated pan-tropical biomass map using multiple reference datasets. Glob. Chang. Biol. 2015. [Google Scholar] [CrossRef] [PubMed]
- Hansen, E.H.; Gobakken, T.; Solberg, S.; Kangas, A.; Ene, L.; Mauya, E.; Næsset, E. Relative efficiency of ALS and InSAR for biomass estimation in a Tanzanian rainforest. Remote Sens. 2015, 7, 9865–9885. [Google Scholar] [CrossRef]
- Molina, P.X.; Asner, G.P.; Abadía, M.F.; Manrique, J.C.O.; Diez, L.A.S.; Valencia, R. Spatially-Explicit testing of a general aboveground carbon density estimation model in a western Amazonian forest using airborne LiDAR. Remote Sens. 2016, 8, 9. [Google Scholar] [CrossRef]
- Lohne, T.P.; Solberg, S.; Næsset, E.; Gobakken, T.; Hansen, E.H.; Zahabu, E. Estimation of tropical forest biomass using radargrammetric DEMs derived from TerraSAR-X stripmap image. In Proceeding of the 5th TerraSAR-X Science Team Meeting, German Aerospace Center (DLR), Oberpfaffenhofen, German, 8 July 2013.
- Solberg, S.; Næsset, E.; Gobakken, T.; Bollandsås, O.M. Forest biomass change estimated from height change in interferometric SAR height models. Carbon Balance Manag. 2014, 9, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Kaasalainen, S.; Holopainen, M.; Karjalainen, M.; Vastaranta, M.; Kankare, V.; Karila, K.; Osmanoglu, B. Combining Lidar and Synthetic Aperture Radar Data to Estimate Forest Biomass: Status and Prospects. Forests 2015, 6, 252–270. [Google Scholar] [CrossRef]
- Global Forest Observations Initiative. Integrating Remote-Sensing and Ground-Based Observations for Estimation of Emissions and Removals of Greenhouse Gases in Forests: Methods and Guidance from the Global Forest Observations Initiative; Group on Earth Observations: Geneva, Switzerland, 2016. [Google Scholar]
- Pelletier, J.; Ramankutty, N.; Potvin, C. Diagnosing the uncertainty and detectability of emission reductions for REDD+ under current capabilities: An example for Panama. Environ. Res. Lett. 2011, 6, 024005. [Google Scholar] [CrossRef]
- Lusiana, B.; van Noordwijk, M.; Johana, F.; Galudra, G.; Suyanto, S.; Cadisch, G. Implications of uncertainty and scale in carbon emission estimates on locally appropriate designs to reduce emissions from deforestation and degradation (REDD+). Mitig. Adapt. Strateg. Glob. Chang. 2014, 19, 757–772. [Google Scholar] [CrossRef]
- Chen, Q.; Laurin, G.V.; Valentini, R. Uncertainty of remotely sensed aboveground biomass over an African tropical forest: Propagating errors from trees to plots to pixels. Remote Sens. Environ. 2015, 160, 134–143. [Google Scholar] [CrossRef]
- Chen, Q.; McRoberts, R.E.; Wang, C.; Radtke, P.J. Forest aboveground biomass mapping and estimation across multiple spatial scales using model-based inference. Remote Sens. Environ. 2016, 18, 350–360. [Google Scholar] [CrossRef]
- Saarela, S.; Holm, S.; Grafström, A.; Schnell, S.; Næsset, E.; Gregoire, T.; Nelson, R.; Ståhl, G. Hierarchical model-based inference for forest inventory utilizing three sources of information. Ann. For. Sci. 2016, 73, 895–910. [Google Scholar] [CrossRef]
- Corona, P. Consolidating new paradigms in large-scale monitoring and assessment of forest ecosystems. Environ. Res. 2016, 144, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Corona, P. Integration of forest mapping and inventory to support forest management. iFor. Biogeosci. For. 2010, 3, 59–64. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Good Practice Guidance for Land Use, land-Use Change and Forestry (IPCC/IGES); Penman, J., Gytarsky, M., Hiraishi, T., Krug, T., Kruger, D., Pipatti, R., Buendia, L., Miwa, K., Ngara, T., Tanabe, K., et al., Eds.; IPCC: Geneva, Switzerland, 2003.
- Joshi, A.R.; Tegel, K.; Manandhar, U.; Aguilar-Amuchastegui, N.; Dinerstein, E.; Eivazi, A.; Gamble, L.; Gautam, B.; Gunia, K.; Gunia, M.; et al. An accurate REDD+ reference level for Terai Arc Landscape, Nepal using LiDAR assisted Multi-source Programme (LAMP). Banko Janakari 2015, 24, 23–33. [Google Scholar] [CrossRef]
- Tomppo, E.; Haakana, M.; Katila, M.; Peräsaari, J. Multi-Source National Forest Inventory—Methods and Applications; Managing Forest Ecosystems; Springer: Berlin, Germany, 2008. [Google Scholar]
- Gregoire, T.G. Design-based and model-based inference in survey sampling: Appreciating the difference. Can. J. For. Res. 1998, 28, 1429–1447. [Google Scholar] [CrossRef]
- Rana, P.; Korhonen, L.; Gautam, B.; Tokola, T. Effect of field plot location on estimating tropical forest above-ground biomass in Nepal using airborne laser scanning data. ISPRS J. Photogramm. Remote Sens. 2014, 94, 55–62. [Google Scholar] [CrossRef]
- Gautam, B.; Peuhkurinen, J.; Kauranne, T.; Gunia, K.; Tegel, K.; Latva-Käyrä, P.; Rana, P.; Eivazi, A.; Kolesnikov, A.; Hämäläinen, J.; et al. Estimation of Forest Carbon Using LiDAR-Assisted Multi-source Programme (LAMP) in Nepal. In Proceedings of the Technical Commission VI, Education and Outreach, Working Group 6, Pokhara, Nepal, 12–13 September 2013.
- Department of Forests, Ministry of Forest and Soil Conservation, GoN. Forest Cover Change Analysis of the Terai Districts (1990/91-2000/01); Department of Forests, Ministry of Forest and Soil Conservation: Kathmandu, Nepal, 2005.
- Department of Forests, Ministry of Forest and Soil Conservation. REDD, forestry and climate change cell. Emission Reductions Project Idea Note; Department of Forests, Ministry of Forest and Soil Conservation: Kathmandu, Nepal, 2014.
- Department of Forests, Ministry of Forest and Soil Conservation, GoN. Hamro Ban; Department of Forests, Ministry of Forest and Soil Conservation: Kathmandu, Nepal, 2013.
- Joshi, A.; Shrestha, M.; Smith, J.; Ahearn, S. Forest Classification of Terai Arc Landscape (TAL) Based on Landsat 7 Satellite Data; Technical Report; WWF-US: Washington, DC, USA, 2003. [Google Scholar]
- Eerikäinen, K. Predicting the height-diameter pattern of planted Pinus kesiya stands in Zambia and Zimbabwe. For. Ecol. Manag. 2003, 175, 355–366. [Google Scholar] [CrossRef]
- Calama, R.; Montero, G. Interregional nonlinear height-diameter model with random coefficients for stone pine in Spain. Can. J. For. Res. 2004, 34, 150–163. [Google Scholar] [CrossRef]
- Mehtätalo, L. A longitudinal height-diameter model for Norway spruce in Finland. Can. J. For. Res. 2004, 34, 131–140. [Google Scholar] [CrossRef]
- Nothdurft, A.; Kublin, E.; Lappi, J. A non-linear hierarchical mixed model to describe tree height growth. Eur. J. For. Res. 2006, 125, 281–289. [Google Scholar] [CrossRef]
- Sharma, M.; Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modelling approach. For. Ecol. Manag. 2007, 249, 187–198. [Google Scholar] [CrossRef]
- Sharma, E.R.; Pukkala, T. Volume Equations and Biomass Prediction of Forest Trees of Nepal; Publication Series of the Ministry of Forests and Soil Conservation of Nepal; Forest Survey and Statistics Division: Kathmandu, Nepal, 1990; pp. 1–16. [Google Scholar]
- Souza, C., Jr.; Roberts, D.A.; Cochrane, M.A. Combining spectral and spatial information to map canopy damage from selective logging and forest fires. Remote Sens. Environ. 2005, 98, 329–343. [Google Scholar] [CrossRef]
- Souza, C.; Siqueira, J.V. ImgTools: A software for optical remotely sensed data analysis. In Proceedings of the XVI Simpósio Brasileiro de Sensoriamento Remoto (SBSR), Foz do Iguaçu-PR, Brazil, 13–18 April 2013.
- Intergovernmental Panel on Climate Change (IPCC). Guidelines for National Greenhouse Gas Inventories. 2006. Available online: http://www.ipcc-nggip.iges.or.jp/public/2006gl/pdf/4_Volume4/V4_04_Ch4_Forest_Land.pdf (accessed on 2 September 2016).
- Junttila, V.; Maltamo, M.; Kauranne, T. Sparse Bayesian Estimation of Forest Stand Characteristics from Airborne Laser Scanning. For. Sci. 2008, 54, 543–552. [Google Scholar]
- Yuan, D.; Elvidge, C.D. Comparison of relative radiometric normalization techniques. ISPRS J. Photogramm. Remote Sens. 1996, 51, 117–126. [Google Scholar] [CrossRef]
- Song, C.; Woodcock, C.E.; Seto, K.C.; Lenney, M.P.; Macomber, S.A. Classification and change detection using landsat TM data: When and how to correct atmospheric effects? Remote Sens. Environ. 2001, 75, 230–244. [Google Scholar] [CrossRef]
- Du, Y.; Teillet, P.M.; Cihlar, J. Radiometric normalization of multitemporal high-resolution satellite images with quality control for land cover change detection. Remote Sens. Environ. 2002, 82, 123–134. [Google Scholar] [CrossRef]
- Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: Making REDD a reality. Environ. Res. Lett. 2007, 2, 045023. [Google Scholar] [CrossRef]
- Canty, M.J.; Nielsen, A.A. Automatic radiometric normalization of multitemporal satellite imagery with the iteratively re-weighted MAD transformation. Remote Sens. Environ. 2008, 112, 1025–1036. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, L.; Lin, H.; Liao, M. Automatic relative radiometric normalization using iteratively weighted least square regression. Int. J. Remote Sens. 2008, 29, 459–470. [Google Scholar] [CrossRef]
- Liu, S.-H.; Lin, C.-W.; Chen, Y.-R.; Tseng, C.-M. Automatic radiometric normalization with genetic algorithms and a Kriging model. Comput. Geosci. 2012, 43, 42–51. [Google Scholar] [CrossRef]
- Eivazi, A.; Kolesnikov, A.; Junttila, V.; Kauranne, T. Variance-preserving mosaicing of multiple satellite images for forest parameter estimation: Radiometric normalization. ISPRS J. Photogramm. Remote Sens. 2015, 105, 120–127. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanré, D. Atmospherically resistant vegetation index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Forest Resource Assessment Nepal Project/Department of Forest Research and Survey. LiDAR Assisted Multisource Programme (LAMP) in Terai Arc Landscape (TAL); Forest Resource Assessment Nepal Project/Department of Forest Research and Survey: Kathmandu, Nepal, 2014. [Google Scholar]
- Næsset, E. Some Challenges in Forest Monitoring—Proposing a “Research Platform” for Development, Training and Validation of Spaceborne Technologies in Brazil. 2009. Available online: http://www.dsr.inpe.br/Brazil_Norway_Workshop/ERIK%20NAESSET_Challenges_in_florest_monitoring _Proposing_a_research_platform_for_development_traning.pdf (accessed on 2 September 2016).
- García, M.; Riaño, D.; Chuvieco, E.; Danson, F.M. Estimating biomass carbon stocks for a Mediterranean forest in central Spain using LiDAR height and intensity data. Remote Sens. Environ. 2010, 114, 816–830. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Stehman, S.V.; Woodcock, C.E. Making better use of accuracy data in land change studies: Estimating accuracy and area and quantifying uncertainity using stratified estimation. Remote Sens. Environ. 2013, 129, 122–131. [Google Scholar] [CrossRef]
- Mauya, E.W.; Hansen, E.H.; Gobakken, T.; Bollandsås, O.M.; Malimbwi, R.E.; Næsset, E. Effects of field plot size on prediction accuracy of aboveground biomass in airborne laser scanning-assisted inventories in tropical rain forests of Tanzania. Carbon Balance Manag. 2015. [Google Scholar] [CrossRef] [PubMed]
- Mascaro, J.; Detto, M.; Asner, G.; Muller-Landau, H. Evaluating uncertainty in mapping forest carbon with airborne LiDAR. Remote Sens. Environ. 2011, 115, 3770–3774. [Google Scholar] [CrossRef]
- Frazer, G.; Magnussen, S.; Wulder, M.; Niemann, K. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E. Assessing effects of positional errors and sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2009, 39, 1036–1052. [Google Scholar] [CrossRef]
- Maltamo, M.; Næsset, E.; Vauhkonen, J. Forestry Applications of Airborne Laser Scanning. Concepts and Case Studies; Managing Forest Ecosystems; Springer: Berlin, Germany, 2014. [Google Scholar]
- Tokola, T. Remote Sensing Concepts and Their Applicability in REDD+ Monitoring. Curr. For. Rep. 2015, 1, 252–260. [Google Scholar] [CrossRef]
- Kandel, P.N. Estimation of above Ground Forest Biomass and Carbon Stock by Integrating Lidar, Satellite Image and Field Measurement in Nepal. J. Nat. Hist. Mus. 2015, 28, 160–170. [Google Scholar]
- Swatantran, A.; Tang, H.; Barrett, T.; DeCola, P.; Dubayah, R. Rapid, High-Resolution Forest Structure and Terrain Mapping over Large Areas using Single Photon Lidar. Sci. Rep. 2016. [Google Scholar] [CrossRef] [PubMed]
- White, H. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econom. J. Econom. Soc. 1980, 48, 817–838. [Google Scholar] [CrossRef]
- Davidson, R.; MacKinnon, J.G. Estimation and Inference in Econometrics; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Ståhl, G.; Saarela, S.; Schnell, S.; Holm, S.; Breidenbach, J.; Healey, S.P.; Patterson, P.L.; Magnussen, S.; Næsset, E.; McRoberts, R.E.; et al. Use of models in large-area forest surveys: Comparing model-assisted, model-based and hybrid estimation. For. Ecosyst. 2016, 3, 1–11. [Google Scholar] [CrossRef]

| Material: | Section | |
| LiDAR: | LiDAR data (5% coverage) | 2.3 |
| Field data: | Vegetation plots (738 plots of 500 m within LiDAR coverage) | 2.4 |
| Satellite: | Satellite data (medium resolution such as Landsat, 100% coverage) | 2.5.1 |
| Step | Contents | |
| 1. | Stratify the forest of the study area into the main forest types and forest condition | 2.3, 2.5.1, |
| classes using satellite data (= forest strata map). (Satellite) | 2.5.4 | |
| 2. | Sampling of locations for LiDAR data acquisition and field plot collection. Weighted | 2.3 |
| random sampling by incorporating the forest strata map, covering all important | ||
| forest types. | ||
| 3. | Calibrate LiDAR-to-AGB model with field based AGB. (LiDAR and Field data) | 2.5.4 |
| 4. LAMP2 | Randomly select 1000 circular LiDAR sample areas of 1 ha size for each forest | 2.5.4 |
| strata within the LiDAR-area. Purpose: They will be used for calculating a mean | ||
| biomass value for each stratum (forest type and condition class). | ||
| 4. LAMP3 | Select 10,000 circular LiDAR sample areas (surrogate plots) using a weighted | 2.6.2 |
| random sampling within the LiDAR area. Weights should be the inverse of LiDAR | ||
| block sampling. Purpose: To be used as training data (surrogate field data) in | ||
| satellite-based model. | ||
| 5. | Use LiDAR-to-AGB model to estimate AGB for the LiDAR sample areas (LAMP2) | 2.5.4, |
| or surrogate plots (LAMP3) | 2.6.2 | |
| 6. LAMP2 | Calculate a mean AGB value for each stratum from the LiDAR-model estimates | 2.5.4 |
| on LiDAR sample areas. To be used for calculating Emission Factors. Combine | ||
| these forest class-specific mean AGB values with the forest strata map of | ||
| the entire area. | ||
| 6. LAMP3 | 1. Extract satellite-based features (band values, vegetation indices) from mosaicked | 2.6.1 |
| satellite-imagery of the entire area. (Satellite) | ||
| 2. Calibrate Satellite-to-AGB model with the surrogate plot AGB estimates. | 2.6.3 | |
| 3. Estimate AGB for each satellite image pixel with the Satellite-to-AGB model. | ||
| 4. Post-process the satellite data based AGB estimates with histogram matching | 2.6.4 | |
| method to avoid saturation effect. | ||
| 7. | The previous steps result in mapped AGB for the entire area, at strata level (LAMP2) | 2.5.4, 2.6.3, |
| or at 1 ha level (LAMP3), respectively. | 2.6.4 | |
| 8. LAMP2 | Time-series analysis of satellite data to generate Activity Data for Reference Level, | 2.5.5–2.5.8 |
| using stratified satellite imagery of two successive time instances T1 and T2. | ||
| 8. LAMP3 | Time-series analysis based on AGB value differences at 1 ha grid level, estimated | 2.6 |
| with the Satellite-to-AGB model from mosaicked satellite-imagery of the entire area | ||
| over the whole time period. | ||
| Variable Name (Unit) | Min | Max | Mean | StD |
|---|---|---|---|---|
| Mean diameter weighted by basal area (cm) | 5.9 | 127.9 | 34.2 | 17.0 |
| Mean tree height weighted by basal area (m) | 2.9 | 36.0 | 15.8 | 6.1 |
| Basal area (m/ha) | 0.1 | 53.4 | 18.4 | 10.6 |
| Number of trees (1/ha) | 20 | 2219 | 679.3 | 450.1 |
| Stem volume (m/ha) | 0.3 | 680.9 | 149.8 | 114.0 |
| Total above-ground biomass (tons/ha) | 0.4 | 829.1 | 189.1 | 142.6 |
| Class | Nr of Plots | Above-Ground Biomass (t/ha) | C and CO2e Values | ||||
|---|---|---|---|---|---|---|---|
| Mean | Min | Max | StD | C (t/ha) | CO2e (t/ha) | ||
| 1-Sal intact | 988 | 235.6 | 20.4 | 509.5 | 84.1 | 110.7 | 406.0 |
| 2-Sal degraded | 969 | 173.2 | 0.0 | 425.3 | 72.9 | 81.4 | 298.5 |
| 3-Salmix intact | 966 | 183.2 | 0.0 | 556.9 | 84.7 | 86.1 | 315.7 |
| 4-Salmix degraded | 946 | 146.4 | 0.0 | 539.6 | 106.2 | 68.8 | 252.3 |
| 5-Othermix intact | 985 | 186.1 | 5.5 | 479.5 | 94.0 | 87.4 | 320.7 |
| 6-Othermix degraded | 943 | 143.2 | 0.4 | 461.6 | 86.8 | 67.3 | 246.8 |
| 7-Riverine intact | 934 | 171.1 | 0.0 | 405.5 | 46.8 | 80.4 | 294.9 |
| 8-Riverine degraded | 979 | 99.4 | 0.0 | 505.6 | 57.9 | 46.7 | 171.3 |
| Change Matrix | Change Class |
|---|---|
| Intact forest to non-forest | Deforestation 1 |
| Intact forest to degraded forest | Degradation |
| Degraded forest to non-forest | Deforestation 2 |
| Non-forest to dense regenerating forest | Regeneration 1 |
| Non-forest to sparse regenerating forest | Regeneration 2 |
| Degraded forest to regenerating forest | Regeneration 3 |
| Regeneration forest to non-forest | Deforestation 3 |
| Forest Type | Transition | Activity | Activity Data (ha) | ||||
|---|---|---|---|---|---|---|---|
| 1999–2002 | 2002–2006 | 2006–2009 | 2009–2011 | 12-Year Total | |||
| Sal Forest | Intact to Deforested | Deforestation 1 | 11,583 | 2085 | 9488 | 17,914 | 41,070 |
| Degraded to Deforested | Deforestation 2 | 4322 | 679 | 615 | 1651 | 7268 | |
| Regenerated to Deforested | Deforestation 3 | 905 | 2117 | 6655 | 9677 | ||
| Intact to Degraded | Degradation | 10,831 | 1342 | 3141 | 17,488 | 32,803 | |
| Deforested to regrowth | Regeneration | 24,635 | 35,951 | 6313 | 10,008 | 76,907 | |
| Sal Mixed | Intact to Deforested | Deforestation 1 | 8487 | 2291 | 10,588 | 20,332 | 41,697 |
| Degraded to Deforested | Deforestation 2 | 7632 | 1395 | 964 | 1927 | 11,918 | |
| Regenerated to Deforested | Deforestation 3 | 1996 | 3405 | 12,821 | 18,222 | ||
| Intact to Degraded | Degradation | 10,186 | 1661 | 10,003 | 10,375 | 32,225 | |
| Deforested to regrowth | Regeneration | 32,597 | 40,999 | 4995 | 11,886 | 90,477 | |
| Other Mixed | Intact to Deforested | Deforestation 1 | 2029 | 273 | 2661 | 3308 | 8271 |
| Degraded to Deforested | Deforestation 2 | 674 | 175 | 514 | 284 | 1647 | |
| Regenerated to Deforested | Deforestation 3 | 174 | 870 | 1536 | 2580 | ||
| Intact to Degraded | Degradation | 1570 | 216 | 380 | 1250 | 3417 | |
| Deforested to regrowth | Regeneration | 2483 | 5239 | 1251 | 3461 | 12,434 | |
| Riverine | Intact to Deforested | Deforestation 1 | 918 | 160 | 255 | 1663 | 2995 |
| Degraded to Deforested | Deforestation 2 | 458 | 59 | 39 | 163 | 719 | |
| Regenerated to Deforested | Deforestation 3 | 76 | 147 | 752 | 974 | ||
| Intact to Degraded | Degradation | 697 | 81 | 225 | 877 | 1881 | |
| Deforested to regrowth | Regeneration | 2202 | 3306 | 510 | 244 | 6262 | |
| Path / Row | Band | a | b |
|---|---|---|---|
| 141/41 | 1 | 2.12 | |
| 2 | 1.62 | ||
| 3 | 1.28 | ||
| 4 | 0 | 0.84 | |
| 5 | 1.02 | ||
| 7 | 1.01 | ||
| 142/41 | 1 | 1 | |
| 2 | 1 | ||
| 3 | 1 | ||
| 4 | 1 | ||
| 5 | 1 | ||
| 7 | 1 | ||
| 143/40 | 1 | 2.16 | |
| 2 | 1.55 | ||
| 3 | 1.23 | ||
| 4 | 1.43 | ||
| 5 | 1.24 | ||
| 7 | 1.17 | ||
| 143/41 | 1 | 1.26 | |
| 2 | 1.18 | ||
| 3 | 1.12 | ||
| 4 | 1.06 | ||
| 5 | 1.15 | ||
| 7 | 1.02 | ||
| 144/40 | 1 | 1.44 | |
| 2 | 1.28 | ||
| 3 | 1.16 | ||
| 4 | 1.22 | ||
| 5 | 1.08 | ||
| 7 | 23.84 | 1.01 |
| Period | CO Emissions (tCO2e) | Total | |
|---|---|---|---|
| Above-Ground | Below-Ground | ||
| 1999–2002 | 13,136,430 | 2,627,286 | 15,763,716 |
| 2002–2006 | 1,736,537 | 347,307 | 2,083,845 |
| 2006–2009 | 9,644,698 | 1,928,940 | 11,573,637 |
| 2009–2011 | 19,020,661 | 3,804,132 | 22,824,793 |
| Total 12-year | 43,538,325 | 8,707,665 | 52,245,991 |
| Average annual | 3,628,193.79 | 725,639 | 4,353,833 |
| 1999–2002 | 2002–2006 | 2006–2009 | 2009–2011 | 12-Year Emissions | |
|---|---|---|---|---|---|
| Kahchanpur | 1,326,570 | 120,105 | 296,008 | 3,499,486 | 5,242,169 |
| Kailali | 3,736,460 | 93,151 | 911,511 | 7,891,560 | 12,632,682 |
| Bardia | 425,756 | 151,066 | 312,516 | 3,116,150 | 4,005,488 |
| Banke | 1,227,909 | 304,491 | 2,515,125 | 567,689 | 4,615,215 |
| Dang | 2,600,210 | 582,332 | 4,759,420 | 892,183 | 8,834,146 |
| Kapilbastu | 1,594,386 | 113,716 | 1,025,029 | 380,993 | 3,114,124 |
| Rupandehi | 597,963 | (24,121) | 72,593 | 224,251 | 870,686 |
| Nawalparasi | 1,869,896 | 171,651 | 758,771 | 456,103 | 3,256,421 |
| Chitwan | 1,388,989 | 267,881 | 250,988 | 1,315,372 | 3,223,230 |
| Parsa | 189,225 | 76,152 | 142,864 | 872,272 | 1,280,513 |
| Bara | 395,579 | 96,825 | 207,383 | 1,615,801 | 2,315,588 |
| Rautahat | 410,772 | 130,596 | 321,429 | 1,992,933 | 2,855,730 |
| Variable | Estimates | Surrogate Plots | RMSE | RMSE (%) | Bias | Bias (%) | ||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | |||||
| AGB, t/ha | 198.2 | 53.1 | 198.1 | 88.1 | 69.8 | 35.2 | 0.12 | 0.06 |
| Volume, m/ha | 157.1 | 42.5 | 157.0 | 71.0 | 56.5 | 36.0 | 0.10 | 0.06 |
| Basal area, m/ha | 19.2 | 4.1 | 19.2 | 6.1 | 4.6 | 23.8 | 0.05 | 0.00 |
| Diameter, cm | 35.0 | 4.3 | 35.0 | 10.2 | 9.3 | 26.6 | 0.02 | 0.00 |
| Height, cm | 16.2 | 2.1 | 16.2 | 4.2 | 3.7 | 22.6 | 0.00 | 0.00 |
| Variable | Estimates | Surrogate Plots | RMSE | RMSE (%) | Bias | Bias (%) | ||
|---|---|---|---|---|---|---|---|---|
| Mean | StD | Mean | StD | |||||
| AGB, t/ha | 198.0 | 88.2 | 198.1 | 88.1 | 77.5 | 39.1 | ||
| Volume, m/ha | 157.0 | 71.1 | 157.0 | 71.0 | 63.0 | 40.1 | ||
| Basal area, m/ha | 19.2 | 6.1 | 19.2 | 6.1 | 5.0 | 25.9 | ||
| Diameter, cm | 35.0 | 10.2 | 35.0 | 10.2 | 11.2 | 31.9 | ||
| Height, cm | 16.2 | 4.2 | 16.2 | 4.2 | 4.3 | 26.4 | ||
| Activity | Intact | Deforestation | Degradation | Regeneration | Total | Mapped Area | Proportion Wi |
|---|---|---|---|---|---|---|---|
| (ha) | (ha) | ||||||
| Intact | 0.704 | 0.016 | 0.008 | 0.142 | 0.871 | 858,910 | 0.871 |
| Deforestation | 0.008 | 0.063 | 0.001 | 0.002 | 0.074 | 72,700 | 0.074 |
| Degraded | 0.003 | 0.005 | 0.024 | 0.000 | 0.032 | 31,398 | 0.032 |
| Regeneration | 0.001 | 0.003 | 0.001 | 0.020 | 0.024 | 23,623 | 0.024 |
| Total | 0.716 | 0.086 | 0.034 | 0.164 | 1.000 | 986,631 | 1.000 |
| Overall accuracy | 0.81 ± 0.09 | ||||||
| Producer’s accuracy | 0.98 ± 0.065 | 0.73 ± 0.024 | 0.72 ± 0.017 | 0.87 ± 0.061 | |||
| User’s | 0.81 ± 0.092 | 0.86 ± 0.007 | 0.76 ± 0.009 | 0.82 ± 0.004 | |||
| Estimates | Ref. Plots | Error | ||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Mean | Std | Mean | Std | RMSE | Rel. RMSE (%) | Bias | Rel. Bias (%) |
| AGB in Tonnes/hectare | 182.8 | 104.2 | 180.4 | 108.5 | 30.8 | 17.1 | 2.4 | 1.3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kauranne, T.; Joshi, A.; Gautam, B.; Manandhar, U.; Nepal, S.; Peuhkurinen, J.; Hämäläinen, J.; Junttila, V.; Gunia, K.; Latva-Käyrä, P.; et al. LiDAR-Assisted Multi-Source Program (LAMP) for Measuring Above Ground Biomass and Forest Carbon. Remote Sens. 2017, 9, 154. https://doi.org/10.3390/rs9020154
Kauranne T, Joshi A, Gautam B, Manandhar U, Nepal S, Peuhkurinen J, Hämäläinen J, Junttila V, Gunia K, Latva-Käyrä P, et al. LiDAR-Assisted Multi-Source Program (LAMP) for Measuring Above Ground Biomass and Forest Carbon. Remote Sensing. 2017; 9(2):154. https://doi.org/10.3390/rs9020154
Chicago/Turabian StyleKauranne, Tuomo, Anup Joshi, Basanta Gautam, Ugan Manandhar, Santosh Nepal, Jussi Peuhkurinen, Jarno Hämäläinen, Virpi Junttila, Katja Gunia, Petri Latva-Käyrä, and et al. 2017. "LiDAR-Assisted Multi-Source Program (LAMP) for Measuring Above Ground Biomass and Forest Carbon" Remote Sensing 9, no. 2: 154. https://doi.org/10.3390/rs9020154
APA StyleKauranne, T., Joshi, A., Gautam, B., Manandhar, U., Nepal, S., Peuhkurinen, J., Hämäläinen, J., Junttila, V., Gunia, K., Latva-Käyrä, P., Kolesnikov, A., Tegel, K., & Leppänen, V. (2017). LiDAR-Assisted Multi-Source Program (LAMP) for Measuring Above Ground Biomass and Forest Carbon. Remote Sensing, 9(2), 154. https://doi.org/10.3390/rs9020154