Construction of Multi-Year Time-Series Profiles of Suspended Particulate Inorganic Matter Concentrations Using Machine Learning Approach
Abstract
1. Introduction
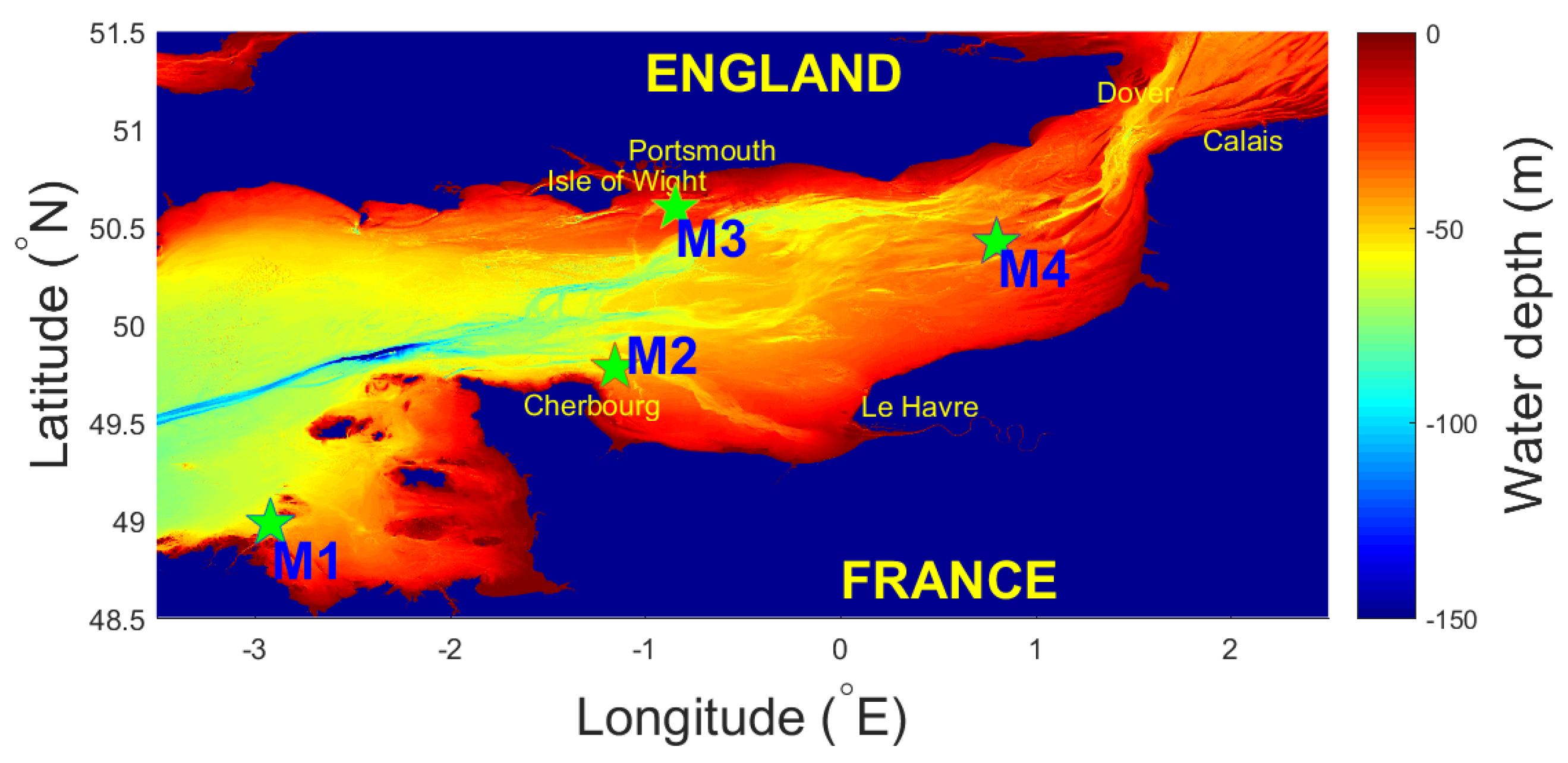
2. Study Area
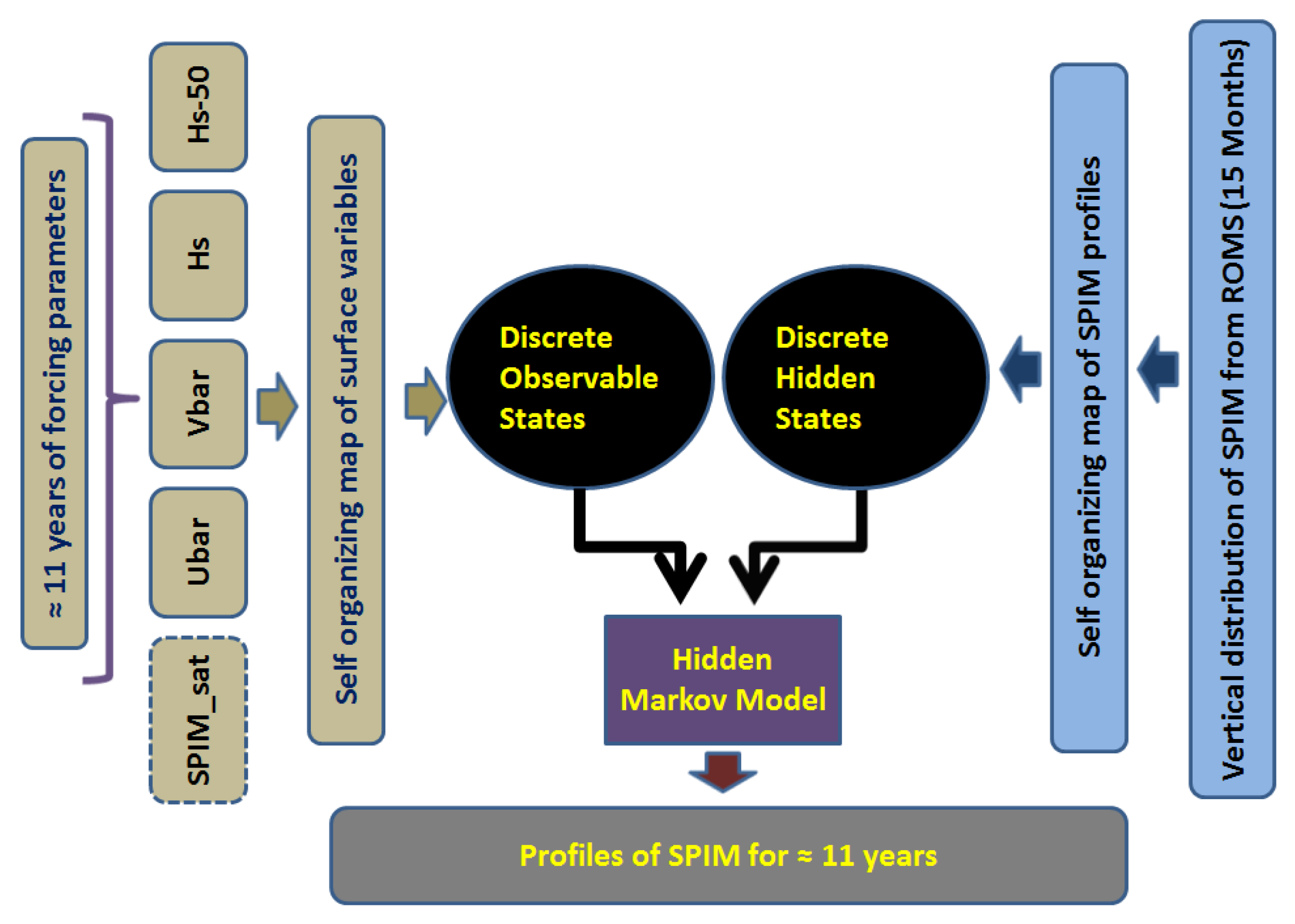
3. Data and Methodology
3.1. Hidden Data
3.2. Observable Data
3.2.1. Significant Wave Height ()
3.2.2. Barotropic Currents
3.3. Self-Organizing Maps
3.4. Hidden Markov Model
3.5. Satellite Data
4. Results and Discussion
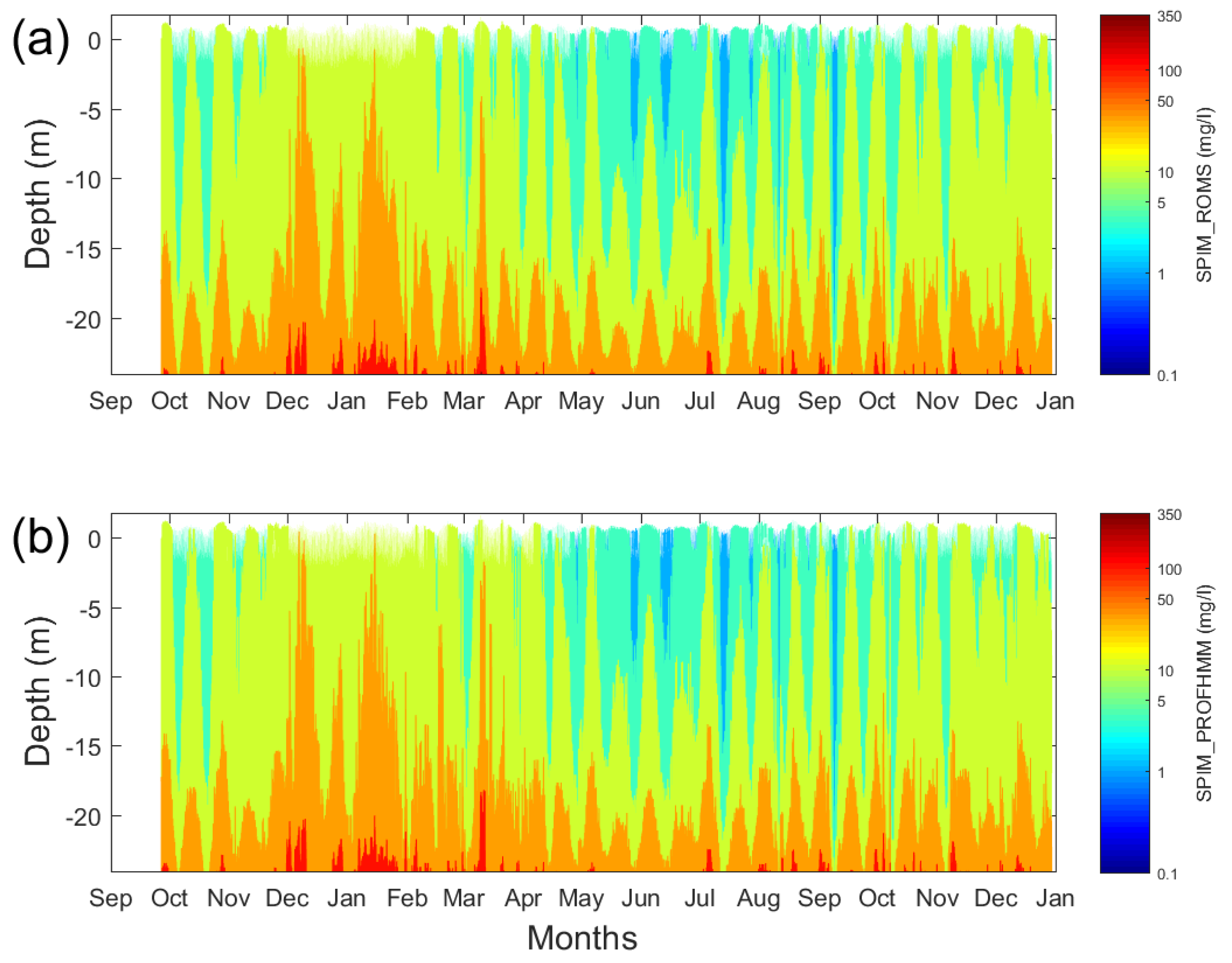
4.1. Output from Learning Phase
4.2. Output from Out-of-Learning Phase
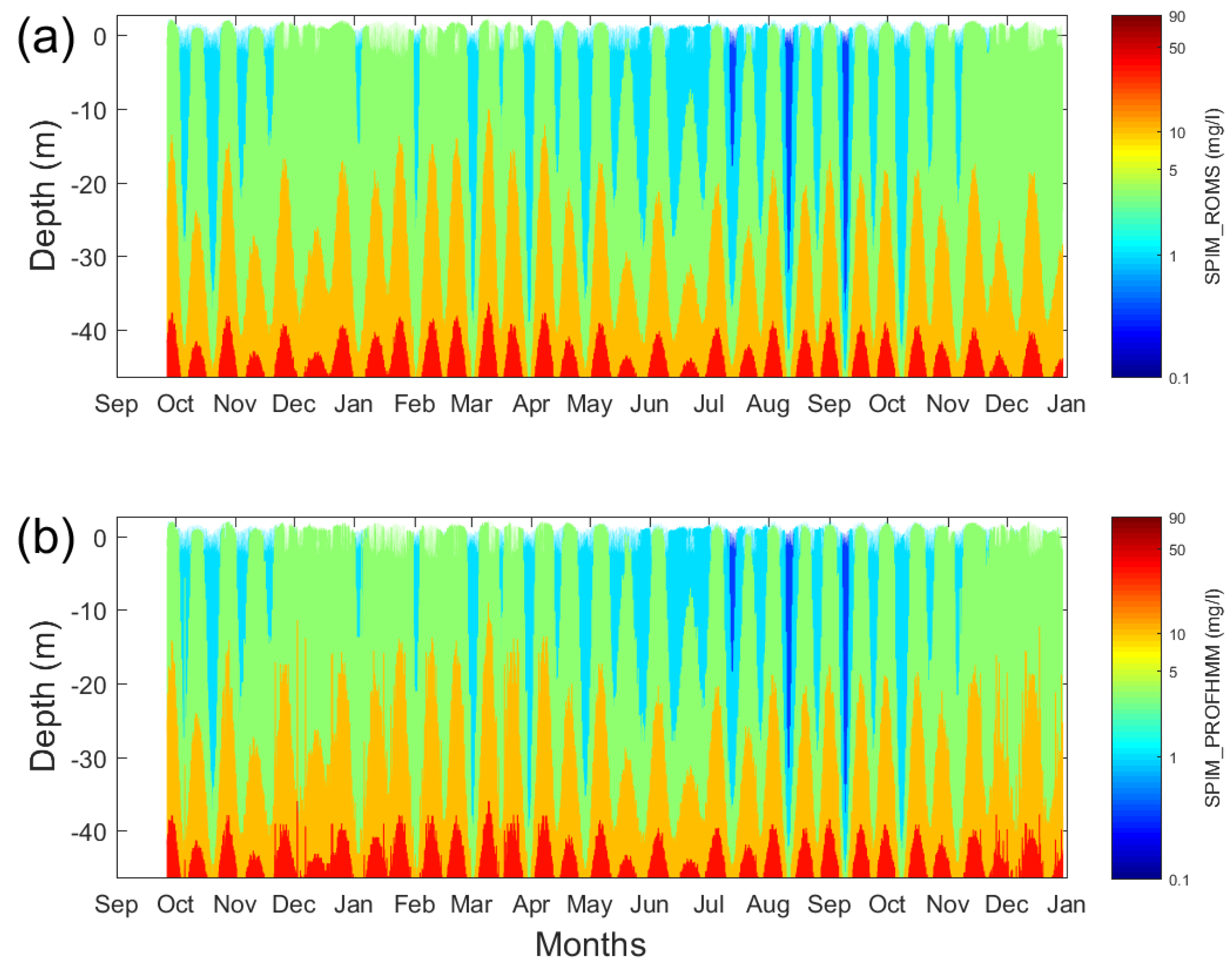
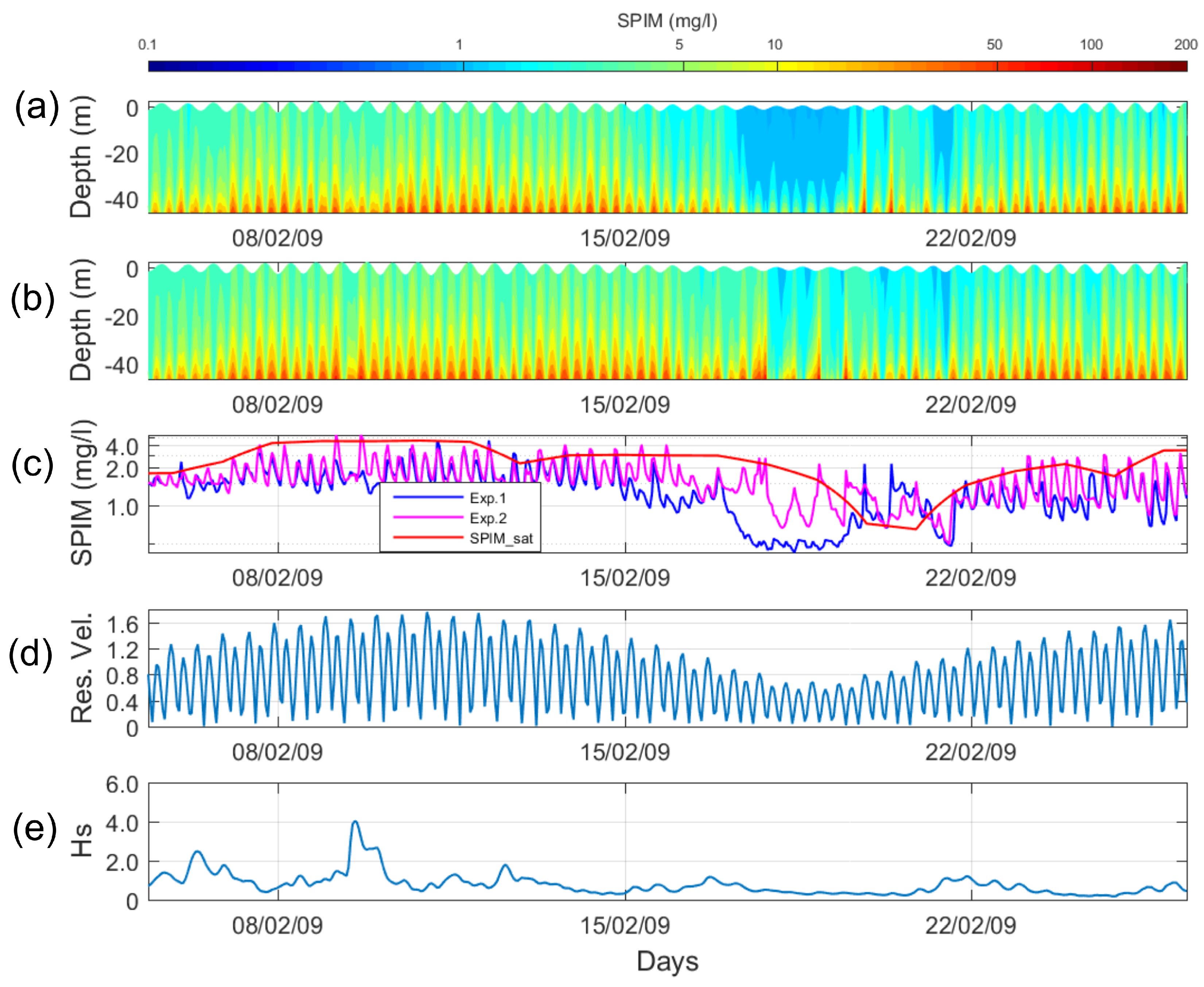
4.2.1. Experiment 1
Time Series of Surface SPIM
- The satellite algorithm overestimates the SPIM concentration when finer particles dominate the suspension during storms [33].
- The kriging interpolation of satellite images becomes imprecise during storms because of the high cloud coverage [45].
- The assumptions in the ROMS model (non-cohesive particles, settling velocity, critical shear stress, etc.) are partially valid [33].
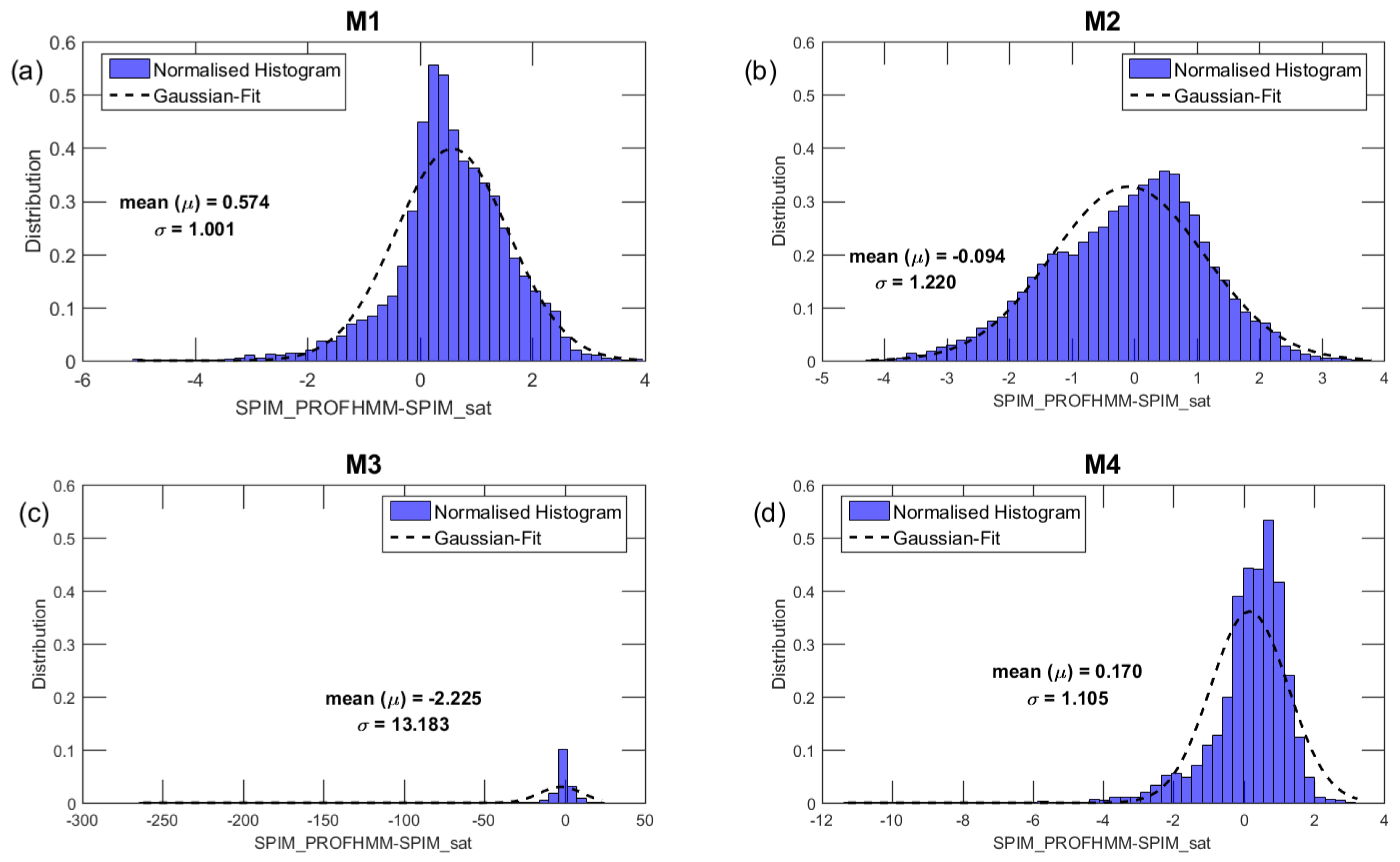
Error Distribution of Surface SPIM
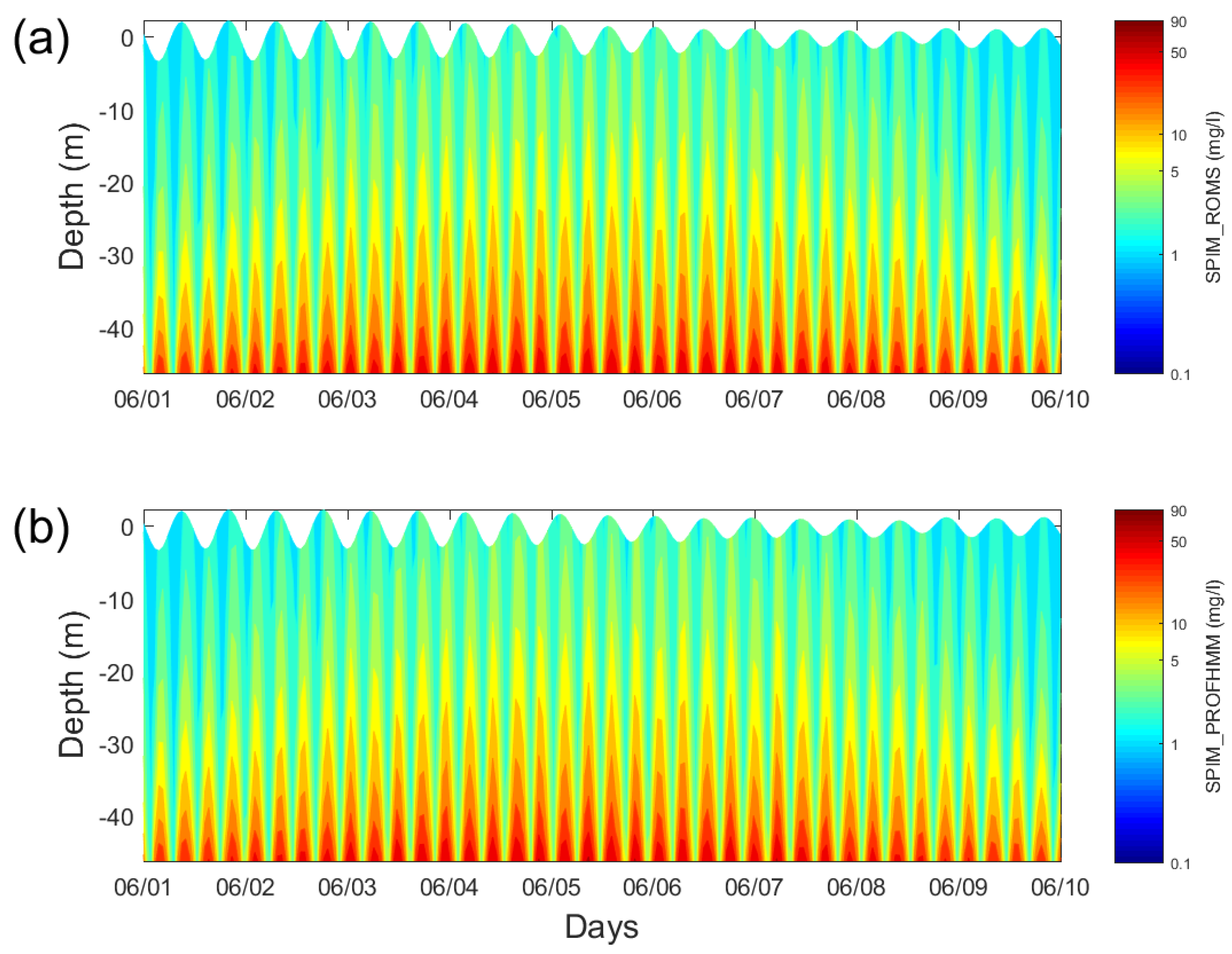
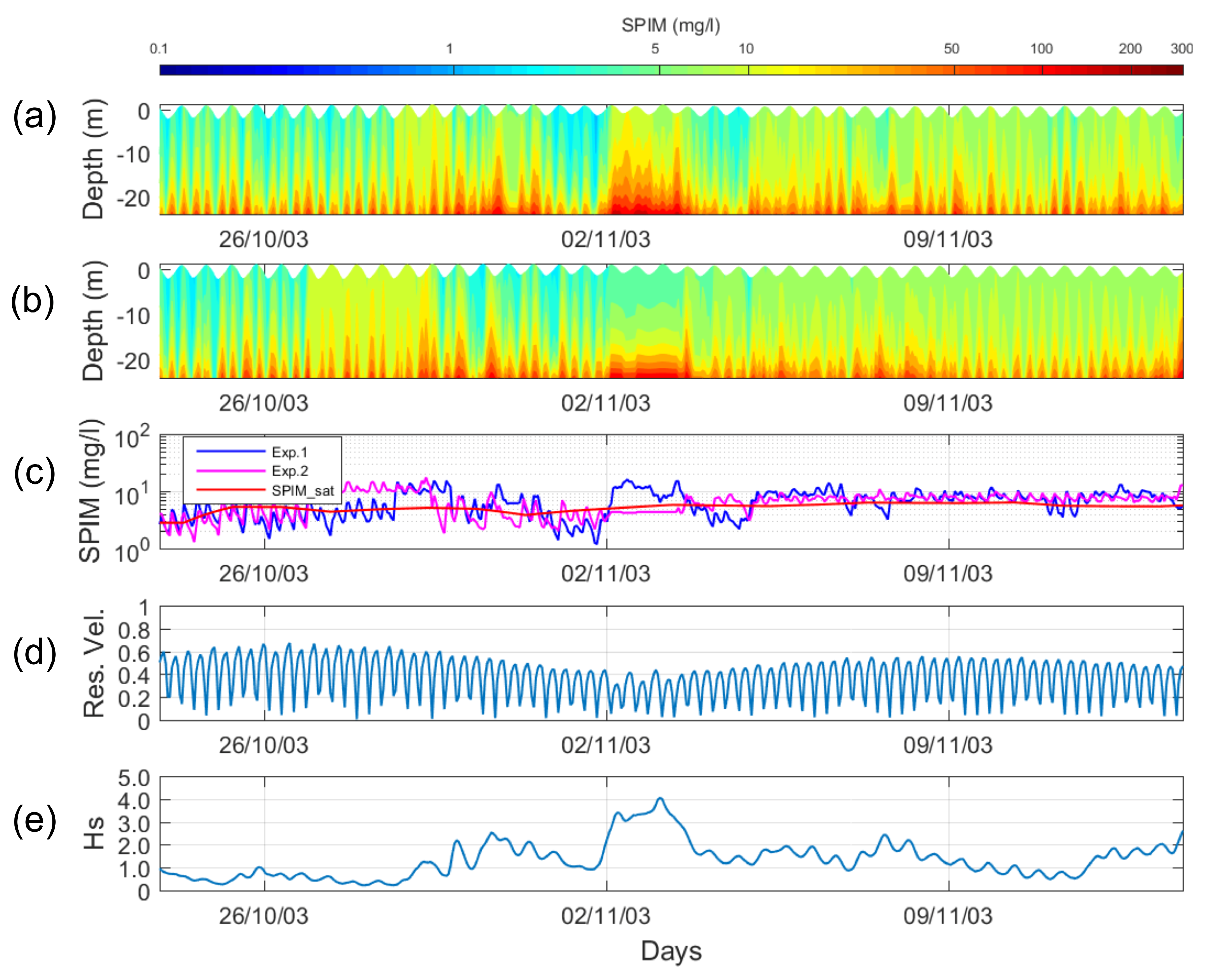
4.2.2. Experiment 2
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SPM | Suspended particulate matter |
| SOMs | Self-organizing maps |
| HMM | Hidden Markov model |
| SPIM | Suspended particulate inorganic matter |
| ROMS | Regional Ocean Modeling System |
| Normalized root-mean-square error | |
| WW3 | Wavewatch III |
| Root-mean-square error | |
| NAP | Non-algal particles |
References
- Zaneveld, J.R.V.; Pegau, W.S. Robust underwater visibility parameter. Opt. Express 2003, 11, 2997–3009. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Shang, S.; Hu, C.; Du, K.; Weidemann, A.; Hou, W.; Lin, J.; Lin, G. Secchi disk depth: A new theory and mechanistic model for underwater visibility. Remote Sens. Environ. 2015, 169, 139–149. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Pattern recognition in lithology classification: Modeling using neural networks, self-organizing maps and genetic algorithms. Hydrogeol. J. 2017, 25, 311–330. [Google Scholar] [CrossRef]
- Diesing, M.; Kroger, S.; Parker, R.; Jenkins, C.; Mason, C.; Weston, K. Predicting the standing stock of organic carbon in surface sediments of the North–West European continental shelf. Biogeochemistry 2017, 135, 183–200. [Google Scholar] [CrossRef]
- Lguensat, R.; Viet, P.H.; Sun, M.; Chen, G.; Fenglin, T.; Chapron, B.; Fablet, R. Data-Driven Interpolation of Sea Level Anomalies Using Analog Data Assimilation. Technical Report. 2017. Available online: https://hal.archives-ouvertes.fr/hal-01609851 (accessed on 22 September 2017).
- Fablet, R.; Viet, P.H.; Lguensat, R. Data-driven Models for the Spatio-Temporal Interpolation of satellite-derived SST Fields. IEEE Trans. Comput. Imaging 2017, 3, 647–657. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Ding, J. Evaluation of water quality based on a machine learning algorithm and water quality index for the Ebinur Lake Watershed, China. Sci. Rep. 2017, 7, 12858. [Google Scholar] [CrossRef] [PubMed]
- Wattelez, G.; Dupouy, C.; Lefevre, J.; Ouillon, S.; Fernandez, J.M.; Juillot, F. Application of the Support Vector Regression Method for Turbidity Assessment with MODIS on a Shallow Coral Reef Lagoon (Voh-Kone-Pouembout, New Caledonia). Water 2017, 9, 737. [Google Scholar] [CrossRef]
- Le Traon, P.Y.; Antoine, D.; Bentamy, A.; Bonekamp, H.; Breivik, L.A.; Chapron, B.; Corlett, G.; Dibarboure, G.; DiGiacomo, P.; Donlon, C.; et al. Use of satellite observations for operational oceanography: Recent achievements and future prospects. J. Oper. Oceanogr. 2015, 8 (Suppl. S1), s12–s27. [Google Scholar] [CrossRef]
- She, J.; Allen, I.; Buch, E.; Crise, A.; Johannessen, J.A.; Le Traon, P.-Y.; Lips, U.; Nolan, G.; Pinardi, N.; Reißmann, J.H.; et al. Developing European operational oceanography for Blue Growth, climate change adaptation and mitigation, and ecosystem-based management. Ocean Sci. 2016, 12, 953–976. [Google Scholar] [CrossRef]
- Ban, Y.; Marullo, S.; Eklundh, L. European Remote Sensing: Progress, challenges, and opportunities. Int. J. Remote Sens. 2017, 38, 1759–1764. [Google Scholar] [CrossRef]
- McCarthy, M.J.; Colna, K.E.; El-Mezayen, M.M.; Laureano-Rosario, A.E.; Méndez-Lázaro, P.; Otis, D.B.; Toro-Farmer, G.; Vega-Rodriguez, M.; Muller-Karger, F.E. Satellite Remote Sensing for Coastal Management: A Review of Successful Applications. Environ. Manag. 2017, 60, 323–339. [Google Scholar] [CrossRef] [PubMed]
- Sasse, T.P.; McNeil, B.I.; Abramowitz, G. A novel method for diagnosing seasonal to inter-annual surface ocean carbon dynamics from bottle data using neural networks. Biogeosciences 2013, 10, 4319. [Google Scholar] [CrossRef]
- Parard, G.; Charantonis, A.A.; Rutgerson, A. Remote sensing algorithm for sea surface CO2 in the Baltic Sea. Biogeosci. Discuss. 2014, 11, 12255–12294. [Google Scholar] [CrossRef]
- Jang, E.; Im, J.; Park, G.H.; Park, Y.G. Estimation of fugacity of carbon dioxide in the East Sea using in situ measurements and Geostationary Ocean Color Imager satellite data. Remote Sens. 2017, 9, 821. [Google Scholar] [CrossRef]
- Saulquin, B.; Fablet, R.; Ailliot, P.; Mercier, G.; Doxaran, D.; Mangin, A.; d’Andon, O.H.F. Characterization of time-varying regimes in remote sensing time series: Application to the forecasting of satellite-derived suspended matter concentrations. IEEE J. STARS 2015, 8, 406–417. [Google Scholar] [CrossRef]
- Chang, N.B.; Bai, K.; Chen, C.F. Integrating multisensor satellite data merging and image reconstruction in support of machine learning for better water quality management. J. Environ. Manag. 2017, 201, 227–240. [Google Scholar] [CrossRef] [PubMed]
- Blondeau-Patissier, D.; Gower, J.F.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef]
- Charantonis, A.A.; Badran, F.; Thiria, S. Retrieving the evolution of vertical profiles of chlorophyll-a from satellite observations, by using hidden Markov models and self-organizing maps. Remote Sens. Environ. 2015, 163, 229–239. [Google Scholar] [CrossRef]
- Krasnopolsky, V.; Nadiga, S.; Mehra, A.; Bayler, E.; Behringer, D. Neural networks technique for filling gaps in satellite measurements: Application to ocean color observations. Comput. Intell. Neurosci. 2016, 2016, 29. [Google Scholar] [CrossRef] [PubMed]
- Kwon, Y.S.; Jang, E.; Im, J.; Baek, S.H.; Park, Y.; Cho, K.H. Developing data-driven models for quantifying Cochlodinium polykrikoides using the Geostationary Ocean Color Imager (GOCI). Int. J. Remote Sens. 2018, 39, 68–83. [Google Scholar] [CrossRef]
- Gokaraju, B.; Durbha, S.S.; King, R.L.; Younan, N.H. A machine learning based spatio-temporal data mining approach for detection of harmful algal blooms in the Gulf of Mexico. IEEE J. STARS 2011, 4, 710–720. [Google Scholar] [CrossRef]
- Vilas, L.G.; Spyrakos, E.; Palenzuela, J.M.T.; Pazos, Y. Support Vector Machine-based method for predicting Pseudo-nitzschia spp. blooms in coastal waters (Galician rias, NW Spain). Prog. Oceanogr. 2014, 124, 66–77. [Google Scholar] [CrossRef]
- Li, Z.; Cassar, N. Satellite estimates of net community production based on O2/Ar observations and comparison to other estimates. Glob. Biogeochem. Cycle 2016, 30, 735–752. [Google Scholar] [CrossRef]
- Pearce, J.; Commodore, A.; Neelon, B.; Boaz, R.; Bozigar, M.; Wilson, S.; Svendsen, E. A novel approach for characterizing neighborhood-level trends in particulate matter using concentration and size fraction distributions: A case study in Charleston, SC. Air Qual. Atmos. Health 2017, 1–12. [Google Scholar] [CrossRef]
- Guillou, N.; Rivier, A.; Gohin, F.; Chapalain, G. Modeling Near-Surface Suspended Sediment Concentration in the English Channel. J. Mar. Sci. Eng. 2015, 3, 193–215. [Google Scholar] [CrossRef]
- Desprez, M. Physical and biological impact of marine aggregate extraction along the French coast of the Eastern English Channel:short-and long-term post-dredging restoration. ICES J. Mar. Sci. 2000, 57, 1428–1438. [Google Scholar] [CrossRef]
- Seuront, L.; Schmitt, F.G. Multiscaling statistical procedures for the exploration of biophysical couplings in intermittent turbulence.PartII.Applications. Deep Sea Res. II 2005, 52, 1325–1343. [Google Scholar] [CrossRef]
- Korotenko, K.A.; Sentchev, A.V.; Schmitt, F.G. Effect of variable winds on current structure and Reynolds stresses in a tidal flow: Analysis of experimental data in the eastern English Channel. Ocean Sci. 2012, 8, 1025–1040. [Google Scholar] [CrossRef]
- Renosh, P.R.; Schmitt, F.G.; Loisel, H.; Sentchev, A.; Mériaux, X. High frequency variability of particle size distribution and its dependency on turbulence over the sea bottom during re-suspension processes. Cont. Shelf Res. 2014, 77, 51–60. [Google Scholar] [CrossRef]
- Renosh, P.R.; Schmitt, F.G.; Loisel, H. Intermittent particle dynamics in marine coastal waters. Nonlinear Process. Geophys. 2015, 22, 633–643. [Google Scholar] [CrossRef]
- Velegrakis, A.F.; Michel, D.; Collins, M.B.; Lafite, R.; Oikonomou, E.K.; Dupont, J.P.; Bishop, C. Sources, sinks and resuspension of suspended particulate matter in the eastern English Channel. Cont. Shelf Res. 1999, 19, 1933–1957. [Google Scholar] [CrossRef]
- Guillou, N.; Rivier, A.; Chapalain, G.; Gohin, F. The impact of tides and waves on near-surface suspended sediment concentrations in the English Channel. Oceanologia 2017, 59, 28–36. [Google Scholar] [CrossRef]
- Rivier, A.; Gohin, F.; Bryére, P.; Petus, C.; Guillou, N.; Chapalain, G. Observed vs. predicted variability in non-algal suspended particulate matter concentration in the English Channel in relation to tides and waves. Geo-Mar. Lett. 2012, 32, 139–151. [Google Scholar] [CrossRef]
- Biscara, L.; Schmitt, T.; Corréard, S.; Creach, R. Modèles numériques de bathymétrie pour la prévision Hydrodynamique du dispositif vigilance vagues-submersions. In Proceedings of the Actes des XIIIèmes Journées Nationales Génie Côtier—Génie Civil, Dunkerque, France, 2–4 July 2014; Volume 155, pp. 2–4. [Google Scholar]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Viterbi, A. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans. Inf. Theory 1967, 13, 260–269. [Google Scholar] [CrossRef]
- Haigh, I.; Nicholls, R.; Wells, N. Rising sea levels in the English Channel 1900 to 2100. Proc. Inst. Civil Eng. Mar. Eng. 2010, 164, 81–92. [Google Scholar] [CrossRef]
- Wadey, M.P.; Nicholls, R.J.; Haigh, I. Understanding a coastal flood event: The 10th March 2008 storm surge event in the Solent, UK. Nat. Hazards 2013, 67, 829–854. [Google Scholar] [CrossRef]
- Soulsby, R.L.; Hamm, L.; Klopman, G.; Myrhaug, D.; Simons, R.R.; Thomas, G.P. Wave-current interaction within and outside the bottom boundary layer. Coast. Eng. 1993, 21, 41–69. [Google Scholar] [CrossRef]
- Roland, A.; Cucco, A.; Ferrarin, C.; Hsu, T.W.; Liau, J.M.; Ou, S.H.; Umgiesser, G.; Zanke, U. On the development and verification of 2-D coupled wave-current model on unstructured meshes. J. Mar. Syst. 2009, 78, S244–S254. [Google Scholar]
- Levier, B.; Benkiran, M.; Reffray, G.; Sotillo, M. IBIRYS: A Regional High Resolution Reanalysis (Physical and Biogeochemical) over the European North East Shelf; EGU: München, Germany, 2014. [Google Scholar]
- Madec, G. NEMO Ocean General Circulation Model Reference Manuel; Internal Report; LODYC/IPSL: Paris, France, 2008. [Google Scholar]
- Sotillo, M.G.; Cailleau, S.; Lorente, P.; Levier, B.; Aznar, R.; Reffray, G.; AmoBaladrón, A.; Chanut, J.; Benkiran, M.; Alvarez-Fanjul, E. The MyOcean IBI Ocean Forecast and Reanalysis Systems: Operational products and roadmap to the future Copernicus Service. J. Oper. Oceanogr. 2008, 8, 63–79. [Google Scholar] [CrossRef]
- Gohin, F.; Loyer, S.; Lunven, M.; Labry, C.; Froidefond, J.M.; Delmas, D.; Huret, M.; Herbland, A. Satellite-derived parameters for biological modelling in coastal waters: Illustration over the eastern continental shelf of the Bay of Biscay. Remote Sens. Environ. 2005, 95, 29–46. [Google Scholar] [CrossRef]
- Gohin, F. Annual cycles of chlorophyll-a, non-algal suspended particulate matter, and turbidity observed from space and in-situ in coastal waters. Ocean Sci. 2011, 7, 705–732. [Google Scholar] [CrossRef]
- Jafar-Sidik, M.; Gohin, F.; Bowers, D.; Howarth, J.; Hull, T. The relationship between Suspended Particulate Matter and Turbidity at a mooring station in a coastal environment: Consequences for satellite-derived products. Oceanologia 2017, 59, 365–378. [Google Scholar] [CrossRef]
- Gohin, F.; Druon, J.N.; Lampert, L. A five channel chlorophyll concentration algorithm applied to SeaWiFS data processed by SeaDAS in coastal waters. Int. J. Remote Sens. 2002, 23, 1639–1661. [Google Scholar] [CrossRef]
- Saulquin, B.; Gohin, F.; Garrello, R. Regional Objective Analysis for Merging High-Resolution MERIS, MODIS/Aqua, and SeaWiFS Chlorophyll-a Data from 1998 to 2008 on the European Atlantic Shelf. IEEE Trans. Geosci. Remote Sens. 2011, 49, 143–154. [Google Scholar] [CrossRef]
- Ruddick, K.; Neukermans, G.; Vanhellemont, Q.; Jolivet, D. Challenges and opportunities for geostationary ocean colour remote sensing of regional seas: A review of recent results. Remote Sens. Environ. 2014, 146, 63–76. [Google Scholar] [CrossRef]
- Liu, X.; Wang, M. Analysis of ocean diurnal variations from the Korean Geostationary Ocean Color Imager measurements using the DINEOF method. Estuar. Coast. Shelf Sci. 2016, 180, 230–241. [Google Scholar] [CrossRef]



| Sand Type | Diameter Range (m) | Mean Diameter (m) |
|---|---|---|
| Sand1 | 0–50 | 25 |
| Sand2 | 50–100 | 75 |
| Sand3 | 100–200 | 150 |
| Sand4 | 200–500 | 350 |
| Sand5 | 500–1000 | 750 |
| Sand6 | 1000–2000 | 1500 |
| M1 | M2 | M3 | M4 | |
|---|---|---|---|---|
| range (mg/L) | 0.05–9.26 | 0.13–7.85 | 0.38–274 | 0.04–14.76 |
| Mean/Bias (mg/L) | 0.57 | 0.17 | ||
| Standard deviation (mg/L) | 1.00 | 1.22 | 13.18 | 1.11 |
| Median (mg/L) | 0.54 | 0.03 | 0.36 | |
| Median absolute deviation (mg/L) | 0.56 | 0.83 | 2.21 | 0.53 |
| Root-mean-square error (mg/L) | 1.15 | 1.22 | 13.37 | 1.12 |
| Normalized root-mean-square error (%) | 12.53 | 15.85 | 4.88 | 7.60 |
| Experiment | Different Error Estimators | M1 | M2 | M3 | M4 |
|---|---|---|---|---|---|
| Exp. 1 | Root-mean-square error (mg/L) | 1.43 | 1.25 | 5.10 | 1.68 |
| Exp. 1 | Normalized root-mean-square error (%) | 1.67 | 1.51 | 1.50 | 1.93 |
| Exp. 2 | Root-mean-square error (mg/L) | 1.92 | 1.47 | 5.75 | 1.39 |
| Exp. 2 | Normalized root-mean-square error (%) | 2.24 | 1.77 | 1.70 | 1.60 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Renosh, P.R.; Jourdin, F.; Charantonis, A.A.; Yala, K.; Rivier, A.; Badran, F.; Thiria, S.; Guillou, N.; Leckler, F.; Gohin, F.; et al. Construction of Multi-Year Time-Series Profiles of Suspended Particulate Inorganic Matter Concentrations Using Machine Learning Approach. Remote Sens. 2017, 9, 1320. https://doi.org/10.3390/rs9121320
Renosh PR, Jourdin F, Charantonis AA, Yala K, Rivier A, Badran F, Thiria S, Guillou N, Leckler F, Gohin F, et al. Construction of Multi-Year Time-Series Profiles of Suspended Particulate Inorganic Matter Concentrations Using Machine Learning Approach. Remote Sensing. 2017; 9(12):1320. https://doi.org/10.3390/rs9121320
Chicago/Turabian StyleRenosh, Pannimpullath R., Frédéric Jourdin, Anastase A. Charantonis, Khalil Yala, Aurélie Rivier, Fouad Badran, Sylvie Thiria, Nicolas Guillou, Fabien Leckler, Francis Gohin, and et al. 2017. "Construction of Multi-Year Time-Series Profiles of Suspended Particulate Inorganic Matter Concentrations Using Machine Learning Approach" Remote Sensing 9, no. 12: 1320. https://doi.org/10.3390/rs9121320
APA StyleRenosh, P. R., Jourdin, F., Charantonis, A. A., Yala, K., Rivier, A., Badran, F., Thiria, S., Guillou, N., Leckler, F., Gohin, F., & Garlan, T. (2017). Construction of Multi-Year Time-Series Profiles of Suspended Particulate Inorganic Matter Concentrations Using Machine Learning Approach. Remote Sensing, 9(12), 1320. https://doi.org/10.3390/rs9121320









