Abstract
Phytoplankton pigments absorb sunlight for photosynthesis, protect the chloroplast from damage caused by excess light energy, and influence the color of the water. Some pigments act as bio-markers and are important for separation of phytoplankton functional types. Among many efforts that have been made to obtain information on phytoplankton pigments from bio-optical properties, Gaussian curves decomposed from phytoplankton absorption spectrum have been used to represent the light absorption of different pigments. We incorporated the Gaussian scheme into a semi-analytical model and obtained the Gaussian curves from remote sensing reflectance. In this study, a series of sensitivity tests were conducted to explore the potential of obtaining the Gaussian curves from multi-spectral satellite remote sensing. Results showed that the Gaussian curves can be retrieved with 35% or less mean unbiased absolute percentage differences from MEdium Resolution Imaging Spectrometer (MERIS) and Moderate Resolution Imaging Spectroradiometer (MODIS)-like sensors. Further, using Lake Erie as an example, the spatial distribution of chlorophyll a and phycocyanin concentrations were obtained from the Gaussian curves and used as metrics for the spatial extent of an intense cyanobacterial bloom occurred in Lake Erie in 2014. The seasonal variations of Gaussian absorption properties in 2011 were further obtained from MERIS imagery. This study shows that it is feasible to obtain Gaussian curves from multi-spectral satellite remote sensing data, and the obtained chlorophyll a and phycocyanin concentrations from these Gaussian peak heights demonstrated potential application to monitor harmful algal blooms (HABs) and identification of phytoplankton groups from satellite ocean color remote sensing semi-analytically.
1. Introduction
Spectral light absorption and backscattering are the two inherent optical properties directly controlling the light field in water and further influencing water color. Optical properties of phytoplankton, specifically the absorption coefficients of the pigments inside them, play a key role in determining both the penetration of radiant energy in water and the use of this radiant energy for photosynthesis. These pigment absorption coefficients and their concentrations are important for understanding photosynthetic rate [1,2], identifying and quantifying phytoplankton functional groups [3] and determining size class distributions ([4,5] and references therein). These properties of phytoplankton and their associated backscattering, along with colored dissolved organic matter absorption and non-algal particle absorption and scattering directly control the light field of water.
With the objective of expanding the ability to detect more pigments than just chlorophyll a, various methods have been proposed [6,7,8]. Most of these methods could obtain one or more pigments in addition to chlorophyll a from Rrs(λ), but the accuracy was influenced by the presence of non-algal particles and dissolved organic matters in the water column. To reduce the influence from components other than phytoplankton, Wang et al. [9] developed a multi-pigment inversion model (MuPI) to obtain information of multiple pigments from hyperspectral Rrs(λ). This model incorporated a Gaussian decomposition scheme into a semi-analytical inversion model and demonstrated that 13 Gaussian curves that contain important phytoplankton pigment information can be retrieved from hyperspectral remote sensing reflectance. The Gaussian scheme was first described by Hoepffner and Sathyendranath [10,11], and was one of the methods proposed to obtain multiple pigments from phytoplankton absorption coefficients [12,13,14,15,16,17]. Hoepffner and Sathyendranath [10] used these Gaussian curves to represent light absorption of different pigments and demonstrated that some of the Gaussian peak heights showed good relationships with phytoplankton pigments, such as peaks at 435 and 675 nm for chlorophyll a, peaks at 643 nm for chlorophyll c, peaks at 460 and 655 nm for chlorophyll b, and peaks at 489 and 582 nm for carotenoids. This Gaussian decomposition scheme sheds light on the potential of obtaining information for multiple phytoplankton pigments beyond chlorophyll a semi-analytically using bio-optical techniques.
Most of the past and current operational ocean color satellite missions are multispectral. It is thus necessary to evaluate the viability and associated uncertainties of obtaining these Gaussian curves from multi-spectral remote sensing data. Using measurements from cyanobacteria bloom waters in different regions, we validated the MuPI performance in obtaining multiple independent Gaussian curves, and the sensitivity of MuPI to the specific spectral bands of existing ocean color satellite sensors. Further, the inversion scheme was applied to Hyperspectral Imager for the Coastal Ocean (HICO), and Moderate Resolution Imaging Spectroradiometer aboard the Aqua satellite (MODIS-Aqua), and MEdium Resolution Imaging Spectrometer (MERIS) imagery over Lake Erie to obtain the spatial distributions of pigment absorption coefficients, chlorophyll a (Chl-a) and phycocyanin (PC) for a cyanobacteria bloom event in the western basin of Lake Erie.
2. Materials and Methods
2.1. In Situ Measurements
2.1.1. Study Areas
The in situ measurements were obtained from different areas at different seasons around the world, which include ponds in the state of Mississippi, U.S.A. (MS), Lake Taihu, China (LT), and Lake Erie, U.S.A. (LE).
Mississippi Pond dataset (MS): This dataset includes 41 samples of remote sensing reflectance (Rrs(λ), sr−1) and absorption coefficients of phytoplankton (aph(λ), m−1), non-algal particles (ad(λ)), and gelbstoff (ag(λ)). This dataset (see Mishra et al. [18] for details) was collected from a series of highly turbid and productive aquaculture ponds at various bloom stages (initiation, peak, and senescence) of cyanobacteria (Chl-a concentration varied from 59 to 1377 mg∙m−3), located in northwestern Mississippi, U.S.A., where cyanobacteria blooms with Planktothrix agardhii as the most abundant species were occurring when the in situ data were collected
Lake Taihu dataset (LT): This dataset includes 45 Rrs(λ) spectra, corresponding spectra of ad(λ), ag(λ), and aph(λ) (350–750 nm) collected from Lake Taihu, China under cyanobacteria bloom conditions (Chl-a: 10–222 mg·m−3) where the dominant species was Microcystis aeruginosa. Water samples and optical data of surface water were collected during two surveys in January–August 2011 and November 2011, respectively.
Lake Erie dataset (LE): This dataset is composed of 36 Rrs(λ), ad(λ), ag(λ), and aph(λ) samples, and 20 Chl-a and PC concentrations. Cyanobacteria blooms dominated by Microcystis aeruginosa have been seasonally reoccurring in the western basin of Lake Erie since the mid-1990s [19]. The field measurements were collected during cruises from 20–23 August 2013 and 18–21 August 2014 in western Lake Erie at 16 and 20 stations, respectively, during the peak cyanobacteria bloom period [20,21], with chlorophyll concentrations ranging from >1 to 100 s of mg·m−3.
Since the ponds are too small for the MODIS and MERIS 1 km spatial resolution imagery, Lake Erie was selected as a local example for application of the method to HICO, MODIS and MERIS imageries to obtain pigment concentrations and Gaussian absorption distribution. The cyanobacteria bloom which occurred in Lake Erie in August 2014 was one of the most serious, causing disruption to the drinking water supply in Toledo, U.S.A. The 2014 cruise was conducted during this event and the sampling locations along with the Chl-a and PC concentrations at each station, are shown in Figure 1, where PC concentrations as high as ~200 mg∙m−3 were noted in the southern portion of Lake Erie.
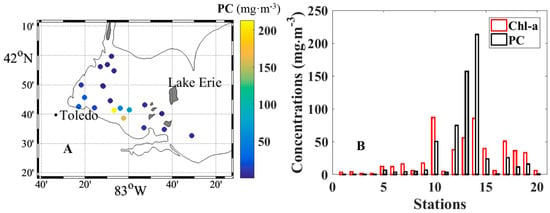
Figure 1.
(A) Sampling locations in the western basin of Lake Erie with different colors reflecting the different phycocyanin (PC) concentrations. (B) The bar chart shows the chlorophyll a (Chl-a) and phycocyanin (PC) concentrations of each station.
2.1.2. Remote Sensing Reflectance
The remote sensing reflectance of the MS dataset was acquired in the range of 400–900 nm with a sampling interval of 0.3 nm by deploying a dual sensor system with two inter-calibrated ocean optics spectroradiometers (Ocean Optics Inc., Dunedin, FL, USA). The in situ Rrs(λ) from LT and LE were measured with a hand-held ASD spectroradiometer (Analytical Spectral Device, Inc. Boulder, Colorado, U.S.A.), from 350 to 1050 nm at 1.4 nm intervals.
2.1.3. Absorption Coefficients
Surface water samples were collected and filtered immediately after the Rrs(λ) measurements and analyzed on the same day in the laboratory. The particulate absorption coefficient was quantified utilizing the transmittance or transmittance/reflectance method of Tassan and Ferrari [22] along with the NASA Ocean Optics Protocols, Revision 4, Volume IV protocol [23]. Percent transmittance and reflectance were measured for each sample filter to calculate the particulate absorption spectrum. Filters were then bleached, and the transmittance and reflectance measured to calculate the absorption coefficients of non-algal particles. The phytoplankton absorption coefficients (aph(λ)) at each station were calculated by subtraction of non-algal particle absorption coefficients from total particle absorption coefficients. The Gaussian peak heights (aGau(λ)) were obtained from aph(λ) using the Gaussian decomposition scheme described in Wang et al. [9], which used a least-square curve fitting technique in Matlab to obtain the aGau(λ). These aGau(λ) were used as ground truth to validate the outputs from Rrs(λ) inversions.
For the MS dataset, a Perkin Elmer Lambda 850 Spectrophotometer (Perkin Elmer Inc., Waltham, MA, USA) was used to measure the absorption coefficient of phytoplankton, detrital matter, and gelbstoff in the 380–750 nm range at 1 nm spectral resolution. Detailed information regarding the environmental characteristics and measurement methods can be found in Mishra et al. [18]. A Shimadzu UV-2401 Spectrophotometer was used for LT. More information about LT and details about water sample collection, measurement protocols, and processing methods can be found in Duan et al. [24] and Ma et al. [25]. Samples from LE were measured with a Perkin-Elmer Lambda 35 UV/Vis Dual-beam Spectrophotometer from 300–800 nm at 1 nm resolution as described in Mouw et al. [26].
2.1.4. Pigment Concentrations and Group Composition
Water samples for Chl-a and PC concentration from Lake Erie were filtered through 0.7 and 0.2 μm glass fiber filters (Whatman GF/F, 25-mm and 47-mm diameter), respectively. The Chl-a was estimated using a Turner Designs 10-AU Fluorometer in the laboratory following the NASA Ocean Optics Protocols, Revision 5, Volume V [23]. Following NASA protocols [27], filters for phycocyanin concentration determination were extracted in phosphate buffer (Ricca Chemical, Arlington, Texas, U.S.A., pH 6.8) using two freeze-thaw cycles, followed by sonication. The concentration of PC was estimated from the relative fluorescence measured using a Turner Aquafluor fluorometer [21]. Phytoplankton populations for the Lake Erie stations in 2013 were also used in this study which were identified and counted using standard light microscopy [21].
2.2. Satellite Imagery
The Hyperspectral Imager for the Coastal Ocean (HICO) was the first space-borne hyperspectral imaging spectrometer designed to sample the coastal ocean. HICO covered selected coastal regions at 90 m spatial resolution with full spectral coverage (380 to 960 nm sampled at 5.73 nm intervals). HICO imagery of the same time frame as in situ measurements in Lake Erie in 2014 was downloaded from the Oregon State University website (http://hico.coas.oregonstate.edu/), and following the steps provided on the website the level 1B (L1B) imagery was atmospherically corrected to level 2 (L2) data using the online version of Tafkaa_6s model, followed by georectification. The HICO Rrs(λ) data have about the same spectral resolution as the in situ measured reflectance (5.73 nm for HICO and 5 nm for original Rrs(λ)). These data were used as an example for MuPI application in hyperspectral satellite imagery.
The Moderate Resolution Imaging Spectroradiometer onboard the Aqua satellite (MODIS-Aqua) launched in 2002 is one of the contemporary satellite ocean color missions. The L1B imagery with 1 km spatial resolution was downloaded from the National Aeronautics and Space Administration (NASA) website (https://ladsweb.nascom.nasa.gov/). The L2 imagery (with 748 nm included in Rrs(λ)) from the same time frame as in situ measurements in Lake Erie in 2014 was obtained using the data processing L2gen from the SeaWiFS Data Analysis System (SeaDAS) software using the standard near infrared (NIR) scheme [28,29,30] for atmospheric correction. MODIS imagery was used as an example of MuPI application to multi-spectral satellite remote sensing data.
MEdium Resolution Imaging Spectrometer (MERIS) on board the European Space Agency’s Envisat platform, was launched in 2002 and ended its mission in May 2012. The L3 seasonal composed imagery and L2 reduced resolution imagery (1 km spatial resolution) was obtained from NASA ocean color website (https://oceancolor.gsfc.nasa.gov/). Lacking coincidence with in situ measurements, the same day imagery of MODIS and MERIS on 3 September 2011 was used for the comparison of the retrieving results. The MERIS seasonal composed imagery in Lake Erie was used to obtain a general seasonal variation of Gaussian absorption coefficients.
2.3. The aGau(λ) Estimation
2.3.1. MuPI Model
To obtain aGau(λ) from remote sensing reflectance, a multi-pigment inversion method [9] was used. The corresponding functions used in this method are included in Table 1. In this method, the Gaussian scheme, which uses 13 Gaussian curves to reconstruct the spectrum of phytoplankton absorption coefficient, was incorporated into the relationship in which Rrs(λ) is a function of total spectral absorption (a(λ)) and backscattering (bb(λ)) coefficients [31,32]. With an Rrs(λ) spectrum as the only input, the function was solved with a spectral optimization method which returns the values of unknowns (aGau(λ), absorption of non-algal particles and gelbstoff: adg(λ), and backscattering coefficient of particles, bbp(λ)), that minimizes the difference between the estimated and input Rrs(λ) spectra. A summarized flowchart of the method is shown in Figure 2. The parameters used for the 13 Gaussian curves in this study are shown in Table 2, which includes the peak locations, widths and empirical relationships between the peak heights.

Table 1.
Summary of the functions and symbols used in multi-pigment inversion model (MuPI).
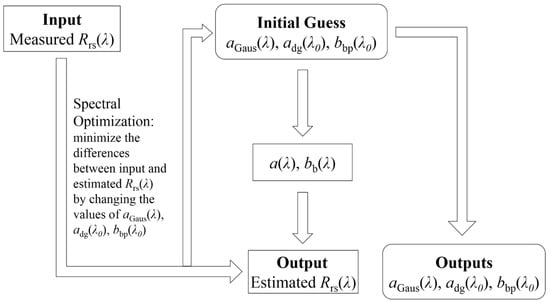
Figure 2.
Flowchart of the inversion method. Utilizing satellite or in situ measured remote sensing reflectance (Rrs(λ)), a spectral optimization method is used to minimize the differences between estimated and measured Rrs(λ) spectra, output values for Gaussian curves (aGau(λ)), non-algal particles and gelbstoff (adg(λ)) and particulate attenuation coefficients (cp) are obtained.

Table 2.
The Gaussian curve peak locations, widths (σ = FWHM/2.35) and the corresponding power-law relationships among the peak heights. The peak heights of the Gaussian curves located at 386.6, 414, 451.7, 484, 515.6, and 677 nm can be estimated from the peak height of the Gaussian curve centered at 435 nm (annotated as x1), those of 548.8, 584.4, 653, and 693.5 nm can be estimated from the peak height at 617.6 nm (x2).
2.3.2. Gaussian Parameters
As with other semi-analytical algorithms (e.g., HOPE [38]; GSM [40], GIOP [36]), aGau(λ) in MuPI were retrieved using a spectral optimization method. The Gaussian scheme used in MuPI plays a critical role in aGau(λ) estimation, and the Gaussian peak heights, locations, and widths are very important factors in the Gaussian scheme. To determine the peak locations and widths of the Gaussian curves, the peaks and troughs of aph(λ) spectra were used as the initial inputs in the optimization process. As shown in Table 2 and Figure 3, a total of 13 Gaussian curves, corresponding to peaks or shoulders of measured aph(λ) spectra, were used to represent the absorption of phytoplankton pigments at different wavelengths: chlorophyll a: 386.6, 414, 435, 677, and 693.5 nm; chlorophyll b: 653 nm; chlorophyll c: 451.7, 584.4, and 636 nm; carotenoids: 484 and 515.6 nm; phycoerythrin: 548.8 nm; and phycocyanin: 617.6 nm. These peak locations and widths (the second and third columns of Table 2) were potentially influenced by pigment composition. Upon further analysis, we found that using fixed values for peak locations and widths in Table 2 cause no more than 5% differences in aph(λ) estimation versus when these peak locations and widths were set as free variables. Comparatively, the peak height of Gaussian curves influenced by pigment concentrations play a critical role in aph(λ) estimation. Thus, in the MuPI method, the peak locations and widths presented in Table 2 were fixed as constants, and the peak heights of these 13 Gaussian curves, containing bio-optical information of phytoplankton pigments, are the parameters to be obtained from remote sensing reflectance.
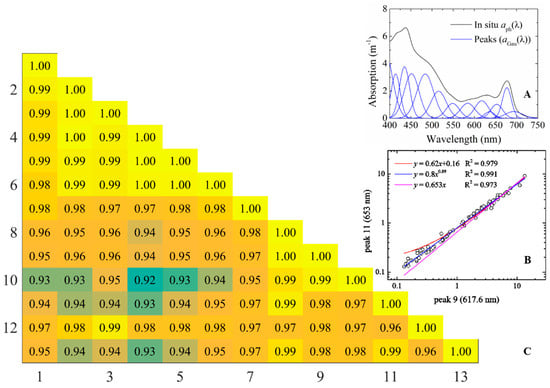
Figure 3.
(A) Example of in situ aph(λ) and corresponding decomposed aGau(λ); (B) The scatter plot shows different functions between peak magnitudes (aGau(λ)) and the corresponding R2; (C) Correlation matrix shows the co-variances among peaks (R2).
It is impractical to retrieve 13 peaks simultaneously from an Rrs(λ) spectrum via spectral optimization because more variables in the function usually means much higher uncertainties in the outputs. In determining the number of independent aGau(λ) to be retrieved from the MuPI model, a series of tests were conducted, and the mean, median, maximum and minimum unbiased absolute percentage difference (UAPDs, Equation (1)) were compared for different datasets when the number of independent aGau(λ) vary among 13, 5 (Peak 2, 5, 7, 9 and 12), 3 (Peak 3, 5 and 9) and 2 (Peak 3 and Peak 9). The combinations of independent aGau(λ) were determined based on the highest correlation coefficients (R2) with other aGau(λ). As expected, an obvious decrease in the percentage differences are noticed when the number of independent aGau(λ) are reduced from 13 to 2 for all three in situ datasets, as shown in Table 3, although the retrieval accuracy varies from dataset to dataset because of the different contributions of phytoplankton to the total absorption (100% × aph(λ)/a(λ), Figure 4). Thus the height of two peaks, here aGau(435) and aGau(617.6), instead of 13, were retrieved as free variables from an Rrs(λ) spectrum to achieve the highest retrieval accuracy from MuPI. This also controls the number of unknowns in the model to maximize its application to different satellite remote sensing data and improve computation efficiencies.
where Ŝ is the estimated value and S is the measured value.

Table 3.
The mean (Mea.), median (Med.), maximum (Max.) and Minimum (Min.) UAPD of different dataset with different number of unknowns (N) to be retrieved from MuPI.
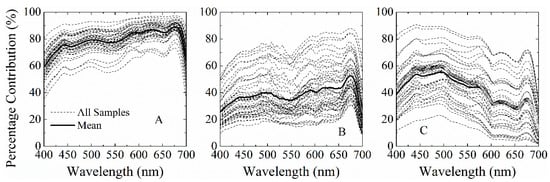
Figure 4.
Percent contribution of phytoplankton absorption coefficients (aph(λ)) to the total absorption coefficient (a(λ) = aw(λ) + adg(λ) + aph(λ), with aw(λ) and adg(λ) as the absorption coefficients of pure seawater and non-algal particles and gelbstoff) for three datasets (all the samples and their mean values): (A) Mississippi ponds (MS); (B) Lake Taihu (LT); and (C) Lake Erie (LE).
Once aGau(435) and aGau(617.6) were obtained from Rrs(λ), the other peaks could be estimated from these two values through a set of relationships shown in Table 2. Whether these relationships can represent data from different regions over different seasons presents uncertainty and a potential error source for aGau(λ) retrieval from MuPI. In our analysis of three datasets, we found that the empirical relationships among aGau(λ) to be very stable. The data from different regions over different seasons follow the trend predicted by the regression line based on one dataset. Figure 5 shows two examples in which all the data points from different datasets scattered tightly around the regression lines.
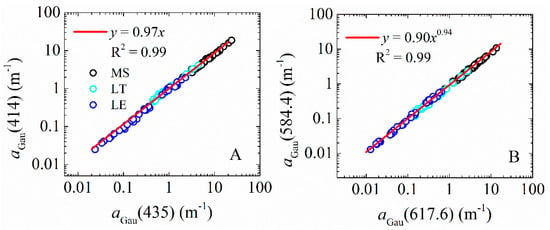
Figure 5.
Example of empirical relationships among aGau(λ) for three different datasets with MS in black, LT in light blue and LE in dark blue: (A) linear relationship between aGau(414) and aGau(435); and (B) power-law relationship between aGau(584.4) and aGau(617.6).
In contrast with the parameters determined in Wang et al. [9], to reduce potential errors updates were made in this study regarding the independent peak heights and their empirical relationships with other peaks. These modifications were made for the following reasons: (1) when further checking the co-variances among aGau(λ) from the MS and LT datasets, it was found that, sometimes, power-law relationships among the peak heights were more robust and representative than the previously adopted linear relationships (Figure 3); and (2) to make the retrievals more meaningful, aGau(435) and aGau(617.6) instead of aGau(515.6) and aGau(584.4) were used as the two independent variables. This change was made because aGau(435) showed a robust relationship with chlorophyll a concentration, and aGau(617.6) with phycocyanin. Further, their absorption coefficients or concentrations directly retrieved from Rrs(λ) can be more widely used in the estimation of phytoplankton biomass, productivity and cyanobacteria bloom detection and monitoring. Further, because of the high co-variation among the peak heights (R2 > 0.92), the selection of different peaks as free variables caused no more than 10% difference in the retrieved results.
2.4. aGau(λ) Spectra Shape
In exploring the aGau(λ) application in HABs detection, a spectral shape analysis was conducted, in which aGau(435), aGau(584.4), and aGau(617.6) were normalized by their respective root of sum of squares,
where the index N represents the total number of wavelengths, and λi corresponds to the wavelengths of 435, 584.4 and 617.6 nm. The naGau(λ) spectra vary over the range between 0 and 1, while it retains the “shapes” pertaining to the original aGau(λ) spectra, i.e., the band ratios of naGau(λ) retain the same as aGau(λ).
2.5. Multi-Spectral Rrs(λ)
To characterize the model performance with multi-spectral Rrs(λ) data as inputs, a set of different spectral band configurations were used (Table 4). This included the existing sensors of Ocean and Land Color Instrument (OLCI), MERIS, MODIS, Visible Infrared Imaging Radiometer Suite (VIIRS), Sentinal-2 Multispectral Instrument (MSI), Landsat-8 Operational Land Imager (OLI) and an All-band configuration that combined all of the existing spectral bands of the different sensors. The inclusion of the All-band configuration was intended to test the sensitivity of the algorithm to specific spectral bands of the existing sensors. The Rrs(λ) of these multiple spectral bands were obtained by applying their spectral response functions (RSF) (https://oceancolor.gsfc.nasa.gov/docs/rsr/rsr_tables/, https://earth.esa.int/web/sentinel/user-guides/sentinel-2-msi/document-library/-/asset_publisher/Wk0TKajiISaR/content/sentinel-2a-spectral-responses) to the in situ hyperspectral data.

Table 4.
The multi-spectral bands used in this study: a composed All-band, OLCI, MERIS, MODIS, VIIRS, MSI and OLI bands.
3. Results
3.1. aGau(λ) from Multi-Spectral Rrs(λ)
The MuPI performance was validated for multi-spectral Rrs(λ) at six different band configurations. Table 5 shows the mean UAPD of 13 aGau(λ) for all three in situ datasets with the spectral bands of different sensors, respectively. Table 6 provides detailed information for LE 2014 data regarding the variation of the mean UAPD in the aGau(λ) retrieval with Rrs(λ) at different spectral configurations. OLCI and MERIS produced similar mean UAPD, which is around 35% for all three datasets and 28% for the LE 2014 data. Compared with MODIS, VIIRS showed slightly higher mean UAPD (All data: VIIRS: 36%, MODIS: 34%; LE 2014: VIIRS: ≤40%, MODIS: ≤37%), which is potentially caused by the lack of a spectral band around 665 nm in VIIRS. MSI and OLI produced the highest uncertainties for aGau(λ) at wavelength longer than 550 nm, but, surprisingly, a ≤50% mean UAPD was achieved for the four spectral bands of the Landsat-8 OLI sensor with the data used here, which demonstrates the potential of applying MuPI to these high spatial resolution satellite remote sensing data.

Table 5.
The mean (Mea.), median (Med.), maximum (Max.), and minimum (Min.) of unbiased absolute percentage differences (UAPD, %) of aGau(λ) estimated from Rrs(λ) with the spectral bands of different sensors for the MS, LT and LE datasets. MERIS+745: MERIS with the 745 nm band; MODIS-645/748: MODIS bands without 645 or 748 nm band.

Table 6.
For LE 2014: The unbiased absolute percentage differences (UAPD, %) of aGau(λ) estimated from Rrs(λ) with the original hyperspectral bands and those at different spectral configuration. P1–P13: 13 Gaussian peaks. MERIS+745: MERIS with the 745 nm band; MODIS-645/748: MODIS bands without 645 or 748 nm band.
By removing and adding specific bands such as 645 and 748 nm for MODIS, and 754 nm in MERIS, differences in the aGau(λ) accuracy were observed. A 10% increase in mean UAPD was observed when the 748 nm band was removed from MODIS, and a 3% decrease in the mean UAPD when adding the 745 nm band to MERIS. However, with the existence of the 748 nm band, the adding and removing of the 645 nm band did not show a large influence (<3% mean UAPD variation). In addition, due to the existence of the 746 nm band in VIIRS, reasonable results were obtained in aGau(λ) retrievals.
Such a result suggests, at least for this dataset of bloom waters, with MuPI there is little impact on the retrieval of aGau(λ) when hyperspectral Rrs(λ) is degraded to multiple-spectral measurements such as MERIS and MODIS-like sensors. This is consistent with conclusions from previous studies that Rrs(λ) data do not need to be as fine as 1 nm in spectral resolution to obtain reliable retrievals of inherent optical properties [41,42,43].
When taking a closer look at the results from the LE 2014 data (Table 6, Figure 6), a mean UAPD of ≤35% was achieved for most of aGau(λ) from Rrs(λ) with MERIS, OLCI, and MODIS bands. The relatively low contributions of phytoplankton absorption coefficients at longer wavelengths was the main reason for the relatively larger uncertainties (e.g., aGau(λ) at 653 nm: ~36% for MODIS and MERIS). In addition, the lack of enough bands between 570 and 660 nm (only 620 nm for MERIS and 645 nm for MODIS) made it difficult to obtain more accurate retrievals.
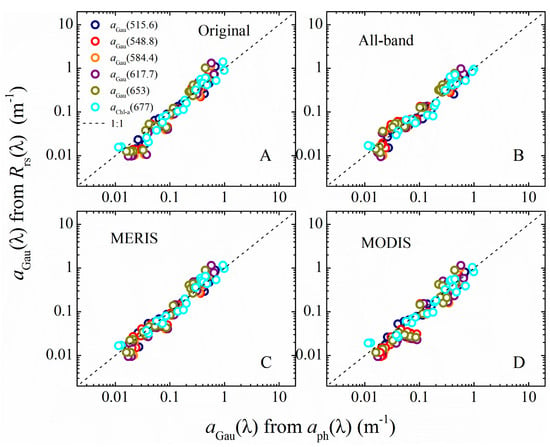
Figure 6.
For LE 2014: aGau(λ) from Gaussian decomposition of measured aph(λ) versus aGau(λ) retrieved from: Rrs(λ) with original hyperspectral bands (A); the combined all sensor bands (B); MERIS bands (C); and MODIS bands (D).
3.2. Chl-a and PC from aGau(λ) for Lake Erie
As one of the most widely used indices for phytoplankton, concentration and light absorption coefficients of chlorophyll a (Chl-a) have been the focus of many studies [33,44,45,46,47]. Previous studies [9,10,17] have indicated that some Gaussian peak heights (aGau(λ)) obtained from aph(λ), such as peaks around 390, 413, 435 and 675 nm, represent the absorption properties of chlorophyll a. Phycocyanin (PC), the bio-marker of the blue-green cyanobacteria, is an important indicator for cyanobacteria biomass [6,7,48]. Based on the regression analysis between aGau(λ), Chl-a and PC from the LE dataset, the Gaussian peaks at 386.6, 414, 435 and 677 nm showed high correlation coefficients with Chl-a concentration with R2 of 0.95, 0.96, 0.97, and 0.98, respectively; and the Gaussian peaks at 617.6 nm showed a 0.93 correlation coefficient with PC concentration. The empirical relationships for Chl-a and PC estimation from aGau(677) and aGau(617.6) were obtained, as shown in Figure 7. The above results further highlight the values of using aGau(λ) as a proxy to obtain pigment absorption or concentration, which may be used to map cyanobacteria bloom waters from ocean color imagery.
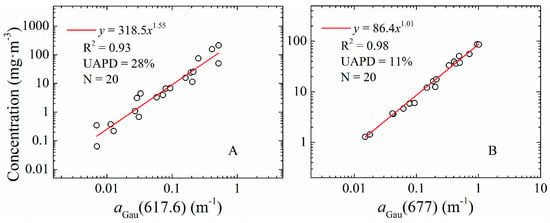
Figure 7.
Co-variation between the measured: phycocyanin (A); and chlorophyll a (B) concentrations, and the Gaussian peak heights (aGau(λ)) centered at 677 and 617.6 nm; and the corresponding relationship, R-square the mean UAPD, and the sample number (N).
3.3. aGau(λ) versus Group Composition
In analysis of the aGau(λ) and cell counts from LE 2013 measurements, we found the spectral shapes formed by aGau(435), aGau(584.4), and aGau(617.6) vary with the composition of cyanobacteria species at different locations in western basin of Lake Erie, as shown in Figure 8. As shown in Table 2, the aGau(435), aGau(584.4), and aGau(617.6) contain absorption properties of pigments Chl-a, PE, and PC, respectively. The variation of pigment compositions, especially the different intracellular Chl-a:PE:PC ratios of the cyanobacteria at the species level is the main reason of the spectral shape variation. This can potentially be used in separating different cyanobacteria species in the bloom waters.
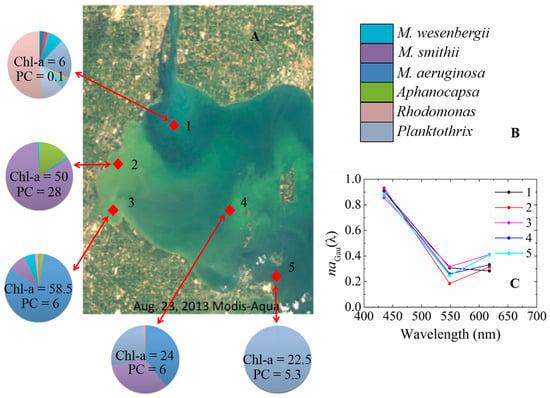
Figure 8.
The different aGau(λ) shapes corresponding to different locations and different species composition: (A) MODIS-Aqua true color image in western basin of Lake Erie on 23 August 2013; (B) cyanobacteria species composition in different locations of Lake Erie for August 2013, with the numbers for PC and Chl-a as the concentrations for these two pigments (mg∙m−3), and M. as Microcystis; and (C) the different spectral shapes of aGau(λ) corresponding to different species composition in different locations in western basin of Lake Erie.
3.4. Pigment and aGau(λ) Retrieval from Satellite Imagery
3.4.1. Validation of Satellite Remote Sensing Data
Before applying MuPI to satellite imagery for aGau(λ) retrieval, the Rrs(λ) data from HICO and MODIS imagery for Lake Erie were first assessed with in situ measurements.
Three criteria were employed to find matchups: (1) Within ±2 days; (2) median of a 3 × 3 box, with no masks of land or clouds; and (3) coefficients of variance smaller than 0.15. The spectral response function was applied to the in situ Rrs(λ) spectrum before comparing it with satellite data. Most of the bands have a mean difference within 35% for Rrs(λ) for both sensors. At the shorter wavelengths (≤500 nm for HICO, and 412 and 443 nm for MODIS), the mean UAPD was as high as 65% and some satellite Rrs(λ) were even negative values because of the poor atmospheric correction for optically complex inland waters [49,50]. For MODIS, the mean UAPD of Rrs(λ) at 748 nm was 52%, possibly due to low Rrs(λ) values at this band and the influence from residual and likely uncorrected oxygen and water vapor absorption in the atmosphere.
Since the main focus of this work is the retrieval of aGau(λ) from Rrs(λ), we took advantage of the aGau(λ) information from the Rrs(λ) spectrum in the longer wavelengths (>500 nm for HICO and >480 nm for MODIS) in the model application, to minimize the influence of ineffective atmospheric correction on the shorter bands of satellite Rrs(λ). To validate this adjustment, MuPI was first applied to in situ measured Rrs(λ) with HICO and MODIS bands but without data from the shorter wavelengths (≤500 nm for HICO and 412 and 443 nm for MODIS). The retrieved aGau(λ) from such Rrs(λ) agreed quite well with aGau(λ) from in situ aph(λ) decomposition, with the mean UAPD ≤38% for HICO, and ≤48% for MODIS bands (Table 7). The estimated Chl-a concentration has a mean UAPD of 28% which is better than the results from the standard products [45] and those shown in Pan et al. [8], and the mean UAPD for the estimated PC concentration is 32% which is consistent or even better than that reported in the literature [6,7,48]. Figure 9 presents one match-up of satellite and in situ Rrs(λ) spectra and the estimated Rrs(λ) spectra from MuPI for both HICO and MODIS, as well as, the 13 derived aGau(λ) from the corresponding spectrum. The aGau(λ) from the corresponding satellite and in situ match-up data showed the same trend.

Table 7.
The mean (Mea.) and median (Med.) of unbiased absolute percentage differences of aGau(λ) estimated from Rrs(λ) of HICO and MODIS satellite imagery.
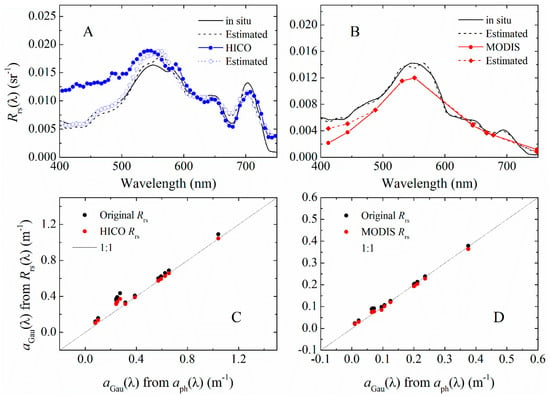
Figure 9.
(A) Example spectra of in situ and HICO measured (Rrs(λ)), and their corresponding estimated spectra from MuPI; (B) example spectra of in situ and MODIS measured (Rrs(λ)), and their corresponding estimated spectra from MuPI; and (C,D) the 13 aGau(λ) derived from in situ, HICO and MODIS Rrs(λ) were plotting against the aGau(λ) from decomposition of in situ measured aph(λ).
3.4.2. Chl-a and PC from HICO and MODIS Imagery
We further explored the aGau(λ) distribution obtained from HICO and MODIS of the western basin of Lake Erie. The MuPI scheme was applied without using Rrs(λ) data at the shorter spectral bands (those <500 nm for HICO and <480 nm for MODIS). The power-law relationships obtained in Section 3.4 between aGau(677) and Chl-a, and aGau(617.6) and PC concentration were applied to the obtained aGau(λ) images to map the spatial distribution of Chl-a and PC concentration (Figure 10).
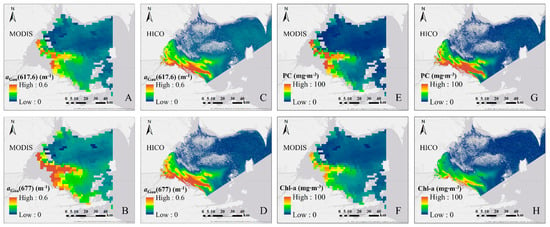
Figure 10.
The spatial distributions of aGau(λ) (m−1) centered at 617.6 and 677 nm in western basin of Lake Erie from: MODIS (13 August 2014, 17:50:00 UTC) (A,B), and HICO (15 August 2014, 21:56:18 UTC) (C,D) remote sensing imagery; the distribution of phycocyanin (PC) and chlorophyll a concentrations (Chl-a) derived from MODIS (E,F) and HICO imageries (G,H).
The estimated spatial distributions of Chl-a and PC from MODIS showed a similar pattern with those from HICO. A two-day difference exists between the HICO (15 August 2014) and MODIS (13 August 2014) observations due to the availability of satellite image, which explains the slightly different locations of the high biomass patches as shown in Figure 9. The non-value patches with in HICO image was a result of the poor Rrs(λ) quality due to the failing of the atmospheric correction.
3.4.3. MODIS and MERIS Imagery over Lake Erie
MERIS imagery did not coincide with the in situ observations used in this study. Thus, to provide an example of MERIS imagery, aGau(λ) were retrieved from MERIS imagery on 3 September 2011. MODIS imagery of this day was also considered.
As shown in Figure 11, similar patterns for high and low absorption patches were noticed for the two sensors, but the two images showed different magnitudes of aGau(λ). In further analysis of the Rrs(λ) from these two sensors at the same locations, good agreement was observed, as shown in Figure 12. The existence of 709 nm band in MERIS could be the main reason for the differences in the retrieval results. The patch of high values in the MERIS (marked with solid star: ★) imagery was not included in MODIS because the standard L1B to L2 processing in SeaDAS masked those pixels as clouds. Further validation and evaluation of MERIS and MODIS Rrs(λ) with in situ data are necessary to have a better understanding of the differences in the results, which is beyond the scope of the current work.
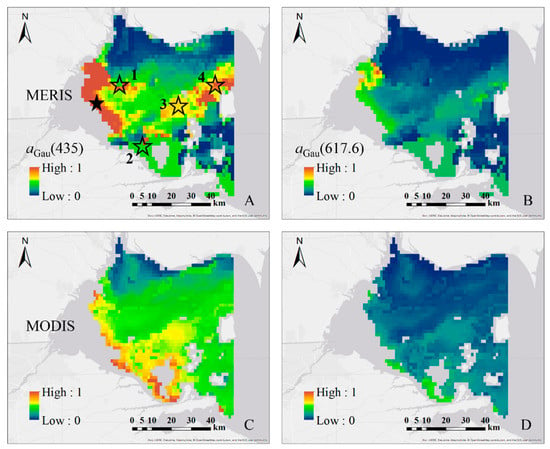
Figure 11.
The spatial distributions of aGau(435) and aGau(617.6) in western basin of Lake Erie estimated from: MERIS (3 September 2011, 15:43:50 UTC) (A,B); and MODIS (3 September 2011, 18:55:00 UTC) (C,D) remote sensing reflectance imagery. The stars on (A) shows the locations of the mismatch between MERIS and MODIS imagery.
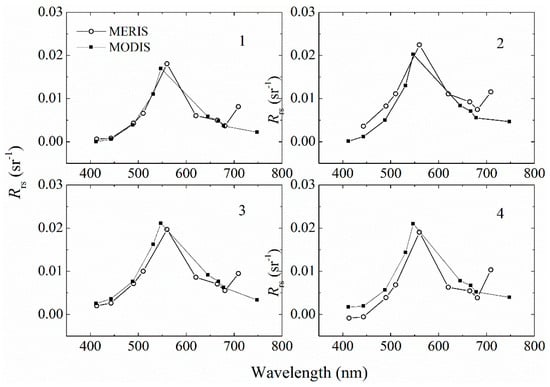
Figure 12.
The Rrs(λ) from MODIS and MERIS imagery at the same locations. The 1, 2, 3, and 4 correspond to the locations marked in Figure 11A.
3.4.4. The Seasonal Variation of aGau(λ) from MERIS Imagery
We further explored the seasonal variation of aGau(435) and aGau(617.6) in Lake Erie retrieved from MERIS seasonal composed 4 km Rrs(λ) imagery (Figure 13). The differences in the spatial distribution of high pigment absorption patches in Spring, Summer, Autumn and Winter were captured. An obvious summer bloom in western basin of Lake Erie is shown in the figure.
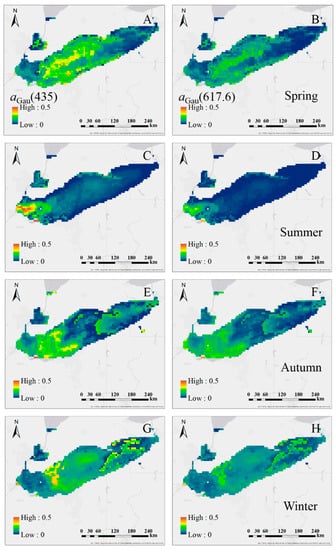
Figure 13.
The distribution of aGau(435) and aGau(617.6) in Lake Erie in: spring (A,B); summer (C,D); autumn (E,F); and winter (G,H).
4. Discussion
4.1. Spectral Requirements for aGau(λ) Retrieval
In the retrieval of aGau(λ) from in situ Rrs(λ) data, we found that a band around 695–715 nm is important for accurate aGau(λ) estimation in bloom waters. This is consistent with previous studies for the estimation of Chl-a in turbid productive waters [51,52,53,54]. Fundamentally, for phytoplankton bloom waters, the reflectance at wavelengths 695–715 nm can be augmented in the same way as occurs with terrestrial plants [51,52,53]. Lacking a proper spectral band within this spectral region for MODIS, the near-infrared band at 748 nm was included when inverting MODIS Rrs(λ). Although higher uncertainties at 748 nm band were noticed (Section 3.4.1), the inclusion of the band at 748 nm results in much more reasonable aGau(λ) retrieval from MODIS-Aqua measured Rrs(λ) (Figure 9, Table 7) versus without Rrs(λ) at this band. The same results were noticed in Section 3.1 for the aGau(λ) retrieval from Rrs(λ) at VIIRS and MSI spectral bands.
4.2. The seasonal aGau(λ) Variation in Lake Erie
The MERIS derived seasonal aGau(435) and aGau(617.6) variation in Lake Erie follows the pattern recorded in the literature [55,56]. In the central basin of Lake Erie, the different patterns, as shown in Figure 13, are due to the greater nutrients in the spring and autumn, and lower availability in the summer as a result of water stratification. The nutrient inputs due to agricultural activities as well as an expanding non-native mussel population, along with the light and temperature changes in different seasons form the main drivers for the different algal bloom patterns in Lake Erie during the four seasons [55,56,57,58,59]. As discovered in Moon [55], the biomass and taxonomic composition and the dominant taxa of surface assemblages varied in different seasons, which can be explained by the light, temperature and nutrient combinations in different seasons, and the strong spatial variability associated with mesoscale physical processes such as upwelling and basin-scale circulation [59].
4.3. Pigment Retrieval and HABs Detection
In this study, MuPI as a semi-analytical inversion scheme was applied to retrieve multiple Gaussian curves from satellite remote sensing data. As demonstrated in previous study [10], these Gaussian curves are related to the different phytoplankton pigments.
This phytoplankton pigment information has been used in the quantification of phytoplankton community composition, at least to a functional group level ([5] and the references therein), because many pigments are particular to specific taxonomic groups or even species [1]. However, only limited work has been conducted to obtain these phytoplankton pigments from satellite remote sensing data. Pan et al. [8] and Moisan et al. [60], as two of them, attempted to obtain 12 and 18 different phytoplankton pigments from satellite remote sensing data, respectively, but both of them are empirical approach based. Pan et al. [8] proposed using empirical relationships of 12 different phytoplankton pigments with the same band ratios of satellite Rrs(λ) around 490 nm to 550 nm. However, using 490 and 550 nm alone is not a good strategy for multiple pigments, as different pigments have different absorption peaks and troughs at different wavelengths [1]. Compared with Pan et al. [8], Moisan et al. [60] directly used the Chl-a product of satellite remote sensing to estimate aph(λ), then decompose this aph(λ) to 18 pigments based on their specific absorption coefficients. However, this satellite Chl-a product used similar empirical algorithm and spectral bands as in Pan et al. [8]. As both works were focused on coastal waters, another large uncertainty comes from non-algal particles and gelbstoff in these waters, which have a big influence on wavelengths shorter than 550 nm, and this influence cannot be eliminated by the band-ratio based algorithm. Compared with these works, MuPI not only considers the contribution of non-algal particles and gelbstoff in the coastal or inland waters, but also the different absorption properties of pigments, as shown in Table 1 and Table 2.
Another application of the pigment information is in HAB detection. The algorithms for HAB detection are usually based on Chl-a and its anomalies [47], or marker pigments, such as phycocyanin (PC) for cyanobacteria [6,7,18,48,61]. With MuPI, a successful discrimination of phycocyanin (PC) and Chl-a was achieved in this study. Limited by the dataset, the estimation of other pigment concentrations (phycoerythrin, chlorophyll b and c, carotenoids) from aGau(λ), as demonstrated in Hoepffner and Sathyendranath [10], could not be conducted here.
Cyanobacteria dominated HABs are increasing globally and presenting a major environmental and human health issue. Extensive Microsystis blooms with toxin production occur during summer and fall in different regions around the world and Microcystis contamination has been documented at many regions including Pinto Lake (California), Lake Erie (U.S.A.) and Lake Taihu (China) [6,7,21,61]. Other common bloom-forming pelagic genera include Aphanizomenon, Anabaena, Rhodomonas and Planktothrix. However, since toxicity is primarily associated with Microcystis, these other cyanobacteria blooms are generally considered nuisance blooms which will not cause acutely dangers to humans and wildlife [62], but they are frequently present in impacted water bodies (Figure 8). However, the ability to discriminate the different bloom-causing species is one of the challenges that existing algorithms are facing. In our analysis with aGau(λ) in Section 3.3, the possibility of discriminating different cyanobacteria species was shown. The variation of the spectral shape defined by aGau(435), aGau(584.4), and aGau(617.6) was found vary with different species and their composition in the water body as a result of the variation in pigment ratios [6]. This result showed the potential of MuPI in the application of separating species in HAB waters, which will be useful in detecting and monitoring potential toxin producers. However, because of data limitation, this potential is not fully addressed in this study, but it will be further explored with a larger dataset in the future.
5. Conclusions
In this study, the MuPI model was validated for obtaining the peak heights of Gaussian curves (aGau(λ)) from multi-spectral satellite remote sensing data. The model performance was validated in the retrieval accuracy of aGau(λ) with Rrs(λ) of six multi-spectral band configurations, and the spectral requirements were discussed. Less than 35% of mean unbiased absolute percentage differences were achieved for aGau(λ) from Rrs(λ) spectra with OLCI, MERIS and MODIS bands, and less than 45% for VIIRS, MSI and OLI bands. Using data from the western basin of Lake Erie as an example, the Rrs(λ) obtained from HICO and MODIS satellites were validated with in situ data over cyanobacterial bloom waters in Lake Erie, and the spatial distributions of aGau(λ) and the concentrations of chlorophyll a and phycocyanin were obtained, where the patches of cyanobacteria bloom were clearly presented. A seasonal distribution of pigment absorption coefficients was obtained from MERIS seasonal composed imagery of 2011 for Lake Erie. These results demonstrate that, with MuPI, it is possible to analytically retrieve information of not only Chl-a, but also PC and potentially other pigments, which will significantly enhance our capability to characterize and evaluate the status of phytoplankton blooms and discriminate phytoplankton groups using satellite ocean color remote sensing.
Supplementary Materials
The algorithm code is available online at http://www.mdpi.com/2072-4292/9/12/1309/s1.
Acknowledgments
We greatly appreciate the constructive comments and suggestions from three anonymous reviewers. We thank Oregon State University for providing the HICO imagery, the National Aeronautics and Space Administration (NASA) for providing MODIS, MERIS imageries. We are in debt to Ronghua Ma, Deepak Mishra and Tim Moore for in situ measurements in Lake Taihu (China), MS ponds and Lake Erie. We are grateful to Timothy Moore for making the combination of phytoplankton composition pie charts and the MODIS-Aqua true color image for Figure 8. Support from NASA’s Ocean Biology and Biogeochemistry and Water and Energy Cycle Programs, and the National Oceanic and Atmospheric Administration (NOAA) JPSS VIIRS Ocean Color Cal/Val Project is greatly appreciated. Mouw was supported by grants NNX14AB80G, 1R01ES021929-01 and OCE-1313783.
Author Contributions
Guoqing Wang and Zhongping Lee framed the research question; Colleen Mouw provided in situ data and helped in data analysis; Guoqing Wang carried out the study and drafted the manuscript; all co-authors provided critical revisions to the manuscript and helped in analyzing and interpretation of the results.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jeffrey, S.W.; Mantoura, R.F.C.; Wright, S.W. Phytoplankton Pigments in Oceanography: Guidelines to Modern Methods (Monographs on Oceanographic Methodology); UNESCO Publishing: Paris, France, 1997; p. 661. [Google Scholar]
- Sosik, H.M.; Mitchell, B.G. Light absorption by phytoplankton, photosynthetic pigments and detritus in the California Current System. Deep Sea Res. Part I 1995, 42, 1717–1748. [Google Scholar] [CrossRef]
- Schlüter, L.; Møhlenberg, F.; Havskum, H.; Larsen, S. The use of phytoplankton pigments for identifying and quantifying phytoplankton groups in coastal areas: Testing the influence of light and nutrients on pigment/chlorophyll a ratios. Mar. Ecol. Prog. Ser. 2000, 192, 49–63. [Google Scholar] [CrossRef]
- The International Ocean-Colour Coordinating Group (IOCCG). Phytoplankton Functional Types from Space; Sathyendranath, S., Ed.; Reports of the International Ocean-Colour Coordinating Group, No. 15; IOCCG: Dartmouth, NS, Canada, 2014. [Google Scholar]
- Mouw, C.B.; Hardman-Mountford, N.J.; Alvain, S.; Bracher, A.; Brewin, R.J.W.; Bricaud, A.; Ciotti, A.M.; Devred, E.; Fujiwara, A.; Hirata, T.; et al. A Consumer’s Guide to Satellite Remote Sensing of Multiple Phytoplankton Groups in the Global Ocean. Front. Mar. Sci. 2017, 4. [Google Scholar] [CrossRef]
- Simis, S.G.; Peters, S.W.; Gons, H.J. Remote sensing of the cyanobacterial pigment phycocyanin in turbid inland water. Limnol. Oceanogr. 2005, 50, 237–245. [Google Scholar] [CrossRef]
- Wynne, T.T.; Stumpf, R.P.; Tomlinson, M.C.; Warner, R.A.; Tester, P.A.; Dyble, J.; Fahnenstiel, G.L. Relating spectral shape to cyanobacterial blooms in the Laurentian Great Lakes. Int. J. Remote Sens. 2008, 29, 3665–3672. [Google Scholar] [CrossRef]
- Pan, X.; Mannino, A.; Russ, M.E.; Hooker, S.B.; Harding, L.W. Remote sensing of phytoplankton pigment distribution in the United States northeast coast. Remote Sens. Environ. 2010, 114, 2403–2416. [Google Scholar] [CrossRef]
- Wang, G.; Lee, Z.; Mishra, D.R.; Ma, R. Retrieving absorption coefficients of multiple phytoplankton pigments from hyperspectral remote sensing reflectance measured over cyanobacteria bloom waters. Limnol. Oceanogr. Methods 2016, 14, 432–447. [Google Scholar] [CrossRef]
- Hoepffner, N.; Sathyendranath, S. Effect of pigment composition on absorption properties of phytoplankton. Mar. Ecol. Prog. Ser. 1991, 73, 11–23. [Google Scholar] [CrossRef]
- Hoepffner, N.; Sathyendranath, S. Determination of the major groups of phytoplankton pigments from the absorption spectra of total particulate matter. J. Geophys. Res. 1993, 98, 22789–22803. [Google Scholar] [CrossRef]
- Bidigare, R.R.; Morrow, J.H.; Kiefer, D.A. Derivative analysis of spectral absorption by photosynthetic pigments in the western Sargasso Sea. J. Mar. Res. 1989, 47, 323–341. [Google Scholar] [CrossRef]
- Bidigare, R.R.; Ondrusek, M.E.; Morrow, J.H.; Kiefer, D.A. In-vivo absorption properties of algal pigments. Proc. SPIE 1990, 1302. [Google Scholar] [CrossRef]
- Bricaud, A.; Claustre, H.; Ras, J.; Oubelkheir, K. Natural variability of phytoplanktonic absorption in oceanic waters: Influence of the size structure of algal populations. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Lohrenz, S.E.; Weidemann, A.D.; Tuel, M. Phytoplankton spectral absorption as influenced by community size structure and pigment composition. J. Plankton Res. 2003, 25, 35–61. [Google Scholar] [CrossRef]
- Moisan, J.R.; Moisan, T.A.; Linkswiler, M.A. An inverse modeling approach to estimating phytoplankton pigment concentrations from phytoplankton absorption spectra. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Chase, A.; Boss, E.; Zaneveld, R.; Bricaud, A.; Claustre, H.; Ras, J.; Dall’Olmo, G.; Westberry, T.K. Decomposition of in situ particulate absorption spectra. Methods Oceanogr. 2013, 7, 110–124. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R.; Lee, Z.; Tucker, C.S. Quantifying cyanobacterial phycocyanin concentration in turbid productive waters: A quasi-analytical approach. Remote Sens. Environ. 2013, 133, 141–151. [Google Scholar] [CrossRef]
- Michalak, A.M.; Anderson, E.J.; Beletsky, D.; Boland, S.; Bosch, N.S.; Bridgeman, T.B.; Chaffin, J.D.; Cho, K.; Confesor, R.; Daloğlu, I.; et al. Record-setting algal bloom in Lake Erie caused by agricultural and meteorological trends consistent with expected future conditions. Proc. Natl. Acad. Sci. USA 2013, 110, 6448–6452. [Google Scholar] [CrossRef] [PubMed]
- Mouw, C.B.; Ciochetto, A.; Moore, T.S.; Twardowski, M.; Sullivan, J.; Yu, A. SeaWiFS Bio-Optical Storage System (SeaBASS). NASA, 2014. Available online: https://seabass.gsfc.nasa.gov/archive/URI/Mouw/NIH-NSF_Lake_Erie/URI_Lake_Erie_2014/archive (accessed on 20 July 2017).
- Moore, T.S.; Mouw, C.B.; Sullivan, J.M.; Twardowski, M.S.; Burtner, A.M.; Ciochetto, A.B.; McFarland, M.N.; Nayak, A.R.; Paladino, D.; Stockley, N.D.; et al. Bio-optical Properties of Cyanobacteria Blooms in Western Lake Erie. Front. Mar. Sci. 2017, 4, 201–220. [Google Scholar] [CrossRef]
- Tassan, S.; Ferrari, G.M. An alternative approach to absorption measurements of aquatic particles retained on filters. Limnol. Oceanogr. 1995, 40, 1358–1368. [Google Scholar] [CrossRef]
- Mitchell, B.G.; Kahru, M.; Wieland, J.; Stramska, M. Determination of spectral absorption coefficients of particles, dissolved material and phytoplankton for discrete water samples. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Revision 4, Volume IV: Inherent Optical Properties: Instruments, Characterizations, Field Measurements and Data Analysis Protocols; Mueller, J.L., Fargion, G.S., McClain, C.R., Eds.; NASA/TM-2003-211621; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2003; pp. 39–64. [Google Scholar]
- Duan, H.; Ma, R.; Zhang, Y.; Loiselle, S.A.; Xu, J.; Zhao, C.; Zhou, L.; Shang, L. A new three-band algorithm for estimating chlorophyll concentrations in turbid inland lakes. Environ. Res. Lett. 2010, 5. [Google Scholar] [CrossRef]
- Ma, R.H.; Tang, J.W.; Dai, J.F. Bio-optical model with optimal parameter suitable for Taihu Lake in water colour remote sensing. Int. J. Remote Sens. 2006, 27, 4305–4328. [Google Scholar] [CrossRef]
- Mouw, C.B.; Ciochetto, A.B.; Grunert, B.; Yu, A. Expanding understanding of optical variability in Lake Superior with a four-year dataset. Earth Syst. Sci. Data Discuss. 2017, 10. [Google Scholar] [CrossRef]
- Horváth, H.; Kovács, A.W.; Riddick, C.; Présing, M. Extraction methods for phycocyanin determination in freshwater filamentous cyanobacteria and their application in a shallow lake. Eur. J. Phycol. 2013, 48, 278–286. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, Z.; Franz, B.A.; McClain, C.R.; Kwiatkowska, E.J.; Werdell, J.; Shettle, E.P.; Holben, B.N. New aerosol models for the retrieval of aerosol optical thickness and normalized water-leaving radiances from the SeaWiFS and MODIS sensors over coastal regions and open oceans. Appl. Opt. 2010, 49, 5545–5560. [Google Scholar] [CrossRef] [PubMed]
- Bailey, S.W.; Franz, B.A.; Werdell, P.J. Estimation of near-infrared water-leaving reflectance for satellite ocean color data processing. Opt. Express 2010, 18, 7521–7527. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Morel, A. Optics of marine particles and marine optics. In Particle Analysis in Oceanography; Springer: Berlin/Heidelberg, Germany, 1991; pp. 141–188. [Google Scholar]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Wei, J.; Voss, K.; Lewis, M.; Bricaud, A.; Huot, Y. Hyperspectral absorption coefficient of “pure” seawater in the range of 350–550 nm inverted from remote sensing reflectance. Appl. Opt. 2015, 54, 546–558. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [PubMed]
- Werdell, P.J.; Franz, B.A.; Bailey, S.W.; Feldman, G.C.; Boss, E.; Brando, V.E.; Dowell, M.; Hirata, T.; Lavender, S.J.; Mangin, A.; et al. Generalized ocean color inversion model for retrieving marine inherent optical properties. Appl. Opt. 2013, 52, 2019–2037. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. 1. A semianalytical model. Appl. Opt. 1998, 37, 6329–6338. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [PubMed]
- Huang, S.; Li, Y.; Shang, S.; Shang, S. Impact of computational methods and spectral models on the retrieval of optical properties via spectral optimization. Opt. Express 2013, 21, 6257–6273. [Google Scholar] [CrossRef] [PubMed]
- Maritorena, S.; Siegel, D.A.; Peterson, A.R. Optimization of a semianalytical ocean color model for global-scale applications. Appl. Opt. 2002, 41, 2705–2714. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.L. Effect of spectral band numbers on the retrieval of water column and bottom properties from ocean color data. Appl. Opt. 2002, 41, 2191–2201. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.; Arnone, R.; He, M. Determination of primary spectral bands for remote sensing of aquatic environments. Sensors 2007, 7, 3428–3441. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Shang, S.; Hu, C.; Zibordi, G. Spectral interdependence of remote-sensing reflectance and its implications on the design of ocean color satellite sensors. Appl. Opt. 2014, 53, 3301–3310. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R.; Clark, D.K.; Brown, J.W.; Brown, O.B.; Evans, R.H.; Broenkow, W.W. Phytoplankton pigment concentrations in the Middle Atlantic Bight: Comparison of ship determinations and CZCS estimates. Appl. Opt. 1983, 22, 20–36. [Google Scholar] [CrossRef] [PubMed]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Hu, C.; Muller-Karger, F.E.; Taylor, C.J.; Carder, K.L.; Kelble, C.; Johns, E.; Heil, C.A. Red tide detection and tracing using MODIS fluorescence data: A regional example in SW Florida coastal waters. Remote Sens. Environ. 2005, 97, 311–321. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. A novel remote sensing algorithm to quantify phycocyanin in cyanobacterial algal blooms. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Mouw, C.B.; Greb, S.; Aurin, D.; DiGiacomo, P.M.; Lee, Z.; Twardowski, M.; Binding, C.; Hu, C.; Ma, R.; Moses, W. Aquatic color radiometry remote sensing of coastal and inland waters: Challenges and recommendations for future satellite missions. Remote Sens. Environ. 2015, 160, 15–30. [Google Scholar] [CrossRef]
- Wang, M.; Son, S.; Shi, W. Evaluation of MODIS SWIR and NIR-SWIR atmospheric correction algorithms using SeaBASS data. Remote Sens. Environ. 2009, 113, 635–644. [Google Scholar] [CrossRef]
- Dekker, A.G.; Malthus, T.J.; Wijnen, M.M.; Seyhan, E. Remote sensing as a tool for assessing water quality in Loosdrecht lakes. In Restoration and Recovery of Shallow Eutrophic Lake Ecosystems in The Netherlands; Springer: Dordrecht, The Netherlands, 1992; pp. 137–159. [Google Scholar]
- Gower, J.F.R.; Doerffer, R.; Borstad, G.A. Interpretation of the 685 nm peak in water-leaving radiance spectra in terms of fluorescence, absorption and scattering, and its observation by MERIS. Int. J. Remote Sens. 1999, 20, 1771–1786. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Borstad, G.; Brown, L. Detection of intense plankton blooms using the 709 nm band of the MERIS imaging spectrometer. Int. J. Remote Sens. 2005, 26, 2005–2012. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A.; Rundquist, D.C.; Leavitt, B.; Barrow, T.; Holz, J.C. Assessing the potential of SeaWiFS and MODIS for estimating chlorophyll concentration in turbid productive waters using red and near-infrared bands. Remote Sens. Environ. 2005, 96, 176–187. [Google Scholar] [CrossRef]
- Moon, J.B.; Carrick, H.J. Seasonal variation of phytoplankton nutrient limitation in Lake Erie. Aquat. Microb. Ecol. 2007, 48, 61–71. [Google Scholar] [CrossRef]
- Leon, L.F.; Smith, R.E.; Hipsey, M.R.; Bocaniov, S.A.; Higgins, S.N.; Hecky, R.E.; Antenucci, J.P.; Imberger, J.A.; Guildford, S.J. Application of a 3D hydrodynamic–biological model for seasonal and spatial dynamics of water quality and phytoplankton in Lake Erie. J. Great Lakes Res. 2011, 37, 41–53. [Google Scholar] [CrossRef]
- Vanderploeg, H.A.; Liebig, J.R.; Carmichael, W.W.; Agy, M.A.; Johengen, T.H.; Fahnenstiel, G.L.; Nalepa, T.F. Zebra mussel (Dreissena polymorpha) selective filtration promoted toxic Microcystis blooms in Saginaw Bay (Lake Huron) and Lake Erie. Can. J. Fish. Aquat. Sci. 2001, 58, 1208–1221. [Google Scholar] [CrossRef]
- Binding, C.; Greenberg, T.; Bukata, R. An analysis of MODIS-derived algal and mineral turbidity in Lake Erie. J. Great Lakes Res. 2012, 38, 107–116. [Google Scholar] [CrossRef]
- Sayers, M.; Fahnenstiel, G.L.; Shuchman, R.A.; Whitley, M. Cyanobacteria blooms in three eutrophic basins of the Great Lakes: A comparative analysis using satellite remote sensing. Int. J. Remote Sens. 2016, 37, 4148–4171. [Google Scholar] [CrossRef]
- Moisan, T.A.; Rufty, K.M.; Moisan, J.R.; Linkswiler, M.A. Satellite Observations of Phytoplankton Functional Type Spatial Distributions, Phenology, Diversity, and Ecotones. Front. Mar. Sci. 2017, 4. [Google Scholar] [CrossRef]
- Kudela, R.M.; Palacios, S.L.; Austerberry, D.C.; Accorsi, E.K.; Guild, L.S.; Torres-Perez, J. Application of hyperspectral remote sensing to cyanobacterial blooms in inland waters. Remote Sens. Environ. 2015, 167, 196–205. [Google Scholar] [CrossRef]
- Kudela, R.M. Characterization and deployment of Solid Phase Adsorption Toxin Tracking (SPATT) resin for monitoring of microcystins in fresh and saltwater. Harmful Algae 2011, 11, 117–125. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).