Atmospheric Profile Retrieval Algorithm for Next Generation Geostationary Satellite of Korea and Its Application to the Advanced Himawari Imager
Abstract
1. Introduction
2. Data and Methods
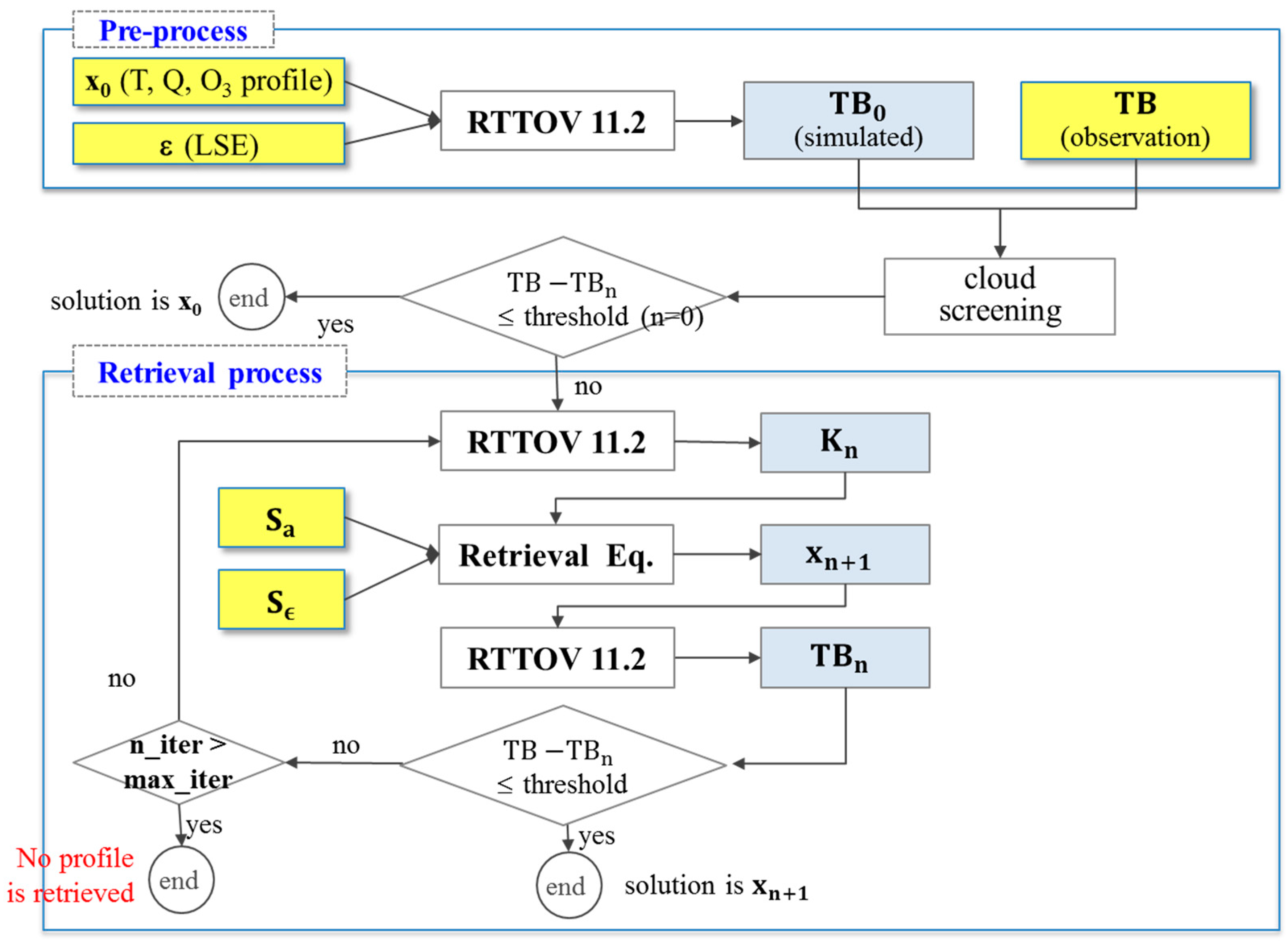
2.1. Retrieval Method
2.2. Data
2.2.1. Satellite Measurements
2.2.2. First Guess Profile
2.2.3. Background Error Covariance
2.2.4. Observation Error Covariance
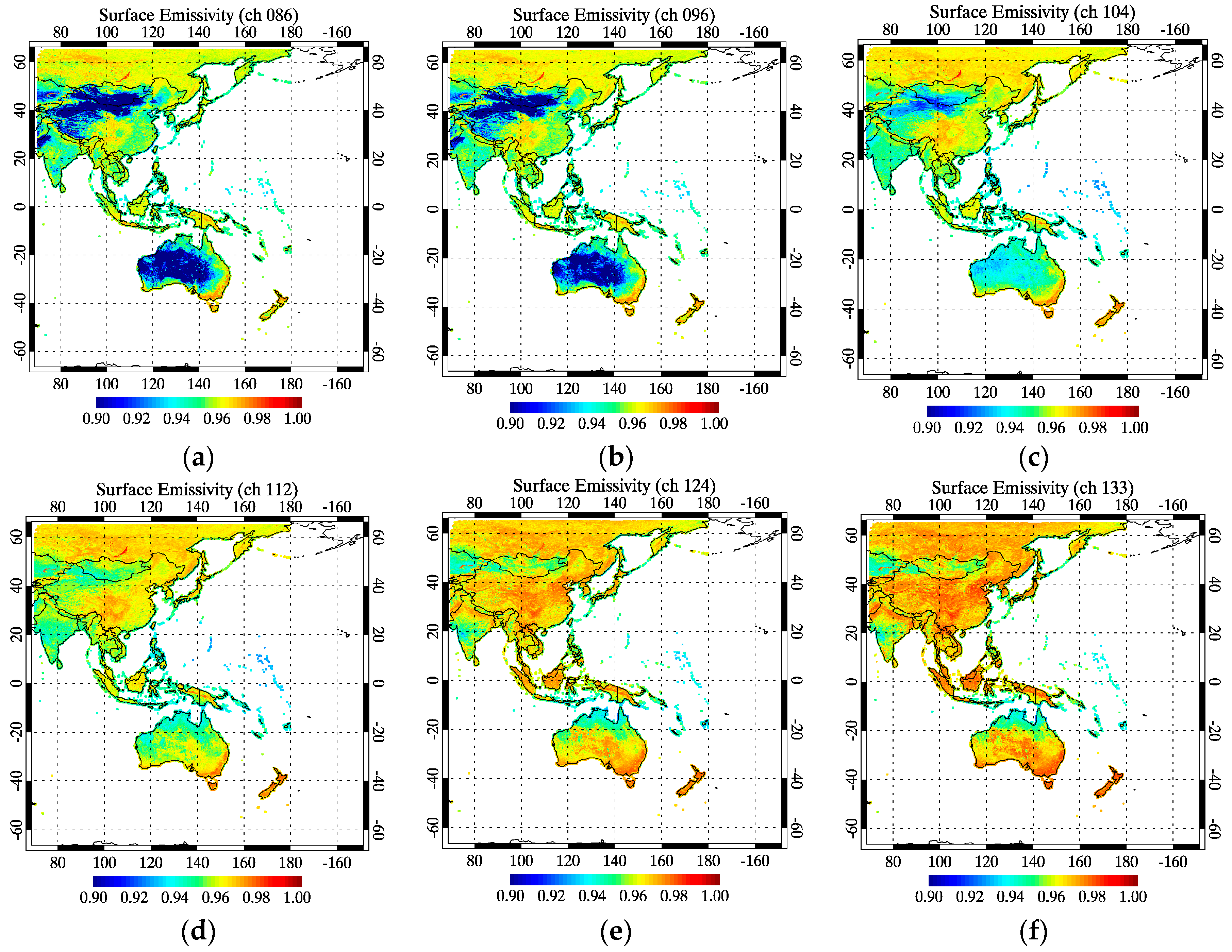
2.2.5. Land Surface Emissivity
2.3. Summary
3. Results
3.1. Algorithm Characterization
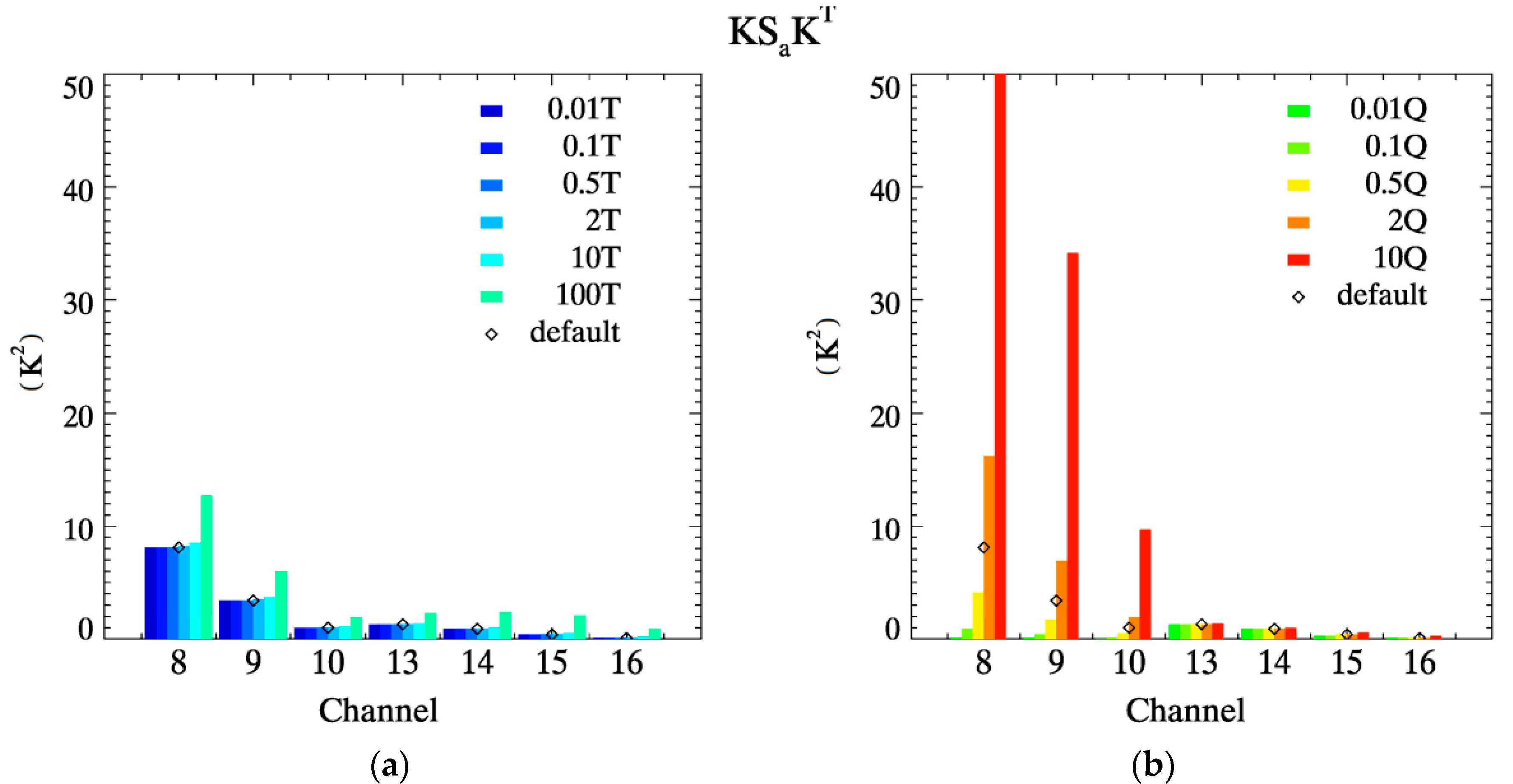
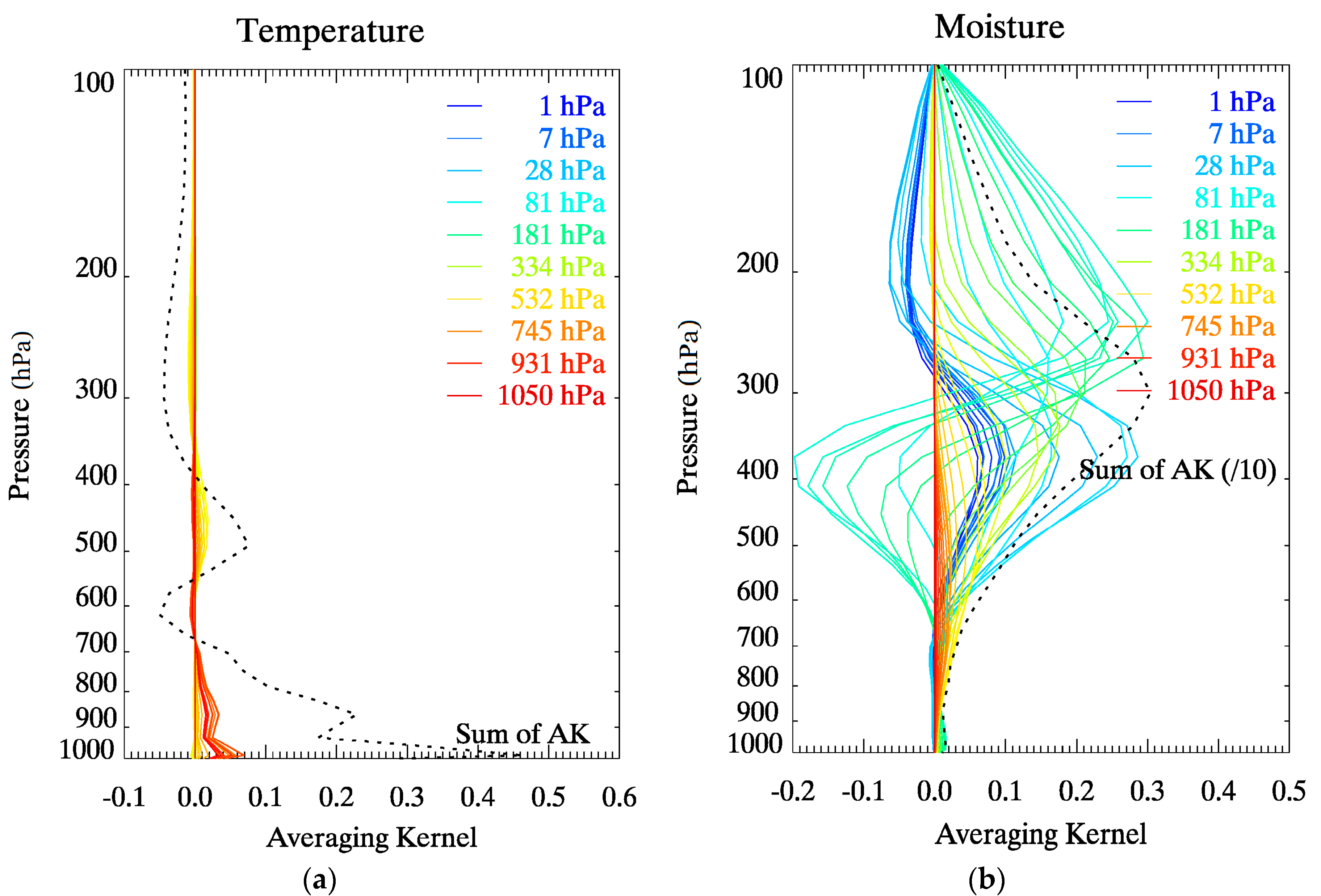
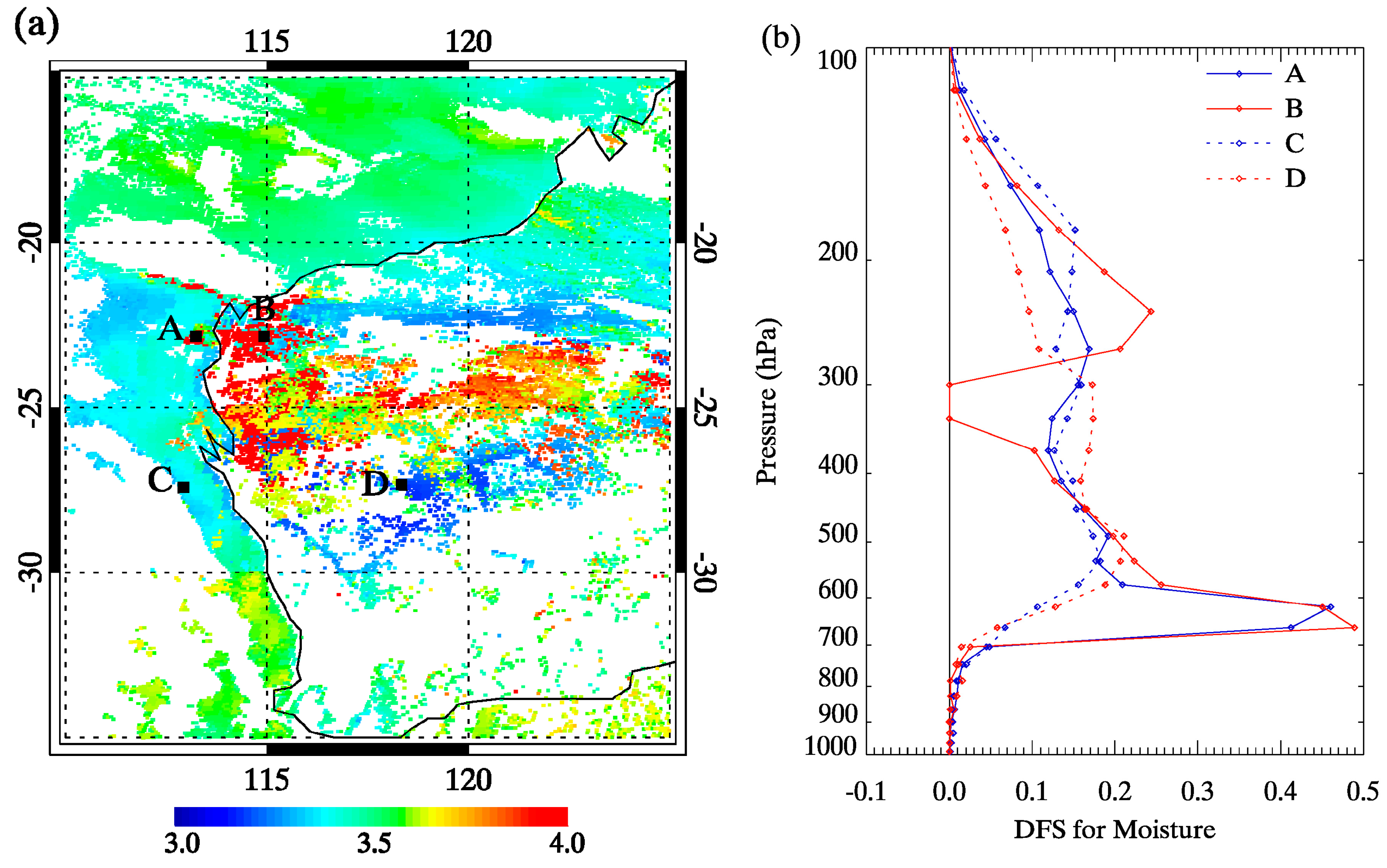
3.1.1. Information Contents of Measurements
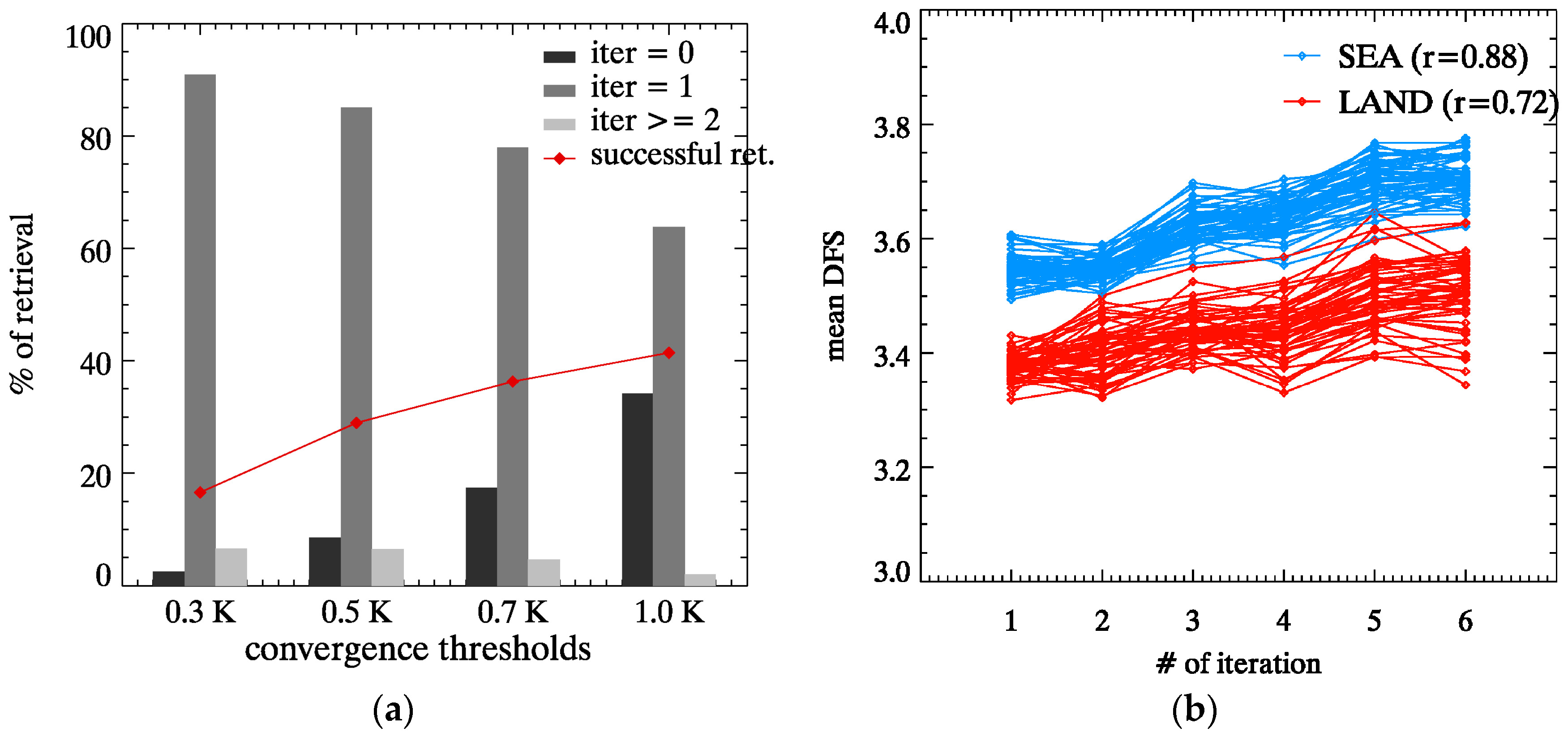
3.1.2. Convergence Threshold and Iteration
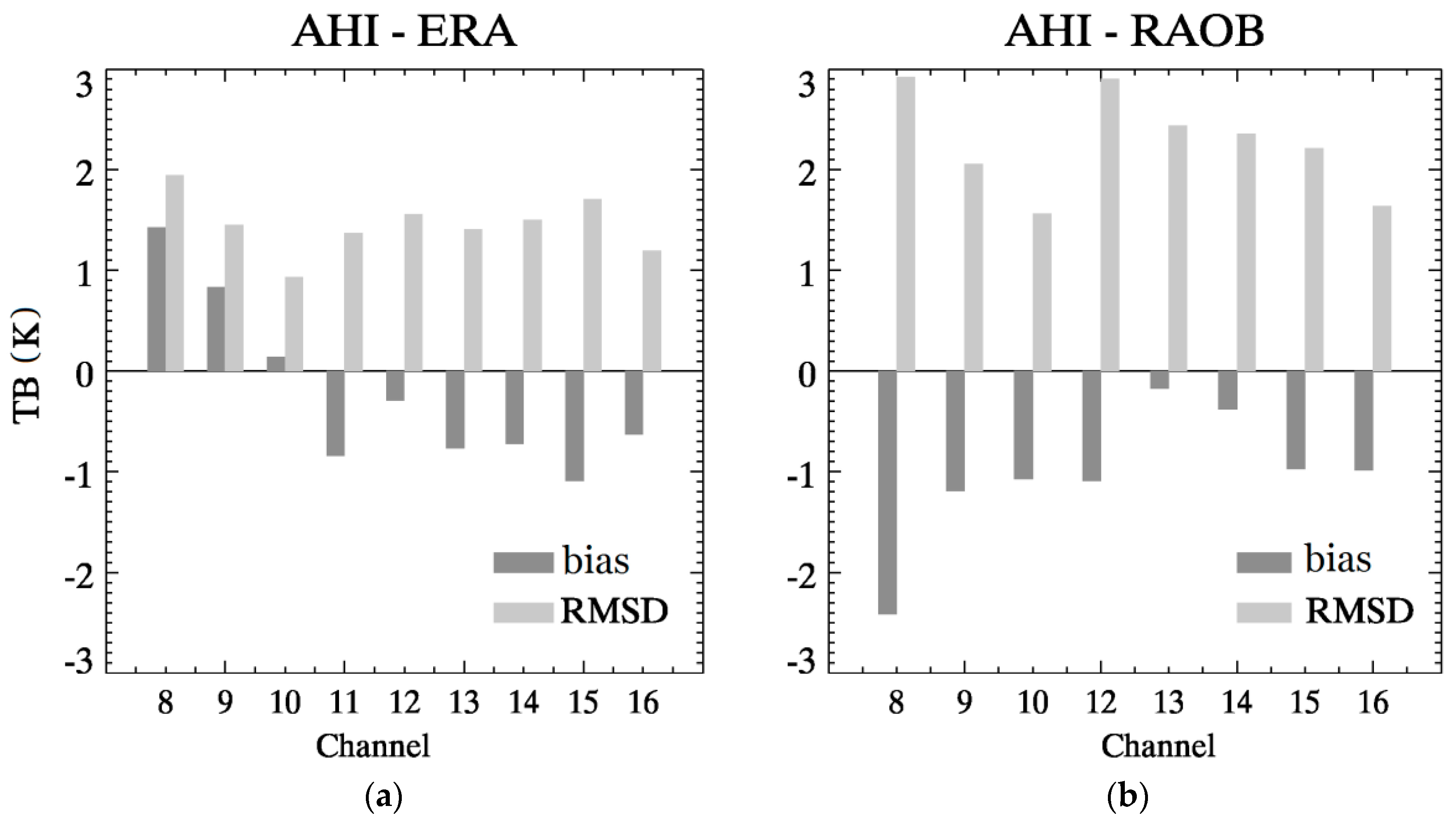
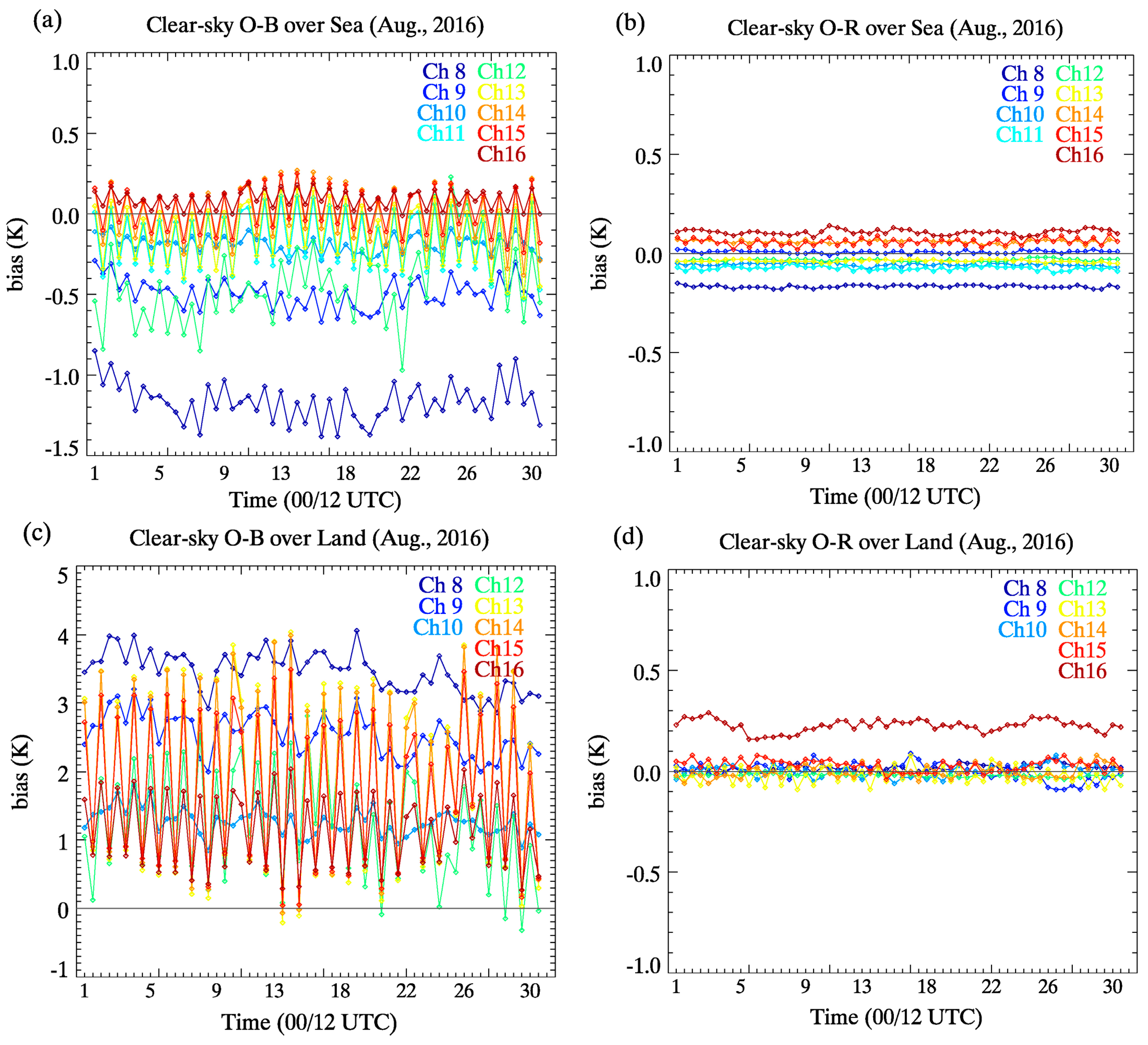
3.1.3. TB Departures
3.2. Validation Results
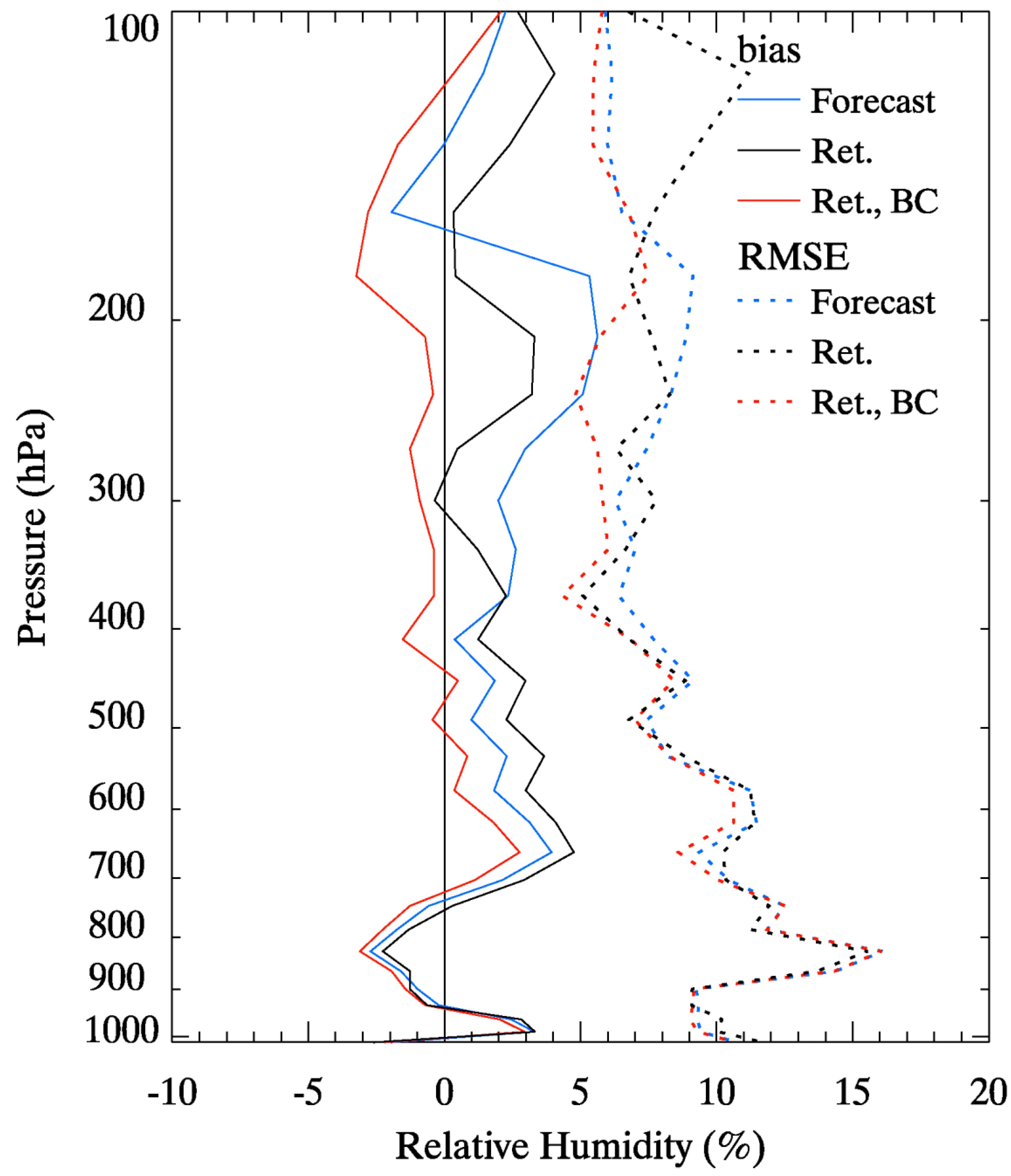
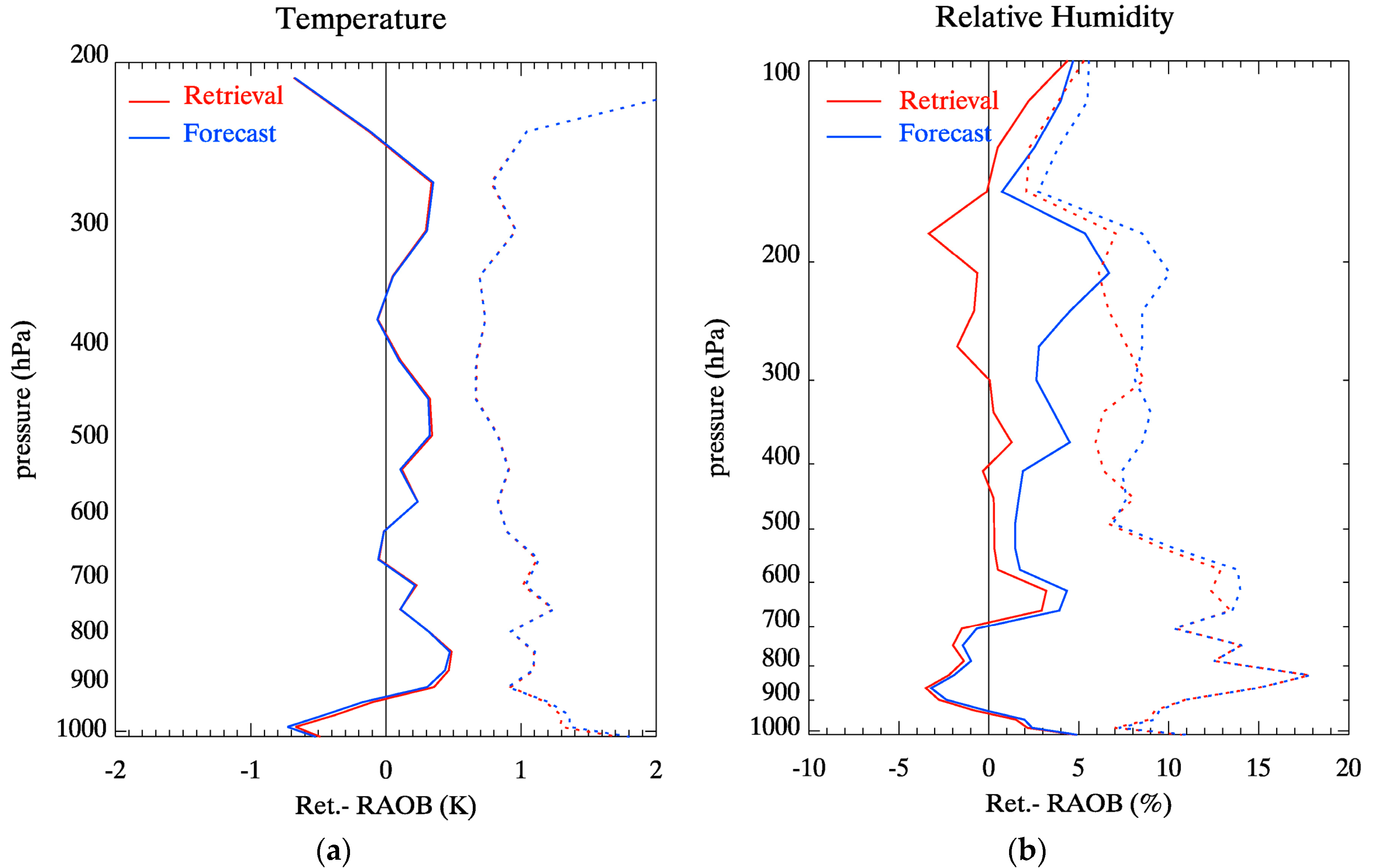
3.2.1. Retrieved Profiles
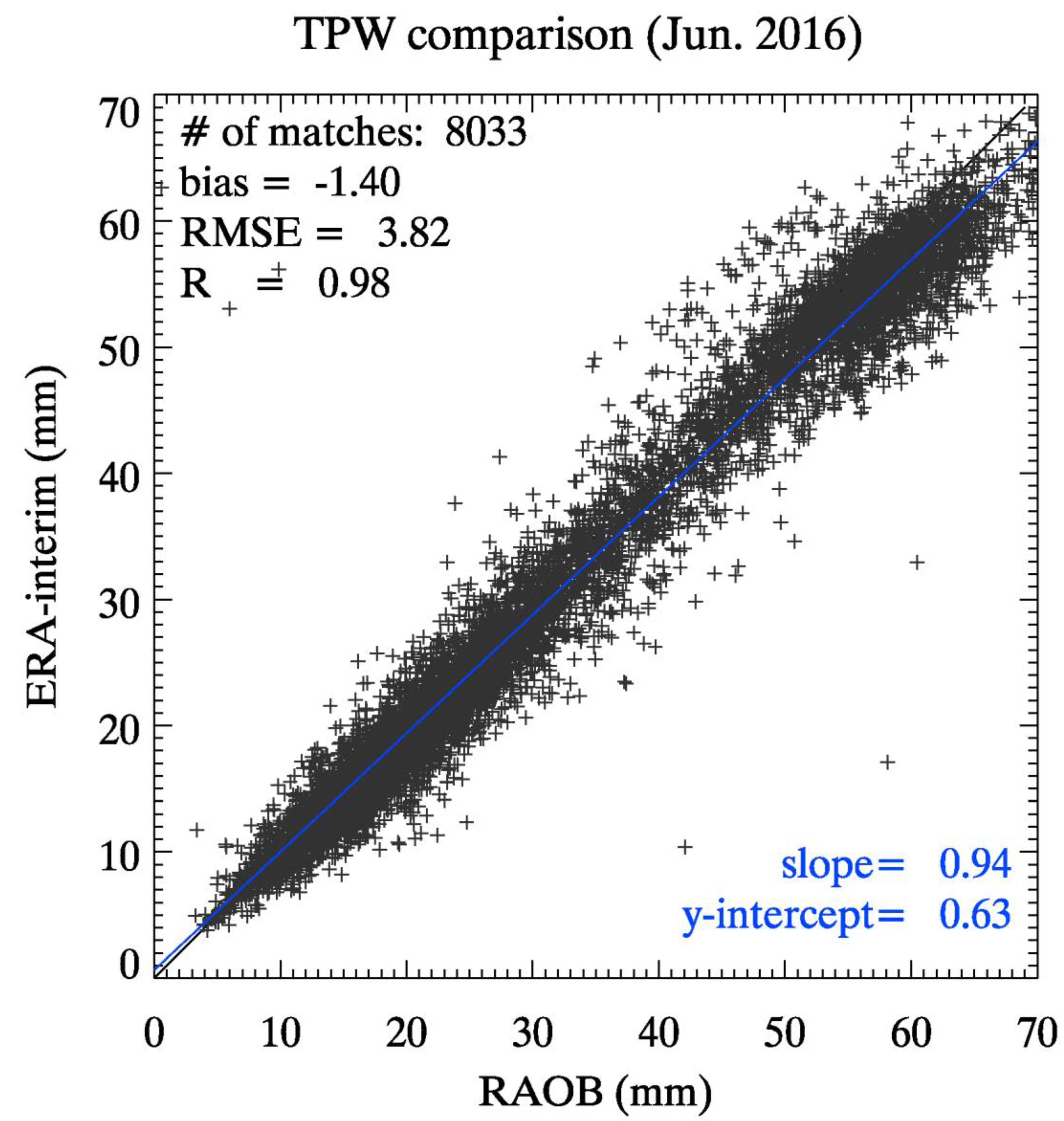
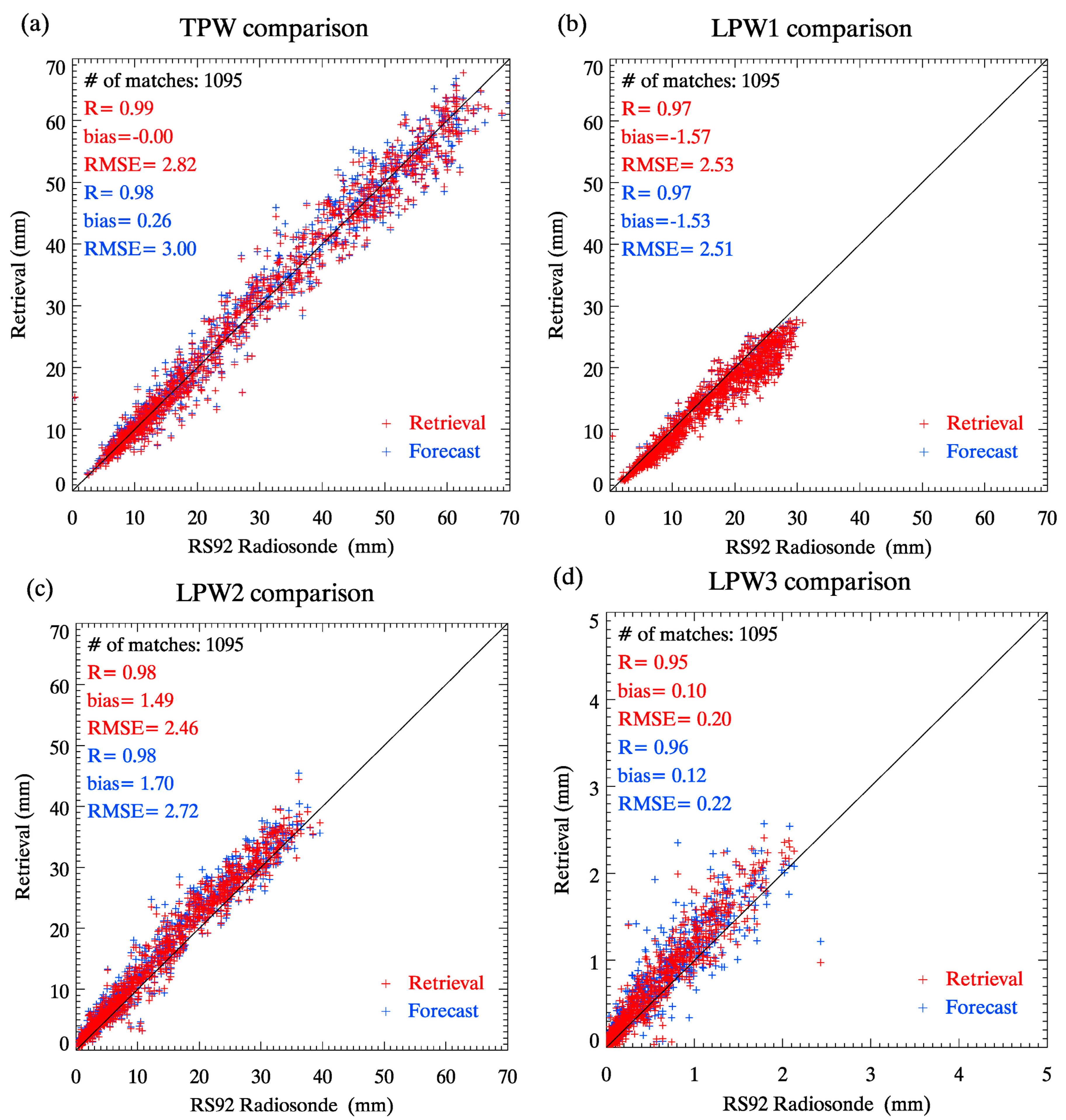
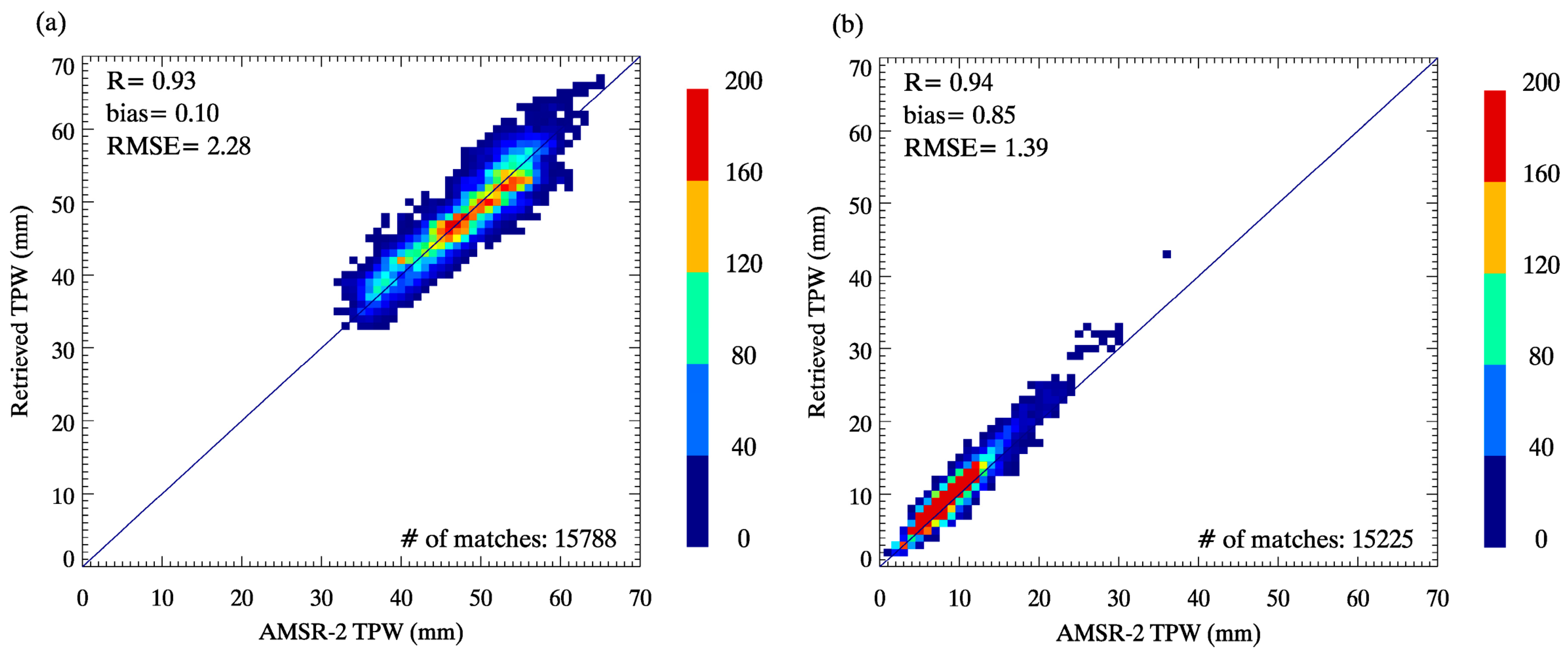
3.2.2. Derived TPW
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ambrosetti, P. Statement of Guidance for Nowcasting and Very Short Range Forecasting (VSRF). World Meteorological Organization. Available online: http://www.wmo.int/pages/prog/www/OSY/SOG/SoG-Nowcasting-VSRF.pdf (accessed on 10 October 2017).
- Lee, J.; Lee, S.-W.; Han, S.-O.; Lee, S.-J.; Jang, D.-E. The Impact of Satellite Observations on the UM-4DVar Analysis and Prediction System at KMA. Atmos. Korean Meteorol. Soc. 2011, 21, 85–93. (In Korean) [Google Scholar]
- Schmit, T.J.; Li, J.; Gurka, J.J.; Goldberg, M.D.; Schrab, K.J.; Li, J.; Feltz, W.F. GOES-R Advanced Baseline Imager and the Continuation of Current Sounder Products. J. Appl. Meteorol. Climatol. 2008, 47, 2696–2711. [Google Scholar] [CrossRef]
- Jin, X.; Li, J.; Schmit, T.J.; Li, J.; Goldberg, M.D.; Gurka, J.J. Retrieving clear-sky atmospheric parameters from SEVIRI and ABI infrared radiances. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Menzel, W.P.; Schmit, T.J.; Nelson, J.P., III; Daniels, J.; Ackerman, S.A. GOES sounding improvement and applications to severe storm nowcasting. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Lee, Y.-K.; Li, Z.; Li, J. Evaluation of the GOES-R ABI LAP Retrieval Algorithm Using the GOES-13 Sounder. J. Atmos. Ocean. Technol. 2014, 31, 3–19. [Google Scholar] [CrossRef]
- KMA. Status Report on the Current and Future Satellite Systems by KMA; Presented to CGMS-43 Plenary Session, Agenda Item [E.1]; University Corporation for Atmospheric Research (UCAR): Boulder, CO, USA, 2015. [Google Scholar]
- Rodgers, C.D. Retrieval of atmospheric temperature and composition from remote measurements of thermal radiation. Rev. Geophys. 1976, 14, 609–624. [Google Scholar] [CrossRef]
- Ma, X.L.; Schmit, T.J.; Smith, W.L. A nonlinear physical retrieval algorithm—Its application to the GOES-8/9 sounder. J. Appl. Meteorol. 1999, 38, 501–513. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; Taylor, F.W., Ed.; World Scientific Publishing: Singapore, 2000; Volume 2, pp. 21–41, 81–99. ISBN 981-02-2740-X. [Google Scholar]
- Li, J.; Schmit, T.J.; Jin, X.; Martin, G. GOES-R Advanced Baseline Imager (ABI) Algorithm Theoretical Basis Document for Legacy Atmospheric Moisture Profile, Legacy Atmospheric Temperature Profile, Total Precipitable Water and Derived Atmospheric Stability Indices; U.S. Department of Commerce: Washington, DC, USA; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA; National Environmental Satellite, Data and Information Service: Silver Spring, MD, USA, 2012.
- Eyre, J.R. Inversion of cloudy satellite sounding radiances by nonlinear optimal estimation. I: Theory and simulation for TOVS. Q. J. R. Meteorol. Soc. 1989, 115, 1001–1026. [Google Scholar] [CrossRef]
- Matricardi, M.; Chevallier, F.; Kelly, G.; Thepaut, J.-N. An improved general fast radiative transfer model for the assimilation of radiance observations. Q. J. R. Meteorol. Soc. 2004, 130, 153–173. [Google Scholar] [CrossRef]
- Renshaw, R. Bias Correction Procedures for ATOVS—A Brief Guide: Bias Correction of (A)TOVS Radiances. Available online: http://nwpsaf.eu/oldsite/deliverables/aapp/biasguide.htm (accessed on 22 September 2017).
- Zou, X.; Zhuge, X.; Weng, F. Characterization of Bias of Advanced Himawari Imager Infrared Observations from NWP Background Simulations Using CRTM and RTTOV. J. Atmos. Ocean. Technol. 2016, 33, 2553–2567. [Google Scholar] [CrossRef]
- Hewison, T.J.; Wu, X.; Yu, F.; Tahara, Y.; Hu, X.; Kim, D.; Koenig, M. GSICS Inter-Calibration of Infrared Channels of Geostationary Imagers Using Metop/IASI. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1160–1170. [Google Scholar] [CrossRef]
- McPeters, R.D.; Labow, G.J. Climatology 2011: An MLS and sonde derived ozone climatology for satellite retrieval algorithms. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Ha, S.; Ahn, M.-H.; Lee, S.J. Possibility of an improved total ozone information from the high performance geostationary imager data. Presented at Asia Oceania Geosciences Society, Singapore, 6–11 August 2017. [Google Scholar]
- Bannister, R.N. A review of forecast error covariance statistics in atmospheric variational data assimilation. I: Characteristics and measurements of forecast error covariances. Q. J. R. Meteorol. Soc. 2008, 134, 1951–1970. [Google Scholar] [CrossRef]
- Stewart, L.M.; Dance, S.L.; Nichols, N.K. Data assimilation with correlated observation errors: Experiments with a 1-D shallow water model. Tellus A Dyn. Meteorol. Oceanogr. 2013, 65. [Google Scholar] [CrossRef]
- Yao, Z.; Li, J.; Li, J.; Zhang, H. Surface emissivity impact on temperature and moisture soundings from hyperspectral infrared radiance measurements. J. Appl. Meteorol. Climatol. 2011, 50, 1225–1235. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Weisz, E.; Schmit, T.; Goldberg, M.; Zhou, D. The simultaneous retrieval of hyperspectral IR emissivity spectrum along with temperature and moisture profiles from AIRS. Int. Soc. Opt. Eng. 2007, 66840L. [Google Scholar] [CrossRef]
- Seemann, S.W.; Borbas, E.E.; LI, J.; Menzel, W.P.; Gumley, L.E. MODIS Atmospheric Profile Retrieval Algorithm Theoretical Basis Document; ATBD07 Version 6; Cooperative Institute for Meteorological Satellite Studies, University of Wisconsin-Madison: Madison, WI, USA, 25 October 2006. [Google Scholar]
- Maddy, E.S.; Barnet, C.D. Vertical Resolution Estimates in Version 5 of AIRS Operational Retrievals. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2375–2384. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; de Leeuw, G. Satellite Aerosol Remote Sensing over Land; Springer Science & Business Media: Berlin, Germany, 2009; pp. 228–235. ISBN 978-3-540-69397-0. [Google Scholar]
- Chung, E.-S.; Soden, B.J.; Sohn, B.J.; Schmetz, J. An assessment of the diurnal variation of upper tropospheric humidity in reanalysis data sets. J. Geophys. Res. Atmos. 2013, 118, 3425–3430. [Google Scholar] [CrossRef]
- Noh, Y.-C.; Sohn, B.-J.; Kim, Y.; Joo, S.; Bell, W. Evaluation of temperature and humidity profiles of Unified Model and ECMWF analyses using GRUAN radiosonde observations. Atmosphere 2016, 7, 94. [Google Scholar] [CrossRef]
- Moradi, I.; Arkin, P.; Ferraro, R.; Eriksson, P.; Fetzer, E. Diurnal variation of tropospheric relative humidity in tropical regions. Atmos. Chem. Phys. 2016, 16, 6913–6929. [Google Scholar] [CrossRef]
- Sun, B.; Reale, A.; Seidel, D.J.; Hunt, D.C. Comparing radiosonde and COSMIC atmospheric profile data to quantify differences among radiosonde types and the effects of imperfect collocation on comparison statistics. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Soden, B.J.; Lanzante, J.R. An assessment of satellite and radiosonde climatologies of upper tropospheric water vapor. J. Clim. 1996, 9, 1235–1250. [Google Scholar] [CrossRef]
- Ingleby, B. An Assessment of Different Radiosonde Types 2015/2016; ECMWF Technical Memorandum No. 807; European Centre for Medium Range Weather Forecasts: Reading, UK, 2017. [Google Scholar]
- Ingleby, B. On the Accuracy of Different Radiosonde Types—WMO. TECO-2016 Madrid, 30 September 2016. Available online: www.wmo.int/pages/prog/www/IMOP/meetings/Upper-Air/ET-IOC-3/Doc3.1(1).pdf (accessed on 11 August 2017).
- JAXA. Status of A R2 Level-2 Products (Algorithm Ver. 2.00). 2015. Available online: suzaku.eorc.jaxa.jp/GCOM_W/materials/product/AMSR2_L2_2.pdf (accessed on 25 September 2017).
- Duncan, D.I.; Kummerow, C.D. A 1DVAR retrieval applied to GMI: Algorithm description, validation and sensitivities. J. Geophys. Res. Atmos. 2016, 121, 7415–7429. [Google Scholar] [CrossRef]
- EUMETSAT. Product Tutorial on Total Precipitable Water Content Products. 2014. Available online: http://www.eumetrain.org/data/3/359/print_3.htm#page_1.0.0 (accessed on 11 October 2017).
- Li, J.; Gerth, J.; Lee, Y.-K.; Li, Z.; Schmit, T.J.; Wang, P.; Bachmeier, S. High resolution all-sky water vapor products from new generation of geostationary satellites and their applications in weather forecasts. Presented at the 7th Asia-Oceania Meteorological Satellite Users’ Conference, Songdo City, Korea, 24–27 October 2016. [Google Scholar]
- Kwon, E.-H.; Sohn, B.J.; Smith, W.L.; Li, J. Validating IASI temperature and moisture sounding retrievals over East Asia using radiosonde observations. J. Atmos. Ocean. Technol. 2012, 29, 1250–1262. [Google Scholar] [CrossRef]
- Kown, E.-H.; Li, J.; Li, J.; Shon, B.J.; Weisz, E. Use of total precipitable water classification of a priori error and quality control in atmospheric temperature and water vapor sounding retrieval. Adv. Atmos. Sci. 2012, 29, 263–273. [Google Scholar] [CrossRef]

| Channel | AMI GK-2A | AHI Himawari-8 | ABI GOES-R |
|---|---|---|---|
| VIS | 0.47 | 0.46 | 0.47 |
| 0.51 | 0.51 | ||
| 0.64 | 0.64 | 0.64 | |
| 0.856 | 0.86 | 0.865 | |
| NIR | 1.38 | 1.378 | |
| 1.61 | 1.6 | 1.61 | |
| 2.3 | 2.25 | ||
| SWIR | 3.8 | 3.9 | 3.90 |
| IR | 6.2 | 6.2 | 6.185 |
| 6.95 | 6.9 | 6.95 | |
| 7.3 | 7.3 | 7.34 | |
| 8.6 | 8.6 | 8.50 | |
| 9.6 | 9.6 | 9.61 | |
| 10.4 | 10.4 | 10.35 | |
| 11.2 | 11.2 | 11.2 | |
| 12.36 | 12.4 | 12.3 | |
| 13.3 | 13.3 | 13.3 |
| Measurements (TB) | AHI TBs from 9 infrared channels (6.2, 6.9, 7.3, 8.6 *, 9.6, 10.4, 11.2, 12.4, 13.3) |
| First-Guess () | T and Q: 6 to 11 h KMA UM forecast |
| O3: monthly climatology improved using OMI total ozone | |
| Observation Error Covariance () | Error covariance for instrument noise (NEdT) and RTM error |
| Background Error Covariance () | T and Q: B-matrix used in KMA OPS 1DVar |
| O3: B-matrix used in ECMWF 1DVar | |
| LSE | Monthly climatology generated from CIMSS global LSE database |
| RTM | RTTOV v.11.2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.J.; Ahn, M.-H.; Chung, S.-R. Atmospheric Profile Retrieval Algorithm for Next Generation Geostationary Satellite of Korea and Its Application to the Advanced Himawari Imager. Remote Sens. 2017, 9, 1294. https://doi.org/10.3390/rs9121294
Lee SJ, Ahn M-H, Chung S-R. Atmospheric Profile Retrieval Algorithm for Next Generation Geostationary Satellite of Korea and Its Application to the Advanced Himawari Imager. Remote Sensing. 2017; 9(12):1294. https://doi.org/10.3390/rs9121294
Chicago/Turabian StyleLee, Su Jeong, Myoung-Hwan Ahn, and Sung-Rae Chung. 2017. "Atmospheric Profile Retrieval Algorithm for Next Generation Geostationary Satellite of Korea and Its Application to the Advanced Himawari Imager" Remote Sensing 9, no. 12: 1294. https://doi.org/10.3390/rs9121294
APA StyleLee, S. J., Ahn, M.-H., & Chung, S.-R. (2017). Atmospheric Profile Retrieval Algorithm for Next Generation Geostationary Satellite of Korea and Its Application to the Advanced Himawari Imager. Remote Sensing, 9(12), 1294. https://doi.org/10.3390/rs9121294






