3.1. TES Algorithm
The Temperature-Emissivity Separation (TES) method was first proposed in [
10] to obtain LST and LSE from the five TIR ASTER channels. TES is applied to channel
i at-surface radiance (
Lsurf,i), as given by Equation (3):
where
is Planck’s function for the effective wavelength
λi of each ASTER band at surface temperature
T,
is the channel emissivity and
is the downwelling atmospheric irradiance. TES starts with the Normalized Emissivity Method (NEM) module [
19], in which the at-surface radiances obtained from the atmospherically-corrected at-sensor radiances are introduced into Equation (3) using an initial surface emissivity value, generally 0.99, for all channels and pixels, and the Planck radiance
is retrieved for each band:
Planck radiances are then inverted obtaining five temperature values. The maximum temperature value (
TNEM) is chosen as the first approximation to the LST. Using
TNEM in Equation (3), new emissivity values are retrieved for each band (
):
values are used to retrieve the temperature-independent
index (
spectrum):
where
is the mean value of NEM emissivities of the five TIR bands. Then, the difference between maximum and minimum
β values is calculated (maximum-minimum difference or
MMD). The
MMD is related to the minimum value of the emissivity spectrum (
) in accordance with an empirical relationship (calibration curve), which is obtained using a set of spectra of rocks, soils, vegetation, snow and water given in the ASTER library [
35]. Hulley and Hook in [
12] obtained a new expression, which adjusts better to vegetated covers since they used a larger number of vegetated cover types to estimate the
MMD regression curve, which is:
This expression was compared with the one given by Gillespie et al. in [
10]. The difference between both expressions according to the
MMD value is shown in
Figure 2. This difference is higher for
MMD values between 0.05 and 0.15, showing a maximum disagreement up to 1% in the minimum emissivity estimation.
Finally, the emissivity spectrum is calculated using
together with the
β spectrum.
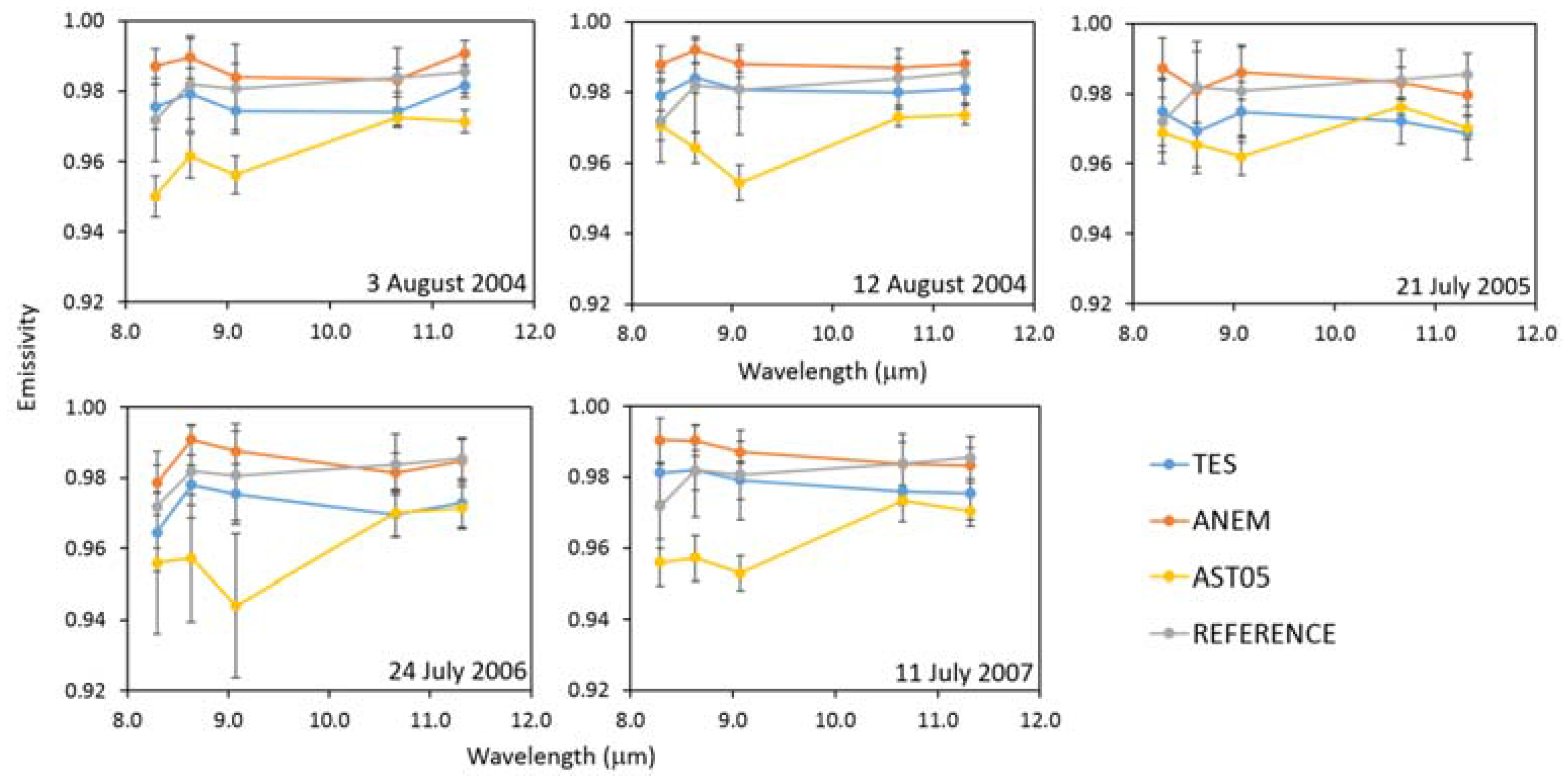
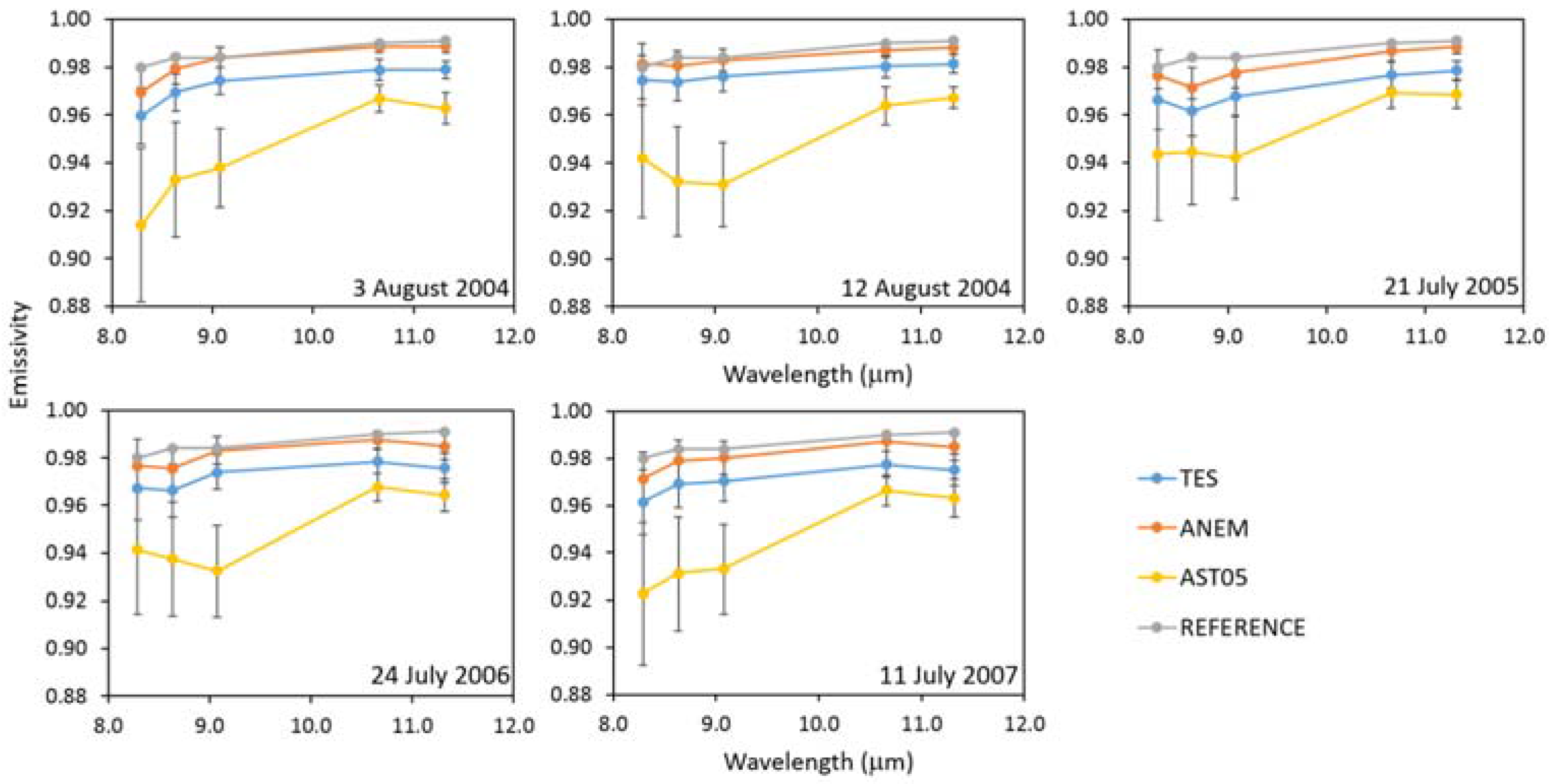
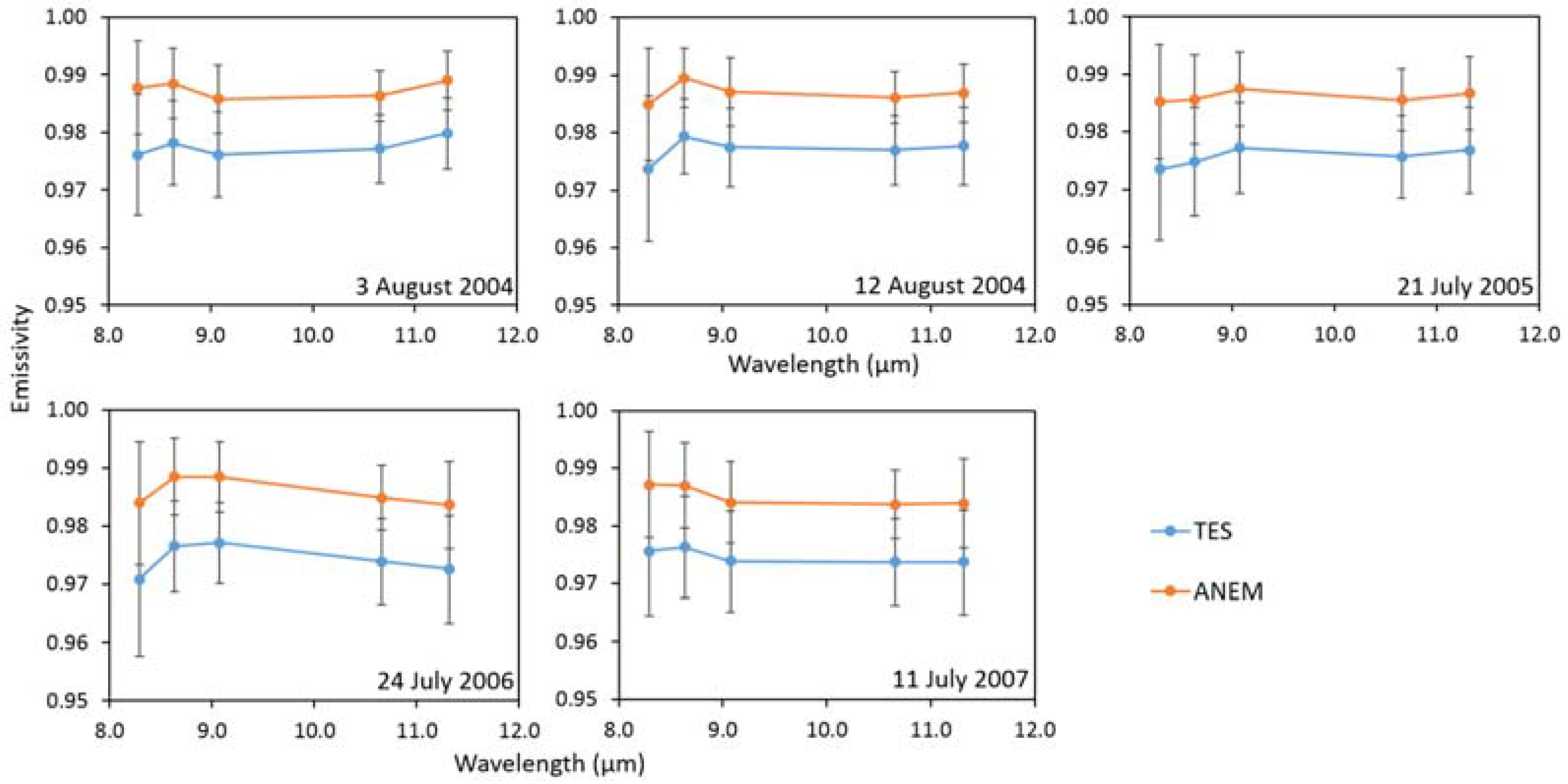
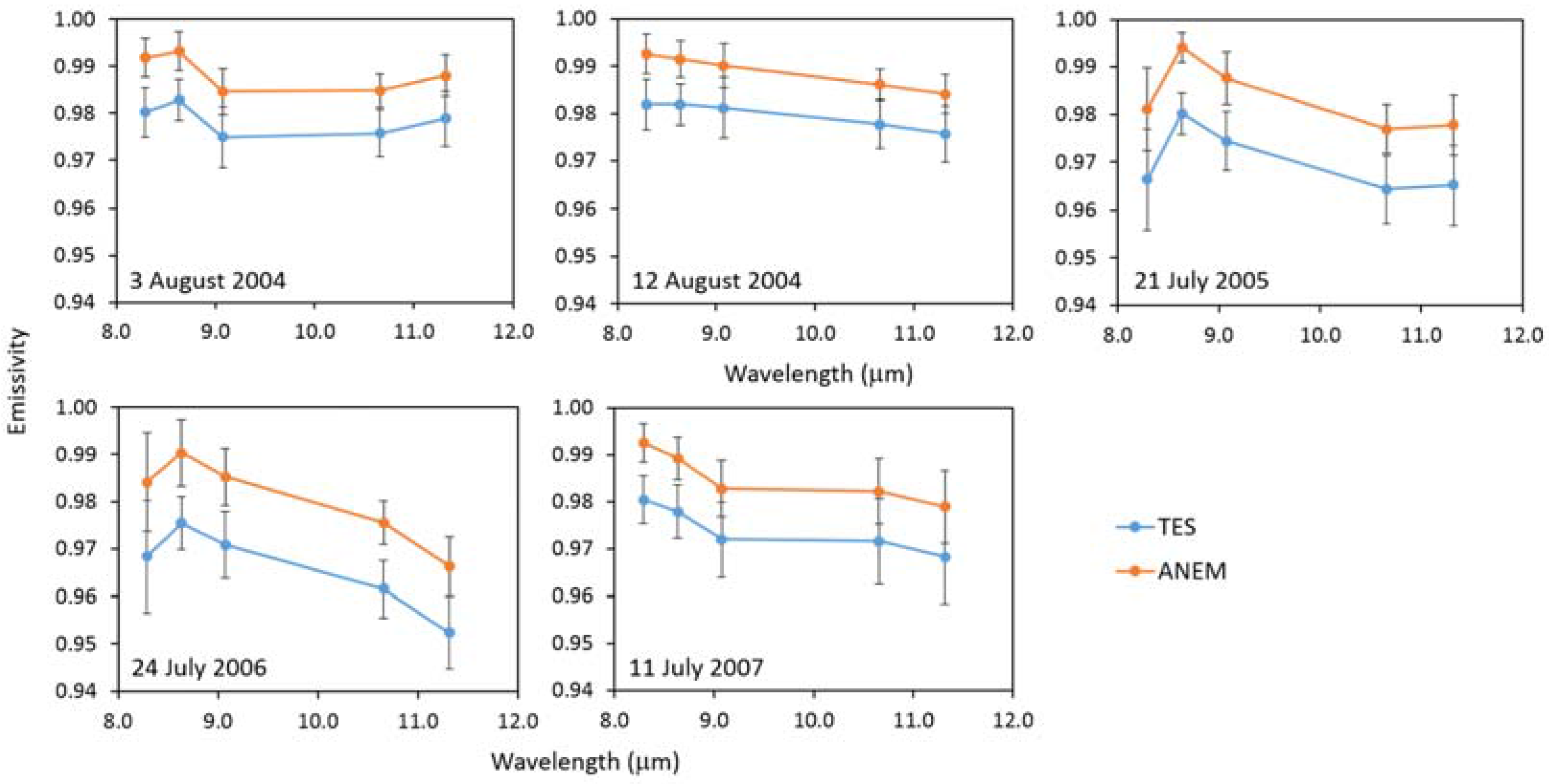
The emissivity spectra obtained from Equation (8) are then used in Equation (4), from which five new temperatures are retrieved. These new temperatures should be equal, but often, they present small differences. If these differences are lower than the noise equivalent temperature difference (NEΔT) of ASTER (±0.3 K), then the maximum of the obtained temperature values is considered as the best estimate of LST.
3.2. ANEM Algorithm
The Adjusted Normalized Emissivity Method (ANEM) was proposed in [
18] as a combination of the Vegetation Cover Method (VCM) [
20,
36] and NEM [
19], explained in
Section 3.1. In ANEM, the emissivity introduced as the input in NEM is retrieved with VCM depending on the vegetation fraction of each pixel in the scene. As a consequence, a different value of emissivity is used for each pixel as initial emissivity for NEM, instead of a unique value for all pixels.
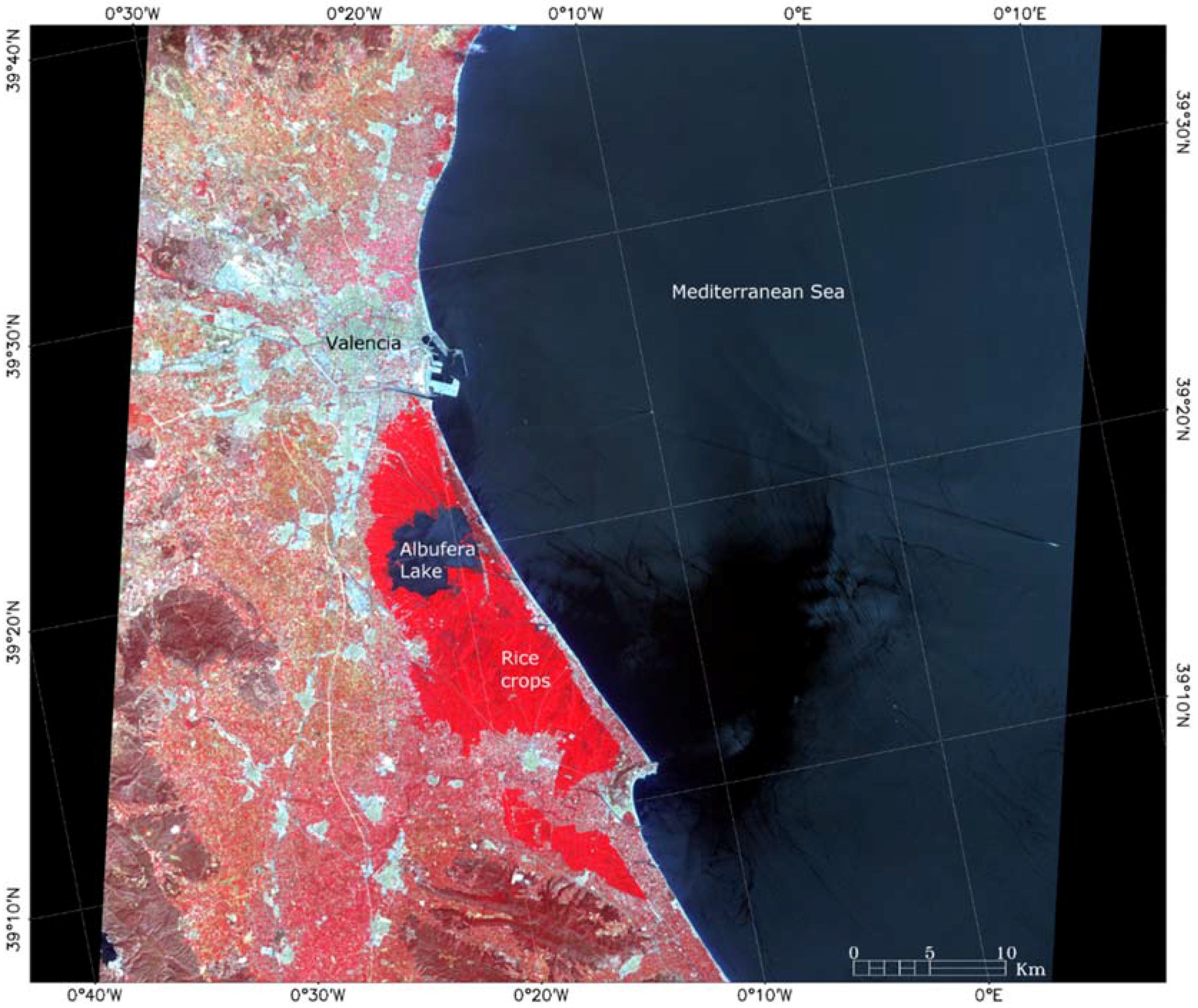
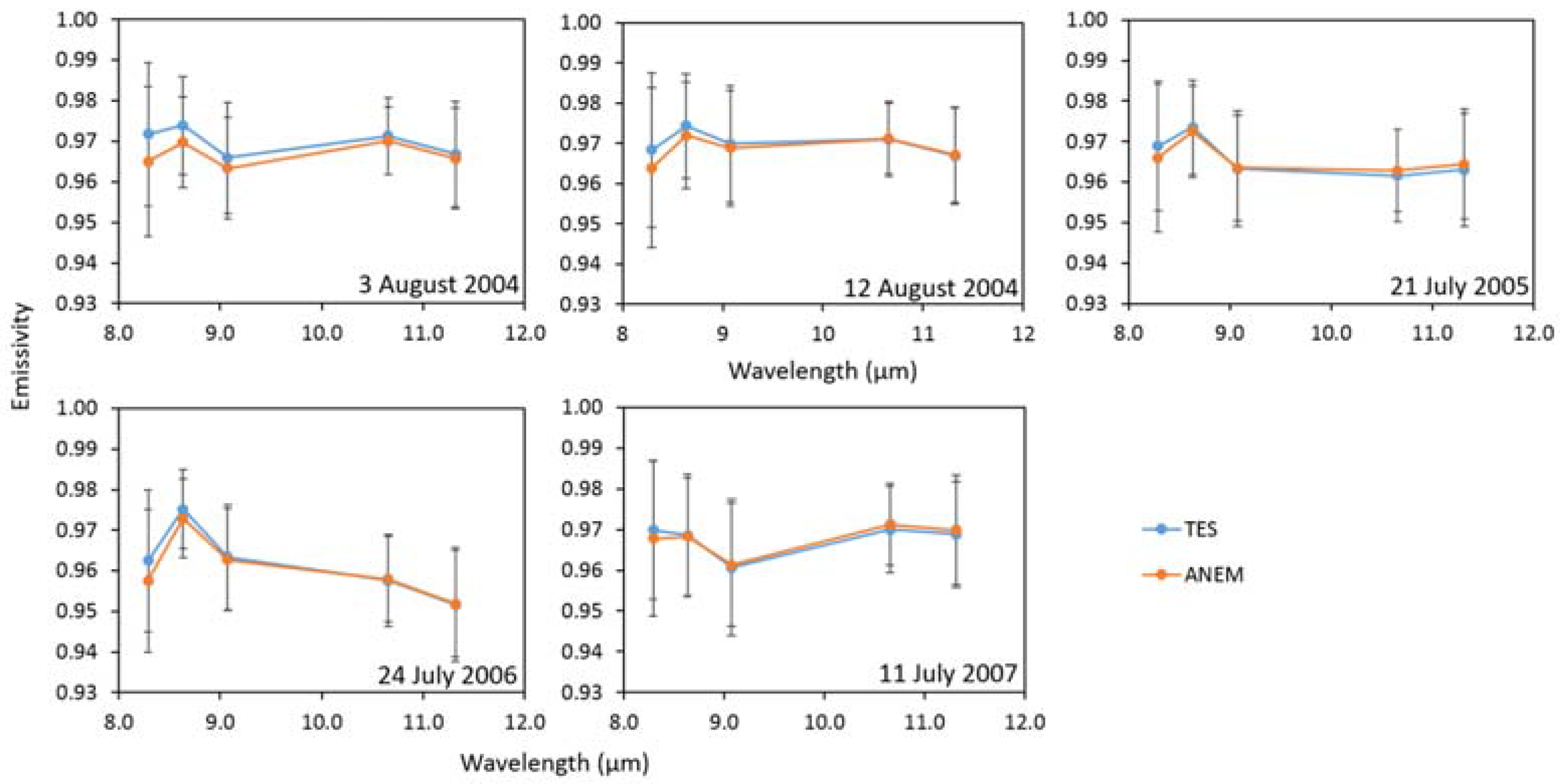
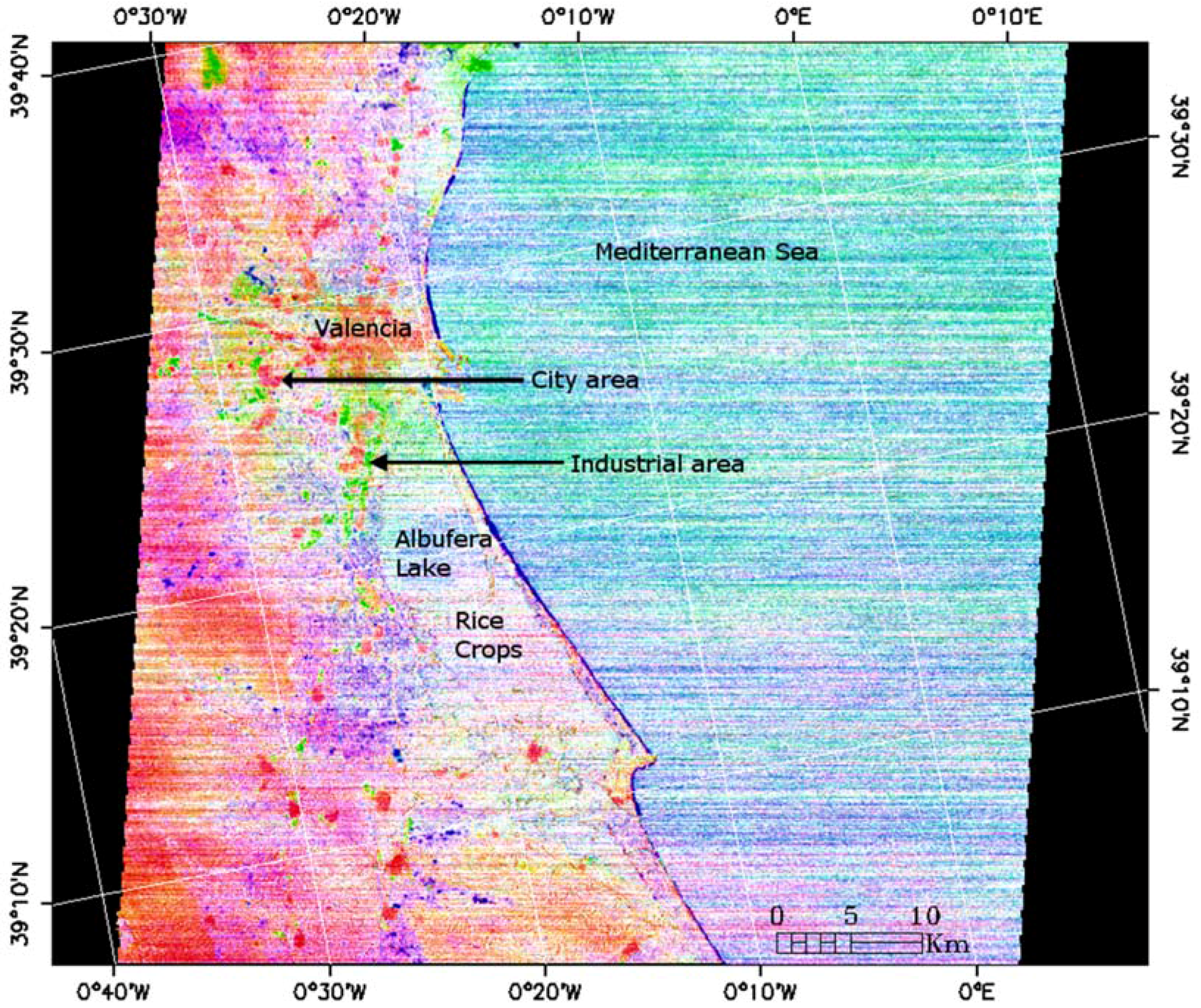
To apply ANEM, it is required to distinguish between natural areas, urban areas and water using the corresponding masks in the scene. They were obtained using ASTER Shortwave Infrared (SWIR) bands (Bands 4–9) with a supervised classification using a Mahalanobis distance of 30 m. We selected the following regions of interest: natural areas including different types of agricultural fields (mainly rice paddies and orange groves) and forested areas; urban areas such as the city of Valencia and other smaller towns around it; and water areas of the Mediterranean Sea and the Albufera Lake. The VCM is applied for natural areas. The effective emissivity of a heterogeneous and rough surface is calculated as:
where
and
are the emissivities of vegetation and soil pixels in band
i, respectively,
is the vegetation fractional cover and
is a term related to the internal reflections between vegetation and soil that depend on the surface structure (cavity term), which is given in [
37]:
The
and
values (see
Table 5) were estimated from the spectra provided in the ASTER spectral library. For vegetation,
was calculated as the average emissivity of green vegetation samples (grass and conifer) for each of the five ASTER TIR bands; while for soil, the procedure is the same, but using 65 soil samples, including 23 aridisols, 11 entisols, 10 mollisols, 9 alfisols, 8 inceptisols, 2 vertisols, 1 spodosol and 1 ultisol. Before the estimation, the different emissivity spectra were integrated with the filter functions of the five ASTER TIR channels to get band-integrated emissivities corresponding to each spectrum.
Different values of vegetation fraction between 0 and 1 were introduced into Equation (9) together with the coefficients given in
Table 5. For each value of
Pv, five different effective emissivity values were retrieved, one per band, then the maximum value was taken. The obtained emissivity maximum values were adjusted against
Pv, with a correlation coefficient of 0.987, resulting in Equation (11), which directly provides the maximum emissivity value to be introduced into NEM as a function of the vegetation fraction:
The vegetation fraction needed in Equation (11) was calculated following the procedure proposed in [
20]:
where
is the Normalized Difference Vegetation Index (NDVI) [
38] of each pixel,
and
are the minimum and maximum NDVI values of the area, which are representative of bare soil and dense vegetation, respectively, and
, where
(
) is the at-surface reflectance value in the red (ASTER Band 2) and near-infrared (ASTER band 3) over pixels where the values
(
) are found. Then, the NDVI image was resized to the SWIR pixel size in order to take the
and
values from the histogram of the scene taking into consideration only the pixels belonging to the natural areas mask. Using the cumulative histogram, the mean value of the pixels between percentiles 4 and 7 was used to calculate
, while the mean of the pixels with percentiles between 93 and 96 of the NDVI distribution was used to obtain
.
Since the previous procedure is not applicable in the case of urban zones and water surfaces, an input emissivity value for the NEM module was determined for them. For water, the emissivity values for the ASTER channels were obtained from Niclòs et al. in [
30] (see
Table 4). The maximum value was taken as ε
max = 0.991 corresponding to ASTER Band 14.
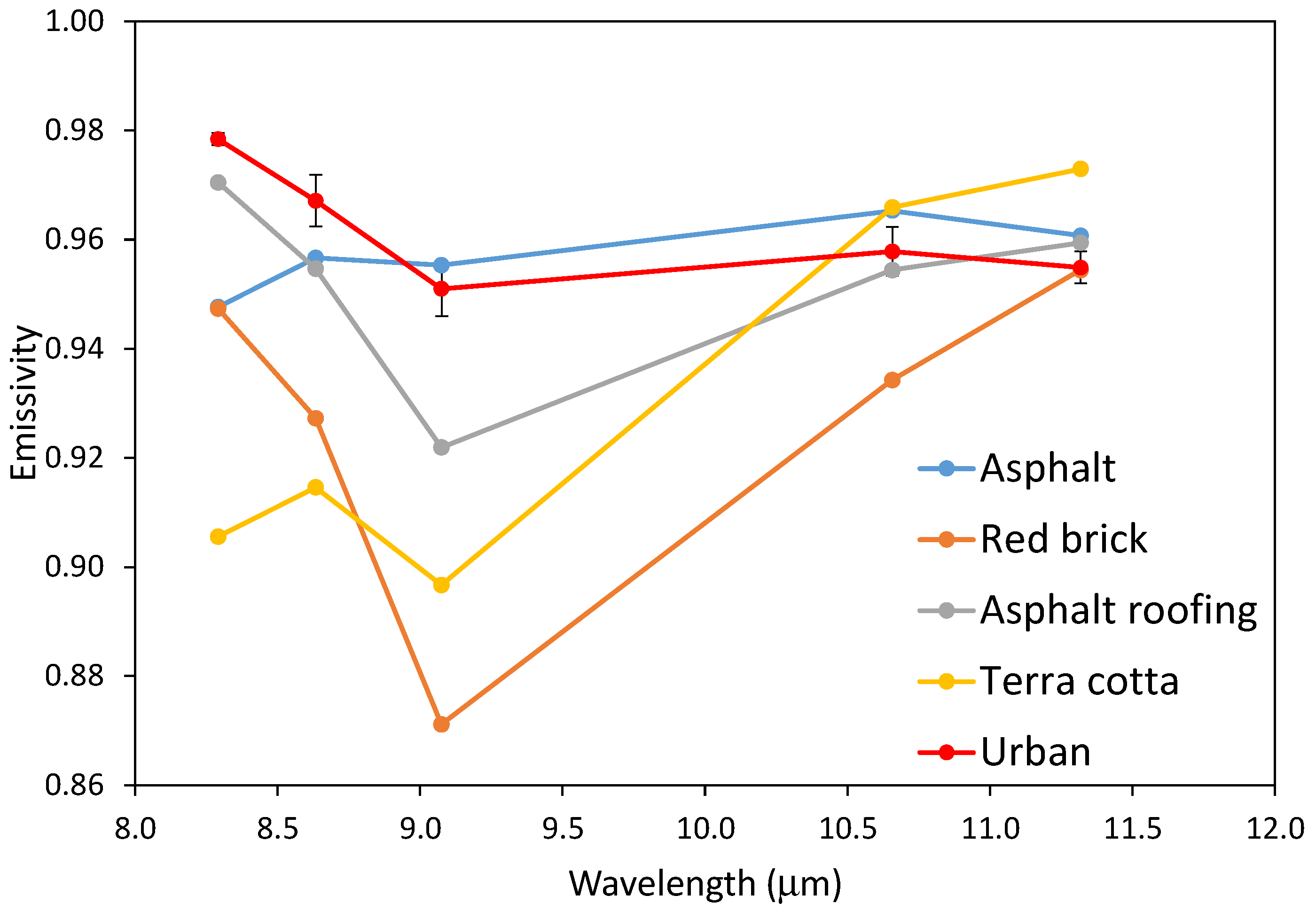
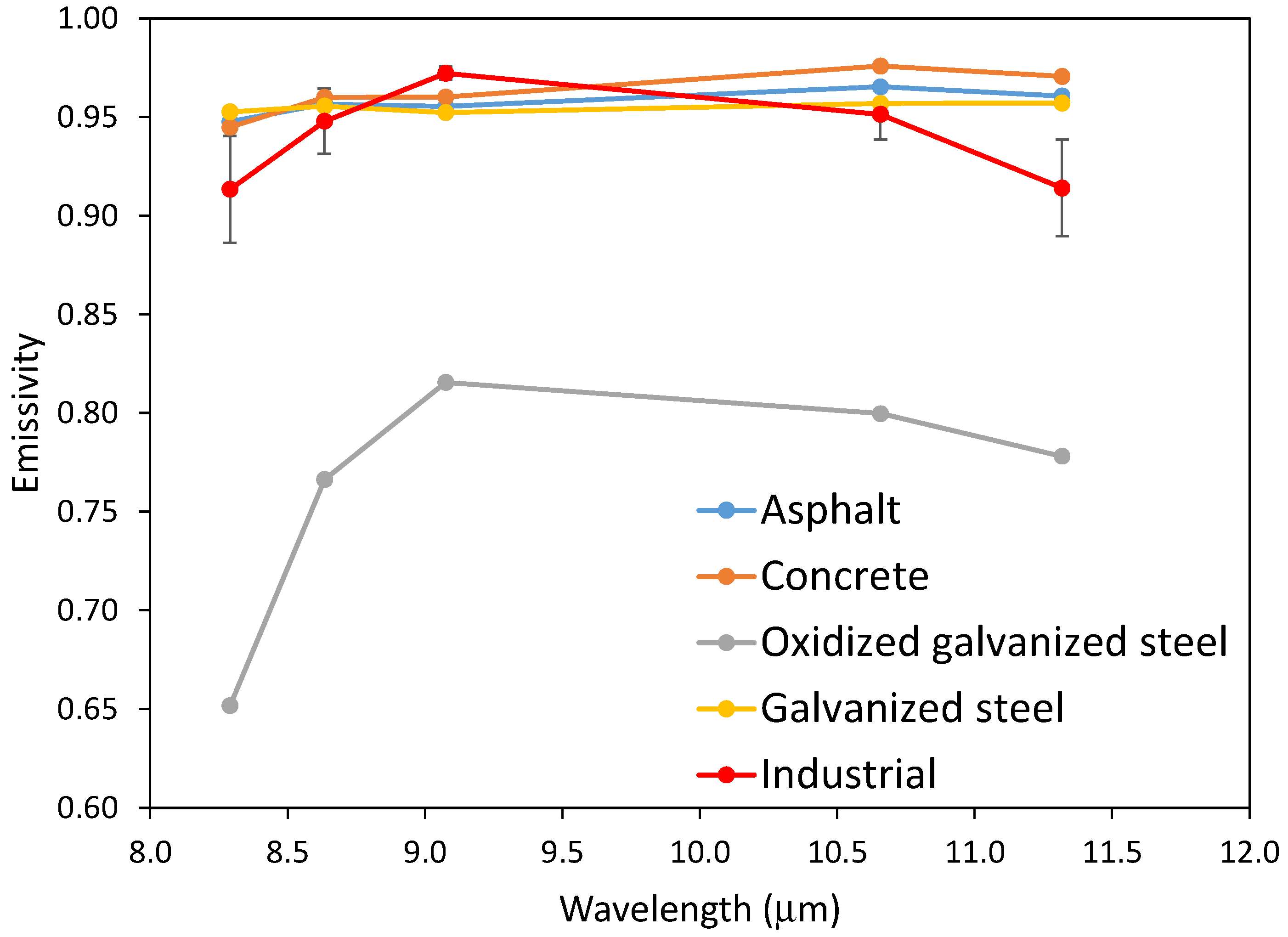
For urban areas, the ASTER library spectra of manmade materials were divided into three groups: construction concrete (to estimate the emissivity of building walls), road asphalts and tars (to estimate the emissivity of streets) and roofing materials (emissivity of building tops). All the spectra in these groups were integrated with the filter functions. For each group, the average and the standard deviation were calculated, obtaining three values of emissivity with a given uncertainty (see
Table 6). With these values, the effective emissivity of the urban areas was determined using the model of Caselles and Sobrino described in [
39]:
where
is the roofing materials emissivity (building tops),
is road asphalts and tars emissivity (streets),
is construction concrete emissivity (building walls),
is the roof proportion,
H is the height of components in the urban area and
S is the separation between these components.
In the calculations, different combinations of the aspect ratio
H/
S (from 0.5–10, at intervals of 0.5) and
(from 0.2–0.8, at intervals of 0.05) were considered for the possible urban structures. Using these values, urban emissivity values were simulated using a random procedure considering that the different variables in Equation (13) were normally distributed around a mean value, given by the mean values in
Table 6, with a standard deviation given by the corresponding uncertainties in that table. Each simulation in this procedure gives as a result an emissivity for the urban area. The procedure was repeated 25 times, from which the final urban emissivity value was calculated as the average of the 25 different obtained values. It was checked that the use of a larger number of repetitions did not change the obtained average value and the standard deviation. The final values and uncertainties for the urban emissivity at the ASTER bands are shown in
Table 6.
In the ANEM algorithm, the VCM emissivity values for the natural areas must be calculated for each scene; however, the estimated values for water and urban areas can be used for every ASTER scene and do not need to be estimated again.