Abstract
Synthetic Aperture Radar Tomography (TomoSAR) allows the reconstruction of the 3D reflectivity of natural volume scatterers such as forests, thus providing an opportunity to infer structure information in 3D. In this paper, the potential of TomoSAR data at L-band to monitor temporal variations of forest structure is addressed using simulated and experimental datasets. First, 3D reflectivity profiles were extracted by means of TomoSAR reconstruction based on a Compressive Sensing (CS) approach. Next, two complementary indices for the description of horizontal and vertical forest structure were defined and estimated by means of the distribution of local maxima of the reconstructed reflectivity profiles. To assess the sensitivity and consistency of the proposed methodology, variations of these indices for different types of forest changes in simulated as well as in real scenarios were analyzed and assessed against different sources of reference data: airborne Lidar measurements, high resolution optical images, and forest inventory data. The forest structure maps obtained indicated the potential to distinguish between different forest stages and the identification of different types of forest structure changes induced by logging, natural disturbance, or forest management.
1. Introduction
Forests are three-dimensional (3D) ecosystems whose 3D structure is strongly affected by dynamic processes such as growth, regeneration, decay and disturbance, and thus closely related to their history, diversity, function, microclimate and yield [1]. Accordingly, 3D forest structure information is important for understanding and modelling the succession, function and development of forest ecosystems, and provides insight into ecological processes and forest dynamics. At the same time, forest structure information is essential for the development of accurate forest biomass estimators that are required to better understand and quantify the contribution of forest ecosystems to the global carbon cycle [2,3,4].
Forest structure monitoring has traditionally been performed by inventory measurements that provide accurate estimates of a number of (single) trees and stand parameters. However, inventory measurements are demanding in time and resources so that they are usually performed at smaller scales with rather low update rates. Given this, spaceborne Synthetic Aperture Radar (SAR) imaging configurations provide continuous forest mapping with global coverage at spatial and temporal resolutions relevant to the detection of changes on the forests. This, combined with the fact that radar signals—especially at lower frequencies—penetrate even dense forest canopies interacting with forest structure components at different heights, make SAR an important element in the context of global forest monitoring.
Indeed, in the last few years, a significant effort has been made to demonstrate and validate the potential of conventional SAR configurations to reflect spatial biomass distribution by means of SAR measurements [5]. The introduction of SAR interferometry was a critical step, as interferometric measurements have an increased sensitivity to vertical structure elements of forest. Indeed, the use of polarimetric interferometric measurements has allowed the model based estimation of vertical forest structure parameters such as forest height [6,7,8,9]. In order to reconstruct more detailed vertical distribution of scatterers, multi-baseline interferometric acquisitions have been used [10]. More recently, tomographic acquisitions (TomoSAR), that can be seen as an extension of multi-baseline interferometric acquisitions, have been used to reconstruct the 3D radar reflectivity of forests, to explore for mapping 3D forest structure, and to improve biomass estimators [11,12,13,14,15,16]. These activities were complemented by a number of ground-based [17,18,19,20] and airborne SAR experiments [21] aiming to quantify the impact of temporal decorrelation on the effect of weather and seasonal conditions on a temporal series of TomoSAR data rather than to analyse forest structure dynamics [22,23,24]. The promising results achieved initiated the implementation of TomoSAR acquisition modes in future spaceborne SAR missions, such as Biomass [25] or Tandem-L [26], for mapping at a global scale structural forest parameters and improving biomass estimations.
With respect to forest structure mapping, SAR configurations have a number of advantages when compared to other remote sensing techniques. Compared to optical and hyperspectral imaging configurations, SAR measurements provide significantly higher sensitivity to the vertical arrangement of forest elements due to the ability to penetrate through the vegetation layer and interact with forest structure components at different heights. Compared to Lidar configurations that allow accurate measurements of vertical forest structure, SAR configurations have the advantage of a higher penetration ability through clouds and into/through vegetation as well as in the realization of wide imaging swaths that allows large and global scale coverage at high temporal resolutions.
Motivated by this, this paper explores the potential of L-band TomoSAR data to monitor forest structure changes as induced by natural or anthropogenic disturbances such as logging, fire and forest management. To do this, a methodology for characterising physical forest structure by means of two descriptors that can be derived from TomoSAR data at L-band was used. First, a set of simulated data from a process-based forest model was used to demonstrate the concept of the proposed methodology. In a second step, real experimental datasets acquired over a temperate forest in the south of Germany were employed to test the robustness and consistency of the forest structure estimation methodology with respect to non-structural temporal changes in the forest, together with its sensitivity to structural variations. For the validation of the achieved results, different sources of reference data, including optical data, airborne Lidar measurements and forest inventory data, were used.
2. From Tomographic SAR Measurements to Forest Structure Estimation
Section 2.1 summarizes the principles of TomoSAR imaging for extracting vertical reflectivity profiles from a set of images [10]. Section 2.2 describes the link between the extracted vertical reflectivity profiles and physical forest structure.
2.1. Tomographic SAR Imaging
Provided that the frequency band employed is low enough to penetrate the canopy, multiple SAR acquisitions over the same area with a slightly different incidence angle can allow a 3D reconstruction of the forest reflectivity at a given frequency and polarization. In the following, we refer to the resolution of the SAR images as SLC (single look complex) resolution in range and azimuth.
In particular, the set of SAR images define vector :
A scatterer at a given height introduces a phase difference in the set of interferometric pairs of the images in . These phase differences define the so called steering vector at a given height as:
where is the vertical wavenumber for the ith pair of images and is defined as follows:
where is the wavelength; is the distance to the scatterer; is the incidence angle; and is the orthogonal distance between two acquisitions. The maximum value of gives the theoretical vertical resolution, while the minimum gives the non-ambiguous height interval [10].
From Equation (1), the multi-image covariance matrix can be defined as:
where denotes the expectation; and the Hermitian or transpose conjugate operator. It should be noted that the estimation of the expectation of a stochastic process requires several realizations of that process, which is generally not available in real datasets. Therefore, the process is assumed to be ergodic and is approximated by spatial averaging. This spatial average or multilook operation degrades the SLC resolution. We will refer to tomographic resolution to the one achieved after multilook.
From the steering vector defined in Equation (2), the steering matrix is defined as:
Then, with Equations (4) and (5), the TomoSAR inversion problem can be expressed as [10,27]:
where is the reflectivity matrix whose number of rows equals the number of elements in height, and its number of columns is the number of available polarimetric channels. Since the number of measurements is usually lower than the number of scattering elements along the height, the system in Equation (6) is underdetermined. Several tomographic algorithms, parametric or non-parametric, can be applied to solve it and estimate the 3D radar reflectivity. Among the non-parametric algorithms, Fourier beamforming is coherent, energy preserving, and does not require any a priori assumptions. However, it achieves limited vertical resolution and is prone to ambiguities if the number of baselines is low and/or they are irregularly distributed. With better vertical resolution capabilities, Capon beamforming is currently the standard algorithm most widely employed in the tomographic SAR community [28,29,30]. Aiming to achieve finer vertical resolutions, algorithms based on Compressive Sensing (CS) techniques have been proposed to solve the underdetermined system in Equation (6), and have been successfully applied to urban [31,32] and forest scenarios [33].
It should be noted that different inversion algorithms lead to different reconstructed reflectivity profiles. Therefore, the ability to reflect forest structure variability is may be affected by the technique employed in the inversion [34]. In this paper, vertical reflectivity profiles were obtained through an algorithm based on CS [27], i.e., Equation (6) was solved by convex optimization as:
where , is a wavelet projection matrix; are the wavelet coefficients stands for the mixed norm; and indicates semi-definite positiveness. With this, matrix T contains for every pixel in range and azimuth a reflectivity profile representing the distribution of scatters along height.
2.2. Forest Structure Estimation
In the following, 3D forest structure is understood as the vertical and horizontal arrangement of trees and/or tree elements in space. It is a critical parameter in forest ecology inherently related to ecological processes, forest stand dynamics and forest management practices [35,36]. Furthermore, it is an indicator of biodiversity, disturbance, growth and yield [1]. Despite the difficulties in finding an appropriate characterization for forest structure for a wide range of applications, spatial scales and forest types, it is commonly assumed that two essential aspects of forest structure are the heterogeneity in the position and size of the trees within a stand. Based on this, a systematic framework for the discrimination of ecologically significant structure classes has recently been suggested [37,38], which proposes two complementary measures: one for the horizontal, and one for the vertical structure. In the literature, different measures have been proposed for the estimation of horizontal and vertical forest structure from field data [39,40,41,42,43,44]. In the following the horizontal structure as the standard density index from [44] is used:
where is the number of trees per hectare; and is the mean diameter at breast height. Regarding the estimation of vertical structure , the standard deviation of individual tree heights is used:
Essentially, the horizontal structure index mainly reflects the density of the tallest trees in the unit area considered, while the vertical structure index accounts for the diversity of tree heights. Therefore, according to its structural complexity, a forest stand can be classified in a horizontal/vertical plane (HV plane in the following) as shown in Figure 1.
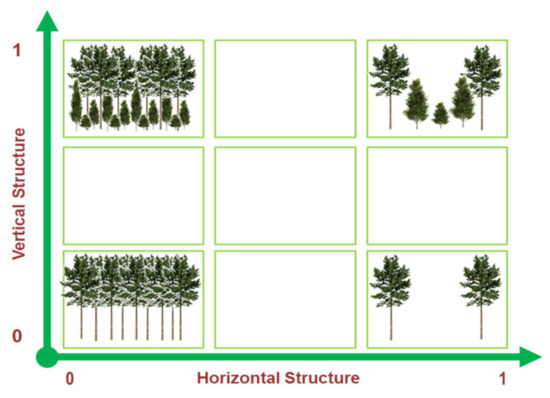
Figure 1.
Horizontal/vertical structure plane proposed for forest structure classification.
Particular airborne SAR techniques such as multi-aspect TomoSAR [45] or holographic SAR [46] can reach higher resolutions and allow the estimation of individual tree profiles. However, this paper is focused on conventional spaceborne acquisitions at low frequencies. In this case, the achievable resolutions do not allow discriminating between individual trees and extracting single-tree parameters. Therefore, any individual-based measure such as and in Equations (8) and (9), cannot be directly estimated from the SAR data used in this paper and instead, indirect correspondences need to be explored to reflect forest structure. In this sense, the presence of a group of trees of similar height is reflected in the reflectivity profiles as a number of peaks (i.e., the maxima of the reconstructed vertical reflectivity profiles) in the range of heights occupied by the canopy [47]. Accordingly, the characterization of forest structure by means of the 3D distribution of peaks in a statistical way appears sensible [34]. Following the characterization of structure from the field data, two complementary indices of structure were estimated from the 3D distribution of reflectivity peaks, one for the horizontal and one for the vertical structure.
Therefore, as a first step, the peaks for every reflectivity profile in the range and azimuth were extracted from the radar reflectivity representing the distribution of scatters along height . Then, A three-dimensional (range, azimuth, height) matrix is the defined with ones at the position of every peak. From this matrix, the horizontal and vertical indicators were estimated.
The horizontal structure descriptor is related to the density of peaks in the upper layer of the forest for a given unit structure window. This upper layer was defined as the range of heights from to , where is defined as the height of the highest peak and is equal to or 5 m, when 60% of the maximum height was lower than 5. As an example, Figure 2 shows the peaks obtained from the reflectivity profile and the green dots represent the peaks in the top layer. The horizontal descriptor was then estimated for every pixel in the image as the total number of peaks in the upper layer in the unit window centered on that pixel, divided by the area of this unit window:
where represents the size of the unit structure window (50 m × 50 m); the sub-index represents the height dimension; and is the area in square meters of the unit structure window. It is worth mentioning that independent of the resolution of the SLC images, the peaks of matrix were projected in a grid of 1 m × 1 m before counting the number of peaks in the unit structure window. This allows us to normalize the number of peaks when systems at different resolutions were employed.
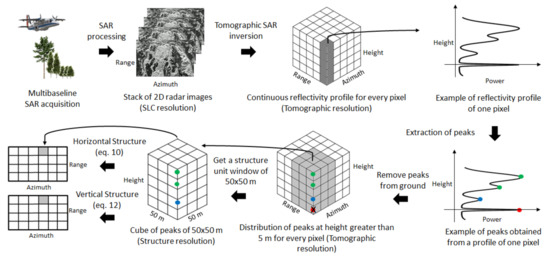
Figure 2.
Steps to estimate forest structure using multibaseline Synthetic Aperture Radar (SAR) measurements.
Once the horizontal descriptor is computed for every pixel in the image, for the whole image is normalized as:
where represents the maximum in the image, or in the set of images to be compared.
Regarding the vertical structure descriptor , a mask of 5 m (empirically set) was first applied to avoid peaks produced by the ground (red peak in Figure 2). Then, the vertical descriptor is defined for every pixel in the image as:
where is a vector with the heights at which at least one peak is found in the unit structure window; is the length of ; and represents the mean of vector . For example, if in a given area the heights in meters of the peaks are then and . Finally, the vertical descriptor is normalized by its maximum within the image (or within the set of images that are going to be compared). It is worth mentioning that since the vertical structure index is reflected by the dispersion of the heights of the peaks, it is not significantly affected by changes in the vertical resolution of the system employed. It should be mentioned that similar measures can be found in the literature for waveform Lidar [48,49].
Furthermore, it is important to note here that system and, even more so, seasonal or environmental variability of the forest may affect the tomographic reflectivity and impact the estimation of structure indices. However, the location of the reflectivity peaks appears to be significantly more robust against system and environmental variability than other profile parameters [37]. This is the reason why the estimation of the structure indices relies only on the position of the peaks and ignores absolute or even relative intensity information.
The main steps to obtain the horizontal and vertical forest structure descriptors using multibaseline SAR measurements are shown in Figure 2.
3. Simulated Data
The proposed methodology was first applied on a set of simulated data. The data were generated in two steps. First, an individual-based forest model was used to generate the distribution of trees within stands for different forest conditions. Second, the multi-image covariance matrix was estimated for a set of vertical wavenumbers at a given spatial resolution. Both steps are described below.
3.1. The Forest Model
Forest-gap models are well-established tools used to investigate forest dynamics, and are able to account for processes such as growth, mortality and regeneration on the tree level, and thus able to simulate a wide range of different forest structure types [50,51]. In this study, FORMIND, an individual and process-based forest gap model designed especially for tropical and temperate forests was used. A detailed description of the model can be found in [52,53] where an African tropical forest parametrization was used for forest succession over 500 years on a scale of 100 hectares [54]. The advantage of employing complex tropical forest scenes in simulations is that they show higher complexity, mainly in the vertical structure, which allows for a better assessment of the effect of the different processes.
Six different scenarios were simulated and investigated. For each of them, FORMIND generated the full tree list including position, stem diameter and height for each individual tree. The normalized distribution of tree heights for each of the six scenarios is shown in Figure 3.
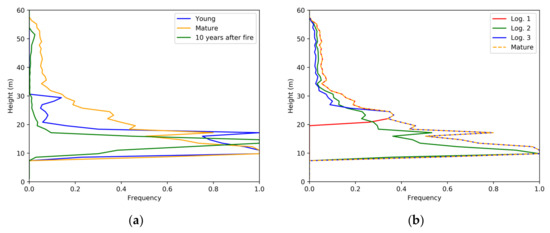
Figure 3.
Distribution of heights for the simulated forest scenarios: (a) three scenarios derived from a young forest stand, after long term changes; and (b) three scenarios derived after performing a logging action on a mature forest.
The first three scenarios represent three different stages from the long term forest evolution:
- The young forest represents an undisturbed early-succession forest at an age of 50 years (see Figure 4a). The majority of trees have heights between 10–18 m. The sharp mode at the height of 18 m is partly due to the fixed height-to-stem diameter relationship used by the forest model.
 Figure 4. Representation of simulated forest: (a) young forest: example of undisturbed forest after 50 years; (b) mature forest: example of undisturbed forest after 500 years; and (c) mature forest 10 years after a fire event.
Figure 4. Representation of simulated forest: (a) young forest: example of undisturbed forest after 50 years; (b) mature forest: example of undisturbed forest after 500 years; and (c) mature forest 10 years after a fire event. - The forest after a fire event represents a forest 10 years after a fire event (which occurred in the year 490). For each tree, a (fire) survival rate is estimated depending on tree size and species-specific fire tolerance [52], which leads to a very heterogeneous forest landscape after the fire that consists of disturbed and undisturbed forest patches (see Figure 4c). The tree height distribution is now less uniform (see Figure 3a), and the number of tall trees is very low with respect to the number of trees below 20 m, as only a few old trees survived the fire. Moreover, in the 10 years after the fire, a dense homogeneous layer of young trees of around 15 m tall has grown beneath.
The latter three scenarios represent three different disturbance types of the mature forest:
- Logging 1 corresponds to firewood removal or “thinning from below”: all trees below 20 m are logged (see Figure 5b). The effect of cutting all trees below a certain threshold is clearly visible in the tree height distribution shown in Figure 3b.
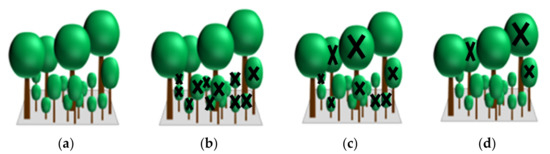 Figure 5. Representation of simulated forest for logging actions: (a) mature undisturbed forest; (b) Logging 1: example of firewood removal or thinning from below; (c) Logging 2: example of diseased trees or free thinning; and (d) Logging 3: example of selective logging of big trees or thinning from above.
Figure 5. Representation of simulated forest for logging actions: (a) mature undisturbed forest; (b) Logging 1: example of firewood removal or thinning from below; (c) Logging 2: example of diseased trees or free thinning; and (d) Logging 3: example of selective logging of big trees or thinning from above. - Logging 2 is an example of diseased trees or “free thinning” where 60% of the trees (independent on their height) are randomly removed, as represented in Figure 5c. When 60% of the trees are randomly removed, the tree height distribution is also affected (see Figure 3b), as the more frequent heights are proportionally more penalized by the action.
3.2. From Simulated Forest Stands to Reflectivity Profiles
Starting from the single tree parameters, vertical reflectivity profiles were simulated. This was implemented in a very pragmatic and simple way as the objective of this task was to demonstrate the underlying principle rather than to assess a given performance. Given the simplifications in the forest simulations and the modelling of the 3D radar reflectivity, the results shown in this section provide a first consistency test, but do not pretend to constitute on their own a sufficient quantitative assessment of the proposed methodology.
The individual steps are described below and the flowchart is shown in Figure 6.
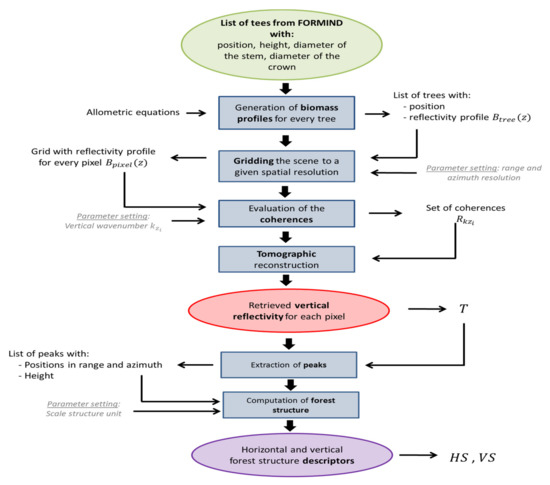
Figure 6.
Flowchart of the simulation of vertical reflectivity profiles from forest stands simulated by FORMIND.
First, for every tree in the list, the distribution of biomass was estimated, taking into account the height of the tree as well as the diameter of its crown and stem. In the model, the tree canopies were assumed to be spherical and the stems cylinders for all trees. With this, the volume at each vertical slice at 0.5 m was computed to obtain the biomass from the volume, and different allometric equations were employed for the trunk, the crown, and tree species, using different wood densities. Once the vertical profile of the biomass for every tree was estimated, the scene was gridded to a given spatial resolution in range and azimuth. In the results below, a spatial resolution of 10 × 10 m was assumed. For each grid cell, the individual contributions of the different trees within the cell were added before applying an extinction factor :
In the results shown in this paper, the extinction was set to 0.05 m−1. Neither interactions between the trees nor polarimetric diversity were accounted. Once the number and distribution of wavenumbers was set, the elements of the multi-image covariance matrix were obtained as:
Ten baselines were considered with kz equally distributed between 0.05 and 0.4 [rad/m] and a spatial multilook of 5 × 5 px was employed for the estimation of the covariance matrix. No temporal decorrelation effects were taken into account. The reflectivity profiles were reconstructed from , as discussed in Section 2.1.
It is worth noting that, despite much higher densities of shorter trees, tall trees produced significantly higher values of power density in the reconstructed vertical reflectivity profiles. This was not only due to the larger volume of taller trees, but was also a result of the applied attenuation that blurred the presence of shorter trees in the reconstructed 3D reflectivity.
3.3. Results and Discussion
From the retrieved reflectivity profiles, the peaks were extracted and finally, the horizontal and vertical structure indices were estimated as per Equations (10)–(12). The density distribution of the obtained indices on the HV plane are shown in Figure 7.
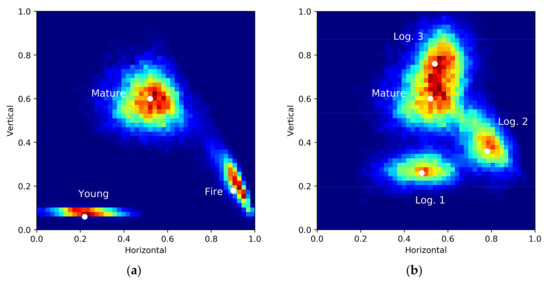
Figure 7a shows the density distribution of the loci of the horizontal and vertical structure indices in the HV plane for the first three scenarios; the white dots indicate the location of the most frequent value in the histogram. The three scenarios can be clearly distinguished from each other. The structure complexity increased significantly in the evolution from young to mature forest (500 years later). The increase in the vertical complexity was predominant and was reflected by an increase of the vertical structure index. At the same time, the transition from a dense layer of younger trees to a less dense mature forest was also reflected by an increase of the horizontal structure index.
The mature forest 10 years after the major fire event significantly decreased the vertical structure as most of the younger trees had a similar height of around 15 m, and only a few (old) tall trees remained. As these tall trees were scattered across the stand, they increased the horizontal heterogeneity that is reflected by the increase of the horizontal structure index.
Figure 7b shows the density distribution of the loci of the horizontal and vertical structure indices in the HV plane for the three disturbance scenarios; the white dots indicate the location of the maximum density of each distribution. All three logging scenarios could be clearly distinguished from each other and from the undisturbed forest cases. The different ways that trees are removed induce different changes in the HV plane. For each change, the point cloud was translated to a different position in the plane. In the case of Logging 1, removing trees selectively to their height had a noticeable effect on the vertical structure complexity, which was reflected by a decrease in the vertical structure index (with respect to the undisturbed case). In the case of Logging 2, the random thinning increased the horizontal structure index (associated to a decrease of forest density) combined with a significant decrease of the vertical index; reflecting the fact that given the uneven original distribution of tree heights, the random logging affected more trees with a more frequent range of heights (in this case, the lower ones with heights below 20 m). Finally, when a number of tall trees with heights above a given threshold were removed, as in the case of Logging 3, the presence of lower trees was enhanced, thus leading to an increase in the vertical structure index.
4. Forest Structure Dynamics on a Real Scenario
4.1. Description of the Test Site
After the tests were performed using simulated data, the proposed approach was applied on real SAR data. To achieve this, we used three quad polarimetric multibaseline datasets acquired by DLR’s (German Aerospace Center) airborne SAR system [56,57] in a repeat pass interferometric mode over the same forest in 2008, 2012 and 2016. The forest selected is located in Traunstein in the south-eastern part of Germany and constitutes a managed forest in a temperate climate, with coniferous, deciduous and mixed stands. Due to the close-to-nature forest management approach, the forest stands are heterogeneous in terms of structure and species richness. Figure 8 shows a stand classification of development stages based on field inventory data. Five major stages were identified in this classification [58]. First, the young stage in this test site (represented in dark blue in Figure 8) is mainly constituted by stands of young trees with low density. The stands in the growth stage (represented in light blue) are fast-growing, constituted mainly by a dense layer of short trees. It should be noted that although the polygons were classified as growth stage, they show a high variability and in most of them, a few scattered tall trees still remain above the short trees. The mature stage in this forest (represented in green) is formed by tall trees that are densely and homogeneously distributed. In the transition stage (represented in orange), small trees grew under older taller trees where the older tall trees are significantly denser than in the growth stage. Finally, stands in the plenter stage (represented in red) have a high variety of tree heights. This plenterwald is the most noticeable feature in terms of structure in the forest under study, and is the result of decades of management practices aimed at boosting structure.
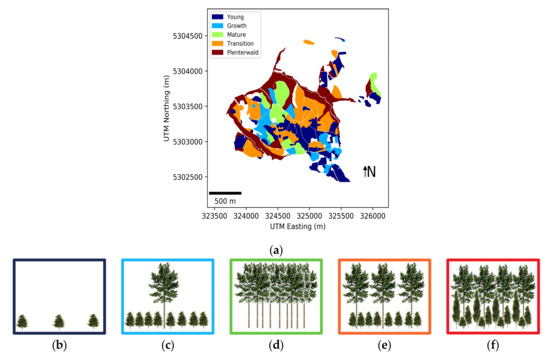
Figure 8.
(a) Classification of the test site according to different development stages. Representation of trees distribution at the different development stages: (b) young; (c) growth; (d) mature; (e) transition; and (f) plenterwald.
In terms of structure, the early stand stages, namely the young and the growth stages, refer to the low structural complexity describing the succession from established transition until the cumulation of growth. Increasing structural complexity is characteristic of the transition, particularly for the plenter stage, with the highest structural complexity. Regarding the mature stage stands in Traunstein, despite their age they exhibited a low complexity since most of the trees are of similar height.
4.2. Radar Data
As mentioned above, three multibaseline datasets at the L-band were acquired over the Traunstein area in a repeat pass interferometric mode. It should be noted that, besides taking place under different weather and seasonal conditions (as detailed in Table 1), different viewing geometries, resolutions and baseline distributions were employed for the different acquisitions. Since each of the tomographic sets was acquired by the same sensor and in the same day (separated only by minutes), system or environmental variability can be ignored within each of the sets. The three tomographic sets were then processed and calibrated (geometrically and radiometrically) to the same standards.

Table 1.
Main parameters of the multibaseline L-band dataset over the Traunstein forest.
4.3. Reference Data
To assess the validity of the results obtained, several sources of reference data were used. Their main specifications are summarized in Table 2. On the one hand, high resolution aerial optical images (2009, 2012) as well as airborne Lidar data (2008 and 2012) were available. On the other hand, in situ data acquired on the basis of inventory plots were considered. These sampled the area under study following a 100 m grid, recording at each grid node the most relevant trees inside a circular area of around 12.5 m radius. Not all trees were reported in the inventory plot, depending on their diameter at breast height and their distance to the center of the plot [58,59]. It is worth mentioning that this scale is too small to allow a direct comparison on a local scale with the estimates from radar data obtained at a scale of 50 m × 50 m.

Table 2.
Main specifications of the different sources of reference data available in this study.
This set of inventory plots was employed to estimate the main development stages at different polygons previously determined and obtain the reference map shown in Figure 8. It should be noted that the polygons were defined following organizational divisions and not according to uniformity of forest type. Furthermore, the polygons included roads, paths, and other man-made targets that introduced important alterations of the estimated structure from the remote sensing data in the form of local discontinuities. Even if local, these discontinuities incurred significant variations that had a non-negligible effect on the structures averaged over the polygons.
Therefore, forest stands inside the predefined polygons were subject to high variability and this introduced uncertainties when averaging the estimated structures over the polygons.
4.4. Results and Discussion
Following the proposed methodology, maps of horizontal and vertical structure were generated for 2008, 2012 and 2016, at a scale of 50 m × 50 m. First, the values of and were averaged over the polygons, classifying the stands in the five development stages shown in Figure 8, the results of which are shown in Figure 9. Figure 10 reflects how the mean values of horizontal and vertical structure for the five different polygons considered were distributed in the HV plane and how they varied across the three datasets.
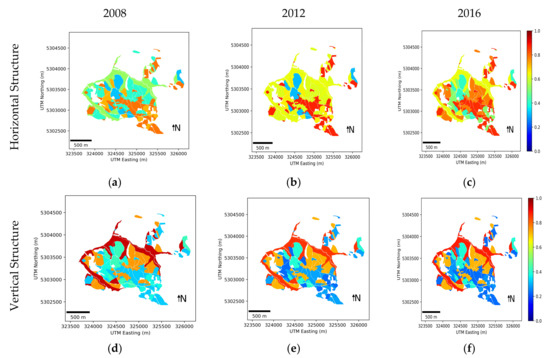
Figure 9.
Horizontal and vertical forest structure in Traunstein averaged over the five predefined polygons, representing different growth stages. Horizontal structure in: (a) 2008; (b) 2012; and (c) 2016. Vertical structure in: (d) 2008; (e) 2012; and (f) 2016.
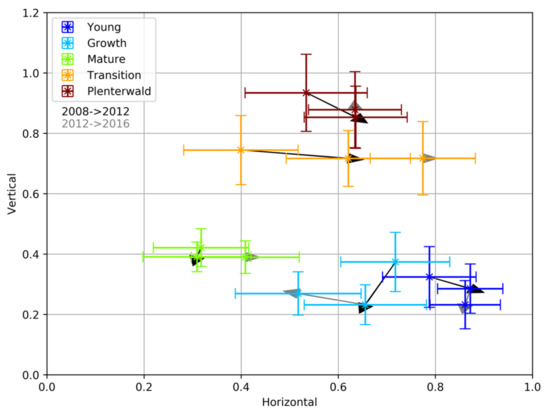
Figure 10.
Distribution of the mean estimated structure in the horizontal/vertical (HV) plane for five polygons defined in Figure 8 at different development stages, and its temporal evolution between 2008 and 2016.
First, it was observed that the five development stages were characterized by different signatures in terms of structure and structure changes. They appeared at different positions in the HV plane and their evolution in this space across the three acquisitions was also different in terms of the magnitude and direction of the vectors representing the variations in structure. The complexity of the different development stages (introduced in Section 4.1) was effectively reflected through the vertical index. The forests at young, growth, and mature stages had low values in contrast to the transition and the plenter stages, whose complexity was reflected by significantly higher values. The horizontal index varies from 0.3 for the dense mature forest to 0.9 for the sparse young forest reflecting the difference in the density of the highest trees in each polygon.
Comparing the estimated structure indices for 2008, 2012 and 2016, it was seen that in general, they did not change significantly, given the range of variability within each stage except for the transition and the growth stands. These two types of forest were the ones most altered by the forest management practices and, therefore, were more dynamic in terms of structure change in such a relatively short time span. It was interesting to observe for these two stages the different direction of the vectors representing the variation in the values of the structure indices between 2008 and 2016. For the transition stand with an initial vertical high value and low horizontal structure value, the value of the horizontal index increased from 2008 to 2012, and further still in 2016. On the contrary, for the growth stage, the horizontal index decreased from 2008 to 2016.
However, to gauge the significance of these previous results, it should be observed that the high variability inside polygons produced by the way they were defined (already discussed in Section 4.1), resulted in a high dispersion of the indices around the mean values for the different stages represented in Figure 10. Furthermore, the variations in structure, essentially due to forest management actions, took place only locally and affected less than 10% of the area considered. This fact reduced the significance of the estimated structure changes when they were averaged over the polygons. The extent of the changes in the area were evaluated from differences in the maps of Lidar heights from 2008 and 2012 given that the changes were only due to forest management actions and, as a consequence, they necessarily produced a change in the height of the forest at high resolution. Figure 11 shows the map of Lidar heights in 2008 (see Figure 11a), in 2012 (see Figure 11b), and the map of absolute differences (see Figure 11c). In the latter, it was observed that most of the area remained undisturbed (represented in dark blue) and changes (represented in other colors) occurred only locally.

Figure 11.
Map of Lidar height over the test site: (a) 2008; (b) 2012; and (c) the height difference between 2008 and 2012.
Similarly, the local extent of the variations in the forest structure was also observed in the maps generated from the TomoSAR data (see Figure 12). The main patterns in both the horizontal and vertical estimated structures were analogous, and significant variations occurred only locally. To compare the match between the intensity and location of logging action—as identified from the height variations with the Lidar measurements and by the changes in the maps of forest structure estimated from TomoSAR—two classes were defined (change and no change) both for the Lidar and TomoSAR maps. In particular, for the TomoSAR dataset, we extracted the map of change in horizontal (or vertical) forest structure by direct subtraction of horizontal (or vertical) forest structure estimated from the TomoSAR data in 2008 and 2012. We then estimated a single map of structure change by aggregating the changes in the horizontal and the vertical dimensions. To define the classes, a threshold was applied to keep only the most significant variations (the threshold was empirically set to 0.3 in the examples provided in this Section). Regarding the Lidar dataset, a map of change was also similarly estimated by applying a threshold (empirically to forest height differences greater than 10 m) to the map of height differences in Figure 11c. The two maps of forest change obtained from the TomoSAR data and the Lidar height were superimposed and are shown in Figure 13.
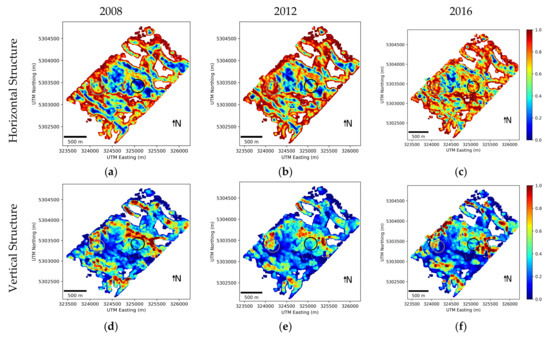
Figure 12.
Forest structure maps estimated from TomoSAR. Horizontal structure in: (a) 2008; (b) 2012; and (c) 2016. Vertical structure in: (d) 2008; (e) 2012; and (f) 2016.
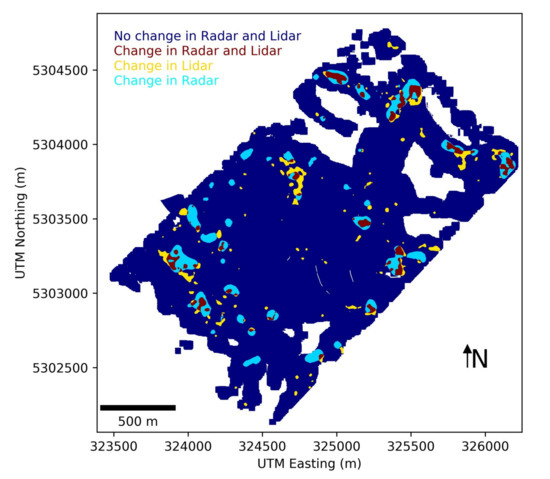
Figure 13.
Map of forest change as identified from Lidar height and from forest structure estimated from TomoSAR data at the L-band.
It was observed that both sources highlight the same areas as more affected by changes between 2008 and 2012. Regarding the discrepancies, the differences in the extension and orientation of the area affected by changes were mainly due to the different resolutions and geometries of the two sources. Both sources provided the same class in 92% of the cases.
In the forest structure estimated from the TomoSAR data, four cases were distinguished by considering the direction of the variation (horizontal or vertical):
- -
- no change was identified either in the horizontal or in the vertical estimated structure;
- -
- horizontal structure varied whereas vertical structure remained stable;
- -
- vertical structure varied whereas horizontal structure remained stable;
- -
- both horizontal and vertical structures varied simultaneously.
Results are shown in Figure 14. As already discussed in Section 3.3, different types of forest management action led to different directions of displacement of the loci of the values of horizontal and vertical structure in the HV plane: some changes were mostly noticeable as a variation in the horizontal structure (light blue areas in Figure 14), whereas others mainly affected the estimated vertical structure (yellow areas in Figure 14). To further assess the sensitivity of the proposed methodology to identify the type of forest structure change, two examples were considered in the following sub-sections: one for the horizontal structure change (highlighted by a black circle in Figure 12 and Figure 14), and one for the vertical (highlighted by a grey circle in Figure 12 and Figure 14).
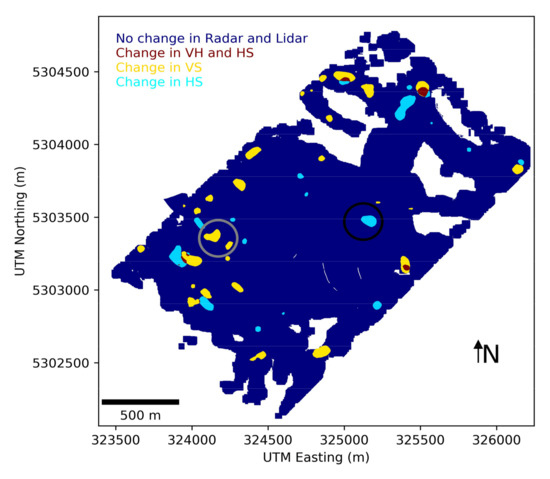
Figure 14.
Map of forest change as identified from forest structure estimated from TomoSAR data at the L-band and discriminating between horizontal and vertical structure variations.
4.4.1. First Example of Local Forest Structure Change in the Area under Study
The first example considered is a transition stand where between 2008 and 2012 a number of trees were logged, independent of their height, resulting in a clearing of a small area depicted in Figure 15d,e, and noticeable in the optical images (see Figure 15a,b). It should be noted that, even if less representative, other logging actions of different types occurred during this period and in the area considered. For example, it was observed (in the parts highlighted by white circles) that a few tall trees were removed, leaving the shorter trees below.
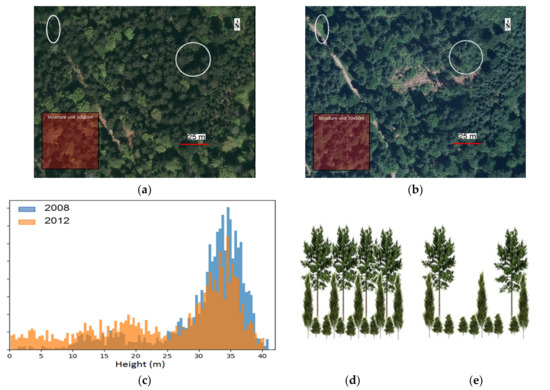
Figure 15.
Main type of forest logging in the area considered in the first example of forest change. Optical images of the area in: (a) 2009; (b) 2012; and (c) a histogram of Lidar heights in the area considered in the first example of forest change in 2008 and 2012. Representation of local tree distributions (d) before; and (e) after logging.
This type of logging, where trees are removed independently of their height, reduces the density of the highest trees, while the distribution of trees according to their height before and after the action remains essentially preserved. Figure 15c shows the histograms of Lidar heights within the plot in 2008 and 2012. This can be used as a proxy of tree-height frequency distribution for the stand. For accurate interpretation, it is worth noting that the height was estimated from the first Lidar return associated to the highest elements of the canopy. When these tall trees were removed, the vegetation below became apparent, which produced an increase in the number of samples at smaller heights. Bearing this in mind, the histograms reflect the reduction of a significant number of tall trees between 25–40 m that resulted in a flattening of the histogram, but the effect is rather small. In terms of structure, the logging action considered in the first example essentially produced a change mainly in the horizontal dimension, given that the density of trees in the top layer was significantly reduced. Regarding the vertical structure, it exhibited only a slight increase as the distribution of heights of the remaining trees was only slightly altered. This was reflected in the maps of the estimated forest structure, as shown in the area highlighted by a black circle in Figure 12, as well as in the representation of the evolution of structure indices in this area in the HV plane (see Figure 16). In Figure 16, the vector representing the variation in the values of the structure indices between 2008 and 2016 reflected an important increase in the horizontal direction. This increased the significance of the changes as estimated by the structure indices. Finally, it is worth mentioning that the results shown in this Section for this example of logging were consistent with the results obtained in Section 3.3 for the simulated scenario where a number of trees were removed randomly independent of their height (Logging 2).
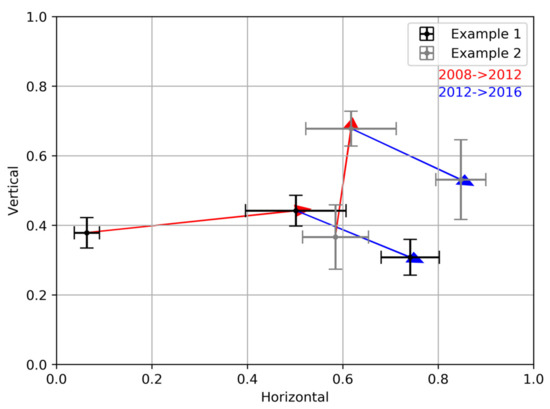
Figure 16.
Evolution of the estimated structure for the two examples of local areas considered from 2008 to 2016.
4.4.2. Second Example of Local Forest Structure Change in the Area under Study
In the second example, a number of tall trees were logged in a transition stand, leaving shorter trees mainly undisturbed. This can be observed in the optical images, particularly in the shadows of the tall trees on the road crossing the stand (see Figure 17a,b). As in the first example, it should be noted that other logging actions of different types have occurred in this area in the period considered. For example, a local clearing can be clearly observed (highlighted by a white circle).
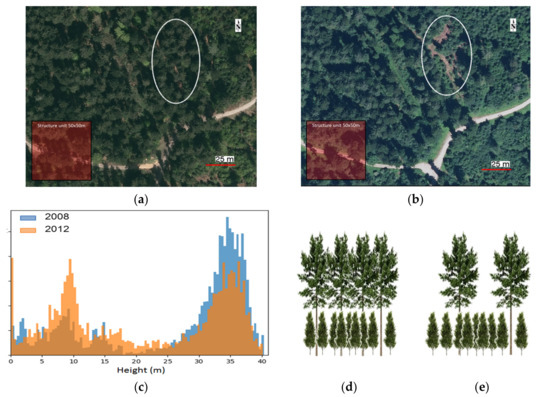
Figure 17.
Main type of forest logging in the area considered in the second example of forest change. Optical images of the area in: (a) 2009; (b) 2012; and (c) the histogram of Lidar heights in the area considered in the second example of forest change in 2008 and 2012. Representation of local tree distribution (d) before; and (e) after logging.
In this case, the number of tall trees decreased; but, in contrast with the previous example, since the shorter trees were not removed the distribution of tree height was modified. Accordingly, Figure 17c shows the histograms of Lidar heights in 2008 and 2012 indicating a significant reduction in the tree heights ranging between 25–40 m, where at the same time there was a noticeable increase in the tree heights between 5–15 m: the presence of two modes was significantly enhanced. Consequently, this type of logging increased the vertical heterogeneity and hence the vertical structure index, as shown in Figure 16. Horizontal structure increased as long as some trees in the top layer were still preserved. This was also implied in the forest structure maps shown in Figure 12, and in the HV plane in Figure 16 by the difference in the direction of the structure change vector in the two examples considered. This result is consistent with the results obtained for the simulated scenario, defined as Logging 3, in Section 3.3.
5. Conclusions
In this paper, a methodology to detect and interpret forest structure changes using L-band tomographic SAR acquisitions was proposed and tested. The link between the L-band tomographic-reconstructed 3D forest reflectivity, which may depend on acquisition and instrument parameters, and the physical forest structure was established by using a recently introduced 2D (i.e., horizontal and vertical) structure characterization concept [37,38]. Accordingly, a pair of vertical and horizontal structure indices was defined derived from the 3D distribution of the peaks of the reconstructed reflectivity function [34]. It was then possible to represent different forest structure conditions on a two-dimensional HV structure plane defined by these two indices. In this sense, different changes in forest structure can be represented on the HV structure plane by vectors with different directions and magnitudes. The length of the vector was associated to the extent (or amount) of structure change, while its direction represented the change in the distribution of trees occurring depending on their height.
The sensitivity and consistency of the proposed structure indices to natural or anthropogenic variations in forest structure was tested on simulated as well as real experimental data. The application of the proposed methodology on simulated data—despite the simplifications in the derivation of the 3D reflectivity from the FORMIND simulations—allowed us to demonstrate the underlying principle for a large diversity of forest structure scenarios. Furthermore, it was shown that changes in forest structure caused either by natural (undisturbed) forest evolution, or by disturbances such as a fire event or different logging scenarios, impacted in different ways on the horizontal and vertical forest structure, and that these changes were projected into the two proposed structure indices.
The proposed methodology was then applied to three sets of tomographic L-band data acquired over the same temperate forest (Traunstein) in 2008, 2012 and 2016 with the aim of validating its ability to detect structural changes occurring in the time between the acquisitions. During this time, the main changes in the site were triggered by natural evolution as well as forest management in terms of logging selected trees and the opening of paths at local scales. For the interpretation and validation of the achieved results, different sources of reference data were available: airborne Lidar measurements, high resolution optical images, and forest inventory data. The results clearly showed that even subtle changes in the vertical as well as horizontal structure of the individual stands were reflected in the 3D L-band reflectivity, and thus in the derived horizontal and/or vertical structure indices. The obtained forest structure maps were comparable and consistent; between them, they exhibited similar global behavior and the differences occurred only locally, as expected and confirmed by the reference data. Local changes were distinctly identified as variations in the estimated structure descriptors; and, consistent with the simulated scenarios, logging of different natures led to different directions of the change vectors on the HV structure plane, even by using data acquired by two different SAR sensors (E-SAR in 2008, and F-SAR in 2012 and 2016) with different viewing geometries, different spatial resolutions, and different spatial track distributions. It was then verified, at the L-band, that the fact that the definition of the two structure indices relied only on the 3D location of the reflectivity peaks made them more robust against variations in the shape of the reflectivity profiles induced by non-structural variability, as long as the main scattering contributions associated with the reflectivity peaks did not change their location.
A drawback in the estimation of forest structure and forest structure changes in real scenarios through statistical measures like the ones employed in this paper is the non-uniformity of the stands that induces border effects. These discontinuities might be caused by the presence of contributions not due to vegetation, such as a road, path, or other man-made targets, but also by structure distributions changing rapidly in space. The extent of the variations introduced by these discontinuities in the forest structure indices was partly determined by the scale of the structure unit window employed. However, the dimensions of this window were difficult to set optimally with no a priori information, since this is site-dependent. Furthermore, a compromise exists between spatial resolution and accuracy of the indices, besides other considerations on system resolution. The effect of scale in the indices will be further addressed in future studies.
Finally, it should be pointed out that a critical point in forest studies with real data is validation. In this paper, field inventory data, Lidar measurements, and high resolution optical images were extensively cross-checked. However, as discussed and justified, the usability of the available field data for quantitative validation was insufficient. Other scenarios with field information at larger scales that are more compatible with remote sensing studies are available, but the temporal series of multibaseline SAR data have yet to be acquired.
Acknowledgments
This study was supported by the HGF Alliance HA-310 Remote Sensing and Earth Systems Dynamics.
Author Contributions
V.C.B. and M.T.A. developed and implemented the algorithms as well as the interpretation of the results, and wrote and revised the manuscript. R.F. provided the FORMIND simulations, contributed to Section 3.1 of the manuscript, and helped in the interpretation of the results. M.H. provided the ground data and contributed to Section 4.1 and Section 4.3 of the manuscript as well as in the interpretation of the results. K.P. supervised the work, contributed to the main ideas, and revised the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Spies, T.A. Forest Structure: A Key to the Ecosystem. Northwest Sci. 1998, 72, 34–36. [Google Scholar]
- Grace, J. Understanding and managing the global carbon cycle. J. Ecol. 2004, 92, 189–202. [Google Scholar] [CrossRef]
- Gatti, L.V.; Gloor, M.; Miller, J.B.; Doughty, C.E.; Malhi, Y.; Domingues, L.G.; Basso, L.S.; Martinewski, A.; Correia, C.S.C.; Borges, V.F.; et al. Drought sensitivity of Amazonian carbon balance revealed by atmospheric measurements. Nature 2014, 506, 76–80. [Google Scholar] [CrossRef] [PubMed]
- Frolkin, S.; Palace, M.W.; Clark, D.B.; Chambers, J.Q.; Shugart, H.H.; Hurtt, G.C. Forest disturbance and recovery: A general review in the context of spaceborne remote sensing of impacts on aboveground biomass and canopy structure. J. Geophys. Res. Biogeosci. 2009, 114. [Google Scholar] [CrossRef]
- Beaudoin, A.; Le Toan, T.; Goze, S.; Nezry, E.; Lopes, A.; Mougin, E.; Hsu, C.C.; Han, H.C.; Kong, J.A.; Shin, R.T. Retrieval of forest biomass from SAR data. Int. J. Remote Sens. 1994, 15, 2777–2796. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Siqueira, P.R. The Vertical Structure of Vegetated Land Surfaces from Interferometric and polarimetric Radar. Radio Sci. 2000, 35, 141–177. [Google Scholar] [CrossRef]
- Garestier, F.; Dubois-Fernandez, P.; Guyon, D.; Le Toan, T. Forest Biophysical Parameter Estimation Using L- and P-Band Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3379–3388. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K. Three-stage inversion process for polarimetric SAR interferometry. IEE Proc. Radar Sonar Navig. 2003, 150, 125–134. [Google Scholar] [CrossRef]
- Reigber, A.; Moreira, A. First demonstration of airborne SAR tomography using multibaseline L-band data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2142–4152. [Google Scholar] [CrossRef]
- Frey, O.; Meier, E. Analyzing Tomographic SAR Data of a Forest with Respect to Frequency, Polarization, and Focusing Technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3648–3659. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Reigber, A. Estimation of Forest Structure, Ground, and Canopy Layer Characteristics from Multibaseline Polarimetric Interferometric SAR Data. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1086–1104. [Google Scholar] [CrossRef]
- Toraño, A.; Pardini, M.; Hajnsek, I.; Papathanassiou, K. Forest Above-Ground Biomass Estimation from Vertical Reflectivity Profiles at L-Band. IEEE Trans. Geosci. Remote Sens. Lett. 2015, 12, 2379–2383. [Google Scholar] [CrossRef]
- Tebaldini, S.; Rocca, F. Multibaseline Polarimetric SAR Tomography of a Boreal Forest at P- and L-Bands. IEEE Trans. Geosci. Remote Sens. 2012, 50, 232–246. [Google Scholar] [CrossRef]
- Aguilera, E.; Nannini, M.; Reigber, A. Wavelet-based compressed sensing for SAR tomography of forested areas. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5283–5295. [Google Scholar] [CrossRef]
- Pardini, M.; Papathanassiou, K. Sub-Canopy Topography Estimation: Experiments with Multibaseline SAR Data at L-Band. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 4954–4957. [Google Scholar]
- Dinh, H.T.M.; Tebaldini, S.; Rocca, F.; Koleck, T.; Borderies, P.; Albinet, C.; Villard, L.; Hamadi, A.; Loan, T.L. Ground-Based Array for Tomographic Imaging of the Tropical Forest in P-Band. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4460–4472. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Tebaldini, S.; Rocca, F.; Toan, T.L. The Impact of Temporal Decorrelation on BIOMASS Tomography of Tropical Forests. IEEE Trans. Geosci. Remote Sens. Lett. 2015, 12, 1297–1301. [Google Scholar] [CrossRef]
- Albinet, C.; Koleck, T.; Le Toan, T.; Borderies, P.; Villard, L.; Hamadi, A.; Laurin, G.V.; Nicolini, G.; Valentini, R. First Results of AFRISCAT, a Tower-Based Radar Experiment in African Forest. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 5356–5358. [Google Scholar] [CrossRef]
- Monteith, A.; Soja, M.; Ulander, L.; Eriksson, L. BOREALSCAT: A Tower-Based Tomographic and Polarimetric Radar Experiment in the Boreal Forest at P-, L- and C-Band. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 7458–7461. [Google Scholar]
- Lee, S.K.; Kugler, F.; Papathanassiou, K.; Hajnsek, I. Quantification of Temporal Decorrelation Effects at L-Band for Polarimetric SAR Interferometry Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1351–1367. [Google Scholar] [CrossRef]
- Simard, M.; Hensley, S.; Lavalle, M.; Dubayah, R.; Pinto, N.; Hofton, M. An Empirical Assessment of Temporal Decorrelation Using the Uninhabited Aerial Vehicle Synthetic Aperture Radar over Forested Landscapes. Remote Sens. 2012, 4, 975–986. [Google Scholar] [CrossRef]
- Pardini, M.; Cantini, A.; Kugler, F.; Papathanassiou, K.; Lombardini, F. Monitoring dynamics in time of forest vertical structure with multibaseline PolInSAR data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 3366–3369. [Google Scholar]
- Pardini, M.; Cantini, A.; Lombardini, F.; Papathanassiou, K. 3-D Structure of Forests: First Analysis of Tomogram Changes Due to Weather and Seasonal Effects at L-Band. In Proceedings of the 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014. [Google Scholar]
- Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.; Younis, M.; Lopez-Dekker, P.; Huber, S.; Villano, M.; Pardini, M.; Eineder, M.; et al. A Highly Innovative Bistatic SAR Mission for Global Observation of Dynamic Processes on the Earth’s Surface. IEEE Geosci. Remote Sens. Mag. 2015, 3, 8–23. [Google Scholar] [CrossRef]
- Cazcarra-Bes, V.; Tello-Alonso, M.; Papathanassiou, K. 3D Forest Structure Estimation from SAR Tomography by means of a Full Rank Polarimetric Inversion based on Compressive Sensing, POLINSAR. In Proceedings of the 7th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry, Frascati, Italy, 26–30 January 2015. [Google Scholar]
- Capon, J. High resolution frequency wavenumber spectrum analysis. Proc. IEEE 1969, 150, 125–134. [Google Scholar] [CrossRef]
- Lombardini, F.; Reigber, A. Adaptive spectral estimation for multibaseline SAR tomography with airborne L-band data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003. [Google Scholar]
- Nannini, M.; Scheiber, R.; Horn, R.; Moreira, A. First 3-D reconstructions of targets hidden beneath foliage by means of polarimetric SAR tomography. IEEE Trans. Geosci. Remote Sens. Lett. 2012, 9, 60–64. [Google Scholar] [CrossRef]
- Budillon, A.; Evangelista, A.; Schirinzi, G. Three-dimensional SAR focusing from multipass signals using compressive sampling. IEEE Trans. Geosci. Remote Sens. 2011, 49, 488–499. [Google Scholar] [CrossRef]
- Zhu, X.; Bamler, R. Tomographic SAR Inversion by L1-norm Regularization—The Compressive Sensing Approach. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3839–3846. [Google Scholar] [CrossRef]
- Aguilera, E.P. Synthetic Aperture Radar Tomography—Compressed Sensing Models and Algorithms. Ph.D. Thesis, Technical University of Berlin, Berlin, Germany, 2014. [Google Scholar]
- Tello-Alonso, M.; Cazcarra-Bes, V.; Pardini, M.; Papathanassiou, K. Assessment of forest structure estimation by means of SAR tomography: Potential and limitations. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 32–35. [Google Scholar]
- Snyder, M. What is Forest Stand Structure and How Is It Measured? North. Woodl. 2010, 64, 15. [Google Scholar]
- Pretzsch, H. Forest Dynamics, Growth and Yield; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–39. [Google Scholar]
- Tello-Alonso, M.; Cazcarra-Bes, V.; Pardini, M.; Papathanassiou, K. Structural classification of forests by means of L-band tomographic SAR. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 5288–5291. [Google Scholar]
- Bohn, F.J.; Huth, A. The importance of forest structure to biodiversity—Productivity relationships. R. Soc. Open Sci. 2017, 4, 160521. [Google Scholar] [CrossRef] [PubMed]
- Shugart, H.H. A Theory of Forest Dynamics; The Blackburn Press: Caldwell, NJ, USA, 1984; p. 278. ISBN 9781930665750. [Google Scholar]
- Zenner, E.K.; Hibbs, D.E. A New Method for Modeling the Heterogeneity of Forest Structure. For. Ecol. Manag. 2000, 129, 75–87. [Google Scholar] [CrossRef]
- Pommerening, A. Approaches to quantifying forest structures. For. Int. J. For. Res. 2002, 75, 305–324. [Google Scholar] [CrossRef]
- Del Rio, M.; Pretzsch, H.; Alberdi, I.; Bielak, K.; Bravo, F.; Brunner, A.; Condés, S.; Ducey, M.J.; Fonseca, T.; von Lüpke, N.; et al. Characterization of the structure, dynamics, and productivity of mixed-species stands: Review and perspectives. Eur. J. For. Res. 2016, 135, 23–49. [Google Scholar] [CrossRef]
- Noss, R.F. Indicators for Monitoring Biodiversity: A Hierarchical Approach. Conserv. Biol. 1990. [Google Scholar] [CrossRef]
- Reineke, L.H. Perfecting a stand-density index for even-aged forest. J. Agric. Res. 1933, 46, 627–638. [Google Scholar]
- Schmitt, M.; Shahzad, M.; Zhu, X.X. Reconstruction of individual trees from multi-aspect TomoSAR data. Remote Sens. Environ. 2015, 165, 175–185. [Google Scholar] [CrossRef]
- Ponce, O.; Prats-Iraola, P.; Scheiber, R.; Reigber, A.; Moreira, A. First Airborne Demonstration of Holographic SAR Tomography with Fully Polarimetric Multicircular Acquisitions at L-Band. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6170–6196. [Google Scholar] [CrossRef]
- Matthew, B.; Woodhouse, I.H. Vertical backscatter profile of forests predicted by a macroecological plant model. Int. J. Remote Sens. 2013, 34, 1026–1040. [Google Scholar] [CrossRef]
- Palace, M.W.; Sullivan, F.B.; Ducey, M.J.; Treuhaft, R.N.; Herrick, C.; Shimbo, J.Z.; Mota-E-Silva, J. Estimating forest structure in a tropical forest using field measurements, a synthetic model and discrete return lidar data. Remote Sens. Environ. 2015, 161, 1–11. [Google Scholar] [CrossRef]
- Whitehurst, A.S.; Swatantran, A.; Blair, J.B.; Hofton, M.A.; Dubayah, R. Characterization of Canopy Layering in Forested Ecosystems Using Full Waveform Lidar. Remote Sens. 2013, 5, 2014–2036. [Google Scholar] [CrossRef]
- Botkin, D.B. Forest Dynamics: An Ecological Model; Oxford University Press: Oxford, NY, USA, 1993; p. 309. ISBN 0-19-506555-7. [Google Scholar]
- Bugmann, H. A review of forest gap models. Clim. Chang. 2001, 51, 259–305. [Google Scholar] [CrossRef]
- Fischer, R.; Bohn, F.; Dantas de Paula, M.; Dislich, C.; Groeneveld, J.; Gutiérrez, A.G.; Kazmierczak, M.; Knapp, N.; Lehmann, S.; Paulick, S.; et al. Lessons learned from applying a forest gap model to understand ecosystem and carbon dynamics of complex tropical forests. Ecol. Model. 2016, 326, 124–133. [Google Scholar] [CrossRef]
- Huth, A.; Ditzer, T.; Bossel, H. The Rain Forest Growth Model FORMIX3. Model Description and Analysis of Forest Growth and Logging Scenarios for the Deramakot Forest Reserve (Malaysia); Goltze, E.: Göttingen, Germany, 1998; pp. 1–182. ISBN 9783884523858. [Google Scholar]
- Fischer, R.; Ensslin, A.; Rutten, G.; Fischer, M.; Schellenberger Costa, D.; Kleyer, M.; Hemp, A.; Paulick, S.; Huth, A. Simulating carbon stocks and fluxes of an African tropical montane forest with an individual-based forest model. PLoS ONE 2015, 10, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Knapp, D.E.; Broadbent, E.N.; Paulo, J.C.; Oliveira, M.K.; Silva, J.N. Selective Logging in the Brazilian Amazon. Science 2005, 310, 480–482. [Google Scholar] [CrossRef] [PubMed]
- Horn, R. The DLR airbone SAR project E-SAR. In Proceedings of the Geoscience and Remote Sensing Symposium—Remote Sensing for a Sustainable Future, Lincoln, NE, USA, 31 May 1996. [Google Scholar]
- Horn, R.; Nottensteiner, A.; Reigber, A.; Fischer, J.; Scheiber, R. F-SAR—DLR’s new multifrequency polarimetric airborne SAR. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Abdullahi, S.; Kugler, F.; Pretzsch, H. Prediction of stem volume in complex temperate forest stands using TanDEM-X SAR data. Remote Sens. Environ. 2016, 174, 197–211. [Google Scholar] [CrossRef]
- Bayerischen Staatsforsten. Richtlinie Für Die Mittel—Und Langfristige Forstbetriebsplanung in Den Bayerischen Staatsforsten; Bayerischen Staatsforsten: Regensburg, Germany, 2011. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).