Estimating Snow Depth Using Multi-Source Data Fusion Based on the D-InSAR Method and 3DVAR Fusion Algorithm
Abstract
:1. Introduction
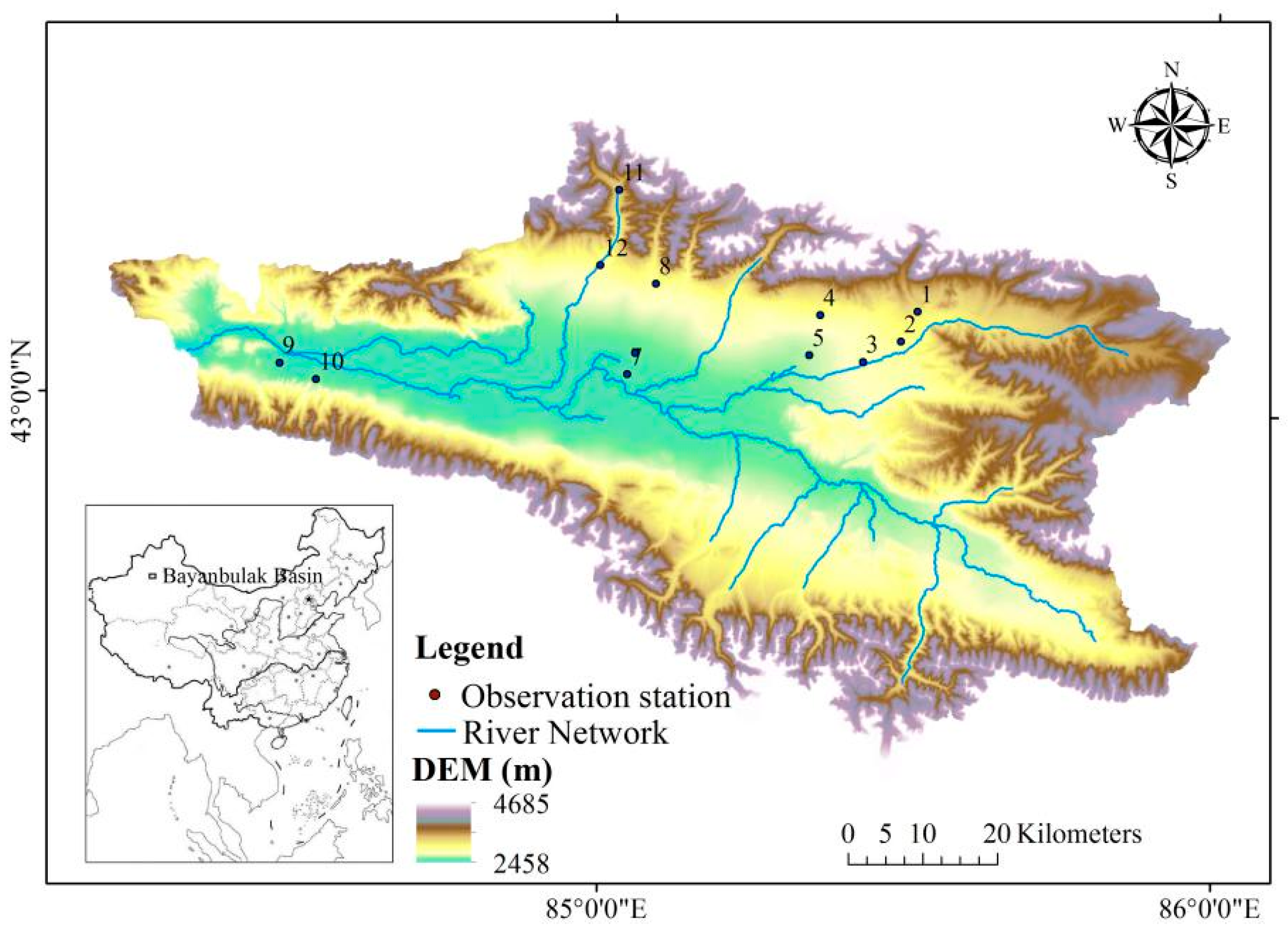
2. Study Area
3. Data Collection and Preprocessing
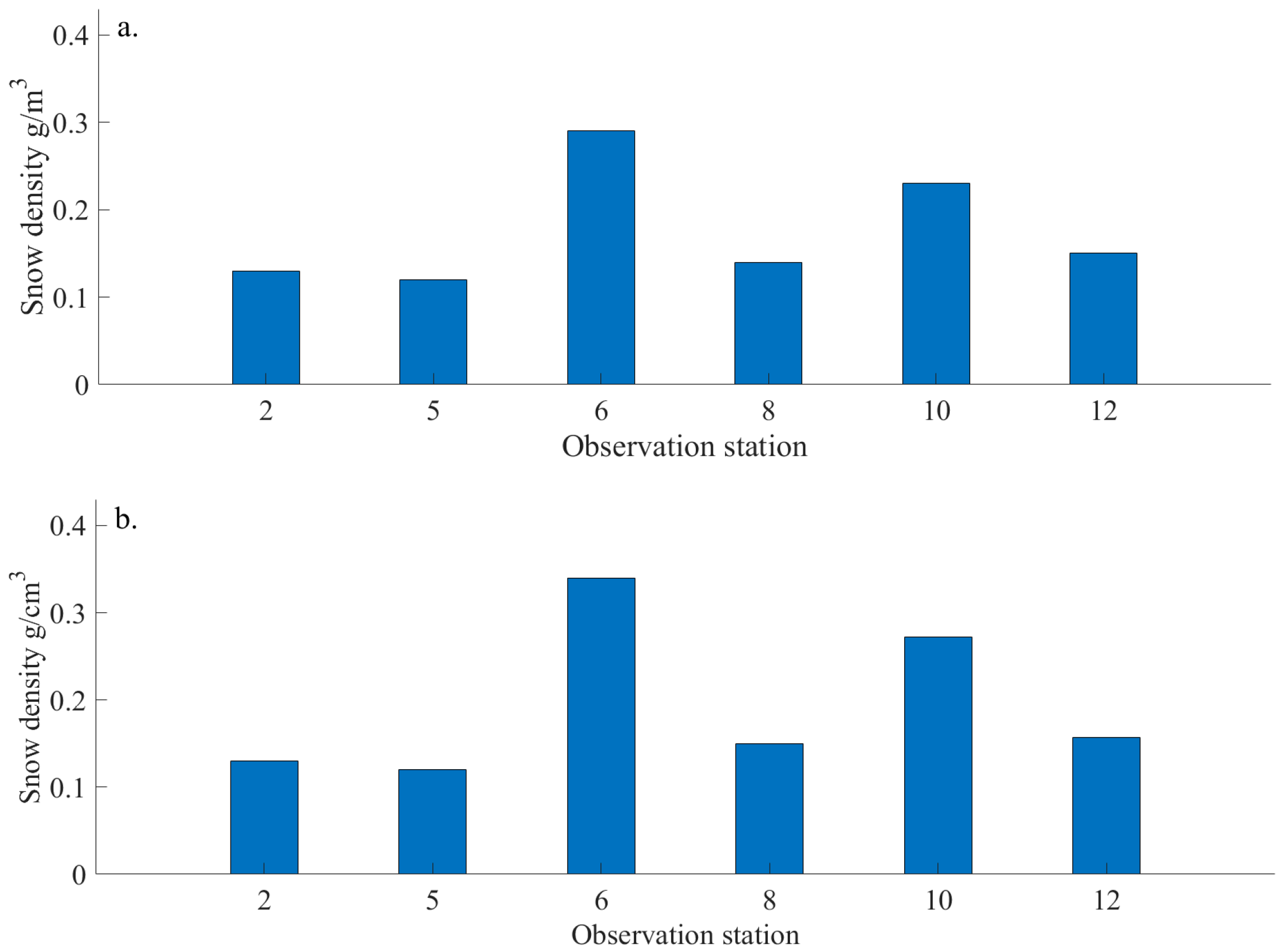
3.1. Field Data Collection
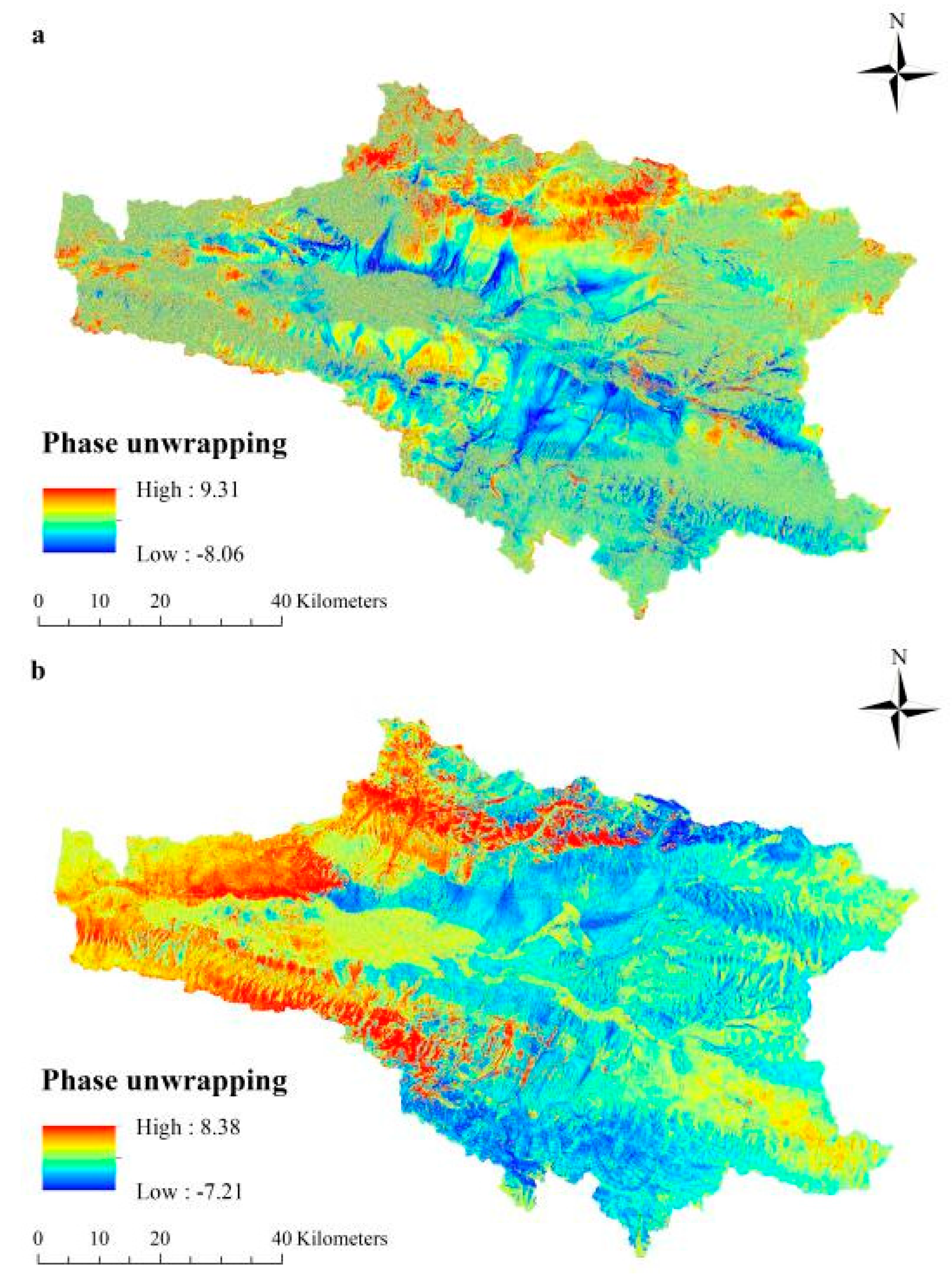
3.2. Sentinel-1 SAR Images and Preprocessing
- (1)
- Precise matching of the master and slave images. Orbital parameters were used to roughly determine the deviation between the master and slave images. For a precise matching of image pairs, the R-D model that was developed by Brown [35] and earth model equation were used. After the calculation of the matched model, the real and imaginary parts of image pairs were resampled to calculate the interferogram. The bilinear interpolation method was adopted for this process.
- (2)
- Generation of the interferogram. After the resampling of the real and imaginary parts of the image pairs, the master image and slave image were subjected to conjugate multiplication. Then, the interferometric phase images were generated.
- (3)
- Removal of flat earth effect and terrain height effect. Since the flat earth effect and terrain height effect are contained in the InSAR interferogram, they needed to be removed before phase unwrapping to obtain the phase information concerning snow depth [36].
- (4)
- (5)
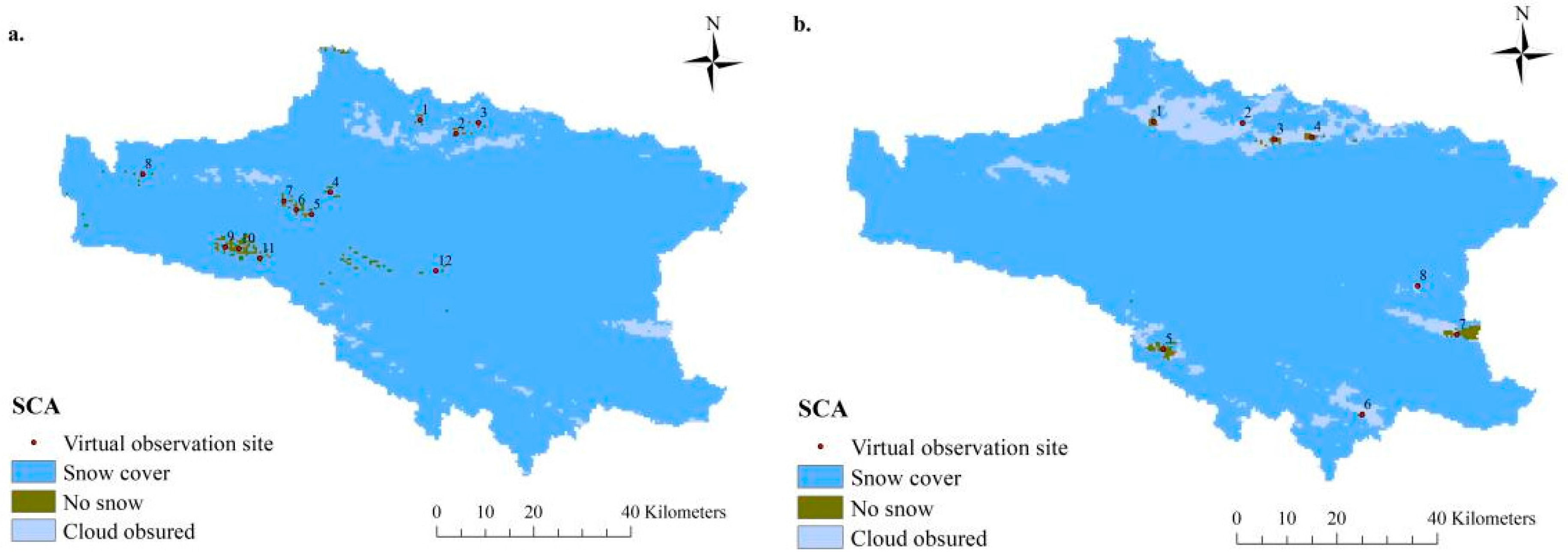
3.3. Processing of the Moderate Resolution Imaging Spectrometer (MODIS) Snow Cover Data and Virtual Site Arrangement
- (1)
- There is no snow in the eight neighbouring pixels of the virtual station.
- (2)
- The distance between the observation stations could be no less than the smallest distance between the existing stations after adding the virtual stations to achieve an even distribution and density of observation stations.
4. Methodology
4.1. Snow Depth Inversion Algorithm
4.2. The Cokriging Model
4.3. The 3DVAR Land Data Assimilation System Scheme
4.3.1. Cost Function
4.3.2. The Background and Observation Error Model
4.3.3. The Principle of 3DVAR and the Cost Function Minimization Algorithm
5. Results
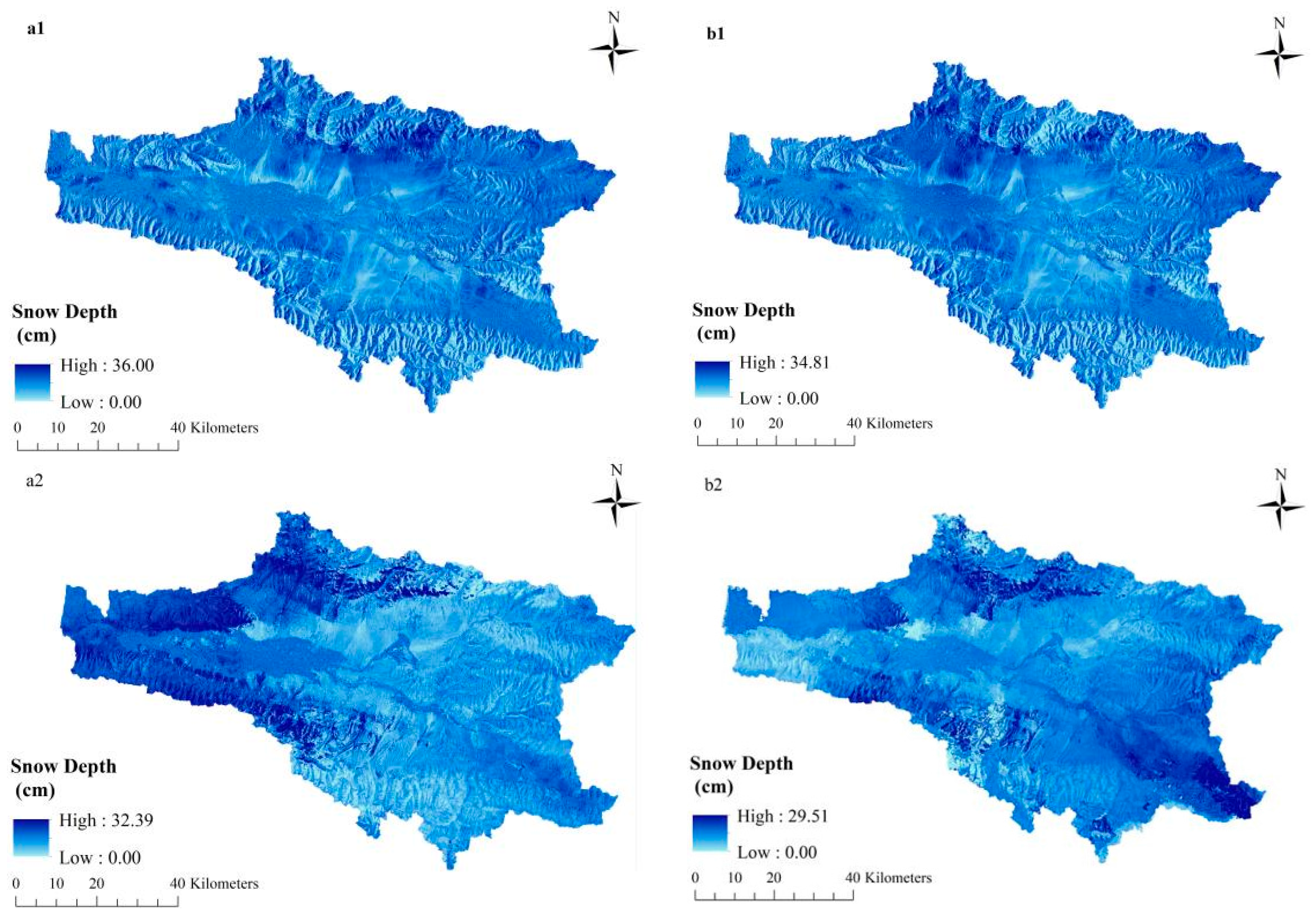
5.1. Inversion Results for Snow Depth
5.2. Background Error Covariance and Observed Error Covariance in the 3DVAR Fusion Algorithm
5.2.1. Establishment of the Background Error Covariance in the 3DVAR Fusion Algorithm
5.2.2. Establishment of the Observation Error Covariance in the 3DVAR Fusion Algorithm
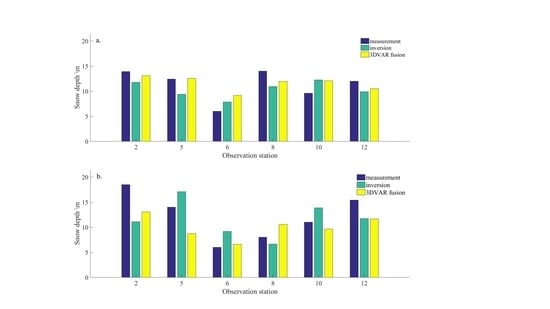
5.3. Estimation of Snow Depth Based on the 3DVAR Fusion Algorithm
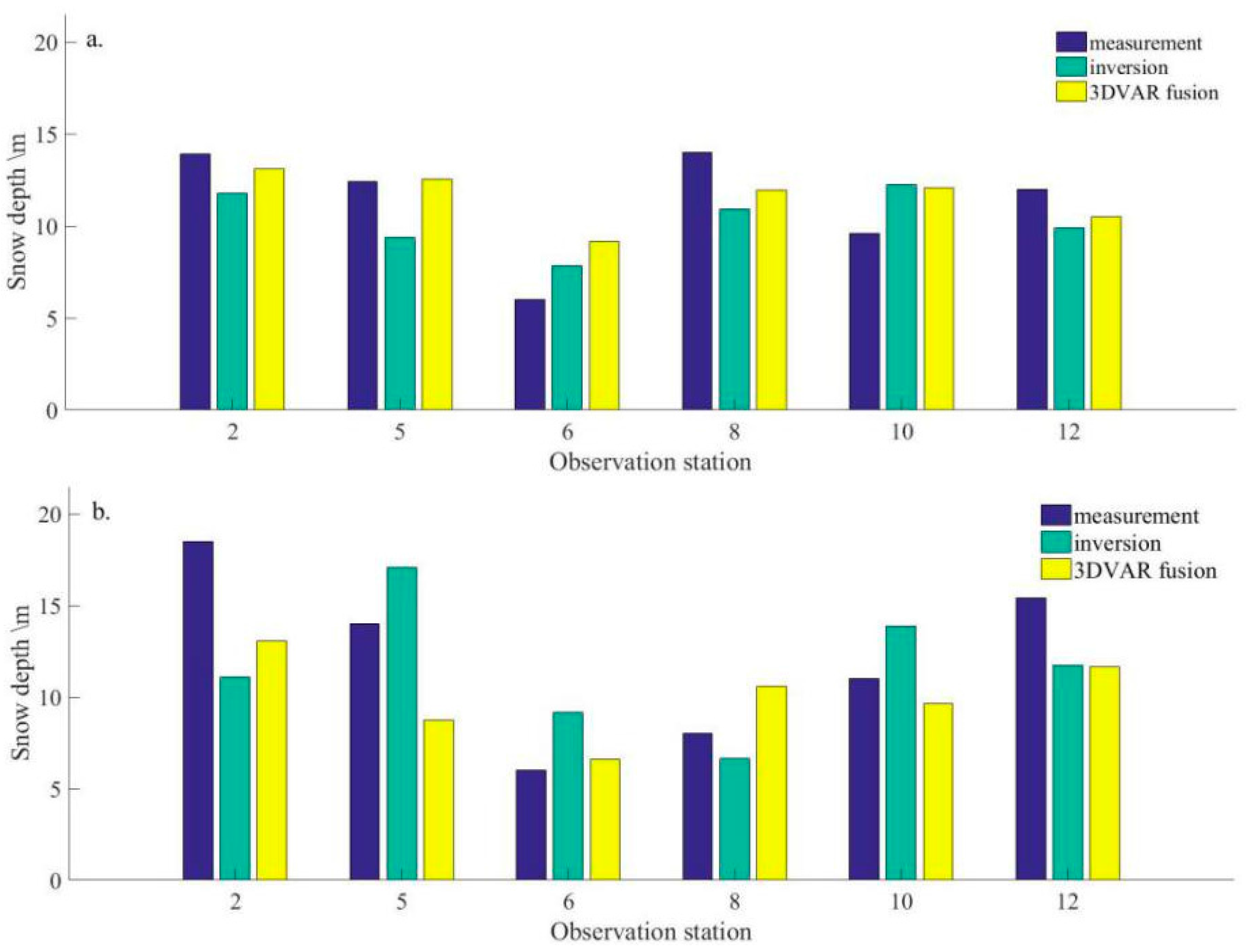
5.4. Evaluation of Accuracy
6. Discussion
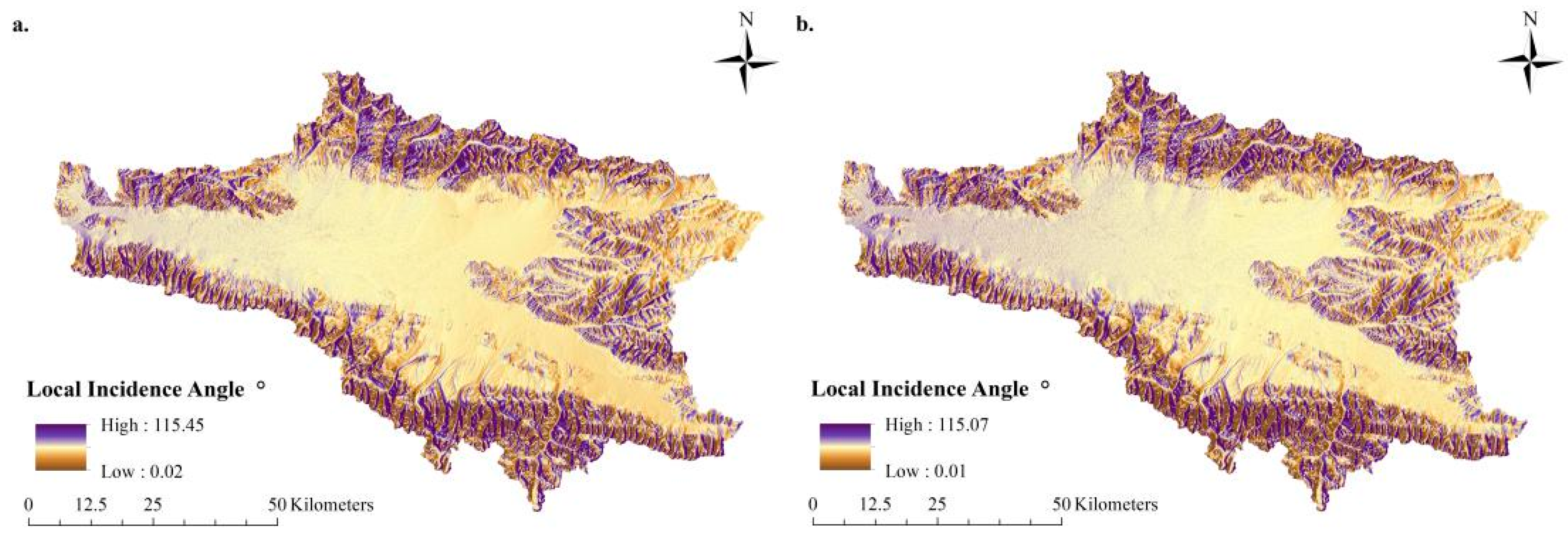
6.1. Factors Influencing Snow Depth Inversion Error in Relation to Spatial Variation
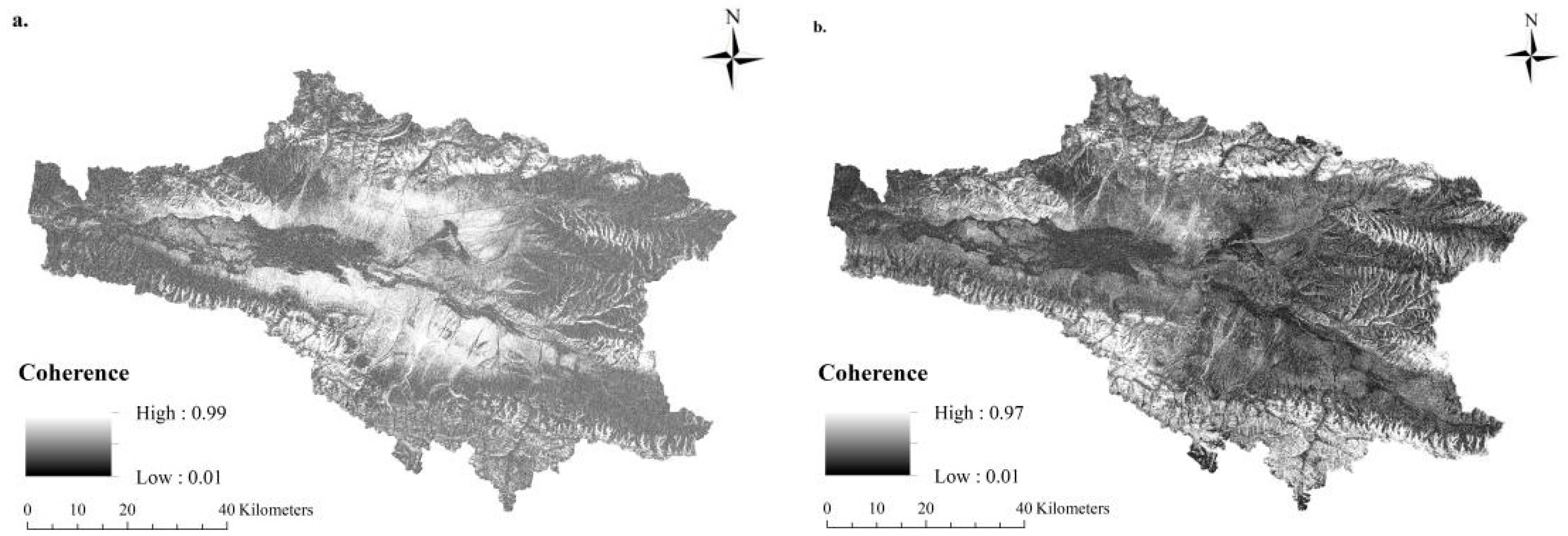
6.2. Limitations of D-InSAR Method
6.3. Limitations Related to the Establishment of Background Error and Observation Error in the 3DVAR Fusion Algorithm
6.4. Limitations of the Data Fusion Methods
7. Conclusions
- (1)
- After correct preprocessing of Sentinel-1 data, the SAR differential interferometry technology of the two-pass method can be utilized for snow depth inversion. However, the variance of certain factors, such as coherence, may influence the accuracy of snow depth inversion. The inversion in this study, which was based on D-InSAR, is a face-to-face process. Therefore, it is more difficult to guarantee a high coherence for a whole region than it is for limited points. It is possible to make use of the SAR differential interferometry technology of the two-pass method to select limited points in areas of high coherence to acquire snow depth.
- (2)
- The study introduced the background and observation error covariance to obtain the minimal analysis vector that would satisfy the cost function, that is, by making use of observation data to correct snow depth inversion. The study indicated that after the 3DVAR fusion, every accuracy indicator of snow depth inversion had been improved.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, T. Influence of the seasonal snow cover on the ground thermal regime: An overview. Rev. Geophys. 2005, 43, 589–590. [Google Scholar] [CrossRef]
- Zimov, S.A.; Schuur, E.A.G.; Chapin, F.S. Permafrost and the Global Carbon Budget. Science 2006, 312, 1612–1613. [Google Scholar] [CrossRef] [PubMed]
- Tarnocai, C.; Canadell, J.G.; Schuur, E.A.G. Soil organic carbon pools in the northern circumpolar permafrost region. Glob. Biogeochem. Cycles 2009, 23, 2607–2617. [Google Scholar] [CrossRef]
- Bocchiola, D.; Janetti, E.B.; Gorni, E. Regional evaluation of three day snow depth for avalanche hazard mapping in switzerland. Nat. Hazards Earth Syst. Sci. 2008, 8, 685–705. [Google Scholar]
- Marshall, S.E.; Roads, J.O.; Glatzmaier, G.A. Snow hydrology in a general circulation model. J. Clim. 1994, 7, 1251–1269. [Google Scholar] [CrossRef]
- Mccreight, J.L.; Small, E.E.; Larson, K.M. Snow depth, density, and SWE estimates derived from GPS reflection data: Validation in the western U.S. Water Resour. Res. 2014, 50, 6892–6909. [Google Scholar] [CrossRef]
- Liang, J.Y.; Liu, X.P.; Huang, K.N.; Chen, Y.N. Improved snow depth retrieval by integrating microwave brightness temperature and visible/infrared reflectance. Remote Sens. Environ. 2015, 156, 500–509. [Google Scholar] [CrossRef]
- Robinson, D.; Kunzi, K.; Kukla, G.; Rott, H. Comparative utility of microwave and shortwave satellite data for all-weather charting of snow cover. Nature 1984, 312, 434–435. [Google Scholar] [CrossRef]
- Dai, L.; Che, T.; Ding, Y. Inter-Calibrating SMMR, SSM/I and SSMI/S Data to Improve the Consistency of Snow-Depth Products in China. Remote Sens. 2015, 7, 7212–7230. [Google Scholar] [CrossRef]
- Foster, J.L.; Chang, A.; Hall, D.K. Comparison of snow mass estimates from a prototype passive microwave snow algorithm, a revised algorithm and a snow depth climatology. Remote Sens. Environ. 1997, 62, 132–142. [Google Scholar] [CrossRef]
- Nikraftar, Z.; Hasanlou, M.; Esmaeilzadeh, M. Novel Snow Depth Retrieval Method Using Time Series Ssmi Passive Microwave Imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B8, 525–530. [Google Scholar] [CrossRef]
- Armstrong, R.L.; Brodzik, M.J. Hemispheric-scale comparison and evaluation of passive-microwave snow algorithms. Ann. Glaciol. 2001, 34, 38–44. [Google Scholar] [CrossRef]
- Storvold, R.; Malnes, E.; Larsen, Y. SAR Remote Sensing of Snow Parameters in Norwegian Areas—Current Status and Future Perspective. J. Electromagn. Waves Appl. 2006, 20, 1751–1759. [Google Scholar] [CrossRef]
- Praveen, K.; Thakur, S.P.; Aggarwal, P.K. Snow physical parameters estimation using space-based Synthetic Aperture Radar. Geocarto Int. 2012, 27, 263–288. [Google Scholar]
- Shi, J.C.; Dozier, J. Estimation of snow water equivalence using SIR-C/X-SAR. I. Inferring snow density and subsurface properties. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2465–2474. [Google Scholar]
- Wu, T.D.; Chen, K.S.; Shi, J.C. A transition model for the reflection coefficient in surface scattering. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2040–2050. [Google Scholar]
- Cui, Y.; Xiong, C.; Lemmetyinen, J. Estimating Snow Water Equivalent with Backscattering at X and Ku Band Based on Absorption Loss. Remote Sens. 2016, 8, 505. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Q.; Zhao, C.; Yang, C.; Sun, Q.; Chen, W. Monitoring land subsidence in the southern part of the lower liaohe plain, china with a multi-track ps-insar technique. Remote Sens. Environ. 2017, 188, 73–84. [Google Scholar] [CrossRef]
- Bozzano, F.; Mazzanti, P.; Perissin, D. Basin Scale Assessment of Landslides Geomorphological Setting by Advanced InSAR Analysis. Remote Sens. 2017, 9, 267. [Google Scholar] [CrossRef]
- Polcari, M.; Palano, M.; Fernández, J.; Samsonov, S.V.; Stramondo, S.; Zerbini, S. 3D displacement field retrieved by integrating sentinel-1 InSAR and GPS data: The 2014 South Napa earthquake. Eur. J. Remote Sens. 2016, 49, 1–13. [Google Scholar] [CrossRef]
- Evans, J.R.; Kruse, F.A. Determination of snow depth using elevation differences determined by interferometric SAR (InSAR). Geosci. Remote Sens. Symp. 2014, 125, 962–965. [Google Scholar]
- Oveisgharan, S.; Zebker, H.A. Estimating Snow Accumulation from InSAR Correlation Observations. IEEE Trans. Geosci. Remote Sens. 2006, 45, 10–20. [Google Scholar] [CrossRef]
- Leinss, S.; Lemmetyinen, J.; Wiesmann, A. Interferometric and polarimetric methods to determine SWE, fresh snow depth and the anisotropy of dry snow. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]
- Guneriussen, T.; Hogda, K.A.; Johnsen, H. InSAR for estimation of changes in snow water equivalent of dry snow. IEEE Trans. Geosci. Remote Sens. 2002, 39, 2101–2108. [Google Scholar] [CrossRef]
- Deeb, E.J.; Forster, R.R.; Kane, D.L. Monitoring snowpack evolution using interferometric synthetic aperture radar on the North Slope of Alaska, USA. Int. J. Remote Sens. 2011, 32, 3985–4003. [Google Scholar] [CrossRef]
- Wei, M.; Sandwell, D.T. Decorrelation of L-Band and C-Band Interferometry over Vegetated Areas in California. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2942–2952. [Google Scholar]
- Nagler, T.; Rott, H.; Ripper, E.; Bippus, G.; Hetzenecker, M. Advancements for snowmelt monitoring by means of sentinel-1 SAR. Remote Sens. 2016, 8, 348. [Google Scholar] [CrossRef]
- Reichle, R.H. Data assimilation methods in the Earth sciences. Adv. Water Resour. 2008, 31, 1411–1418. [Google Scholar] [CrossRef]
- Gauthier, P.; Tanguay, M.; Laroche, S.; Pellerin, S.; Morneau, J. Extension of 3DVAR to 4DVAR: implementation of 4DVAR at the meteorological service of Canada. Mon. Weather Rev. 2006, 135, 2339–2354. [Google Scholar] [CrossRef]
- Kleist, D.T.; Parrish, D.F.; Derber, J.C.; Treadon, R.; Errico, R.M.; Yang, R. Improving incremental balance in the gsi 3DVAR analysis system. Mon. Weather Rev. 2009, 137, 1046–1060. [Google Scholar] [CrossRef]
- Zhao, K.; Xue, M. Assimilation of coastal doppler radar data with the arps 3DVAR and cloud analysis for the prediction of hurricane IKE (2008). Geophys. Res. Lett. 2009, 36, 91–100. [Google Scholar] [CrossRef]
- Peng, S.; Zeng, X.; Li, Z. A three-dimensional variational data assimilation system for the South China Sea: Preliminary results from observing system simulation experiments. Ocean Dyn. 2016, 66, 737–750. [Google Scholar] [CrossRef]
- Métivier, F.; Devauchelle, O.; Chauvet, H. Geometry of meandering and braided gravel-bed threads from the Bayanbulak Grassland, Tianshan, P.R. China. Earth Surf. Dyn. 2016, 4, 273–283. [Google Scholar] [CrossRef]
- Zhang, B.; Yao, Y.; Cheng, W. Human-Induced Changes to Biodiversity and Alpine Pastureland in the Bayanbulak Region of the East Tienshan Mountains. Mt. Res. Dev. 2002, 22, 383–389. [Google Scholar] [CrossRef]
- Liu, X.; Ma, H.; Sun, W. Study on the geolocation algorithm of space-borne SAR image. In Advances in Machine Vision, Image Processing and Pattern Analysis, Proceedings of the International Workshop on Intelligent Computing in Pattern Analysis/Synthesis: Xi’an, China, 26–27 August 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 270–280. [Google Scholar]
- Liu, G.; Fan, J.H.; Zhao, F.; Mao, K.B.; Dou, C.Y. Monitoring elevation change of glaciers on Geladandong Mountain using TanDEM-X SAR interferometry. J. Mt. Sci. 2017, 14, 859–869. [Google Scholar] [CrossRef]
- Song, H.; Sun, Y. InSAR phase filtering using spatially adapted total generalized variation. Remote Sens. Lett. 2017, 8, 370–379. [Google Scholar] [CrossRef]
- Yu, X.; Yang, H.; Peng, J. A modified Goldstein algorithm for InSAR interferogram filtering. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 1051–1054. [Google Scholar]
- Atzori, S.; Chiarabba, C.; Devoti, R. Anomalous far-field geodetic signature related to the 2009 L’Aquila (central Italy) earthquake. Terra Nova 2014, 25, 343–351. [Google Scholar] [CrossRef]
- Deng, J.; Huang, X.; Feng, Q. Toward Improved Daily Cloud-Free Fractional Snow Cover Mapping with Multi-Source Remote Sensing Data in China. Remote Sens. 2015, 7, 6986–7006. [Google Scholar] [CrossRef]
- Yang, G.; Xie, H.; Ning, L. Toward advanced daily cloud-free snow cover and snow water equivalent products from Terra–Aqua MODIS and Aqua AMSR-E measurements. J. Hydrol. 2010, 385, 23–35. [Google Scholar]
- Mhawej, M.; Faour, G.; Fayad, A. Towards an enhanced method to map snow cover areas and derive snow-water equivalent in Lebanon. J. Hydrol. 2014, 513, 274–282. [Google Scholar] [CrossRef]
- Huang, C.L.; Wang, H.W.; Hou, J.L. Estimating spatial distribution of daily snow depth with kriging methods: Combination of MODIS snow cover area data and ground-based observations. Cryosphere Discuss. 2015, 9, 4997–5020. [Google Scholar] [CrossRef]
- Li, H. Snow depth derived from repeat-pass InSAR sounding. J. Glaciol. Geocryol. 2014, 36, 517–526. [Google Scholar]
- Harshburger, B.J.; Humes, K.S.; Walden, V.P. Spatial interpolation of snow water equivalency using surface observations and remotely sensed images of snow-covered area. Hydrol. Process. 2010, 24, 1285–1295. [Google Scholar] [CrossRef]
- Cuomo, S.; Galletti, A.; Giunta, G. Numerical Effects of the Gaussian Recursive Filters in Solving Linear Systems in the 3Dvar Case Study. Numer. Math. Theory Methods Appl. 2017, 10, 520–540. [Google Scholar] [CrossRef]
- Che, T.; Dai, L.; Wang, J. Estimation of snow depth and snow water equivalent distribution using airborne microwave radiometry in the Binggou Watershed, the upper reaches of the Heihe River basin. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 23–32. [Google Scholar] [CrossRef]
- Kumar, V.; Venkataraman, G. SAR interferometric coherence analysis for snow cover mapping in the western Himalayan region. Int. J. Digit. Earth 2011, 4, 78–90. [Google Scholar] [CrossRef]
- Leinss, S.; Parrella, G.; Hajnsek, I. Snow height determination by polarimetric phase differences in X-band SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 7, 3794–3810. [Google Scholar] [CrossRef]
- Leinss, S.; Löwe, H.; Proksch, M. Anisotropy of seasonal snow measured by polarimetric phase differences in radar time series. Cryosphere Discuss. 2015, 9, 6061–6123. [Google Scholar] [CrossRef]
- Sun, S.; Tao, C.; Jian, W. Estimation and Analysis of Snow Water Equivalents Based on C-Band SAR Data and Field Measurements. Arct. Antarct. Alp. Res. 2015, 47, 313–326. [Google Scholar] [CrossRef]
| Master Image | Slave Image | Temporal Baseline (Day) | Perpendicular Baseline (m) | Polarisation Mode |
|---|---|---|---|---|
| 31 October 2016 | 18 December 2016 | 48 | 15.91 | VV |
| 31 October 2016 | 11 January 2017 | 72 | 11.15 | VV |
| Time Frame | Method | R2 | RE | RMSE | MEE | MAEE |
|---|---|---|---|---|---|---|
| (%) | (cm) | |||||
| 31 October 2016–18 December 2016 | Inversion | 0.31 | 21.83 | 2.51 | −0.97 | 2.47 |
| 3DVAR fusion | 0.50 | 14.86 | 1.96 | 0.25 | 1.68 | |
| 31 October 2016–11 January 2017 | Inversion | 0.27 | 29.60 | 4.04 | −0.55 | 3.60 |
| 3DVAR fusion | 0.46 | 26.01 | 3.65 | −2.10 | 3.16 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, L.; Yang, J.; Chen, X.; Hao, J. Estimating Snow Depth Using Multi-Source Data Fusion Based on the D-InSAR Method and 3DVAR Fusion Algorithm. Remote Sens. 2017, 9, 1195. https://doi.org/10.3390/rs9111195
Liu Y, Li L, Yang J, Chen X, Hao J. Estimating Snow Depth Using Multi-Source Data Fusion Based on the D-InSAR Method and 3DVAR Fusion Algorithm. Remote Sensing. 2017; 9(11):1195. https://doi.org/10.3390/rs9111195
Chicago/Turabian StyleLiu, Yang, Lanhai Li, Jinming Yang, Xi Chen, and Jiansheng Hao. 2017. "Estimating Snow Depth Using Multi-Source Data Fusion Based on the D-InSAR Method and 3DVAR Fusion Algorithm" Remote Sensing 9, no. 11: 1195. https://doi.org/10.3390/rs9111195
APA StyleLiu, Y., Li, L., Yang, J., Chen, X., & Hao, J. (2017). Estimating Snow Depth Using Multi-Source Data Fusion Based on the D-InSAR Method and 3DVAR Fusion Algorithm. Remote Sensing, 9(11), 1195. https://doi.org/10.3390/rs9111195