1. Introduction
Remote sensing of oceans and coastal zones is a key technology for monitoring spatial-temporal distribution of the river plume into sea and understanding of the land-ocean interaction processes. Satellite retrievals of inherent optical parameters (IOPs) of waters such as absorption and scattering characteristics is one of the most important applications of ocean color remote sensing [
1]. Furthermore, chlorophyll, chromophoric dissolved organic matter (CDOM), suspended sediment and other water component concentrations can be derived from IOPs, which leads to further estimations of phytoplankton biomass, primary productivity and heat flux [
2]. The IOPs mainly include absorption coefficient (
a(
λ), see
Table 1 for symbols and definitions) and backscattering coefficient. They are the source of the satellite remote sensing to quantify ocean water information [
3], and key parameters of bio-optical models [
4]. CDOM absorption coefficient is often used as a tracer to evaluate the amount of nutrients carried by Changjiang diluted water. Numerous applications of remote sensing have allowed to retrieve main components of water (i.e., phytoplankton, non-pigmented particles and CDOM) worldwide [
5,
6,
7]. In CDOM-rich regions, such as North America and northern Europe, CDOM determines the optical properties of marine waters to a large extent and its existence can affect marine biogeochemical processes by the light absorption. Bricaud et al. [
8] pointed out that even low concentrations of CDOM in the open sea may have an effect on absorption and hence on ocean color similar to that of low or moderate algal biomass; Nieke et al. [
9] supported the possibility of using light absorption characteristics of CDOM in coastal waters strongly influenced by freshwater runoff in the Estuary and Gulf of St. Lawrence system (Canada); Darecki et al. [
10] found a strong influence of CDOM absorption on the quantitative and qualitative features of spectral reflectance of in two different water bodies with similar chlorophyll content in the Baltic Sea; Hu et al. [
11] estimated
ag to study occurrence and distribution of red tides in coastal waters off South Florida; Bowers et al. [
12] used salinity to determinate
ag in an estuary for exploring the river discharge.
A number of algorithms were proposed to quantify
ag(
λ) from spectral measurements of ocean water. Empirical algorithms [
13,
14,
15,
16,
17,
18,
19] were mostly based on spectral reflectance ratios to calculate
ag(
λ), and these algorithms required adequate data to parameterize the model and may only be valid for specific locations. Algorithms based on statistical modeling [
18,
20,
21,
22,
23,
24], such as optimization (Garver-Siegel-Maritorena, GSM), matrix inversion algorithm, artificial neural network (aNN) and Linear Matrix Inversion (LMI) algorithm, used some semi-analytical methodologies, but required knowledge about specific biochemical parameters [
5]. Semi-analytical algorithms [
25,
26,
27] mostly use
Rrs(
λ) to calculate IOPs and further to estimate biochemical parameters, which incorporate both empirical parameters and bio-optical models. The quasi-analytical algorithm (QAA) developed by Lee et al. [
28] was widely applied during the last decade. Several updated versions were presented in following years [
29,
30,
31]. Recent version (QAA_v6) has been presented online by Lee [
31].
Although the QAA algorithm is widely used [
30,
32,
33,
34,
35], some researches pointed out that there are still large uncertainties in deriving optical properties for optically complex Case 2 waters [
36,
37,
38]. Under the joint influences of river runoffs, tidal currents, marine circulations, etc., the hydrodynamic and biogeochemical environment in the Changjiang estuary and its adjacent coastal waters is unique, characterizing by high turbidity and complicated optical properties [
39,
40,
41]. Among these drivers, the Changjiang diluted water with low salinity and high levels of nutrients and suspended sediment [
42,
43,
44,
45] makes greatest contribution to the optical complexity in the region of Changjiang River mouth due to its obvious seasonal changes. Compared to the clear oceanic waters, due to the lack of in situ data support, an application of QAA in the Changjiang estuarine and coastal waters is rarely reported in the literature.
Therefore, improvements to QAA over optically complex and highly turbid waters is in great demand considering successful absorption retrieval from ocean color remote sensing would provide a considerable advance in the release of satellite product and estimation of water components in the future. The objective of this study is to improve QAA algorithm and enhance an accuracy of QAA retrieval from satellite data in the Changjiang estuarine and coastal waters. The applicability of QAA is tested in the study area at first and then we perform a verification and calibration of QAA based on large amounts of in situ data accumulated during 9 voyage surveys from 2011 to 2015. Moreover, we calibrate the QAA_v6 and propose QAA_cj for retrieving both total and CDOM spectral absorption coefficients. Through applying to GOCI level-1 products, QAA_cj is finally validated with in situ data and compared with QAA_v6.
2. Materials and Methods
2.1. Shipborne Samplings and Measurements
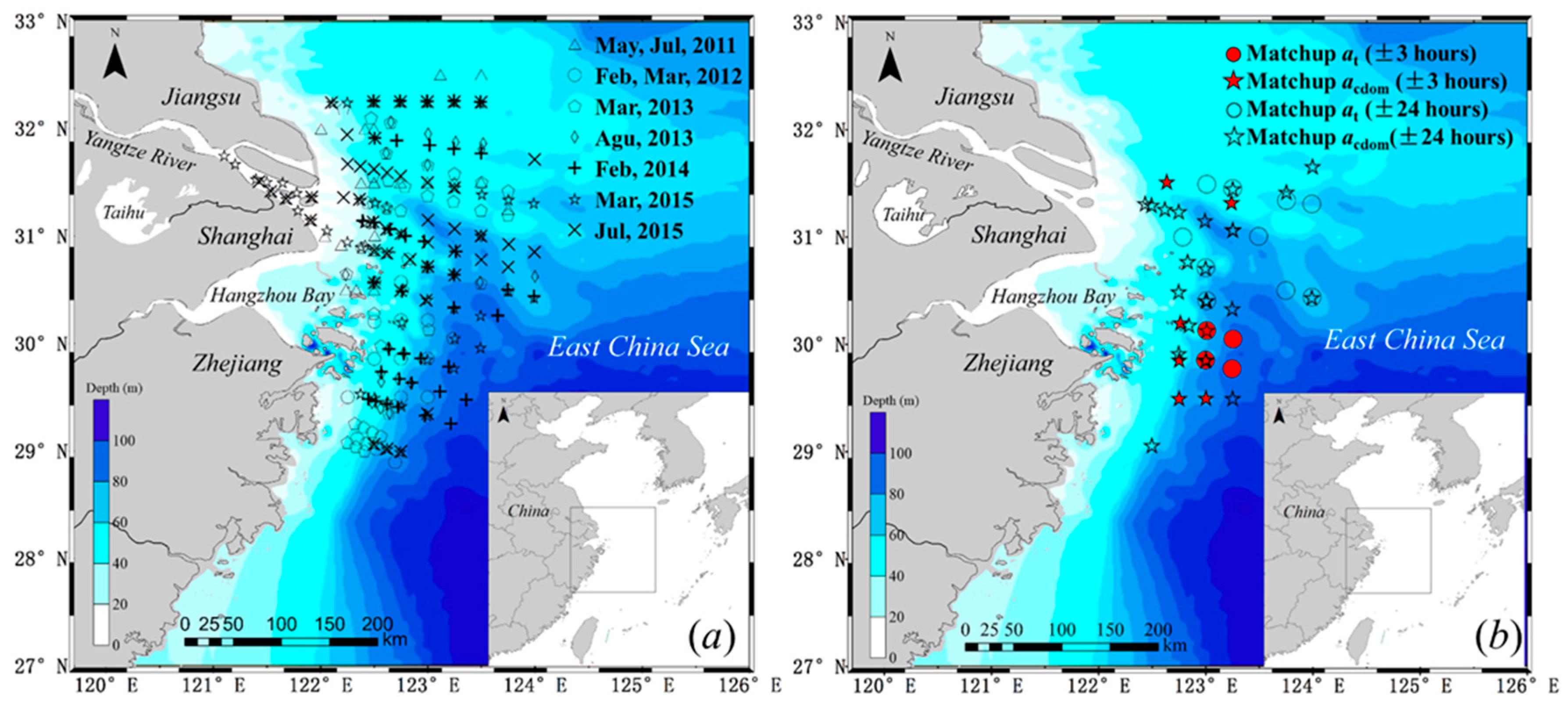
Water samples were collected during nine cruise campaigns in the Changjiang estuarine and coastal waters from 2011 to 2015. Spectral radiometric parameters (i.e., spectral downwelling irradiance,
Ed, spectral incident radiance,
Ls, total spectral upwelling radiance,
Ltot) for estimating
Rrs(
λ) were measured by Hyperspectral surface acquisition system (HyperSAS, Satlantic Inc.
®, Halifax, NS, Canada). A total of 371 surface data samples was collected. Two radiance sensors were pointed to the sea and sky, respectively, at an optimal zenith angle of 40°, and at an optimal azimuth angle of 135° away from the sun, in order to maximally avoid the wind speed impact and minimize solar glitter effects [
46].
Spectral absorption coefficients a(λ, z) and attenuation coefficients c(λ, z) (z is the depth in meters) were measured in situ by WETLabs® absorption and attenuation meter (ac-s) during downcasts and upcasts as water flowed through the ac-s meter. A total of 479 data samples of a was obtained. bb(λ, z) values were measured simultaneously by WETLabs® ECO-BB9 backscattering sensors (at wavelengths of 412, 440, 488, 510, 532, 595, 650, 676, and 715 nm, and at a scattering angle of 117°). 515 data samples of bbp were collected.
CDOM water samples were obtained through filtration on shipboard using a 0.22 µm polycarbonate membrane (Millipore, 47 mm diameter, MilliporeSigma, Burlington, MA, USA) under low vacuum immediately after sampling. The membranes were soaked in 10% HCl for 15 min and then rinsed by Milli-Q water three times before filtration. The filtered CDOM samples were collected in borosilicate glass vials, and then stored in a −40 °C refrigerator. All vials were pre-soaked in 10% HCl for 24 h, rinsed by Milli-Q water for three times, and pre-combusted at 450 °C for 5 h. A total of 551 data samples were obtained.
Data processing methods were detailed in
Section 2.2. A total of 181 matchups containing simultaneous data of
Rrs,
a and
bb were obtained. Furthermore, SPSS software (IBM
®, version 22.0) was used to control data quality. Excluding the sampling data deviating from the mean values more than ±3σ, 144 matchup data were reserved for the analysis. In addition, 159 matchup data of
ag and
Rrs were collected. All matchup locations are shown in
Figure 1a. Meanwhile, two sets of matchup data were randomly divided into two parts, of which 70% were used to calibrate algorithm, and 30% to validate algorithm.
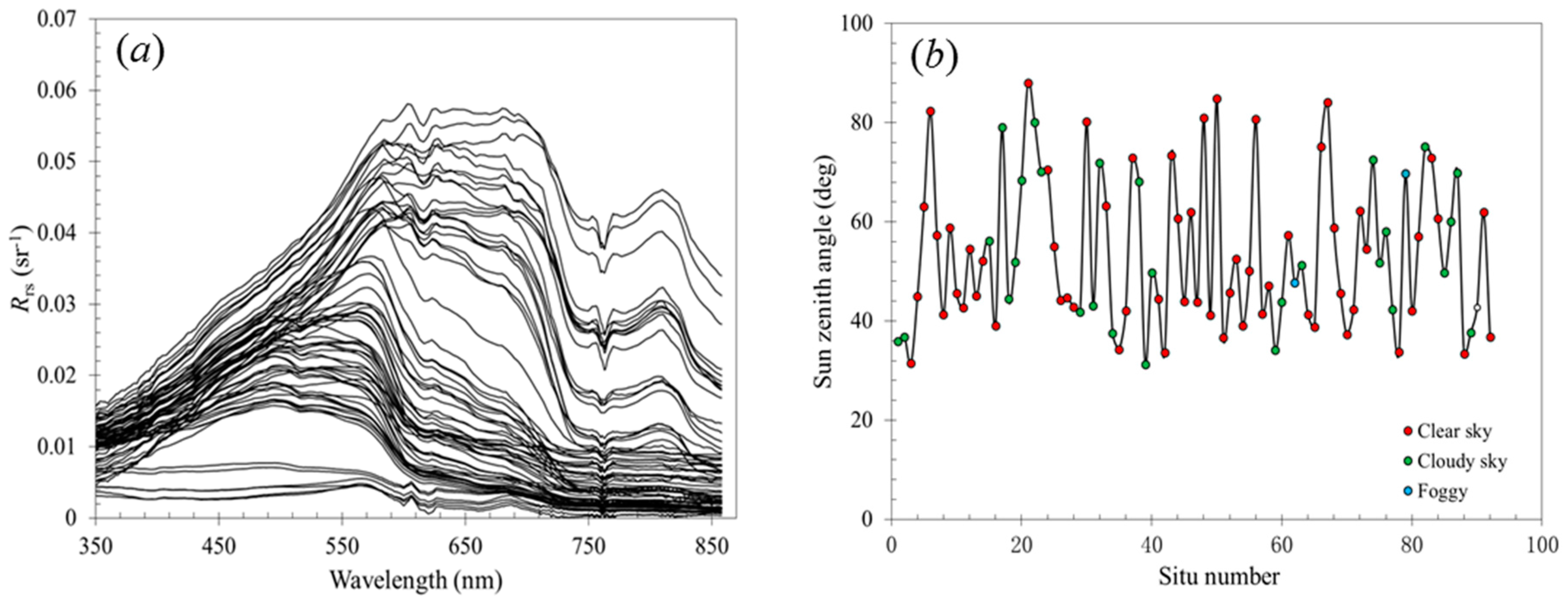
Typical spectra of remote-sensing reflectance collected in the Changjiang estuarine and its adjacent coastal waters are shown in
Figure 2a,b shows the sun zenith angle and weather conditions of in situ
Rrs(
λ) validation data.
2.2. Data Processing
Through in situ measurements of downwelling spectral irradiance,
Ed(
λ), incident spectral radiance,
Ls(
λ), total upwelling spectral radiance,
Ltot(
λ),
Rrs(
λ) is estimated by Sokoletsky and Shen [
47]:
where
ρsky(
λ) stands for a ratio of spectral reflected sky radiance, and
Ls,sky(
λ) for incident spectral sky radiance. The estimations of
ρsky(
λ),
Ls,sky(
λ) and
Rrs(
λ) were detailed in Sokoletsky and Shen [
47].
Because
a(
λ) is affected by temperature, salinity, pure water absorption and total scattering, it must be corrected [
47,
48,
49]. For the most important and simultaneously the most difficult scattering correction procedure for the
anw(
λ), we have used a modified Boss’s method (MBM) which was described in Sokoletsky and Shen [
47]. The average of
a(
λ, z) in depths of 0.5~1.5 m is adopted for the surface data.
bbp(
λ) is calculated using a scale factor supplied by the WETLabs Inc. [
48]. The specific correction method of
bbp is described in Sokoletsky and Shen [
47]. In turbid waters,
bbp at
λ < 488 nm measured by ECO-BB9 is generally too low due to absorption effects. Therefore, a spectral power function fitting was conducted, based on
bbp(
λ, z) values measured at
λ ≥ 488 nm [
47]. In this study, the average of
bbp(
λ, z) in depths of 0.5 to 1.5 m is adopted for the surface values.
In laboratory, CDOM samples were unfrozen and warmed to room temperature under dark light conditions. CDOM absorbance spectra,
D(
λ), were measured by PerkinElmer Lambda 1050 UV/VIS spectrophotometer.
ag(
λ) was derived as follows [
39]:
where
a′
g(
λ) represent uncorrected values of
ag(
λ) at wavelength
λ,
λ in nm;
l is the length of cuvette,
l = 0.1 m. Further, these initial values were scattering corrected as follows [
8]:
where
ag(
λ) is the final CDOM absorption coefficient.
2.3. Satellite Images
Satellite images were captured by the Geostationary Ocean Color Imager (GOCI) launched by Korean Ocean Satellite Center, which is the world’s first geostationary ocean color observation sensor [
50]. GOCI image covers 2500 × 2500 square kilometers, including Bohai Sea, Yellow Sea and East China Sea. GOCI collects eight images per day between 8:00 to 15:00 (Beijing time) at each hour, in a 500 m spatial resolution. GOCI has 6 visible wavebands centered at 412, 443, 490, 555, 660, 680 nm, and two near-infrared wavebands centered at 745 and 865 nm. GOCI data and products can be downloaded from official website (
http://kosc.kiost.ac). This study used GOCI level-1 top-of-atmosphere (TOA) radiance data. Through performing atmospheric correction method proposed by Pan et al. [
51], which is applicable for the Changjiang estuarine and coastal waters, the TOA radiance data are then inversed into the water surface remote-sensing spectral reflectance
Rrs(
λ). Afterwards, GOCI images
Rrs(
λ) were used for CDOM retrieval. Quasi-synchronous matchups between GOCI overpass observations and ground samplings were available during 6 March 2012 and 22 March 2015. A time window between in situ and satellite data was set at ±3 h for the Changjiang estuary, and ±24 h for the outer oceanic area. A mean value from a 3 × 3 pixel box centered at each sampling site is used aiming to reduce sensor and algorithm noise. A total of 28 images were obtained. Locations and time intervals of matchup samples are shown in
Figure 1b.
2.4. QAA_v6
The QAA_v6 is developed from QAA that is based on the relationship between
rrs and IOPs from Gordon et al. [
52]:
where the values of g
0 = 0.089 and g
1 = 0.1245 were accepted in this study in accordance with the QAA_v6.
rrs(
λ) has a computable relation with
Rrs(
λ) according to the following Equation (1) (QAA_v6, step 0),which can be derived from
Rrs to obtain IOPs:
The QAA_v6 algorithm was divided into two parts: in the first part, reference wavelength λ0 was selected, and then bbp(λ) and a(λ) were estimated by semi-analytical and analytical algorithms. In this process, aph(λ), ag(λ), and ad(λ) were not taken into account. In the second part, the total absorption coefficient which was derived from the first part was decomposed into absorption coefficients of its major components.
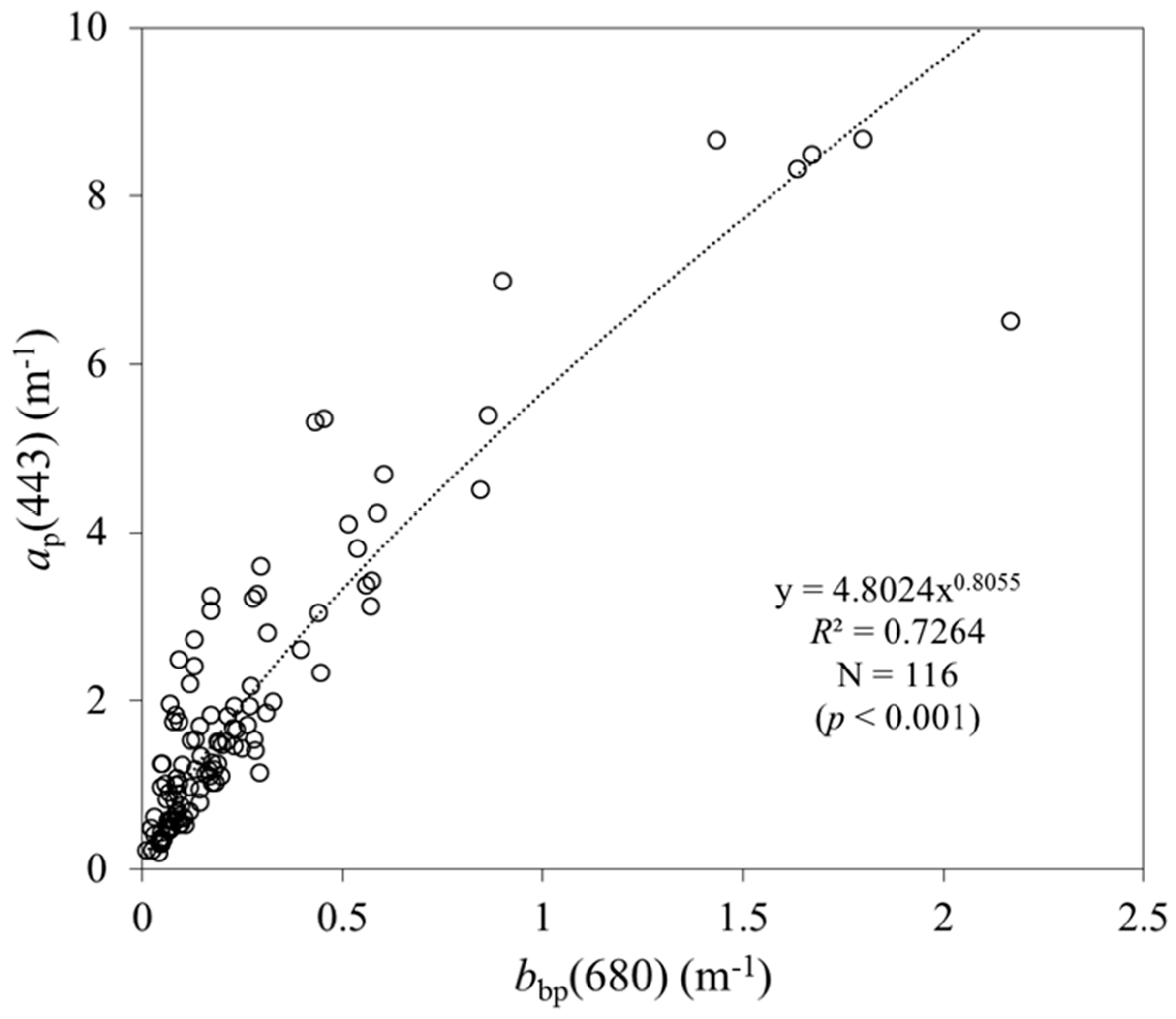
In the first part of the algorithm, two reference wavelengths were used in QAA_v6, which are 55X (here X means any number from 0 to 9; for example, it was 5 in previous versions of the QAA (version 1, 2, 3 and 4)) and 670 nm, designed for oceanic and coastal waters, respectively. The a(λ0) could be estimated from Rrs(443), Rrs(490), Rrs(55X), and Rrs(670) according to empirical formula (QAA_v6, step 2):
If
Rrs(670) < 0.0015 sr
−1:
where
a(
λ0) is an empirical coefficient relating to the specific study area,
h0 = −1.146,
h1 = −1.366,
h2 = −0.469. Therefore, it is calibrated by fitting Equation (7) by using in situ data in the study area, which is detailed in
Section 3.1.
bb(
λ) is expressed by Lee [
31] (QAA_v6, step 5):
where
Y is an empirical coefficient relating to the specific study area. Therefore, it is calibrated by fitting Equation (8) using in situ data in the study area, which is detailed in
Section 3.1.
In the second part,
a(
λ), was decomposed into two partial absorption coefficients:
adg(
λ) and
aph(
λ). The expression for
adg is given by Lee [
31] (QAA_v6, step 9):
where
S is the exponential slope for
adg(
λ). According to QAA_v6,
S values can be estimated by spectral ratio (QAA_v6, step 8):
Since
S values are influenced by CDOM and phytoplankton detritus, they are difficult to estimate accurately. In this study, we reestablished the empirical formula based on in situ data, which is detailed in
Section 3.1.
2.5. QAA_CDOM
To retrieve
ag, the mixture variable
adg needs to be further decomposed to
ag and
ad. However, the QAA_v6 cannot separate
ag from
adg so far. In this study, we use QAA_CDOM algorithm proposed by Zhu and Yu [
26] and Zhu et al. [
27] to separate
ag(443) and
ad(443) by:
where
j1 and
j2 are calculated by fitting Equation (11) by using in situ data in the study area, which is detailed in
Section 3.1.
Zhu and Yu [
26] and Zhu et al. [
27] used the in situ data (water types vary from clear Case 1 to turbid Case 2) to prove the effectiveness of this algorithm. The algorithm takes an advantage of
bbp(555) to estimate
ap(443). Therefore,
ag(443) can eventually be obtained by subtracting
ap(443) and
aw(443) from
a(443) estimated by the QAA_v6.
2.6. Accuracy Assessment
The accuracy of calibration algorithm can be evaluated by four statistical indices, root-mean-square-error (RMSE), mean absolute relative error (MARE), bias and the coefficient of determination (
R2). These indices are defined as follows (
N is the number of samples):
where
Xest,i and
Xmea,i are predicted and in situ values of optical parameters, respectively.
4. Discussion
CDOM absorption is a major variable in remote sensing algorithms for deriving concentrations of optically active components of sea water [
56]. Based on the spectral absorption characteristic of CDOM, Del Castillo and Miller [
14], D’Sa and Miller [
18] and Ficek et al. [
13] established statistical relationships between
ag and
Rrs ratio (using different wavelengths) in Mississippi River and the Baltic. Using
Rrs(
λ) to calculate
a and further to separate out
adg and
aph, semi-analytical models, such as GSM [
23] and QAA [
28], were developed based on IOCCG dataset and in situ data, while Brando and Dekker [
5] and Hoge and Lyon [
22] developed models using in situ data in Fitzroy Estuary and U.S. Middle Atlantic Bight.
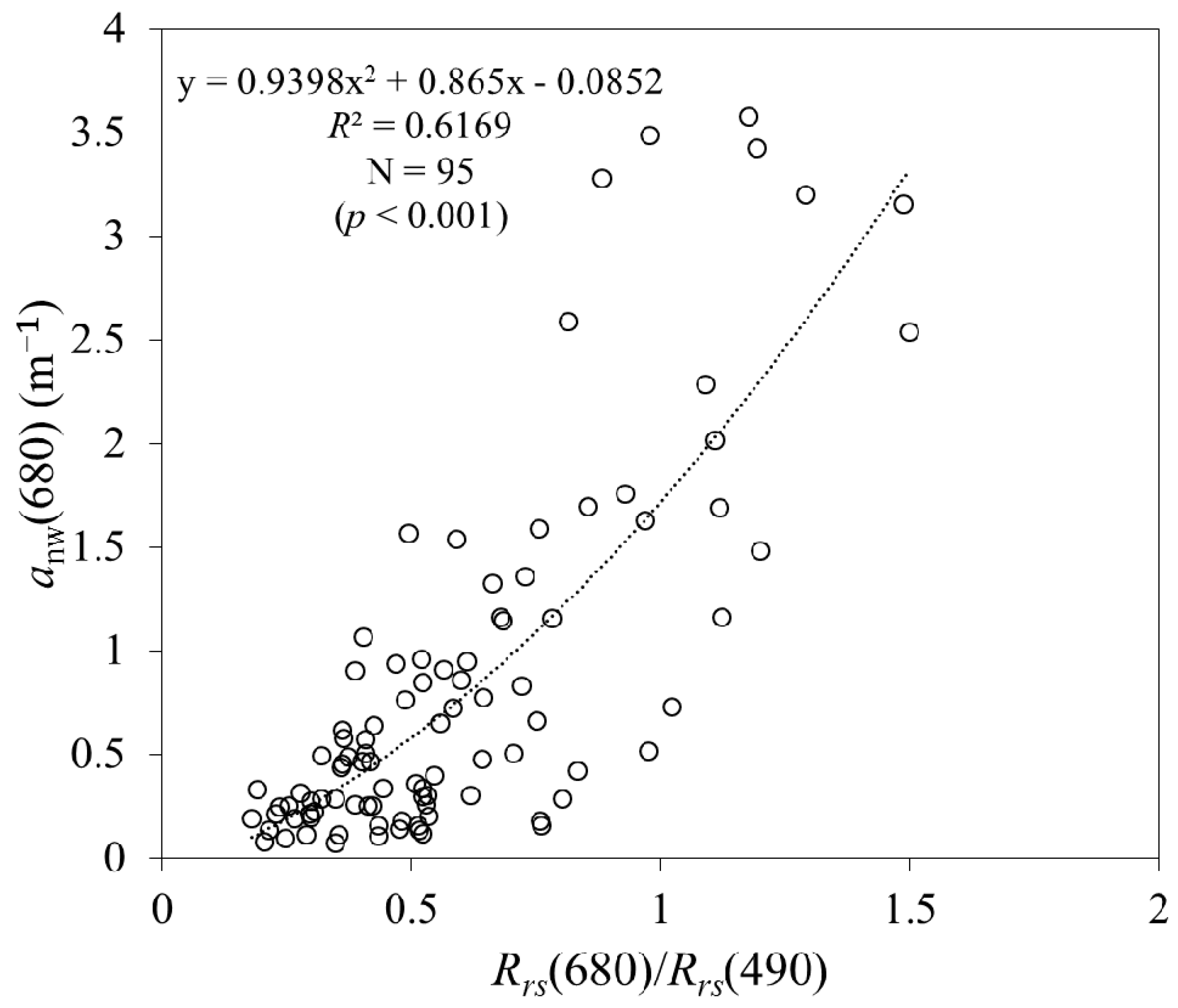
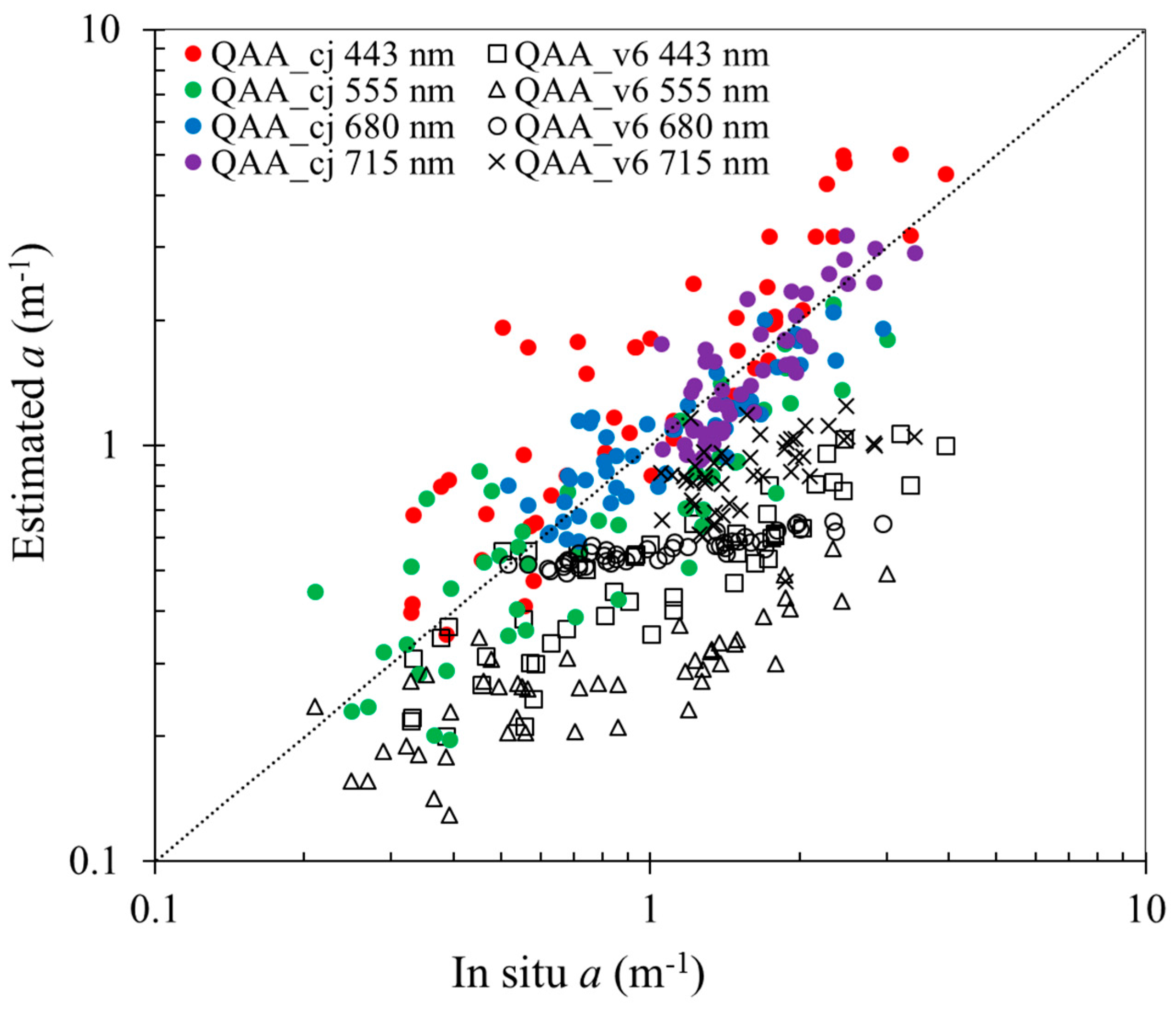
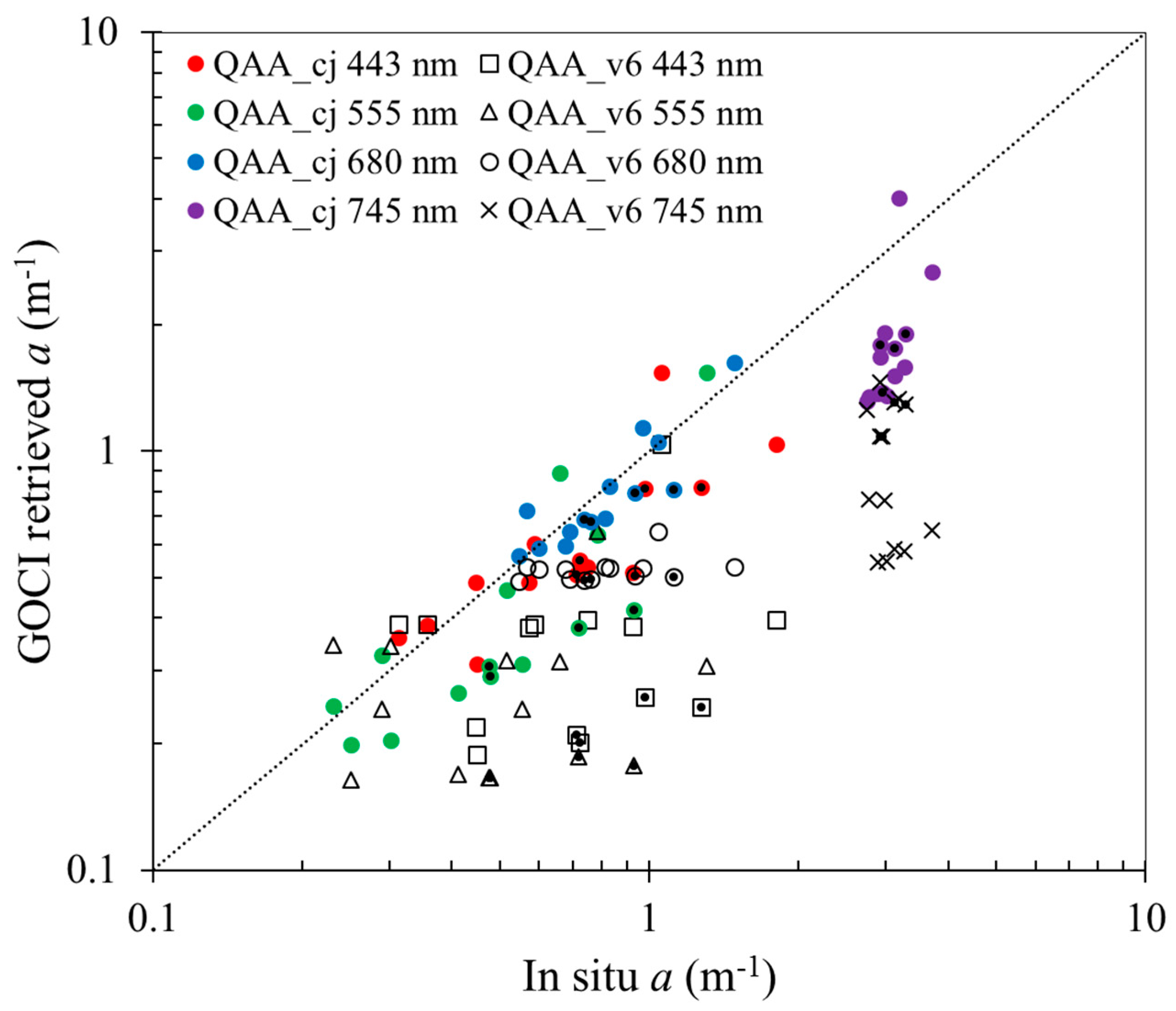
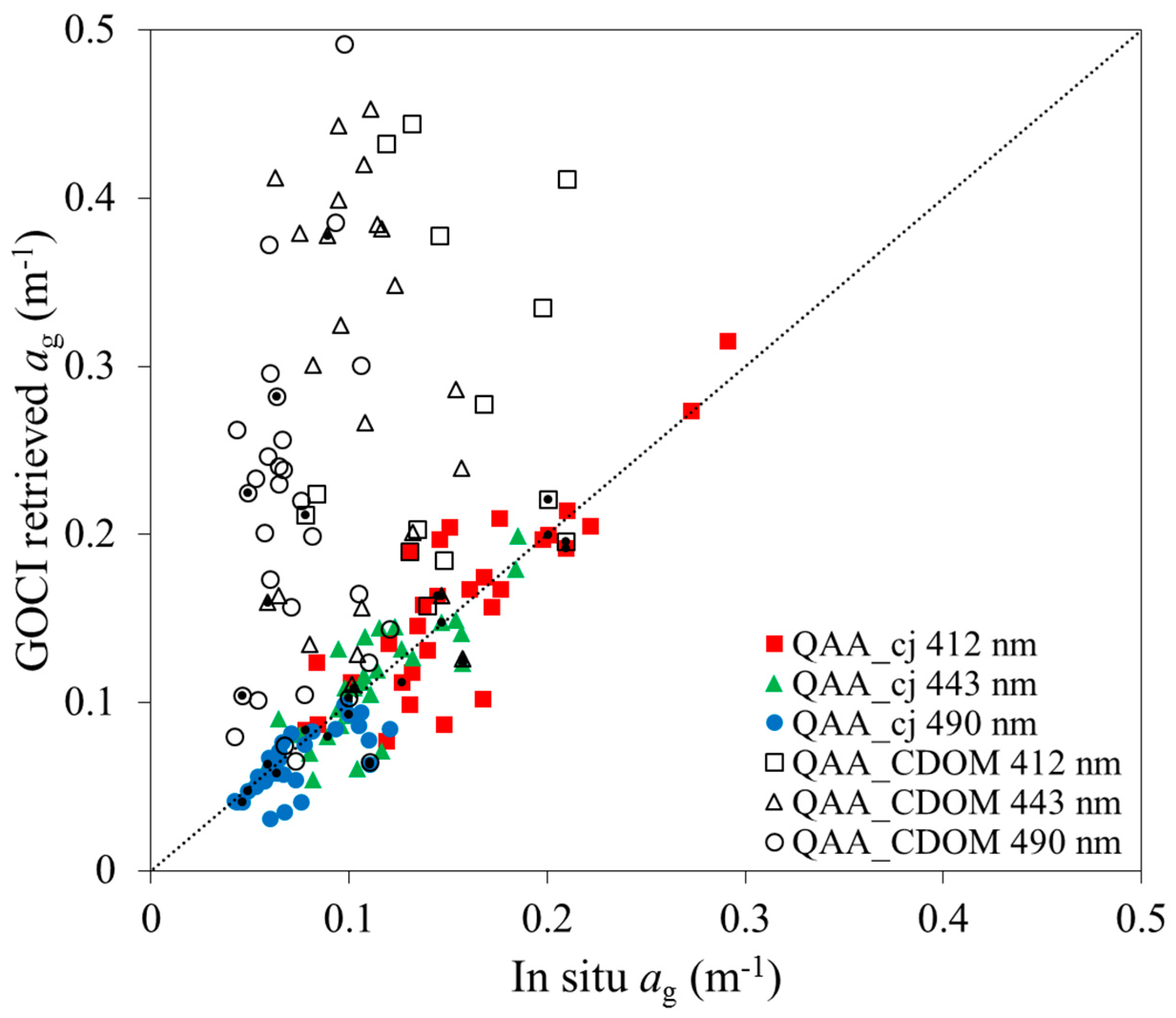
The QAA_cj algorithm was developed to give an opportunity to obtain more accurate estimates for both total and partial absorption coefficients in highly turbid waters, such as the Changjiang estuarine and coastal waters. For this purpose, we calibrated empirical parameters of the QAA_v6 and QAA_CDOM algorithms. Proofs of improvement made in these algorithms are shown in
Table 4,
Table 5,
Table 6 and
Table 7 and
Figure 6,
Figure 7,
Figure 8,
Figure 9 and
Figure 10. For example, a total absorption coefficient
a(
λ) retrieved by QAA_v6 was underestimated in highly turbid waters, while QAA_cj-based values were closer to in situ data (
Table 4,
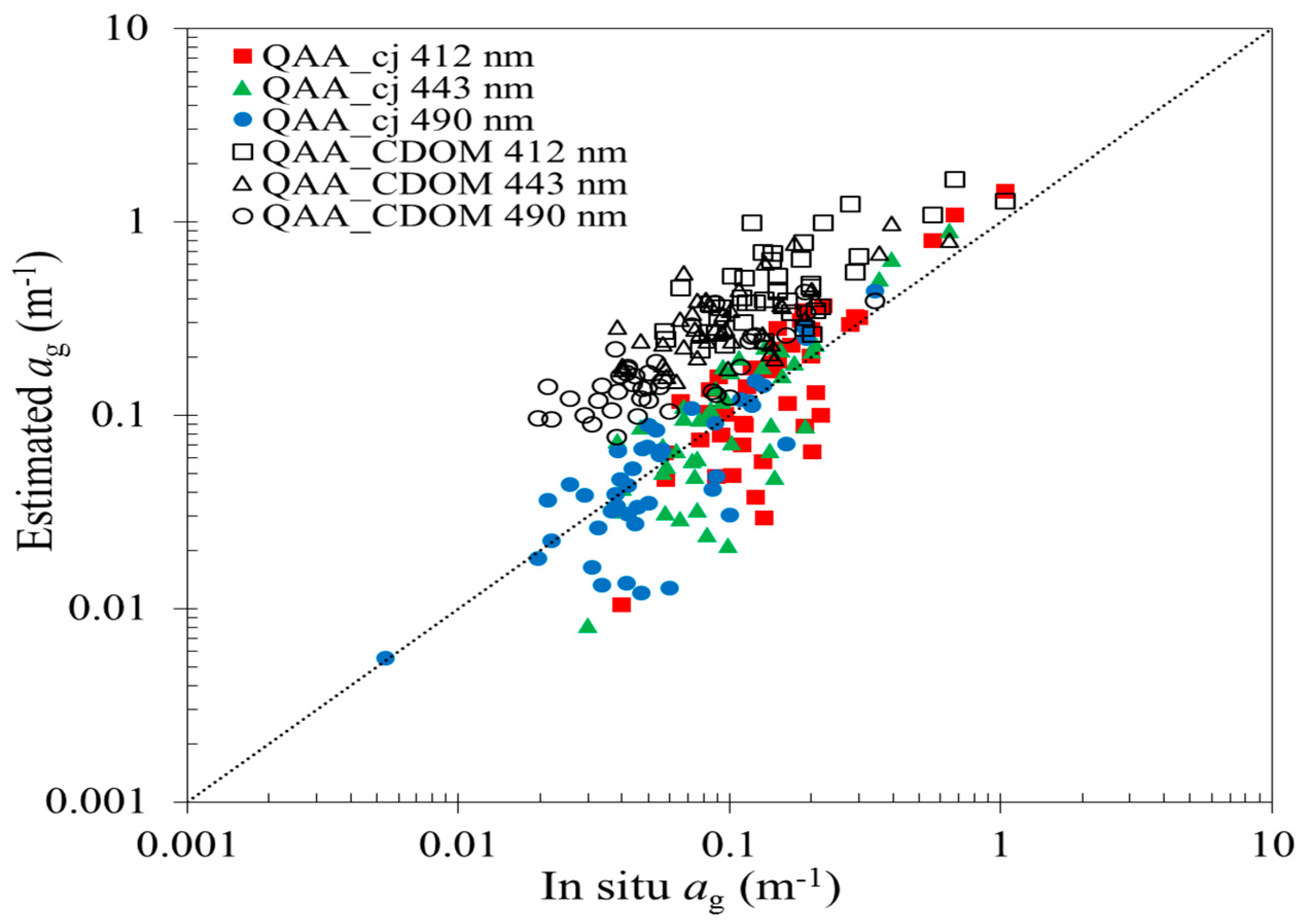
Figure 7). As for CDOM spectral absorption
ag(
λ), on the one hand it could not be estimated by the QAA algorithm and on the other hand it was overestimated by the QAA_CDOM algorithm (
Figure 8), while the QAA_cj retrieved value of
ag(443) has RMSE and
R2 of 0.07 m
−1 and 0.90, respectively, compared with in situ data (
Table 5). Nevertheless, the accuracy of
ag(
λ) derived from the QAA_cj in highly turbid waters still remains to be a challenge.
We also wish to note that our findings may have great values not only for numerous scientists and for decision makers working for the East China estuarine and coastal waters, but also for many other investigators. As it has been found by Sokoletsky et al. [
57], the biogeochemistry-optical relationships for the East China estuarine and coastal waters are very similar to that of the Gironde Estuary [
58] and the Southern North Sea [
59]. Thus, these findings really allow generalizing all conclusions of our study.
Since the aim of the study was the investigation of underwater IOPs, we used a conversion from the surface remote-sensing reflectance
Rrs(
λ) to its underwater analog,
rrs(
λ). Therefore, in this study, we used the formula proposed by Sokoletsky et al. [
57] to calculate
rrs(
λ) from
Rrs(
λ). Sokoletsky and Shen [
47] showed that although relations between
Rrs(
λ) and
rrs(
λ) are close for different models, the particular model parameters may play an important role in the inversion results. In addition, we have used only clear and cloudless sky conditions to measure
Rrs(
λ) to do calculations more simple and closer to remote-sensing results,
Figure 2b.
Equation (4) is an approximation to the exact solution of the radiative transfer equation [
60], which may cause a normalized (to the mean value) root-mean-square error of about 20% [
61]. Moreover, it is inappropriate to regard parameters of this equation (i.e., g
0 and g
1) as constants. These parameters are associated with the solar zenith angle and water properties, and vary with water composition scattering properties [
62]. Consequently, g
0 and g
1 have influence on
bb(
λ), when using QAA, it will further affect the inversion accuracy of
a(
λ). Lee et al. [
62] partitioned and weighted parameter
g according to the molecular (water itself) and particulate contributions to the backscattering coefficient. In this study, however, this approach was not exploited.
According to Lee et al. [
63], the
a(
λ0) and
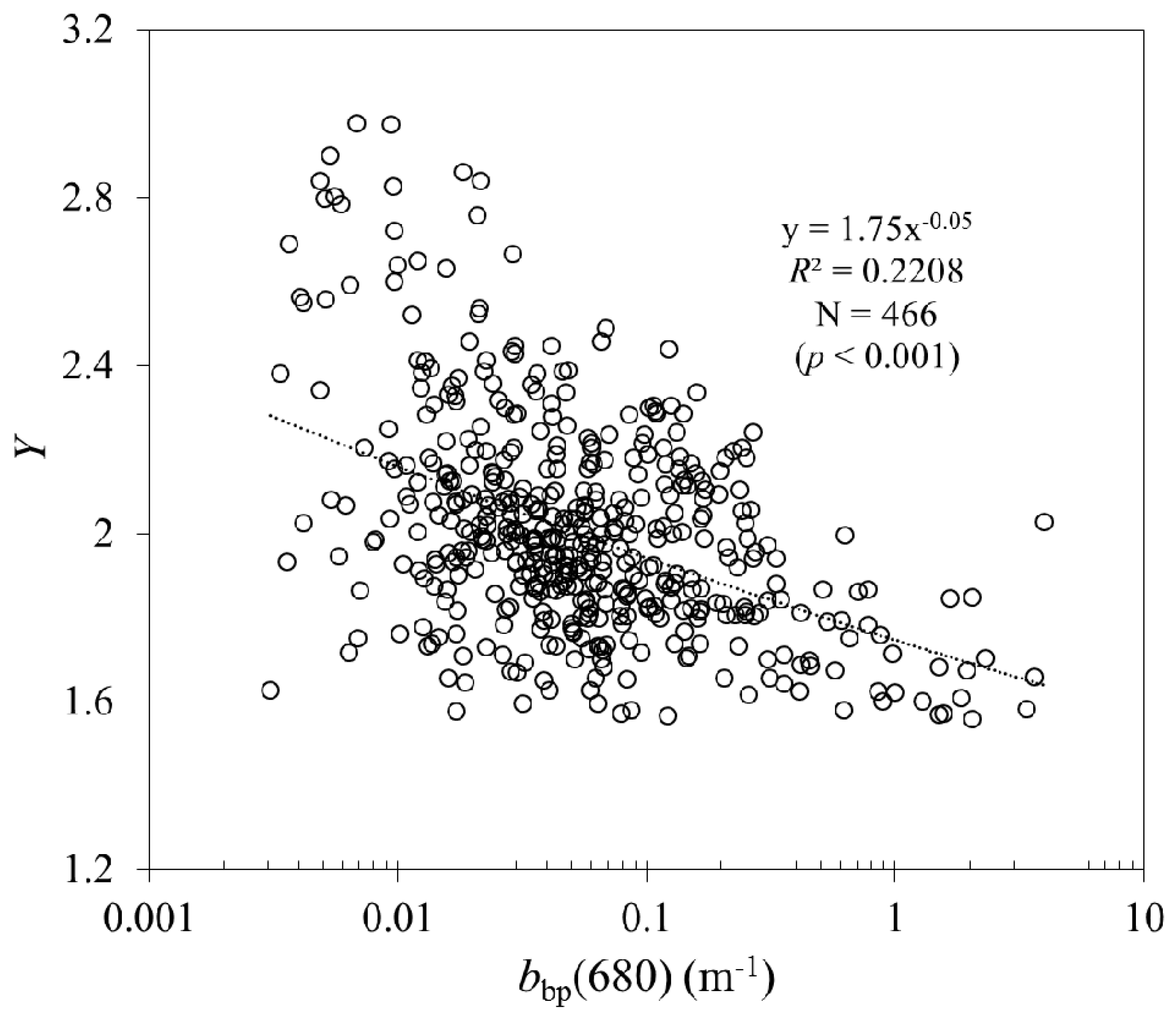
Y have an impact on performance of the QAA.
Y is a parameter which describes spectral variation of
bbp(
λ) [
64], and the variation of
Y depends on water composition and size of particles according to the Mie theory [
65]. Yang et al. [
38] found that
Y values have a great impact on the retrieval results, particularly in the shorter spectral bands.
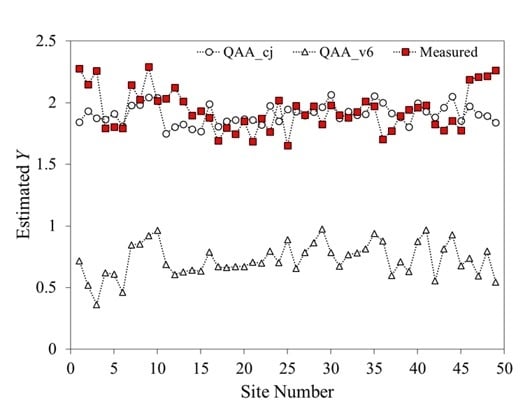
Figure 6 shows that the QAA_v6 algorithm has a low accuracy in estimating
Y, which perhaps caused by the insufficient capability of this algorithm considering the complex optical features of the Changjiang estuarine and coastal waters. The ranges of
Y values derived from the QAA_cj and the QAA_v6 are from 1.5 to 2.5 and from 0.3 to 1, respectively (
Figure 6). Even though our algorithm for
Y (Equation 19) does not yield a reasonable correlation with the measured values (
Figure 6), we have chosen to keep it for generalization purposes, and we are planning to improve the
Y model in the following study.
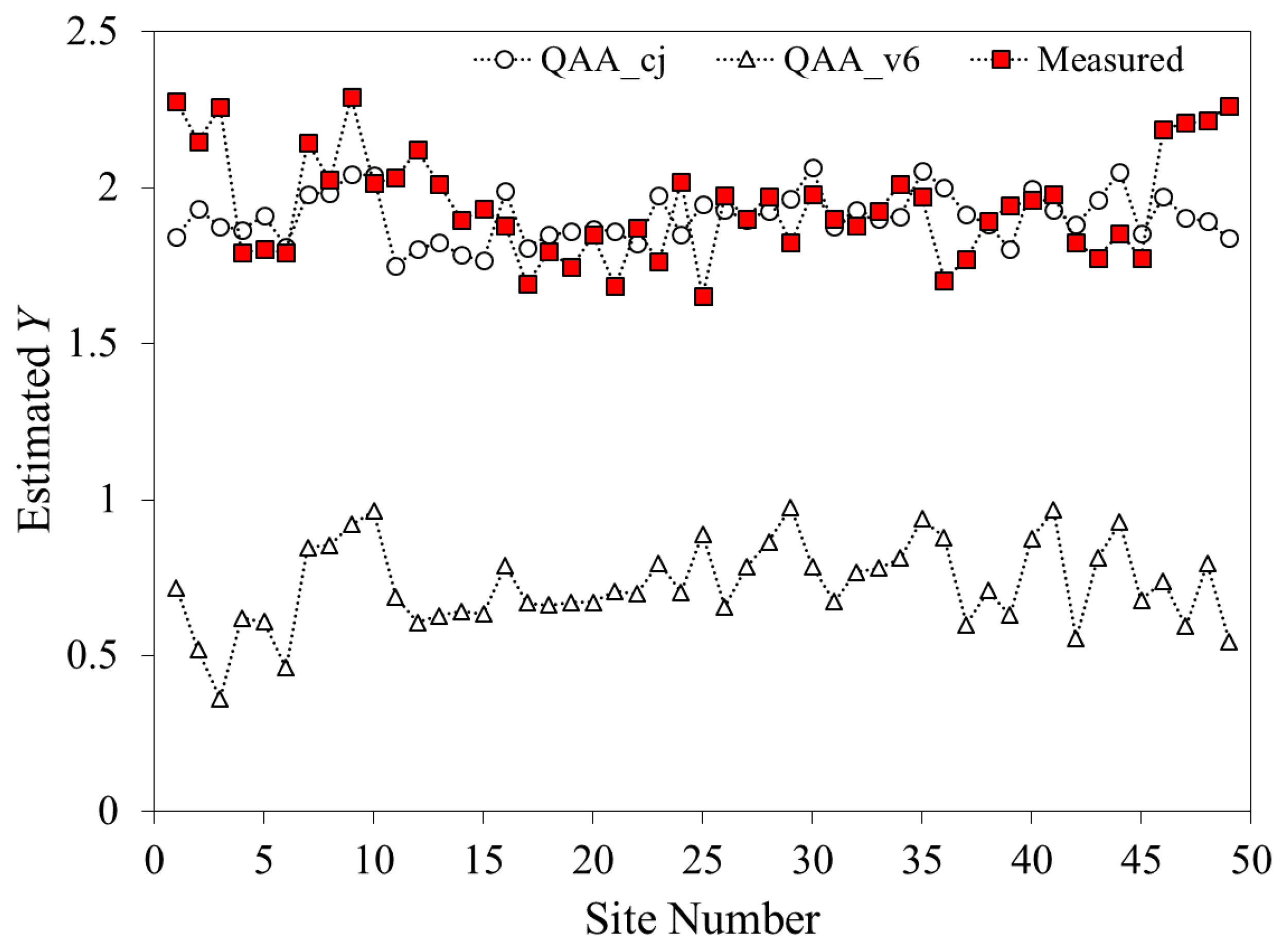
In this study, we have changed the reference wavelength from 670 nm to 680 nm. Although it is an insignificant change of spectral, the retrieval accuracy of calibrated formula was improved effectively when applied to Changjiang estuarine and coastal waters (
Table 4 and
Table 5). We reproduced
a(
λ) and
ag(
λ) from the GOCI images using the QAA_v6, QAA_CDOM and QAA_cj algorithms, and presented the comparison results in
Figure 9 and
Figure 10. As shown in
Figure 9, differences between our algorithm and in situ data is smaller than those between the QAA_v6 and in situ data for the whole blue to near infrared spectral range. Similar findings were found for the
ag(
λ) retrieving in the blue spectral domain (
Figure 10).
Some contradicting results derived from QAA algorithm were discovered from existing literature as well. For example, investigations by Qin et al. [
66] and Shanmugam et al. [
67] have shown that there is a lower accuracy for retrieving absorption components in some regions of the ocean by QAA. Zheng et al. [
68] have also shown that the accuracy of QAA algorithm (v5) varied greatly in deriving
a(
λ) (from 2% to 28%) and
bb(
λ) (from 8% to 14%) depending on wavelength and ocean site. In addition, Zhu et al. [
69] compared and verified 15 CDOM retrieval algorithms (empirical, semi-analytical, optimization, and matrix inversion algorithms), and pointed out that the QAA_CDOM algorithm was optimal. The reason of this is that CDOM has negligible backscattering, whereas inorganic particles have strong backscattering, even in longer wavelength [
27]. Several researches find that QAA_CDOM has a good accuracy in obtaining the
ap(
λ) from
bbp(
λ) [
26,
27,
69]. However, QAA_CDOM has some empirical parameters, which are required to be calibrated according to specific study area.
Figure 10 shows that after calibration,
ag(
λ) has a significant improvement at 412, 443, 490 nm. It seems obvious that better accuracy in
ag(
λ) leads to improvement of a retrieval accuracy for
aph and
ad.
5. Conclusions
Through calibration and validation, we improved empirical parameters of QAA_v6 and QAA_CDOM IOPs algorithms, and thus developed a new algorithm, namely, QAA_cj, which is suitable for the highly turbid Changjiang estuary and adjacent areas. Results of validation prove that QAA_cj has a better accuracy in retrieving a(λ) and ag(λ), compared with the QAA_v6 and QAA_CDOM. a(λ) derived from QAA_cj is in a good agreement with in situ and GOCI data, where RMSE ranges from 0.35 to 1.17 m−1, MARE from 0.11 to 0.52, bias from −1.23 to 0.66 m−1 and R2 is from 0.28 to 0.82. As for ag(λ), RMSE ranges from 0.035 to 0.12 m−1, MARE from 0.14 to 0.42, bias from −0.0086 to 0.033 m−1 and R2 is from 0.53 to 0.92.
The improvement of a(λ) and ag(λ) retrieval accuracy will help to provide theoretical basis for the release of satellite product and further study on optical properties. Reliable CDOM products can provide information on the internal movements and nutrients structure of Changjiang diluted water and mechanisms of hydrodynamics in the Changjiang estuarine and coastal waters. The trace of CDOM can advance our understanding of the land-ocean interaction processes through monitoring spatial-temporal distribution of the river plume into sea. In the future, we will focus on exploring the relationships between environmental factors and optical parameters, in combination with satellite data and physical models.