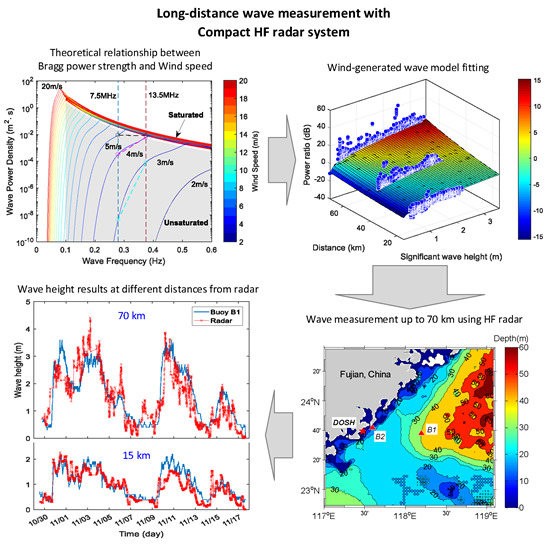
Wave Height Estimation from First-Order Backscatter of a Dual-Frequency High Frequency Radar
Abstract
:1. Introduction
2. Theory and Method
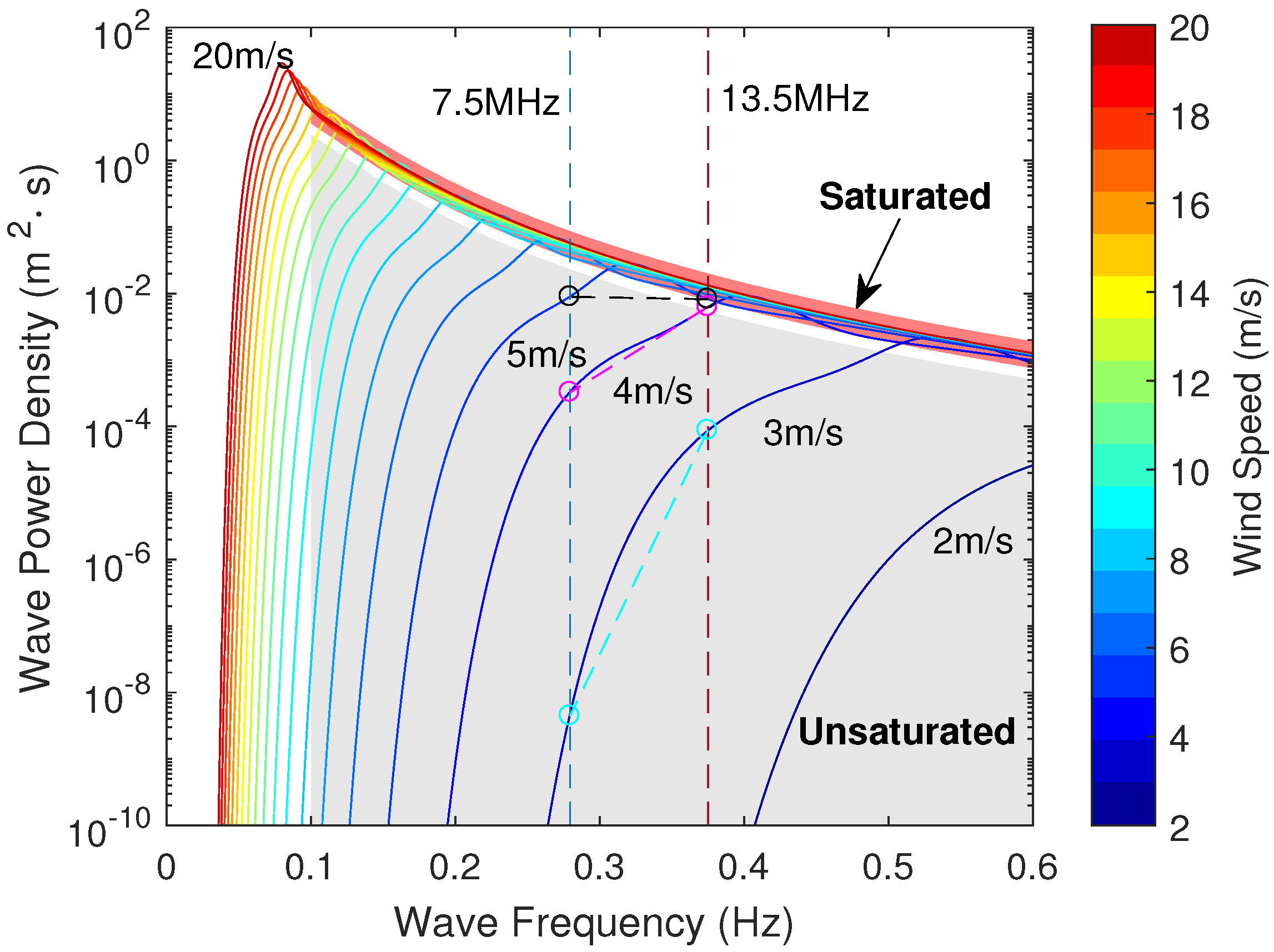
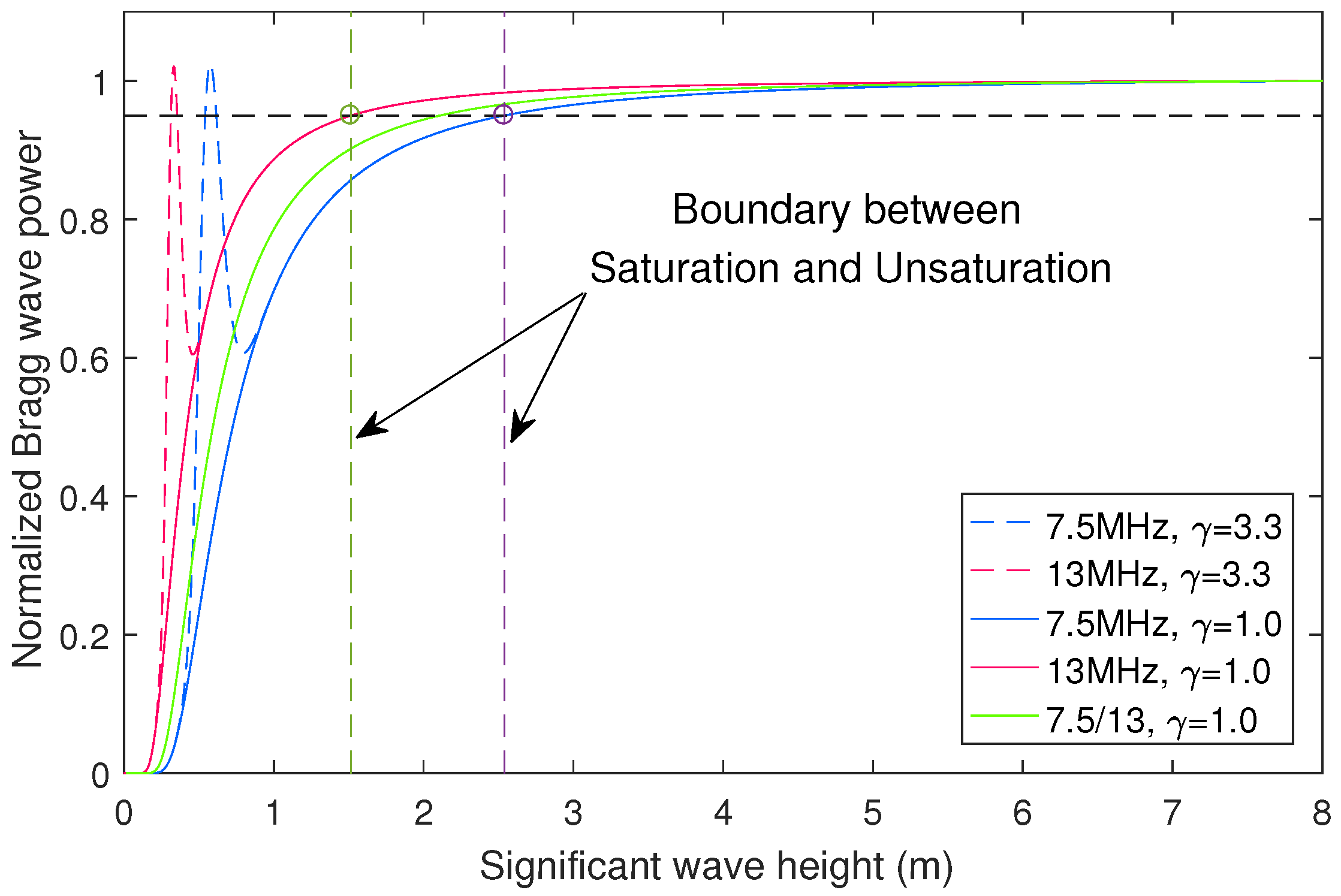
2.1. Relationship between First-order Echo Power and Wave Height
2.2. Model of Dual-Frequency Power Ratio with Wave height and Distance
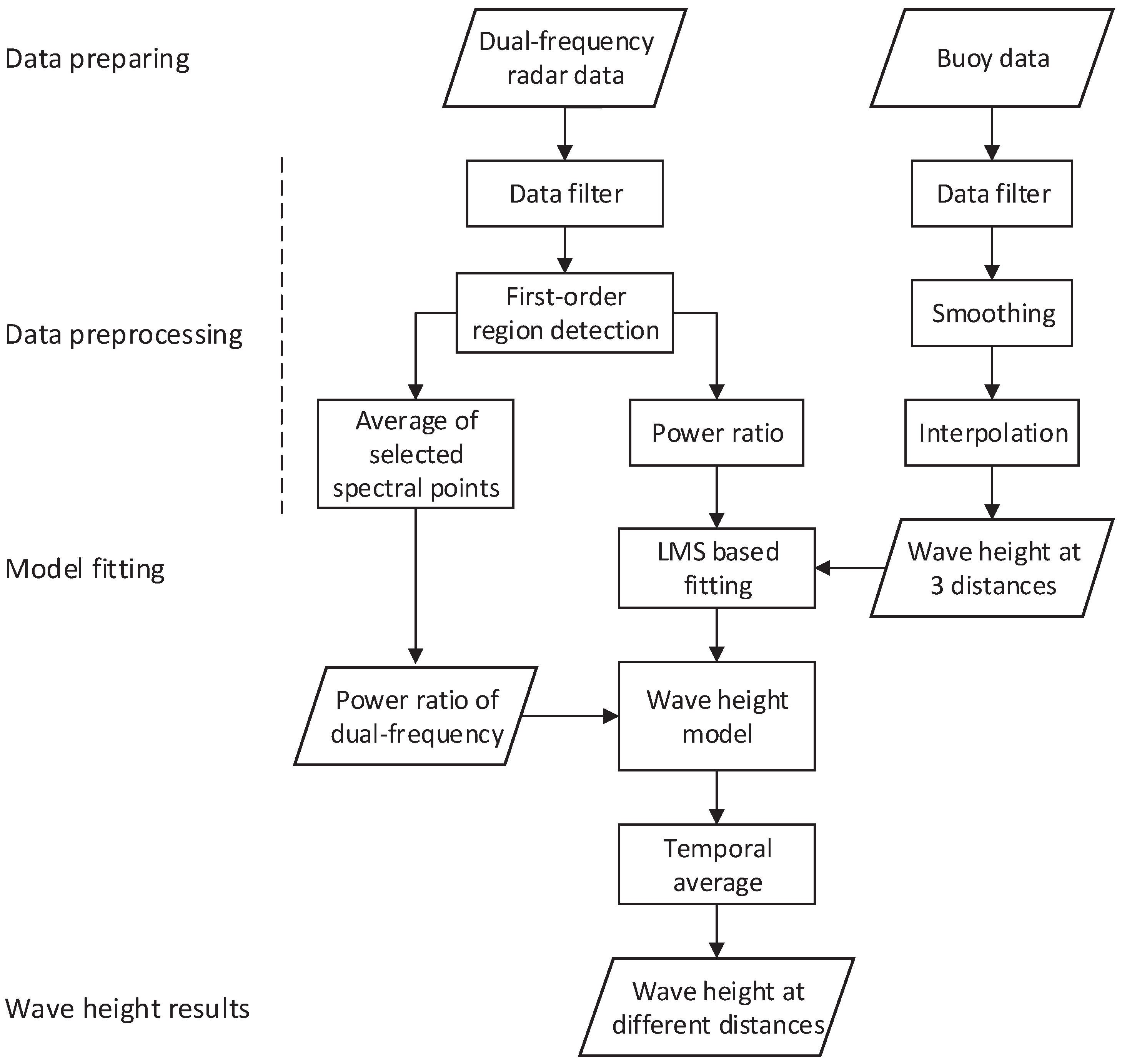
2.3. Block Diagram of the Wave Height Estimation
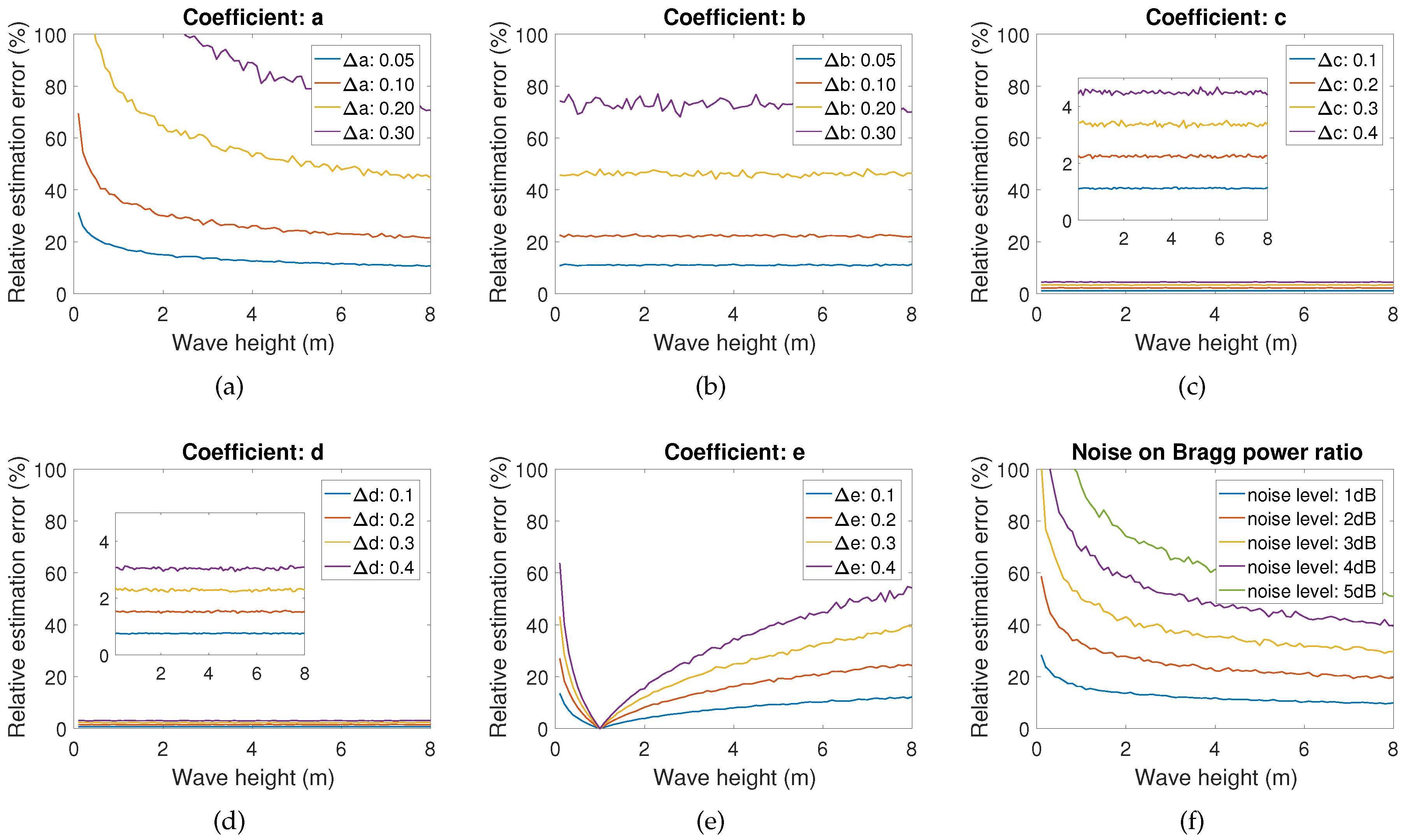
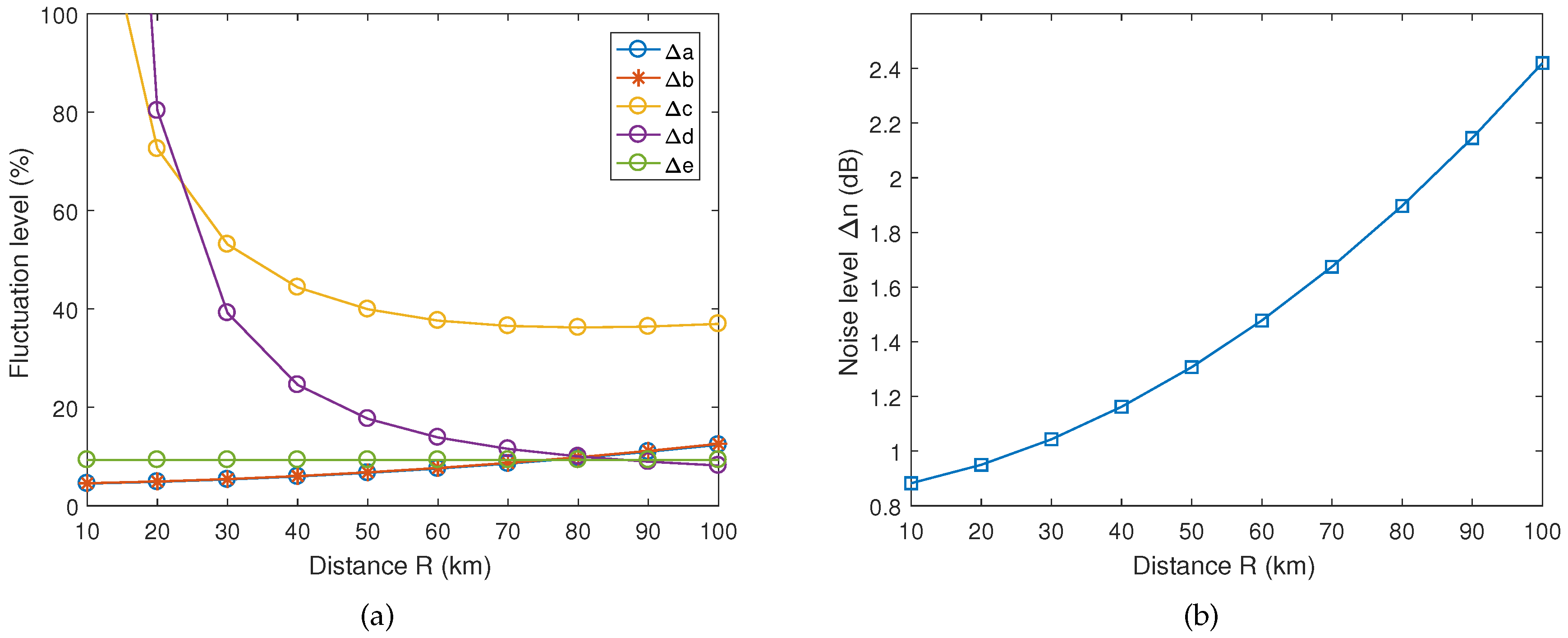
3. Numerical Analysis
4. Experimental Results
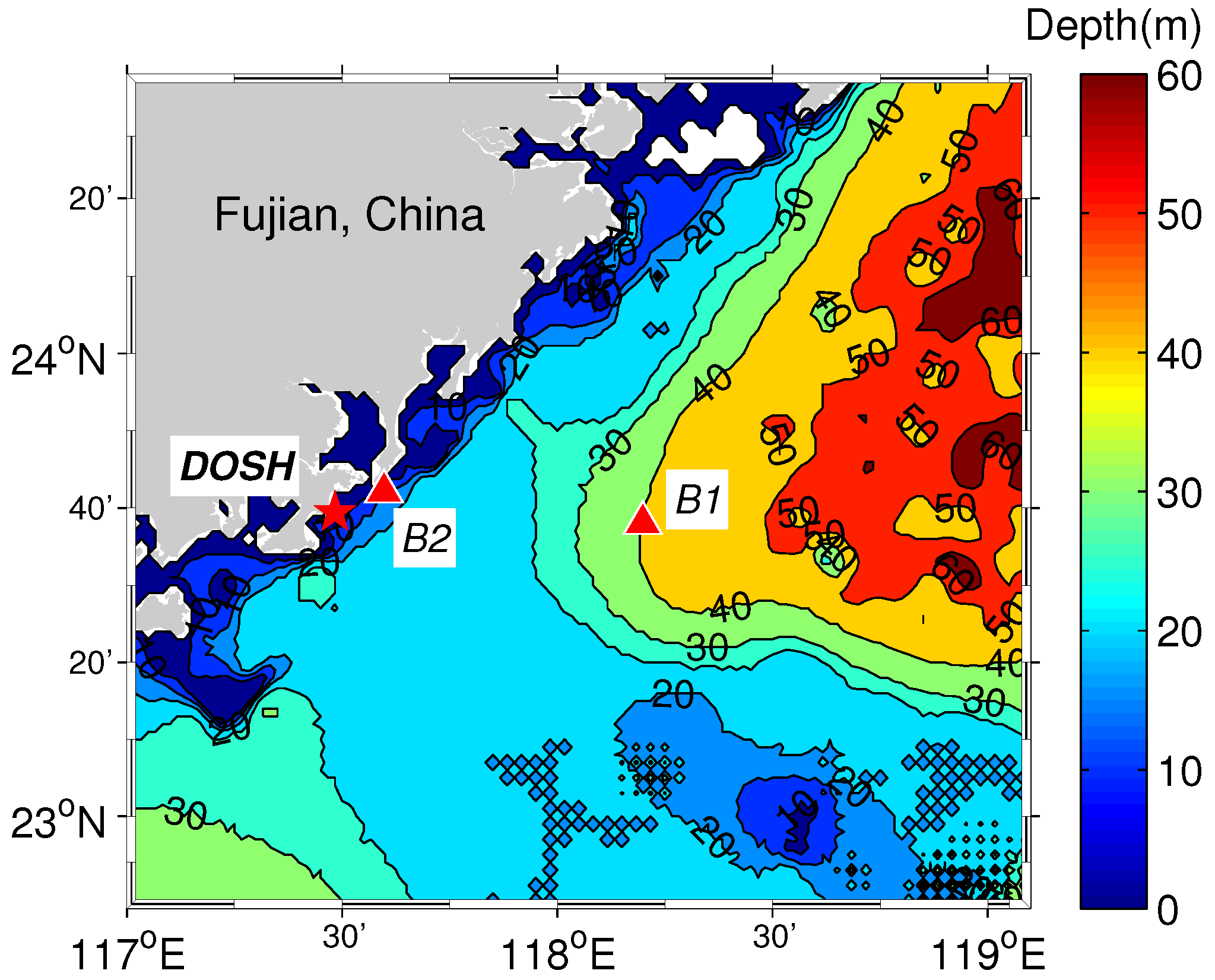
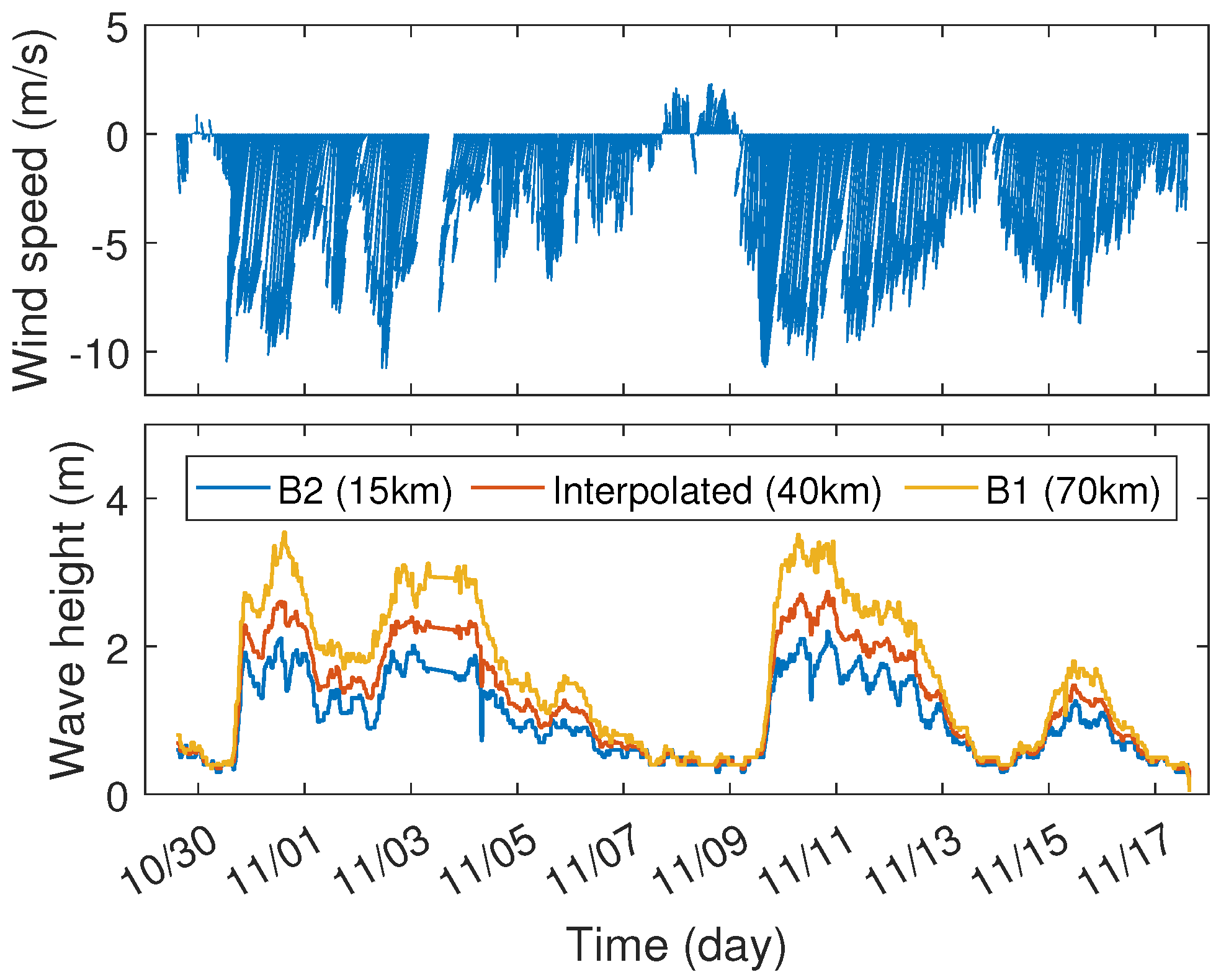
4.1. Experiment Data Description
4.2. Results of Model Fitting and Wave Height Estimation
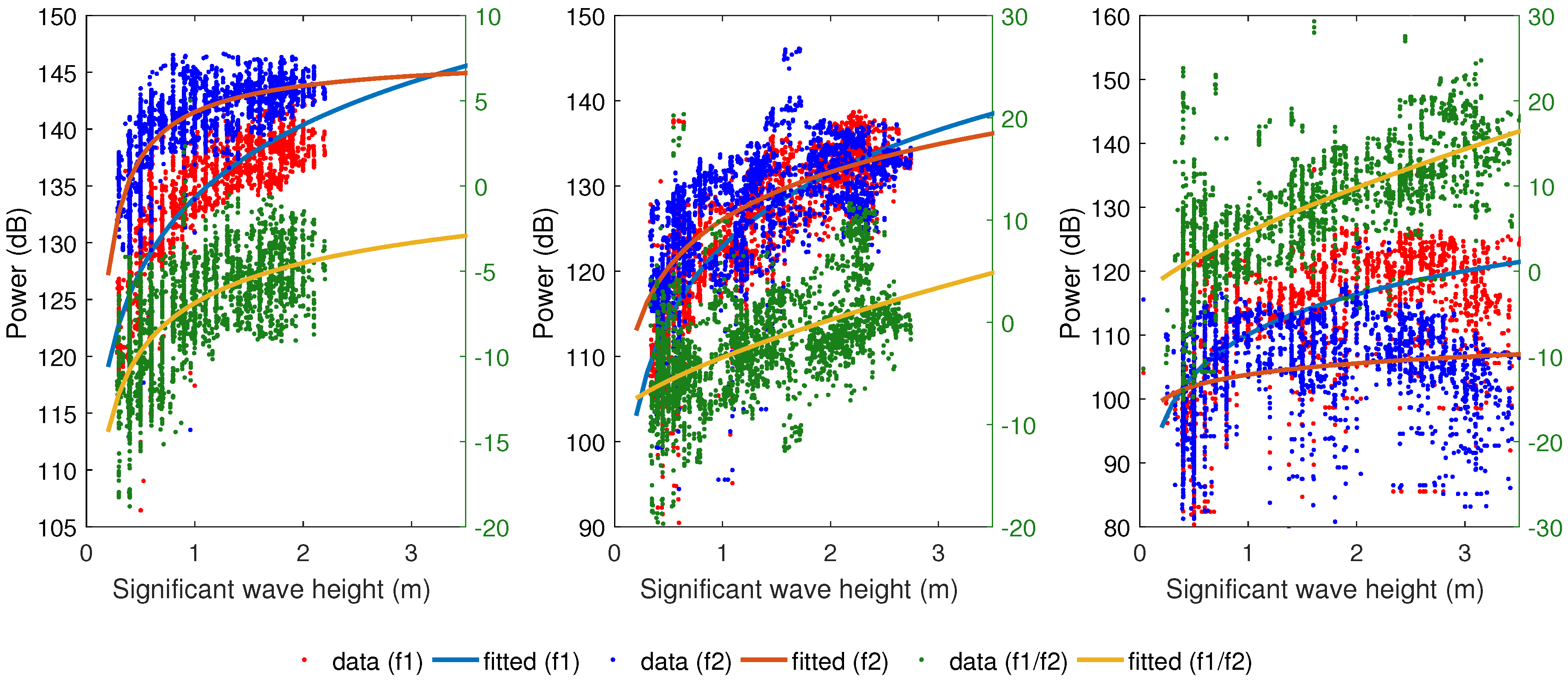
4.2.1. Two-dimensional fitting: Bragg power and
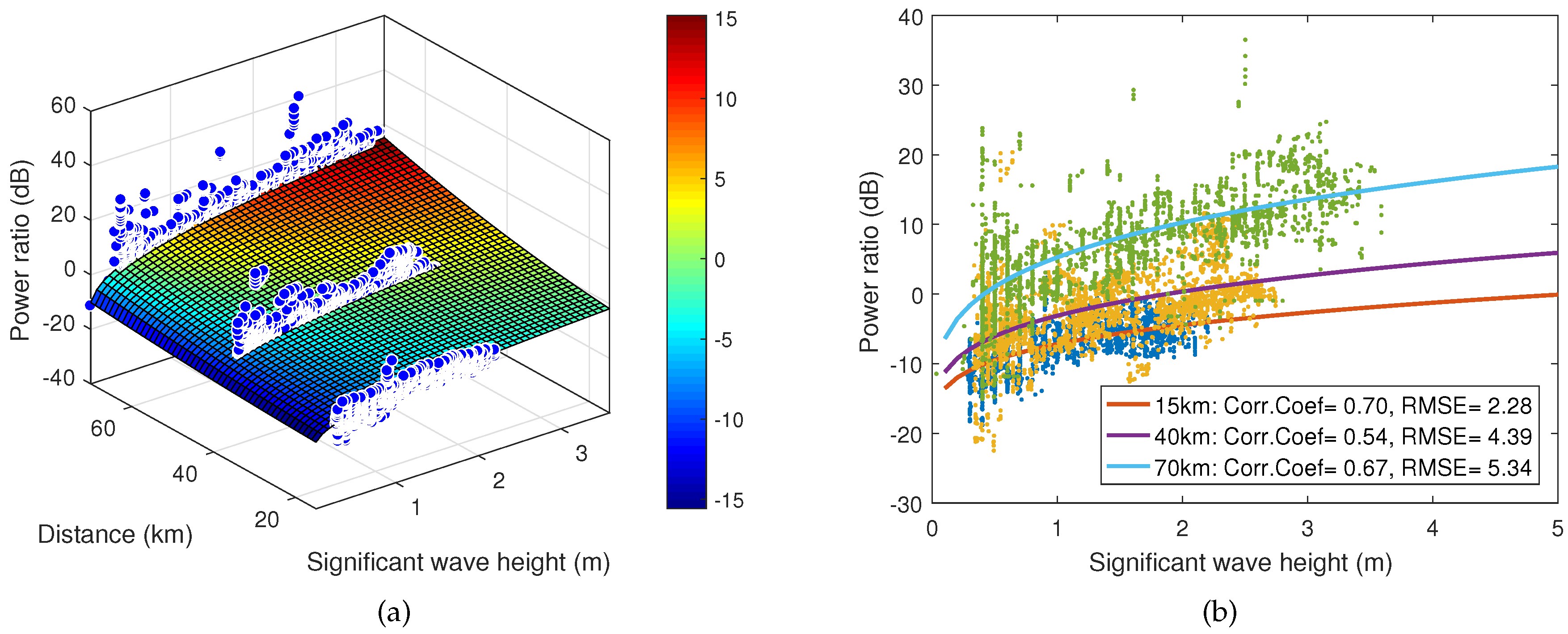
4.2.2. Three-dimensional fitting: Bragg power ratio and
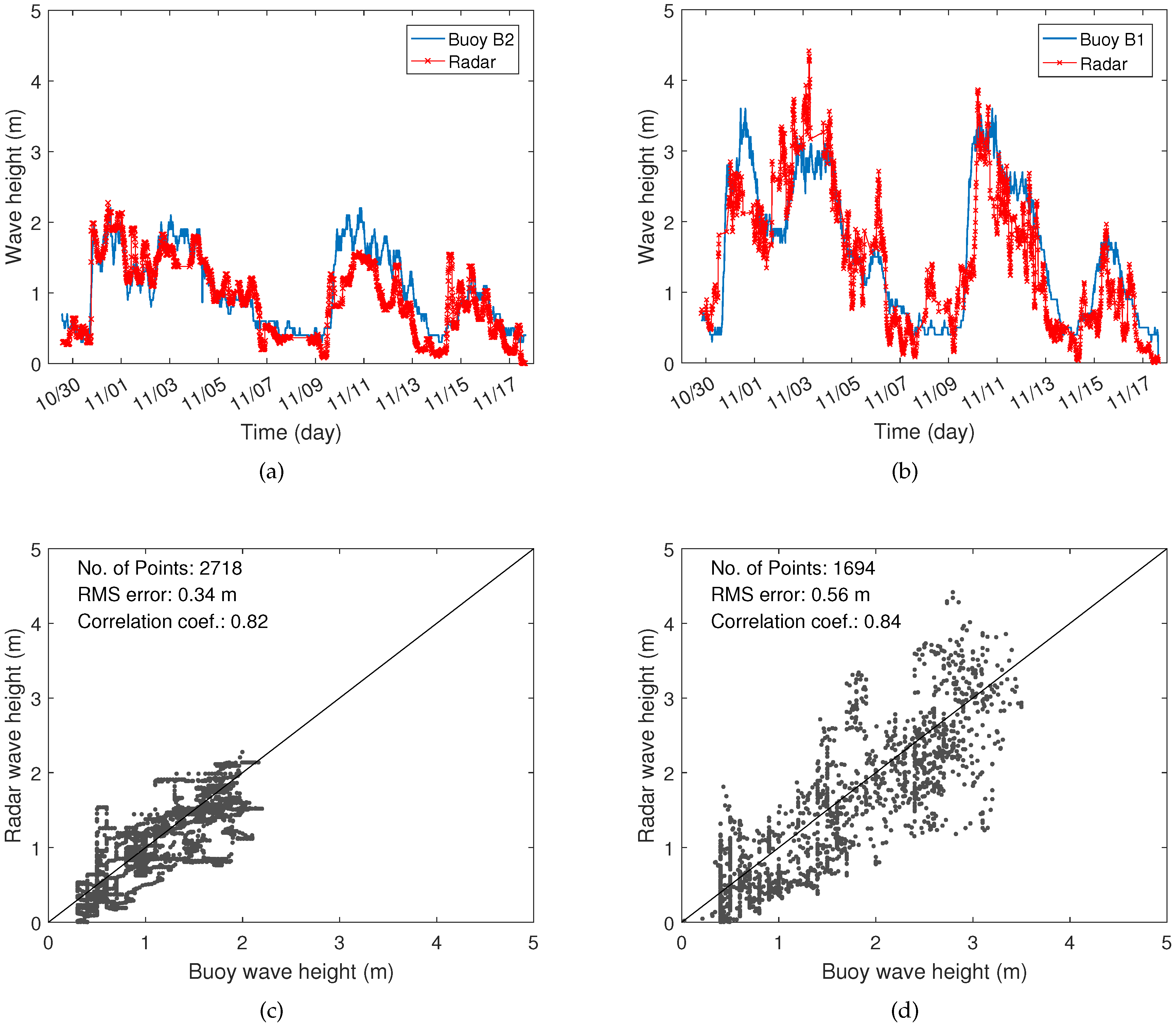
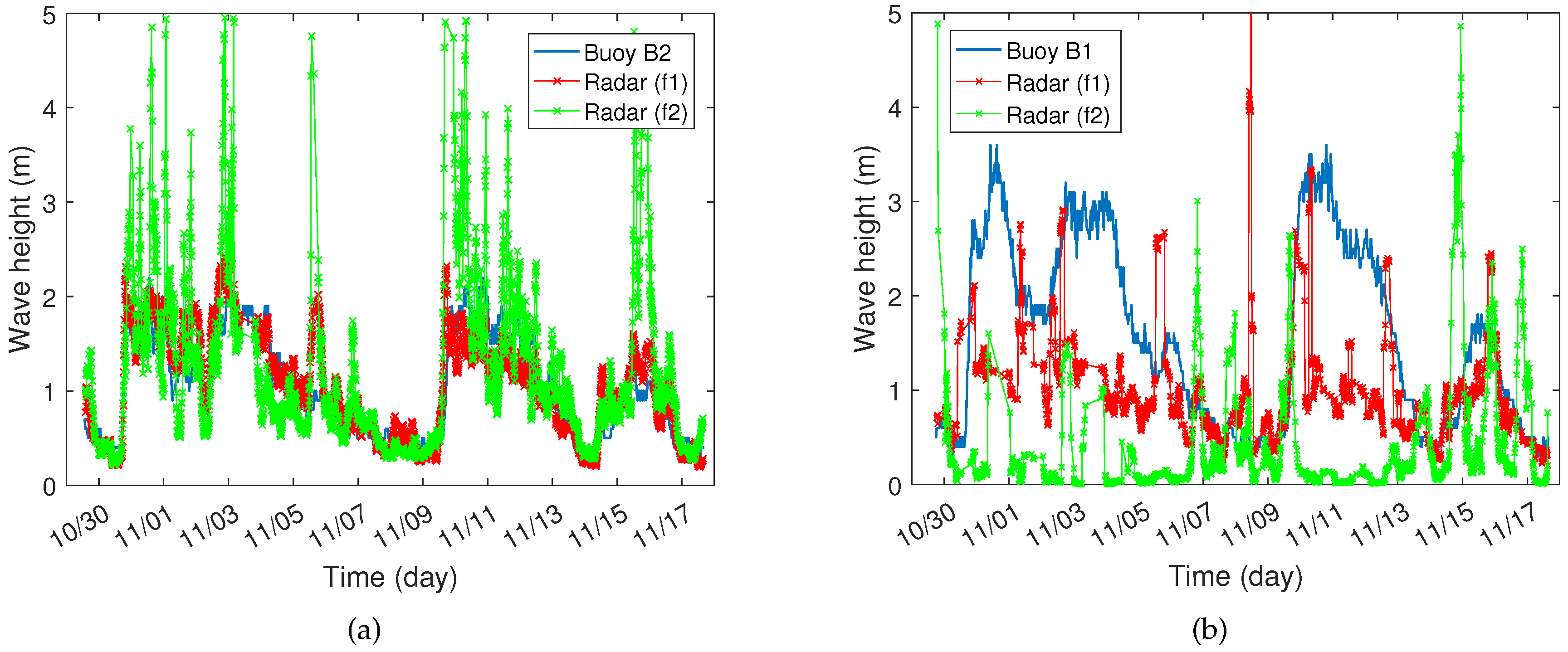
4.2.3. Wave Height Estimation Results
5. Discussion
6. Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Barrick, D.E. First-order theory and analysis of MF/HF/VHF scatter from the sea. IEEE Trans. Antennas Propag. 1972, AP-20, 2–10. [Google Scholar] [CrossRef]
- Barrick, D.E. The ocean waveheight nondirectional spectrum from inversion of the HF sea-echo Doppler spectrum. Remote Sens. Environ. 1977, 6, 201–227. [Google Scholar] [CrossRef]
- Lipa, B.J.; Nyden, B. Directional wave information from the SeaSonde. IEEE J. Ocean. Eng. 2005, 30, 221–231. [Google Scholar] [CrossRef]
- Gurgel, K.W.; Essen, H.H.; Schlick, T. An Empirical Method to Derive Ocean Waves From Second-Order Bragg Scattering: Prospects and Limitations. IEEE J. Ocean. Eng. 2006, 31, 804–811. [Google Scholar] [CrossRef]
- Wyatt, L.R. Limits to the inversion of HF radar backscatter for ocean wave measurement. J. Atmos. Ocean. Technol. 2000, 17, 1651–1666. [Google Scholar] [CrossRef]
- Wyatt, L.R. Wave measurements from the Australian Coastal Ocean Radar Network. In Proceedings of the OCEANS 2014—TAIPEI, Taipei, Taiwan, 7–10 April 2014; pp. 1–5. [Google Scholar]
- Hisaki, Y. Development of HF radar inversion algorithm for spectrum estimation (HIAS). J. Geophys. Res. Oceans 2015, 120, 1725–1740. [Google Scholar] [CrossRef]
- Wyatt, L.R.; Liakhovetski, G.; Graber, H.C.; Haus, B.K. Factors Affecting the Accuracy of SHOWEX HF Radar Wave Measurements. J. Atmos. Ocean. Technol. 2005, 22, 847–859. [Google Scholar] [CrossRef]
- Shen, W.; Gurgel, K.W.; Voulgaris, G.; Schlick, T.; Stammer, D. Wind-speed inversion from HF radar first-order backscatter signal. Ocean Dyn. 2012, 62, 105–121. [Google Scholar] [CrossRef]
- Kirincich, A. Remote Sensing of the Surface Wind Field over the Coastal Ocean via Direct Calibration of HF Radar Backscatter Power. J. Atmos. Ocean. Technol. 2016, 33, 1377–1392. [Google Scholar] [CrossRef]
- Zhou, H.; Wen, B. Wave Height Extraction From the First-Order Bragg Peaks in High-Frequency Radars. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2296–2300. [Google Scholar] [CrossRef]
- Tian, Y.; Wen, B.; Zhou, H. Measurement of High and Low Waves Using Dual-Frequency Broad-Beam HF Radar. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1599–1603. [Google Scholar] [CrossRef]
- Milsom, J.D. HF Groundwave Radar Equations. In Proceedings of the Seventh International Conference on (Conf. Publ. No. 441) HF Radio Systems and Techniques, Nottingham, UK, 7–10 July 1997; pp. 285–290. [Google Scholar]
- Grosdidier, S.; Baussard, A.; Khenchaf, A. HFSW Radar Model: Simulation and Measurement. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3539–3549. [Google Scholar] [CrossRef]
- Shearman, E.D.R. Propagation and scattering in MF/HF groundwave radar. IEE Proc. F Commun. Radar Signal Process. 1983, 130, 579–590. [Google Scholar] [CrossRef]
- Leong, H. On the Feasibility of Using Measured Sea Clutter Continuum In HFSWR to Validate Modelled Ground-Wave Propagation Attenuation in Rough Sea; Defence R&D Canada: Ottawa, ON, Canada, 2012. [Google Scholar]
- Barrick, D.E. Theory of HF and VHF Propagation Across the Rough Sea, part I & II. Radio Sci. 1971, 6, 517–533. [Google Scholar]
- Hasselmann, K.; Barnett, T.; Bouws, E.; Carlson, H.; Cartwright, D.; Enke, K.; Ewing, J.; Gienapp, H.; Hasselmann, D.; Kruseman, P.; et al. Measurements of wind wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Dtsch. Hydrogr. Z 1973, 12, 1–95. [Google Scholar]
- Pierson, W.; Moskowitz, L. A proposed spectral form for fully developed wind seas based upon the similarity theory of S.A. Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Phillips, O.M. The Dynamics of the Upper Ocean; Cambridge University Press: Cambridge, UK, 1966. [Google Scholar]
- Long, A.; Trizna, D. Mapping of North Atlantic winds by HF radar sea backscatter interpretation. IEEE Trans. Antennas Propag. 1973, 21, 680–685. [Google Scholar] [CrossRef]
- Lipa, B.J.; Barrick, D.E. Methods for the extraction of long-period ocean wave parameters from narrow beam HF radar sea echo. Radio Sci. 1980, 15, 843–853. [Google Scholar] [CrossRef]
- Naderi, M.; Pätzold, M. Design and analysis of a one-dimensional sea surface simulator using the sum-of-sinusoids principle. In Proceedings of the OCEANS 2015—MTS/IEEE Washington, Washington, DC, USA, 19–22 October 2015; pp. 1–7. [Google Scholar]
- Tyler, G.L.; Teague, C.C.; Stewart, R.H.; Peterson, A.M.; Munk, W.H.; Joy, J.W. Wave directional spectra from synthetic aperture observations of radio scatter. Deep Sea Res. 1974, 21, 989–1016. [Google Scholar] [CrossRef]
- Codar. SesSonde general specifications. Available online: http://www.codar.com/images/products/SeaSonde/1A-SeaSonde_v2_20100331.pdf. (accessed on 27 September 2017).
- Tian, Y.; Wen, B.; Tan, J.; Li, K.; Yan, Z.; Jing, Y. A new fully-digital HF radar system for oceanographical remote sensing. IEICE Electron. Express 2013, 10, 1–6. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Merz, C.R. Assessment of CODAR SeaSonde and WERA HF Radars in Mapping Surface Currents on the West Florida Shelf. J. Atmos. Ocean. Technol. 2014, 31, 1363–1382. [Google Scholar] [CrossRef]
- Li, Z.; Wen, B.; Tian, Y. Design and Implementation of a Dual-Frequency Compact Antenna System for HF Radar. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1887–1890. [Google Scholar] [CrossRef]
| Frequency (MHz) | Transmit Antenna | Transmit Power (W) | Receive Antenna | Range Resolution (km) | CIT (s) | |
|---|---|---|---|---|---|---|
| 7.5 | Monopole | 100 | Crossed-Loop | 5 | 553 | |
| 13.5 | 2.5 | 553 |
| Distance (R) | Frequency | a | b | c | RMSE (dB) | Corr. Coef. |
|---|---|---|---|---|---|---|
| 15(km) | −8662 | 8796 | 0.001052 | 2.94 | 0.87 | |
| 146.9 | −5.396 | −0.806 | 2.62 | 0.76 | ||
| 6.629 | −13.50 | −0.2759 | 2.25 | 0.70 | ||
| 40(km) | −3141 | 3264 | 0.003795 | 4.65 | 0.86 | |
| −6368 | 6494 | 0.001243 | 5.28 | 0.70 | ||
| −9.373 | 5.93 | 0.6965 | 4.38 | 0.54 | ||
| 70(km) | −9224 | 9334 | 0.0009802 | 8.02 | 0.65 | |
| −3390 | 3495 | 0.000667 | 7.64 | 0.25 | ||
| −3.434 | 8.017 | 0.7232 | 5.30 | 0.68 |
| Item | Fitting coefficients in Equation (15) | ||||
|---|---|---|---|---|---|
| a | b | c | d | e | |
| 95% confidence bound | −24.31 ∼ −19.93 | 11.48 ∼ 16.04 | 0.025 ∼ 0.069 | 0.0019 ∼ 0.0024 | 0.217 ∼ 0.265 |
| Mean value | −22.12 | 13.76 | 0.047 | 0.0021 | 0.241 |
| Absolute uncertainty | |||||
| Relative uncertainty | 9.9% | 16.6% | 46.4% | 11.8% | 9.9% |
| Distance (R) | Frequency | No. of points | RMSE (dB) | Corr. Coef. |
|---|---|---|---|---|
| 15(km) | 2829 | 0.28 | 0.86 | |
| 2734 | 0.68 | 0.66 | ||
| 2718 | 0.34 | 0.82 | ||
| 70(km) | 1677 | 1.01 | 0.40 | |
| 1648 | 1.65 | −0.26 | ||
| 1694 | 0.56 | 0.84 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Wen, B.; Zhou, H.; Wang, C.; Yang, J.; Huang, W. Wave Height Estimation from First-Order Backscatter of a Dual-Frequency High Frequency Radar. Remote Sens. 2017, 9, 1186. https://doi.org/10.3390/rs9111186
Tian Y, Wen B, Zhou H, Wang C, Yang J, Huang W. Wave Height Estimation from First-Order Backscatter of a Dual-Frequency High Frequency Radar. Remote Sensing. 2017; 9(11):1186. https://doi.org/10.3390/rs9111186
Chicago/Turabian StyleTian, Yingwei, Biyang Wen, Hao Zhou, Caijun Wang, Jing Yang, and Weimin Huang. 2017. "Wave Height Estimation from First-Order Backscatter of a Dual-Frequency High Frequency Radar" Remote Sensing 9, no. 11: 1186. https://doi.org/10.3390/rs9111186
APA StyleTian, Y., Wen, B., Zhou, H., Wang, C., Yang, J., & Huang, W. (2017). Wave Height Estimation from First-Order Backscatter of a Dual-Frequency High Frequency Radar. Remote Sensing, 9(11), 1186. https://doi.org/10.3390/rs9111186