Davos-Laret Remote Sensing Field Laboratory: 2016/2017 Winter Season L-Band Measurements Data-Processing and Analysis
Abstract
1. Introduction
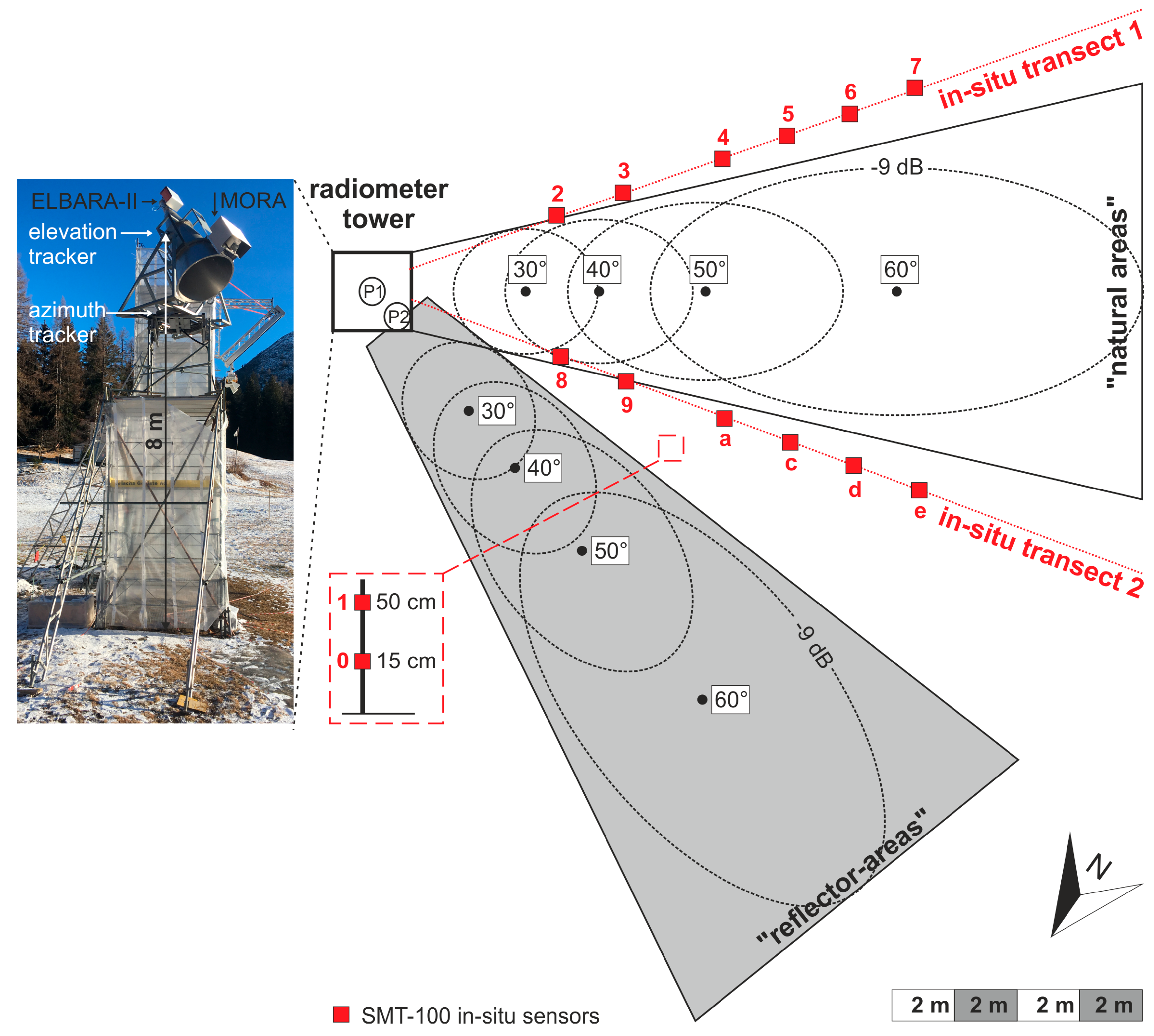
2. Test-Site Description
- The second generation ELBARA-II of the ETH L-band radiometer (ELBARA) operating at horizontal and vertical polarization within the protected part of the L-band (1400–1427 MHz). ELBARA-II technical specifications and its performance under field conditions are outlined by Schwank et al. [17,27]. The first generation ELBARA was designed and constructed in 2001 at the Institute of Applied Physics, University of Bern [28]. A number of ELBARA-II radiometers were produced by the company Gamma Remote Sensing AG (Gümligen, Switzerland) with the main purpose of calibration and validation activities supporting ESA’s SMOS mission [18]. The ELBARA-II assembly, mounted atop an 8-meter tower, includes a tracking system to allow for automated observations of brightness temperatures at different nadir angles and azimuth. For the work presented here, ELBARA-II is the key remote sensing instrument.
- The SnowScat scatterometer is a fully polarimetric, coherent stepped-frequency continuous wave radar operating in the frequency range 9–18 GHz [31]. It is mounted on a rail and attached to a 10-m tower, which allows for elevation and azimuth scanning over the site. Using Synthetic Aperture Radar (SAR) techniques, 3D backscatter maps of the site are made indicating parameters such as radiation penetration depth and snow water equivalent of dry snow.
3. In-Situ Measurements
3.1. Snow Density Profiles
3.2. Permittivity, Temperature, and Precipitation
4. L-Band Radiometry and Raw Data Processing
4.1. L-Band Brightness Temperatures
4.1.1. Active Cold Source (ACS) Calibration Using Sky Measurements
4.1.2. Antenna Brightness Temperatures
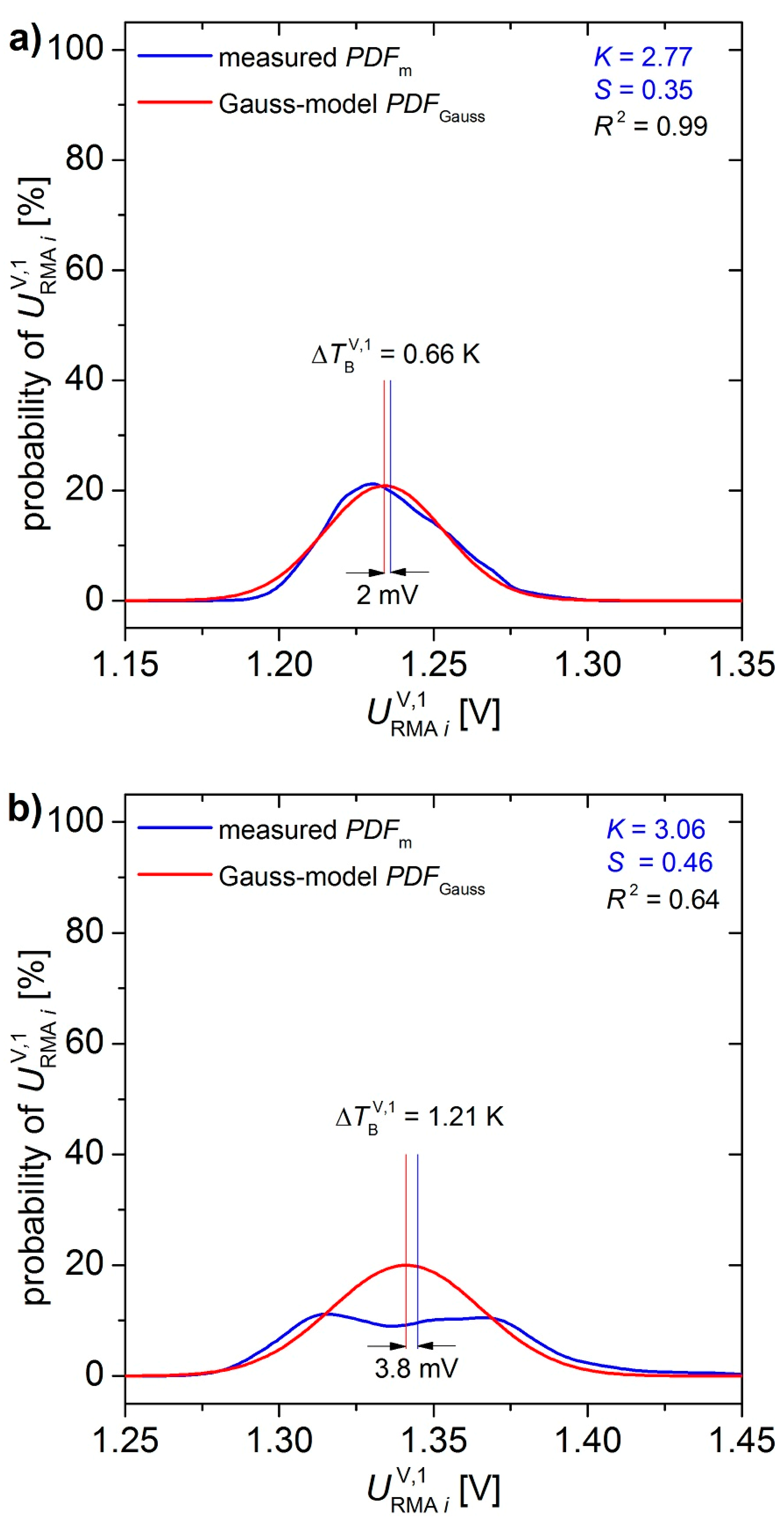
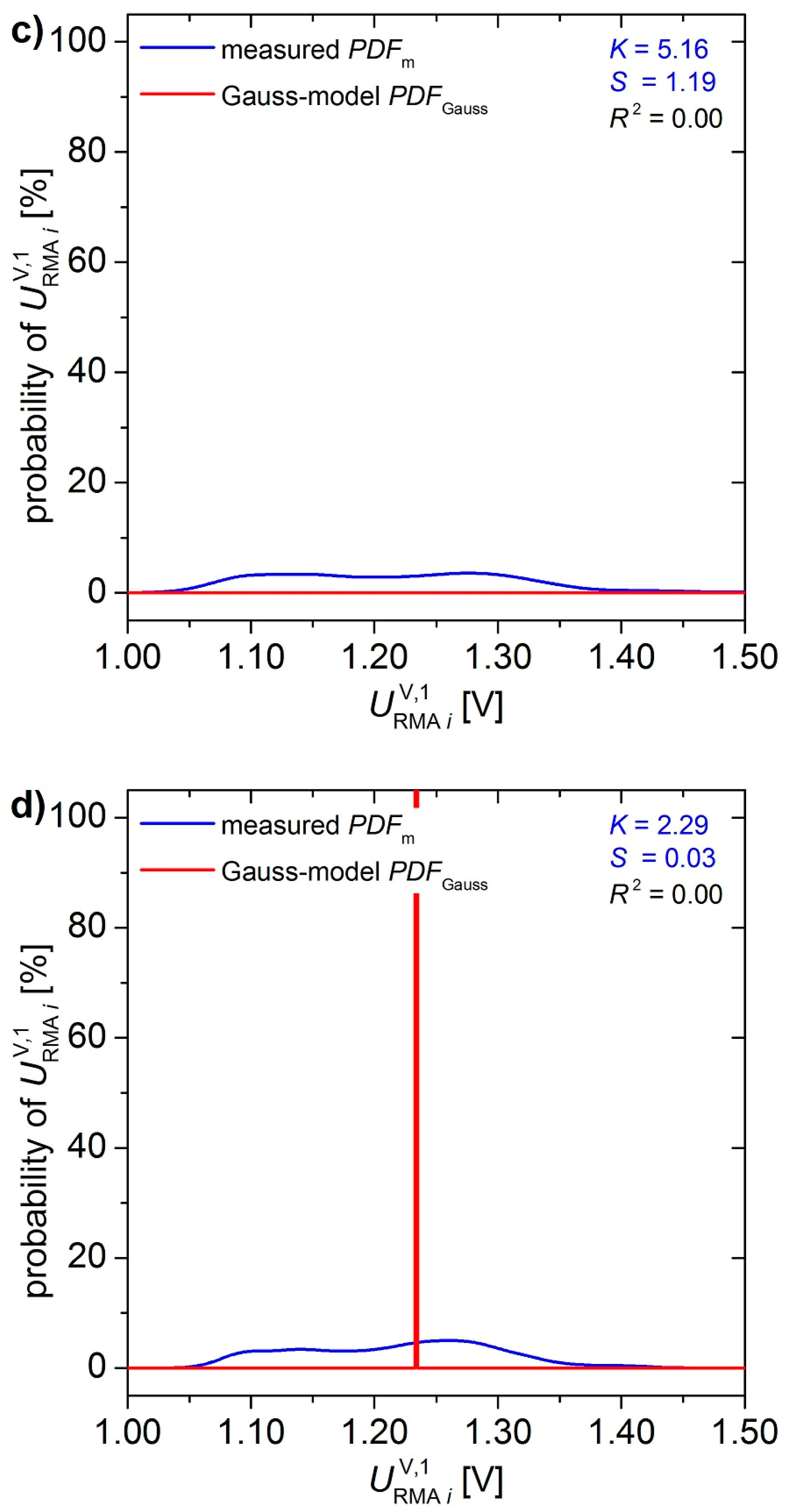
4.2. Radio Frequency Interference Detection and Mitigation
- The starting value of is set to the mean of the measured sample .
- The codomain of is restricted by the lowest measurement to
- The starting value of is set to corresponding to the typical standard deviation of a sample measured on the resistive noise source.
- The codomain of is restricted to
4.3. Effective Transmission Losses and ACS Temperatures
4.4. Brightness Temperatures of “Reflector Areas”
5. Analysis of Brightness Temperatures
5.1. Methodology for the Analysis of L-Band Brightness Temperatures’ Response to Snow Liquid Water
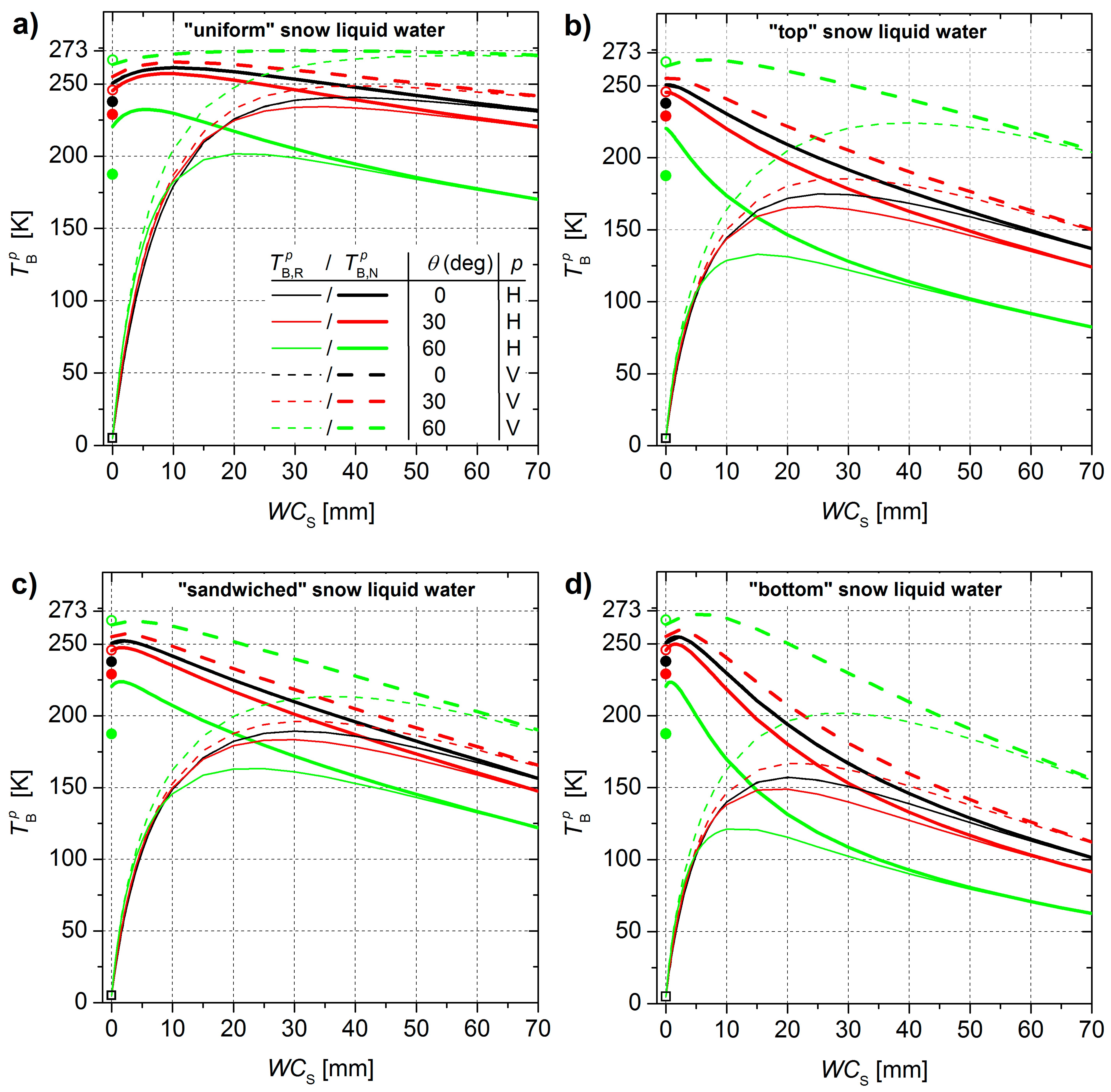
5.2. Sensitivities of Brightness Temperatures to Liquid Snow Water
5.3. Analysis of Measured Brightness Temperatures
6. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mätzler, C. Cost action 712: Microwave radiometry. In Remote Sensing of Atmosphere and Ocean from Space: Models, Instruments and Techniques; Springer: Berlin, Germany, 2002; pp. 231–246. [Google Scholar]
- Jackson, T.J.; Schmugge, T.J. Passive microwave remote sensing system for soil moisture: Some supporting research. IEEE Trans. Geosci. Remote Sens. 1989, 27, 225–235. [Google Scholar] [CrossRef]
- Rautiainen, K.; Lemmetyinen, J.; Pulliainen, J.; Vehviläinen, J.; Drusch, M.; Kontu, A.; Kainulainen, J.; Seppänen, J. L-Band Radiometer Observations of Soil Processes in Boreal and Subarctic Environments. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1483–1497. [Google Scholar] [CrossRef]
- Rautiainen, K.; Lemmetyinen, J.; Schwank, M.; Kontu, A.; Ménard, C.B.; Mätzler, C.; Drusch, M.; Wiesmann, A.; Ikonen, J.; Pulliainen, J. Detection of soil freezing from L-band passive microwave observations. Remote Sens. Environ. 2014, 147, 206–218. [Google Scholar] [CrossRef]
- Macelloni, G.; Brogioni, M.; Pampaloni, P.; Cagnati, A.; Drinkwater, M.R. DOMEX 2004: An experimental campaign at Dome-C Antarctica for the calibration of spaceborne low-frequency microwave radiometers. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2642–2653. [Google Scholar] [CrossRef]
- Roy, A.; Toose, P.; Williamson, M.; Rowlandson, T.; Derksen, C.; Royer, A.; Berg, A.A.; Lemmetyinen, J.; Arnold, L. Response of L-Band brightness temperatures to freeze/thaw and snow dynamics in a prairie environment from ground-based radiometer measurements. Remote Sens. Environ. 2017, 191, 67–80. [Google Scholar] [CrossRef]
- Zheng, D.; Wang, X.; van der Velde, R.; Zeng, Y.; Wen, J.; Wang, Z.; Schwank, M.; Ferrazzoli, P.; Su, Z. L-Band Microwave Emission of Soil Freeze-Thaw Process in the Third Pole Environment. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5324–5338. [Google Scholar] [CrossRef]
- Mätzler, C.; Hüppi, R. Review of Signature Studies for Microwave Remote Sensing of Snowpacks. Adv. Space Res. 1989, 9, 253–265. [Google Scholar] [CrossRef]
- Mätzler, C. Improved Born Approximation for scattering of radiation in a granular medium. J. Appl. Phys. 1998, 83, 6111–6117. [Google Scholar] [CrossRef]
- Wiesmann, A.; Mätzler, C. Microwave emission model of layered snowpacks. Remote Sens. Environ. 1999, 70, 307–316. [Google Scholar] [CrossRef]
- Liang, D.; Xu, X.; Tsang, L.; Andreadis, K.M.; Josberger, E.G. The Effects of Layers in Dry Snow on Its Passive Microwave Emissions Using Dense Media Radiative Transfer Theory Based on the Quasicrystalline Approximation (QCA/DMRT). IEEE Trans. Geosci. Remote Sens. 2008, 46, 3663–3671. [Google Scholar] [CrossRef]
- Harlow, R.C.; Essery, R. Tundra Snow Emissivities at MHS Frequencies: MEMLS Validation Using Airborne Microwave Data Measured During CLPX-II. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4262–4278. [Google Scholar] [CrossRef]
- Schwank, M.; Rautiainen, K.; Mätzler, C.; Stähli, M.; Lemmetyinen, J.; Pulliainen, J.; Vehviläinen, J.; Kontu, A.; Ikonen, J.; Ménard, C.B.; et al. Model for microwave emission of a snow-covered ground with focus on L band. Remote Sens. Environ. 2014, 154, 180–191. [Google Scholar] [CrossRef]
- Schwank, M.; Mätzler, C.; Wiesmann, A.; Wegmüller, U.; Pulliainen, J.; Lemmetyinen, J.; Rautiainen, K.; Derksen, C.; Toose, P.; Drusch, M. Snow Density and Ground Permittivity Retrieved from L-Band Radiometry: A Synthetic Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3833–3845. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Schwank, M.; Rautiainen, K.; Kontu, A.; Parkkinen, T.; Mätzler, C.; Wiesmann, A.; Wegmüller, U.; Derksen, C.; Toose, P.; et al. Snow density and ground permittivity retrieved from L-band radiometry: Application to experimental data. Remote Sens. Environ. 2016, 180, 377–391. [Google Scholar] [CrossRef]
- Naderpour, R.; Schwank, M.; Mätzler, C.; Lemmetyinen, J.; Steffen, K. Snow Density and Ground Permittivity Retrieved From L-Band Radiometry: A Retrieval Sensitivity Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3148–3161. [Google Scholar] [CrossRef]
- Schwank, M.; Wiesmann, A.; Werner, C.; Mätzler, C.; Weber, D.; Murk, A.; Völksch, I.; Wegmüller, U. ELBARA II, An L-Band Radiometer System for Soil Moisture Research. Sensors 2010, 10, 584–612. [Google Scholar] [CrossRef] [PubMed]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- De Jeu, R.; Holmes, T.R.H.; Owe, M. Deriving land surface parameters from 3 different vegetated sites with the ELBARA 1.4 GHz passive microwave radiometer. In Proceedings of the Remote Sensing of Agriculture, Ecosystems, and Hydrology V (SPIE), Barcelona, Spain, 8–12 September 2003; Volume 5232. [Google Scholar]
- Saleh, K.; Wigneron, J.-P.; Waldteufel, P.; de Rosnay, P.; Schwank, M.; Calvet, J.-C.; Kerr, Y.H. Estimates of Surface Soil Moisture under Grass Covers using L-band Radiometry. Remote Sens. Environ. 2007, 109, 42–53. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Chanzy, A.; Kerr, Y.H.; Lawrence, H.; Shi, J.; Escorihuela, M.J.; Mironov, V.; Mialon, A.; Demontoux, F.; de Rosnay, P.; et al. Evaluating an Improved Parameterization of the Soil Emission in L-MEB. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1177–1189. [Google Scholar] [CrossRef]
- Hofer, R.; Mätzler, C. Investigations on snow parameters by radiometry in the 3- to 60-mm wavelength region. J. Geophys. Res. 1980, 85, 453. [Google Scholar] [CrossRef]
- Mätzler, C.; Aebischer, H.; Schanda, E. Microwave dielectric properties of surface snow. IEEE J. Ocean. Eng. 1984, 9, 366–371. [Google Scholar] [CrossRef]
- Pulliainen, J.; Hallikainen, M. Retrieval of Regional Snow Water Equivalent from Space-Borne Passive Microwave Observations. Remote Sens. Environ. 2001, 75, 76–85. [Google Scholar] [CrossRef]
- Kaleschke, L.; Tian-Kunze, X.; Maaß, N.; Mäkynen, M.; Drusch, M. Sea ice thickness retrieval from SMOS brightness temperatures during the Arctic freeze-up period. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Bogena, H.R.; Huisman, J.A.; Schilling, B.; Weuthen, A.; Vereecken, H. Effective calibration of low-cost soil water content sensors. Sensors 2017, 17, 208. [Google Scholar] [CrossRef] [PubMed]
- Schwank, M.; Wigneron, J.P.; Lopez-Baeza, E.; Völksch, I.; Mätzler, C.; Kerr, Y. L-Band Radiative Properties of Vine Vegetation at the SMOS Cal/Val Site MELBEX III. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1587–1601. [Google Scholar] [CrossRef]
- Mätzler, C.; Weber, D.; Wüthrich, M.; Schneeberger, K.; Stamm, C.; Wydler, H.; Fluhler, H. ELBARA, the ETH L-band radiometer for soil-moisture research. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003; Volume 5, pp. 3058–3060. [Google Scholar]
- Institue of Applied Physics. Handbook of the MORA 11.4 GHz Radiometer; Institue of Applied Physics: Bern, Switzerland, 1991. [Google Scholar]
- Guglielmetti, M.; Schwank, M.; Mätzler, C.; Oberdörster, C.; Vanderborght, J.; Flühler, H. FOSMEX: Forest Soil Moisture Experiments with Microwave Radiometry. IEEE Trans. Geosci. Remote Sens. 2008, 46, 727–735. [Google Scholar] [CrossRef]
- Werner, C.; Wiesmann, A.; Strozzi, T.; Schneebeli, M.; Matzler, C. The snowscat ground-based polarimetric scatterometer: Calibration and initial measurements from Davos Switzerland. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 2363–2366. [Google Scholar]
- Pellarin, T.; Wigneron, J.-P.; Calvet, J.-C.; Berger, M.; Douville, H.; Ferrazzoli, P.; Kerr, Y.H.; Lopez-Baeza, E.; Pulliainen, J.; Simmonds, L.P. Two-year global simulation of L-band brightness temperatures over land. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2135–2139. [Google Scholar] [CrossRef]
- Loth, B.; Graf, H.-F.; Oberhuber, J.M. Snow cover model for global climate simulations. J. Geophys. Res. 1993, 98, 10451–10464. [Google Scholar] [CrossRef]
- Tarongi, J.M.; Camps, A. Normality Analysis for RFI Detection in Microwave Radiometry. Remote Sens. 2010, 2, 191–210. [Google Scholar] [CrossRef]
- Le Vine, D.M. ESTAR experience with RFI at L-band and implications for future passive microwave remote sensing from space. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 847–849. [Google Scholar]
- Li, L.; Njoku, E.G.; Im, E.; Chang, P.S.; Germain, K.S. A preliminary survey of radio-frequency interference over the US in Aqua AMSR-E data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 380–390. [Google Scholar] [CrossRef]
- Njoku, E.G.; Ashcroft, P.; Chan, T.K.; Li, L. Global survey and statistics of radio-frequency interference in AMSR-E land observations. IEEE Trans. Geosci. Remote Sens. 2005, 43, 938–947. [Google Scholar] [CrossRef]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Lilliefors, H.W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Ruf, C.S.; Gross, S.M.; Misra, S. RFI detection and mitigation for microwave radiometry with an agile digital detector. IEEE Trans. Geosci. Remote Sens. 2006, 44, 694–706. [Google Scholar] [CrossRef]
- Roo, R.D.D.; Misra, S.; Ruf, C.S. Sensitivity of the Kurtosis Statistic as a Detector of Pulsed Sinusoidal RFI. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1938–1946. [Google Scholar] [CrossRef]
- Misra, S.; Ruf, C.S. Detection of Radio-Frequency Interference for the Aquarius Radiometer. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3123–3128. [Google Scholar] [CrossRef]
- Johnson, J.T.; Potter, L.C. Performance Study of Algorithms for Detecting Pulsed Sinusoidal Interference in Microwave Radiometry. IEEE Trans. Geosci. Remote Sens. 2009, 47, 628–636. [Google Scholar] [CrossRef]
- Schwank, M.; Guglielmetti, M.; Mätzler, C.; Flühler, H. Testing a New Model for the L-band Radiation of Moist Leaf Litter. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1982–1994. [Google Scholar] [CrossRef]
- Wigneron, J.-P.; Kerr, Y.; Waldteufel, P.; Saleh, K.; Richaume, P.; Ferrazzoli, P.; Escorihuela, M.-J.; Grant, J.P.; Hornbuckle, B.; de Rosnay, P.; et al. L-band microwave emission of the biosphere (L-MEB) model: Description and calibration against experimental data sets over crop fields. Remote Sens. Environ. 2007, 107, 639–655. [Google Scholar] [CrossRef]
- Mätzler, C.; Wiesmann, A. Extension of the microwave emission model of layered snowpacks to coarse-grained snow. Remote Sens. Environ. 1998, 70, 317–325. [Google Scholar] [CrossRef]
- Wigneron, J.-P.; Laguerre, L.; Kerr, Y.H. A simple parameterization of the L-band microwave emission from rough agricultural soils. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1697–1707. [Google Scholar] [CrossRef]
- Flores, A.N.; Entekhabi, D.; Bras, R.L.; Ivanov, V.Y. Hillslope-Scale Controls on Remote Sensing of Soil Moisture with Microwave Radiometry. In Proceedings of the 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; pp. II-695–II-698. [Google Scholar]
- Mätzler, C.; Wiesmann, A. Documentation for MEMLS, Version 3 ‘Microwave Emission Model of Layered Snowpacks’. MEMLS Manual, Version: 04.05.12. 2012. Available online: http://www.iap.unibe.ch/publications/pub-detail.php?lang=de&id=236 (accessed on 17 November 2017).
- Hallikainen, M.; Ulaby, F.; Dobson, M.; El-Rayes, M. Dielectric measurements of soils in the 3- to 37-GHz band between −50 °C and 23 °C. In Proceedings of the IGARSS’84: Remote Sensing, from Research Towards Operational Use, Strasbourg, France, 27–30 August 1984. [Google Scholar]
- Liebe, H.J.; Hufford, G.A.; Manabe, T. A model for the complex permittivity of water at frequencies below 1 THz. Int. J. Infrared Millim. Waves 1991, 12, 659–675. [Google Scholar] [CrossRef]
- Wigneron, J.-P.; Jackson, T.; O’Neill, P.; de Lannoy, G.; de Rosnay, P.; Walker, J.; Ferrazzoli, P.; Mironov, V.; Bircher, S.; Grant, J. Modelling the passive microwave signature from land surfaces: A review of recent results and application to the L-band SMOS & SMAP soil moisture retrieval algorithms. Remote Sens. Environ. 2017, 192, 238–262. [Google Scholar]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS Soil Moisture Retrieval Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar]
- Entekhabi, D.; Njoku, E.G.; Neill, P.E.O.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naderpour, R.; Schwank, M.; Mätzler, C. Davos-Laret Remote Sensing Field Laboratory: 2016/2017 Winter Season L-Band Measurements Data-Processing and Analysis. Remote Sens. 2017, 9, 1185. https://doi.org/10.3390/rs9111185
Naderpour R, Schwank M, Mätzler C. Davos-Laret Remote Sensing Field Laboratory: 2016/2017 Winter Season L-Band Measurements Data-Processing and Analysis. Remote Sensing. 2017; 9(11):1185. https://doi.org/10.3390/rs9111185
Chicago/Turabian StyleNaderpour, Reza, Mike Schwank, and Christian Mätzler. 2017. "Davos-Laret Remote Sensing Field Laboratory: 2016/2017 Winter Season L-Band Measurements Data-Processing and Analysis" Remote Sensing 9, no. 11: 1185. https://doi.org/10.3390/rs9111185
APA StyleNaderpour, R., Schwank, M., & Mätzler, C. (2017). Davos-Laret Remote Sensing Field Laboratory: 2016/2017 Winter Season L-Band Measurements Data-Processing and Analysis. Remote Sensing, 9(11), 1185. https://doi.org/10.3390/rs9111185




