2. Materials and Methods
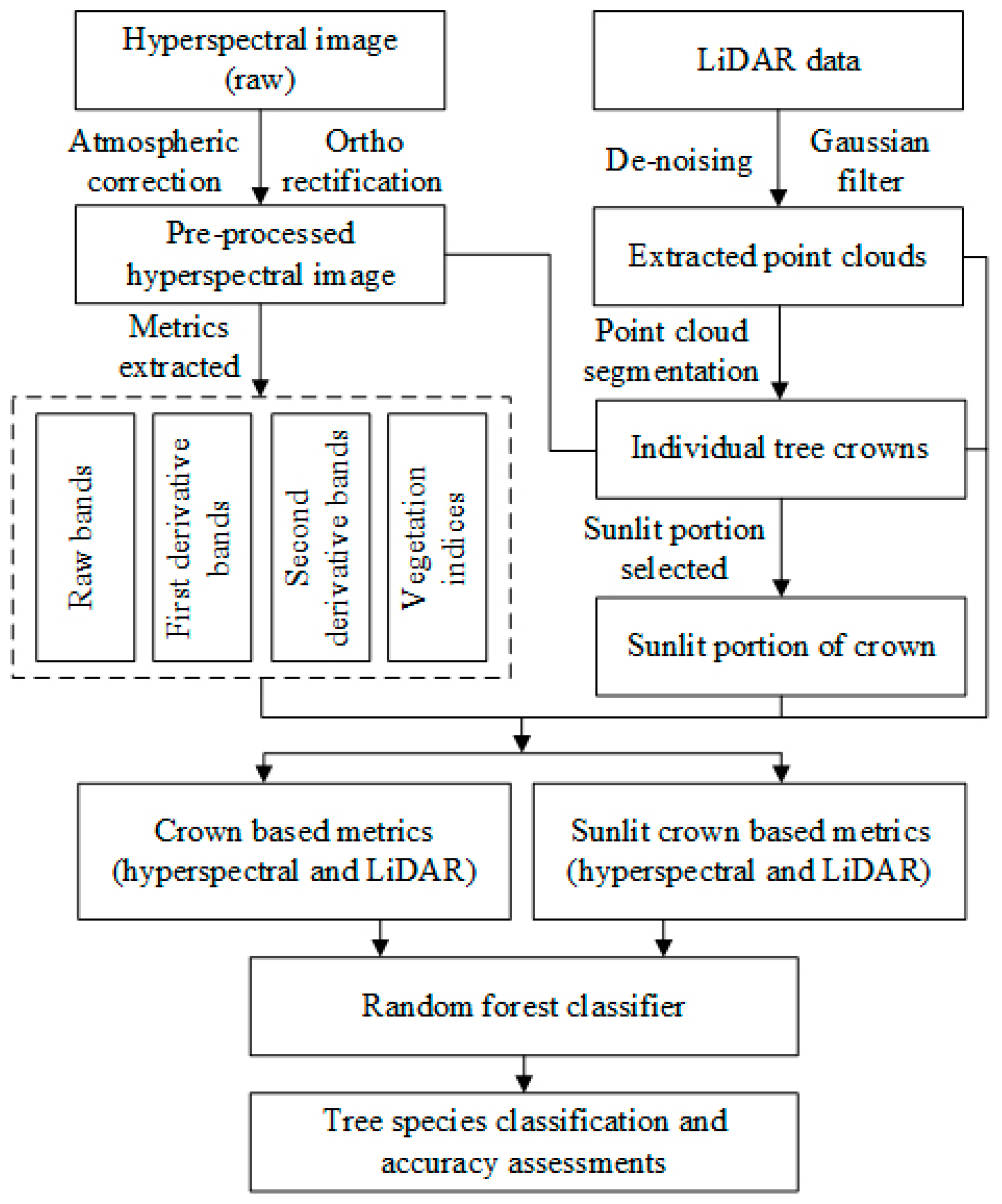
A general overview of the technique route for tree-species classification is shown in
Figure 1. First, the hyperspectral raw data were preprocessed to minimize the impacts of atmospheric interference and terrain distortion. Second, four sets of metrics (raw bands, first derivative bands, second derivative bands and vegetation indices) were calculated and subsequently selected using principal component analysis (PCA). Third, each individual tree crown was extracted using point cloud segmentation algorithm (PCS) by the LiDAR data after de-noising and filtering, and then sunlit portions in each crown were selected from hyperspectral data. Finally, the LiDAR metrics computed from discrete LiDAR data within crowns and the hyperspectral metrics in individual tree crown and in sunlit portions were utilized to Random Forest classifier to discriminate five tree-species at two levels of classification.
2.1. Study Site
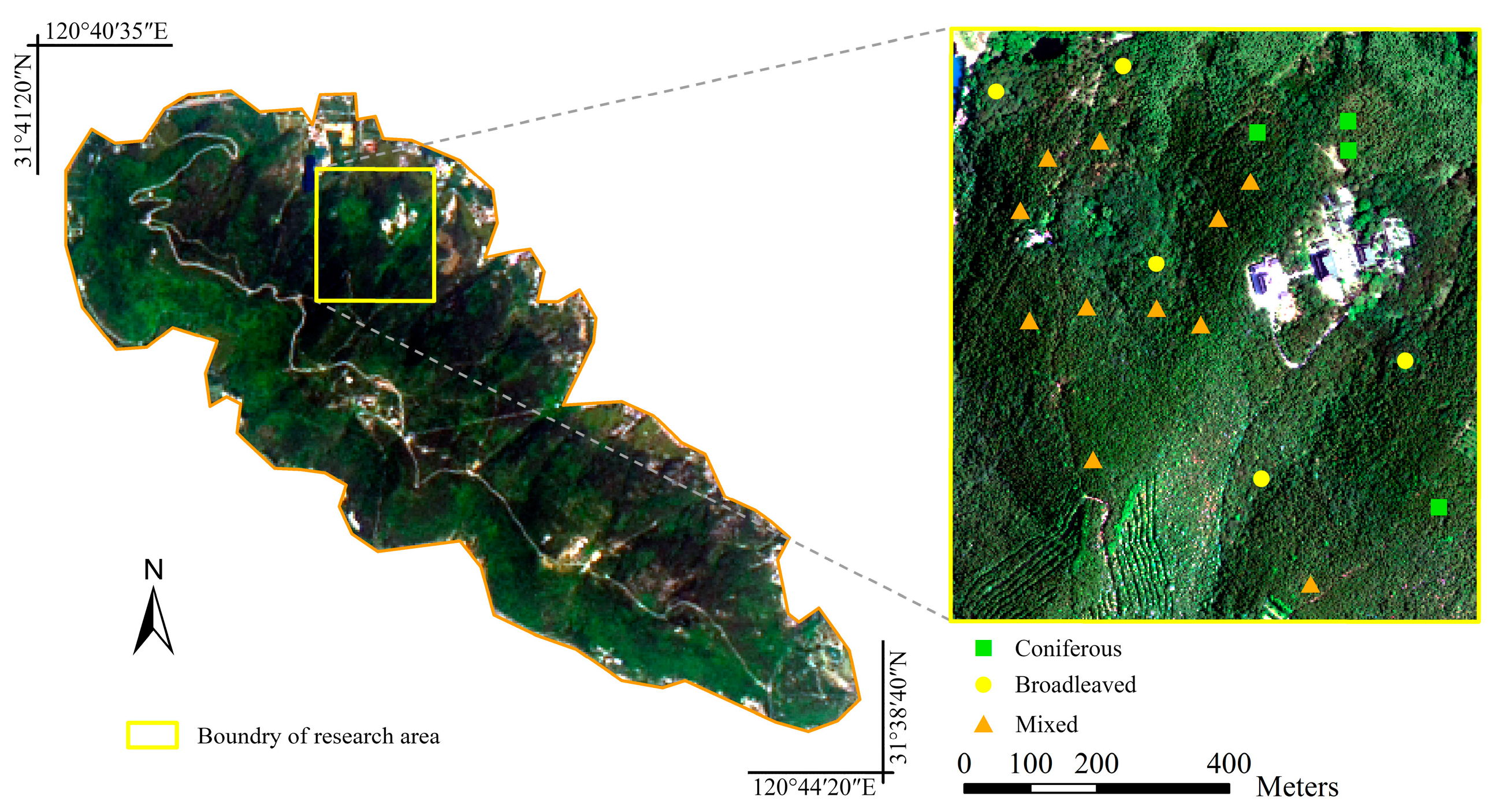
This study was conducted at Yushan Forest, a state-operated forest and national forest park, in the town of Changshu in Jiangsu Province, southeast China (120°42′9.4″E, 31°40′4.1″N) (
Figure 2). It covers approximately 1103 ha, with an elevation ranging between 20 and 261 m above sea level. It is situated in the north subtropical monsoon climatic region with an annual precipitation of 1062.5 mm. The Yushan forest belongs to the north subtropical secondary forest, and it can be classified to coniferous dominated, broadleaved dominated and mixed forests [
71]. The main coniferous tree-species are Chinese fir (
Cunninghamia lanceolata (Lamb.) Hook.) and Masson pine (
Pinus massoniana Lamb.). The major broadleaved tree-species include Sweet gum (
Liquidambar formosana Hance) and Sawtooth oak (
Quercus acutissima Carruth.), mixed with Chinese chestnut (
Castanea mollissima BL.).
2.2. Field Data
In this study, inventory data of field plots were obtained from the forest survey (under a leaf-on condition). A total of 20 square field plots (30 × 30 m
2) were established within the study site in August 2013, guided by data from an existing pre-stratified stand inventory data (2012). These plots were designed to cover a range of species composition, age classes, and site indices, and can be divided into three types based on species composition: (i) coniferous dominated forest (
n = 4); (ii) broadleaved dominated forest (
n = 5); and (iii) mixed species forest (
n = 11). The position of the center of field plots were assessed by Trimble GeoXH6000 GPS units, corrected with high precision real-time differential signals received from the Jiangsu Continuously Operating Reference Stations (JSCORS), resulting in a sub-meter accuracy [
71].
Individual tree within each plot with a diameter at breast height (DBH) larger than 5 cm was measured. The measurements included position, species, tree top height, height to crown base, and crown width in both cardinal directions. DBH was measured using a diameter tape for all trees. The calculation of position was based on the direction and distance of trees relative to the plot center. Tree top height was measured using a Vertex IV hypsometer. Crown widths were obtained as the average of two values measured along two perpendicular directions from the location of tree top. Moreover, the crown class, i.e., dominant, co-dominant, intermediate and overtopped, were also recorded. Since the intermediate and overtopped trees have little chance of being detected from above, they were excluded from the data analysis and classification. The statistics of the forest characteristics of three forest types are summarized in
Table 1.
2.3. Remote Sensing Data
The hyperspectral and LiDAR data were acquired simultaneously by the LiCHy (Hyperspectral, LiDAR and CCD) Airborne Observation System [
72] which was operated at 900 m above ground level with a flight path covering the entire Yushan Forest. Hyperspectral data were obtained using AISA Eagle sensor with 3.3 nm spectral resolution. The data employed were already georeferenced by the data provider. LiDAR data were acquired using a Riegl LMS-Q680i scanner with 360 kHz pulse repetition frequency and a scanning angle of ±30° from nadir. The average ground point distances of the dataset were 0.49 m (within a scanline) and 0.48 m (between scanlines) in a single scan, and the pulse density was three times higher in the overlapping regions. The specifications of hyperspectral and LiDAR data are summarized in
Table 2.
2.4. Data Pre-Processing
The hyperspectral images were atmospherically corrected using the Empirical line model with the field reflectance spectra (dark and bright targets where each target recorded ten curves) obtained by ASD FieldSpec spectrometer (Analytical Spectral Devices, Boulder, CO, USA). Then, the background noise of LiDAR data was suppressed by de-noising process and smoothed by a Gaussian filter. A 0.5 m digital terrain model (DTM) and digital surface model (DSM) were created by calculating the average elevation from the ground points and highest points within each cell, respectively, and the cells that contained no points were interpolated by linear interpolation of neighboring cells. The DTM of the study area was subtracted from the elevation value of each point to compute the normalized point cloud. Finally, the geometric corrections of the hyperspectral images were implemented with a nearest-neighbor interpolation using the DSM data to minimize terrain distortions and register hyperspectral data to LiDAR data. The number of ground control points (GCP) was more than 30 in the hyperspectral image of each plots (30 × 30 m2). The overall accuracy of geometric correction was higher than 0.25 m.
2.5. Hyperspectral Metrics Calculation
The spectral reflectance is important to classify tree-species because it can be applied to record the biophysical and biochemical attributes of vegetation such as leaf area index (LAI), biomass, and presence of pigments (e.g., chlorophyll and carotenoid) [
73,
74,
75]. All bands (64 bands) including the area of visible, red edge and near infrared were chosen in this study.
Derivative analysis is often used to enhance the target features and meanwhile weaken noises like illumination and soil background [
76]. The first and second order derivatives are used most commonly. In this study, derivatives for metrics were extracted using reflectance data, and the first and second derivative bands (128 bands) were calculated.
Hyperspectral vegetation indices have been developed based on specific absorption features that quantify biophysical and biochemical indicators best. Various narrowband vegetation indices calculated from hyperspectral image helped detect and map tree-species [
19,
20]. Here, a set of 20 narrowband vegetation indices was calculated and summarized in
Table 3. The definitions and references are presented below.
2.6. Individual Tree Detection
The point cloud segmentation (PCS) algorithm of Li et al. [
52] was applied to detect individual trees. It was a top-to-bottom region growing approach to segment trees individually and sequentially from point cloud. The algorithm started from a tree top and “grow” an individual tree by including nearby points based on the relative spacing. Points with a spacing smaller than a specified threshold were classified as the target tree, and the threshold was approximately equal to the crown radius. Additionally, the shape index (SI) was added to improve the accuracy of segmentation by avoiding the elongated branch. The PCS algorithm was implemented using LiForest (GreenValley International, Berkeley, CA, USA) software, and the space threshold was equal to the mean crown radius of each corresponding forest type (coniferous = 1.45 m, broadleaved = 2.40 m and mixed = 1.91 m). The results of segmentation were point cloud which contained the attribute of tree ID, and points from the same tree had same ID. For each detected tree, the tree position, tree height and crown area were estimated and compared to the corresponding tree in the field. It was considered correct when a detected tree was located within the crown of the field inventory tree. The point cloud of detected tree was rasterized to image to match with hyperspectral image, and the value of each pixel was assigned as point ID appeared most frequently. The pixels had the same value in rasterized image were considered as a part of the same tree, and the range of crown was the boundary of pixels with the same value.
To evaluate the accuracy of tree detection, three measures including recall (
r, represents the tree detection rate), precision (
p, represents the precision of detected trees) and
F1-score (
F1, presents the overall accuracy taking both omission and commission in consideration) were introduced using the following equations [
92,
93].
where
Nt is the number of the detected trees which exist in field position,
No is the number of the trees which were omitted by algorithm, and
Nc is the number of the detected trees which do not exist in field.
2.7. LiDAR Metrics Calculation
Discrete LiDAR metrics are descriptive structure statistics, and they are calculated from the height normalized LiDAR point cloud. In the study, 12 metrics for each tree were calculated, including: (i) selected height measures, i.e., percentile heights (
h25,
h50,
h75 and
h95), minimum height (
hmin) and maximum height (
hmax); (ii) selected canopy’s return density measures, i.e., canopy return densities (
d2,
d4,
d6 and
d8); (iii) variation of tree height, i.e., coefficient of variation of heights (
hcv); and (iv) canopy cover, i.e., canopy cover above 2 m (
CC). A summary of the LiDAR metrics and descriptions is given in
Table 4.
Previous studies have found that first returns have more stable capabilities for forest biophysical attribute estimation than all returns [
94]. Therefore, LiDAR metrics were computed by first returns. Metrics of percentile height and canopy return density were generated from first returns which were higher than 2 m above ground to exclude returns from low-lying vegetation.
2.8. Sunlit Portion in Individual Tree Crown
Previous studies have demonstrated that the spectral signal from sunlit crown was dominated by first order scattering and the impacts of soil and shadows were minimal, therefore it was appropriate for foliage or canopy modeling [
95]. The sunlit crown was defined as all the pixels within an individual tree crown that had reflectance values in near infrared band greater than the mean value of crown in that band [
96]. In this study, the pixels in each crown with reflectance values in 800 nm higher than the mean value were selected as sunlit crown.
2.9. Hyperspectral Metrics and the Selection
The individual tree crown and sunlit crown metrics were extracted from hyperspectral metrics using spatial statistical analysis. Metrics at the two levels both included raw reflectance bands (n = 64), derivative bands (n = 128) and vegetation indices (n = 20).
In general, hyperspectral imagery was considered to be suited for tree-species classification due to its high spectral resolution and a large amount of hyperspectral metrics. However, the high dimension of spectral data would cause Hughes phenomenon and always perform ineffectively in classification [
97,
98]. As result, it was necessary to optimize the hyperspectral metrics and reduce dimension of spectral data. The Principal Component Analysis (PCA) which aimed to calculate a subspace of orthogonal projections in accordance with the maximized variance of the whole metrics, therefore was widely applied in hyperspectral metrics optimization [
99,
100]. In this study, the PCA algorithm was used to reduce the dimension of the hyperspectral metrics. The best 20 metrics, which had high correlation with the first three principle components, were correspondingly selected from reflectance bands, derivative bands and vegetation indices at both the whole crown and sunlit crown level.
2.10. Random Forest and Classification
The Random Forest classifier is a non-parametric ensemble of decision trees which have been trained using bootstrap samples of training data. A number of trees are constructed based on random feature subset and it is faster to grow a large number of decision trees without pruning. In random forest, only the best among a subset of candidate features are selected randomly to determine the split at each node. Approximately one-third of samples that are not used in the bootstrapped training data are called the out-of-bag (OOB) samples, which offer unbiased estimates of the training error and could be used to evaluate the relative importance of features.
In total, 587 samples including Chinese chestnut (C.C: n = 117), Sweet gum (S.G: n = 100), Sawtooth oak (S.O: n = 114), Masson pine (M.P: n = 130) and Chinese fir (C.F: n = 126) were classified at two levels (five tree-species and two forest-types). Random forest classifiers were trained using training dataset, while the classification accuracies were assessed by the validation dataset. The training and validation datasets were allocated randomly, and the proportion of training dataset and validation dataset were 60% and 40%, respectively. The number of decision trees was set to 1000 to ensure that each sample was classified more than once. The classification accuracies were assessed by overall accuracy (OA), the producer’s and user’s accuracy.
In this study, the LiDAR metrics (12 metrics) and the hyperspectral metrics (80 metrics selected by the indices of PCA) were selected again using the correlation analysis (the metrics that strongly correlated with other metrics were excluded) before classification, and the number of retained LiDAR metrics and hyperspectral metrics (whole crown and sunlit crown metrics) were eight and thirty, respectively. The classification of five tree-species and two forest-types were both divided into four parts: (i) using LiDAR metrics (n = 8) and sunlit hyperspectral metrics (n = 30) to classify tree-species (SA); (ii) using LiDAR metrics (n = 8) and crown hyperspectral metrics (n = 30) to classify tree-species (CA); (iii) using sunlit hyperspectral metrics (n = 30) to classify tree-species (SH); and (iv) using crown hyperspectral metrics (n = 30) to classify tree-species (CH). In order to select the most important metrics, metrics were eliminated from random forest classifier one by one. The order in which metrics ruled out were controlled by the ranking for importance (the mean decrease in Gini index) of each metric in each loop, and the last metric was eliminated.
3. Results
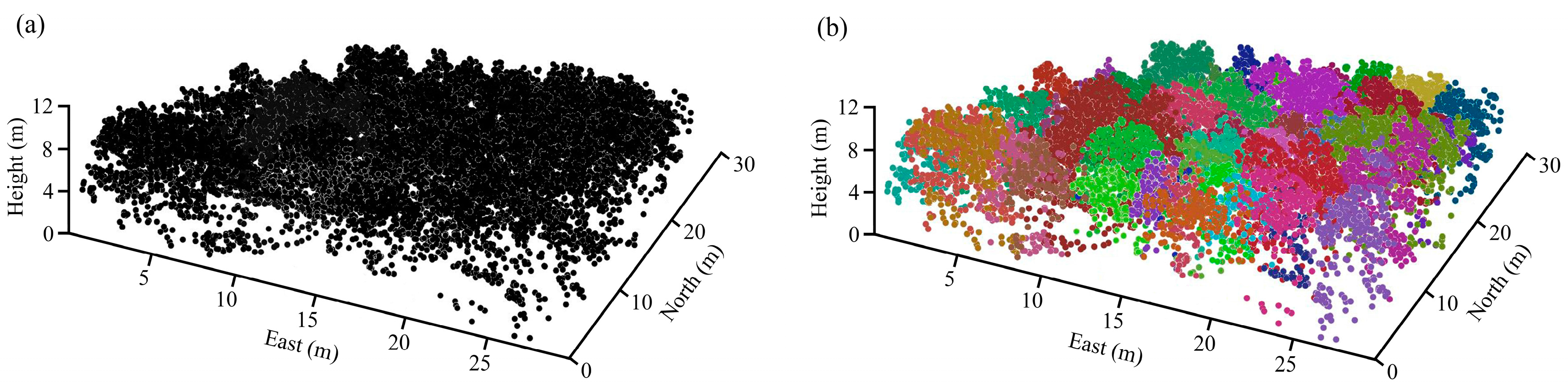
Figure 3 shows the result of individual tree detection using PCS algorithm in one plot (30 × 30 m
2). Furthermore, visual inspection indicated that the algorithm succeed in segmenting subtropical forest trees. In total, 587 (80.1%) of dominate and co-dominate trees were correctly detected in all of the 20 plots. The error of omission (the number of trees which was not detected by PCS algorithm) was 146 (19.9%), and the error of commission (the number of detected trees which did not exist in the field) was 97 (14.2%). The
F1-score of coniferous dominated plots was highest (88.2%), followed by the broadleaved dominated plots (85.7%), and the mixed plots was lowest (80.3%) (
Table 5). It was likely due to the crown of coniferous trees which tended to be compact and relatively isolate from each other. However, the broadleaved trees were rounded and more likely to overlay, and the structure of mixed plots was more complicated than coniferous dominated and broadleaved dominated plots. The accuracy of estimated tree height and diameter were also assessed using inventory data. The accuracy of estimated crown diameter (RMSE = 0.36 m, rRMSE = 9.5% observed mean crown diameter) was less than the tree height (RMSE = 0.48 m, rRMSE = 4.6% observed mean height).
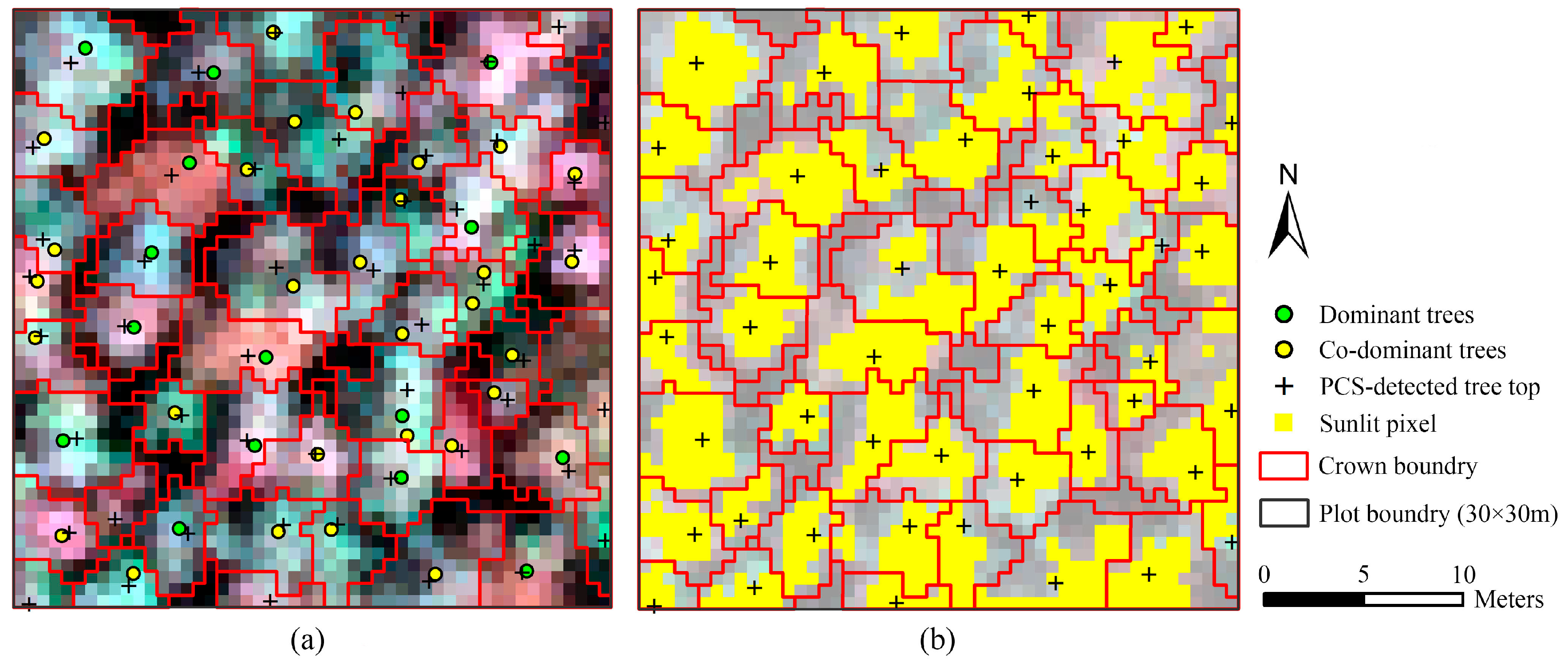
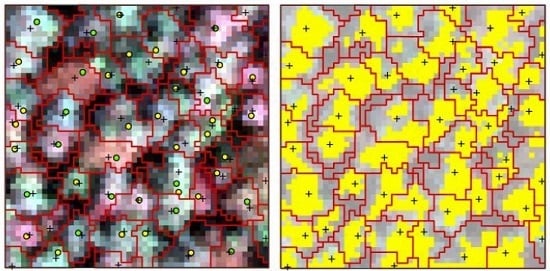
The point clouds of each tree extracted by PCS algorithm were rasterized to the image, which was matched with hyperspectral data; therefore, the boundary of each individual tree was consistent with hyperspectral image. One sample plot of hyperspectral imagery with detected tree tops, crown boundaries and the tops of linked trees in field is shown in
Figure 4a. The portions in each crown with reflectance values in the band of 800 nm higher than the mean value were selected as sunlit crown. The detected trees and sunlit portion in each crown can be seen in
Figure 4b.
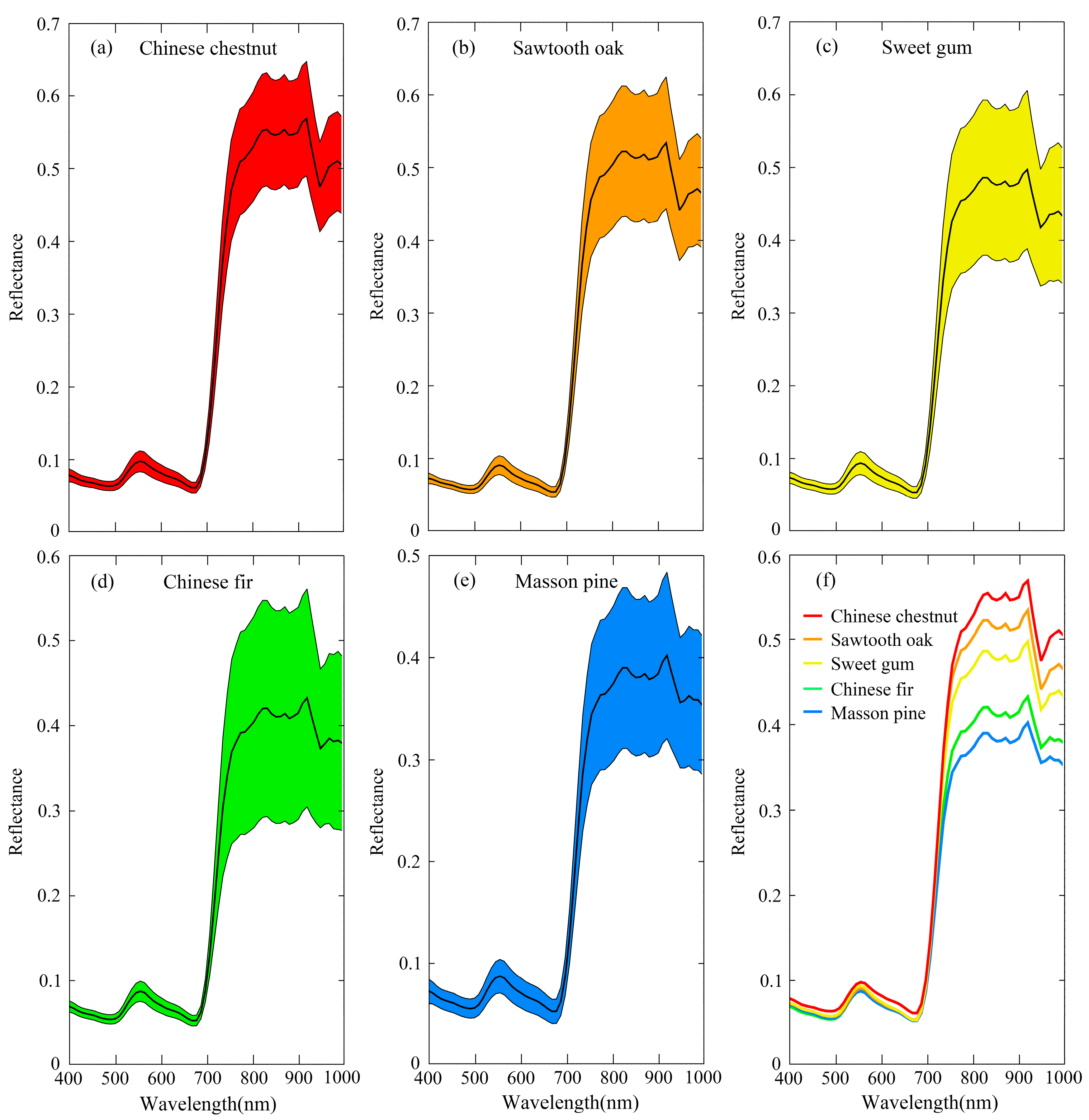
The reflectance of five tree-species extracted from sunlit crown indicated that the species exhibited various spectral responses, especially in the areas of near infrared. It was noted by the difference sizes of envelopes (
Figure 5a–e) and the mean spectral reflectance in
Figure 5f. The hyperspectral metrics were also calculated based on this premise. With the PCA algorithm, 20 best metrics were correspondingly selected from reflectance bands, derivative bands and vegetation indices at both whole crown and sunlit crown level. The result of best metrics selected from sunlit crown metrics is shown in
Figure 6. The metrics are mainly located in the regions of visible, red edge and near infrared.
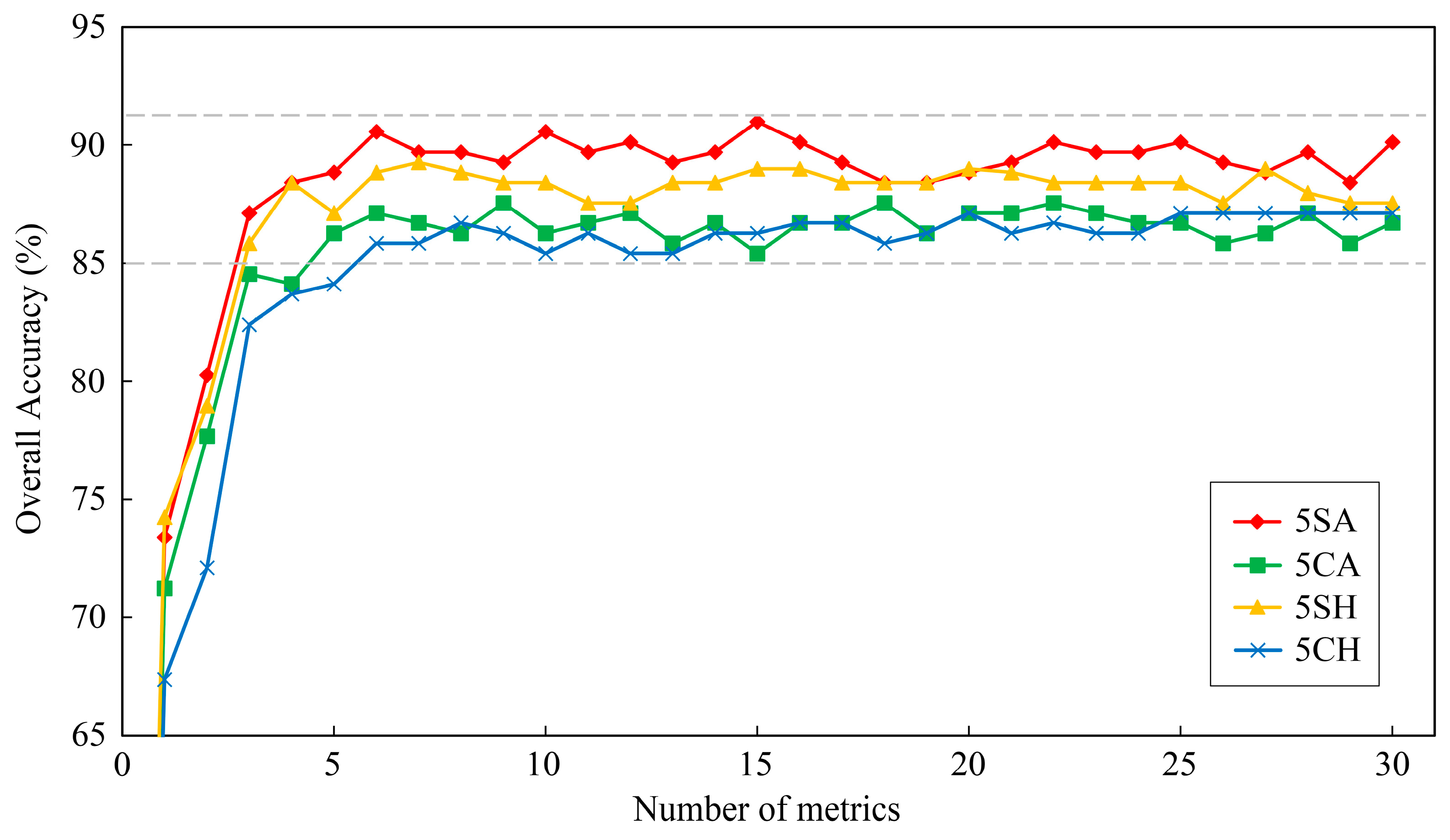
Figure 7 presents the overall accuracies of five tree-species classifications using random forest classifier with respect to the reduction of metrics numbers (0–30). When the number of metrics was less than six, the overall accuracies of classifications decreased by the reduction of the number of metrics in most cases. Then, the overall accuracies were tend to be stable at the certain numerical range when metrics number was larger than six. Therefore, only few selected metrics could be used to classify tree-species effectively, and six was the optimal number of metrics for five tree-species classifications in this study. The top-six important metrics were selected as the most important metrics for five tree-species classifications (
Table 6). Classification using LiDAR and sunlit hyperspectral metrics (5SA) performed best, followed by classification using sunlit hyperspectral metrics (5SH) and classification using LiDAR and crown hyperspectral metrics (5CA), and the classification using crown hyperspectral metrics (5CH) performed worst. The classifications using LiDAR and hyperspectral metrics had better performance than classifications using only hyperspectral metrics; therefore, the fusion of hyperspectral and LiDAR data could improve the accuracy of tree-species classification in subtropical forests. In addition, the classifications using sunlit crown metrics also outperformed the classifications using whole crown metrics, which indicated that the metrics extracted from sunlit crown had lower within-species variance and could be used to enhance the species separability.
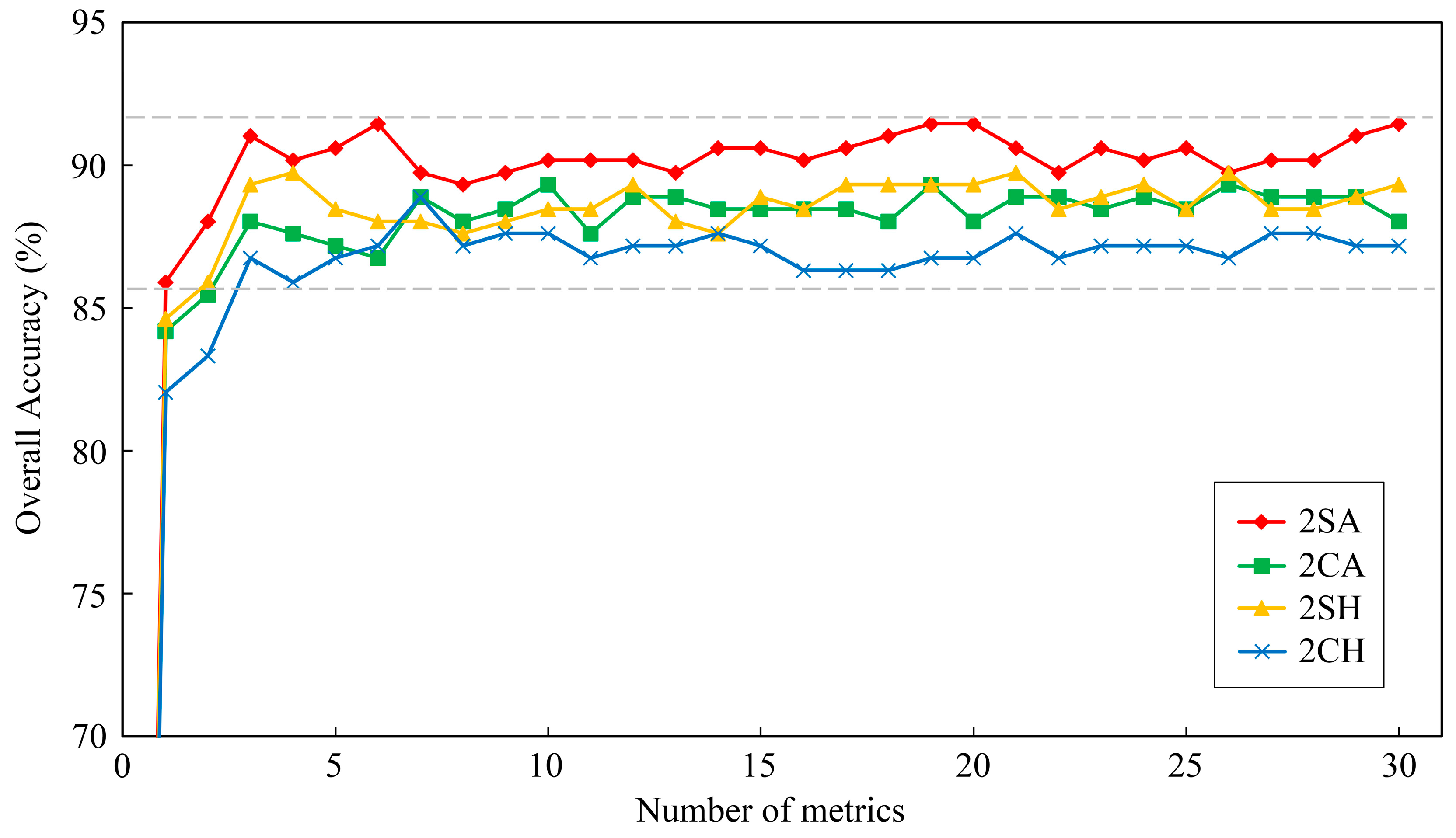
Similarly,
Figure 8 displays the overall accuracies of two forest-types classifications with respect to the reduction of metrics number (0–30). When the number of metrics was less than three, the overall accuracies of classifications decreased by the reduction of the number of metrics in all cases. Then, the overall accuracies tended to be stable at certain numerical range when metrics number was larger than three. Therefore, only few selected metrics could also be used to classify forest types effectively, and three was the optimal number of metrics for two forest-types classification in this study. The top-three important metrics were selected as the most important metrics for two forest-types classification (
Table 6). For two forest-types classification, classification using LiDAR and sunlit hyperspectral metrics (2SA) performed best, followed by classification using sunlit hyperspectral metrics (2SH) and classification using LiDAR and crown hyperspectral metrics (2CA), and the classification using crown hyperspectral metrics (2CH) performed worst. The classifications using LiDAR and hyperspectral metrics had better performance than classifications using only hyperspectral metrics, which demonstrated that the fusion of hyperspectral and LiDAR data could also improve the accuracy of two forest-types classification in subtropical forests. Meanwhile, the classifications using sunlit crown metrics outperformed the classifications using whole crown metrics, and it indicated that the metrics extracted from sunlit crown had lower within-type variance and could be used to enhance the separability of forest types as well.
The confusion matrix and accuracies of classifications using the most important metrics at two classification levels, i.e., all five tree-species and two forest-types are shown in
Table 7 and
Table 8, respectively. Classifications of two forest-types using three most important metrics (overall accuracy = 86.7–91.0%) have slightly higher accuracies than the classifications of five tree-species using six most important metrics (overall accuracy = 85.8–90.6%). In both classifications of five tree-species and two forest-types, classification using LiDAR and sunlit hyperspectral metrics had highest accuracy (overall accuracy = 90.6% and 91.0%), followed by classification using sunlit hyperspectral metrics (overall accuracy = 88.8% and 89.3%) and classification using LiDAR and crown hyperspectral metrics (overall accuracy = 87.1% and 88.0%), sequentially, and the classification using crown hyperspectral metrics had lowest accuracy (overall accuracy = 85.8% and 86.7%). The classifications using LiDAR and hyperspectral metrics (overall accuracy = 87.1–91.0%) performed better than the classifications using only hyperspectral metrics (overall accuracy = 85.8–89.3%), and the classifications using sunlit crown metrics (overall accuracy = 88.8–91.0%) outperformed using whole crown metrics (overall accuracy = 85.8–88.0%).
4. Discussion
The tree-species classification would have better performance because the fusion of hyperspectral and LiDAR data could achieve the combination of spectral and structure information [
62,
63,
101]. In this study, although the classifications using hyperspectral metrics showed a relative good performance (overall accuracies were stable over 85%), the classifications using LiDAR and hyperspectral metrics performed better and had higher accuracies. Moreover, the improvements of overall accuracies were from 0.4% to 5.6% except few cases caused by the effect of Hughes phenomenon (
Figure 7 and
Figure 8). Furthermore, compared with the classifications using only hyperspectral metrics, the mean omission and commission of classifications using LiDAR and hyperspectral metrics decreased by 1.5% and 1.6%, respectively (
Table 7 and
Table 8). Cao et al. [
16] classified tree-species using only full-waveform LiDAR data with random forest classifier in the same study area of subtropical forests. Compared with our results, lower overall accuracies were obtained in six tree-species (68.6%) and two forest-types (86.2%) classification. Alonzo et al. [
63] reported a 4.2% increase of classification overall accuracy for the addition of LiDAR data to hyperspectral metrics in urban forests located on Santa Barbara, California. Jones et al. [
23] classified 11 tree-species using the fused hyperspectral and LiDAR data at pixel-level in temperate forests of coastal southwestern Canada and found that the producer’s accuracy increased 5.1–11.6% compared with using single dataset, which was slightly higher than reported in this study. The reason for the slight lower improvement of accuracy in our study may be due to the complexity of multilayered subtropical forest which decline the capability of LiDAR metrics to discriminate tree-species.
Traditionally, the individual tree crown (ITC) was manually delineated on RGB false color image, or automatically delineated based on image segmentation algorithm on optical image and LiDAR-derived canopy height model (CHM). The result of crown delineation using optical image was influenced by the image quality which depended on many factors (e.g., sensor status, illumination and view geometry), and the segmentation algorithm using LiDAR-derived CHM was not ideal as the CHM which had inherent errors during the interpolating process from point cloud to gridded model. The PCS algorithm is a method to segment individual tree from point cloud directly. It could provide three dimensional structure information of each tree and avoid the limitation of using CHM. In this study, the PCS algorithm was a top-to-bottom region growing approach that segmented trees individually and sequentially from point cloud. In total, 587 (80.1%) of dominate and co-dominate trees were correctly detected and the overall accuracy was 82.9%. Cao et al. [
16] applied local maximum filtering algorithm to detect individual tree in the same research area, and the 78.5% of dominate and co-dominate trees were correctly detected. The slightly lower detection accuracy compared with this study may be caused by the errors of CHM and the smooth median filtering. The accuracy of estimated crown diameter (rRMSE = 9.5%) by PCS algorithm was lower than tree height (rRMSE = 4.6%), which may be owing to the overlapping of adjacent canopy in subtropical forest.
Based on the selected result of hyperspectral metrics extracted from sunlit crown using PCA algorithm (
Figure 6), three spectral regions were identified. Two regions in the visible band (500–600 nm and 680–750 nm) included blue edge, green peak, part of yellow edge, red valley and red edge. Previous studies had used these bands to separate tree-species at various scales [
20,
102,
103]. They were related to nitrogen, pigment content, vegetation vigor, light use efficiency, plant stress and biophysical quantities, and all these properties were supposed to differ among species [
104,
105,
106]. The other region was in the near infrared band (800–900 nm) which had high reflectance due to multiple-scattering within leaf structure such as spongy mesophyll. The region was related to cell structure, biophysical quantity and yield (e.g., biomass and LAI) [
107,
108]. Clark et al. [
15] found that the species differences were mainly focused in NIR region at canopy scale. It was also confirmed in this study that the difference of five tree-species was maximum in NIR bands (
Figure 5f).
In hyperspectral image, the crown spectral values may exhibit bimodal tendencies related to the sunlit and shadow parts [
96], and the multiple-scattering among tree crown may lead to noisy spectral values. The sunlit crown values were dominated by first-order scattering from canopy and the influences of soil background, trunk and branch were minimum. Therefore, using metrics extracted from sunlit crown may improve the classification accuracy. This hypothesis was confirmed by our results that the classifications using sunlit crown metrics (overall accuracies stable at 87.1–91.5%) had better performance than using whole crown metrics (overall accuracies stable at 85.4–89.3%), and the mean improvement of overall accuracy was 2.3% (
Figure 7 and
Figure 8). The classification of 17 tree-species in tropical forests undertaken by Feret et al. [
13] showed similar results. Meanwhile, compared with the classifications using whole crown metrics, the omission and commission of classifications using sunlit metrics were declined 0–7.5% and 0–8.6%, respectively (
Table 7 and
Table 8).
With the one by one elimination of the input selected metrics after decorrelation, the overall accuracies were stable at certain numerical range (standard deviation = 0.53–0.64%) at the beginning, and then started decrease since the remaining metrics could not provide sufficient information for species discrimination. The number of input metrics of last point before the decline of overall accuracies was seen as the optimal number of metrics for classification. In this study, six and three were the optimal number of metrics for five tree-species and two forest-types classification, respectively. The top-ranked six or three metrics were selected as the most important metrics. Compared with highest overall accuracies of each classification, the overall accuracies of five tree-species and two forest-types classification using the most important metrics descended only 0.4–1.3% and 0.4–2.1%, respectively. Therefore, the classifications using the most important metrics improved the overall accuracies significantly and these metrics could be used to classify tree-species efficiently, which is consistent with the previous studies [
16,
99].
The point clouds metrics have significant relationship with three dimensional structure proprieties of canopy [
57,
109,
110]. During the classifications, the LiDAR metrics
hcv,
h95 and
d2 were selected as the most important metrics (
Table 6).
hcv indicated the height variation of all first returns, and it could reflect the canopy structure of different species. At the study site, coniferous trees usually have dense and homogenous tower-shaped crown which lead to a relative low height variance of first return within crown. Meanwhile, the broadleaved trees have loose and heterogeneous ovoid crown which lead to a high height variance of first return within crown.
hcv is sensitive to this difference, which makes it possible to be a good metric for species discrimination.
h95 is also a good indicator of classifying tree-species since it is upper percentile height which can reflect the height of trees in some extent. Furthermore, the forest in study area is under a mature or near mature condition, therefore, the tree height is approaching the maximum value, resulting the differences of height among different species.
d2 is the percentage of first return above the 20 quantiles to total number of first returns, and the crown with dense foliage and branch could reduce the number of points in lower height, thereby
d2 could be used to describe the dense of crown. The species with different crown density will lead to the various
d2, and thus it could be effectively applied to classify tree-species.
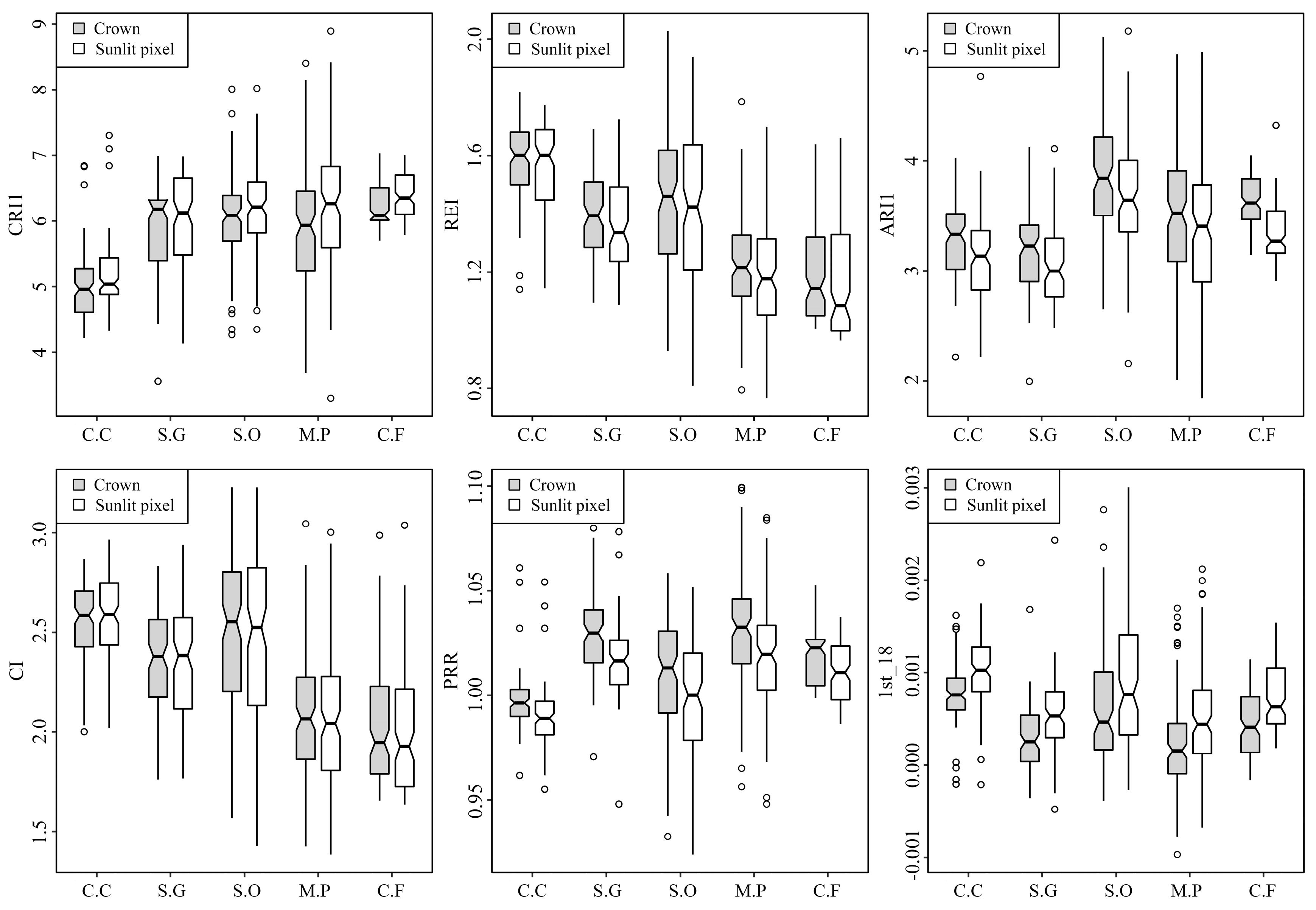
Previous studies have verified the significant effects of hyperspectral metrics for tree-species classification [
13,
63], and this study also showed the obvious advantages of hyperspectral metrics. The overall accuracies of classifications using only hyperspectral metrics were greater than 85% and the overall accuracies were higher after adding LiDAR metrics. Six frequently used hyperspectral metrics (i.e., CRI1, REI, ARI1, CI, PRR and 1st_18) were selected from the most important metrics. For each metric, the differences of five tree-species are significant (
Figure 9). CRI1, ARI1 and CI are metrics representing reflectance of carotenoid, anthocyanin and chlorophyll, respectively, and are correlated with the content of pigments directly. Therefore, the content of pigments in five tree-species will lead these three metrics to vary with different tree-species. Gitelson et al. [
84] found that REI had a strong relationship with canopy content of chlorophyll (R
2 = 0.94, RMSE = 0.15 g/m
2), and can be used to estimate the content of chlorophyll accurately. Therefore, it was applied to classify tree-species effectively in this study, and the distribution of box plot was similar to CI. PRR is a metrics used to measure the efficiency of light use which may be influenced by content of pigments and the crown surface structure. As a result, tree-species (e.g.,
Masson pine) with high content of pigments and dense crown have high light use efficiency. It has been proved that classification using first-order derivative metrics outperformed using reflectance metrics [
111]. 1st_18 is the value of first-order derivative in 553 nm correlated with chlorophyll and biomass which can be used to assess vegetation fertility level and biophysical quantity, thus it is a good indicator to classify five tree-species in subtropical forest.
To compare the six metrics selected from most important metrics, CRI1, ARI1, PRR and 1st_18 were all calculated using green bands, and REI and CI were calculated using red edge bands. Green band and red edge region were both verified as informative areas of spectrum in vegetation studies [
112], which is similar with the results of band selection using PCA algorithm (
Figure 6). CRI1, ARI1, PRR and 1st_18 all had different values in sunlit crown and whole crown, yet the ranges of REI and CI in sunlit crown and whole crown were similar (
Figure 9). Therefore, CRI1, ARI1, PRR and 1st_18 might be more sensitive to illumination than REI and CI. It could be explained that the green bands had shorter wavelength and the value was more likely influenced by scattering in crown than red edge bands [
113].