Evaluation and Aggregation Properties of Thermal Infra-Red-Based Evapotranspiration Algorithms from 100 m to the km Scale over a Semi-Arid Irrigated Agricultural Area
Abstract
1. Introduction
- To investigate ET flux scaling properties from HR to LR using data from the same sensor (i.e., ASTER), as well as data stemming from different sensors onboard the same platform (i.e., ASTER, MODIS).
- To develop and evaluate new and existing scaling relationships based on easily obtainable RS quantities to relate local HR and LR roughness lengths.
2. Data
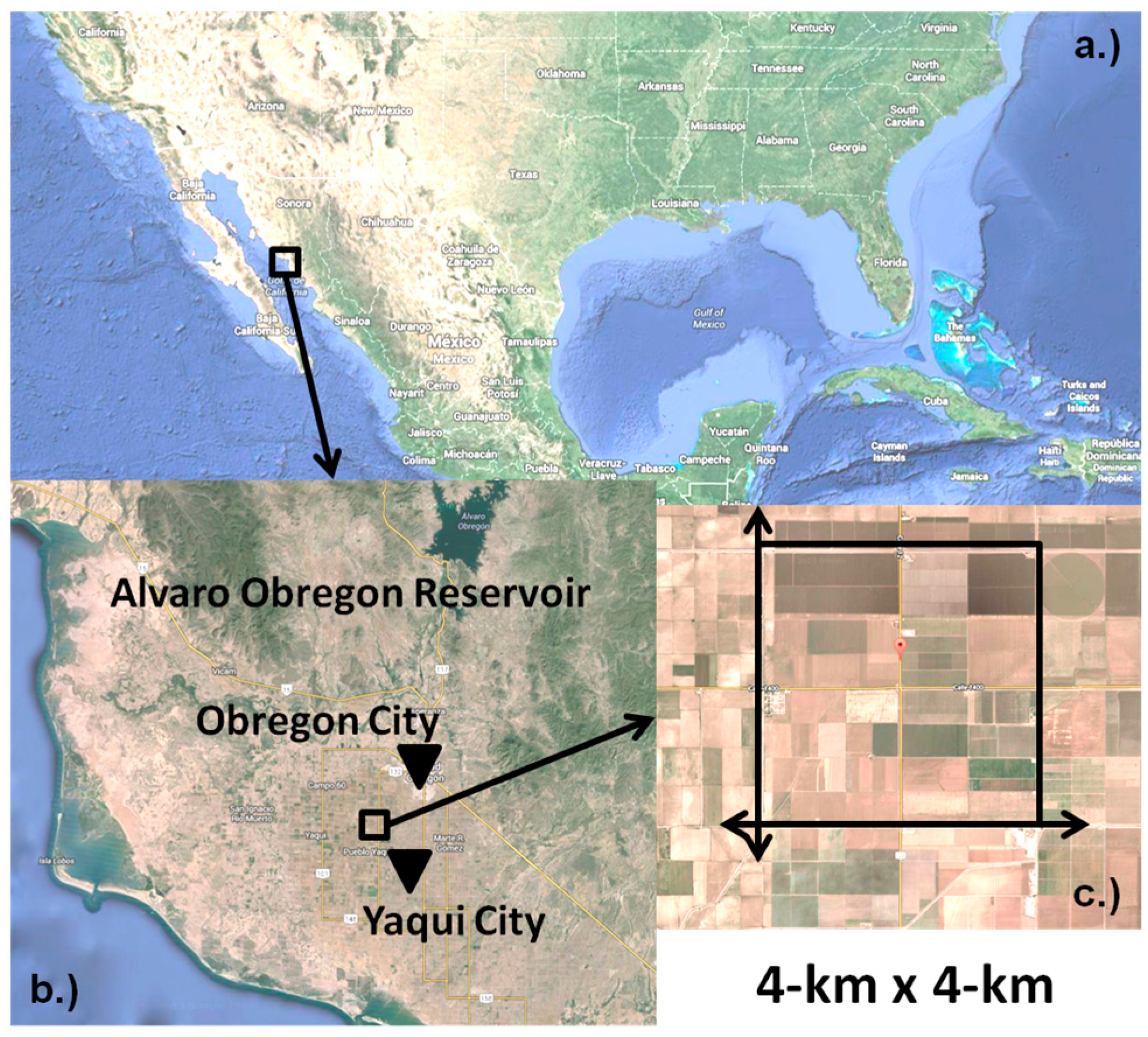
2.1. Study Area
2.2. In Situ Measurements
2.3. Remote Sensing Data
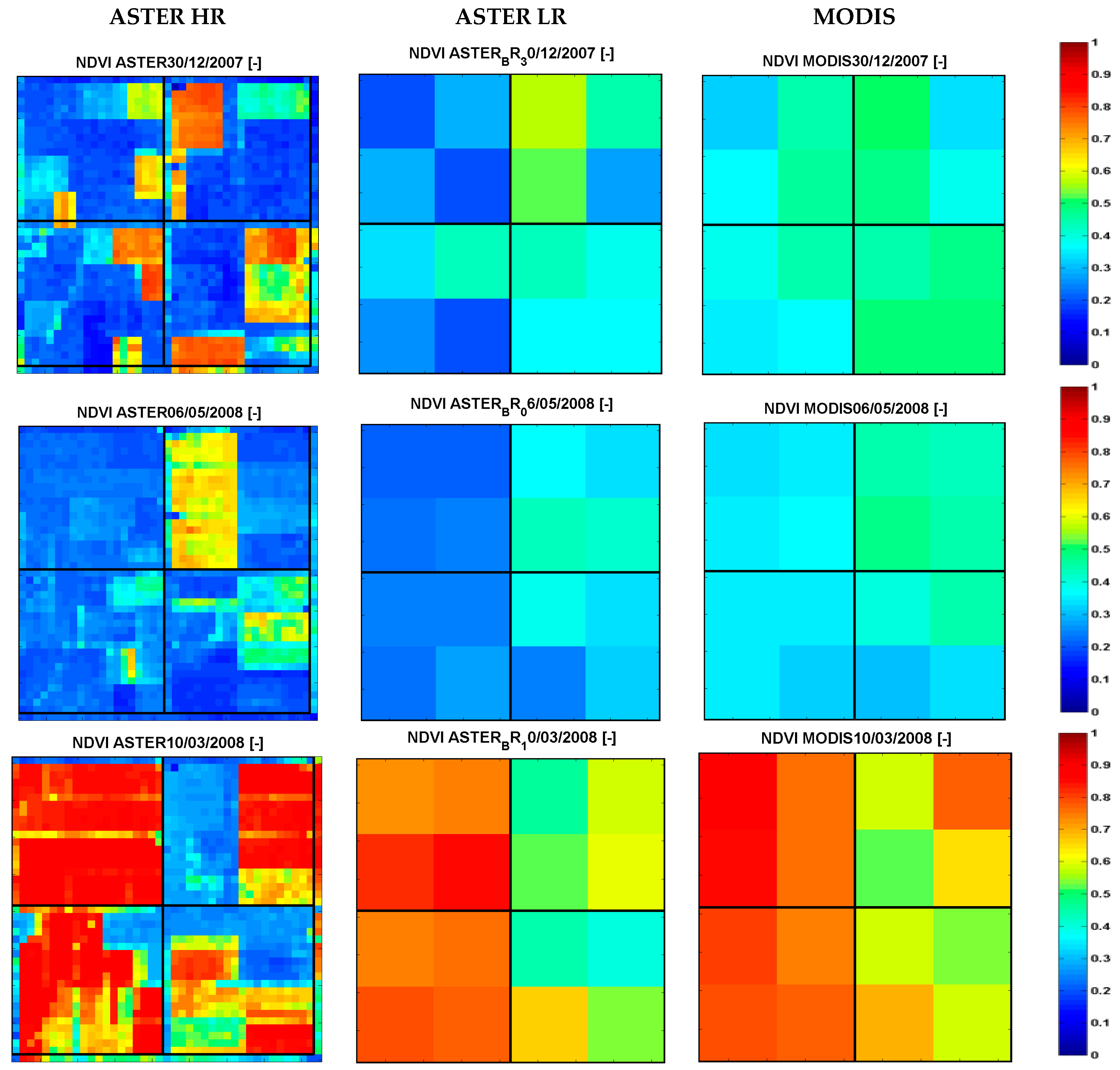
2.4. Remote Sensing Data Preprocessing
3. Energy Balance Models Parameterization and ET Calculation
3.1. Available Energy
3.2. SEBS Model
3.3. TSEB Model
3.4. Daily ET Fluxes Generation
4. Methods
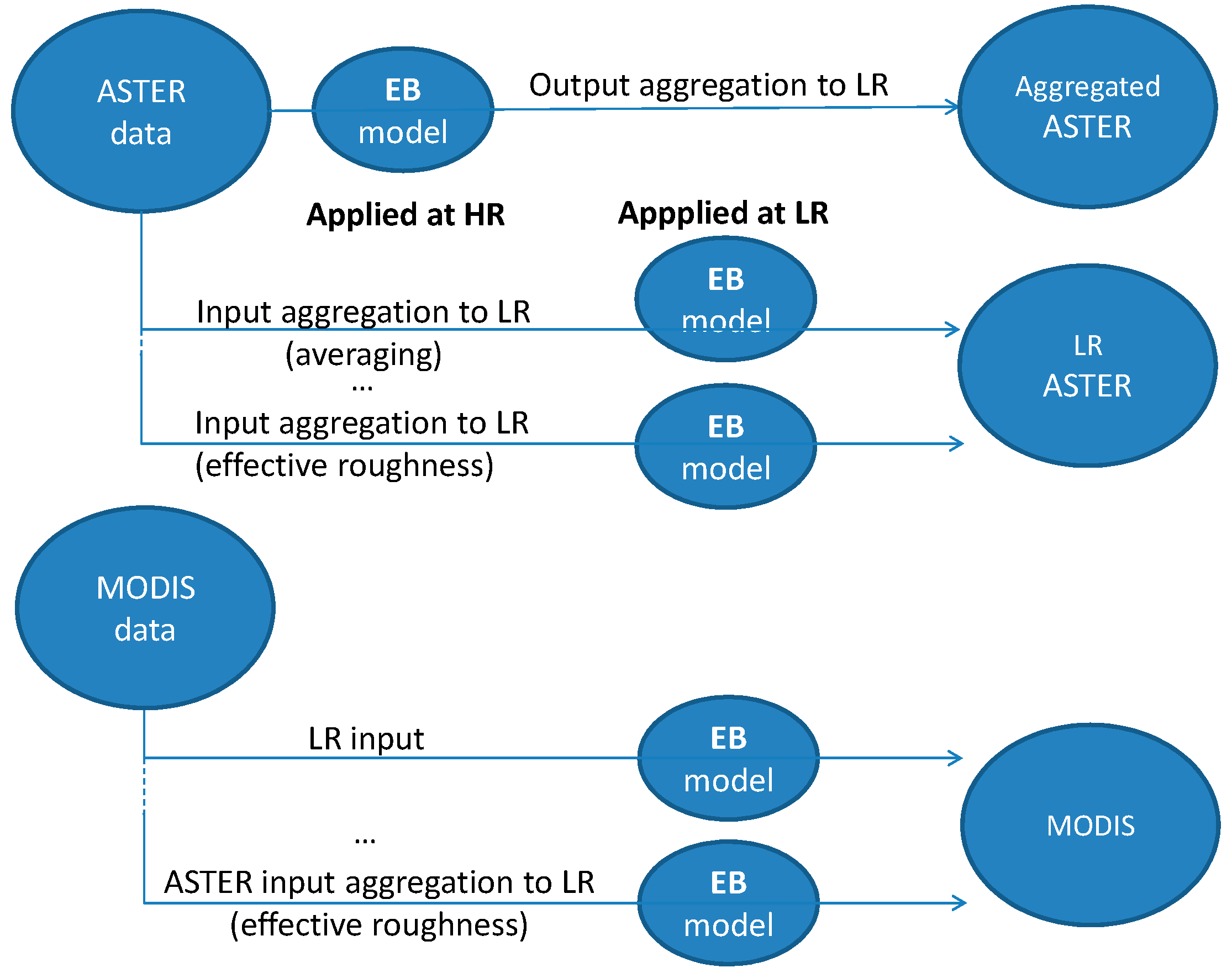
4.1. General Design of the Experiments
- In a preliminary step, HR maps of ET were computed with both models from ASTER products (dataset named ‘HR-ASTER’ including spectral surface reflectances, spectral surface emissivities, radiative surface temperature and surface fluxes). ET maps were evaluated against the eddy correlation measurements performed in seven crop fields. These maps were aggregated at the kilometric resolution to be used in the following steps as a reference dataset to evaluate ET maps obtained at low resolution. This aggregation was done considering that surface fluxes can be averaged using a simple arithmetic mean. The reference dataset at low resolution was named ‘agg-ASTER’.
- In the second step, LR maps of ET were produced from the high-resolution ASTER products aggregated at the kilometric resolution (equivalent to MODIS resolution). LR RS products were used for all inputs of both models. This dataset was named ‘LR-ASTER’. ET maps at LR were evaluated against ‘agg-ASTER’ ET maps. Since both input datasets at LR and HR came from the same sensor, the biases between the two estimations of ET were only related to how the nonlinear relationships in the model translates the variability of inputs at HR into an average LR outputs that can be significantly different than the one generated using LR inputs.
- In a third step, LR maps of ET were produced from the MODIS products (surface temperature, emissivities, albedo, NDVI) at 2 km resolution, as it would be done in a standard application of SEBS and TSEB using MODIS data. These dataset (named ‘MODIS’) was evaluated against ‘agg-ASTER’ ET maps. In this case, differences between ET maps were related to a combination of the differences in products, input parameter derivations and heterogeneity/nonlinearity issues.
- In a fourth step, we analysed the possibility to derive SEBS and TSEB input parameters at low resolution by aggregating parameters estimated from high-resolution data. This scenario considered the possible use of high-resolution images in the solar domain from Earth observation satellites for deriving model inputs at the kilometric resolution. Decametric information are now increasingly available, in particular thanks to Sentinel2 satellites. We expected that this scenario would provide a deeper analysis of the potential source of biases in deriving ET and to develop more adequate aggregation rules for the relevant inputs.
4.2. Estimating Surface Parameters at HR from ASTER Products
4.3. Estimating Surface Parameters at LR from ASTER Product
4.4. Estimating Surface Parameters at LR from MODIS Product
4.5. Aggregation Rules for the Input Parameters
5. Results
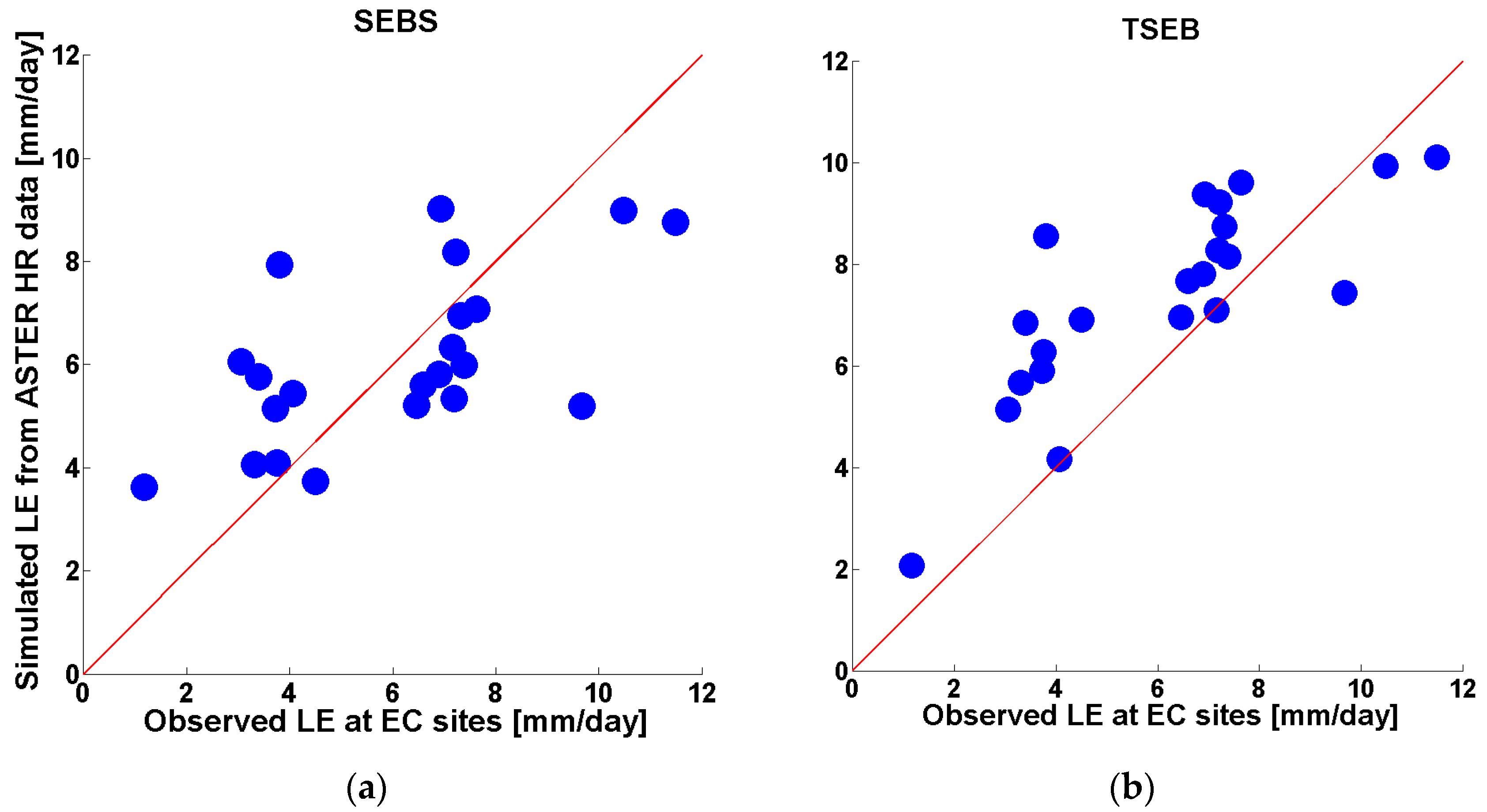
5.1. Preliminary Step: Evaluation of Flux Estimations at High Resolution from ASTER Data
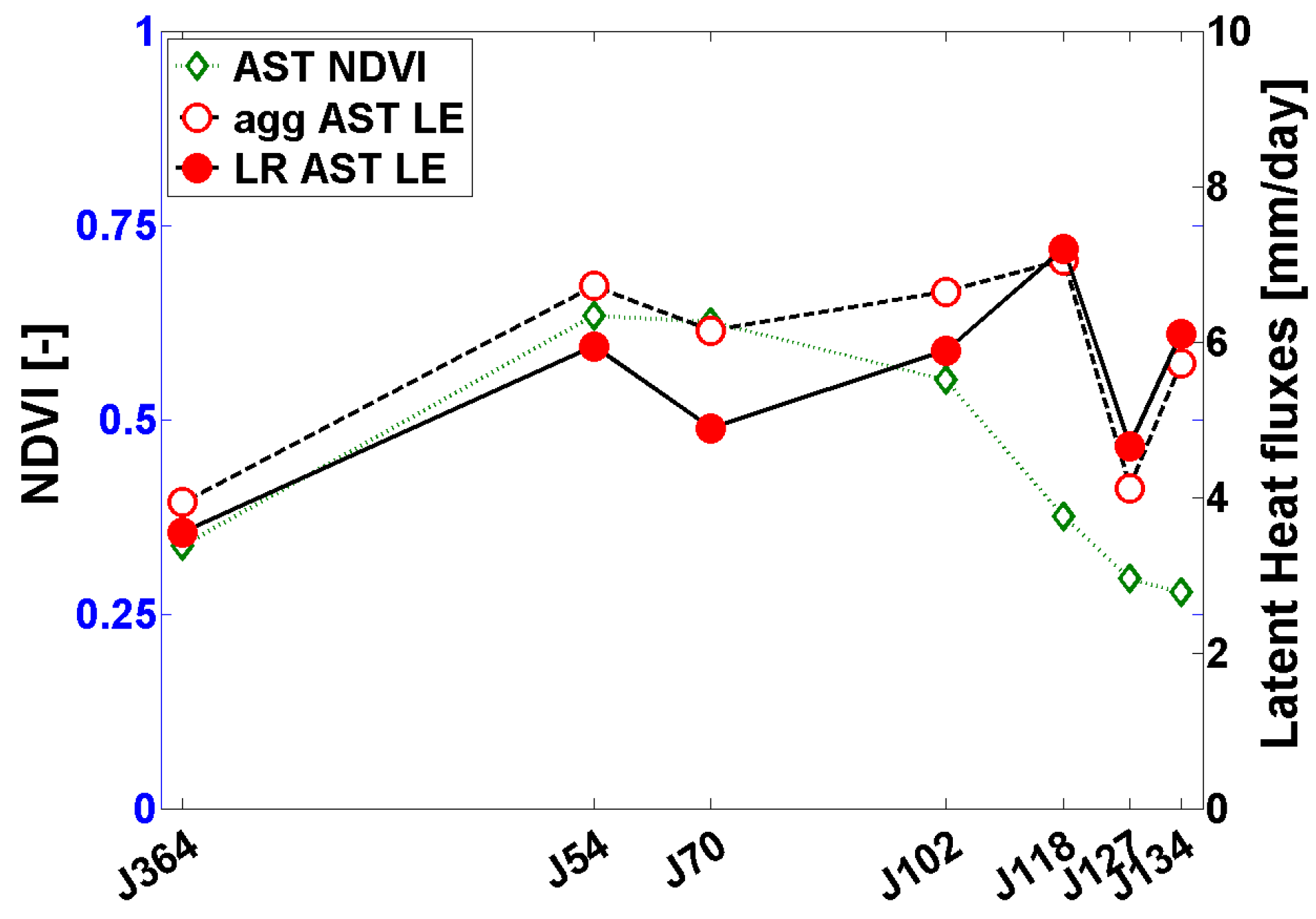
5.2. Flux Estimation at Low Resolution from ASTER LR Data and MODIS Data
5.2.1. Available Energy
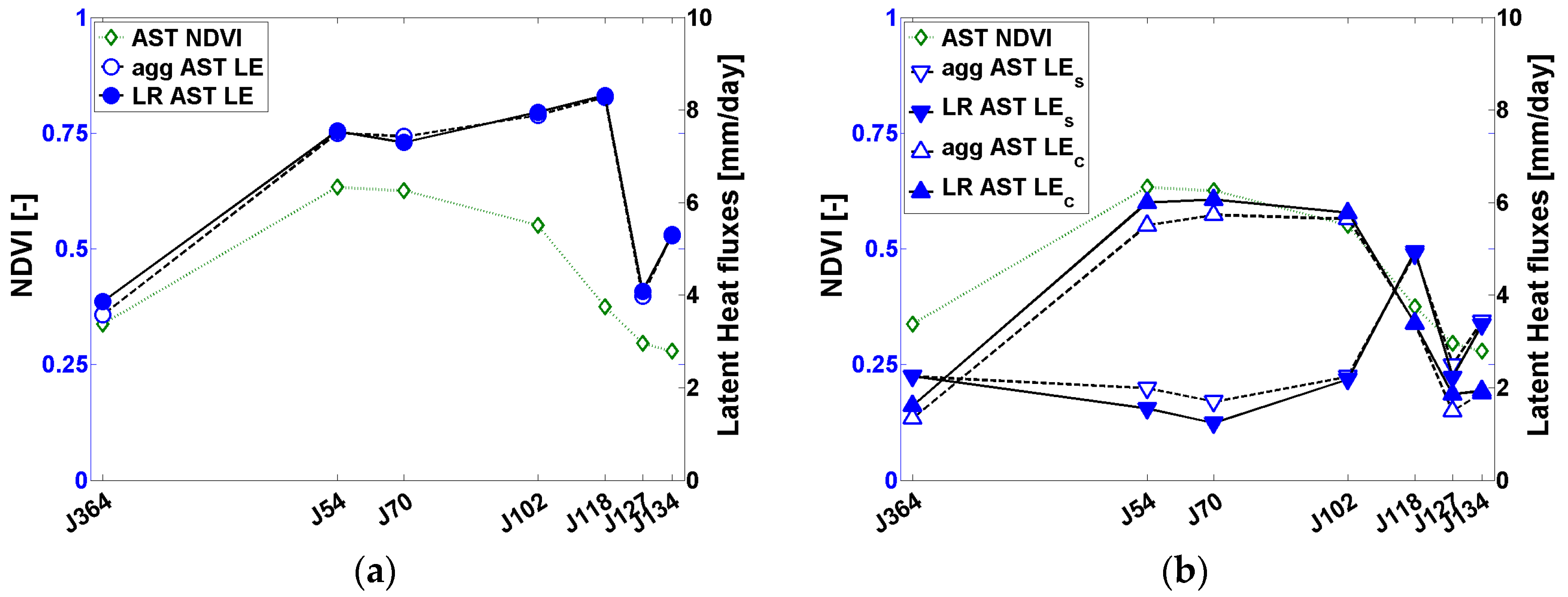
5.2.2. Estimation of ET from LR ASTER with SEBS
5.2.3. Estimation of ET from LR ASTER with TSEB
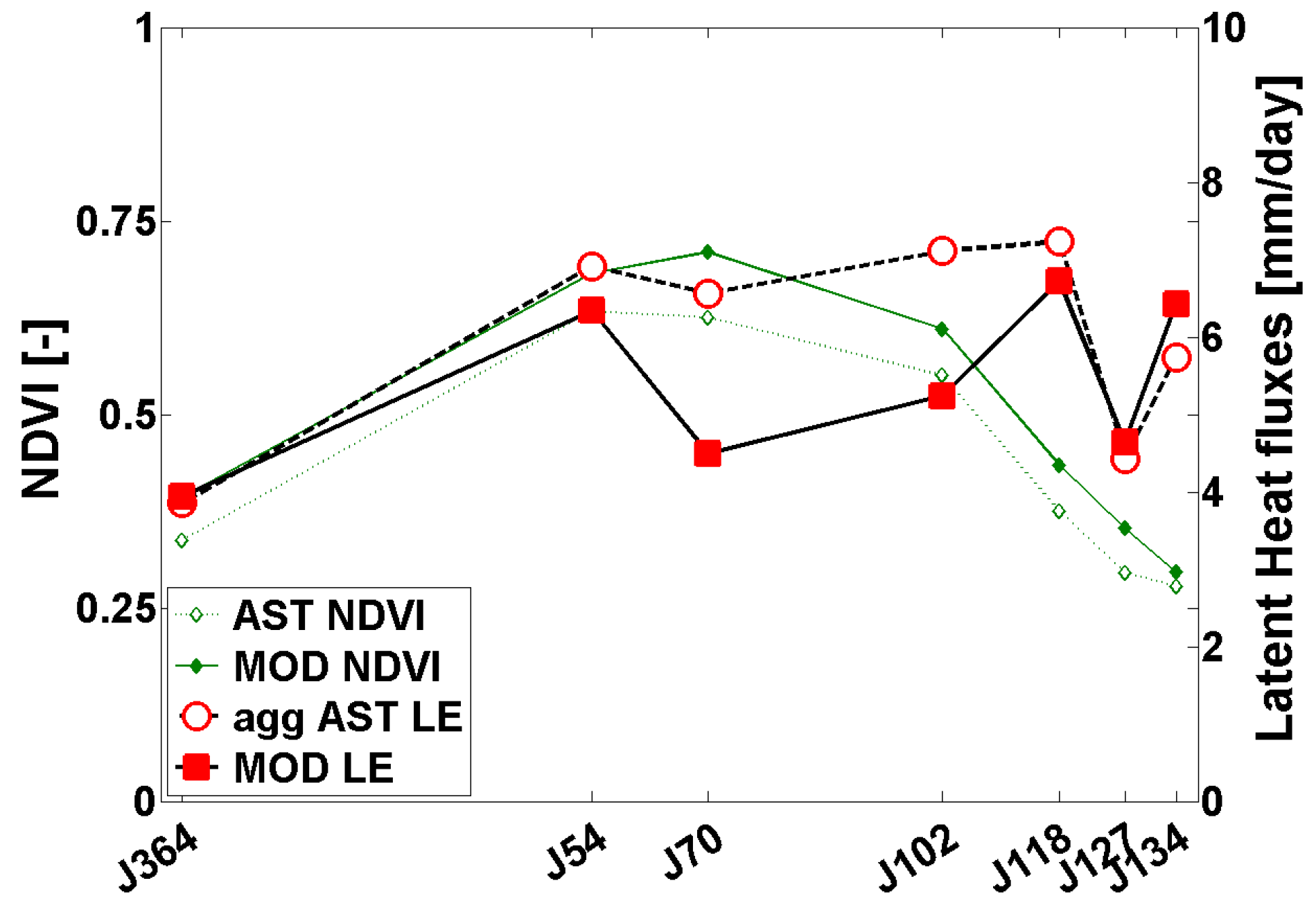
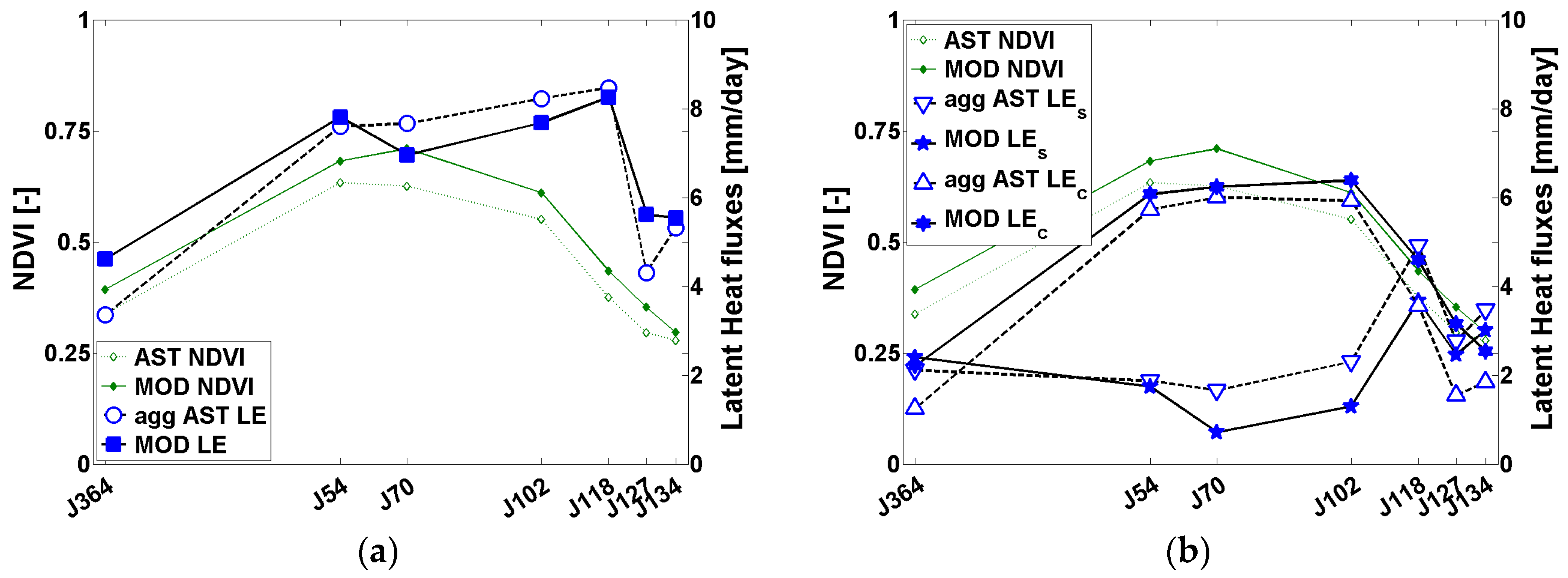
5.2.4. Estimation of ET from MODIS Data with SEBS
5.2.5. Estimation of ET from MODIS Data with TSEB
5.3. Test of Effective Roughness Length Parameterization at Low Resolution
Evaluation
6. Discussion
6.1. Discussion on Flux Estimation at Low Resolution
- TSEB had significantly higher or similar scaling performances (flux conservation across scales) as SEBS, respectively, with LR ASTER data and MODIS data;
- SEBS had similar scaling performances with LR ASTER and MODIS data;
- TSEB scaling performances were significantly lower with MODIS data than with LR ASTER data (for ET mapping as well as for ET partitioning in E and T);
- With TSEB, relative biases between the soil and the vegetation offset each other when one considers the whole season.
6.2. Discussion on the Efficiency of Aggregation Rules
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Leduc, C.; Pulido-Bosch, A.; Remini, B. Anthropization of groundwater resources in the Mediterranean region: Processes and challenges. Hydrogeol. J. 2017, 25, 1529–1547. [Google Scholar] [CrossRef]
- Saadi, S.; Simonneaux, V.; Boulet, G.; Raimbault, B.; Mougenot, B.; Fanise, P.; Ayari, H.; Lili-Chabaane, Z. Monitoring irrigation consumption using high resolution NDVI image time series: Calibration and validation in the Kairouan Plain (Tunisia). Remote Sens. 2015, 7, 13005–13028. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M.; Hain, C.R.; Mecikalski, J.R.; Schultz, L.; Gonzalez-Dugo, M.P.; Cammalleri, C.; d’Urso, G.; Pimstein, A.; et al. Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrol. Earth Syst. Sci. 2011, 15, 223–239. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S. A methodology for estimation of surface evapotranspiration over large areas using remote sensing observations. Geophys. Res. Lett. 1999, 26, 2773–2776. [Google Scholar] [CrossRef]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Roerink, G.J.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth Part B Hydrol. Oceans Atmos. 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Merlin, O.; Chirouze, J.; Olioso, A.; Jarlan, L.; Chehbouni, G.; Boulet, G. An image-based four-source surface energy balance model to estimate crop evapotranspiration from solar reflectance/thermal emission data (SEB-4S). Agric. For. Meteorol. 2014, 184, 188–203. [Google Scholar] [CrossRef]
- Tang, R.L.; Li, Z.L.; Chen, K.S.; Jia, Y.Y.; Li, C.R.; Sun, X.M. Spatial-scale effect on the SEBAL model for evapotranspiration estimation using remote sensing data. Agric. For. Meteorol. 2013, 174, 28–42. [Google Scholar] [CrossRef]
- Galleguillos, M.; Jacob, F.; Prévot, L.; French, A.; Lagacherie, P. Comparison of two temperature differencing methods to estimate daily evapotranspiration over a Mediterranean vineyard watershed from ASTER data. Remote Sens. Environ. 2011, 115, 1326–1340. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. Assessing the impact of end-member selection on the accuracy of satellite-based spatial variability models for actual evapotranspiration estimation. Water Resour. Res. 2013, 49, 2601–2618. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.Q.; Neale, C.M.U. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Gao, F.; Hain, C.R.; Kustas, W.P. Mapping daily evapotranspiration at field scales over rainfed and irrigated agricultural areas using remote sensing data fusion. Agric. For. Meteorol. 2014, 186, 1–11. [Google Scholar] [CrossRef]
- Chen, X.H.; Li, W.T.; Chen, J.; Rao, Y.H.; Yamaguchi, Y. A combination of TsHARP and thin plate spline interpolation for spatial sharpening of thermal imagery. Remote Sens. 2014, 6, 2845–2863. [Google Scholar] [CrossRef]
- Mechri, R.; Ottle, C.; Pannekoucke, O.; Kallel, A. Genetic particle filter application to land surface temperature downscaling. J. Geophys. Res. Atmos. 2014, 119, 2131–2146. [Google Scholar] [CrossRef]
- Merlin, O.; Duchemin, B.; Hagolle, O.; Jacob, F.; Coudert, B.; Chehbouni, G.; Dedieu, G.; Garatuza, J.; Kerr, Y. Disaggregation of modis surface temperature over an agricultural area using a time series of formosat-2 images. Remote Sens. Environ. 2010, 114, 2500–2512. [Google Scholar] [CrossRef]
- Zhan, W.F.; Chen, Y.H.; Zhou, J.; Wang, J.F.; Liu, W.Y.; Voogt, J.; Zhu, X.L.; Quan, J.L.; Li, J. Disaggregation of remotely sensed land surface temperature: Literature survey, taxonomy, issues, and caveats. Remote Sens. Environ. 2013, 131, 119–139. [Google Scholar] [CrossRef]
- Boulet, G.; Olioso, A.; Ceschia, E.; Marloie, O.; Coudert, B.; Rivalland, V.; Chirouze, J.; Chehbouni, G. An empirical expression to relate aerodynamic and surface temperatures for use within single-source energy balance models. Agric. For. Meteorol. 2012, 161, 148–155. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Boulet, G.; Mougenot, B.; Lhomme, J.P.; Fanise, P.; Lili-Chabaane, Z.; Olioso, A.; Bahir, M.; Rivalland, V.; Jarlan, L.; Merlin, O.; et al. The sparse model for the prediction of water stress and evapotranspiration components from thermal infra-red data and its evaluation over irrigated and rainfed wheat. Hydrol. Earth Syst. Sci. 2015, 19, 4653–4672. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Chirouze, J.; Boulet, G.; Jarlan, L.; Fieuzal, R.; Rodriguez, J.C.; Ezzahar, J.; Er-Raki, S.; Bigeard, G.; Merlin, O.; Garatuza-Payan, J.; et al. Intercomparison of four remote-sensing-based energy balance methods to retrieve surface evapotranspiration and water stress of irrigated fields in semi-arid climate. Hydrol. Earth Syst. Sci. 2014, 18, 1165–1188. [Google Scholar] [CrossRef]
- Su, Z.; Dorigo, W.; Fernández-Prieto, D.; Van Helvoirt, M.; Hungershoefer, K.; de Jeu, R.; Parinussa, R.; Timmermans, J.; Roebeling, R.; Schröder, M.; et al. Earth observation Water Cycle Multi-Mission Observation Strategy (WACMOS). Hydrol. Earth Syst. Sci. Discuss. 2010, 7, 7899–7956. [Google Scholar] [CrossRef]
- Jia, L.; Su, Z.B.; van den Hurk, B.; Menenti, M.; Moene, A.; De Bruin, H.A.R.; Yrisarry, J.J.B.; Ibanez, M.; Cuesta, A. Estimation of sensible heat flux using the Surface Energy Balance System (SEBS) and ATSR measurements. Phys. Chem. Earth 2003, 28, 75–88. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, S.; Xu, Z.; Chen, Y.; Zhu, M. Validation of remotely sensed evapotranspiration over the Hai River Basin, China. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Kleissl, J.; Hong, S.H.; Hendrickx, J.M.H. New Mexico scintillometer network supporting remote sensing and hydrologic and meteorological models. Bull. Am. Meteorol. Soc. 2009, 90, 207–218. [Google Scholar] [CrossRef]
- Tang, R.L.; Li, Z.L.; Jia, Y.Y.; Li, C.R.; Sun, X.M.; Kustas, W.P.; Anderson, M.C. An intercomparison of three remote sensing-based energy balance models using large aperture scintillometer measurements over a wheat-corn production region. Remote Sens. Environ. 2011, 115, 3187–3202. [Google Scholar] [CrossRef]
- Corbari, C.; Mancini, M.; Su, Z.; Li, J. Evapotranspiration estimate from water balance closure using satellite data for the Upper Yangtze River basin. Hydrol. Res. 2014, 45, 603–614. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Su, H.; Wood, E.F.; McCabe, M.F.; Su, Z. Evaluation of remotely sensed evapotranspiration over the CEOP eop-1 reference sites. J. Meteorol. Soc. Jpn. 2007, 85A, 439–459. [Google Scholar] [CrossRef]
- Su, H.B.; McCabe, M.F.; Wood, E.F.; Su, Z.; Prueger, J.H. Modeling evapotranspiration during SMACEX: Comparing two approaches for local- and regional-scale prediction. J. Hydrometeorol. 2005, 6, 910–922. [Google Scholar] [CrossRef]
- Verstraeten, W.W.; Veroustraete, F.; Feyen, J. Estimating evapotranspiration of European forests from NOAA-imagery at satellite overpass time: Towards an operational processing chain for integrated optical and thermal sensor data products. Remote Sens. Environ. 2005, 96, 256–276. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Allard, D.; Garrigue, S.; Leroy, M.; Jeanjean, H.; Fernandes, R.; Myneni, R.B.; Privette, J.; Morisette, J.; et al. Valeri: A network of sites and a methodology for the validation of medium spatial resolution land satellite products. Remote Sens. Environ. 2013, 76, 36–39. [Google Scholar]
- Mira, M.; Weiss, M.; Baret, F.; Courault, D.; Hagolle, O.; Gallego-Elvira, B.; Olioso, A. The MODIS (collection V006) BRDF/albedo product MCD43D: Temporal course evaluated over agricultural landscape. Remote Sens. Environ. 2015, 170, 216–228. [Google Scholar] [CrossRef]
- Etchanchu, J.; Rivalland, V.; Gascoin, S.; Cros, J.; Brut, A.; Boulet, G. Effects of multi-temporal high-resolution remote sensing products on simulated hydrometeorological variables in a cultivated area (southwestern France). Hydrol. Earth Syst. Sci. Discuss. 2017, 2017, 1–23. [Google Scholar] [CrossRef]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ. 2006, 105, 271–285. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Walker, J.P. Effects of spatial aggregation on the multi-scale estimation of evapotranspiration. Remote Sens. Environ. 2013, 131, 51–62. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluating the effects of subpixel heterogeneity on pixel average fluxes. Remote Sens. Environ. 2000, 74, 327–342. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M.; Shmugge, T.J.; Anderson, M.C. Mapping surface energy fluxes with radiometric temperature. In Thermal Remote Sensing in Land Surface Processes; CRC Press: Boca Raton, FL, USA, 2004; pp. 205–253. [Google Scholar]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Chehbouni, A.; Njoku, E.G.; Lhomme, J.P.; Kerr, Y.H. Approaches for averaging surface parameters and fluxes over heterogeneous terrain. J. Clim. 1995, 8, 1386–1393. [Google Scholar] [CrossRef]
- Kim, C.P.; Stricker, J.N.M.; Feddes, R.A. Impact of soil heterogeneity on the water budget of the unsaturated zone. Water Resour. Res. 1997, 33, 991–999. [Google Scholar] [CrossRef]
- Wassenaar, T.; Olioso, A.; Hasager, C.; Jacob, F.; Chehbouni, A. Estimation of evapotranspiration on heterogeneous pixels. In Proceedings of the First International Symposium on Recent Advances in Quantitative Remote Sensing, Valencia, Spain, 16–20 September 2002; Sobrino, J.A., Ed.; Publicacions de la Universitat de València: Valencia, Spain, 2002; pp. 458–465. [Google Scholar]
- Taylor, P.A. Comments and further analysis on effective roughness lengths for use in numerical 3-dimensional models. Bound.-Layer Meteorol. 1987, 39, 403–418. [Google Scholar] [CrossRef]
- Byun, K.; Liaqat, U.W.; Choi, M. Dual-model approaches for evapotranspiration analyses over homo- and heterogeneous land surface conditions. Agric. For. Meteorol. 2014, 197, 169–187. [Google Scholar] [CrossRef]
- Choi, M.; Kustas, W.P.; Anderson, M.C.; Allen, R.G.; Li, F.Q.; Kjaersgaard, J.H. An intercomparison of three remote sensing-based surface energy balance algorithms over a corn and soybean production region (Iowa, US) during SMACEX. Agric. For. Meteorol. 2009, 149, 2082–2097. [Google Scholar] [CrossRef]
- Hasager, C.B.; Jensen, N.O.; Olioso, A. Land cover, surface temperature and leaf area index maps from satellites used for the aggregation of momentum and temperature roughnesses. In Proceedings of the First International Symposium on Recent Advances in Quantitative Remote Sensing, Valencia, Spain, 16–20 September 2002; pp. 466–473. [Google Scholar]
- Michel, D.; Jiménez, C.; Miralles, D.G.; Jung, M.; Hirschi, M.; Ershadi, A.; Martens, B.; McCabe, M.F.; Fisher, J.B.; Mu, Q.; et al. The WACMOS-ET project—Part 1: Tower-scale evaluation of four remote-sensing-based evapotranspiration algorithms. Hydrol. Earth Syst. Sci. 2016, 20, 803–822. [Google Scholar] [CrossRef]
- Jacob, F.; Olioso, A.; Gu, X.F.; Su, Z.B.; Seguin, B. Mapping surface fluxes using airborne visible, near infrared, thermal infrared remote sensing data and a spatialized surface energy balance model. Agronomie 2002, 22, 669–680. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Li, F.; Prueger, J.H.; Mecikalski, J.R. Effects of vegetation clumping on two-source model estimates of surface energy fluxes from an agricultural landscape during SMACEX. J. Hydrometeorol. 2005, 6, 892–909. [Google Scholar] [CrossRef]
- Timmermans, W.J.; van der Kwast, J.; Gieske, A.S.M.; Su, Z.; Olioso, A.; Jia, L.; Elbers, J. Intercomparison of energy flux models using ASTER imagery at the SPARC 2004 site (Barrax, Spain). In Proceedings of the SPARC Final Workshop, Enschede, The Netherlands, 4–5 July 2005; p. 8. [Google Scholar]
- French, A.N.; Jacob, F.; Anderson, M.C.; Kustas, W.P.; Timmermans, W.; Gieske, A.; Su, Z.; Su, H.; McCabe, M.F.; Li, F.; et al. Surface energy fluxes with the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) at the Iowa 2002 SMACEX site (USA). Remote Sens. Environ. 2005, 99, 55–65. [Google Scholar] [CrossRef]
- Van der Kwast, J.; Timmermans, W.; Gieske, A.; Su, Z.; Olioso, A.; Jia, L.; Elbers, J.; Karssenberg, D.; de Jong, S. Evaluation of the Surface Energy Balance System (SEBS) applied to ASTER imagery with flux-measurements at the SPARC 2004 site (Barrax, Spain). Hydrol. Earth Syst. Sci. 2009, 13, 1337–1347. [Google Scholar] [CrossRef]
- Delogu, E.; Boulet, G.; Olioso, A.; Coudert, B.; Chirouze, J.; Ceschia, E.; Le Dantec, V.; Marloie, O.; Chehbouni, G.; Lagouarde, J.P. Reconstruction of temporal variations of evapotranspiration using instantaneous estimates at the time of satellite overpass. Hydrol. Earth Syst. Sci. 2012, 16, 2995–3010. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. Fluxnet: A new tool to study the temporal and spatial variability of ecosystem–scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Brutsaert, W. Aspects of bulk atmospheric boundary layer similarity under free-convective conditions. Rev. Geophys. 1999, 37, 439–451. [Google Scholar] [CrossRef]
- Su, Z.; Schmugge, T.; Kustas, W.P.; Massman, W.J. An evaluation of two models for estimation of the roughness height for heat transfer between the land surface and the atmosphere. J. Appl. Meteorol. 2001, 40, 1933–1951. [Google Scholar] [CrossRef]
- Gomez, M.; Olioso, A.; Sobrino, J.A.; Jacob, F. Retrieval of evapotranspiration over the Alpilles/ReSeDA experimental site using airborne POLDER sensor and a thermal camera. Remote Sens. Environ. 2005, 96, 399–408. [Google Scholar] [CrossRef]
- Liang, S.L. Narrowband to broadband conversions of land surface albedo I algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Ogawa, K.; Schmugge, T.; Rokugawa, S. Estimating broadband emissivity of arid regions and its seasonal variations using thermal infrared remote sensing. IEEE Trans. Geosci. Remote Sens. 2008, 46, 334–343. [Google Scholar] [CrossRef]
- Fieuzal, R.; Duchemin, B.; Jarlan, L.; Zribi, M.; Baup, F.; Merlin, O.; Hagolle, O.; Garatuza-Payan, J. Combined use of optical and radar satellite data for the monitoring of irrigation and soil moisture of wheat crops. Hydrol. Earth Syst. Sci. 2011, 15, 1117–1129. [Google Scholar] [CrossRef]
- Lewis, P.; Barnsley, M.J. Influence of the sky radiance distribution on various formulations of the earth surface albedo. In Proceedings of the 6th International Symposium on Physical Measurements and Signatures in Remote Sensing, Val d’Isere, France, 17–21 January 1994; pp. 707–716. [Google Scholar]
- Lucht, W.; Schaaf, C.B.; Strahler, A.H. An algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Trans. Geosci. Remote Sens. 2000, 38, 977–998. [Google Scholar] [CrossRef]
- Liang, S. An optimization algorithm for separating land surface temperature and emissivity from multispectral thermal infrared imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 264–274. [Google Scholar] [CrossRef]
- Bouguerzaz, F.A.; Olioso, A.; Raffy, M. Modelling radiative and energy balance on heterogeneous areas from remotely-sensed radiances. Can. J. Remote Sens. 1999, 25, 412–424. [Google Scholar] [CrossRef]
- Boulet, G.; Kalma, J.D.; Braud, I.; Vauclin, M. An assessment of effective land surface parameterisation in regional-scale water balance studies. J. Hydrol. 1999, 217, 225–238. [Google Scholar] [CrossRef]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]

| Sensor | Products | Frequency | Resolution [m] | Bands/Product/Subdatasets |
|---|---|---|---|---|
| ASTER | AST07XT—VNIR | 16 days | 15 | Band1 |
| Band2 | ||||
| Band3N | ||||
| AST07XT—SWIR | 30 | Band4 | ||
| Band5 | ||||
| Band6 | ||||
| Band7 | ||||
| Band8 | ||||
| Band9 | ||||
| AST05 | 90 | Surface emissivity [-] | ||
| AST08 | 90 | Surface temperature [°K] | ||
| MODIS | MOD11A1 | Daily | ~1000 | Surface temperature [°K] |
| Emissivity Band31 | ||||
| Emissivity Band32 | ||||
| QC_Day (Quality control) | ||||
| MOD13A2 | 16 days | ~1000 | NDVI | |
| VI Quality QA (Quality control) | ||||
| MOD15A2 | 8 days | ~1000 | Lai_1 km | |
| FparLai_QC (Quality control) | ||||
| MCD43B3 | 16 days | ~1000 | Black Sky Albedo SW | |
| White Sky Albedo SW |
| Date | —RS | —agg lin | —agg geo | —agg har | —grad |
|---|---|---|---|---|---|
| Relative bias [–] | |||||
| 30/12/2007 (J364) | −0.10 | −0.10 | −0.06 | 0.05 | −0.15 |
| 23/02/2008 (J54) | −0.11 | −0.09 | −0.05 | 0.00 | −0.07 |
| 10/03/2008 (J70) | −0.20 | −0.15 | −0.09 | 0.00 | −0.17 |
| 11/04/2008 (J102) | −0.11 | −0.09 | −0.07 | −0.01 | −0.08 |
| 27/04/2008 (J118) | 0.02 | 0.00 | 0.01 | 0.05 | 0.00 |
| 06/05/2008 (J127) | 0.13 | −0.10 | −0.08 | 0.10 | −0.02 |
| 13/05/2008 (J134) | 0.07 | −0.07 | −0.06 | 0.06 | −0.10 |
| Seasonal | −0.05 | −0.08 | −0.05 | 0.03 | −0.08 |
| RMSE [mm/day] | |||||
| 30/12/2007 (J364) | 0.74 | 0.62 | 0.44 | 0.36 | 1.09 |
| 23/02/2008 (J54) | 1.49 | 1.08 | 0.88 | 0.70 | 1.34 |
| 10/03/2008 (J70) | 1.48 | 1.11 | 0.76 | 0.57 | 1.61 |
| 11/04/2008 (J102) | 1.01 | 0.75 | 0.56 | 0.34 | 1.03 |
| 27/04/2008 (J118) | 0.48 | 0.33 | 0.28 | 0.42 | 0.45 |
| 06/05/2008 (J127) | 1.12 | 0.60 | 0.55 | 0.65 | 1.26 |
| 13/05/2008 (J134) | 0.79 | 0.54 | 0.55 | 0.47 | 1.27 |
| Seasonal | 1.08 | 0.77 | 0.60 | 0.52 | 1.20 |
| Date | —RS | —Agg Lin | —Agg Geo | —Agg Harmonic | —Grad |
|---|---|---|---|---|---|
| Relative bias [-] | |||||
| 30/12/2007 (J364) | 0.02 | 0.12 | 0.18 | 0.18 | 0.07 |
| 23/02/2008 (J54) | −0.08 | 0.02 | 0.05 | −0.02 | −0.04 |
| 10/03/2008 (J70) | −0.32 | −0.12 | −0.08 | −0.16 | −0.19 |
| 11/04/2008 (J102) | −0.26 | −0.21 | −0.18 | −0.14 | −0.17 |
| 27/04/2008 (J118) | −0.07 | −0.13 | −0.11 | −0.01 | −0.03 |
| 06/05/2008 (J127) | 0.05 | −0.24 | −0.11 | 0.11 | 0.09 |
| 13/05/2008 (J134) | 0.12 | −0.03 | 0.03 | 0.04 | −0.02 |
| Seasonal | −0.10 | −0.09 | −0.04 | −0.02 | −0.06 |
| RMSE [mm/day] | |||||
| 30/12/2007 (J364) | 0.35 | 0.65 | 0.73 | 0.70 | 0.35 |
| 23/02/2008 (J54) | 0.65 | 0.47 | 0.53 | 0.48 | 0.56 |
| 10/03/2008 (J70) | 2.13 | 0.84 | 0.59 | 1.21 | 1.36 |
| 11/04/2008 (J102) | 2.04 | 1.68 | 1.42 | 1.20 | 1.40 |
| 27/04/2008 (J118) | 0.62 | 1.08 | 0.89 | 0.28 | 0.30 |
| 06/05/2008 (J127) | 0.69 | 1.39 | 1.04 | 0.62 | 0.53 |
| 13/05/2008 (J134) | 0.74 | 0.40 | 0.27 | 0.44 | 0.68 |
| Seasonal | 1.23 | 1.03 | 0.86 | 0.78 | 0.85 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahir, M.; Boulet, G.; Olioso, A.; Rivalland, V.; Gallego-Elvira, B.; Mira, M.; Rodriguez, J.-C.; Jarlan, L.; Merlin, O. Evaluation and Aggregation Properties of Thermal Infra-Red-Based Evapotranspiration Algorithms from 100 m to the km Scale over a Semi-Arid Irrigated Agricultural Area. Remote Sens. 2017, 9, 1178. https://doi.org/10.3390/rs9111178
Bahir M, Boulet G, Olioso A, Rivalland V, Gallego-Elvira B, Mira M, Rodriguez J-C, Jarlan L, Merlin O. Evaluation and Aggregation Properties of Thermal Infra-Red-Based Evapotranspiration Algorithms from 100 m to the km Scale over a Semi-Arid Irrigated Agricultural Area. Remote Sensing. 2017; 9(11):1178. https://doi.org/10.3390/rs9111178
Chicago/Turabian StyleBahir, Malik, Gilles Boulet, Albert Olioso, Vincent Rivalland, Belen Gallego-Elvira, Maria Mira, Julio-Cesar Rodriguez, Lionel Jarlan, and Olivier Merlin. 2017. "Evaluation and Aggregation Properties of Thermal Infra-Red-Based Evapotranspiration Algorithms from 100 m to the km Scale over a Semi-Arid Irrigated Agricultural Area" Remote Sensing 9, no. 11: 1178. https://doi.org/10.3390/rs9111178
APA StyleBahir, M., Boulet, G., Olioso, A., Rivalland, V., Gallego-Elvira, B., Mira, M., Rodriguez, J.-C., Jarlan, L., & Merlin, O. (2017). Evaluation and Aggregation Properties of Thermal Infra-Red-Based Evapotranspiration Algorithms from 100 m to the km Scale over a Semi-Arid Irrigated Agricultural Area. Remote Sensing, 9(11), 1178. https://doi.org/10.3390/rs9111178









