A New Method to Map Groundwater Table in Peatlands Using Unmanned Aerial Vehicles
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sets
2.2.1. Remote Sensing Data
2.2.2. Groundwater Measurements
2.2.3. Ground Control Points
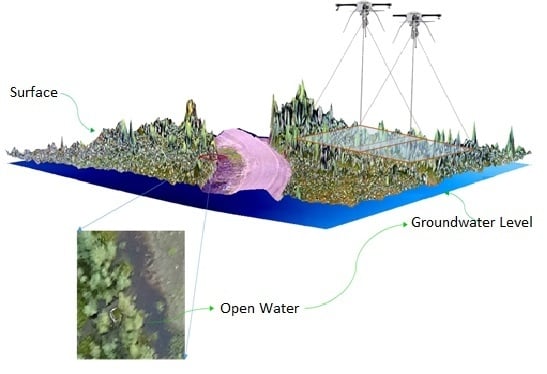
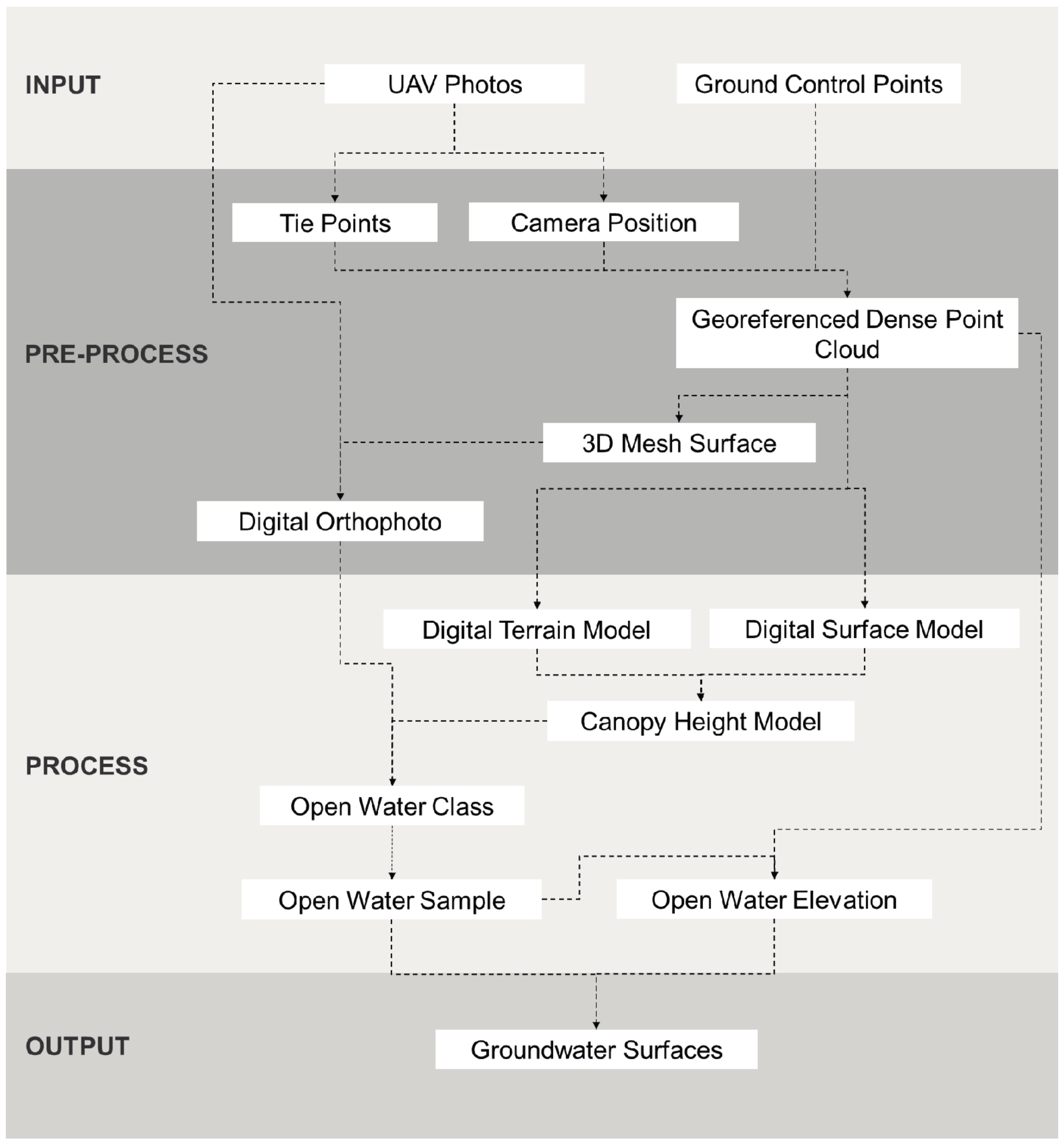
2.3. Workflow
2.3.1. Pre-Processing
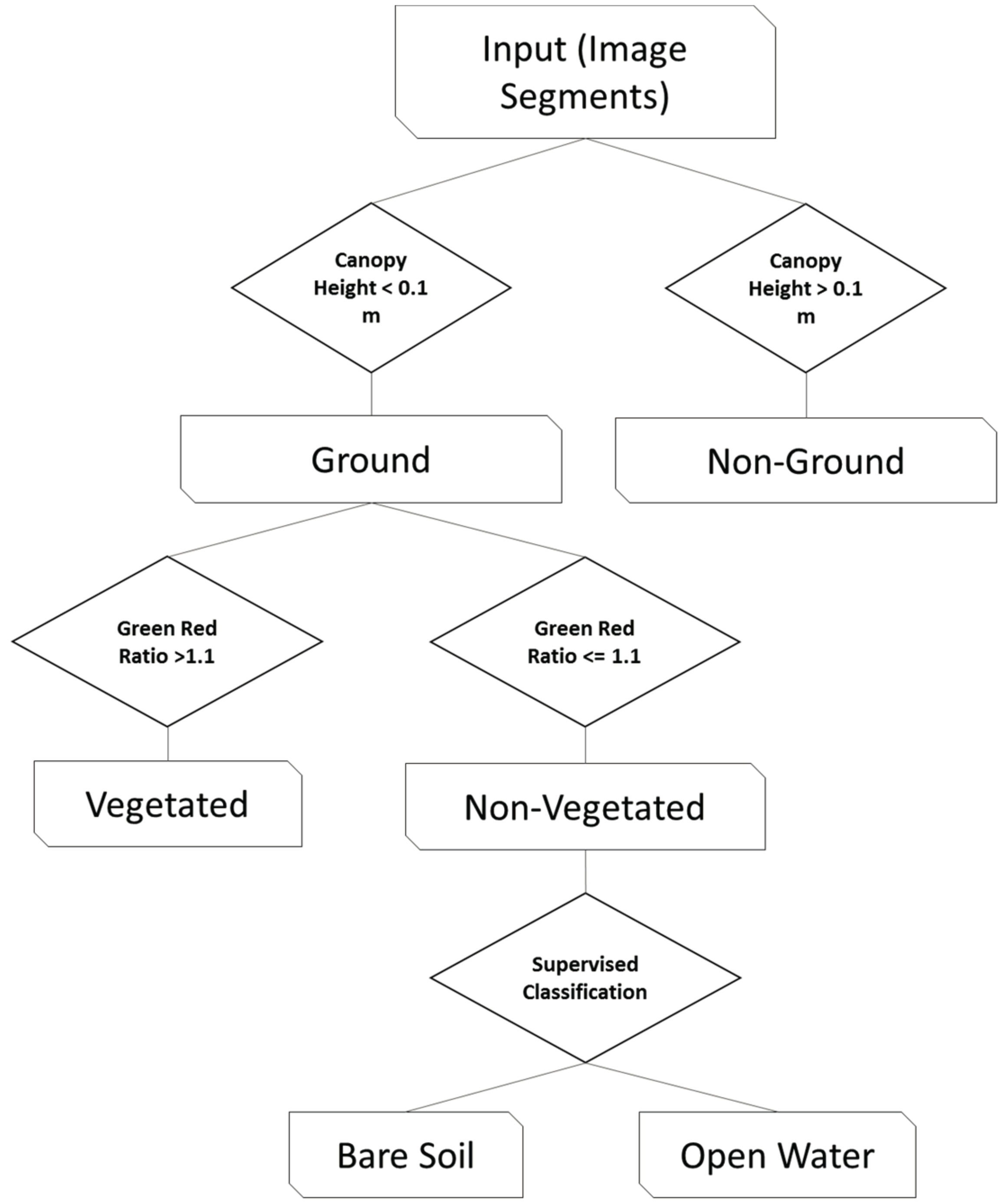
2.3.2. Extracting Open Water
2.3.3. Sampling Open Water
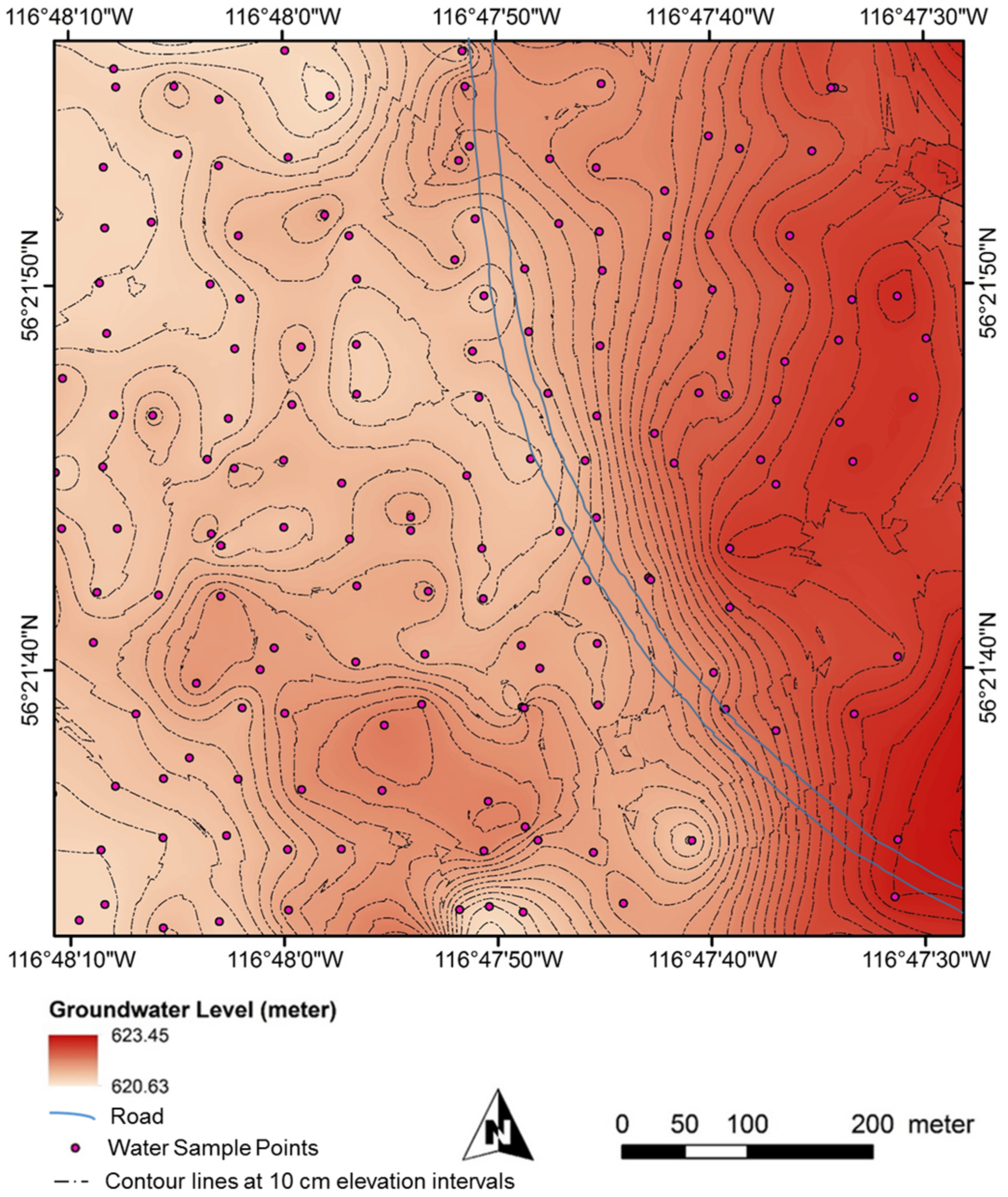
2.3.4. Creating Ground-Water-Level and Depth-to-Water Surfaces
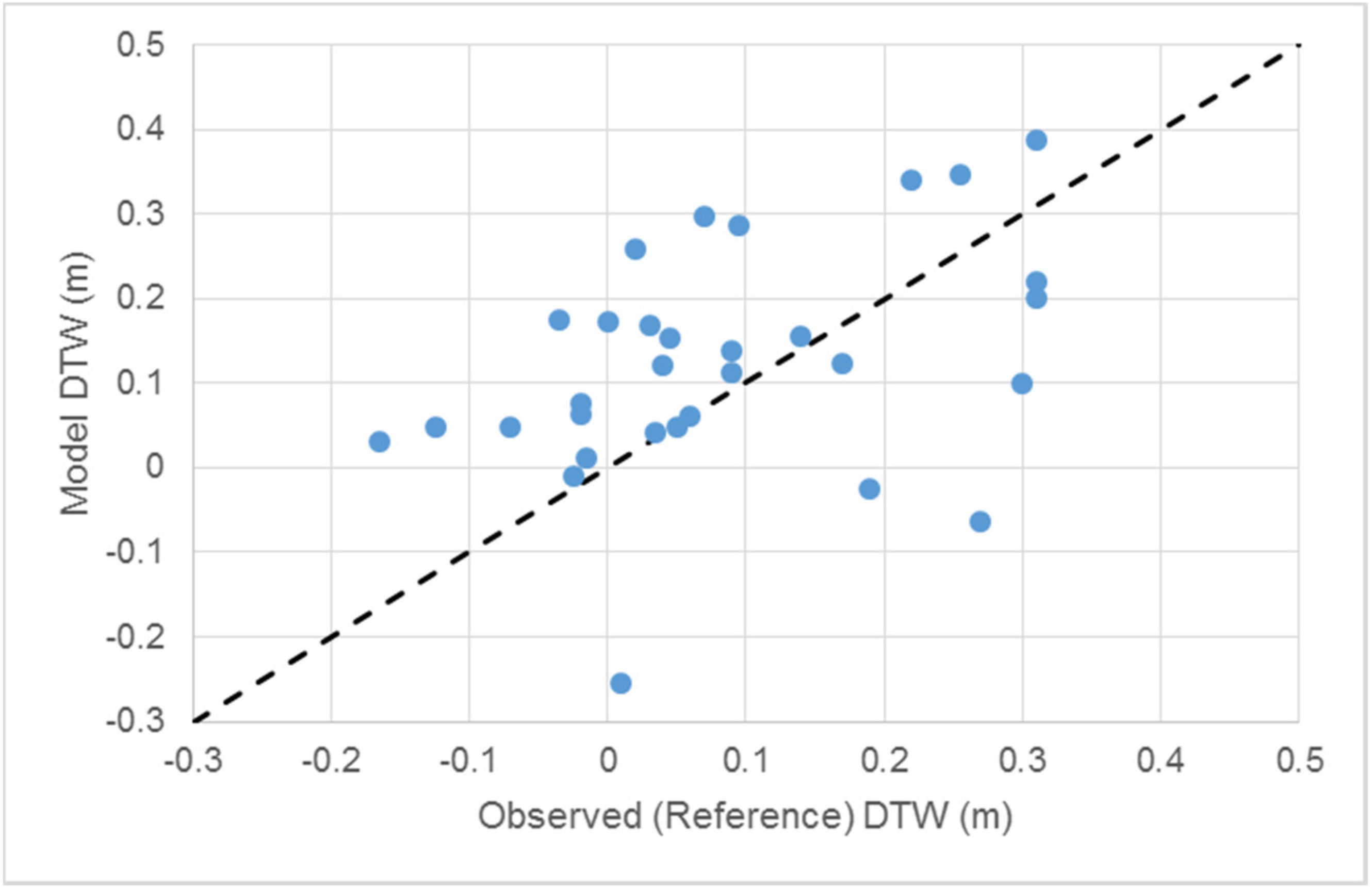
2.4. Validation
3. Results
Spatial Distribution of Model Errors
4. Discussion
- (i)
- Our method does not require any field measurements to be able to generate groundwater surfaces,
- (ii)
- If available, a large number of reference points can be used in the interpolation process that can lead to more accurate estimates, and
- (iii)
- When compared to ground-based measurements, our workflow can be scaled across much larger study areas.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wieder, R.K.; Vitt, D.H. (Eds.) Boreal Peatland Ecosystems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 188, pp. 1–2. [Google Scholar]
- Tarnocai, C.; Kettles, I.M.; Lacelle, B. Peatlands of Canada; Open File 6561 (Digital Database), CD-ROM; Geological Survey of Canada: Ottawa, ON, Canada, 2011.
- Posa, M.R.; Wijedasa, L.S.; Corlett, R.T. Biodiversity and conservation of tropical peat swamp forests. BioScience 2011, 61, 49–57. [Google Scholar] [CrossRef]
- Harris, A.; Bryant, R.G. A multi-scale remote sensing approach for monitoring northern peatland hydrology: Present possibilities and future challenges. J. Environ. Manag. 2009, 90, 2178–2188. [Google Scholar] [CrossRef] [PubMed]
- Dinsmore, K.J.; Skiba, U.M.; Billett, M.F.; Rees, R.M. Effect of water table on greenhouse gas emissions from peatland mesocosms. Plant Soil 2009, 318, 229. [Google Scholar] [CrossRef]
- Jungkunst, H.F.; Flessa, H.; Scherber, C.; Fiedler, S. Groundwater level controls CO2, N2O and CH4 fluxes of three different hydromorphic soil types of a temperate forest ecosystem. Soil Biol. Biochem. 2008, 40, 2047–2054. [Google Scholar] [CrossRef]
- Frolking, S.; Roulet, N.T.; Moore, T.R.; Lafleur, P.M.; Bubier, J.L.; Crill, P.M. Modeling seasonal to annual carbon balance of Mer Bleue Bog, Ontario, Canada. Glob. Biogeochem. Cycles 2002, 16, 4-1–4-21. [Google Scholar] [CrossRef]
- Vazquez-Amabile, G.G.; Engel, B.A. Use of SWAT to compute groundwater table depth and streamflow in the Muscatatuck River watershed. Trans. ASAE 2005, 48, 991–1003. [Google Scholar] [CrossRef]
- Lee, D.R.; Cherry, J.A. A field exercise on groundwater flow using seepage meters and mini-piezometers. J. Geol. Educ. 1979, 27, 6–10. [Google Scholar] [CrossRef]
- Jha, M.K.; Chowdary, V.M.; Chowdhury, A. Groundwater assessment in Salboni Block, West Bengal (India) using remote sensing, geographical information system and multi-criteria decision analysis techniques. Hydrogeol. J. 2010, 18, 1713–1728. [Google Scholar] [CrossRef]
- Walter, B.P.; Heimann, M.; Matthews, E. Modeling modern methane emissions from natural wetlands: 1. Model description and results. J. Geophys. Res. Atmos. 2001, 106, 34189–34206. [Google Scholar] [CrossRef]
- Brunner, P.; Franssen, H.J.; Kgotlhang, L.; Bauer-Gottwein, P.; Kinzelbach, W. How can remote sensing contribute in groundwater modeling? Hydrogeol. J. 2007, 15, 5–18. [Google Scholar] [CrossRef]
- Waters, P.; Greenbaum, D.; Smart, P.L.; Osmaston, H. Applications of remote sensing to groundwater hydrology. Remote Sens. Rev. 1990, 4, 223–264. [Google Scholar] [CrossRef]
- Meingast, K.M.; Falkowski, M.J.; Kane, E.S.; Potvin, L.R.; Benscoter, B.W.; Smith, A.M.; Bourgeau-Chavez, L.L.; Miller, M.E. Spectral detection of near-surface moisture content and water-table position in northern peatland ecosystems. Remote Sens. Environ. 2014, 152, 536–546. [Google Scholar] [CrossRef]
- Takada, M.; Mishima, Y.; Natsume, S. Estimation of surface soil properties in peatland using ALOS/PALSAR. Landsc. Ecol. Eng. 2009, 5, 45–58. [Google Scholar] [CrossRef]
- Zhang, Y.; Wegehenkel, M. Integration of MODIS data into a simple model for the spatial distributed simulation of soil water content and evapotranspiration. Remote Sens. Environ. 2006, 104, 393–408. [Google Scholar] [CrossRef]
- Stromberg, J.C.; Tiller, R.; Richter, B. Effects of groundwater decline on riparian vegetation of semiarid regions: the San Pedro, Arizona. Ecol. Appl. 1996, 6, 113–131. [Google Scholar] [CrossRef]
- Harris, A.; Bryant, R.G.; Baird, A.J. Detecting near-surface moisture stress in Sphagnum spp. Remote Sens. Environ. 2005, 97, 371–381. [Google Scholar] [CrossRef]
- Lovitt, J.; Rahman, M.M.; McDermid, G.J. Assessing the Value of UAV Photogrammetry for Characterizing Terrain in Complex Peatlands. Remote Sens. 2017, 9, 715. [Google Scholar]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Ingram, H.A. Size and shape in raised mire ecosystems: A geophysical model. Nature 1982, 297, 300–303. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–5. [Google Scholar] [CrossRef]
- Rosnell, T.; Honkavaara, E. Point cloud generation from aerial image data acquired by a quadrocopter type micro unmanned aerial vehicle and a digital still camera. Sensors 2012, 12, 453–480. [Google Scholar] [CrossRef] [PubMed]
- Niethammer, U.; James, M.R.; Rothmund, S.; Travelletti, J.; Joswig, M. UAV-based remote sensing of the Super-Sauze landslide: Evaluation and results. Eng. Geol. 2012, 128, 2–11. [Google Scholar] [CrossRef]
- Remondino, F.; Barazzetti, L.; Nex, F.; Scaioni, M.; Sarazzi, D. UAV photogrammetry for mapping and 3d modeling–current status and future perspectives. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, C22. [Google Scholar] [CrossRef]
- Hugenholtz, C.H.; Whitehead, K.; Brown, O.W.; Barchyn, T.E.; Moorman, B.J.; LeClair, A.; Riddell, K.; Hamilton, T. Geomorphological mapping with a small unmanned aircraft system (sUAS): Feature detection and accuracy assessment of a photogrammetrically-derived digital terrain model. Geomorphology 2013, 194, 16–24. [Google Scholar] [CrossRef]
- Woodget, A.S.; Carbonneau, P.E.; Visser, F.; Maddock, I.P. Quantifying submerged fluvial topography using hyperspatial resolution UAS imagery and structure from motion photogrammetry. Earth Surf. Process. Landf. 2015, 40, 47–64. [Google Scholar] [CrossRef]
- Vitt, D.H.; Halsey, L.A.; Bauer, I.E.; Campbell, C. Spatial and temporal trends in carbon storage of peatlands of continental western Canada through the Holocene. Can. J. Earth Sci. 2000, 37, 683–693. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Jaud, M.; Passot, S.; LeBivic, R.; Delacourt, C.; Grandjean, P.; Le Dantec, N. Assessing the Accuracy of High Resolution Digital Surface Models Computed by PhotoScan® and MicMac® in Sub-Optimal Survey Conditions. Remote Sens. 2016, 8, 465. [Google Scholar] [CrossRef]
- Benassi, F.; Dall’Asta, E.; Diotri, F.; Forlani, G.; Di Cella, U.M.; Roncella, R.; Santise, M. Testing accuracy and repeatability of UAV blocks oriented with GNSS-supported aerial triangulation. Remote Sens. 2017, 9, 172. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; Van der Meer, F.; Van der Werff, H.; Van Coillie, F.; et al. Geographic object-based image analysis–towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.M.; Hay, G.J.; Couloigner, I.; Hemachandran, B. Transforming Image-Objects into Multiscale Fields: A GEOBIA Approach to Mitigate Urban Microclimatic Variability within H-Res Thermal Infrared Airborne Flight-Lines. Remote Sens. 2014, 6, 9435–9457. [Google Scholar] [CrossRef]
- Gnanachandrasamy, G.; Ramkumar, T.; Venkatramanan, S.; Vasudevan, S.; Chung, S.Y.; Bagyaraj, M. Accessing groundwater quality in lower part of Nagapattinam district, Southern India: Using hydrogeochemistry and GIS interpolation techniques. Appl. Water Sci. 2015, 5, 39–55. [Google Scholar] [CrossRef]
- Selvam, S.; Manimaran, G.; Sivasubramanian, P.; Balasubramanian, N.; Seshunarayana, T. GIS-based evaluation of water quality index of groundwater resources around Tuticorin coastal city, South India. Environ. Earth Sci. 2014, 71, 2847–2867. [Google Scholar] [CrossRef]
- Yao, L.; Huo, Z.; Feng, S.; Mao, X.; Kang, S.; Chen, J.; Xu, J.; Steenhuis, T.S. Evaluation of spatial interpolation methods for groundwater level in an arid inland oasis, northwest China. Environ. Earth Sci. 2014, 71, 1911–1924. [Google Scholar] [CrossRef]
- Laaha, G.; Skoien, J.O.; Bloschl, G. Spatial prediction on river networks: comparison of top-kriging with regional regression. Hydrol. Process. 2014, 28, 315–324. [Google Scholar] [CrossRef]
- Sun, Y.; Kang, S.; Li, F.; Zhang, L. Comparison of interpolation methods for depth to groundwater and its temporal and spatial variations in the Minqin oasis of northwest China. Environ. Model. Softw. 2009, 24, 1163–1170. [Google Scholar] [CrossRef]
- Weltzin, J.F.; Bridgham, S.D.; Pastor, J.; Chen, J.; Harth, C. Potential effects of warming and drying on peatland plant community composition. Glob. Chang. Biol. 2003, 9, 141–151. [Google Scholar] [CrossRef]
- Charman, D.J.; Amesbury, M.J.; Hinchliffe, W.; Hughes, P.D.; Mallon, G.; Blake, W.H.; Daley, T.J.; Gallego-Sala, A.V.; Mauquoy, D. Drivers of Holocene peatland carbon accumulation across a climate gradient in northeastern North America. Quat. Sci. Rev. 2015, 121, 110–119. [Google Scholar] [CrossRef]
- Turetsky, M.R.; Benscoter, B.; Page, S.; Rein, G.; Van Der Werf, G.R.; Watts, A. Global vulnerability of peatlands to fire and carbon loss. Nat. Geosci. 2015, 8, 11–14. [Google Scholar] [CrossRef]
- Kettridge, N.; Turetsky, M.R.; Sherwood, J.H.; Thompson, D.K.; Miller, C.A.; Benscoter, B.W.; Flannigan, M.D.; Wotton, B.M.; Waddington, J.M. Moderate drop in water table increases peatland vulnerability to post-fire regime shift. Sci. Rep. 2015, 5, 8063. [Google Scholar] [CrossRef] [PubMed]
- Chimner, R.A.; Pypker, T.G.; Hribljan, J.A.; Moore, P.A.; Waddington, J.M. Multi-decadal changes in water table levels alter peatland carbon cycling. Ecosystems 2017, 20, 1042–1057. [Google Scholar] [CrossRef]
- Miller, C.A.; Benscoter, B.W.; Turetsky, M.R. The effect of long-term drying associated with experimental drainage and road construction on vegetation composition and productivity in boreal fens. Wetl Ecol. Manag. 2015, 23, 845–854. [Google Scholar] [CrossRef]
- Strack, M.; Softa, D.; Bird, M.; Xu, B. Impact of winter roads on boreal peatland carbon exchange. Glob. Chang. Biol. 2017. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, S.H.; Sedghamiz, A. Application and evaluation of kriging and cokriging methods on groundwater depth mapping. Environ. Monit. Assess. 2008, 138, 357–368. [Google Scholar] [CrossRef] [PubMed]
- Buchanan, S.; Triantafilis, J. Mapping water table depth using geophysical and environmental variables. Groundwater 2009, 47, 80–96. [Google Scholar] [CrossRef] [PubMed]


| Minimum Absolute Error (cm) | Maximum Absolute Error (cm) | Root Mean Square Error (cm) | Mean Error (cm) | |
|---|---|---|---|---|
| Ground Water Level | 0.6 | 50.5 | 22.0 | −0.9 |
| Depth to Water | 0.0 | 65.3 | 20.3 | −7.0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.M.; McDermid, G.J.; Strack, M.; Lovitt, J. A New Method to Map Groundwater Table in Peatlands Using Unmanned Aerial Vehicles. Remote Sens. 2017, 9, 1057. https://doi.org/10.3390/rs9101057
Rahman MM, McDermid GJ, Strack M, Lovitt J. A New Method to Map Groundwater Table in Peatlands Using Unmanned Aerial Vehicles. Remote Sensing. 2017; 9(10):1057. https://doi.org/10.3390/rs9101057
Chicago/Turabian StyleRahman, Mir Mustafizur, Gregory J. McDermid, Maria Strack, and Julie Lovitt. 2017. "A New Method to Map Groundwater Table in Peatlands Using Unmanned Aerial Vehicles" Remote Sensing 9, no. 10: 1057. https://doi.org/10.3390/rs9101057
APA StyleRahman, M. M., McDermid, G. J., Strack, M., & Lovitt, J. (2017). A New Method to Map Groundwater Table in Peatlands Using Unmanned Aerial Vehicles. Remote Sensing, 9(10), 1057. https://doi.org/10.3390/rs9101057